Область допустимых значений

На этой странице вы узнаете

• В чем парадокс ОДЗ?
• Что будет, если разделить число на \(0\)? 
• Как обмануть ОДЗ?

Существует ли абсолютная свобода? 

В жизни, возможно, сами того не осознавая, мы имеем ряд ограничений: моральные принципы, наше воспитание, общественное мнение и даже законы. Так и в математике: невозможно выполнять преобразования и не встретить ограничений. 

Именно про ограничения мы сегодня будем разговаривать. А сейчас попробуем ответить на вопрос: что именно ограничивает математика?

Значение переменных

В математике ключевую роль играют далеко не числа, о чем мы уже говорили в этой статье. Но как числа могут быть не важны в математике?

Математика – это наука не только про сложение или вычитание, ее возможности куда шире. В том числе с ее помощью можно строить целые модели, то есть описывать реальные ситуации на математическом языке, а после применять эти модели ко множеству случаев в жизни.

Например, мы можем описать с помощью математики схемы выплат по кредиту. Однако каждый кредит отличается друг от друга: процентной ставкой, суммой, взятой в кредит или сроком его погашения. Неужели каждый раз придется составлять новую математическую модель?

Разумеется, нет! Именно для этого придумали переменные.

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах. Обычно переменные обозначаются буквами. 

Другими словами, сумму кредита мы можем выразить не числом, а буквой, и после подставлять вместо этой буквы любое значение. Например, мы можем сказать, что кредит взят на сумму S рублей, и при этом S может быть равна как 1 млн. рублей, так и 100 000 рублей, в зависимости от того, какое значение мы сами зададим. 

Именно для переменных и созданы ограничения в математике. Почему так случилось? Дело в том, что для некоторых выражений (которые мы обязательно рассмотрим дальше) существуют значения, при которых они не могут существовать. И тогда возникает парадокс: вместо переменной мы можем подставить любое число, но при этом не с любым числом выражение будет существовать. Тут нам на помощь и приходят ограничения. 

Но пока что вернемся к переменной. Как мы уже выяснили, она может принимать любое значение, кроме тех, при которых выражения не могут существовать. Разделим их. 

Допустимые значения переменной – это значения переменной, при которых выражение имеет смысл. 

Выражение имеет смысл, если при данных значениях переменной можно посчитать его значение.

Недопустимые значения переменной – это такие значения, при которых выражение не имеет смысла. 

Но можно ли как-то объединить все допустимые значения переменной? Не будем же мы выписывать много-много чисел каждый раз, чтобы понять, какое значение может принимать переменная? Разумеется, нет, нам достаточно будет задать лишь множество. 

Область допустимых значений

Этим самым множеством будет область допустимых значений (далее – ОДЗ). 

Область допустимых значений – это множество всех переменных, при которых выражение имеет смысл, или, иначе говоря, это множество всех допустимых значений переменной. 

При решении уравнений или неравенств очень важно правильно найти ОДЗ. Поскольку в ОДЗ входят только те значения, которые может принимать переменная, то такие ограничения – наша подсказка, что может входить в ответ. Бывают случаи, когда переменная при решении может принимать недопустимые значения, и очень важно исключить их перед самим ответом. 

В чем парадокс ОДЗ? Обратим внимание, что в ОДЗ входят только те значения, при которых существует выражение. Однако при решении мы будем искать недопустимые значения переменных.  В этом и заключается парадокс: мы ищем «неправильные» ответы, чтобы в итоге прийти к «правильным».  То есть при поиске ОДЗ мы идем от обратного: ищем переменные, при которых не будет существовать выражение, а после исключаем их из ответа.

ОДЗ можно искать по-разному. Это может быть как аналитический метод, когда решаются уравнения, неравенства или их системы, так и графический, когда используют графики функций. Однако в этой статье мы будем рассматривать только аналитический метод. 

Разумеется, ОДЗ есть далеко не во всех выражениях. В каких случаях нам стоит обратить на нее внимание?

В первую очередь важно следить за «опасными» выражениями. Какие выражения можно к ним отнести?

• Дроби,
• корни четной степени,
• логарифмы,
• тригонометрические функции,
• модуль,
• показательные функции. 

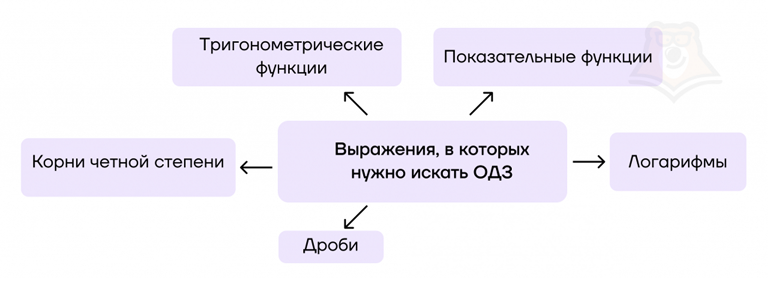
Если в примере нам встретится кто-то из них, то это красный флаг, сигнализирующий о том, что необходимо искать ОДЗ. 

Разберемся, как найти ОДЗ для каждого из этих случаев. 

ОДЗ в выражениях с дробями

Начнем мы с дробей. С помощью дроби записывается деление. Например, выражения \(10:2\) и \(\frac{10}{2}\) являются одинаковыми, но записаны по-разному. 

Все, что записано над дробной чертой, называется числителем (в нашем случае это \(10\)). Числитель является делимым. А вот под чертой записан знаменатель (в нашем случае это \(2\)), который является делителем. Результат вычисления дроби будет частным. 

Однако не для каждой дроби нужно искать ОДЗ! Как же так?

Все дело в том, что для дробей существует единственное ограничение: делить на \(0\) нельзя. 

Следовательно, и ОДЗ нужно искать только в том случае, когда в знаменателе дроби может появиться \(0\), иными словами, когда в знаменателе дроби будет стоять переменная. 

• Например, в дроби \(\frac{x}{2}\) в знаменателе даже при особом желании \(0\) не появится – там стоит число, которое не меняет своего значения.

• А вот если мы возьмем дробь \(\frac{2}{x}\), то тут уже есть опасность, что х примет значение \(x=0\). 

Если в выражении встречается дробь, в знаменателе которой стоит переменная, необходимо найти ОДЗ. 

ОДЗ для дроби: знаменатель не может быть равен \(0\). 

Что будет, если разделить число на \(0\)? При решении уравнений и неравенств, преобразованиях, даже в ОДЗ, мы всегда говорим: делить на \(0\) нельзя! Но так ли это? На самом деле, делить на \(0\) можно, и при этом мы получим бесконечность. Но выполнить такое действие можно только с комплексными числами, которые не рассматриваются (или рассматриваются кратко) в курсе школьной математики.  Поскольку мы постоянно работаем с вещественными числами (в которые входят все множества натуральных, целых, рациональных и иррациональных чисел), то делить на \(0\) все-таки нельзя.

Бывают случаи, когда переменная стоит и в числителе, и в знаменателе. Как тогда искать ОДЗ?

Точно также. Даже если переменная в числителе, это никак не влияет на ее допустимые значения: если числитель дроби будет равен \(0\), то вся дробь будет равна \(0\) (если \(0\) разделить на любое число, то получится \(0\)). Следовательно, в этом случае мы можем не обращать внимания на числитель и при поиске ОДЗ работать только со знаменателем. 

Рассмотрим такое уравнение на примере №20 ОГЭ по математике. 

Задание. Решите уравнение \(\frac{2x^2-2x-60}{x^2-25}=1\).
Решение. Первым делом необходимо записать ОДЗ, если в уравнении есть «опасное» место. В нашем случае это знаменатель дроби, который не может быть равен \(0\).

ОДЗ: \(x^2-25\neq 0\)

Раскроем выражение по формуле сокращенного умножения \(a^2-b^2=(a-b)(a+b)\):

\((x-5)(x+5)\neq 0\)

Если произведение множителей равно \(0\), то каждый множитель равен \(0\). Следовательно:

\(x-5\neq 0\) и \(x+5\neq 0\)
\(x\neq 5\) и \(x\neq -5\)

Это и будет нашей ОДЗ. 

Теперь перейдем к решению уравнения. Поскольку мы нашли ОДЗ, мы можем умножить уравнение на знаменатель дроби, не теряя корни:

\(\frac{2x^2-2x-60}{x^2-25}=1|*x^2-25\)
\(2x^2-2x-60=x^2-25\)

Перенесем все слагаемые в одну сторону:

\(2x^2-2x-60-x^2+25=0\)
\(x^2-2x-35=0\)

Решим уравнение с помощью дискриминанта:

\(D=b^2-4ac=4-4*1*(-35)=4+140=144\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{2+12}{2}=7\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{2-12}{2}=-5\) – не удовлетворяет ОДЗ.

Следовательно, в ответ необходимо записать только корень \(x=7\). 

Ответ: 7 

Мы разобрались с дробями. Какие же опасности нас поджидают, если мы столкнемся с корнем?

ОДЗ корня

Про корни мы уже говорили в статье «Понятие корня». Вспомним, что корни бывают четной (кратной 2) и нечетной (не кратной 2) степени. При этом ограничений для корней нечетной степени нет. 

А вот с корнями четной степени уже все намного интереснее. 

Вспомним, что извлечение корня – обратная операция возведению в степень. Если мы возведем число в четную степень (например, 2), какой результат мы получим? Попробуем возвести числа в степень 2:

• \((-7)^2=49\)
• \(0^2=0\)
• \(7^2=49\)

Как мы видим, мы не можем получить отрицательное число при возведении в четную степень. Это связано с простым правилом: «минус на минус дают плюс». 

Следовательно, наименьшее число, которое мы можем получить при возведении в четную степень – это \(0\) (и только при возведении 0 в четную степень). Следовательно, и наименьшее число, которое может стоять под знаком корня – это \(0\). 

Если в выражении встречается корень четной степени, необходимо найти ОДЗ. 

ОДЗ корня: подкоренное выражение больше или равно 0. 

Не существует корня четной степени, подкоренным выражением которого будет отрицательное число. Например, если мы попробуем извлечь корень \(\sqrt{-49}\), у нас ничего не получится. А вот для корня \(\sqrt{49}\) мы получим ответ \(7\). 

Попробуем решить уравнение \(\sqrt{8-x}=4+x\). Мы видим корень, а значит, нам необходимо найти ОДЗ. 

Итак, мы записываем слово ОДЗ и пишем неравенство \(8-x\geq 0\), решаем его: \(x\leq 8\) и на этом заканчиваем поиск ОДЗ и переходим к решению самого уравнения. 

Поздравляем! Мы получили \(0\) баллов за задание на экзамене. 

Важно: при поиске ОДЗ необходимо учитывать все ограничения, которые встречаются в уравнении (неравенстве). Если не будет учтено хотя бы одно, то ОДЗ найдено неправильно, что влечет за собой снятие всех баллов за задание даже в случае, когда уравнение (неравенство) решено верно.

При этом ОДЗ ищется до решения уравнения (неравенства), поскольку при преобразовании выражений можно потерять какое-либо условие и ОДЗ не будет полным (также при преобразовании ОДЗ может расшириться и его придется дописывать). 

Как обмануть ОДЗ? На самом деле, есть одна хитрость, позволяющая не выписывать все-все-все ограничения в выражении. И эта хитрость кроется в названии.  Если при решении вместо слова «ОДЗ» мы напишем «Ограничения», то необходимость выписывать все условия исчезает. Однако и тут есть свои подводные камни: в ограничениях должны быть выписаны все значимые для данного выражения условия. Это удобно в случаях, когда в ОДЗ дублируются несколько ограничений, которые после нужно объединять.

Но какое же ОДЗ тогда верное? 

Тут мы сталкиваемся с особенностью уравнений: если одна часть равна другой, то они имеют и одинаковые знаки. Поскольку при извлечении корня четной степени может получиться только неотрицательное число, то и вторая часть уравнения должна быть неотрицательной. Иначе мы сталкиваемся с ситуацией, когда положительное число равно отрицательному, что невозможно. 

Так мы подобрались к еще одному ограничению для корня четной степени. 

Корень четной степени может быть равен только неотрицательному числу. 

Как оказалось, в нашем, казалось бы простом, уравнении целых два ограничения. А теперь попробуем снова решить его! 

Итак, мы имеем уравнение \(\sqrt{8-x}=4+x\). 

Подкоренное выражение неотрицательно, а также неотрицательна правая часть уравнения. Составим систему неравенств:

Решим каждое неравенство и получим:

Осталось отметить решения неравенств на числовой прямой и найти их пересечение: 

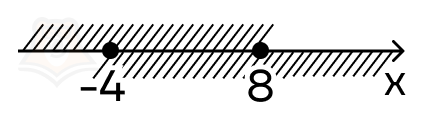
Следовательно, решением системы неравенств и ОДЗ нашего уравнения будет: \(x\in [-4;8]\). 

Осталось решить иррациональное уравнение. 

Возведем обе части уравнения в квадрат и получим:

\((\sqrt{8-x})^2=(4+x)^2\)
\(8-x=(4+x)^2\)

Применим формулу сокращенного умножения: \((a+b)^2=a^2+2ab+b^2\).

\(8-x=16+8x+x^2\)

Перенесем все значения в одну сторону и приведем подобные слагаемые:

\(x^2+8x+16-8+x=0\)
\(x^2+9x+8=0\)

Решим квадратное уравнение с помощью дискриминанта:

\(D=b^2-4ac=9^2-4*1*8=81-32=49\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-9+7}{2*1}=-1\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-9-7}{2*1}=-8\)

Мы нашли корни уравнения. Осталось сравнить их с ОДЗ. Для этого нанесем на числовую прямую найденные значения:

ОДЗ принадлежит только корень \(–1\), следовательно, он и будет ответом. 

Ответ: \(–1\). 

По сравнению с дробью, корень имеет целых два ограничения? Куда больше?

ОДЗ логарифма

Логарифм действительно имеет еще больше ограничений. Но для начала вспомним, что это за зверь такой.

Логарифм — это число, в которое нужно возвести основание a, чтобы получить число \(b\).

Логарифм записывается в виде \(log_ab\), где \(а\) – основание логарифма, а \(b\) – его аргумент. 

Например, мы возводим число \(4\) в \(3\) степень и получаем: \(4^3=64\). Тогда, чтобы найти степень, в которую мы возвели число, мы можем воспользоваться логарифмом: \(log_464=3\). 

\(a^x=b\Leftrightarrow x=log_ab\)

Какие же ограничения существуют для логарифма?

• Основание логарифма строго больше \(0\) и не равно \(1\).
• Аргумент логарифма всегда строго больше \(0\). 

Следовательно, мы получаем целых три ограничения:

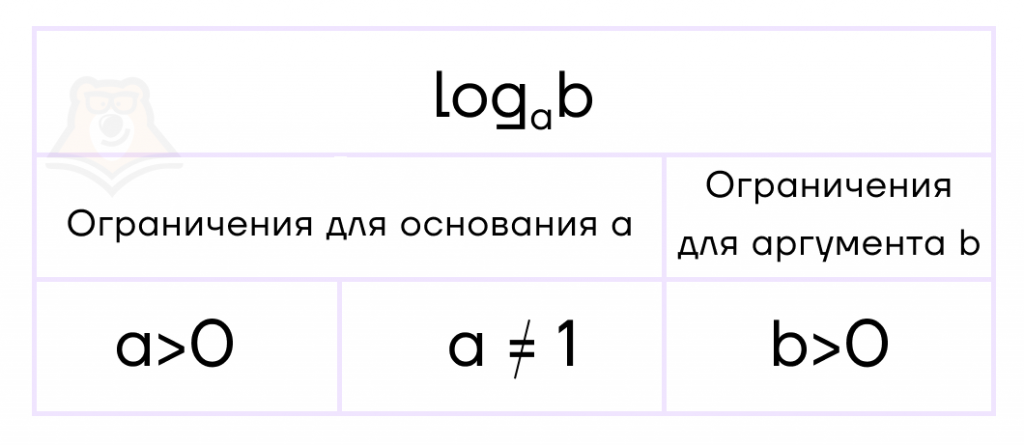
Подробнее, почему в логарифме существуют такие ограничения, можно прочесть в статье, на которую мы ссылались выше. А сейчас попробуем решить уравнение.

\(log_x(24-5x)=2\)

Запишем ОДЗ. Поскольку переменная есть и в аргументе, и в основании, у нас получится система из трех выражений:

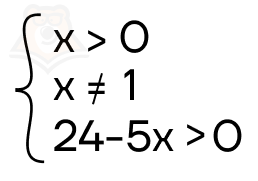
Преобразуем третье неравенство:

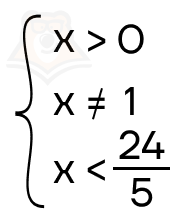
Обозначим решения на числовой прямой:

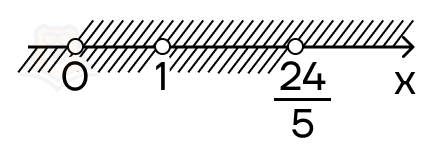
ОДЗ этого логарифма будет: \(x\in (0;1)\cup (1;\frac{24}{5})\). 

Перейдем к решению уравнения. Преобразуем логарифм по его определению:

\(log_x(24-5x)=2 => x^2=24-5x\)
\(x^2+5x-24=0\)

Решим квадратное уравнение с помощью дискриминанта:

\(D=b^2-4ac=5^2-4*1*(-24)=25+96=121\)
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-5+11}{2*1}=3\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-5-11}{2*1}=-8\)

Сравнивая с ОДЗ определяем, что уравнение будет существовать только при \(x=3\). 

Ответ: \(3\). 

«Страшнее» логарифма может звучать разве что тригонометрия. А значит, пора приступить и к ней! 

ОДЗ тригонометрических функций

Тригонометрия – огромный раздел в математике, но сегодня мы кратко рассмотрим лишь его часть. А именно мы поговорим про синусы, косинусы, тангенсы и котангенсы.

Начнем с ОДЗ синуса и косинуса. Вспомним, что синус – это отношение противолежащего катета прямоугольного треугольника к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе. 

\(sin(\gamma)=\frac{a}{c}\)
\(cos(\gamma)=\frac{b}{c}\)

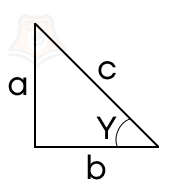
Какая же опасность подстерегает нас тут? Одно из свойств треугольника: против большей стороны лежит больший угол. Самый большой угол в прямоугольном треугольнике – прямой угол, напротив которого лежит гипотенуза. Следовательно, гипотенуза – самая большая сторона прямоугольного треугольника. 

А теперь посмотрим на отношения, из которых выводятся синус и косинус: они оба получается путем деления катета на гипотенузу. Катеты всегда будут меньше, а значит, мы делим меньшее число на большее. 

Какой результат мы получим в этом случае? Число в любом случае будет меньше или равно 1! 

Если в выражении встречаются синус или косинус, необходимо найти ОДЗ. 

ОДЗ синуса и косинуса: синус и косинус больше или равны –1, но меньше или равны 1. 

\(-1\leq sin x\leq 1\)
\(-1\leq cos x\leq 1\)

Важное замечание: это ограничение касается именно значений синуса или косинуса, при этом их аргумент может принимать любое значение. Иначе говоря, \(sin x\neq 2\), но х может быть равен 2. 

Мы рассмотрели синус и косинус, но что не так с тангенсом и котангенсом?

Вспомним, что: \(tg(x)=\frac{sin(x)}{cos(x)}\) и \(ctg(x)=\frac{cos(x)}{sin(x)}\).

Вот мы и столкнулись с ОДЗ! Внимательно посмотрим на знаменатель: он не может быть равен \(0\). Следовательно:

• Для тангенса: косинус не может быть равен \(0\).
• Для котангенса: синус не может быть равен \(0\). 

По тригонометрической окружности легко можно определить значения, при которых выполняются эти условия:

• Для тангенса: \(cos(x)\neq 0=>x\neq \frac{\pi}{2}+n, n\in Z\).
• Для котангенса: \(sin(x)\neq 0=>x\neq \pi n, n\in Z\). 

Если в выражении встречаются тангенс или котангенс, то необходимо найти ОДЗ. 

ОДЗ тангенса: \(cos(x)\neq 0=>x\neq \frac{\pi}{2}+n, n\in Z\)
ОДЗ котангенса: \(sin(x)\neq 0=>x\neq \pi n, n\in Z\)

Рассмотрим еще одно «опасное» выражение: модуль. 

ОДЗ модуля

Про модуль мы подробно разговаривали в этой статье. 

Модуль — расстояние от любой точки на числовой прямой до начала координат. 

Иначе сказать, модуль берет только цифры и не обращает внимание на знаки. Например:

• \(|3|=3\)
• \(|-3|=3\)

Результатом вычисления модуля всегда будет положительное число. Следовательно, если в уравнении попадется модуль, он может быть равен только неотрицательному числу. 

Допустим, мы имеем уравнение \(|x^2-4x+1|=x+3\). В этом случае в ОДЗ попадает правая часть уравнения: \(x+3\geq 0\). 

Если в уравнении встречается модуль, необходимо найти ОДЗ. 

ОДЗ модуля: модуль может быть равен только неотрицательному числу. 

И последнее, что нам осталось узнать: ОДЗ показательной функции. 

ОДЗ показательной функции 

Про показательные функции мы уже говорили в статье «Показательная и логарифмическая функции». 

Показательная функция имеет вид \(y=a^x\). 

Какое же тут может быть ОДЗ? Оказывается, основание степени должно быть строго больше \(0\) и не равняться \(1\). Подробнее, откуда взялось такое ограничение, вы можете прочесть в статье про показательную функцию. 

Если в уравнении встречается показательная функция, необходимо найти ОДЗ.

ОДЗ показательной функции: в функции вида \(y=a^x\) основание степени \(a>0\) и \(a\neq 1\). 

Однако в отличие от всех предыдущих ограничений, ОДЗ тут искать нужно только в том случае, если в основании стоит переменная. Например, если нам дана функция \((2+x)^{-9+6x}=(2+x)^{x^2}\) мы должны написать ОДЗ: \(2+x>0\). 

Мы рассмотрели все ограничения, которые могут встретиться в выражениях. Но если в выражении встречаются сразу и корень, и дробь, и тригонометрия, и все-все-все? В этом случае необходимо будет составлять систему со всеми ограничениями, присутствующими в выражении. Рассмотрим такой пример. 

Решим пункт а) задания №12 ЕГЭ по профильной математике. 
Задание. а) Решите уравнение \(\frac{(ctg(x)-1)log_{29}(4cos^2(x))}{log_{73}(\frac{2\sqrt{3}}{3}sin(x))}=0\).

Решение. В данном уравнении сразу несколько выражений, для которых нужна ОДЗ: это дробь, тригонометрические функции и логарифмы. Нам необходимо составить систему с каждым ограничением.

В первую очередь знаменатель дроби не равен \(0\), следовательно:
\(log_{73}(\frac{2\sqrt{3}}{3}sin(x))\neq 0\). 

Поскольку в уравнении есть синус и косинус, то \(-1\leq sin(x)\leq 1\) и \(-1\leq cos(x)\leq 1\). Для котангенса: \(sin(x)\neq 0\). 

И последнее: аргументы логарифма должны быть строго больше \(0\). Тогда \(4cos^2(x)>0\) и \(\frac{2\sqrt{3}}{3}sin(x)>0\). 

Теперь составим систему:

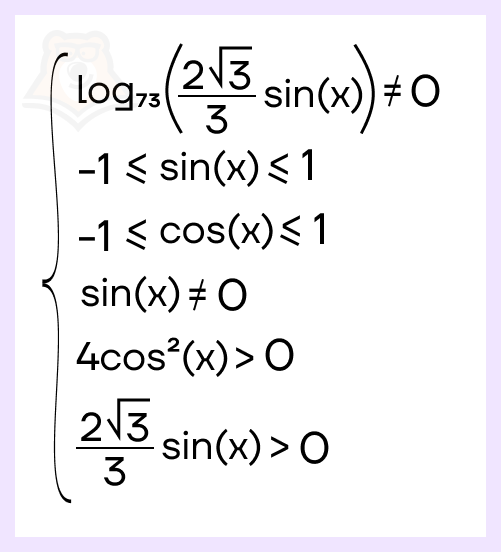
Рассмотрим каждое условие. Логарифм преобразуем по его определению, тогда:

\(\frac{2\sqrt{3}}{3}sin(x)\neq 73^0=>\frac{2\sqrt{3}}{3}sin(x)\neq 1=>sin(x)\neq \frac{3}{2\sqrt{3}}=>sin(x)\neq \frac{\sqrt{3}*\sqrt{3}}{2\sqrt{3}}\)

Откуда получаем:

\(sin(x)\neq \frac{\sqrt{3}}{2}\)

Решая простейшее тригонометрическое уравнение:

Второе и третьей условие не будем трогать. 

По четвертому условию нашей системы \(sin(x)\neq 0 => x\neq \pi n, n\in Z\). 

Рассмотрим неравенство \(4cos^2(x)>0\). Поскольку косинус стоит в квадрате, то он всегда будет неотрицательным числом (так как степень четная). Однако из-за строгости знака он не может равняться \(0\), тогда мы можем перейти к выражению:

\(cos(x)\neq 0=>x\neq \frac{\pi}{2}+\pi n, n\in Z\)

И последнее неравенство в ОДЗ: \(\frac{2\sqrt{3}}{3}sin(x)>0\). Разделим его на \(\frac{2\sqrt{3}}{3}\) и получим: \(sin(x)>0\). Эта запись означает, что корни уравнения должны лежать в первой и второй четвертях тригонометрической окружности. 

Снова запишем систему:

Заметим, что записи \(x\neq \pi n, n\in Z\) и \(sin(x)>0\) можно объединить, поскольку неравенство имеет строгий знак, а значит учитывает условие \(sin(x)\neq 0\). 
Тогда получаем ОДЗ:

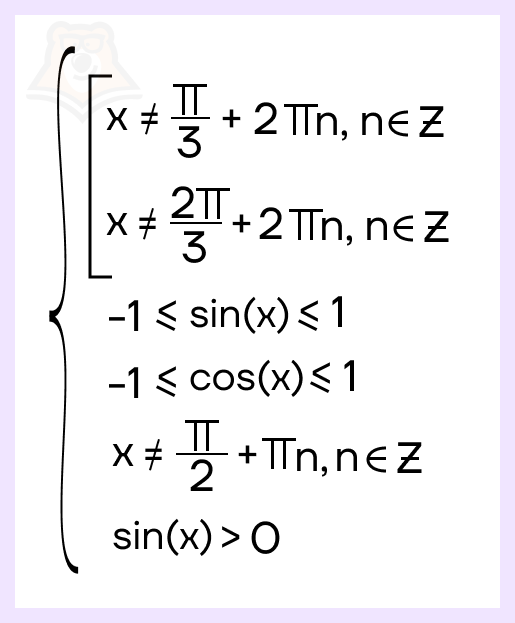
Теперь перейдем к решению самого уравнения \(\frac{(ctg(x)-1)log_{29}(4cos^2(x))}{log_{73}(\frac{2\sqrt{3}}{3}sin(x))}=0\). Чтобы уравнение решалось, числитель должен быть равен \(0\), а знаменатель наоборот (однако знаменатель мы уже учли в ОДЗ и можем не обращать на него внимания). Тогда мы переходим к уравнению:

\((ctg(x)-1)log_{29}(4cos^2(x))=0\)

Если произведение множителей равно \(0\), то каждый множитель равен \(0\), откуда:

\(ctg(x)-1=0\) и \(log_{29}(4cos^2(x))=0\)

Решим первое уравнение:

\(ctg(x)-1=0\)
\(ctg(x)=1\)
\(x=\frac{\pi}{4}+\pi n, n\in Z\)

Решим второе уравнение:

\(log_{29}(4cos^2(x))=0\)

По свойству логарифма:

\(4cos^2(x)=1\)
\(cos^2(x)=\frac{1}{4}\)
\(cos(x)=\pm \frac{1}{2}\)

Если \(cos(x)=\frac{1}{2}\), то \(x=\pm \frac{\pi}{3}+2\pi n, n\in Z\).
Если \(cos(x)=-\frac{1}{2}\), то \(x=\pm \frac{2\pi}{3}+2\pi n, n\in Z\).

Отметим все условия ОДЗ и полученные корни уравнения на тригонометрической окружности:

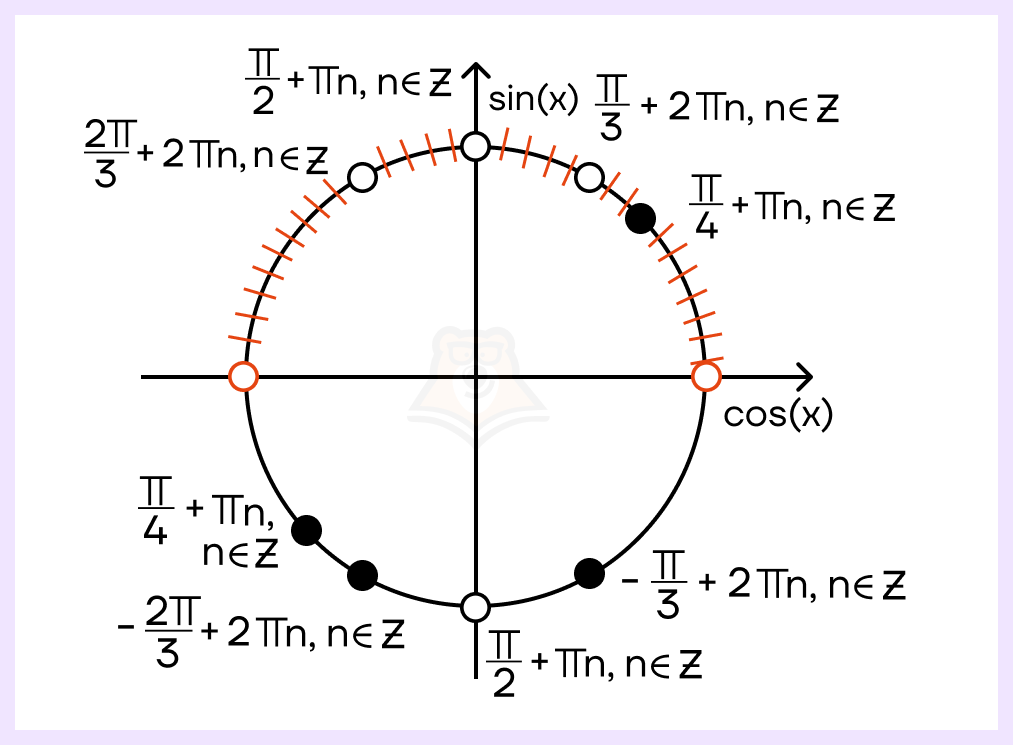
Условиям ОДЗ удовлетворяет только корень \(x=\frac{\pi}{4}+\pi n, n\in Z\), причем только та точка, которая лежит в первой четверти. Следовательно, ответом будет: \(x=\frac{\pi}{4}+2\pi n, n\in Z\). 

Ответ: \(x=\frac{\pi}{4}+2\pi n, n\in Z\)

Сегодня мы стали неуязвимее: теперь мы знаем все слабые места математических выражений. А значит, мы не запутаемся при решении сложных заданий и справимся даже с самой большой ОДЗ! 

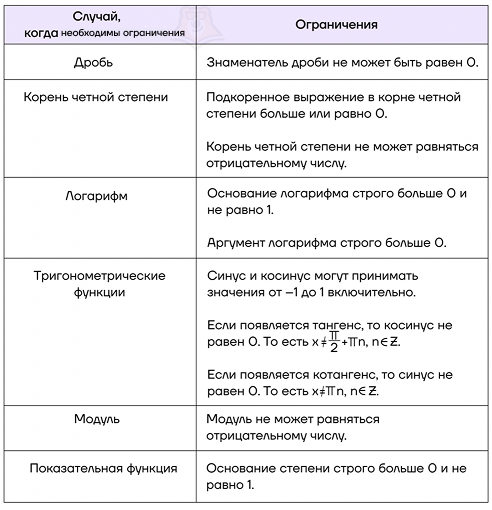
А для удобства мы собрали все ОДЗ в одной таблице. 

Область допустимых значений важна при решении уравнений и неравенств. Поэтому теперь вы можете смело постигать «Целые рациональные, дробно-рациональные и иррациональные уравнения». 

Термины

Множество – совокупность нескольких элементов, объединенных каким-либо свойством.

Основание степени – число, которое возводят в какую-либо степень. 

Система – несколько уравнений (неравенств), для которых необходимо найти значение переменных, которые удовлетворяют каждому уравнению (неравенству) в системе.  

Числовая прямая – это прямая, на которой отмечены начало отсчета, положительное направление и дан масштаб для измерения длин. Другими словами, это прямая, на которой расставлены целые числа по порядку.  

Фактчек

• При решении уравнений и неравенств можно столкнуться с выражениями, для которых необходимы ограничения. В этом случае на помощь приходит область допустимых значений – это все значения, которые может принимать переменная. 
• ОДЗ необходимо искать в случаях, когда в выражении встречаются дроби, корни, логарифмы, тригонометрические функции, модуль и показательные функции. 
• Знаменатель дроби не может быть равен \(0\). 
• Подкоренное выражение в корне четной степени больше или равно \(0\). Также корень четной степени не может быть равен отрицательному числу. 
• Основание логарифма строго больше \(0\) и не равно \(1\). Аргумент логарифма строго больше \(0\). 
• Синус и косинус могут принимать значения от \(-1\) до \(1\) включительно. Если в выражении появляется тангенс, то косинус не может быть равен \(0\). Если в выражении появляется котангенс, то синус не равен \(0\). 
• Модуль не может равняться отрицательному числу. 
• Основание показательной функции должно быть строго больше \(0\) и не равняться \(1\). 

Проверь себя 

Задание 1.
Выберите верное утверждение:

1. В ОДЗ можно найти только одно ограничение.
2. В ОДЗ необходимо найти все ограничения.
3. В ОДЗ включаются значения, которым не может равняться переменная.
4. ОДЗ расшифровывается как «область дозволенных значений».

Задание 2.
Какая ОДЗ в выражении \(\frac{x-4}{x+2}\)?

1. \(x\neq 0\)
2. \(x\neq -2\)
3. \(x\neq 4\)
4. В данном выражении ОДЗ не требуется. 

Задание 3.
Какая ОДЗ у тангенса? 

1. \(x\neq \frac{\pi}{2}+2\pi n, n\in Z\)
2. \(x\neq \pi n, n\in Z\)
3. \(x\neq \frac{\pi}{2}+n, \pi n\in Z\)
4. \(x\neq 2n, n\in Z\)

Задание 4.
Какая ОДЗ у логарифма \(log_2(x+8)\)?

1. \(x\neq -7\)
2. \(x>0\)
3. \(x\neq -8\)
4. \(x>-8\)

Ответы: 1. – 2; 2. – 2; 3. – 3; 4. – 4.