Параллелограмм

На этой странице вы узнаете

• Чем отличаются признаки от свойств?
• Какая фигура является антагонистом параллелограмма?
• Во что можно поиграть на уроках и вспомнить геометрию?

Когда мы видим изображение с множеством деталей, наш мозг автоматически раскладывает их на простые фигуры. Этот процесс занимает доли секунды. Разные геометрические фигуры вызывают у нас разные ощущения, эмоции и ассоциации. А что будет, если мы задержим взгляд на одной из них и разберем подробнее? 

Четырехугольник

Начнем с так называемой базы. 

Четырехугольник — геометрическая фигура, которая состоит из четырех вершин, которые соединены четырьмя отрезками. 

Важное условие четырехугольника заключается в том, что любые три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.

Мы будем рассматривать выпуклые четырехугольники. Такой четырехугольник расположен в одной полуплоскости относительно прямой, которая содержит любую из его сторон.

Например, вот этот четырехугольник — невыпуклый. 

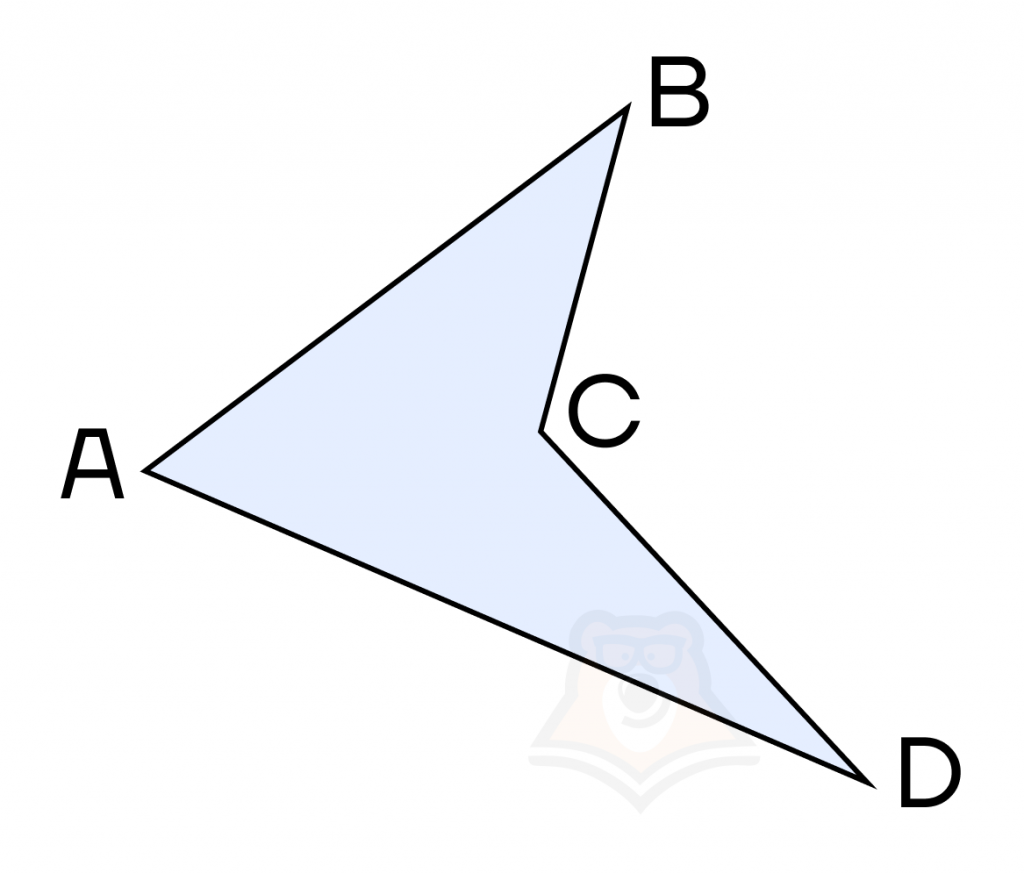
А вот этот — выпуклый. И все четырехугольники, которые мы будем рассматривать дальше, — выпуклые.

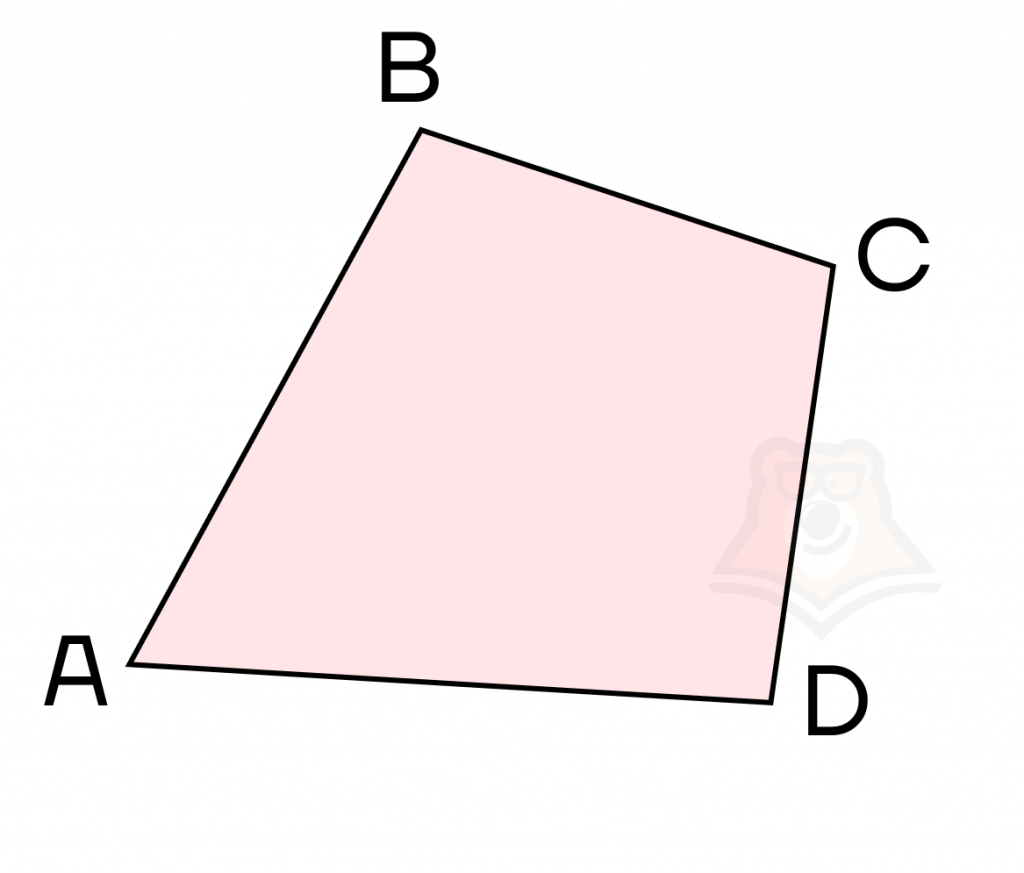
В выпуклом многоугольнике можно посчитать сумму углов по формуле:

\((n-2)*180°\)

Соответственно, для четырехугольника:

\((4-2)*180°=2*180°=360°\)

Итак, теперь мы можем перейти к частным случаям многоугольников.

Параллелограмм

Первым делом разберем параллелограмм.

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны. 

Давайте определим, что значит словосочетание «попарно параллельны». Это значит, что AB||CD, BC||AD.

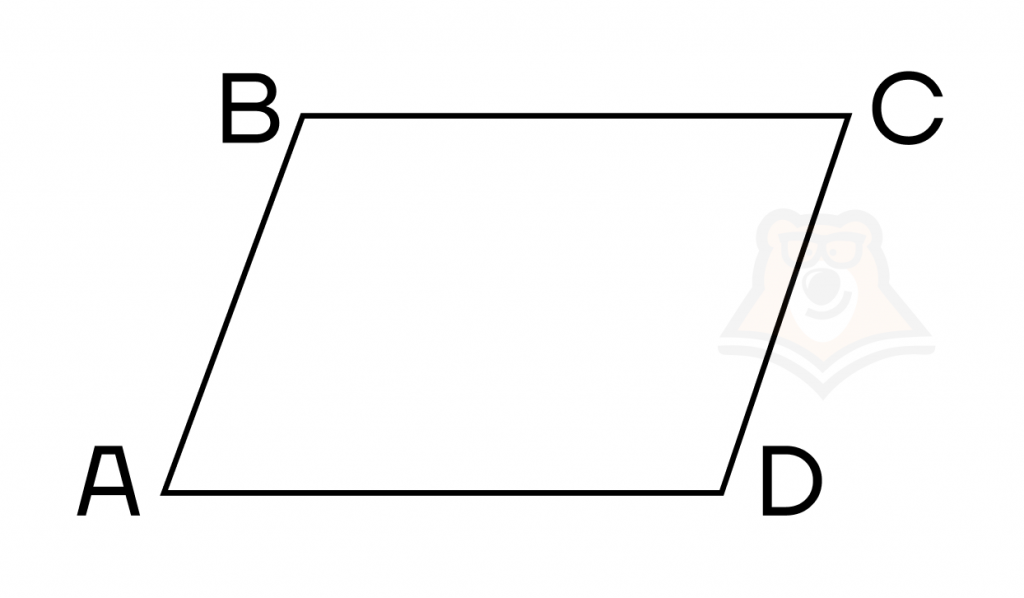
Параллелограмм в обычной жизни мы видим достаточно часто:

Давайте узнаем, какие свойства и признаки есть у параллелограмма.

Все о параллелограмме

Чем отличаются свойства от признаков? Свойства нельзя путать с признаками, хоть они и очень похожи. Например, свойствами параллелограмма обладает фигура, уже являющаяся параллелограммом, а признаки предназначены для выявления параллелограммов среди четырехугольников.

Свойства параллелограмма

1. Противолежащие стороны равны.

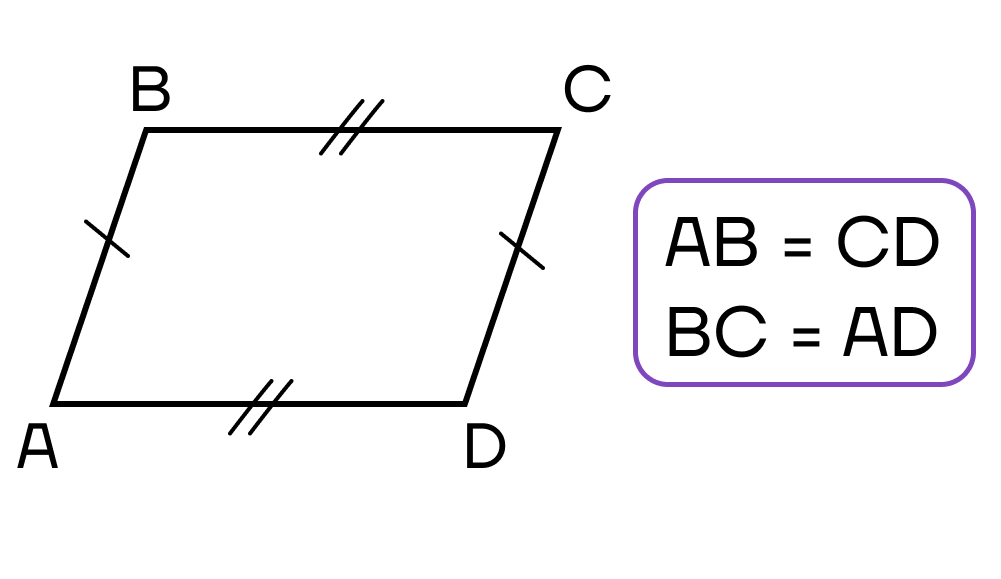
2. Противолежащие стороны параллельны.

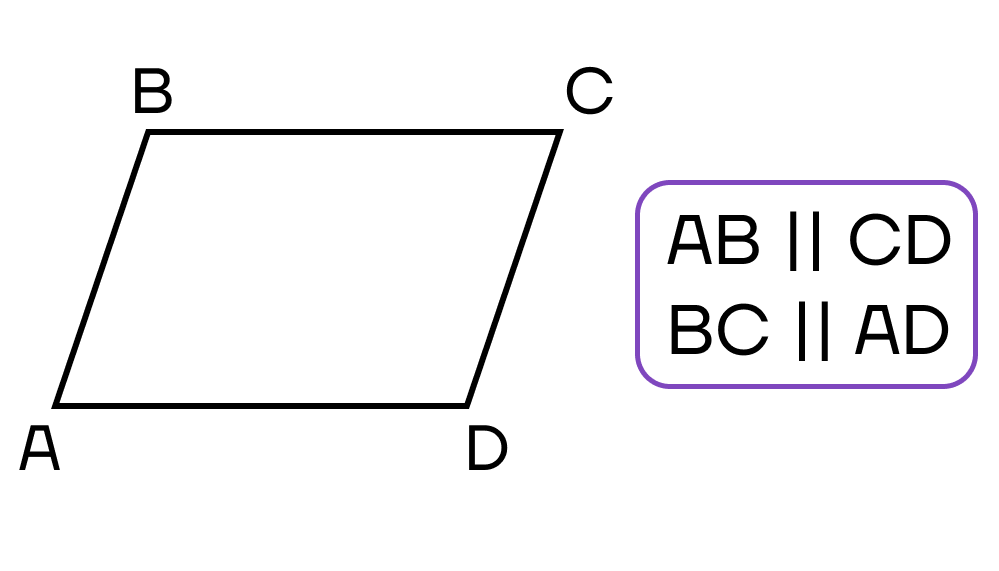
3. Диагонали пересекаются и точкой пересечения делятся пополам.

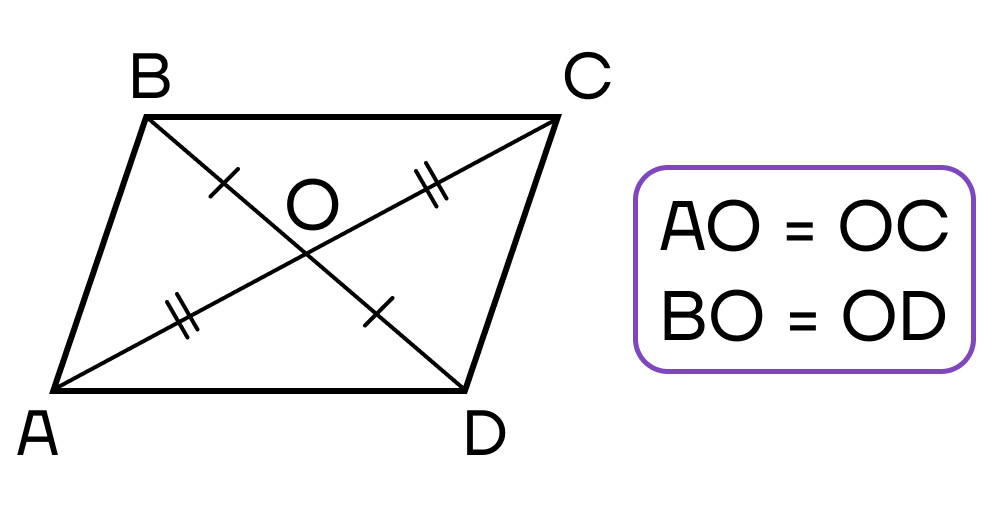
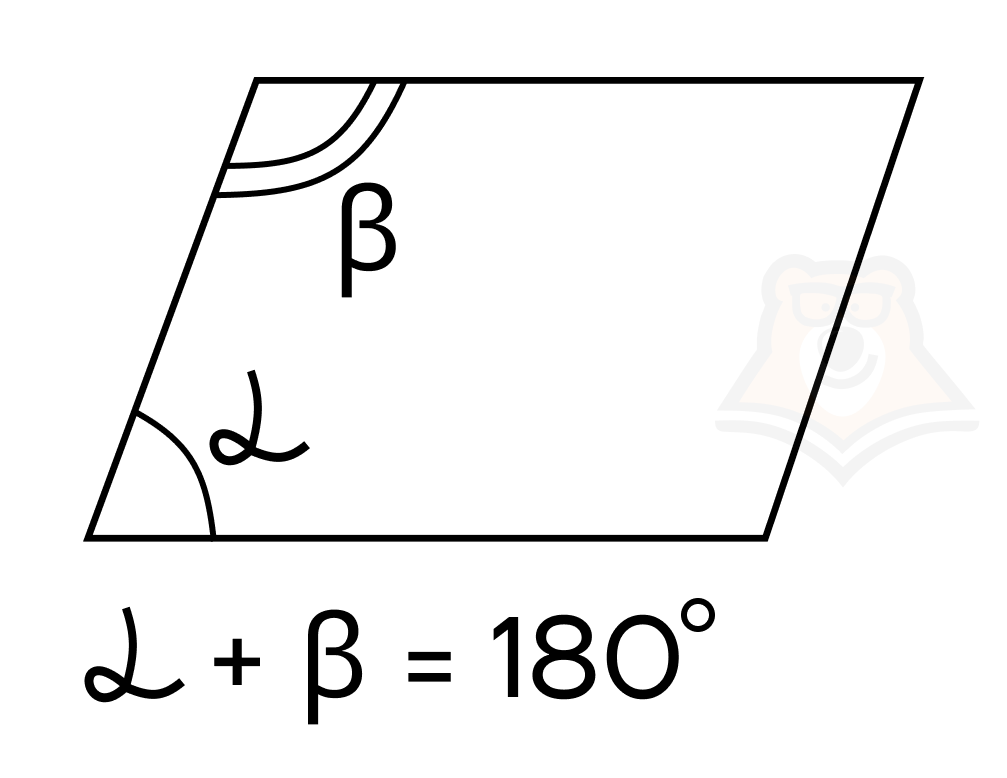
4) Сумма углов прилежащих к любой стороне равна 180°. 

Это так, потому что, как в примере на картинке, стороны AD и BC — параллельные прямые, а AB — секущая. Следовательно, по свойству двух параллельных прямых и секущей, это односторонние углы и их сумма равна 180°.

5) Противолежащие углы попарно равны. Это доказывается через третий признак равенства треугольников, ведь, например, у треугольников ABD и BDC все стороны равны, а значит и углы тоже.

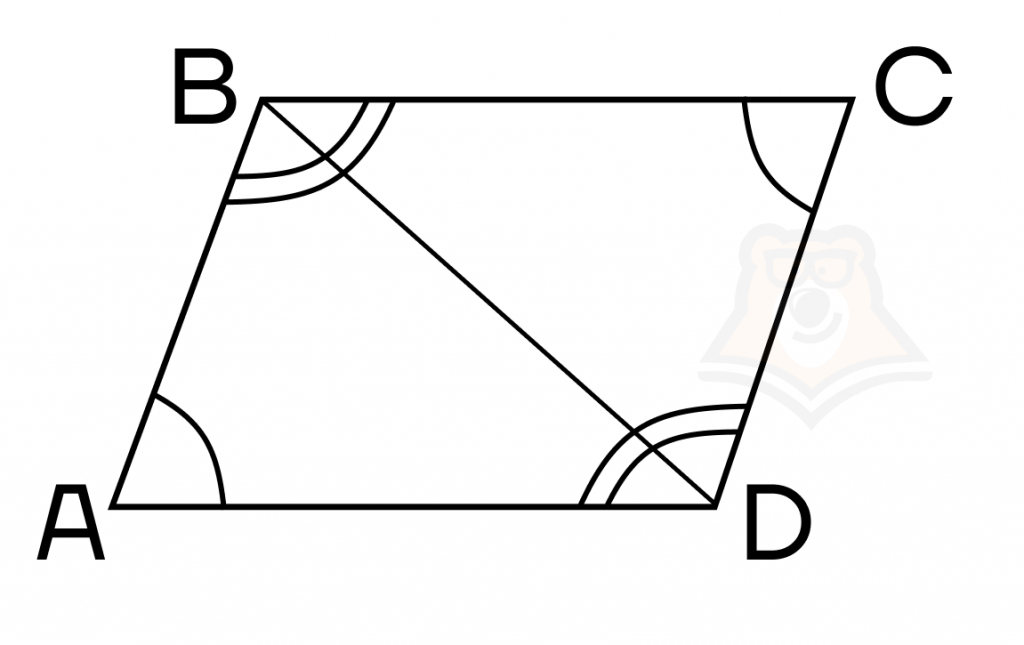
Теперь перейдем к признакам параллелограмма. Это то, что нам помогает понять, что четырехугольник является параллелограммом.

У параллелограмма есть три основных признака. Если для четырехугольника выполняется хотя бы один из признаков, такой четырехугольник можно называть параллелограммом.

Признаки параллелограмма

1. Две противоположные стороны четырехугольника параллельны и равны.

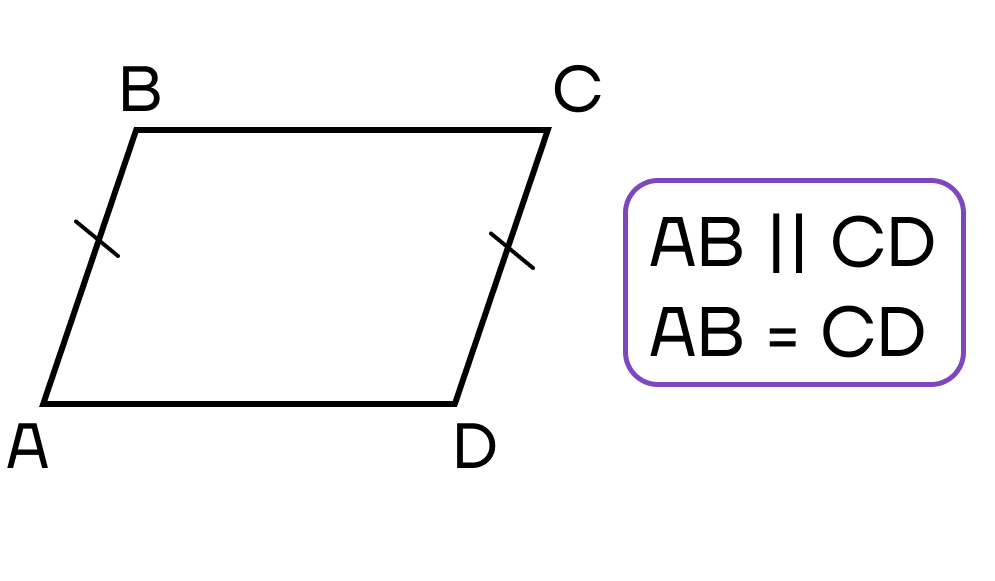
2. Противоположные стороны четырехугольника попарно равны.

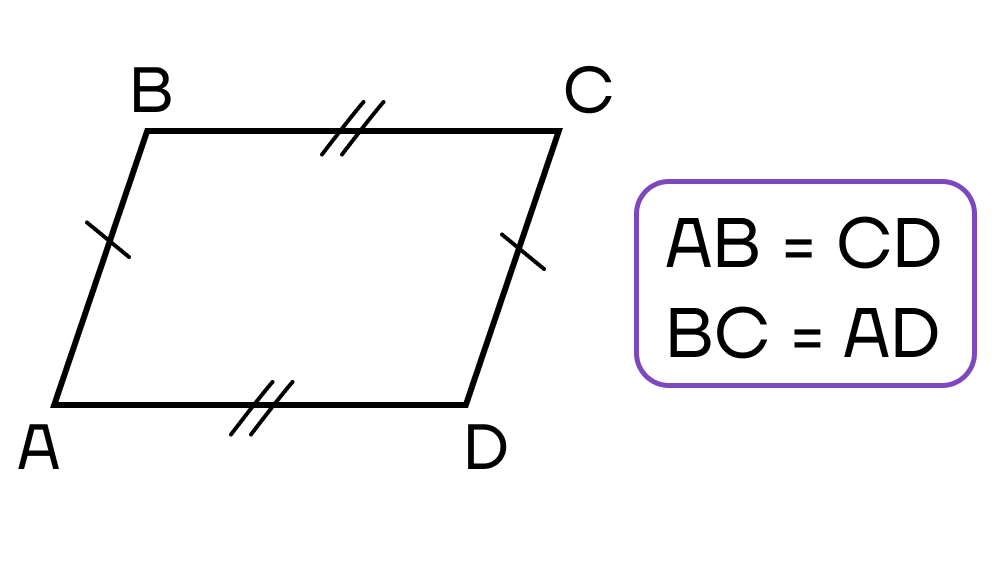
3. Диагонали четырехугольника пересекаются и в точке пересечения делятся пополам.

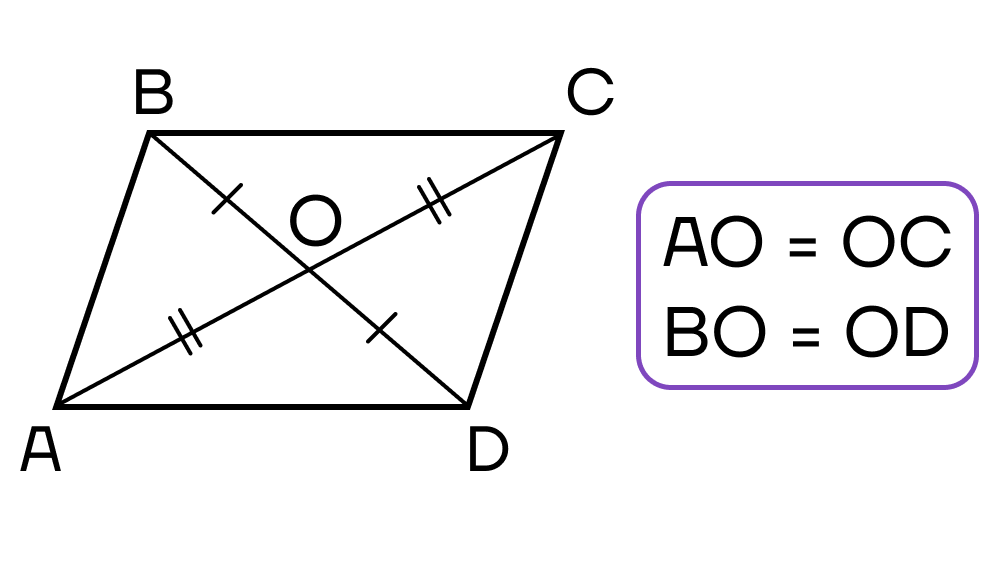
Теперь рассмотрим биссектрису в параллелограмме.

Биссектриса параллелограмма – это луч, исходящий из вершины угла параллелограмма, делящий этот угол на два равных угла и пересекающий одну из сторон параллелограмма.

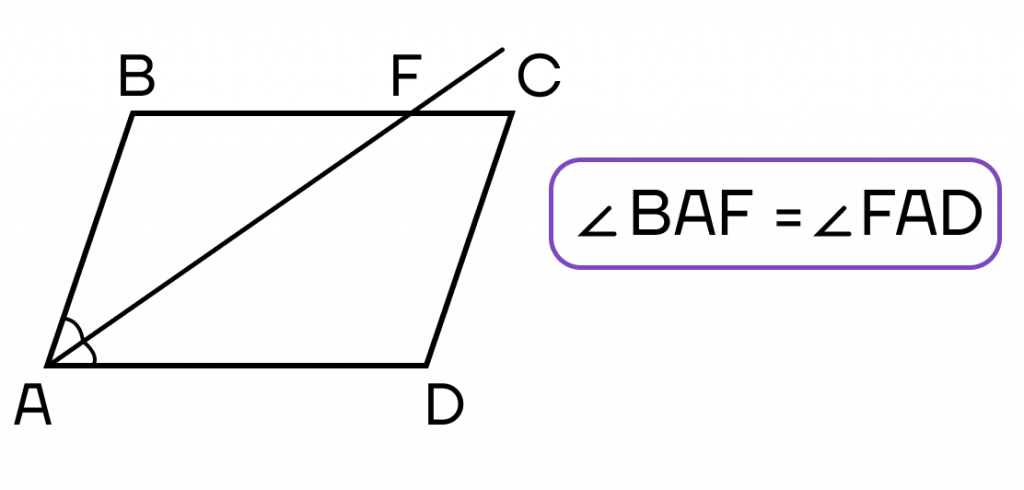
Рассмотрим два полезных факта, связанных с биссектрисой в параллелограмме.

1. Биссектриса, проведенная из угла параллелограмма, отсекает от него равнобедренный треугольник. 

Это тоже доказывается с помощью параллельных прямых. Рассмотрим две параллельные прямые: AD и BC, а также секущую AF. Углы FAD и BFA равны, так как они накрест лежащие. А так как AF — биссектриса, то углы BAF и FAD, углы FAD и BFA тоже, значит и BAF = BFA. Следовательно, треугольник BAF — равнобедренный.

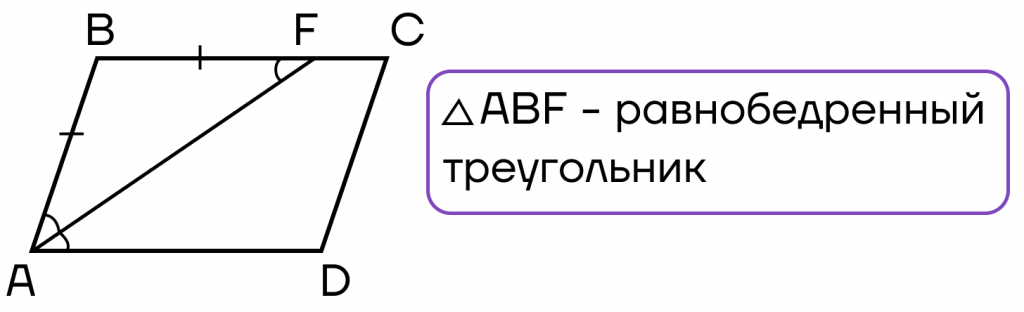
2. Биссектрисы углов, принадлежащих одной стороне параллелограмма, пересекаются под прямым углом.

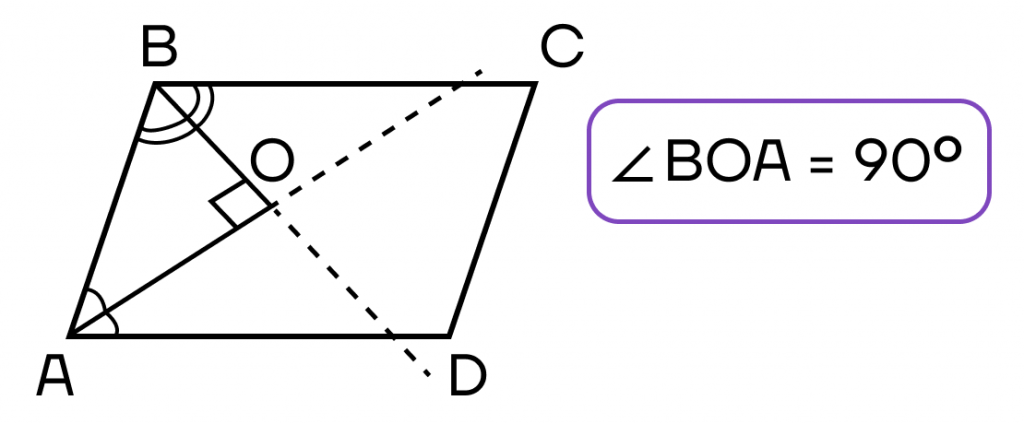
Мы почти закончили изучение параллелограмма. Осталось только рассмотреть формулы для нахождения площади. Их всего три.

1. Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.

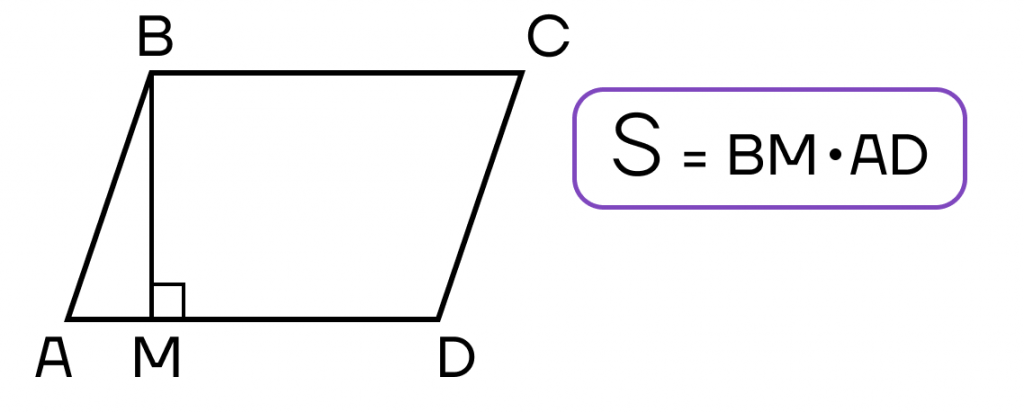
2. Площадь параллелограмма равна произведению двух его соседних сторон на синус угла между ними.

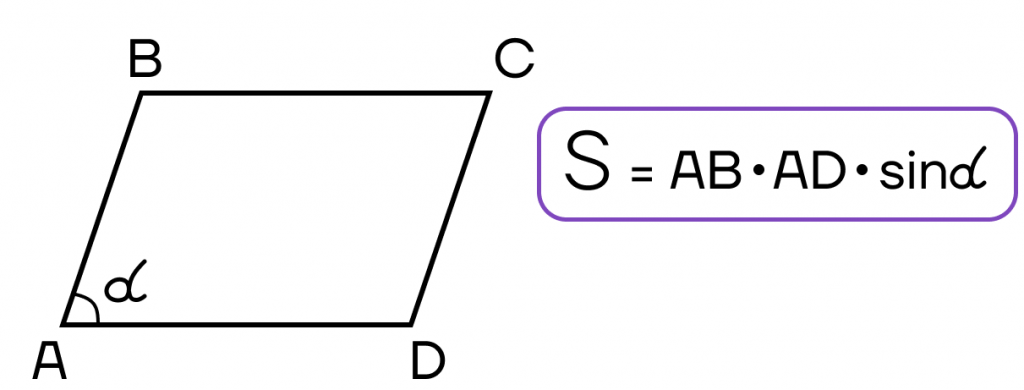
3. Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними.

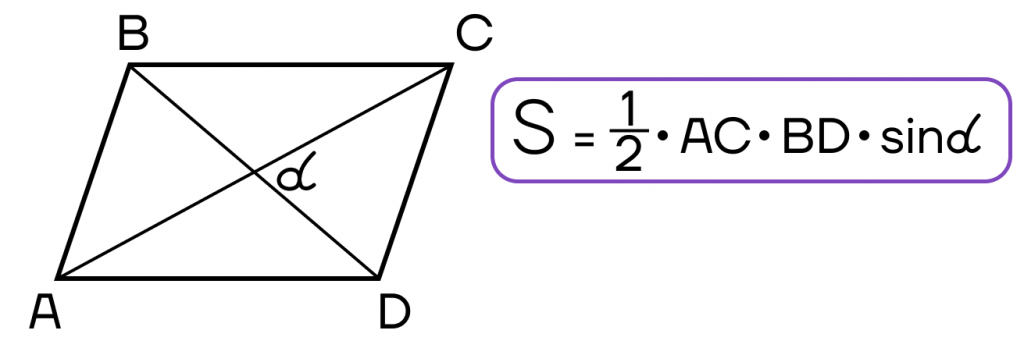
Какая фигура является антагонистом параллелограмма? Есть такая фигура, которая называется «антипараллелограмм». Это плоский и самопересекающийся четырехугольник, в котором две противоположные стороны равны между собой, но не параллельны. Напомним, что у параллелограмма противоположные стороны равны и параллельны между собой.

Мы рассмотрели всю теорию, связанную с параллелограммом. Давайте теперь решим задание для закрепления материала.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.

Задание. Стороны параллелограмма равны 10 и 15. Высота, опущенная на первую сторону, равна 12. Найдите высоту, опущенную на вторую сторону параллелограмма.

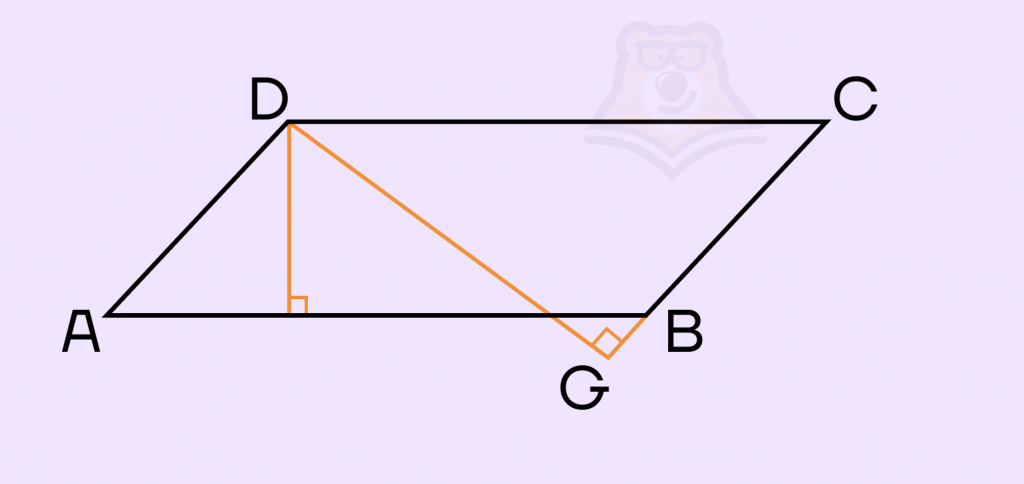
Решение. Примем искомую высоту за x. Как мы уже знаем, площадь параллелограмма можно найти с помощью высоты и стороны, к которой эта высота проведена. Соответственно, с помощью этой формулы мы и можем найти x:

\(S = a*h_1=b*h_2\)
\(S=10*12=15*h_2\)
\(h_2=\frac{10*12}{15}\)
\(h_2=8\)

Ответ: 8

На этом мы закончили изучение параллелограмма, так что можем двигаться дальше!

Прямоугольник

Хоть мы и закончили с параллелограммом, он с нами еще не закончил, и вот почему.

Прямоугольник — это параллелограмм. Но с одной особенностью — у прямоугольника углы по 90°.

Прямоугольник часто называют частным случаем параллелограмма. Из этого следует, что для прямоугольника применимы те же признаки и свойства, что для параллелограмма, но и имеется ряд собственных.

В жизни прямоугольник тоже встречается достаточно часто. Например, вы можете увидеть его в двери, картине или фотографии:

• 

• 

Все о прямоугольнике

Начнем со свойств прямоугольника.

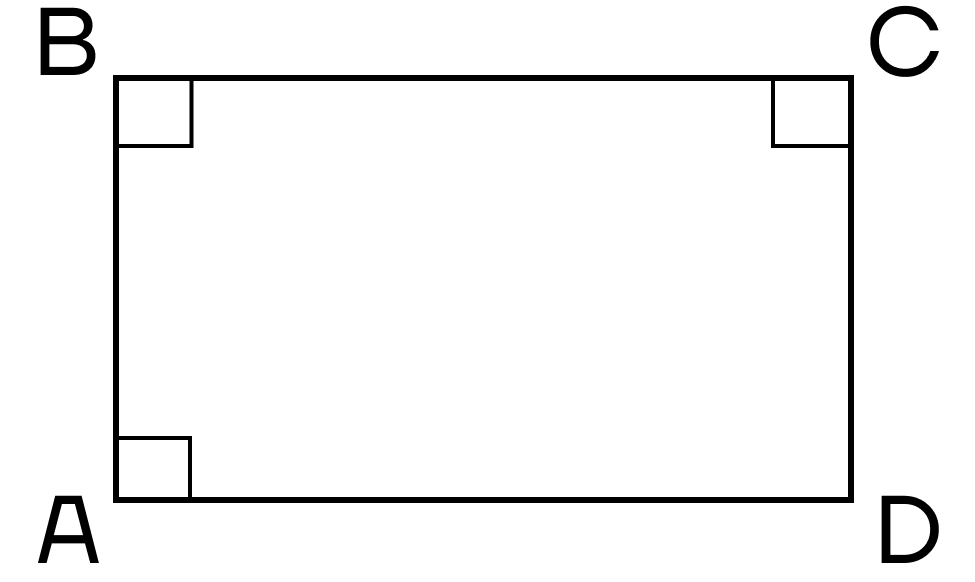
1. Все углы прямые.

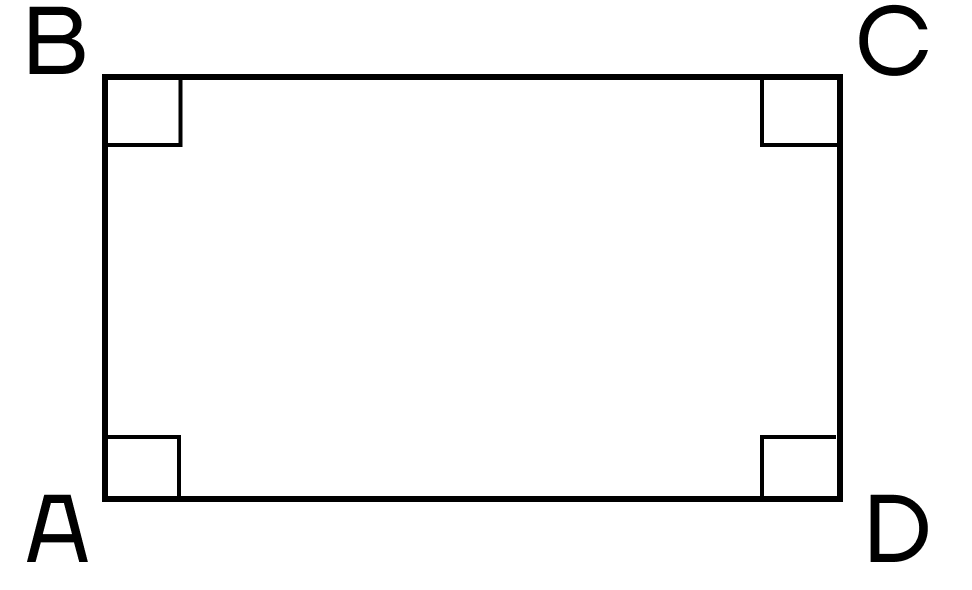
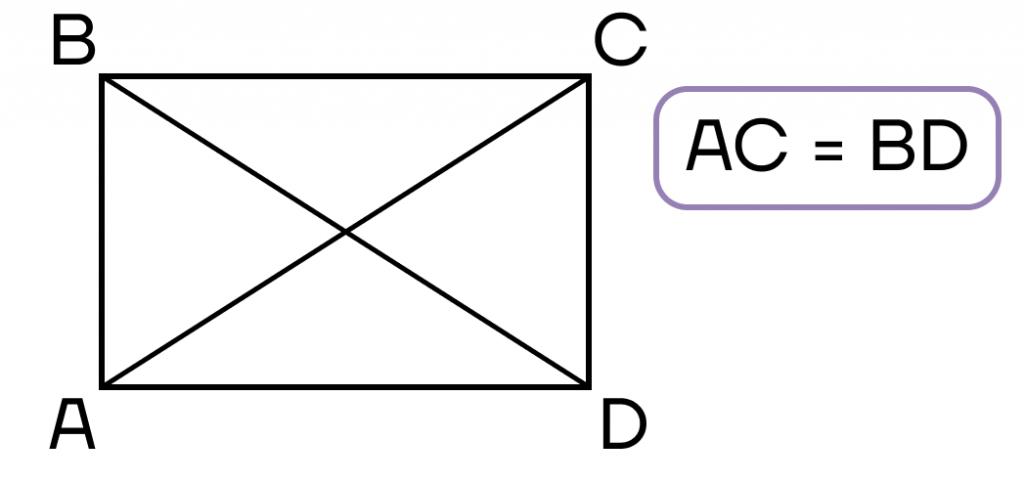
2. Диагонали равны.

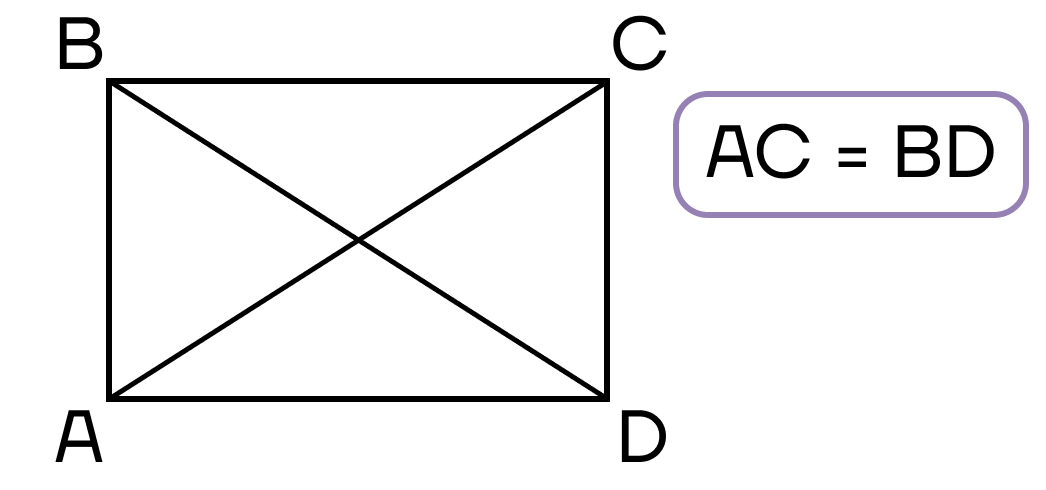
3. Стороны прямоугольника одновременно являются и его высотами.

4. Сумма квадратов двух прилежащих сторон равна квадрату диагонали. Это теорема Пифагора.

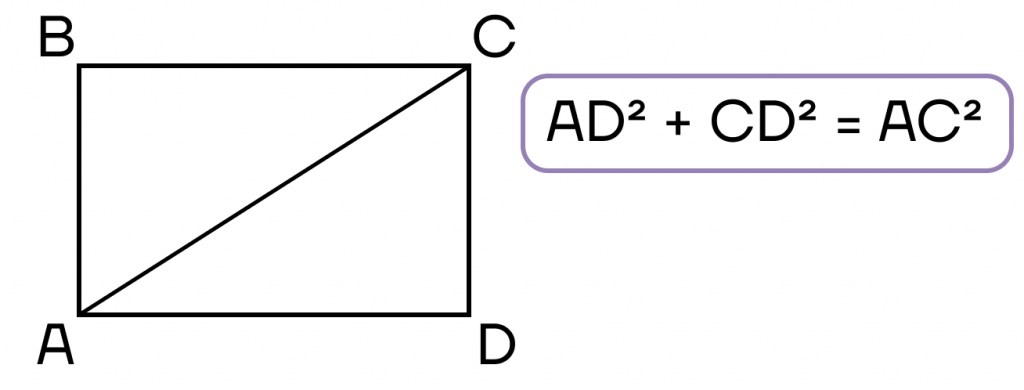
Со свойствами разобрались, теперь рассмотрим признаки.

1. Параллелограмм, имеющий хотя бы один прямой угол, — прямоугольник.

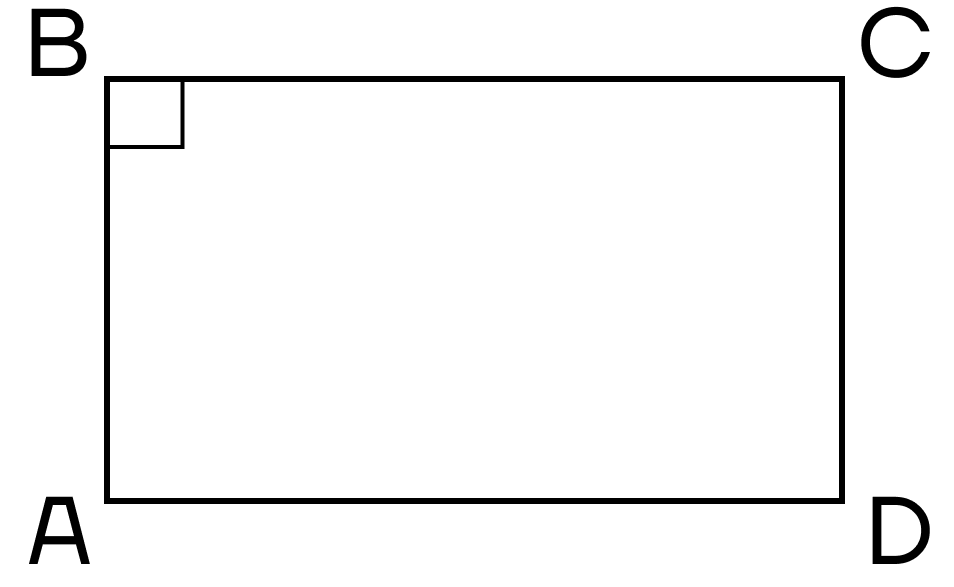
2. Параллелограмм, все углы которого равны, — прямоугольник.

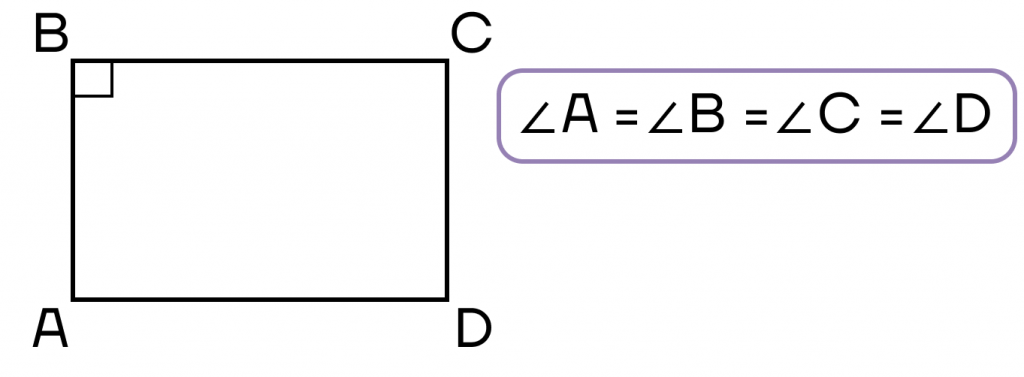
3. Параллелограмм, диагонали которого равны, — прямоугольник.

4. Четырехугольник, у которого три прямых угла, — прямоугольник.

Так, а что там у нас с биссектрисами в прямоугольнике?

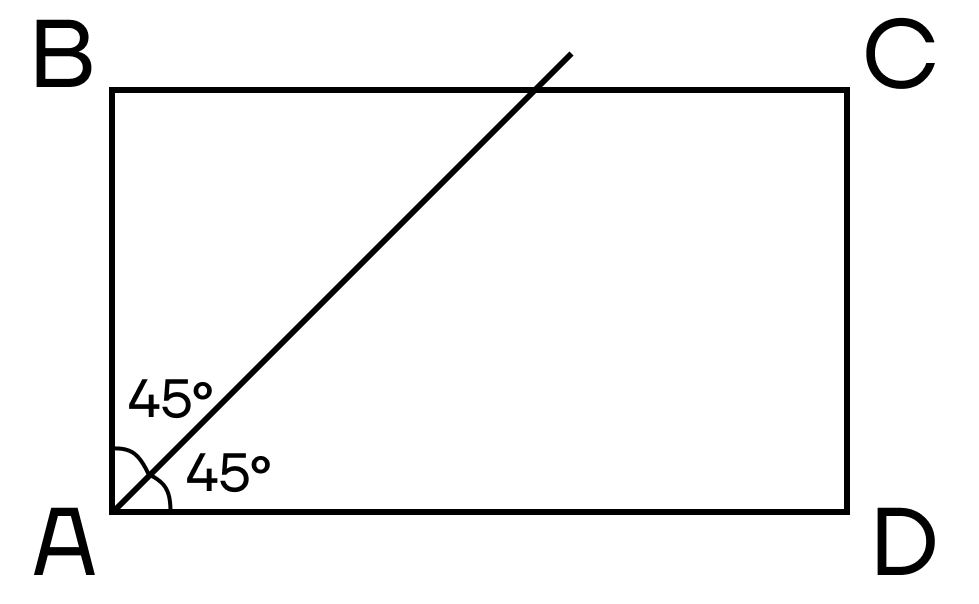
А с биссектрисами все достаточно легко. Биссектриса делит угол прямоугольника на два угла по 45° и пересекает одну из сторон прямоугольника.

Теперь рассмотрим два способа нахождения площади прямоугольника.

1. Площадь прямоугольника равна произведению двух соседних сторон.

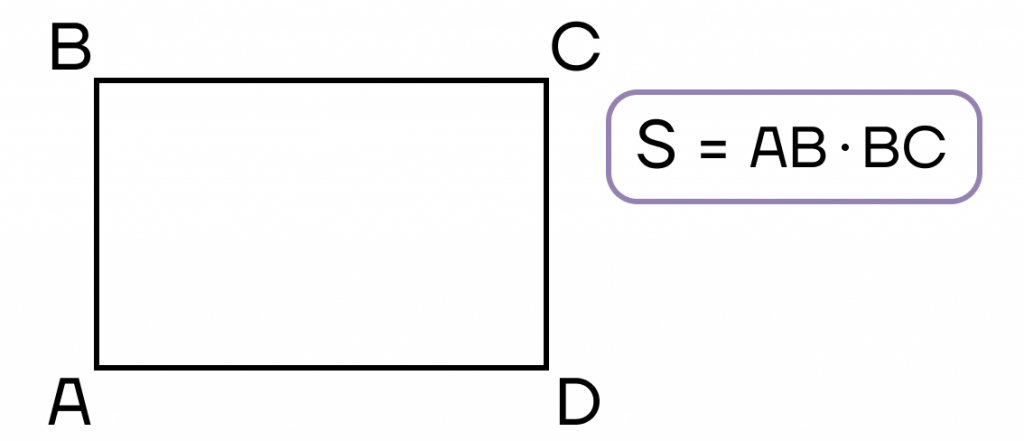
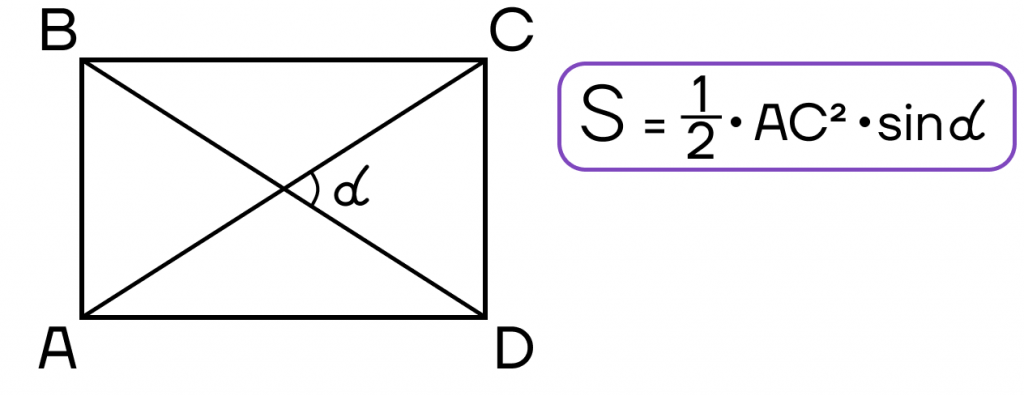
2. Площадь прямоугольника равна половине произведения квадрата диагонали на синус угла между диагоналями.

Во что можно поиграть на уроках и вспомнить геометрию? 1. Итак, запоминайте алгоритм. Бросаете два кубика. 2. Делаете прямоугольник с размером сторон, которые сгенерировал кубик. 3. Новый прямоугольник обязательно должен быть соединен с любым другим вашим прямоугольником. 4. Если это ваш первый прямоугольник, то поместите его в любой угол, а соперник должен поместить свой в противоположный. 5. Если у вас не получается создать прямоугольник с получившимися сторонами, то вы пропускаете ход. 6. Игра заканчивается, когда вся территория занята. Побеждает тот, у кого наибольшая территория.

Давайте закрепим материал на примере.

Решим задание, которое может встретиться на ЕГЭ по профильной математике в задании №1.

Задание. Площадь прямоугольника равна 20. Найдите его большую сторону, если она на 8 больше меньшей стороны.

Решение. Как мы уже знаем, площадь прямоугольника равна произведению длины на ширину. Примем одну сторону прямоугольника за x, тогда вторая равна x + 8.
Тогда:

\(S=x*(x+8)=20\)
\(x^2+8x-20=0\)

Решим квадратное уравнение:

\(D=8^2-4*1*(-20)=64+80=144\)

Корни уравнения:

\(x_{1,2}=\frac{-8\pm 12}{2}\)

Первый корень:

\(x_1=\frac{-8+12}{2}=\frac{4}{2}=2\)

Второй корень:

\(x_2=\frac{-8-12}{2}=-\frac{20}{2}=-10\)

Сторона не может иметь отрицательную длину, поэтому верный корень — первый. Это наименьший корень, а значит больший:

\(x=2+8=10\)

Ответ: 10

На этом заканчивается наша статья, но не тема четырехугольников. В следующей статье мы продолжим изучать их и узнаем про ромб и квадрат. Читайте здесь: «Параллелограмм. Часть 2».

Фактчек

• Четырехугольник — геометрическая фигура из четырех вершин, которые соединены четырьмя отрезками. 
• У четырехугольника любые три точки не лежат на одной прямой, а соединяющие их отрезки не пересекаются.
• Параллелограмм – это выпуклый четырехугольник, у которого стороны попарно параллельны.
• Прямоугольник — это параллелограмм, у которого все углы — прямые.

Проверь себя

Задание 1.
Найдите площадь параллелограмма, если его стороны 5 и 8, а угол между ними 30°. 

1. 40
2. 20
3. 10
4. 25

Задание 2.
Найдите площадь прямоугольника, если его диагональ 12, а угол между диагоналями 60°.

1. \(8\sqrt{3}\)
2. \(6\)
3. \(6\sqrt{3}\)
4. \(4\)

Задание 3.
У четырехугольника диагонали пересекаются под углом 30°, а его стороны попарно параллельны и равны. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Задание 4.
У четырехугольника две противоположные стороны параллельны и равны и есть один прямой угол. Что это за фигура?

1. Квадрат
2. Ромб
3. Прямоугольник
4. Параллелограмм

Ответы: 1. – 2; 2. – 3; 3. – 4; 4. – 3.