Линейные, квадратные и кубические уравнения
На этой странице вы узнаете
- Почему неизвестное обозначают через x?
- Откуда у квадратного уравнения растут корни и сколько их?
- Как находить корни квадратного уравнения, не считая их?
С задачами мы сталкиваемся постоянно. Например, когда ведем ежедневник. И каждый раз возникает вопрос: как успеть решить все-все за день? Неужели нет какого-то понятного и простого алгоритма, который всегда будет работать?
В жизни такой алгоритм вряд ли существует. Но математика здесь преуспела! Главный секрет математики в том, что любую задачу можно решить уравнением. А решить уравнение — значит найти все его корни или доказать, что их нет.
Давай разберемся, как это сделать.
Понятие уравнения
Вспомним, что:
Уравнение — это равенство, содержащее неизвестное, обозначенное буквой.

Представим, что перед нами лежит две коробки: закрытая и открытая. Мы видим, что лежит в открытой. И тут нам говорят: коробки одинаковые! Тогда мы можем сделать вывод, что в первой коробке точно такая же «начинка», как и в открытой.
По такой же логике решаются и уравнения: мы знаем, что с обеих сторон от знака «равно» лежит что-то равнозначное.
Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством.
Например, число 8 будет корнем уравнения \(2x-3=5+x\), потому что равенство \(2*8-3=5+8\) верное.
| Почему неизвестное обозначают через x? Арабские математики в IX веке для записи формул использовали слова. Неизвестную величину они называли «шей», что буквально означает «нечто». Выглядело это примерно так:  Позднее испанские ученые переводили записи на свой язык. Они записывали неизвестное как xei, поскольку в их языке отсутствовал звук [ш]. С появлением формул слово сократилось до одной буквы x. |
Линейные уравнения
Линейное уравнение — это уравнение, в котором неизвестная находится в степени 1.
Вид линейного уравнения:
| \(ax+b=0\), где \(х\) — неизвестная; \(а\) — коэффициент при неизвестной; \(b\) — свободный член. |
Стоит отметить, что а и b в таком уравнение известны, также оба этих числа можно называть коэффициентами.
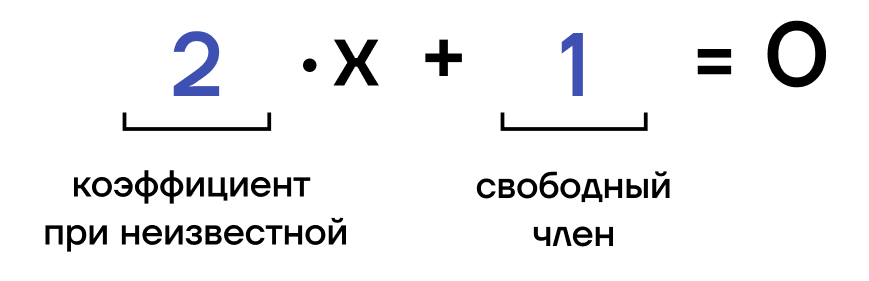
Линейные уравнения — самые простые, ведь в них нет ни степеней, ни корней. Только переменная, обозначаемая буквой, и несколько цифр.
Предположим, что мы играли с собакой пятью игрушками. Вдруг она убежала и вернулась с еще несколькими вещами. Мы удивились: откуда она их только достала? Но в итоге продолжили играть уже 8 игрушками. Так сколько вещей принесла собака?
Если было пять вещей, а стало восемь, ответ очевиден: 3 игрушки. В виде уравнения это можно записать так:
\(5+x=8 => x=3\)
Алгоритм решения линейных уравнений
1. Первым делом нужно выразить х. Иными словами, все буквы должны быть в одной стороне, а все цифры в другой.
2. После распределения букв и цифр по разным сторонам от знака равно нужно посчитать, чему равны левая и правая части уравнения.
3. Найти неизвестную.
А какие инструменты у нас есть, чтобы выражать и находить значения переменных? Преобразования, которые можно совершать:
- Переносить слагаемое в другую часть уравнения с противоположным знаком.
\(x-5=0
x=0+5
x=5\)
Вспомним: цифры и буквы должны быть по разным сторонам от равно, именно поэтому мы перенесли 5. Почему мы поменяли знак? Все просто: значение уравнения не должно поменяться. Иными словами, если мы отнимаем что-то от левой части, то должны отнять и у правой.
- Умножать или делить обе части уравнение на одно и то же число или выражение, которое не равно нулю.
\(3x=12 |: 3\)
\(\frac{3x}{3}=\frac{12}{3}\)
\(x=4\)
Здесь работает такое же правило, как и в предыдущем пункте. Чтобы все было «по-честному», если мы что-то делаем с одной стороной уравнения, то же действие производится и со второй стороной.
Давайте рассмотрим решение линейного уравнения на следующем примере
\(2(x+5)-4x+2=0\)
- Сначала раскроем скобки. Для этого умножим каждое слагаемое в скобке на число перед ней.
\(2*x+2*5-4x+2=0\)
\(2x+10-4x+2=0\)
- Для упрощения сложим подобные слагаемые, то есть слагаемые, у которых совершенно одинаковые переменные. Если у нас просто числа без переменных, то они тоже будут подобными слагаемыми: их сближает отсутствие буквы.
\((2x-4x)+(10+2)=0\)
\(-2x+12=0\)
- А теперь уже известное нам действие: буквы влево, цифры вправо. Поэтому мы переносим число 12 на другую сторону, не забывая поменять знак.
\(-2x=-12\)
Чтобы найти значение х, нужно, чтобы слева переменная была «чистой», то есть без коэффициентов. Поэтому мы делим все уравнение на (-2).
\(\frac{-2x}{-2}=\frac{-12}{-2}\)
\(x=6\)
Значение неизвестной найдено, то есть единственное решение данного уравнения 6.
С линейными уравнениями можно столкнуться и в жизни. Допустим, нам нужно приготовить 570 грамм теста на пирожки.
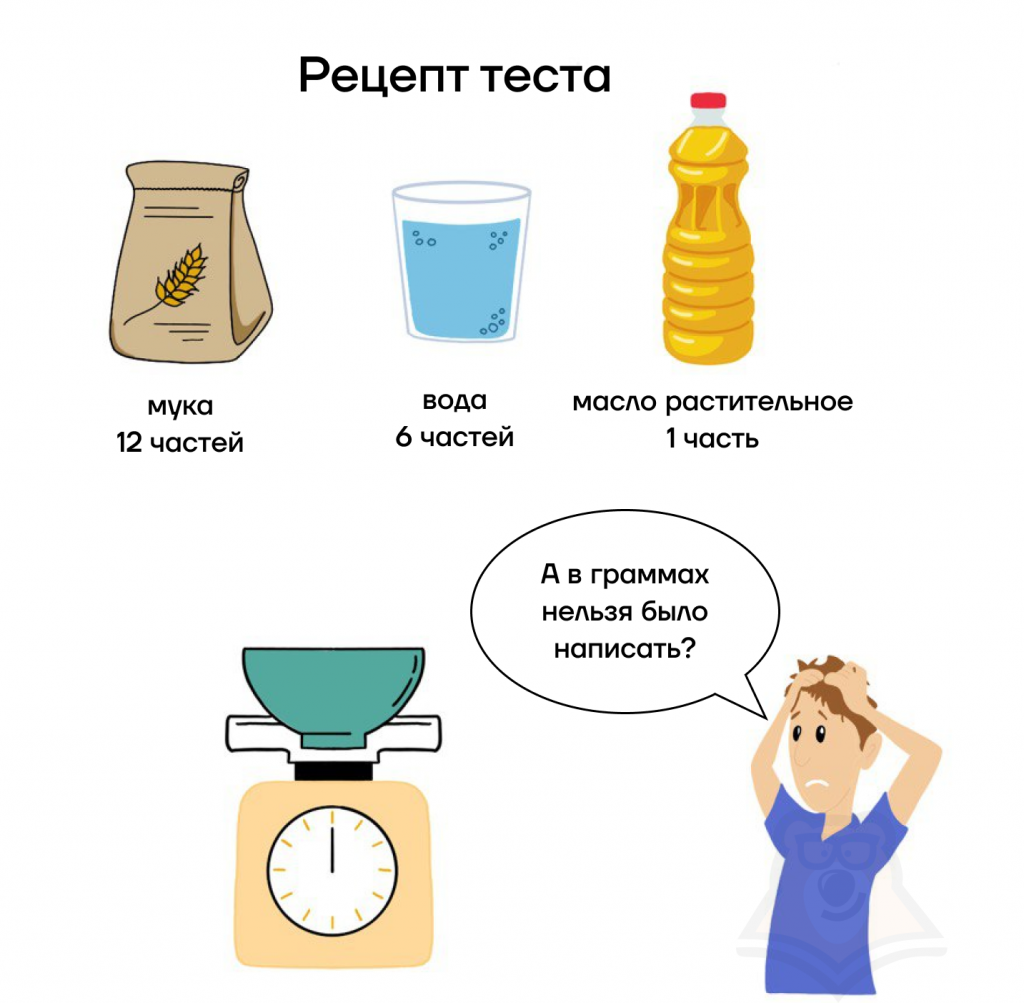
Обозначим вес одной части за x. Составим и решим уравнение для получения этого количества теста:
\(12x+6x+x=570\)
\(19x=570\)
\(x=30\)
Мы узнали, что одна часть — это 30 грамм. Теперь посчитаем, сколько грамм продуктов нам потребуется.
Мука: 12*30=360 грамм.
Вода: 6*30=180 грамм.
Растительное масло: 1*30=30 грамм.
Квадратные уравнения
Мы уже знаем, что такое линейное уравнение. Но как выглядит квадратное? Неужели геометрия пробралась и сюда?
На самом деле все проще: название этого вида уравнения вовсе не связано с геометрическими фигурами: оно происходит от степени.
Квадратное уравнение — это уравнение, в котором неизвестная находится в степени 2.
Вид квадратного уравнения:
| \(ax^2+bx+c=0\), где \(х\) — неизвестная; \(а\) и \(b\) — коэффициенты при неизвестной; \(с\) — свободный член. |
Стоит отметить, что а, b и с — известные числа.
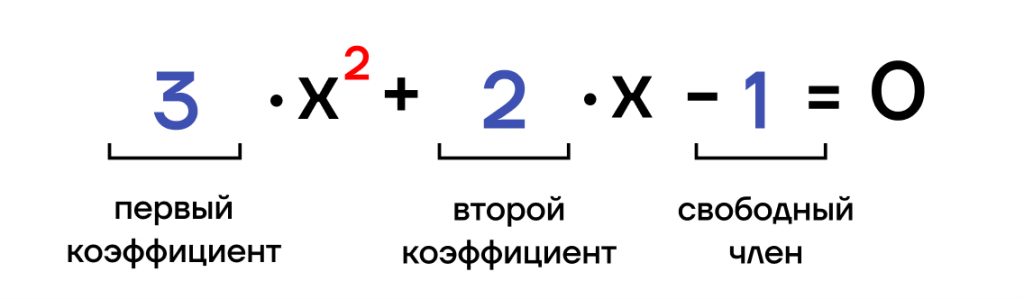
Какими бывают квадратные уравнения?
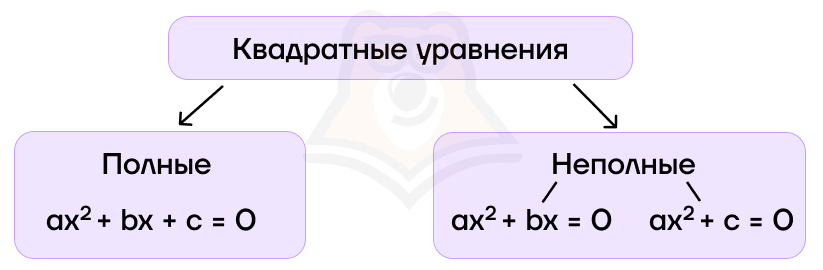
Эти виды квадратных уравнений отличаются тем, что у полного квадратного уравнения есть оба коэффициента и свободный член, а у неполного может отсутствовать или второй коэффициент, или свободный член.
Рассмотрим решение несколько неполных квадратных уравнений на примере:
- \(x^2+2x=0\).
Вспомним, что \(x^2\) — это \(x*x\), а \(2x\) — это \(2*x\). Тогда наше уравнение примет следующий вид:
\(x*x+2*x=0\).
Мы видим общий множитель х, а значит, его можно вынести за скобку:
\(x(x+2)=0\).
Если произведение двух множителей равно 0, то каждый множитель равен 0.
Отсюда мы получаем два уравнения: \(x=0\) и \(x+2=0\), следовательно,
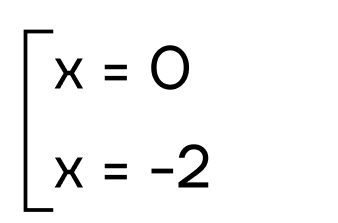
Ответ: 0 и -2.
- \(x^2-4=0\).
Снова воспользуемся простым правилом: буквы влево, цифры вправо:
\(x^2=4\).
А теперь, чтобы найти значение переменной, достаточно будет извлечь квадратный корень:
\(x=±2\).
Почему у нас получилось два числа? Все просто: если возвести в квадрат число 2, то получится 4, также будет и с числом \((-2): (-2)^2=(-2)*(-2)=4\).
Ответ: 2 и -2.
Теперь переходим к другому виду уравнений — полное квадратное уравнение. Оно может иметь 2 корня, 1 корень или не иметь корней. Количество корней зависит от дискриминанта.
Что такое дискриминант?
Дискриминант в квадратном уравнении — это выражение, которое ищется по следующей формуле, где а, b и с берутся из уравнения:
\(D=b^2-4⋅a⋅c\)
| Откуда у квадратного уравнения растут корни и сколько их? Ответ может быть разным, и зависеть он будет именно от дискриминанта. Достаточно запомнить три факта: — Если D > 0, то уравнение имеет 2 корня. — Если D = 0, то уравнение имеет 1 корень. — Если D < 0, то уравнение не имеет корней. |
Неужели мы должны тратить свои силы, чтобы просто узнать, какое количество корней у уравнения? Неужели нельзя сразу решить и узнать ответ? Но дискриминант нас обхитрил: он нужен не только для того, чтобы узнать количество корней, но и для решения уравнения.
Способов решения квадратных уравнений очень много. Рассмотрим самые популярные среди них.
Способы решения квадратных уравнений
- Решение через дискриминант.
Корни квадратного уравнения находятся по этим формулам, где а и b берутся из уравнения, а D — это дискриминант:
\(x_1=\frac{-b+\sqrt{D}}{2⋅a}
x_2=\frac{-b-\sqrt{D}}{2⋅a}\)
Заметим, что у нас появляются \(x_1\) и \(x_2\). Это связано с тем, что в квадратном уравнении ищется 2 корня.
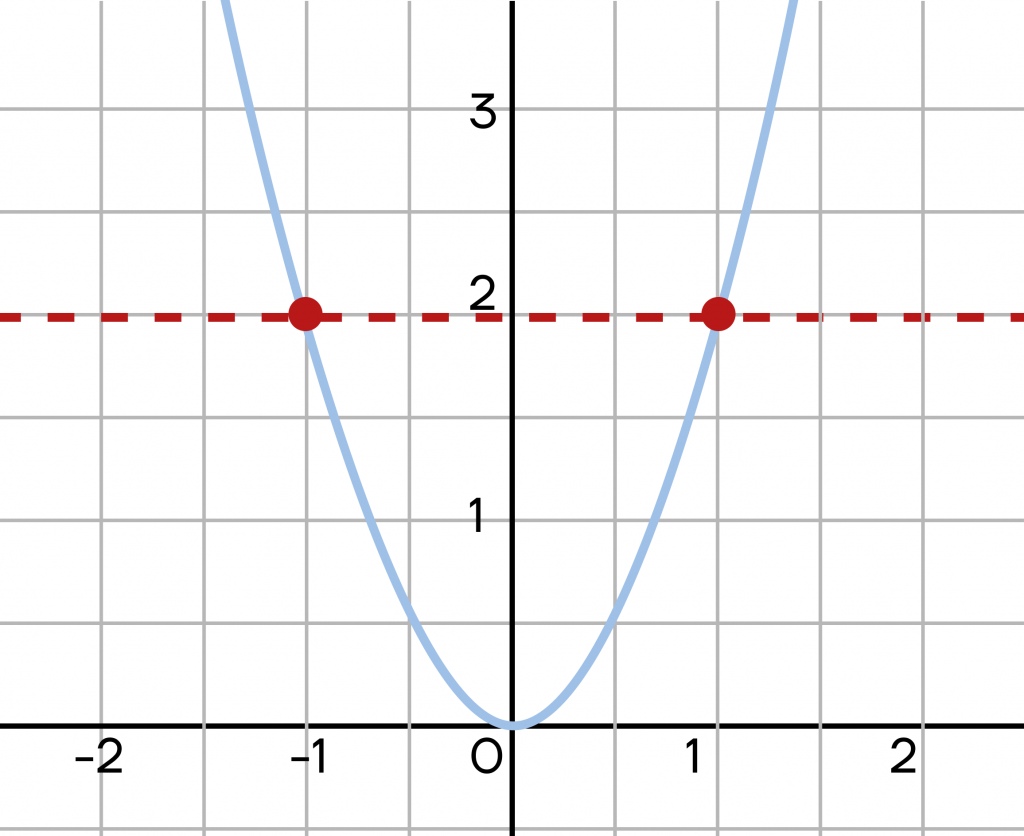
Теперь присмотримся к формулам: они отличаются только тем, что перед корнем из дискриминанта стоит разный знак. Почему так происходит? На самом деле, квадратное уравнение описывает параболу, и если провести в любом ее месте горизонтальную линию, то получим две точки на ветвях. Поэтому мы делаем шаги «в разные стороны». А подробнее про параболы и чтение графиков можно узнать в статье «Основные элементарные функции».
А какой формулой пользоваться в случае, если дискриминант равен 0? Если мы подставим D=0 в данные формулы, то получим:
\(x_1=\frac{-b+\sqrt{D}}{2⋅a}=\frac{-b+\sqrt{0}}{2a}=\frac{-b}{2a}\) и \(x_2=\frac{-b-\sqrt{D}}{2⋅a}=\frac{-b-\sqrt{0}}{2a}=\frac{-b}{2a}\).
Следовательно, \(x_1=x_2\) и можно воспользоваться одной формулой:
\(x_1=\frac{-b}{2⋅a}\)
Алгоритм решения квадратного уравнения через дискриминант
1. Определить, чему равны коэффициенты при каждом члене уравнения. Иными словами, необходимо найти a, b, c.
2. Найти дискриминант по формуле и определить, какое количество корней будет у уравнения. Это поможет не ошибиться в дальнейшем решении.
3. Подставить коэффициенты и дискриминант в формулы и посчитать корни.
- По теореме Виета.
| Как находить корни квадратного уравнения, не считая их? По теореме Виета корни нужно подбирать, то есть искать их не вычисляя, а просто подставляя нужное число. Поэтому она удобна для нахождения рациональных корней (чисел, которые можно представить в виде обыкновенной дроби). В чем заключается теорема Виета? Это система из двух формул, в которую подставляются коэффициенты при переменных. Такую систему нужно лишь запомнить и немного потренироваться ее использовать. А вот что применять: решение через дискриминант или теорему Виета — это дело вкуса. Тем и прекрасна математика: решить один и тот же пример можно несколькими способами, причем ответ всегда будет одинаковым. |
Франсуа Виет выявил интересную связь между коэффициентами квадратного уравнения и корнями этого же уравнения. Эта связь формулируется так:
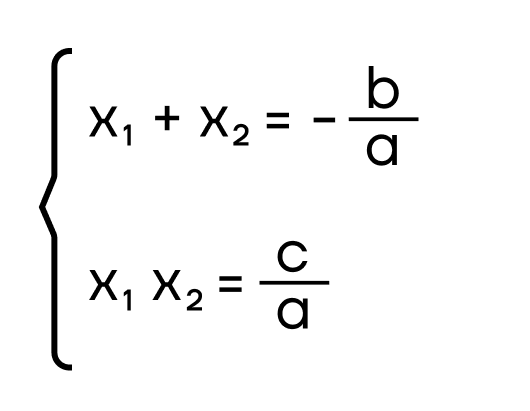 , где , где\(а, b\) и \(с\) — коэффициенты квадратного уравнения; \(x_1\) и \(x_2\) — корни квадратного уравнения. |
Алгоритм решения квадратного уравнения с помощью теоремы Виета
1. Определить, чему равны коэффициенты при каждом члене уравнения.
2. Подставить в формулы известные числа.
3. Найти корни уравнения.
Давайте рассмотрим решение квадратного уравнения на следующем примере
\(2x^2-5x-3=0\).
Коэффициенты нам уже известны: \(a=2, b=-5, c=-3\).
1 способ:
- Найдем дискриминант:
\(D=b^2-4ac=(-5)^2-4⋅2⋅-3=25+24=49\).
- Дискриминант больше нуля, следовательно, у уравнения 2 корня, найдем их:
\(x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-(-5)+\sqrt{49}}{2⋅2}=\frac{5+7}{4}=\frac{12}{4}=3.\)
\(x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-(-5)-\sqrt{49}}{2⋅2}=\frac{5-7}{4}=\frac{-2}{4}=-\frac{1}{2}.\)
Решениями уравнения являются числа \(3\) и \(-\frac{1}{2}\).
2 способ:
- Запишем систему по теореме Виета:
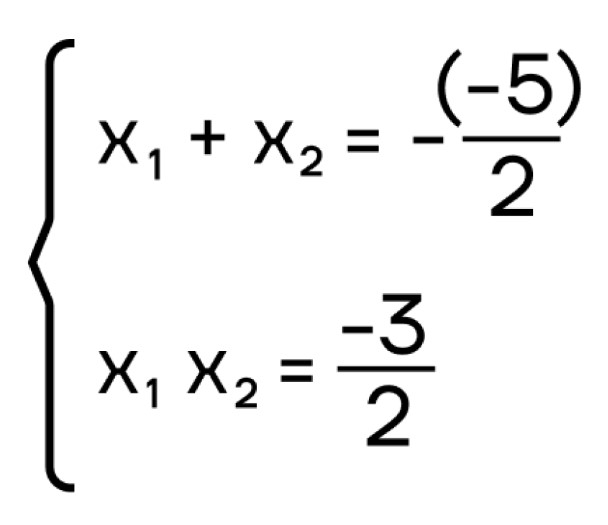
- Теперь подберем такие два числа, чтобы их сумма была \(\frac{5}{2}\), а произведение \((-\frac{3}{2})\), это будут числа \(3\) и \(-\frac{1}{2}\).
Значит, решениями уравнения являются числа \(3\) и \(-\frac{1}{2}\).
Свойства коэффициентов квадратного уравнения
У коэффициентов квадратного уравнения есть свойства, которые позволяют найти корни очень быстро. Разберем их:
- Если \(a+b+c=0\), то \(x_1=1; x_2=\frac{c}{a}\).
- Если \(a+c=b\), то \(x_1= -1; x_2= -\frac{c}{a}\).
Давайте проверим работу этих свойств на примерах.
Пример 1. Найти корни уравнения: \(x^2-3x+2=0\).
Решение. Как мы можем заметить, сумма коэффициентов равна нулю, а это значит, что корни будут такими:
\(x_1=1\)
\(x_2=\frac{2}{1}=2\)
Проверим это, решив уравнение с помощью дискриминанта:
\(D=9-4*1*2=9-8=1\)
\(x_1=\frac{3-1}{2}=1\)
\(x_2=\frac{3+1}{2}=2\)
Супер, первое свойство правда работает. Проверим второе:
Пример 2. Найти корни уравнения: \(x^2+3x+2=0\)
Решение. Вы уже наверняка поняли, что корни будут такими:
\(x_1=-1\)
\(x_2=\frac{2}{1}=-2\)
Проверим это с помощью дискриминанта:
\(D=9-4*1*2=9-8=1\)
\(x_1=\frac{-3-1}{2}=-2\)
\(x_2=\frac{-3+1}{2}=-1\)
И вновь корни совпали при разных способах решения квадратного уравнения. Теперь перейдем к кубическим уравнениям.
Кубические уравнения
Перейдем к последнему виду уравнений. Их название тоже связано не со стереометрией, а со степенью.
Кубическое уравнение — это уравнение, в котором неизвестная находится в степени 3.
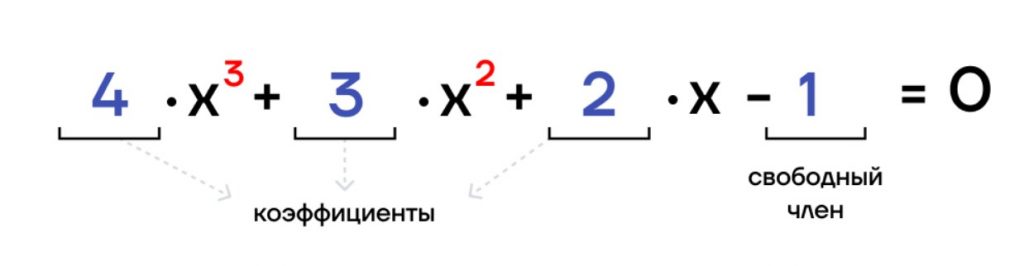
Вид кубического уравнения:
| \(ax^3+bx^2+cx+d=0\), где \(х\) — неизвестная; \(а, b\) и \(с\) — коэффициенты при неизвестной; \(d\) — свободный член. |
Стоит отметить, что а, b, с и d — известные числа.
Преобразования, которые можно совершать в кубических уравнениях:
- Вынесение общего множителя за скобки.
Предположим, у нас есть две тарелки с фруктами, но вот беда: мы любим только апельсины. В каждой тарелке лежит по два апельсина, следовательно, мы можем переложить их в одну тарелку, а все остальные фрукты в другую. После чего довольными пойти кушать апельсины и смотреть сериалы. Таким образом, само содержание тарелок у нас не поменяется, но расположение фруктов в них изменится.
Алгоритм решения кубического уравнения методом вынесения общего множителя за скобку
1. Разложить каждое слагаемое на множители.
2. Вынести за скобку множители, которые есть в обоих слагаемых.
3. Вынести скобку, как общий множитель.
Пример:
\(x^3-2x^2-3x=x*x*x-2*x*x-3*x=x(x^2-2x-3)\).
- Группировка.
В этом случае мы действуем аналогично, но переменная, которую мы выносим за скобку, усложняется: мы перекладываем в другую тарелку не только апельсины, но и бананы.
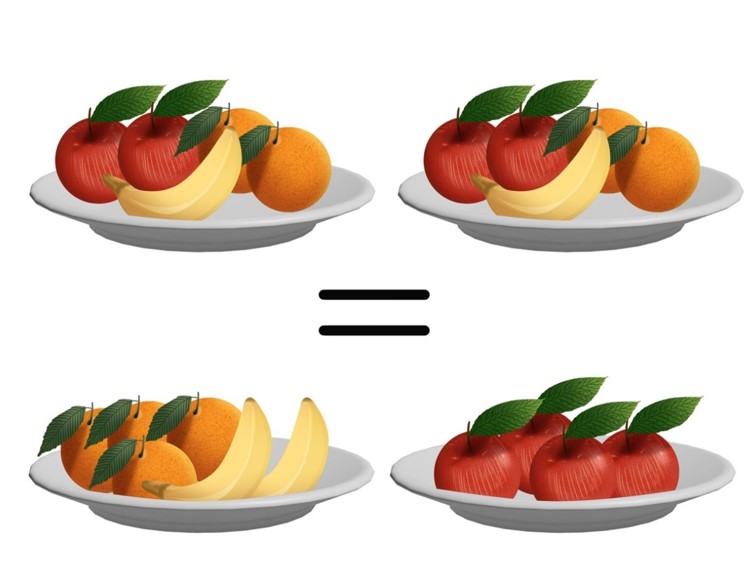
| Алгоритм решения кубического уравнения методом группировки Объединить слагаемые в пары.Вынести общий множитель из каждой скобки, чтобы получились одинаковые скобки.Еще раз вынести общий множитель так, чтобы получилось произведение. |
Пример: \(6x^3+9x^2+8x+12=6x^3+9x^2+8x+12=\)
\(=(3x^2*2x+3x^2*3)+(4*2x+4*3)= 3x^2(2x+3)+4(2x+3)=
=(3x^2+4)(2x+3).\)
Рассмотрим решение кубического уравнения.
\(4x+x^3=x^2+4\)
- Перенесем все слагаемые в левую часть, чтобы дальнейшие преобразования было удобнее совершать.
\(4x+x^3-x^2-4=0.\)
- Заметим, что повторяются четверки, значит, они должны быть в разных группах. При этом у нас есть две переменные, степени которых отличаются не так сильно, тогда их тоже можно развести в разные группы. Получается, что удобнее группировать 1-е и 2-е слагаемые и 3-е и 4-е слагаемые.
\((4x+x^3)-(x^2+4)=0.\)
- Вынесем общий множитель х из первой скобки:
\(x(4+x^2)-(x^2+4)=0.\)
- Вынесем еще один общий множитель \(x^2+4\) за скобки:
\((x-1)(4+x^2)=0.\)
Почему в первой скобке получилось \(х – 1\)? Заметим, что до вынесения общего множителя за скобку, перед вторым слагаемым стоял просто минус. В этом случае запись можно заменить на аналогичную:
\(x(4+x^2)-1*(x^2+4)=0\)
\((x-1)(4+x^2)=0\)
- Чтобы произведение было равно 0, один из множителей должен быть равен 0. Запишем совокупность:
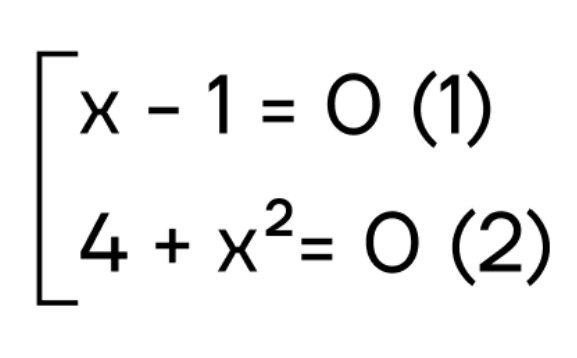
- Решим каждое уравнение отдельно:
| \(x-1=0\) \(x=1\) | \(4+x^2=0\) \(x^2=-4\) Нет решений, так как \(x^2 ≥ 0\) верно для любого х. |
Из этого следует, что у данного уравнения есть только одно решение x=1.
Почему важно уметь решать уравнения? Они могут встретиться во всех заданиях на ОГЭ и ЕГЭ. Уравнения — это основа любой задачи, а значит, их нужно уметь решать, чтобы справляться с более сложными заданиями.
Теперь, когда вы разобрались в линейных, квадратных и кубических уравнениях мы предлагаем вам усложнить задачу и познакомиться с целыми рациональными, дробно-рациональными и иррациональными уравнениями.
Термины
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа (числа, используемые при счете). Например, \(\frac{1}{2}\).
Система уравнений — это два и более равенства, объединенных фигурной скобкой, имеющих несколько решений, которые одновременно являются решениями для всей системы.
Фактчек
- В линейном уравнении неизвестная находится в степени 1. Для решения такого уравнения в одной части уравнения нужно оставить только неизвестную, а в другой собрать все остальное.
- В квадратном уравнении неизвестная в квадрате, то есть в степени 2. Решать такое уравнение можно, например, через дискриминант:
\(D=b^2-4⋅a⋅c\)
\(x_1=\frac{-b+\sqrt{D}}{2⋅a}\)
\(x_2=\frac{-b-\sqrt{D}}{2⋅a}\)
Второй способ решения квадратного уравнения: теорема Виета:
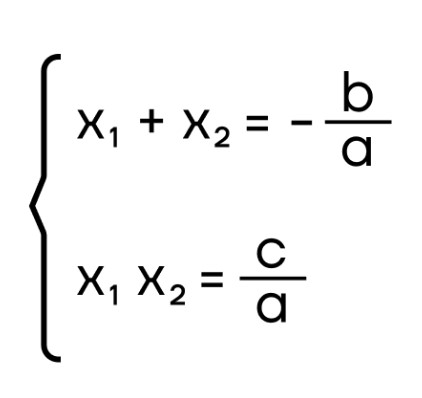
- В кубическом уравнении неизвестная находится в кубе, то есть в степени 3. Для решения такого уравнения используется вынесение общего множителя за скобки и способ группировки.
Проверь себя
Задание 1.
Найдите корень уравнения \(2x+4⋅3-2x=0\).
- 3
- 2
- -2
- -3
Задание 2.
Сколько корней будет у уравнения \(x^2+x-2=0\)?
- нет корней
- один корень
- два корня
- три корня
Задание 3.
Найдите корни уравнения \(x^2+4x-5=0\).
- 1 и 5
- 1 и -5
- 1 и 2
- -1 и 2
Задание 4.
Найдите корни уравнения \(x^2-5x=0\).
- 0 и 5
- 2 и 5
- 25 и 5
- 0 и 4
Задание 5.
Найдите корни уравнения \(12x+4-12x^3-4x^2=0\).
- \(\frac{-1}{3}\)
- \(-1\) и \(1\)
- \(-1, -\frac{1}{3}\) и \(1\)
- \(-1, \frac{1}{3}\) и \(1\)
Ответы: 1. — 4; 2. — 3; 3. — 2; 4. — 1; 5. — 3.
123


 к списку статей
к списку статей