Формулы тригонометрии и простейшие уравнения

На этой странице вы узнаете

• Лайфхак: что делать, если забыл нужную формулу?
• Чем отличаются тригонометрическая функция и аркфункция?
• Какие аркфункции можно «не решать»?

Все помнят Льва Николаевича Толстого? Того самого великого русского писателя, чье лицо с невероятной бородой украшает стену каждого класса литературы буквально каждой российской школы. Удивлены, что он «пробрался» и в математику? Между тем, его перу принадлежит выдающийся для своего времени учебник арифметики. А еще он знаменит своими математическими изречениями, которые люди «растащили» на цитаты задолго до изобретения статусов в социальных сетях. Одно из них гласит:

«Большинство жизненных задач решаются как алгебраические выражения: приведением их к самому простому виду».

Как мы видим, этот совет полезен не только в науке, но и в жизни. Но сегодня мы применим его непосредственно к тригонометрии. А на помощь к нам придут тригонометрические формулы. Давайте же начнем делать сложное простым.

Основные формулы тригонометрии

Тригонометрия – увлекательнейшая наука, которая открывает нам дверцу в мир углов и их значений. Мы уже начали разбирать, как работать с углами, в статьях «Тригонометрическая окружность. Часть 1» и «Тригонометрическая окружность. Часть 2». 

Вспомним чуть подробнее, что такое тригонометрические функции. Это уже знакомые нам синус, косинус, тангенс и котангенс. Они нужны для поиска численного значения угла, то есть для того, чтобы представить угол как число. 

Тригонометрические функции имеют вид sin x, cos x, tg x, ctg x, при этом х – аргумент тригонометрической функции. Разумеется, вместо х может стоять любая буква (переменная) или даже величина угла в градусах или радианах. 

А как выглядят тригонометрические формулы? В этом нам предстоит разобраться. 

Было бы странно начать разбор формул с тех, которые используются крайне редко, правда? Поэтому мы начнем с самого важного: основного тригонометрического тождества.

Слово «тождество» подсказывает нам, что одна часть уравнения равна другой. Так о каком уравнении речь и как выглядит это самое основное тригонометрическое тождество?

\(sin^2x + cos^2x = 1\)

Попробуем доказать данное тождество. Рассмотрим прямоугольный треугольник со сторонами a, b, c и углом .

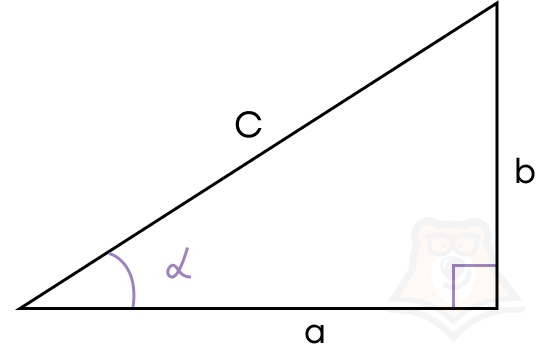
Для дальнейшего решения нам необходимо вспомнить про прямоугольный треугольник, а именно про отношение его сторон и углов. Так, синус – отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе. Запишем эти отношения с помощью переменных: 

\(sin α = \frac{b}{c}\)
\(cos α = \frac{a}{c}\)

Теперь воспользуемся теоремой Пифагора для прямоугольного треугольника. По теореме сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы:

\(a^2+b^2=c^2\)

Разделим получившееся выражение на квадрат длины гипотенузы:

\(\frac{a^2}{c^2}+\frac{b^2}{c^2}=1\)

Итак, что же мы получили? Первым и вторым слагаемым у нас как раз стоят квадраты синуса и косинуса:

\(sin^2a=(\frac{b}{c})^2=\frac{b^2}{c^2}\)
\(cos^2a=(\frac{a}{c})^2=\frac{a^2}{c^2}\)

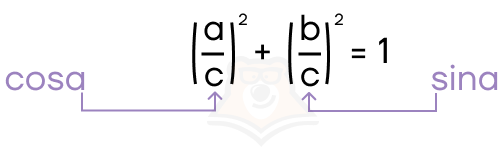
Основное тригонометрическое тождество доказано.

Мы разобрали формулу с синусом и косинусом. Есть ли что-то похожее для тангенса и котангенса? Да, но для обсуждения этого момента нам нужно понаблюдать одну интересную связь. 

Вспомним, что тангенс – отношение противолежащего катета к прилежащему, а котангенс – отношение прилежащего катета к противолежащему.

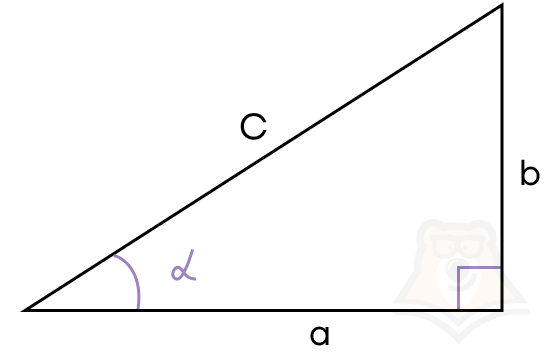
\(tg a=\frac{b}{a}\)
\(ctg a =\frac{a}{b}\)

Попробуем разделить синус на косинус:

\(\frac{sin a}{cos a}=(\frac{b}{c}):(\frac{a}{c})=\frac{b}{c}*\frac{c}{a}=\frac{b}{a}\)

Здесь можно заметить, что мы получили тангенс. Таким образом, мы вывели еще одну важную формулу:

\(tg x=\frac{sin x}{cos x}\)

Но что получится, если разделить не синус на косинус, а наоборот? Проверим:

\(\frac{cos a}{sin a}=(\frac{a}{c}):(\frac{b}{c})=\frac{a}{c}*\frac{c}{b}=\frac{a}{b}\)

Мы получили котангенс! 

\(сtg x=\frac{cos x}{sin x}\)

Теперь попробуем найти связь между тангенсом и котангенсом. Как перейти от одного к другому? Достаточно лишь перевернуть дроби с синусом и косинусом. 

\(\frac{cos x}{sin x}=ctg x => \frac{1}{ctg x}=\frac{1}{\frac{cos x}{sin x}}=\frac{sin x}{cos x}=tg x\)

То есть в этом случае мы получаем равенства с обратными числами:

\(сtg x=\frac{1}{tg x}\)
\(tg  x=\frac{1}{ctg x}\)

Далее давайте рассмотрим, как связаны тангенс и котангенс одного угла. Для этого просто попробуем умножить их друг на друга:

\(tg a*ctg a =\frac{b}{a}*\frac{a}{b}=1\)

Мы получили еще одну важную формулу:

\(tg x*ctg x=1\)

И наконец, попробуем вывести еще одну связь: между котангенсом и синусом, а также тангенсом и косинусом. Для этого вернемся к основному тригонометрическому тождеству:

\(sin^2x + cos^2x = 1\)

Разделим его на квадрат синуса:

\(sin^2x + cos^2x = 1|:(sin^2x)\)
\(\frac{sin^2x}{sin^2x}+\frac{cos^2x}{sin^2x}=\frac{1}{sin^2x}\)
\(1+ctg^2x=\frac{1}{sin^2x}\)

Аналогичным способом можно вывести формулу с косинусом и тангенсом. Запишем получившиеся тождества:

\(1+tg^2x=\frac{1}{cos^2x}\)
\(1+ctg^2x=\frac{1}{sin^2x}\)

Итак, мы разобрали основные формулы в тригонометрии. На этом все? Конечно, нет! В тригонометрии существует множество формул, поэтому продолжим разбор мы уже с более сложными выражениями. 

Преобразование тригонометрических выражений может встретиться вам в №16 ЕГЭ по базовой математике. Разберем один из возможных вариантов этого задания.

Найдите \(7sin x\), если \(cos x=\frac{2\sqrt6}{7}\) и \(x\in(\pi:\frac{3\pi}{2})\).

Решение.
Нам не просто так дан промежуток, к которому принадлежит х. Он необходим, чтобы определить знак (плюс или минус) в ответе. 

Промежуток показывает, что х принадлежит третьей четверти. Синус в третьей четверти отрицателен, значит, ответ будет с минусом. Подробнее про определение знаков тригонометрических функций можно прочесть в статье «Формулы приведения». 

Далее нам необходимо воспользоваться основным тригонометрическим тождеством.
\(sin^2x + cos^2x = 1\)

Выразим из него синус:
\(sin^2x=1-cos^2x\)
\(sin x=\pm\sqrt{1-cos^2x}\)

Поскольку мы уже определили, что синус будет отрицательным, получаем уравнение:
\(sin x=-\sqrt{1-cos^2x}\)

Подставляем значение косинуса и считаем:
\(sin x=-\sqrt{1-(\frac{2\sqrt6}{7})^2}=-\sqrt{1-\frac{4*6}{49}}=-\sqrt{1-\frac{24}{49}}=-\sqrt{\frac{25}{49}}=-\frac{5}{7}\)

В условии нам необходимо найти 7sin x. Следовательно, осталось умножить получившееся значение на 7:
\(7*(-\frac{5}{7})=-5\)

Ответ: -5

Рассмотренные выше формулы в первую очередь отражают связи между тригонометрическими функциями. Однако, с помощью формул можно преобразовывать одну конкретную функцию, например, работать только с синусом или только с котангенсом. 

Но чтобы применять такие формулы, в самой функции должно что-то поменяться. В первую очередь, изменениям подлежит аргумент. Например, в аргументе может стоять отрицательный угол. 

Формулы отрицательных углов

Что такое отрицательный угол и как с ним работать? На самом деле, все просто: чтобы получить отрицательный угол, достаточно поставить перед аргументом минус. Например, sin(-x). 

Применять такой угол при решении выражений с тригонометрическими функциями очень неудобно, поэтому от минуса обычно избавляются. Однако делать это нужно по правилам: нельзя просто его не написать. 

Чтобы правильно избавиться от минуса, нужно понимать, что отрицательные углы напрямую связаны с графиками тригонометрических функций, а именно с четностью функций. Подробнее про четность функции можно прочесть в статье «Определение и график функции».

Четность функции можно сравнить со снежинкой. Если мы посмотрим на нее под микроскопом и мысленно проведем ось посередине, то окажется, что левая и правая части одинаковые. Единственное их отличие – они отзеркалены. 

Также и четные функции: справа и слева они имеют одинаковые отзеркаленные части. 

Четная функция – функция, для которой выполняется равенство \(f(x)=f(-x)\).

Повторим, такие функции симметричны относительно оси ординат. Можно представить, что вместо оси у у нас стоит зеркало, в которой график функции отражается. 

Если мы вспомним графики тригонометрических функций и проверим их симметричность, то заметим, что четным является только косинус. Этим он выделяется среди других функций.

Синус, тангенс и котангенс – нечетные функции. Для них будет справедливо уравнение \(f(-x)=-f(x)\). Их графики не симметричны относительно оси у.

Таким образом, опираясь на четность функции, мы можем вывести четыре формулы:

\(cos(-x)=cos x\)
\(sin(-x)=-sin x\)
\(tg(-x)=-tg x\)
\(ctg(-x)=-ctg x\)

Пользуясь этими формулами, можно легко избавляться от минуса в аргументах функции.

Итак, мы попробовали изменить аргумент с помощью минуса. А если попробовать поставить перед аргументом коэффициент, например, 2?

Формулы двойных углов

Как еще мы можем поколдовать с аргументом? Разобрать двойной угол. 

Из самого названия следует, что аргумент функции будет умножен на 2. Например, \(cos(2x)\). 

Но математики уже позаботились о нас, и чтобы мы не мучились, вывели формулы, по которым просто преобразовать двойной угол и перейти к обычному аргументу. Рассмотрим их. 

\(sin(2x)=2sin x*cos x\)
\(cos(2x)=cos^2x-sin^2x\)
\(tg(2x)=\frac{2tg x}{1-tg^2x}\)
\(ctg(2x)=\frac{ctg^2x-1}{2ctg x}\)

Заметили, что косинус выделился и тут? На самом деле, у него целых три формулы для двойного угла. Попробуем вывести еще две. Для этого вернемся к основному тригонометрическому тождеству и выразим квадрат косинуса:

\(sin^2x+cos^2x=1 =>cos^2x=1-sin^2x\)

Теперь подставим полученное выражение в формулу косинуса двойного угла:

\(cos(2x)=cos^2x-sin^2x=(1-sin^2x)-sin^2x=1-2sin^2x\)

Аналогичным способом выведем формулу двойного угла только через косинусы:

\(sin^2x+cos^2x=1 =>sin^2x=1-cos^2x\)
\(cos(2x)=cos^2x-sin^2x=cos^2x-(1-cos^2x)=cos^2x-1+cos^2x=2cos^2x-1\)

Таким образом, мы получили еще две формулы для двойного угла.

\(cos(2x)=1-2sin^2x\)
\(cos(2x)=2cos^2x-1\)

Важно заметить, что формулы работают в обе стороны. Читать их можно как слева направо, так и справа налево.

Преобразование тригонометрических выражений встречается в №6 ЕГЭ по профильной математике. 

Найдите значение выражения \(11\sqrt{3}-22\sqrt{3}*sin^2(\frac{\pi}{12})\)

Решение.
Заметим, что у нас есть общий множитель \(11\sqrt3\). Вынесем его за скобки:

\(11\sqrt{3}*1-2*11\sqrt{3}*sin^2(\frac{\pi}{12}))=11\sqrt{3}(1-2sin^2(\frac{\pi}{12}))\)

В скобке у нас получилось формула косинуса двойного угла. «Свернем» ее:

\(11\sqrt3*cos(2*\frac{\pi}{12})=11\sqrt3*cos(\frac{\pi}{6})\)

У нас получилось табличное значение косинуса. Подставляем его и считаем ответ:

\(11\sqrt3*\frac{\sqrt3}{2}=\frac{11*3}{2}=16,5\)

Ответ: \(16,5\)

Теперь попробуем еще сильнее усложнить аргумент. Пусть вместо него будет стоять алгебраическое выражение. 

Формулы сложения и вычитания углов

Перейдем к сложению и вычитанию аргумента. В записи задания это обычно выглядит, например, так: \(tg(\alpha+\beta)\) или \(ctg(\alpha-\beta)\). Если повезет, выражение в аргументе может прийти к обычному углу, который достаточно легко посчитать. Однако, не всегда все так просто. 

Например, попробуем посчитать \(sin(45+60)\). В скобках получаем угол в 105 градусов, что не является табличным значением. Что же делать? Считать через аркфункцию? Подробнее про аркфункцию мы поговорим чуть дальше. 

На самом деле, мы можем воспользоваться формулами сложения и вычитания углов. Рассмотрим их.

\(sin(\alpha\pm\beta)=sin\alpha*cos\beta \pm cos \alpha*sin\beta\)
\(cos(\alpha\pm\beta)=cos \alpha*cos\beta \mp sin \alpha*sin\beta\)
\(tg(\alpha\pm\beta)=\frac{tg \alpha \pm tg\beta}{ 1\pm tg \alpha*tg\beta}\)
\(ctg(\alpha\pm\beta)=\frac{ctg \alpha*ctg\beta\mp1}{ctg\beta\mp ctg\beta \pm \alpha}\)

Заметим, что в этих формулах у нас появился знак \(\mp\). Знаки \(\pm\) и \(\mp\) отличаются друг от друга и эту разницу мы сейчас обсудим. 

Знак \(\mp\) означает, что нам нужно использовать противоположный знак тому, который стоит в аргументе. Например, у нас в аргументе стоит +, тогда при преобразовании формулы мы должны поменять его на минус. Например, \(cos(a+\beta)=cos a*cos\beta -sin a*sin\beta\).
Точно так же с этим знаком минус меняется на плюс. 

Если в аргументе стоит привычный \(\pm\), то знаки мы не меняем и используем те же, что даны изначально. Например, \(sin(a+\beta)=sin a*cos \beta+cos a*sin \beta\).

Чтобы точно не запутаться в преобразовании знаков, нужно ориентироваться по одной стороне. Например, если в примере у нас стоит знак сверху, то и все остальные знаки для преобразований мы берем сверху. 

Рассмотрим \(tg(a-\beta)\). Заметим, что в изначальной формуле минус стоит снизу, значит, для преобразований берем только нижние знаки. Получаем:

\(tg(a-\beta)=\frac{tg a-tg\beta}{1+tg a*tg \beta}\)

Теперь попробуем решить наше выражение sin(45+60). Применим формулу и получим:

\(sin(45+60)=sin 45*cos 60+cos 45*sin 60\)

Далее нам просто нужно подставить табличные значения синусов и косинусов. Саму таблицу мы приложили ниже, а подробнее про работу с ней рассказывали в статье «Тригонометрическая окружность. Часть 1».

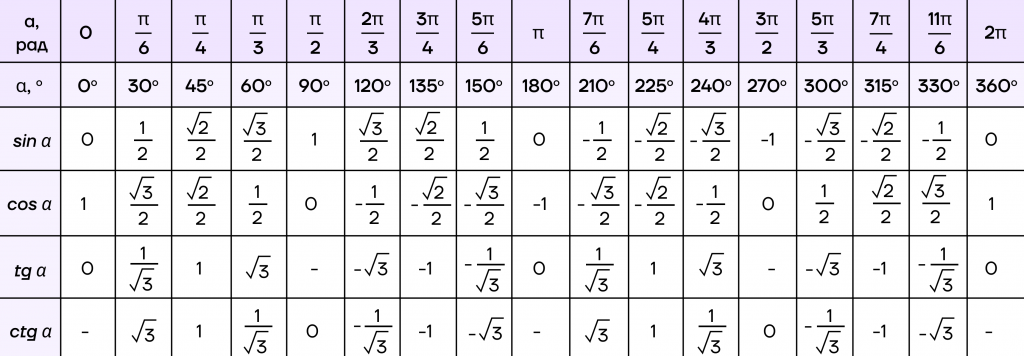
По таблице получаем:

\(sin 45*cos 60+cos 45*sin 60=\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}\)

Осталось посчитать выражение и найти ответ:

\(\frac{\sqrt2}{2}*\frac{1}{2}+\frac{\sqrt2}{2}*\frac{\sqrt3}{2}=\frac{\sqrt2}{4}+\frac{\sqrt6}{4}=\frac{\sqrt2+\sqrt6}{4}\)

Аргументы мы меняли различными способами. Можем ли как-то поменять саму тригонометрическую функцию? Конечно! Например, возведем ее в квадрат. 

Формулы понижения степени

Как считать выражения, в которых тригонометрическая функция стоит в квадрате? Просто возвести табличное значение в квадрат? А если в аргументе не табличное значение, но необходимо воспользоваться аркфункцией (еще немного терпения, мы обязательно разберемся, что же это за зверь такой)? Спойлер: аркфункцией нельзя пользоваться, если тригонометрическая функция стоит в квадрате. 

Как тогда преобразовывать такие выражения? Снова воспользоваться формулами:

\(sin^2x=\frac{1-cos(2x)}{2}\)
\(cos^2x=\frac{1+cos(2x)}{2}\)
\(tg^2x=\frac{1-cos(2x)}{1+cos(2x)}\)
\(ctg^2x=\frac{1+cos(2x)}{1-cos(2x)}\)

Первые две формулы легко вывести из косинуса двойного угла. Например:

\(cos(2x)=1-2sin^2x\)
\(2sin^2x=1-cos(2x)\)
\(sin^2x=\frac{1-cos(2x)}{2}\)

Лайфхак: что делать, если забыл нужную формулу?  Особая прелесть формул в тригонометрии в том, что они неразрывно связаны друг с другом. И если случилось так, что вы забыли одну из формул, ее легко можно вывести из другой! Например, как вывести формулу понижения степени из формулы косинуса двойного угла мы разобрали только что.

Теперь попробуем составить алгебраическое выражение с самими тригонометрическими функциями. Для усложнения задачи у них будут разные аргументы.

Сумма, разность и произведение синуса и косинуса

Нам осталось разобрать еще несколько формул. В этот раз они связаны с действиями, производимыми с самими функциями. Например, с произведением синуса и косинуса. 

Рассмотрим формулы:

\(sin\alpha+sin \beta =2sin(\frac{\alpha+\beta}{2})*cos(\frac{\alpha-\beta}{2})\)
\(sin \alpha-sin \beta=2sin(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)
\(cos \alpha+cos \beta =2cos(\frac{\alpha-\beta}{2})*cos(\frac{\alpha+\beta}{2})\)
\(cos \alpha-cos \beta =-2sin(\frac{\alpha+\beta}{2})*sin(\frac{\alpha-\beta}{2})\)

\(sin \alpha*sin \beta =\frac{1}{2}(cos(\alpha-\beta)-cos(\alpha+\beta))\)
\(cos \alpha*cos \beta =\frac{1}{2}(cos(\alpha-\beta)+cos(\alpha+\beta))\)
\(sin \alpha*cos \beta=\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\)

Заметим, что в формулах разные аргументы. Если они не табличные, то посчитать значение выражения почти нереально. Поэтому, если это возможно, с помощью этих формул мы можем упростить выражение до табличных углов.

Например, попробуем преобразовать выражение \(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})\). 

Рассчитать значение не представляется возможным: в аргументе стоят нетабличные значения. Попробуем преобразовать это выражение с помощью формулы \(sin \alpha*cos\beta =\frac{1}{2}(sin(\alpha-\beta)+sin(\alpha+\beta))\):

\(sin(\frac{3\pi}{8})*cos(\frac{\pi}{8})=\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))\)

Преобразуем выражения в аргументах синусов отдельно:

\(\frac{3\pi}{8}-\frac{\pi}{8}=\frac{3\pi-\pi}{8}=\frac{2\pi}{8}=\frac{\pi}{4}\)
\(\frac{3\pi}{8}+\frac{\pi}{8}=\frac{3\pi+\pi}{8}=\frac{4\pi}{8}=\frac{\pi}{2}\)

Получаем выражение:

\(\frac{1}{2}(sin(\frac{3\pi}{8}-\frac{\pi}{8})+sin(\frac{3\pi}{8}+\frac{\pi}{8}))=\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))\)

Теперь подставим значения из таблицы:

\(\frac{1}{2}(sin(\frac{\pi}{4})+sin(\frac{\pi}{2}))=\frac{1}{2}(\frac{\sqrt2}{2}+1)=\frac{1}{2}*\frac{2+\sqrt2}{2}=\frac{2+\sqrt2}{4}\)

Значение выражения найдено.

Подведем итог. Формулы тригонометрии необходимы для преобразования сложных выражений. А чтобы они были в одном месте, мы составили для вас таблицу.

Итак, мы разобрались, как преобразовывать выражения с тригонометрическими функциями. Какой следующий шаг? Правильно, решение уравнений.

Простейшие тригонометрические уравнения

Вспомним, что уравнение – это выражение с переменной, в котором одна часть равна другой. В тригонометрических уравнениях у нас добавляется лишь одно условие: появляется тригонометрическая функция. 

Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.

В данной статье мы рассмотрим решение простейших тригонометрических уравнений. Они имеют следующий вид:

\(sin x=a\)
\(cos x=a\)
\(tg x=a\)
\(ctg x=a\)

В этой записи а – заданный угол в градусах или радианах. При решении уравнений нам нужно будет найти значение х.

Также заметим, что для синуса и косинуса а может принимать значения от -1 до 1 включительно, что связано с их ограничениями.

Чтобы найти значение аргумента, нам нужно «перевернуть» уравнение, или воспользоваться обратной функцией. А какая функция обратна к тригонометрической?

Аркфункция — это функция, обратная тригонометрической. 

Аркфункции записываются с помощью приставки arc. Например, arcsin, arccos, arctg, arcctg. 

Чем отличаются тригонометрическая функция и аркфункия? Если с помощью тригонометрических функций мы определяем значение тригонометрической функции для заданного угла, то с помощью аркфункций мы ищем угол по значению тригонометрической функции.

Разумеется, для аркфункций есть свои формулы. Выглядят они так:

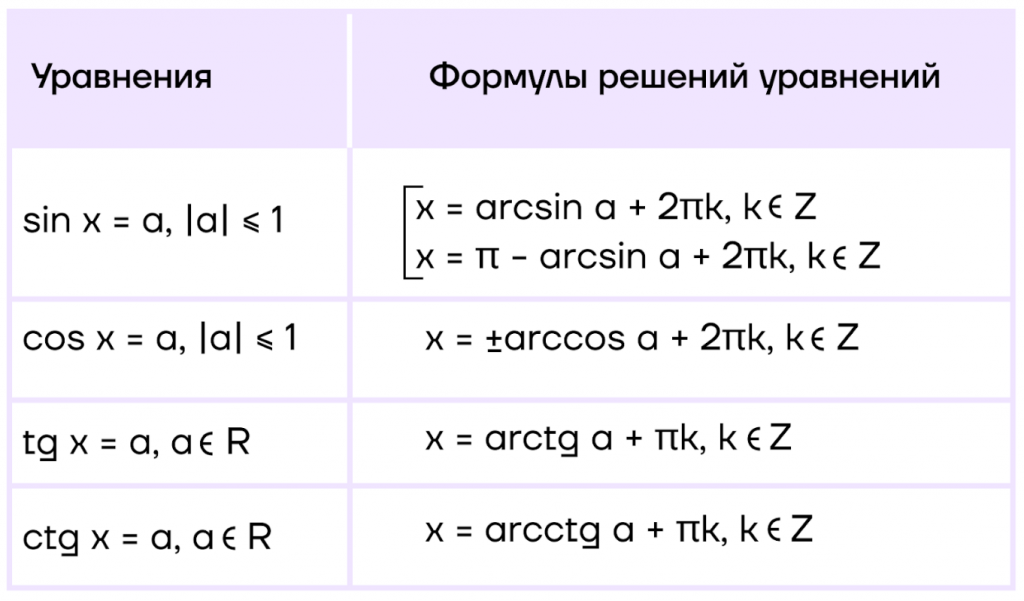
Как пользоваться аркфункциями для решения простейших тригонометрических уравнений?

Алгоритм решения простейших тригонометрических уравнений:

1. Записать уравнение.
2. Записать формулу (формулы) решение этого уравнения, опираясь на таблицу аркфункций выше.
3. Если угол в аркфункции табличный, найти его значение по единичной тригонометрической окружности или по таблице значений углов (см. раздел Формулы сложения и вычитания углов этой статьи).
4. Если угол не табличный, оставить запись через аркфункции.
5. Для табличных углов: вычислить значение выражений. 

Рассмотрим решение таких уравнений на примерах.

Пример 1: cos x = 0,9.

Заметим, что 0,9 – не табличное значение, а значит, нам нужно решить уравнение через аркфункции. Воспользуемся формулами и найдем:

\(x=\pm arccos(0,9)+2\pi k, k\in Z\).

Уравнение решено! 

Важно правильно записывать период. Это связано с тем, что значения тригонометрических функций повторяются на каждом витке окружности, а при решении уравнений нам обязательно учесть все корни. Подробнее про правильную  запись периода мы рассказывали в статье «Тригонометрическая окружность. Часть 2». 

Пример 2: sin x=0.

Здесь нам нужно на секундочку отвлечься от решения. 

Какие аркфункции можно «не решать»? Существует несколько частных случаев, которые решаются вне основных формул аркфункций. Их можно просто запомнить и применять при решении сразу: это случаи, когда угол равен нулю, единице или минус единице.

Рассмотрим, как решать аркфункции в этом случае. Снова воспользуемся таблицей. 

На самом деле, эти случаи можно решить и через обычные формулы для аркфункций, однако в итоге мы придем к этим же значениям. 

Проверим на нашем примере sin x=0. Запишем формулу решения уравнения для синуса. Получаем совокупность:

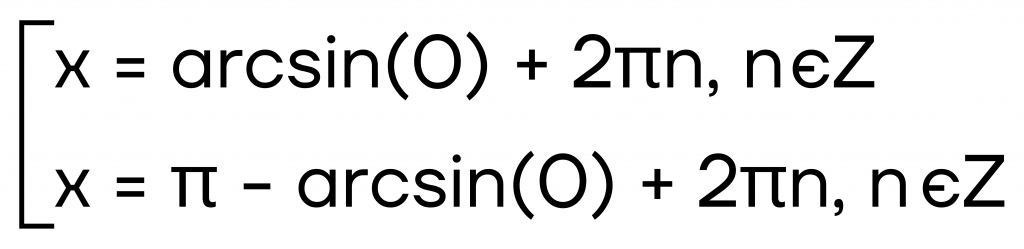
Подставим необходимые данные из таблицы значений углов: 

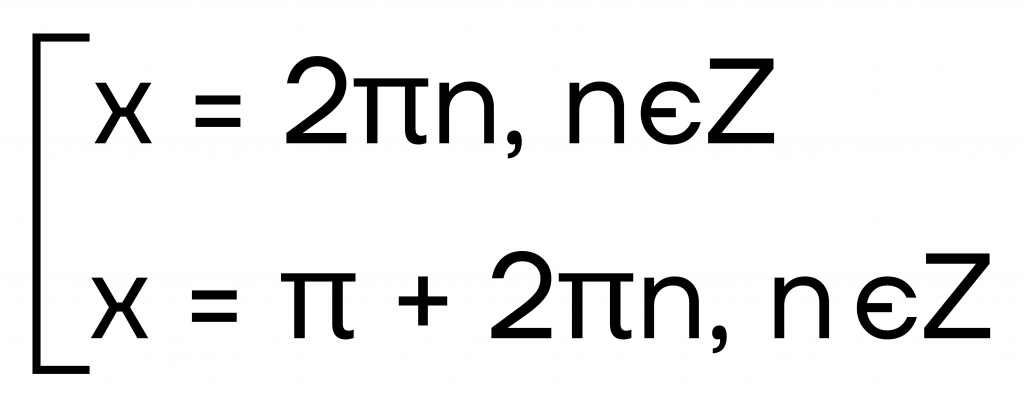
Заметим, что эти два корня лежат через полкруга на окружности. А значит, запись можно упростить до \(x=\pi n, n\in Z\).

Теперь рассмотрим пример простейшего тригонометрического уравнения с табличными значениями угла.

Пример 3: \(sin x =\frac{1}{2}\).

Записываем решение уравнения через аркфункцию:

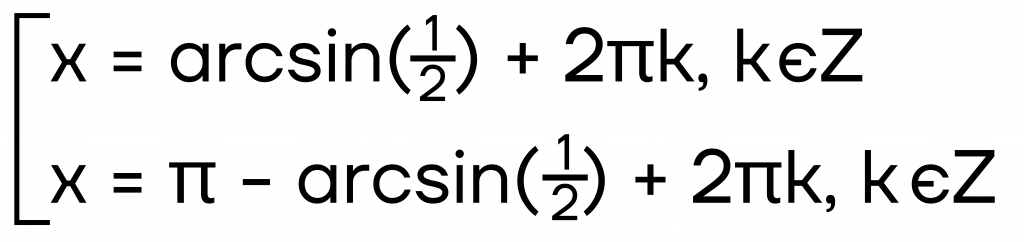
Далее нам нужно вместо аркфункций подставить табличное значение. Находим, при каком угле синус будет равен 12. Это угол 6. 

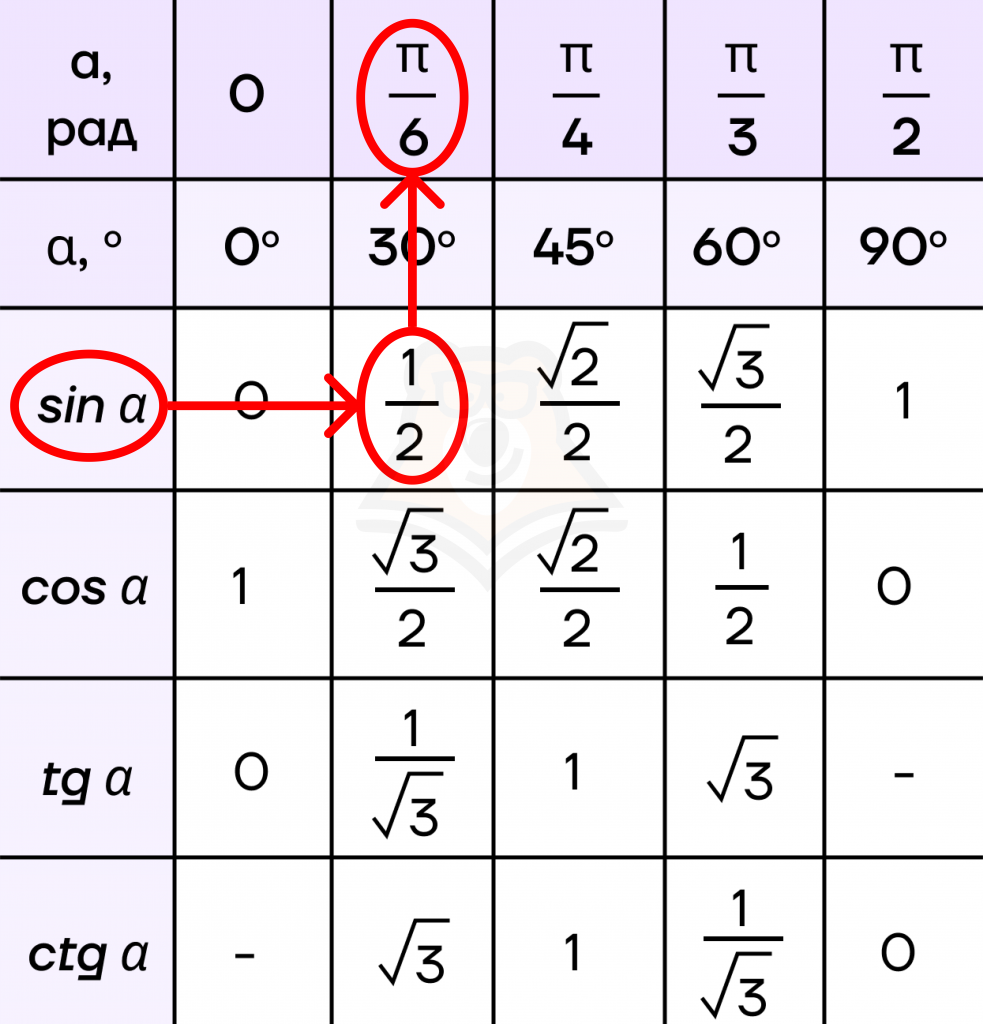
Получаем совокупность:

Осталось посчитать второе уравнение в совокупности:

\(x=\pi-\frac{\pi}{6}+2\pi k, k\in Z\)
\(x=\frac{6\pi-\pi}{6}+2\pi k, k\in Z\)
\(x=\frac{5\pi}{6}+2\pi k, k\in Z\)

Итак, мы получили ответ:

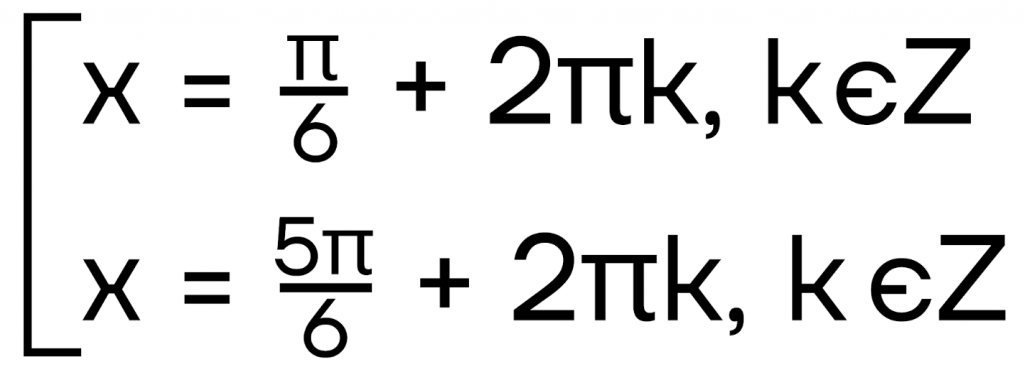
Решению уравнений, в частности, тригонометрических посвящено целое задание на экзамене. Речь про №12 ЕГЭ по профильной математике. 

а) Решите уравнение \(sin(2x)-cos(\frac{10x}{7})*cos(\frac{3x}{7})=sin(\frac{10x}{7})*sin(\frac{3x}{7})\).
б) Найдите корни этого уравнения, принадлежащие отрезку \([\frac{\pi}{2};2\pi]\).

Решение:
а) Перенесем все слагаемые в одну сторону:
\(sin(2x)-cos(\frac{10x}{7})*cos(\frac{3x}{7})-sin(\frac{10x}{7})*sin(\frac{3x}{7})=0\)
\(sin(2x)-(cos(\frac{10x}{7})*cos(\frac{3x}{7})+sin(\frac{10x}{7})*sin(\frac{3x}{7}))=0\)

Заметим, что в скобках у нас получилась формула \(cos(\alpha \pm \beta)=cos \alpha*cos\beta \mp sin \alpha*sin\beta\). «Свернем» ее:

\(sin(2x)-cos(\frac{10x}{7}-\frac{3x}{7})=0\)
\(sin(2x)-cos x=0\)

Раскроем синус двойного угла:

\(2sin x*cos x-cos x=0\)

У нас появился общий множитель – косинус. Вынесем его за скобку:

\(cos x(2sin x-1)=0\)

Если произведение множителей равно 0, то каждый множитель равен 0. Составим совокупность:

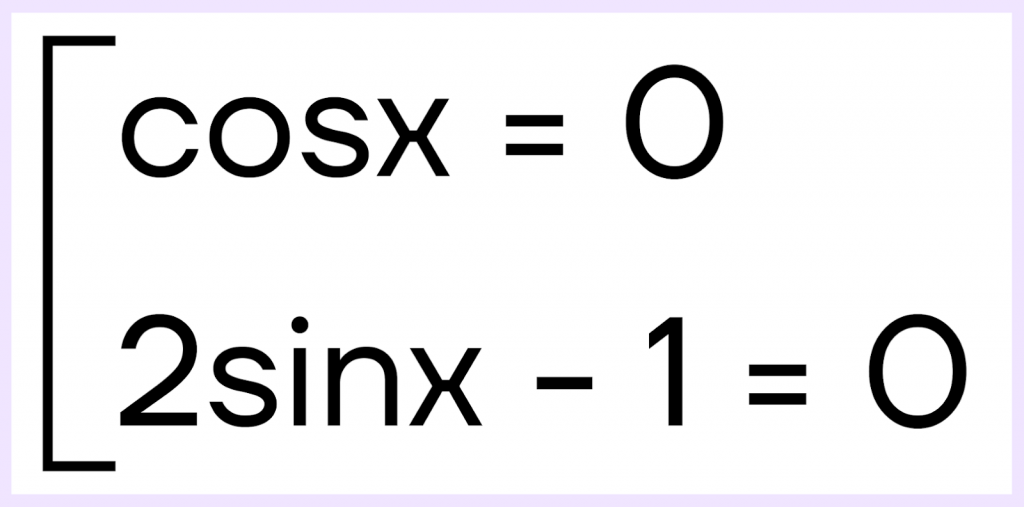
Решим первое уравнение совокупности:
\(cos x=0\)
\(x=\frac{\pi}{2}+\pi k, k \in Z\)

Решим второе уравнение совокупности:
\(2sin x-1=0\)
\(2sin x=1\)
\(sin x=\frac{1}{2}\)

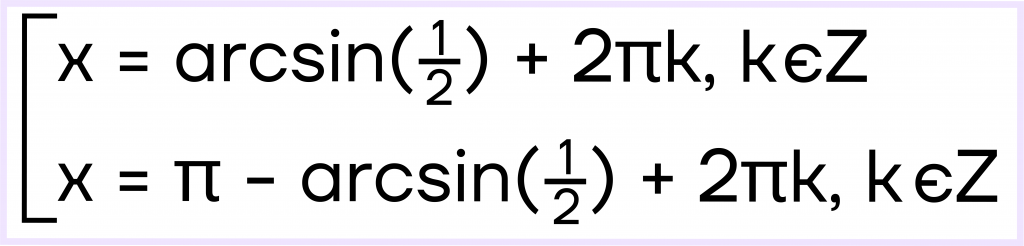
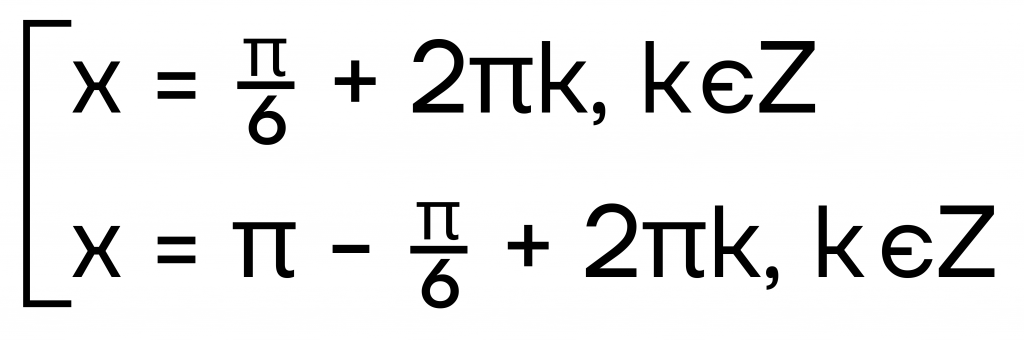
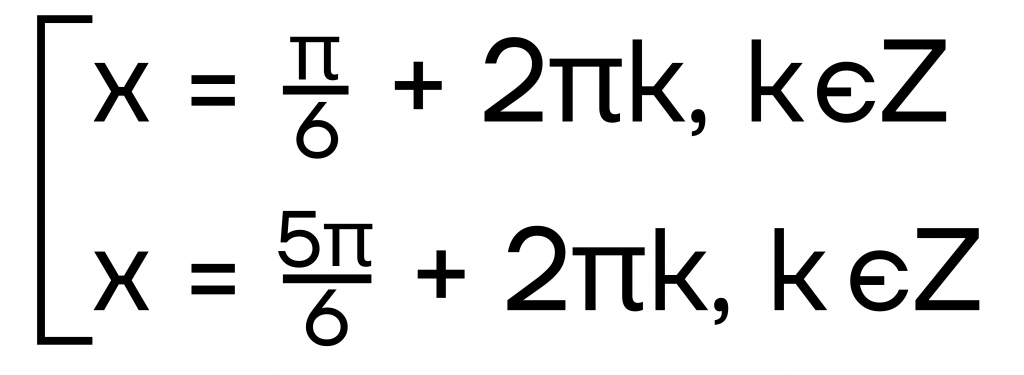
Запишем все ответы к пункту в одной совокупности:

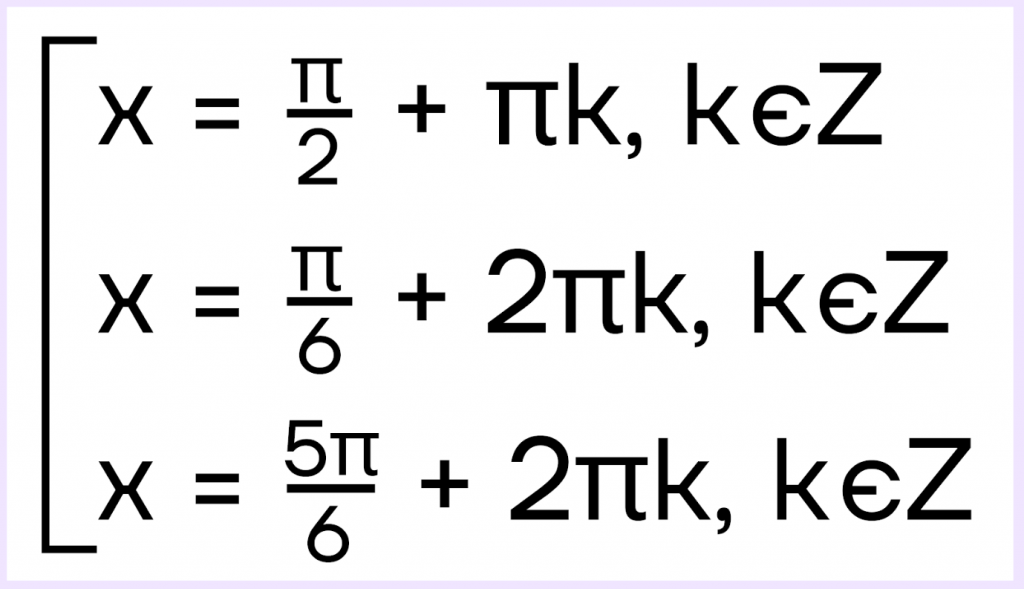
б) Нам необходимо найти все корни, которые лежат в промежутке \([\frac{\pi}{2};2\pi]\). Воспользуемся отбором по окружности. Подробнее про этот вид отбора можно узнать в статье «Тригонометрическая окружность. Часть 2».

Полученные корни отметим черными точками на окружности:

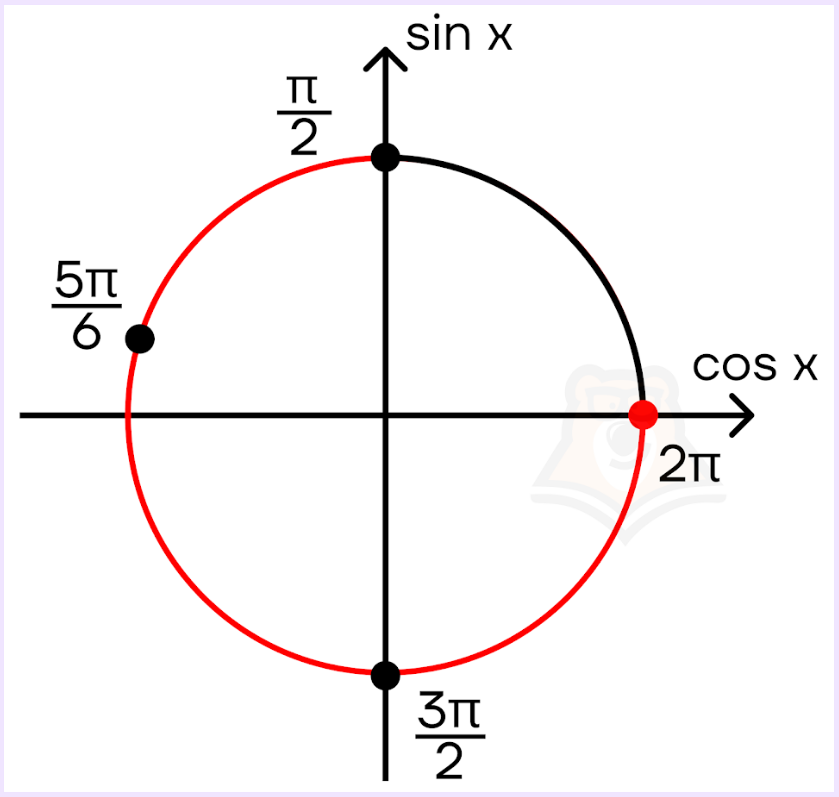
Получаем ответ: \(\frac{\pi}{2}, \frac{5\pi}{6}, \frac{3\pi}{2}\).
Ответ: а) \({\frac{\pi}{2}+\pi k, \frac{\pi}{6}+2\pi k, \frac{5\pi}{6}+2\pi k: k\in Z}\); б) \(\frac{\pi}{2}, \frac{5\pi}{6}, \frac{3\pi}{2}\).

Итак, мы научились работать с тригонометрическими уравнениями и формулами, а значит, нам почти по плечу решение сложных уравнений и неравенств. Остался лишь еще один шаг в изучении тригонометрии, прежде чем мы сможем приступить к их разбору. Этот шаг – «Формулы приведения», о которых вы можете прочесть в нашей следующей статье. 

Термины

Гипотенуза — это сторона прямоугольного треугольника, лежащая против прямого угла.

Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1. Подробно мы разбираем ее в статье «Тригонометрическая окружность. Часть 1».

Катет — это одна из двух сторон, образующих прямой угол в прямоугольном треугольнике.

Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.

Радиан — это способ измерения угла с помощью числа пи (). Чтобы считать углы в радианах, нужно помнить, что \(\pi=180°\), тогда \(90°=\frac{\pi}{2}, 360°=2\pi\) и т.д. 

Фактчек

• Чтобы решать сложные тригонометрические уравнения и неравенства, необходимо уметь преобразовывать выражения. Для этого нужно правильно пользоваться формулами. 
• Условно, формулы можно разделить на несколько групп: основные формулы тригонометрии, формулы отрицательных углов, формулы двойных углов, формулы сложения и вычитания углов, формулы понижения степени, формулы для суммы, разности и произведения синусов и косинусов.
• К основным тригонометрическим формулам в первую очередь относится основное тригонометрическое тождество: \(sin^2x + cos^2x = 1\). Оно и еще несколько других формул раскрывают связь между функциями. 
• Важно запомнить, что формулы работают в обе стороны: их можно читать справа налево и слева направо. Более того, многие формулы можно выводить друг из друга, что значительно упрощает их заучивание.
• Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции. 
• Для решения тригонометрических уравнений необходимо применять аркфункции, то есть функции, обратные тригонометрическим. С помощью аркфункций мы находим угол через значение тригонометрической функции. 

Проверь себя

Задание 1.
Как выглядит основное тригонометрическое тождество?

1. \(sin x+cos x =1\)
2. \(sin^2x+cos^2x=1\)
3. \(cos(2x)=1-2sin^2x\)
4. \(sin x=\frac{1}{cos x}\)

Задание 2.
Какая тригонометрическая функция является четной?

1. котангенс
2. тангенс
3. синус
4. косинус

Задание 3.
Чему равен \(cos(2x)\)?

1. \(2sin x*cos x\)
2. \(sin^2x-cos^2x\)
3. \(2cos^2x-1\)
4. \(1-sin^2x\)

Задание 4.
Выберите правильное решение уравнения \(tg x=a\).

1. \(arctg x+\pi k, k \in Z\)
2. \(\pm arctg x+\pi k, k \in Z\)
3. \(arctg x+2\pi k, k \in Z\)
4. \(arctg x\)

Задание 5.
Решите уравнение \(cos 2x =1\).

1. \(x=-\pi+\pi k, k \in Z\)
2. \(x=2\pi k, k \in Z\)
3. \(x=\pi k, k \in Z\)
4. \(x=-\pi+2\pi k, k \in Z\)

Ответы: 1. — 2; 2. — 4; 3. — 3; 4. — 1; 5. — 3.