Логарифмические уравнения и неравенства
На этой странице вы узнаете
- Что значит расти по экспоненте?
- Как быстро избавиться от логарифмов с одинаковым основанием?
- Как не попасть в аварию в погоне за результатом?
Математики иногда скучают. Иначе как объяснить то, что для понимания этой пугающей многих учеников темы, нужно запомнить единственный факт: «Степень числа и логарифм — разная запись одного и того же математического события». В этой статье мы ближе познакомимся с логарифмами и увидим, что ничего экстремально сложного в них на самом деле нет.
Понятие логарифма
Математика очень интересная наука, действия в которой можно повернуть в обе стороны. Например, возведение в степень и извлечение корня — одно и то же действие, но совершаемое «в разные направления». Это как шарик-маятник, который качается туда-сюда.
Однако помимо извлечения корня степень числа имеет еще одно противодействие: это логарифм. Разберемся, чем же они отличаются.
Итак, извлекая корень, мы находим первоначальное число, которое возвели в степень. Например, если мы вычислим, чему равно \(4^3\), то получим 64. А если извлечем \(\sqrt[3]{64}\), то получим число, которое возводили в степень. Иными словами, извлекая корень, мы находим основание степени.
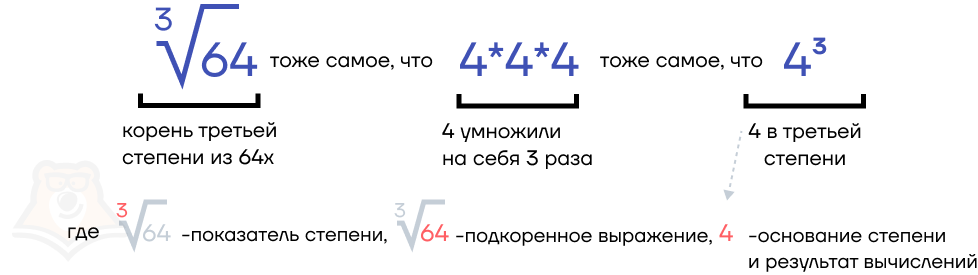
Но что, если мы знаем основание степени и число, полученное при возведении, но при этом не знаем показатель степени? Можем ли мы как-нибудь найти, в какую именно степень возвели то или иное число?
Ответ: да! Для этого и существуют логарифмы. Логарифм отвечает на вопрос: «В какую степень возвести число a, чтобы получилось число b?»
Например, мы возвели двойку в неизвестную степень и получили 4:
\(2^x=4\)
Зададим вопрос: в какую степень нужно возвести 2, чтобы получился такой результат? Ответ приходит сразу — это 2:
\(2^2=4\)
Эту же операцию можно записать значительно короче, если использовать логарифм. Запись будет выглядеть так:
\(log_24=2\)
Вот и всё!
Если понятие «степень» все еще звучит устрашающе, мы написали для вас статью «Действия с натуральными числами».
Изучить весь материал для ЕГЭ и ОГЭ и разобраться с темами любой сложности вы можете на курсах в онлайн-школе «Умскул»! Запишитесь на бесплатную консультацию и узнайте подробности про вебинары, платформу с домашками и пробниками и скидки:
А теперь внедрим в нашу статью немного научности. Что такое логарифм во вселенной математики?
Логарифм — это число, в которое нужно возвести основание a, чтобы получить число b.
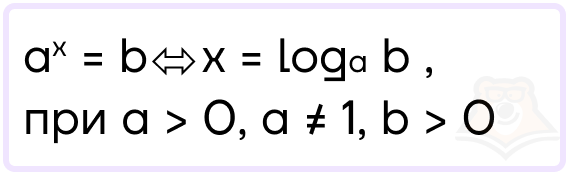
У каждого элемента любой математической функции есть название. Как называются элементы логарифма?
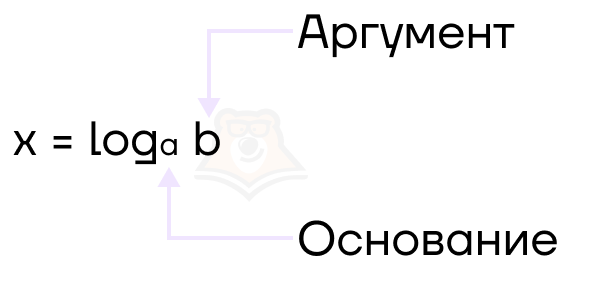
Снова вспомним корни. Корень степени 2 мы записываем без показателя степени, например, \(\sqrt{25}\). Это связано с его распространенностью и «особенностью». Так и в логарифмах существуют свои «краткие записи», применяемые для «особенных» логарифмов. Такими логарифмами являются десятичный и натуральный. Рассмотрим их чуть подробнее.

Десятичный логарифм — это логарифм числа по основанию 10.
Например, нам нужно узнать, в какую степень нужно возвести 10, чтобы получить 100. То есть мы находим \(log_{10}100=2\). Аналогично \(log_{10}1000=3\) или \(log_{10}100000=5\).
Для сокращения записи мы не пишем основание, а само название логарифма немного меняем. Выглядит запись десятичного логарифма следующим образом:
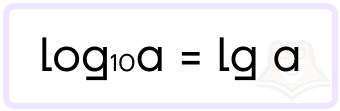
Запись такого логарифма нужно просто запомнить. Но не будет и ошибкой, если записать обычным способом.
Что же с натуральным логарифмом? Аналогично десятичному, в его основании стоит особое число — экспонента.
Экспонента — это такая математическая константа, постоянная (как, например, ускорение свободного падения в физике), которая примерно равна 2,72.
Натуральный логарифм — это логарифм по основанию е (e ≈ 2,72).
Такой логарифм тоже имеет «свою» запись, которую нужно запомнить:
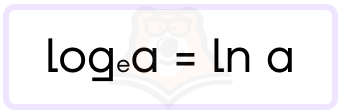
У натурального логарифма в основании стоит число e, которое называется числом Эйлера. На самом деле, это иррациональное число, которое имеет бесконечное количество знаков после запятой, но мы ограничиваемся краткой записью 2,72. Число e играет важную роль во многих разделах математики.

| Что значит расти по экспоненте? Экспонента — это показательная функция \(y=e^x\), где \(e\) — число Эйлера, равное примерно 2,72. Особенность такой функции в том, что число Эйлера многократно умножается на само себя, а значит, неравномерно увеличивается. Примером такого увеличения может быть падение камушка: чем дольше он летит, тем выше его скорость. Другим примером может быть сложный процент, когда сумма вклада или долга увеличивается каждый год на определенное число процентов (про сложные проценты можно узнать в статье «Финансовые задачи. Проценты»). Такой рост называют ростом по экспоненте. На самом деле, экспонента имеет множество интересных свойств, например, ее производная равна ей самой. График экспоненты будет выглядеть как непрерывно и «неравномерно» возрастающая кривая. |
Нельзя обходить такую важную тему, как логарифмы, стороной. Они часто встречаются в заданиях 5, 12 и 14 профильного ЕГЭ по математике или в №17 ЕГЭ по базовой математике. При умелом использовании их свойств можно упростить выражение или заменить запись логарифма на более удобную.
Рассмотрим пример задания из номера 5 первой части ЕГЭ по профильной математике.
Найдите корень уравнения \(log_5(x+121)=4\).
Решение. Немного изменим запись: если возвести 5 в степень 4, то мы получим \(x+121\). Значит, мы можем составить и решить уравнение:
\(x+121=5^4\)
\(x+121=625\)
\(x=504\)
Ответ: 504
Может возникнуть вопрос: неужели при решении каждого логарифмического уравнения или неравенства придется прибегать к «переформулировке»? На самом деле, нет, ведь для упрощения решений существуют свои правила, а главное, свойства логарифмов. Рассмотрим их чуть подробнее.
Основное логарифмическое тождество
Итак, какими свойствами обладает логарифм? Начнем с одного из самых важных, а именно — основного логарифмического тождества.
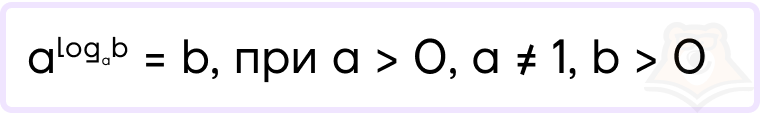
Возможно, вас смутило, что логарифм стоит в степени числа. На самом деле, логарифм — это тоже какое-то число, просто в другой записи. Так, \(3^2\) и \(3^{log_24}=32\) — одно и то же число, но в разных записях.
Разберемся чуть подробнее, как работает тождество. Путь \(a=2, b=4\). Тогда получаем запись:
\(2^{log_24}=4\)
Решим отдельно левую часть:
\(2^{log_24}=2^2=4\)
Получаем, что тождество верно. Но почему это так работает?
Заметим, что при вычислении логарифма мы получаем значение степени x, в которую должны возвести основание а, чтобы получить аргумент b.
\(log_ab=x\), тогда \(a^x=b\)
После этого мы снова возводим то же основание а в ту же степень, и снова получаем аргумент b. То есть делаем одно и то же действие дважды.
\(a^{log_ab}=a^x=b\)
Следовательно, это тождество позволяет сократить вычисление на несколько шагов. Важно: оно будет работать только в случае, когда основания степени и логарифма будут совпадать. Тогда совпадут и аргумент с ответом.
Рассмотрим, почему это не работает при несовпадающих основаниях. Для этого найдем значение выражения \(3^{log_24}\). Итак, \(log_24=2\), значит, мы получаем выражение \(3^2=9\). Очевидно, что \(9\neq4\), соответственно, применить основное тождество логарифмов мы здесь не можем (поскольку \(3\neq2\)).
Данное тождество часто используется для преобразований.
Свойства логарифмов
Логарифмы, как и числа, можно складывать, умножать и делать множество действий с ними. Как не запутаться в них, не производить лишних вычислений и не ошибиться? Для этого нужно хорошо знать все свойства, которые представлены в таблице ниже. Каждое из рассмотренных в таблице свойств можно использовать для преобразований.

Рассмотрим каждое свойство чуть подробнее.
Свойство 1. \(log_ab^m=m*log_ab\).
Попробуем найти значение выражения \(log_28^2\) без применения свойства. Тогда возведем аргумент в степень и получим:
\(log_28^2=log_264\)
Воспользовавшись определение логарифма, заметим, что \(log_264=6\).
Но что делать, если числа окажутся большими, или, более того, у логарифма не будет точного значения — примером такого логарифма может служить \(log_57\). Да и вычисление в несколько действий с большими числами может занять много времени.
Именно поэтому мы применяем это свойство!
\(log_28^2=2*log_28=2*3=6\)
Свойство 2. \(log_{a^n}b=\frac{1}{n}*log_ab\)
Рассмотрим на примере логарифма \(log_{2^2}4\). Посчитаем без свойства:
\(log_{2^2}4=log_44=1\)
Заметим, что:
- в первом свойстве мы увеличивали аргумент логарифма (то есть конечный результат, который получается при возведении числа в степень);
- в этот раз мы увеличиваем уже число, которое возводим в степень.
Сравните:
\(2^2=4\) или \(3^2=9\)
Следовательно, когда мы будем производить «обратные» действия, то есть считать логарифм, то при увеличении основания степени (и сохранении результата возведения в степень), у нас должна уменьшиться сама степень, в которую мы возводим.
Например:
\(2^4=16\) и \(4^2=16\)
Именно поэтому у нас появляется дробь: она уменьшает степень во столько раз, во сколько мы увеличили первоначальное число:
\(log_{2^2}4=\frac{1}{2}log_24=\frac{1}{2}*2=1\)
Свойство 3. \(log_{a^n}b^m=\frac{m}{n}*log_ab\)
Это свойство вытекает из двух предыдущих, просто их соединили вместе. Иначе пришлось бы отдельно выносить степень из аргумента и отдельно из основания логарифма. Сравните:
\(log_{2^3}5^7=7*log_{2^3}5=7*\frac{1}{3}*log_25=\frac{7}{3}log_25\)
или
\(log_{2^3}5^7=\frac{7}{3}log_25\)
Свойство 4. \(log_ab+log_ac=log_a(b*c)\)
Найдем значение выражения \(log_24+log_28\):
\(log_24+log_28=2+3=5\)
Но в случае, когда числа не будут так легко считаться (или вовсе не будут считаться), на помощь придет это свойство:
\(log_512,5+log_52=log_525=2\)
Свойство 5. \(log_ab-log_ac=log_a\frac{b}{c}\)
Аналогично с предыдущим свойством это нужно для упрощения вычислений.
Например:
\(log_318-log_32=log_3\frac{18}{2}=log_39=2\)
Свойства 6 и 7. \(log_aa=1\) и \(log_a1=0\)
Эти свойства напрямую связаны с возведением числа в степень. Достаточно лишь ответить на два вопроса:
- В какую степень нужно возвести число, чтобы получилось такое же число?
- В какую степень нужно возвести любое число, чтобы получить 1?
Ответы на эти вопросы будут 1 и 0. Отсюда и эти свойства:
- Число в степени 1 будет равно само себе: \(log_aa=1\).
- Число в степени 0 будет равно 1: \(log_a1=0\).
Свойство 8. \(log_ab=\frac{log_cb}{log_ca}\)
Это свойство используется в случаях, когда нам нужно представить логарифм с любым другим основанием.
Например:
\(log_25=\frac{log_35}{log_25}\)
Это свойство может пригодиться в решении уравнений и неравенств для упрощения выражений.
Свойство 9. \(log_ab=\frac{1}{log_ba}\)
Что делать, если нам нужно представить логарифм с определенным основанием, которое равно аргументу этого логарифма? Все просто: мы можем поменять основание и аргумент местами, если воспользуемся свойством \(log_ab=\frac{1}{log_ba}\).
Например:
\(log_{27}3=\frac{1}{log_327}=\frac{1}{3}\)
Заметим, что это же выражение можно было решить немного по-другому:
\(log_{27}3=log_{3^3}3=\frac{1}{3}*log_33=\frac{1}{3}\).
В этом случае мы воспользовались свойствами 2 и 6.
Свойство 10. \(a^{log_cb}=b^{log_ca}\)
Еще одно свойство, которое позволяет изменить аргумент логарифма, и при этом не менять значение выражения.
Рассмотрим на примере \(2^{log_24}\):
\(2^{log_24}=2^2=4\)
\(2^{log_24}=4^{log_22}=4^1=4\)
Для более простого запоминания свойств логарифмов предлагаем вам воспользоваться нашими забавными ассоциациями.

Теперь, когда мы знаем свойства логарифмов, мы можем перейти к более сложным преобразованиям — к решениям уравнений и неравенств.
Простейшие логарифмические уравнения
В других статьях мы уже рассматривали разные виды уравнений: линейные, квадратные, показательные и т.п. Настало время узнать про логарифмические уравнения.
Логарифмическое уравнение — это уравнение, в котором неизвестная стоит в аргументе или основании логарифмов.
Иными словами, если в уравнении мы видим логарифм с неизвестной — это логарифмическое уравнение.
Например, \(log_2x=4\) — логарифмическое уравнение.
А вот \(log_25+x=x^2\) не будет логарифмическим уравнением, поскольку неизвестная не стоит ни в аргументе, ни в основании логарифма.
Как решать логарифмические уравнения?
Логарифмическое уравнение нужно привести к такому виду:
\(log_af(x)=log_ag(x)\).
При решении таких уравнений нужно обязательно учитывать, что по определению аргумент логарифма всегда должен быть больше нуля, а основание больше нуля и не должно равняться единице. Эти ограничения называются областью допустимых значений или ОДЗ логарифма.
Область допустимых значений — это те значения, которые может принимать переменная x (или другая буква латинского алфавита) в выражении.
\(log_ab\)
ОДЗ логарифма: a > 0, a ≠ 0, b> 0.
| Как быстро избавиться от логарифмов с одинаковым основанием? Это можно сделать, приравняв аргументы. Почему мы можем так сделать? Представим, что мы возводим некоторое число в степень, это число будет стоять в основании логарифма. Если два логарифма равны, то и степени, в которые мы возвели число, равны. Следовательно, будет равен и результат возведения в степень, то есть аргумент логарифма! \(a^x=b\) \(log_ab=x\) Тогда пусть \(log_ab=log_ac\) \(x=log_ac\) \(a^x=c => b=c\) При этом проверить ОДЗ можно только у одного из логарифмов, поскольку если один из них положителен, а второй равен первому, то и второй будет положительным. Например, если b=2, то из равенства b=c получаем c=b=2. В логарифмических уравнениях встречаются более сложные выражения, которые в дальнейшем мы будем выражать в виде функций — например, f(x) или g(x). Например: |
Алгоритм решения логарифмического уравнения:
1. Написать ОДЗ.
2. Упростить выражения слева и справа от знака равенства, используя свойства логарифмов, если это возможно.
3. Если основания логарифмов одинаковые, избавиться от логарифмов. В противном случае — используя свойства логарифмов, привести к одинаковому основанию, а уже потом совершить эти действия.
4. Решить уравнение и сравнить с ОДЗ, выписать в ответ корни.
Рассмотрим на примере:
\(log_2(5x-4)=log_2(x+8)\)
- В первую очередь найдем ОДЗ. Для этого вспомним, что аргумент логарифма всегда строго положителен:
\(5x-4>0\) и \(x+8>0\)
Найдем возможные значения х:
\(5x>4\) и \(x>-8\)
\(x>\frac{4}{5}\) и \(x>-8\)
Нанесем найденные промежутки на числовую прямую и определим, какие значения может принимать х. Для этого нам нужно будет найти промежутки, которые удовлетворяют обоим неравенствам:
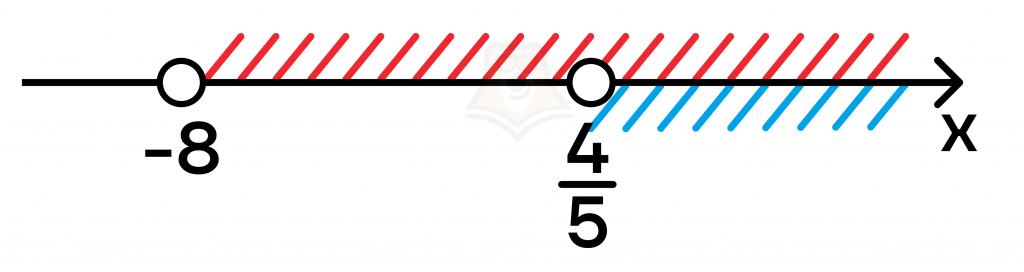
Теперь мы можем определить ОДЗ: \(x \in(\frac{4}{5};+{\infty})\)
- Если в обеих частях уравнения находится логарифм по одинаковому основанию, то можно «скинуть» логарифмы и записать равенство аргументов. Поскольку и у первого, и у второго логарифма основания равны 2, то мы можем приравнять их аргументы:
\(5x-4=x+8\)
- Решим полученное уравнение:
\(5x-x=8+4\)
\(4x=12\)
\(x=3\)
- Подставим в ОДЗ и проверим, подходит ли корень. Поскольку \(3>\frac{4}{5}\), то корень нам подходит.
Ответ: 3.
А теперь немного усложним задачу. Допустим, переменная будет стоять и в основании, и в аргументе логарифма.
Рассмотрим еще одно уравнение:
\(log_2(x-4)=log_{4x}4+log_{4x}x\)
- Найдем ОДЗ. Аргумент логарифма всегда строго больше 0, а основание больше 0 и не равно 1. Тогда получаем следующие неравенства для аргументов логарифмов:
\(x>0\)
\(x-4>0\)
И для оснований логарифмов:
\(4x>0\)
\(4x\neq1\)
Решим неравенства:
\(x>0\)
\(x>4\)
\(x>0\)
\(x\neq\frac{1}{4}\)
Теперь отметим все ограничения на числовой прямой и найдем, чему равна ОДЗ:
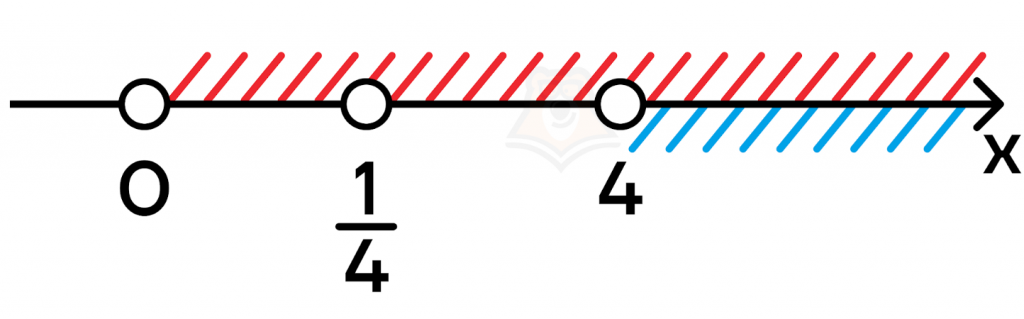
Поскольку нам нужно, чтобы ограничение удовлетворяло всем полученным неравенствам и уравнениям, то \(x\in(4;+{\infty})\).
- Теперь перейдем к решению самого уравнения. По свойствам логарифма (свойства 4 и 6) преобразуем правую часть уравнения:
\(log_2(x-4)=log_{4x}4x\)
\(log_2(x-4)=1\)
- Чтобы отбросить логарифмы и перейти к уравнению с аргументами, необходимо, чтобы их основания были равны. Поскольку основание левого логарифма равно 2, то представим правую часть в виде логарифма с таким же основанием 2:
\(log_2(x-4)=log_22\)
- Отбросим логарифмы и перейдем к уравнению с ними:
\(x-4=2\)
\(x=6\)
Поскольку \(6>4\), то корень принадлежит ОДЗ, а значит, его можно записать в ответ.
Ответ: 6.
Мы разобрали уравнения с логарифмами. Остался вопрос: а как решать неравенства с ними?
Простейшие логарифмические неравенства
Логарифмическое неравенство — это неравенство, в котором переменная стоит в аргументе или основании логарифма.
Для решения логарифмических неравенств тоже можно избавляться от логарифмов.
Делается это уже известным способом — если основания равны, то можно перейти к неравенству с аргументами. При этом нужно обращать внимание на основание логарифма.
Важно!
Если \(0<a<1\), тогда знак неравенства меняется на противоположный.
Если \(a>1\), тогда знак неравенства не меняется.
Разберемся, почему это так работает. Рассмотрим два примера:
\(log_24=2\)
\(log_{\frac{1}{2}}4=log_{2^{-1}}4=-1*log_24=-2\)
Как можно увидеть, если основание логарифма меньше 1, то результат вычислений отрицательный (в случае, если аргумент больше 1). Это связано с тем, что при возведении дробного числа в степень, большую 1, это число только уменьшается, например:
\((\frac{1}{3})^2=\frac{1}{9}\)
Но если мы возведем такое число в отрицательную степень, то получим больший результат:
\((\frac{1}{3})^{-2}=3^2=9\)
Именно поэтому ради избежания путаницы со знаками, при отбрасывании логарифмов с основанием \(0<a<1\) мы меняем знак на противоположный: тем самым мы сразу избавляемся от минуса.
Например:
\(log_{\frac{1}{3}}9>0\)
\(log_{3^{-1}}9>0\)
\(-log_39>0 |*(-1)\)
\(log_39<0\)
А теперь чуть подробнее рассмотрим, как действовать с логарифмическими неравенствами:

Алгоритм решения логарифмического неравенства:
1. Написать ОДЗ.
2. Упростить выражения слева и справа от знака неравенства, используя свойства логарифмов, если это возможно.
3. Если основания логарифмов одинаковые, избавиться от логарифмов по схеме выше. В противном случае — используя свойства логарифмов, привести к одинаковому основанию, а уже потом совершить эти действия.
4. Решить неравенство, пересечь с ОДЗ, записать ответ.
| Как не попасть в аварию в погоне за результатом? Обратим ваше внимание еще раз. Решая как логарифмические уравнения, так и неравенства, можно разогнаться слишком сильно и вылететь с дороги… Чтобы такого не случилось, есть специальный ограничитель неправильных ответов — ОДЗ. Работая с логарифмами и избавляясь от них, всегда следите за показаниями ОДЗ, иначе в ответ попадут лишние корни. |
Логарифмические неравенства могут встретиться в номере 14 ЕГЭ по профильной математике. Рассмотрим один из их примеров:
Решите неравенство: \(log_3^2x-10log_3x\geq-21\)
Решение. Первым делом, найдем ОДЗ. Поскольку переменная стоит только в аргументе логарифма, то и ограничения вводим лишь на аргумент:
\(x>0\)
Перейдем к решению. Заметим, что \(log_3x\) — повторяющееся выражение, а значит, мы можем сделать замену.
Обратим внимание, что у первого логарифма степень стоит именно у логарифма, а не у аргумента.
Пусть \(log_3x=t\), тогда:
\(t^2-10t\geq-21\)
\(t^2-10t+21\geq0\)
Теперь слева у нас получилось квадратное неравенство. Для его решения найдем нули функции, приравняв левую часть к 0:
\(t^2-10t+21=0\)
Найдем корни уравнения с помощью дискриминанта:
\(D=b^2-4ac=10^2-4*1*21=100-84=16\)
\(t_1=\frac{-b+\sqrt{D}}{2a}=\frac{10+4}{2}=7\)
\(t_2=\frac{-b-\sqrt{D}}{2a}=\frac{10-4}{2}=3\)
Воспользуемся методом интервалов (подробнее об этом методе можно прочитать в одноименной статье). Отметим корни на числовой прямой, расставим знаки и найдем промежутки:
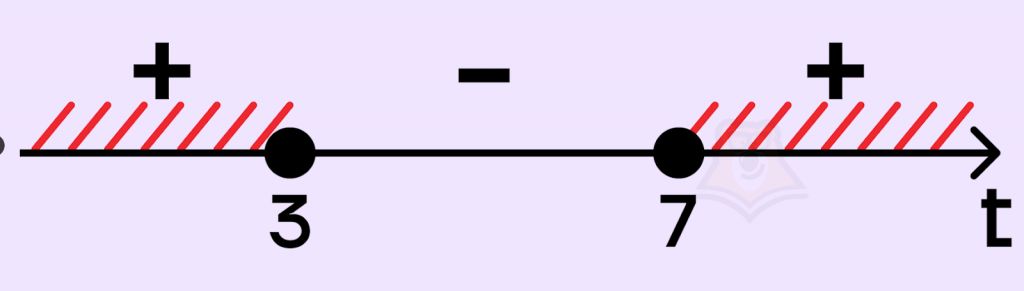
Получаем промежутки:

Сделаем обратную замену:
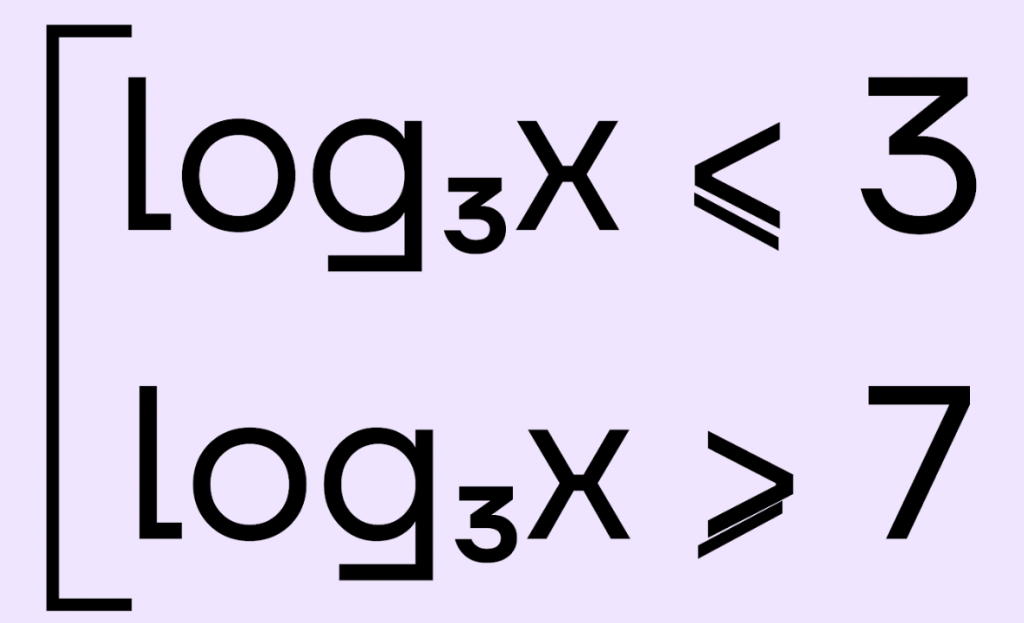
Представим правые части неравенства в виде логарифмов с основанием 3:
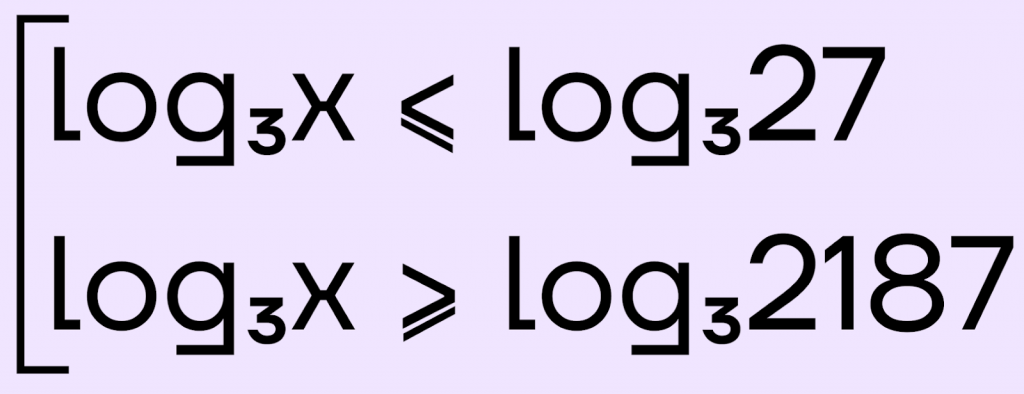
Теперь у нас справа и слева логарифмы с одинаковым основанием, соответственно, мы можем отбросить логарифмы и перейти к неравенствам с аргументами. Поскольку 3>1, то знаки неравенства менять не нужно:
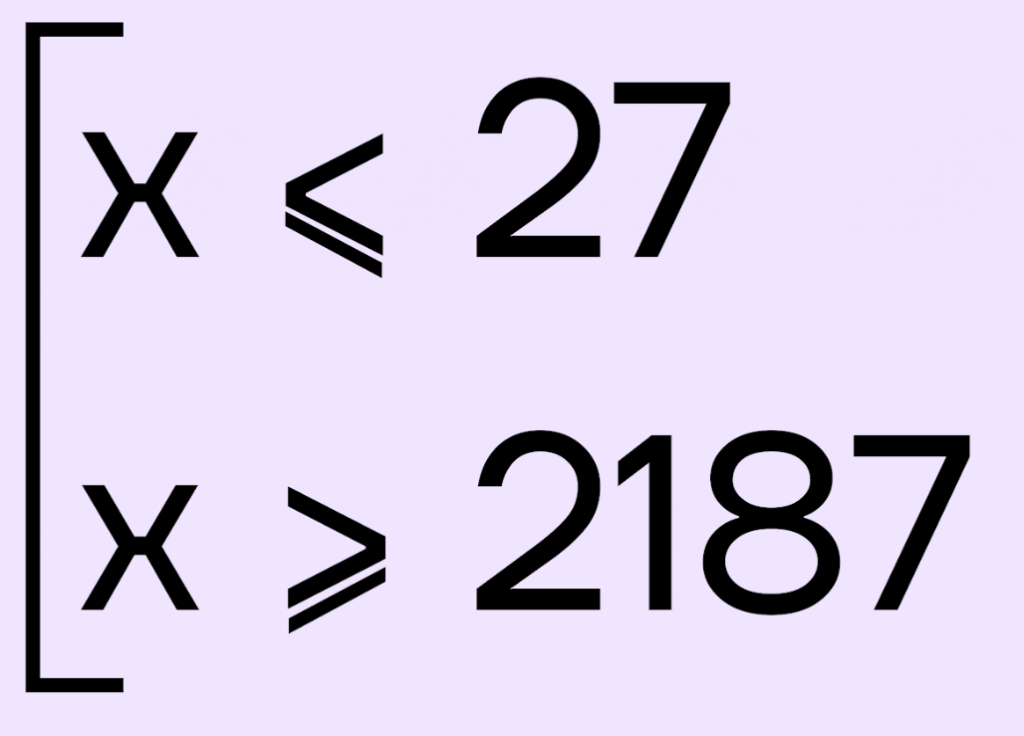
Отметим на числовой прямой полученные промежутки, а также нанесем ОДЗ:
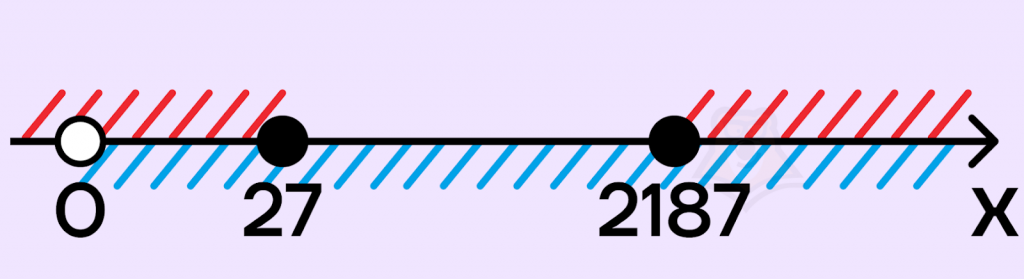
С учетом ОДЗ получаем промежутки: \((0;27]\bigcup[2187;+{\infty})\). Это и будет ответ.
Ответ: \((0;27]\bigcup[2187;+{\infty})\)
Теперь давайте рассмотрим решение неравенства с основанием, которое меньше 1.
\(log_{\frac{1}{5}}x^2\geq log_{\frac{1}{5}}x+2\)
Шаг 1. Напишем ОДЗ. Аргумент логарифма должен быть строго больше 0, поэтому получаем два неравенства:
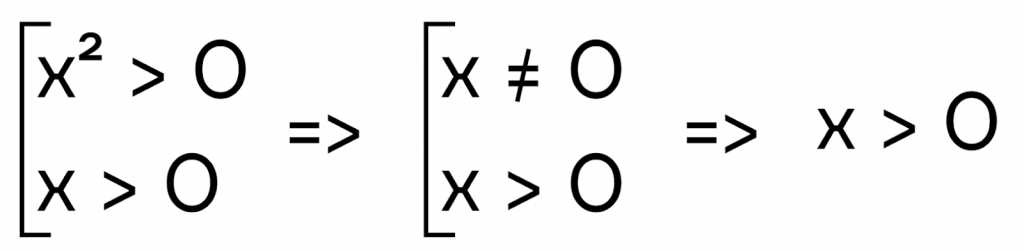
Шаг 2. Преобразуем правую часть. Для этого воспользуемся свойством логарифмов и вынесем степень аргумента перед логарифмом.
Поскольку степень положительная, то мы должны поставить аргумент в модуль, чтобы не потерять отрицательные значения:
\(2*log_{\frac{1}{5}}|x|\geq log_{\frac{1}{5}}x+2\)
Шаг 3. Раскроем модуль. По ОДЗ мы получили, что x>0, а значит, мы можем убрать модуль, поскольку под ним всегда будет стоять положительное число:
\(2*log_{\frac{1}{5}}x\geq log_{\frac{1}{5}}x+2\)
Шаг 4. Перенесем одно слагаемое влево и упростим:
\(2*log_{\frac{1}{5}}x-log_{\frac{1}{5}}x\geq 2\)
\(log_{\frac{1}{5}}x\geq 2\)
Представим правую часть в виде логарифма с основанием \(\frac{1}{5}\):
\(log_{\frac{1}{5}}x\geq log_{\frac{1}{5}}\frac{1}{25}\)
Шаг 5. Отбросим логарифмы. Поскольку \(\frac{1}{5}<1\), то знак неравенства меняется на противоположный:
\(x\geq 125\)
Шаг 6. Отметим полученный промежуток на числовой прямой и нанесем ОДЗ:
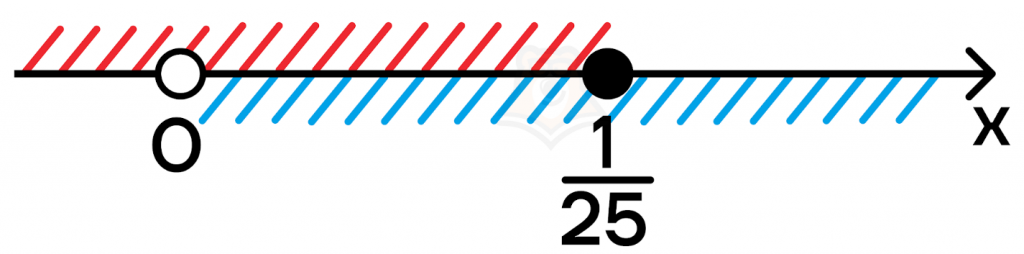
С учетом ОДЗ получаем промежуток \((0;\frac{1}{25}]\).
Ответ: \((0;\frac{1}{25}]\)
Мы рассмотрели логарифмы, уравнения и неравенства с ними. Научиться решать их не так сложно. Практикуйтесь побольше, тогда все обязательно получится. А чтобы продолжить освоение математической науки, рекомендуем вам познакомиться со статьей «Тригонометрическая окружность и графики функций».
Термины
Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле \(D=b^2-4⋅a⋅c\), где а, b и с берутся из уравнения. Подробнее о нем рассказано в статье «Линейные, квадратные и кубические уравнения».
Иррациональные числа — это числа, которые нельзя представить в виде обыкновенной дроби, то есть они не имеют точного значения.
Квадратное неравенство — это такое неравенство, которое можно привести к виду \(ax^2+bx+c ⋁ 0\), где a, b и с — любые числа (причем a ≠ 0), x — неизвестная переменная, а ⋁ — любой из знаков сравнения (> , < , ≤ , ≥ ). Решение таких неравенств мы обсуждаем в статье «Метод интервалов».
Модуль числа — это его абсолютная величина. При взятии модуля мы не учитываем знак этого числа — положительное оно или отрицательное. Модуль числа всегда неотрицателен и обозначается с помощью модульных скобок: |a| ≥ 0. Этому математическому понятию посвящена отдельная статья Учебника.
Нули функции — это значения аргумента, при которых функция равна нулю.
Показательная функция — это функция, у которой неизвестная находится в показателе степени. Например, \(y = 2^x\). Подробнее о ней мы рассказываем в одноименной статье.
Производная функции — это математическое понятие, показывающее скорость изменения функции в определенной точке. Подробнее про производные можно прочесть в статье «Исследование функции с помощью производной».
Фактчек
- Логарифм — это степень, в которую возводится основание логарифма, чтобы получить аргумент.

- Десятичный логарифм — это логарифм числа по основанию 10. Записывается так: lg a.
- Натуральный логарифм — это логарифм по основанию е (e ≈ 2,72). Записывается как ln a.
- Основное логарифмическое тождество: \(a^{log_ab}=b\), при \(a >0, a ≠ 1, b>0\).
- Существуют специальные свойства логарифмов, благодаря которым можно совершать преобразования.
- При решении уравнений и неравенств нельзя забывать про ОДЗ на аргумент и основание логарифма: основание больше нуля и не равно единице, аргумент больше нуля.
- В логарифмических неравенствах при переходе к неравенству аргументов логарифмов знак меняется на противоположный, если значение основания логарифма находится на промежутке от 0 до 1.
Проверь себя
Задание 1.
Решите уравнение \(log_3(x^2+4)=log_3(4x)\).
- 1 и -1
- 2 и -2
- 2
- -1
Задание 2.
Решите уравнение \(log_28=log_{16}(x)+2\).
- 16
- 12
- 1
- 8
Задание 3.
Решите уравнение \(log_2(2x^2)-5=log_2(x) +log_2(x-5)\).
- 0 и \(\frac{16}{3}\)
- 0 и \(\frac{32}{3}\)
- 32
- \(\frac{16}{3}\)
Задание 4.
Решите неравенство \(log_9(x+4)\geq log_9(2x)^2\).
- \([-\frac{4}{3};0)\bigcup(0;4]\)
- \((0;4]\)
- \([-\frac{4}{3};0)\)
- \([-\frac{4}{3};4]\)
Задание 5.
Решите неравенство \(log_{500}500\geq log_2(1+3x)\).
- \((0;\frac{1}{3}]\)
- \((-\frac{1}{3};\frac{1}{3}]\)
- \([-\frac{1}{3};\frac{1}{3}]\)
- (\(-\frac{1}{3};0\)
Ответы:1. — 3; 2. — 1; 3. — 4; 4. — 1; 5. — 2.


 к списку статей
к списку статей