Действия с натуральными числами

На этой странице вы узнаете:

• Как связаны числа и матрешка?
• Упрощаем: как разложить число на простые множители?
• Где могут пригодиться НОК и НОД?

До сих пор существуют племена людей, которые определяют количество только как «один» и «много». Однако мы с вами замахиваемся на понимание одной из самых «высоких» наук — математики. А она, в свою очередь, невозможна без чисел. Чтобы случайно не наступить на математические грабли, надо освоить действия с натуральными числами и разобраться с их свойствами. Предлагаем сделать это в статье.

Действия с натуральными числами

В науках почти всегда что-то можно разделить на группы. Например, в биологии мы сталкиваемся с группами, когда говорим про царства, классы и виды, в русском языке — с частями речи и так далее. Числа в математике также можно разделить на группы, и одна из них — натуральные числа. Но какие числа мы можем отнести к натуральным? Может, те, в которых нет ГМО, консервантов и красителей?

Натуральные числа – это числа, употребляемые при счете.

Натуральные числа начинаются  с 1 и образуются путем сложения некоторого количества единиц. Примерами натуральных чисел могут служить 1, 2, 3, 10, 1320, 130024, 1248640 и т.д. 

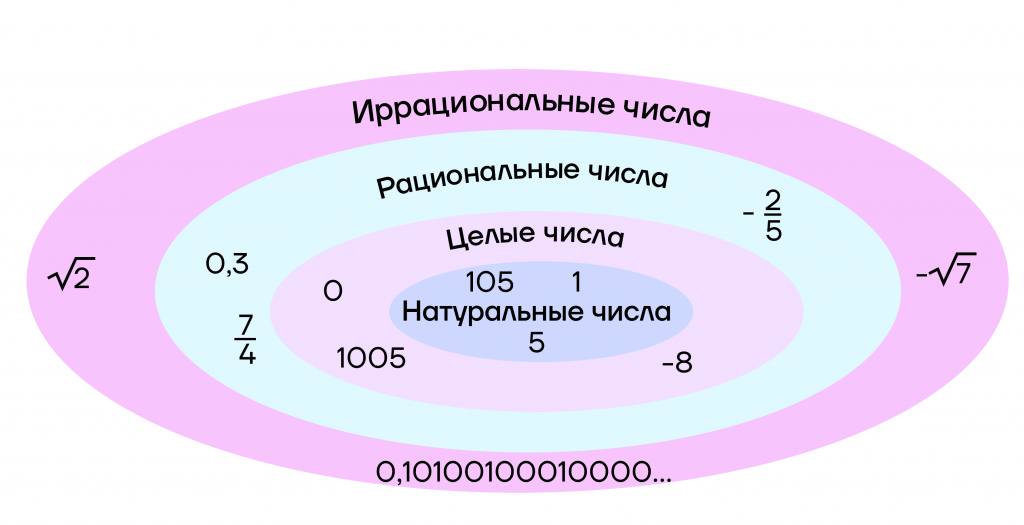
Как связаны числа и матрешка? Существует несколько множеств чисел, и помимо натуральных в них входят целые, рациональные и иррациональные. Чем же они отличаются друг от друга? Целые числа — это понятие включает в себя натуральные числа, а также противоположные натуральным (то есть со знаком минус) и ноль. Иными словами, во множество целых чисел помимо натуральных входят также отрицательные числа и 0. Так, число 5 будет и натуральным, и целым, а число (- 5) — только целым. Рациональные числа — это числа, которые можно представить в виде положительной или отрицательной обыкновенной дроби. То есть к множеству целых чисел добавляются еще и дроби. Например, \(\frac{1}{2}\) или — 8,16. Иррациональные числа — это числа, которые нельзя представить в виде обыкновенной дроби, следовательно, это числа, не имеющие точного значения. В множество иррациональных чисел также входят и рациональные числа. Например, √7=2,6457513… Таким образом, все числа можно представить в виде матрешки: в каждое множество входят все предыдущие множества.

Итак, что еще мы можем делать с натуральными числами, кроме как считать предметы? Рассмотрим основные действия, которые проводятся с натуральными числами, а также то, как их сравнивать.

Сравнение натуральных чисел

Сравнить два натуральных числа ㅡ определить, какое из них больше, а какое — меньше.

Например, сравним числа 5 и 8. Распишем последовательность натуральных чисел от 1 до 10:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10 …

Как мы можем заметить, число 8 стоит правее, то есть позже числа 5, а это значит, что 5 меньше 8. 

Для сравнения используются знаки > и < ㅡ больше и меньше соответственно. То есть ответ для предыдущего вопроса можем записать так: 5 < 8.

Важно отметить, что 0 меньше всех натуральных чисел. Например, 0 < 1, 0 < 31297047.

Теперь давайте сравним сразу три числа, к примеру, 0, 217 и 9. 

Как мы уже обсуждали, 0 меньше всех натуральных чисел. Значит, 0 < 217 и 0 < 9. 

Далее заметим, что число 9 меньше, чем 217, то есть 9 < 217. Это все можно соединить в одно двойное неравенство:

0 < 9 < 217

Для того, чтобы быстро сравнивать натуральные числа, есть парочка лайфхаков:

1. Если у двух натуральных чисел разное количество цифр, то большее из них то, у которого больше цифр. Например, 12345 > 1234, так как у первого числа на одну цифру больше.
2. Если два натуральных числа имеют одинаковое количество цифр, то для того, чтобы определить, какое из них больше, нужно читать число слева направо и найти то, у которого первая отличающаяся цифра будет большее. Например, 12345 < 12356. В данном случае первые три цифры одинаковые, но вот четвертая у второго числа больше, чем у первого.  

Теперь перейдем к операциям над числами.

Сложение

Сложение – это арифметическая операция, в результате которой объединяются единицы двух чисел.

Например, 2 + 3 = 5. 

2 состоит из двух единиц, 3 состоит из трех единиц, тогда

(1 + 1) + (1 + 1 + 1) = 5.  

Допустим, вместо наших единиц будут апельсины. У Саши будет 4 апельсина, а у Маши 3 апельсина. Если девочки сложат апельсины в один пакет,  то получится 7 апельсинов. Это действие можно записать через сложение как 4 + 3 = 7.

Сложение можно записать как

m + n = p, где m и n — слагаемые; p – сумма.

Как и у любого действия в математике, сложение имеет свои свойства, которыми удобно пользоваться при счете. Рассмотрим их.

Свойства сложения:

1 свойство. Переместительное свойство: a+b=b+a.
Иначе можно сказать, что от перемены слагаемых сумма не меняется. 

Например, 1+3=4 и 3+1=4. Если бы у Маши оказалось 4 апельсина, а у Саши 3, то вместе у них также останется 7 апельсинов.  

2 свойство. Сочетательное свойство: a+(b+c)=(a+b)+c.
При сложении чисел не имеет значения, какие из них складывать в первую очередь: сумма не изменится. Например, 1+(2+3)=1+5=6 и (1+2)+3=3+3=6.

Вычитание

Вычитание – это арифметическое действие, обратное сложению.

Если при сложении мы ищем сумму через слагаемые, то в вычитании можем найти слагаемое через сумму и другое слагаемое. Например, 6 — 2 = 4. 

Вычитание можно записать как

p — n = m, где p — уменьшаемое; n – вычитаемое; m — разность.

Свойства вычитания:

1 свойство: а — (b + c) = a — b — c.
Если из числа нужно вычесть сумму других двух чисел, то можно вычесть эти числа последовательно. 

Например, 10 — (2 + 5) = 10 — 2 — 5 = 3. 

2 свойство: (a + b) — c = (a — c) + b.
Если из суммы чисел нужно вычесть другое число, то сначала можно вычесть число из любого слагаемого, а потом сложить получившийся результат и оставшееся число. 

Например, (8 + 2) — 3 = (8 — 3) + 2 = 7. 

Умножение

Умножение – это действие, в результате которого определенное слагаемое берется несколько раз.

Например, в записи 35 * 3, число 35 берется три раза: 35 + 35 + 35. 

Умножение можно записать как

m * n = p, где m и n — множители; p – произведение.

Свойства умножения:

1 свойство. Переместительное: a * b = b * a.
От перестановки множителей произведение не изменяется.

Например, 3 * 4 = 4 * 3 = 12.

2 свойство. Сочетательное свойство умножения: a * (b * c) = (a * b) * c.
От изменения порядка умножения чисел произведение не меняется.

Например, 34 * (2 * 4) = (34 * 2) * 4 = 272. 

3 свойство. Распределительное свойство умножения: a * (b + c) = a * b + a * c.
При умножении числа на сумму, можно умножить это число на каждое слагаемое, а после сложить результаты. 

Например, 2 * (59 + 91) = 2 * 59 + 2 * 91 = 300. 

Деление

Деление – это действие, обратное умножению.

Например, 35 : 5 = 7. 

Деление можно записать как

m : n = p, где m — делимое; n — делитель; p – частное.

Следует запомнить, что делить на 0 натуральные числа нельзя. 

Однако не всегда получается разделить число нацело, тогда при делении появляется остаток. Например, при делении 36 на 8 получается частное 4 и остаток 4. Иначе эту операцию можно записать так: 36 = 8 * 4 + 4. 

Деление с остатком можно записать как

m = n * p + r, где m — делимое; n — делитель; p – частное; r – остаток.

Существуют признаки делимости, которые помогают сразу определить, делится ли число нацело или нет. Вот некоторые из них:

• Число делится на 2, если последняя цифра его записи четная или ноль.
  Так, 1946032 будет делиться на 2, поскольку последняя цифра четная. 

1946032 :2=973016

• Число делится на 3, если сумма его цифр делится на 3.
  Число 951 будет делиться на 3, поскольку 9+5+1=15, 15 : 3=5. 

951 : 3=317 

• Число делится на 4, если две его последние цифры кратны четырем или ноли.
  45216 будет делиться на 4, поскольку 16 кратно 4, тогда

  45216 : 4=11304. 

Так же 700 будет кратно 4, поскольку две последние цифры — ноли, тогда 

700 : 4=175. 

• Число делится на 5, если последняя его цифра 0 или 5.
  Например, 63795 : 5=12759, 25570 : 5=5114. 

• Число делится на 9, если сумма его цифр делится на 9.
  Сумма цифр числа 927 равна 9+2+7=18, то есть кратна 9, поэтому

 927 : 9=103.

• Число делится на 10, если последняя его цифра — ноль. 

Например, 2561470 : 10=256147.

Заметим, что при сложении и умножении натуральных чисел всегда получаются натуральные числа, тогда как при вычитании и делении не всегда получаются натуральные числа (результат будет зависеть от конкретного примера).

Например,

7 — 14 = -7, где -7 – не натуральное число,
21 : 4 = 5,25, где 5,25 – не натуральное число. 

Возведение в степень

Возведение в степень очень похоже на умножение, но чтобы возвести число в степень нужно умножить его на само себя. Сколько раз число будет умножено на само себя, такая степень у него и будет. 

Например, 40⁵ = 40 * 40 * 40 * 40 * 40. 

Возведение в степень можно представить как

mn = p, где m – основание степени; n – показатель степени.

Свойства степеней:

Извлечение корня

Извлечение корня – действие, обратное возведению в степень.

При извлечении корня мы узнаем, в какую степень нужно возвести число, чтобы получилось данное число. 

Извлечение корня можно записать как

\(\sqrt[n]{m} = p\), где n – показатель корня; m – подкоренное выражение; p – корень.

Свойства корней:

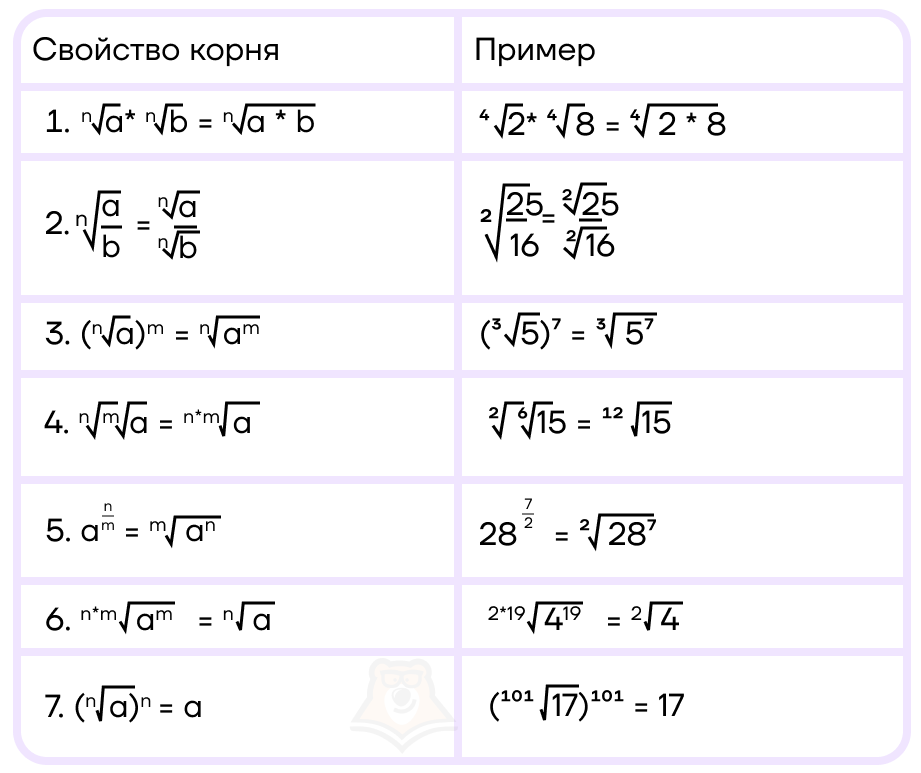
О том, как не запутаться в корнях, смотрите статью «Понятие корня».

Подведем итог:
Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать из них корень.

Действия с числами, разумеется, встречаются во всех заданиях ОГЭ и ЕГЭ. Для примера рассмотрим задание №6 из ОГЭ:

Найдите значение выражения: \(\7*3^3+8*10^-1+15*2^5\).

Решение.
Для решения нам понадобится одно из свойств степеней:

 \(a^-n= \frac{1}{a^n}, a\neq0

Тогда мы можем переписать выражение в виде:

\(7*3^3+8*\frac{1}{10}+15*2^5\)

Возведем числа в степени и посчитаем:

\(7*27+8*\frac{1}{10}+15*32=189+0,8+480=669,8\)

Ответ: 669,8

Разложение числа на простые множители

Для понимания дальнейших рассуждений необходимо ввести понятие простого числа. 

Простое число – это число, которое делится только на себя и на единицу.

Например, у числа 2 делителями будут только 2 и 1, у числа 17 – 17 и 1, у числа 151 – 151 и 1. 

Помимо простых чисел существуют и составные числа – это числа, у которых есть другие делители, кроме 1 и самого себя. 

Любое составное число можно разложить на простые множители (причем только одним способом).

Например, 6 = 2 * 3, где 2 и 3 – простые числа. 

Разложение на простые множители – это действие, в результате которого мы можем представить любое составное число в виде произведения нескольких простых множителей. 

Умение раскладывать числа на простые множители может пригодиться для анализа чисел и их свойств. 

Упрощаем: как разложить число на простые множители? Любое число состоит из нескольких простых множителей. Разложить число на простые множители значит представить это число в виде произведения нескольких его простых множителей. Например, 18 = 2 * 3 * 3

Чтобы разложить число на простые множители, необходимо последовательно делить его на простые множители, начиная с наименьшего возможного. 

Для примера разложим число 123896.

Первый подходящий делитель будет равен 2:

123896 = 61948 * 2.

61948 не является простым числом, поэтому продолжаем раскладывать, следующий делитель также равен 2:

123896 = 30974 * 2 * 2. 

Продолжаем раскладывать число до тех пор, пока справа не получится произведение только из простых чисел:

123896 = 2 * 2 * 2 * 17 * 911.

Для удобства повторяющиеся числа можно записать в виде степеней:

123896 = 2³ * 17*911. 

Процесс разложения на простые множители можно записать в виде столбика, где слева будут получившиеся в результате деления числа, а справа множители. Для примера разложим число 156:

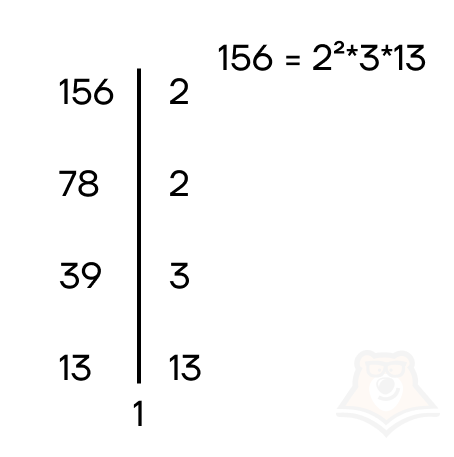
Разложение множителей удобно применять, если необходимо найти все делители числа. Например, в числе 156 мы можем выделить не только простые множители, но и составные: 2 * 2 * 3 = 12 (156 : 12 = 13) или 2 * 3 = 6 (156 : 6 = 26) и т.д. 

Любой делитель числа равен произведению нескольких его простых множителей.

Наибольший общий делитель и наименьшее общее кратное

У любых двух составных чисел можно найти общие делители, то есть такие числа, на которые будут нацело делиться данные числа. 

Например, рассмотрим числа 150 и 315.

Разложим их на простые множители: 150 = 2 * 3 * 5², 315 = 3² * 5 * 7. 

У числа 150 можно выделить следующие делители: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150.

У числа 315: 1, 3, 5, 7, 9, 15, 21, 35, 45, 63, 105, 315. 

Из них совпадают: 3, 5, 15. 

Совпадающие делители будут называться общими, а наибольший из них – наибольшим общим делителем (НОД). Он обозначается D(a,b). 

Если НОД чисел a и b  равен единице, то это взаимно простые числа. Взаимно простыми числами могут быть и составные, например, 15 и 16. 

Чтобы найти НОД чисел, необходимо: 1. Каждое из них разложить на простые множители;  2. Определить, какие из них повторяются; 3. Умножить их друг на друга.

Найдем НОД  чисел 45 и 105:

• 45 = 3² * 5
• 105 = 3 * 5 * 7. 

Совпадающие простые множители: 3 и 5, тогда D(45, 105) = 3 * 5 = 15. 

У любых составных чисел можно найти наименьшее общее кратное (НОК). Это такое число, которое нацело будет делиться на данные числа. 

Например, рассмотрим числа 9 и 12.
Числа, кратные 9: 9, 18, 27, 36, 45, 54, 63, 72 и т.д.
Числа, кратные 12: 12, 24, 36, 48, 60, 72 и т.д.
Среди этих чисел есть повторяющиеся 36 и 72, они будут общими кратными для чисел 9 и 12, а меньшее из них – это наименьшее общее кратное данных чисел (НОК).

Чтобы найти НОК чисел, необходимо:  1. Разложить их на простые множители; 2. Найти произведение всех получившихся простых множителей, при этом взять наибольший показатель степени у каждого.

Например, найдем НОК чисел 184 и 624.
184 = 2³ * 23
624 = 2⁴ * 3 * 13
Тогда К(184, 624) = 2⁴ * 3 * 13 * 23 = 14352. 

Почему мы берем наибольший показатель степени? Поскольку нам нужно, чтобы число делилось нацело, то в него должны быть включены все имеющиеся простые множители. В нашем случае число 2³ уже включено в 2⁴. То есть нам нужно, чтобы НОК делилось не только на 8, но и на 16.

Наименьшее общее кратное двух взаимно простых чисел будет равно произведению этих чисел.

К(а, b) = a * b, где

a, b – взаимно простые числа. 

Между НОК и НОД существует следующая связь: произведение НОК и НОД некоторых чисел равно произведению этих чисел.

D(a, b) * K(a, b) = a * b

Где могут пригодиться НОК и НОД? НОК и НОД активно используются в дробях.  С помощью НОД можно сразу сократить дробь. Например, D(228, 1650) = 6, следовательно дробь с такими числами сразу можно сократить на 6: \(\frac{228}{1650} = \frac{38}{275}\) С помощью НОК можно привести дроби к общему знаменателю. Например, К(6, 22) = 66, тогда дроби \(\frac{1}{6}\) и \(\frac{1}{22}\) можно привести к общему знаменателю и получить \(\frac{11}{66}\) и \(\frac{3}{66}\).

НОК и НОД удобно использовать для вычислений, однако задачи с ним могут встретиться и в самом задании, например, в №18 ЕГЭ по профильной математике. Всего в таком задании три пункта: а, б и в. Решим один из пунктов такого задания. 

Пусть а — наименьшее общее кратное, а b — наибольший общий делитель натуральных чисел х и y, удовлетворяющих условию 2x=92-y.
а) Может ли \(\frac{a}{b}\) быть равным 90?

Решение. 
Важное примечание: для полного понимания логики решения этого задания вам могут потребоваться более глубокие знания математики, в частности, навык решения квадратных уравнений и работы с дискриминантом. Мы подробно рассказали об этом в статье «Линейные, квадратные и кубические уравнения». Пожалуйста, обратитесь к ней в случае необходимости.

Несмотря на то, что это задание считается одним из самых сложных в ЕГЭ, мы можем решить первый пункт, просто подобрав пример. 

Начнем перебирать примеры. Какие числа при делении дадут 90? В первую очередь в голову приходят числа 90 и 1. 

Тогда по свойству НОК и НОД имеем:

\(D(x,y)*K(x,y)=x*y\)
\(90*1=x*y\)
\(xy=90\)

Выразим отсюда х:
\(x=\frac{90}{y}\)

А теперь подставим х в условие:
\(2x=92-y => 2*\frac{90}{y}=92-y=>\frac{180}{y}=92-y\)

Домножим уравнение на y и получим:
\(180=92y-y^2 => y^2-92y+180=0\)

Решим с помощью дискриминанта:

\(D=b^2-4ac=8464-720=7744=> \sqrtD=88\)
\(y_1=\frac{-b+\sqrtD}{2a}=\frac{92+88}{2}=90\)
\(y_2=\frac{-b-\sqrtD}{2a}=\frac{92-88}{2}=2\)

В первом случае х будет равен 1, во втором — 45. Проверим оба этих случая на соответствие условию:

\(2*1=92-90 => 2=2\) — подходит.
\(2*45=92-2=>90=90\) — подходит.

Значит, пример мы подобрали правильно.

Ответ: Да, например, 90 и 1

Рассмотренные операции являются основными для вычислений  в задачах. Применение описанных свойств облегчает и ускоряет счет, что даст дополнительное время на экзамене и сократит количество вычислительных ошибок.

Но могут возникнуть вопросы: в каком порядке выполнять действия? Как выполнять действия с числами разных знаков? Как их округлять? Ответы на все эти вопросы вы найдете в статье «Действия с числами».

Термины

Дискриминант квадратного уравнения — это выражение, равное b² − 4ac.

Квадратное уравнение — это уравнение, в котором неизвестная находится в степени 2.

Фактчек

• Натуральные числа — это числа, используемые при счете. 
• Сравнить два натуральных числа ㅡ определить, какое из них больше, а какое — меньше.
• Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень. При сложении и умножении натуральных чисел можно получить только натуральные числа, а при вычитании и делении — нет. 
• Существуют простые и составные числа. Простые числа делятся только на единицу и само себя; составные числа имеют еще и другие делители. Каждое составное число можно разложить на произведение простых множителей, причем только одним способом. 
• У нескольких чисел можно найти наибольший общий делитель и наименьшее общее кратное. Если НОД двух чисел равен 1, то это взаимно простые числа. НОК двух взаимно простых чисел будет равен произведению этих чисел.
• Произведение НОК и НОД некоторых чисел равно произведению этих чисел.

Фактчек

• Натуральные числа – это числа,  используемые при счете. 
• Натуральные числа можно складывать, вычитать, умножать, делить, возводить в степень и извлекать корень,. При сложении и умножении натуральных чисел можно получить только натуральные числа, а при вычитании и делении – нет. 
• Существуют простые и составные числа: простые числа делятся только на единицу и само себя; составные числа имеют еще и другие делители. Каждое составное число можно разложить на произведение простых множителей, причем только одним способом. 
• У нескольких чисел можно найти наибольший общий делитель и наименьшее общее кратное. Если НОД двух чисел равен 1, то это взаимно простые числа. НОК двух взаимно простых чисел будет равен произведению этих чисел. 
• Произведение НОК и НОД некоторых чисел равно произведению этих чисел. 

Проверь себя

Задание 1.
Какие числа называются натуральными? 

1. Числа, используемые при счете.
2. Все числа, которые существуют. 
3. Все положительные и отрицательные целые числа. 
4. Все четные числа. 

Задание 2. 
Ответь, не вычисляя, какое число делится на 3?

1. 113; 
2. 239; 
3. 158726; 
4. 26841. 

Задание 3. 
Ответь, не вычисляя, какое число делится на 4?

1. 7673438; 
2. 2850;
3. 526982; 
4. 264864. 

Задание 4. 
Какое число является составным?

1. 26;
2. 17;
3. 3;
4. 97.

Задание 5. 
Какое число является простым?

1. 39;
2. 91;
3. 59;
4. 93.

Ответы: 1. — 1 2. — 4 3. — 4 4. — 1 5. — 3