Финансовые задачи

На этой странице вы узнаете

• С помощью какого инструмента можно решить любую экономическую задачу?
• Как сделать «буп» котику и быстро заполнить таблицу?
• Чек-лист: как правильно решать экономические задачи?

Мы ежедневно сталкиваемся с денежными операциями. Покупка вкусняшек, оплата проезда, или приобретение что-то для души — это все финансовые операции. И про кредиты слышали многие из нас. Давайте разберемся, как подходить ко всем этим вопросам математически грамотно. 

Финансовые задачи на каждый день

Кредиты берут и на покупку обычных бытовых вещей и на что-то более внушительное, как машина или квартира. В любом случае при обращении в банк за выдачей кредита каждый должен быть готов столкнуться с разными схемами платежей и понятиями процентов.

Кредит – денежная сумма, предоставляемая банком на определенный срок под определенные условия.

Другими словами, кредит – это «долг» перед банком. 

При этом кредит состоит из:

• Основного долга, то есть суммы, которую мы берем в долг.
• Процентной части, начисляемой на основную сумму. 

Про проценты, в том числе сложные проценты или увеличение и уменьшение числа на процент, можно подробнее прочитать в статье «Финансовые задачи. Проценты». 

Сейчас мы углубимся в основные схемы погашения кредита. На самом деле, их не так много, а если быть точнее, то всего две. Главное их различие в платежах.

Начнем разбираться в кредитах с аннуитетных платежей. 

Аннуитетные платежи

Этот вид платежей встречается достаточно часто. В чем заключается его основная роль? Каждый месяц (или год) сумма выплат одинаковая. 

Например, если мы заключим договор с банком, в котором пропишут, что каждый месяц необходимо выплачивать 10 тысяч рублей — это и будет пример аннуитетных платежей. 

Аннуитетные платежи — такая система выплат, при которых кредит выплачивается раз в год (или в другой период времени в зависимости от договора) равными платежами. 

Главное словосочетание будет «равными платежами». Вне зависимости от остатка долга, платеж меняться не будет. 

Разберемся чуть подробнее. Каждый расчетный период (это может быть месяц, год и т.д.) на кредит начисляются установленные проценты. Следовательно, выплачивая кредит по аннуитетным платежам, мы будем одновременно гасить и долг, и процент. Наш платеж будет складываться из процентов, начисленных на долг и самого тела долга. 

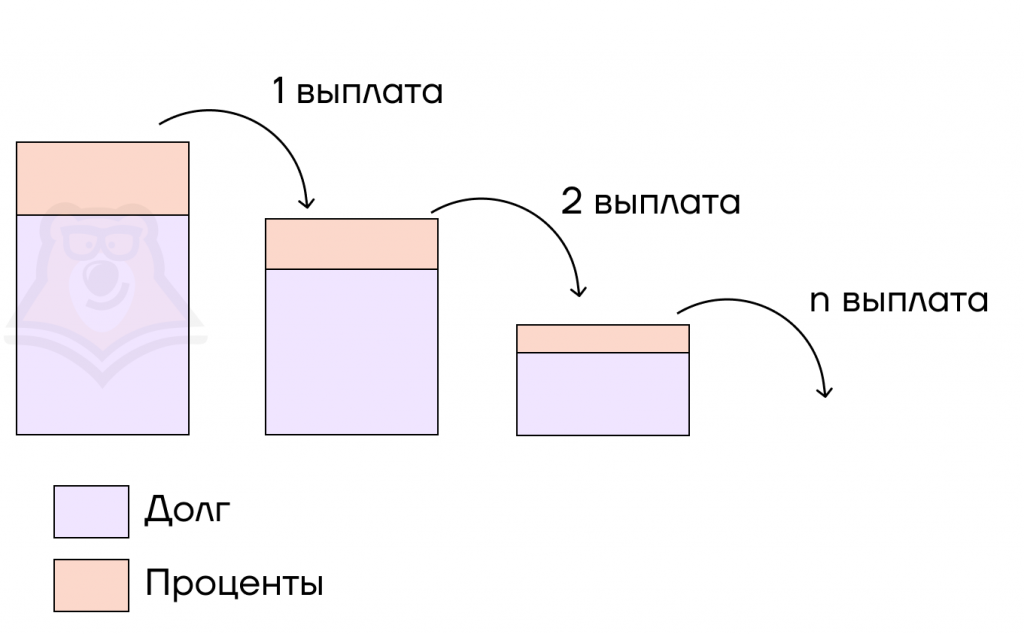
Также вспомним, что чем больше долг, тем больше начисленный на него процент. Поскольку сама выплата не меняется с течением времени, то вначале основная часть выплаты идет на погашение начисленных процентов, а остаток — на погашение самого долга. Со временем их отношение выравнивается и меняется в обратную сторону. 

Схему выплат аннуитетных платежей можно представить следующим образом. На ней видно, что с каждой выплатой уменьшается как сам долг, так и начисленный на него процент. 

Как определить, что перед нами задача на аннуитетные платежи?
Нужно посмотреть на некоторые ключевые слова:

• выплаты равны между собой;
• выплаты фиксированные;
• сам долг уменьшается неравномерно. 

Мы уже вполне готовы решить задачу на аннуитетные платежи. 

Пример 1. Игорь хочет в мае взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— Каждый январь долг возрастает на 10% по сравнению с концом предыдущего года.
— С февраля по май каждого года нужно выплатить часть долга, равную 665,5 тыс. рублей. 

На какую сумму хочет взять кредит Игорь, если он был погашен тремя равными платежами?

Решение. 

Шаг 1. Каждый год кредит будет увеличиваться на 10%, поэтому для удобства решения введем коэффициент \(k=1+\frac{10}{100}=1,1\). Обозначим взятый кредит за S, а ежегодную выплату за \(x=665,5\) тыс. 

Шаг 2. 

С помощью какого инструмента можно решить любую экономическую задачу? Большинство экономических задач можно решить с помощью правильно составленной таблицы. В ней можно отразить всю необходимую информацию для решения задачи. Более того: таблицу можно подстраивать под конкретную задачу, поскольку нет определенного шаблона, как ее заполнять.

Что обычно включается в таблицу:

• остаток на начало периода,
• начисленный процент,
• выплата,
• остаток после выплаты. 

Таблица — очень гибкий инструмент. В зависимости от условия задачи она может меняться. Например, выплату можно разбить на два столбика: процентную часть и часть от основного долга. 

Чуть подробнее разберем составление таблицы. 

Поскольку выплаты фиксированные и равны между собой, мы можем сразу заполнить четвертый столбик:

Что еще нам известно? То, что долг в начале был равен S, а в самом конце полностью выплачен. Значит, на конец периода долг будет равен 0. Заполним соответствующие ячейки:

Дальше мы можем найти долг с начисленными процентами в первый год. Для этого нужно долг умножить на коэффициент.

А теперь решим небольшую задачку: у Маши было 5 яблок. Она отдала два из них подруге. Сколько яблок осталось у Маши? Без раздумий мы можем сразу сказать, что у Маши осталось 3 яблока. Внимательно посмотрим на таблицу: долг перед банком был 1,1S (5 яблок), после чего погасили его часть, равную х (2 яблока). Какой остаток останется? 1,1S – х. 

Было	Убрали	Получили
5 яблок	2 яблока	3 яблока
1,1S	x	1,1S — x

Таким образом, с помощью долга, выплаты и остатка можно составить уравнение: 

• «Долг с процентами» – «выплата» = «остаток». 

Это же уравнение можно немного варьировать, например:

• «Долг с процентами» – «остаток» = «выплата». 
  Этот случай можно использовать, когда нам неизвестна выплата, но известны остальные две величины. 

• «Остаток» + «выплата» = «долг с процентами».
  Этот случай используется в ситуациях, когда неизвестен первоначальный долг. 

В зависимости от условий задачи можно с помощью таблицы всегда выразить неизвестную величину. 

Как сделать «буп» котику и быстро заполнить таблицу? Если в таблице есть столбики «Долг после процентов», «Выплата» и «Остаток», то они связаны принципом БУП: Было, Убрали, Получили. С помощью БУП можно выразить либо долг, либо выплату, либо остаток, достаточно составить уравнение (или его вариацию): «Долг» – «Выплата» = «Остаток». В дальнейшем такую операцию будем называть БУП: Было, Убрали, Получили.

Заполним нужные ячейки. Сразу заметим, что долг без процентов в начале года будет равен остатку на конец предыдущего года.

Выполняем такой же алгоритм со вторым годом: начисляем проценты и ищем остаток. Важно заметить, что проценты начисляются на весь остаток, в том числе на переменную х. 

И по такой же схеме осталось заполнить только последние две ячейки.

Вот и все заполнение таблицы, совсем ничего сложного. Нужно немного рассуждений и операций с числами. 

Шаг 3. Составим итоговое уравнение. Посмотрим на последнюю строчку и вспомним уже выведенную формулу БУП. 

Было: \(1,1(1,12^S-2,1x)=1,1^3S-2,31x\).
Убрали: х.
Получили: 0. 

Тем самым мы получаем уравнение: \(1,1^3S-2,31x-x=0\). Осталось только решить его.

\(1,1^3S-3,31x=0\)
\(S=\frac{3,31x}{1,1^3}\)

Тут уже можно заменить переменные на числа. Вспомним, что \(x=665,5\).

\(S=\frac{3,31*665,5}{1,331}\)
\(S=1655\) тыс.

Ответ: 1655 тысяч рублей. 

Рассмотрим еще одну задачу на аннуитетные платежи. 

Пример 2. В сентябре 2023 года планируется взять кредит. Условия его возврата таковы:
— В январе каждого года долг увеличивается на 20% по сравнению с концом предыдущего года.
— С февраля по сентябрь нужно выплатить часть долга одним платежом.
Известно, что кредит был погашен двумя равными платежами. Найдите, на какую сумму был взят кредит, если сумма его выплат на  136 тыс. больше суммы взятого кредита. 

Решение. 

1. Для начала введем переменные. S — кредит, х — выплаты в 1 и 2 год, \(k=1+\frac{20}{100}=1,2\) — коэффициент увеличения. 

2. Составим таблицу:

3. Теперь составим уравнение: 

\(1,2(1,2S-x)-x=0\)
\(1,2^2S-1,2x-x=0\)
\(1,44S-2,2x=0\). 

4. Внимательно прочитаем условие и отметим, что сумма выплат на 136 тысяч больше суммы кредита. Как найти сумму выплат? Нужно посмотреть на таблицу. В ней расписаны все наши выплаты, а значит, их просто нужно сложить. Получается, что сумма выплат равна 2х.

Составим еще одно уравнение, опираясь на условие задачи: 2x = S+136.

5. Мы получили два уравнения. Поскольку нам необходимо найти S, достаточно выразить х в одном из них и подставить в другое. 

\(2x=S+136\)
\(x=0,5S+68\)

Тогда в уравнении \(1,44S-2,2x=0\) получаем:

\(1,44S-2,2(0,5S+68)=0\).
\(1,44S-1,1S-68=0\)
\(0,34S=68\)
\(S= \frac{68}{0,34}\)
\(S=200\) тыс. 

Ответ: 200 тыс. рублей.

Мы решили уже целых две задачи! Закрепим результат, разобрав еще один интересный пример. 

Пример 3. Юля хочет взять в кредит 150 тысяч рублей под 10% годовых. Погашение кредита происходит раз в год равными платежами (кроме последней выплаты). На какое минимальное количество лет Юля должна взять кредит, чтобы ежегодные выплаты были не более 50 тысяч рублей? 

Решение. Притормозим на минутку. Сначала рассмотрим еще одну логическую задачу, которая поможет в решении. 

Маша решила раздать шарики прохожим. Всего у нее 10 шариков. В каком случае большее количество людей получит шарики: если Маша будет раздавать по два или по одному шарику? 

Если Маша раздает по одному шарику, то их получит 10 человек. А если по 2, то их получит 5 человек. Чем больше шариков Маша отдает одному человеку, тем меньше людей получит шарики. 

В нашей задаче приводятся такие же рассуждения: чем больше выплату будет делать Юля, тем меньше лет она будет выплачивать кредит. То есть ее ежегодная выплата должна иметь максимальное значение, а по условию задачи это 50 тысяч рублей. 

Шаг 1. Составим таблицу. Коэффициент увеличения будет равен \(1+\frac{10}{100}=1,1\). 

В этой задаче в таблице удобнее сразу считать величины, а не подставлять переменные. 

Заполним первую строчку. Долг без процентов равен 150 тысяч, после начисления процентов он будет равняться \(150*1,1=165\) тысяч. 

Как мы определили выше, выплата должна равняться 50 тысяч. Тогда остаток: \(165-50=115\) тысяч.

Шаг 2. Аналогично считаем и заполняем все следующие строчки до тех пор, пока долг после начисления процентов не станет меньше 50:

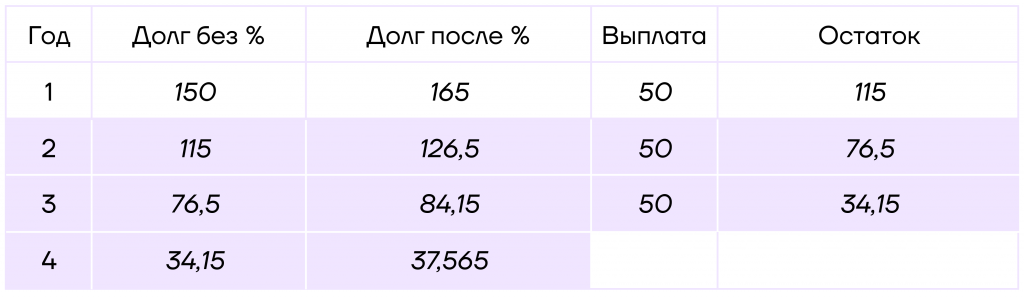
Шаг 3. Заметим, что после этой выплаты есть возможность полностью погасить кредит. Следовательно, остаток будет равен 0. 

Тогда выплата равна \(37,565-0=37,565\). 

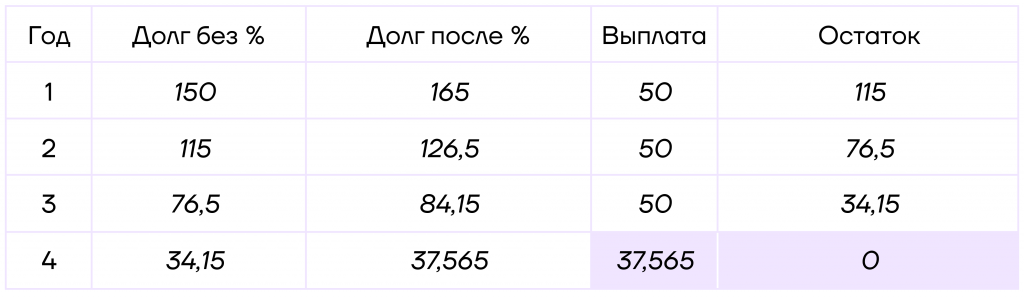
Таким образом, с помощью только таблицы мы решили задачу. Минимальное число лет, на которое Юля может взять кредит — 4 года, что видно из таблицы. 

Ответ: 4. 

Дифференцированные платежи

Разобравшись в аннуитетных платежах, следует перейти к дифференцированным. В них также нет ничего сложного. Главное их отличие от аннуитетных в том, что долг будет уменьшаться на одну и ту же величину.

Дифференцированные платежи — такая система выплат, при которой сумма долга уменьшается равномерно. 

В этом случае сумма кредита делится на несколько равных частей, которые выплачиваются банку вместе с начисленными на остаток процентами. Из этих двух частей будет складываться платеж: причем с каждым месяцем (годом) платеж будет уменьшаться, поскольку будет уменьшаться и процент, который начисляется на остаток. 

В отличие от аннуитетных платежей, выплаты в дифференцированных платежах не фиксированные. Со временем выплаты будут уменьшаться. 

Представим схему выплат дифференцированных платежей. Например, кредит S взяли на 4 года. Следовательно, каждый год он будет уменьшаться на \(frac{1}{4}S\) часть, а проценты будут начисляться уже на остаток. 

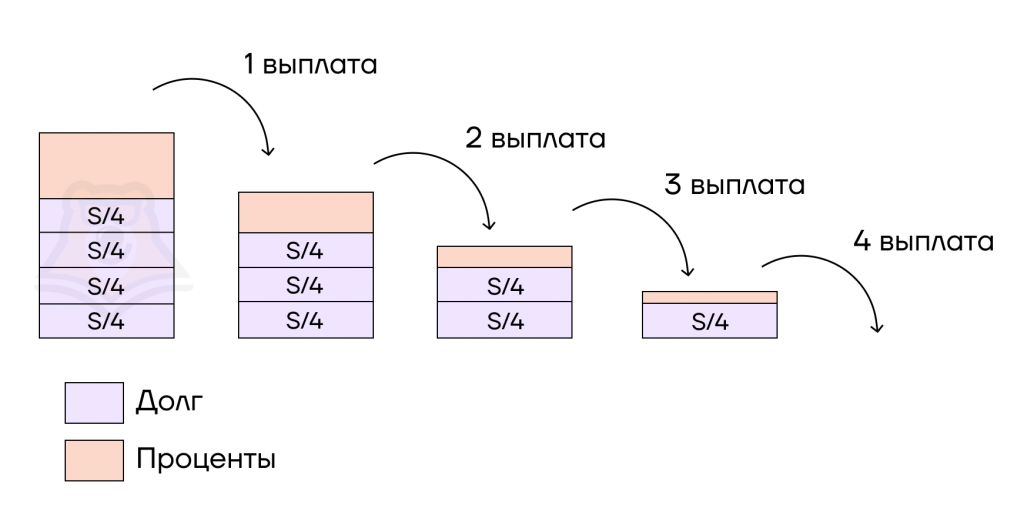
Ключевые слова, чтобы определить, что перед нами схема с дифференцированными платежами:

• платежи разные;
• каждый платеж меньше предыдущего;
• долг уменьшается на одну и ту же величину. 

Рассмотрим примеры задач на дифференцированные платежи. 

Пример 4. Вася взял кредит в банке на сумму 1 млн рублей под 10% годовых. Условия его возврата таковы:
— После начисления процентов необходимо выплатить часть долга.
— После каждой выплаты долг должен быть на одну и ту же сумму меньше долга до выплаты.
— Кредит должен быть выплачен за 5 лет.

Найдите общую сумму выплат по кредиту. 

Решение. 

1. Составим таблицу. Для этого введем коэффициент увеличения \(k=1+\frac{10}{100}=1+0,1=1,1\). 

Заметим, что кредит взят на 5 лет, а сумма долга уменьшается равномерно. Следовательно, каждый год долг должен уменьшаться на \(\frac{1}{5}=0,2\) млн рублей.

Таким образом, мы можем заполнить последний столбик таблицы: достаточно просто вычитать каждый год из долга 0,2 млн рублей. Также мы сразу можем заполнить второй столбик таблицы, для этого достаточно переносить данные из последнего столбика. 

2. Теперь, зная долг до процентов, мы можем узнать долг после процентов:

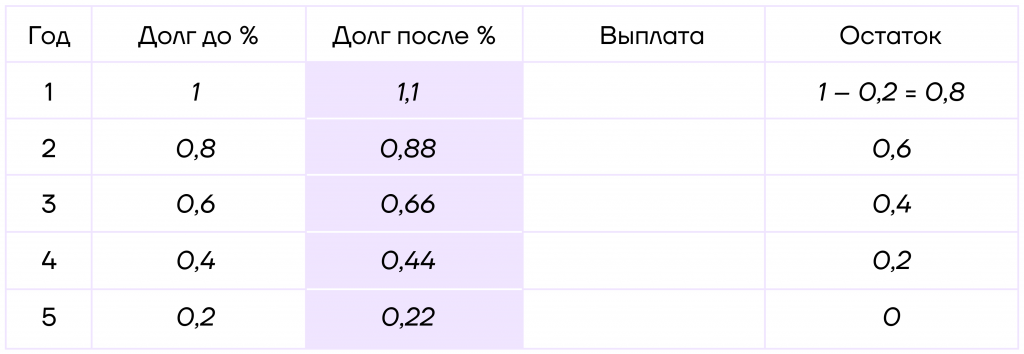
3. Осталось найти выплату. А для этого мы можем использовать все тот же БУП. 

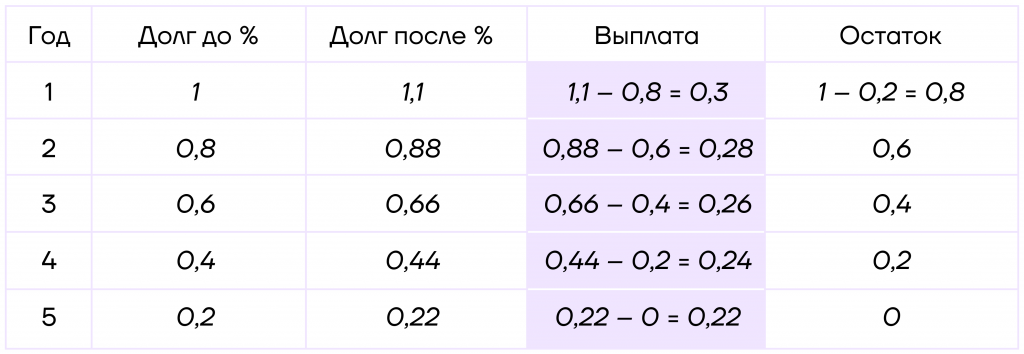
4. Теперь мы можем  найти сумму выплат, для этого нужно сложить все выплаты, которые были произведены по кредиту:

\(0,3+0,28+0,26+0,24+0,22 = 1,3\) млн рублей. 

Ответ: 1,3 млн рублей. 

На примере этой задачи составим схему того, как выплачивался кредит. Она поможет нагляднее понять, как работает схема выплат при дифференцированных платежах. 

А как решать задачи, если мы знаем сумму только одной выплаты? 

Пример 5. Лиза взяла кредит в банке на 12 месяцев. Условия его возврата таковы:
— 1 числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
— со 2 по 14 число каждого месяца необходимо выплатить часть долга;
— 15 числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15 число предыдущего месяца. 

Какая сумма была взята в кредит, если известно, что 11 платеж составил 165 тысяч рублей?

Решение. 

Шаг 1. Пусть S — кредит. Отметим, что кредит каждый месяц будет уменьшаться на \(\frac{S}{12}\).

В этот раз составим немного другую таблицу, а именно разобьем выплату на проценты и основную часть от долга. Также таблица на 12 месяцев слишком большая (а в задачах могут встретиться таблицы еще больше), поэтому мы будем рассматривать только первые два и последние три месяца. 

Сразу заполним все данные, которые нам известны. 

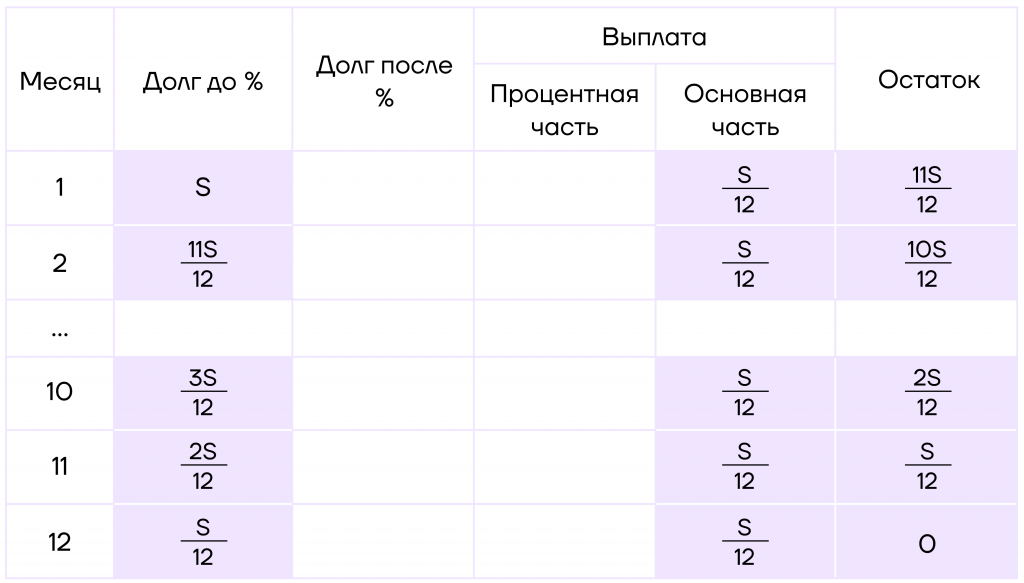
Шаг 2. Теперь будем начислять процент. 

Введем переменную \(k=\frac{5}{100}\). Заметим, что это не коэффициент увеличения, а значит, долг после начисления процентов будет состоять из основной части и процентной. Заполним третий столбик: 

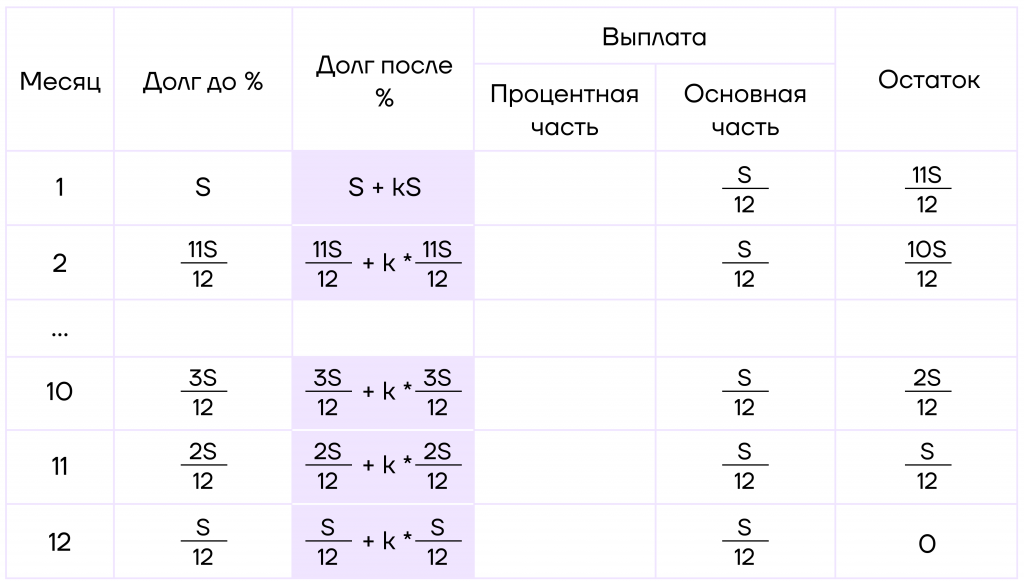
Чтобы закончить заполнение таблицы, вспомним БУП и найдем, чему будет равна процентная часть выплаты. 

Было: \(S+kS\)
Убрали: \(x+\frac{S}{12}\)
Осталось: \(\frac{11S}{12}\)

Тогда получаем: \(S+kS-(x+\frac{S}{12})=\frac{11S}{12}\)
\(S+kS-x-\frac{S}{12}=\frac{11S}{12}\)
\(\frac{11S}{12}+kS-x=\frac{11S}{12}\)
\(x=kS\) — это данные для четвертого столбика. 

Найти остальные ячейки можно таким же способом, но проще будет переносить процентную часть из третьего столбика. 

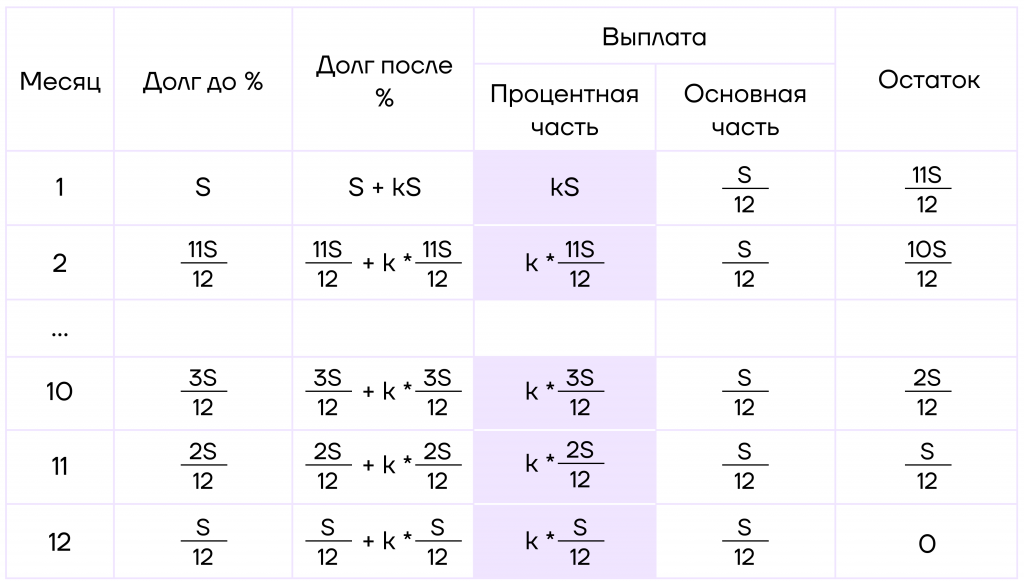
Таблица составлена. 

Шаг 3. Осталось найти, чему равен 11-ый платеж. Для этого нужно найти выплату в 11-ом месяц, то есть сложить эти ячейки:

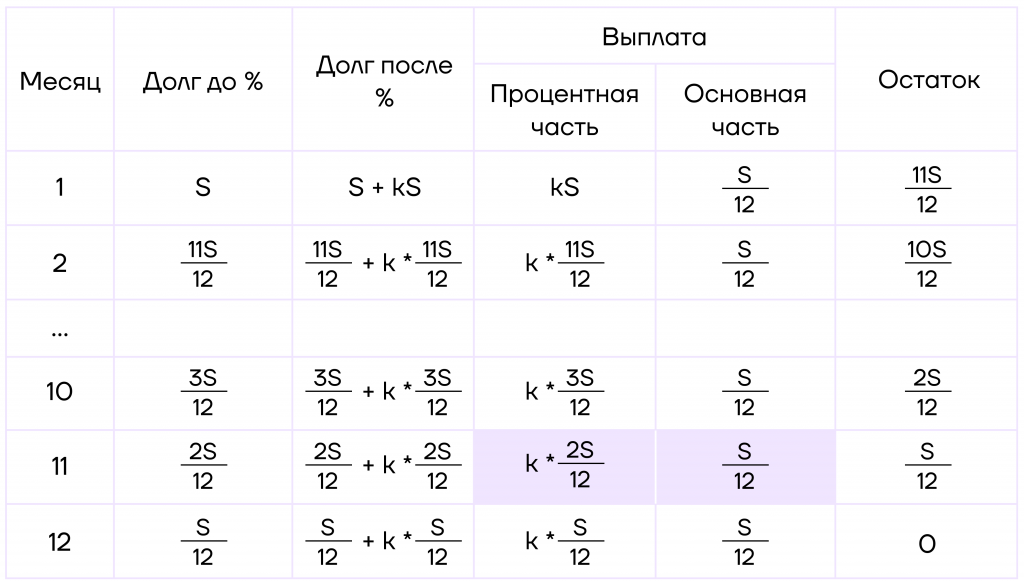
Получаем \(k*\frac{2S}{12}+\frac{S}{12}=165\).

Подставляем вместо коэффициентов известные величины и решаем уравнение. 

\(\frac{S}{12}(2k+1)=165\)
\(\frac{S}{12}(2*0,05+1)=165\)
\(S(0,1+1)=1980\)
\(1,1S=1980\)
\(S=1800\) тыс.

Ответ: 1800 тысяч рублей. 

Теперь попробуем найти не сумму кредита, а количество лет, на которое он взят. Ничего сложного в этом тоже нет. 

Пример 6. В октябре планируется взять кредит на сумму 15 млн рублей на целое число лет. Условия его возврата таковы:
— Каждый март долг возрастает на 10% по сравнению с концом предыдущего месяца.
— С марта по октябрь необходимо выплатить часть долга.
— В октябре каждого года долг будет на одну и ту же сумму меньше долга на октябрь предыдущего года. 

На сколько лет планируется взять кредит, если сумма выплат после его полного погашения составила 22,5 млн рублей? 

Решение. 

1. Пусть \(k=\frac{10}{100}, S = 15\) млн — кредит, n — количество лет, на которое взят кредит. 

Заметим, что каждый год долг будет уменьшаться на \(\frac{S}{n}\) лет. 

2. Составим таблицу. Поскольку нам неизвестно количество лет, рассматриваться будут только первые два и последние два года. 

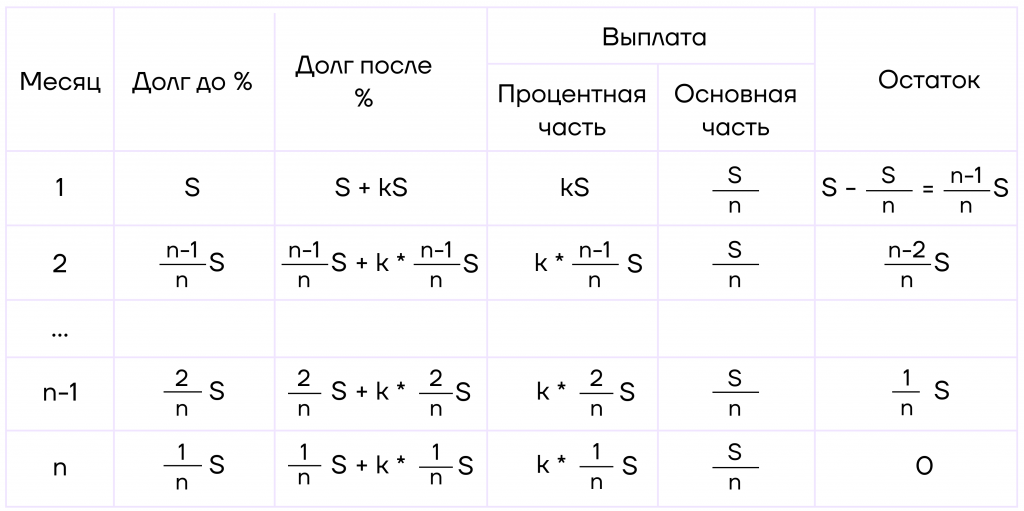
Сумма выплат — это сумма всех платежей, которые были внесены за кредит. 

В таблице это будет сумма этих ячеек. Отметим, что между 2 и n-1 месяцем есть еще все оставшиеся выплаты, которые просто не прописаны в таблицы. Эти выплаты также обязательно учесть в уравнении. 

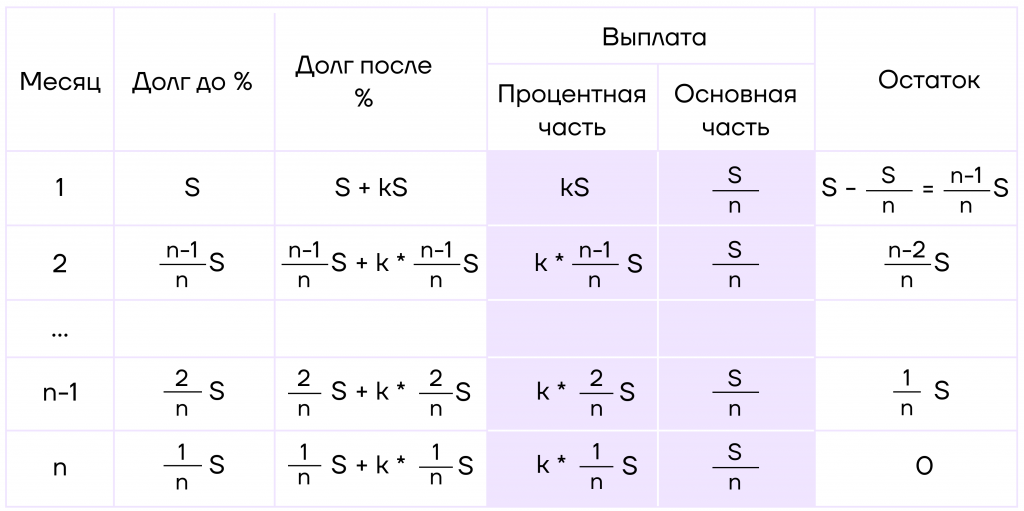
3. Составим уравнение: 

\(kS+\frac{S}{n}+k*\frac{n-1}{n}S+\frac{S}{n}+…+k*\frac{2}{n}S+\frac{S}{n}+k*\frac{1}{n}s+\frac{S}{n}=22,5\)

Немного по-другому сгруппируем слагаемые и вынесем общие множители за скобку:

\(kS(1+\frac{n-1}{n}+…+\frac{2}{n}+\frac{1}{n})+n*\frac{S}{n}=22,5\)
\(kS(\frac{n}{n}+\frac{n-1}{n}+…+\frac{2}{n}+\frac{1}{n})+S=22,5\)

4. Заметим, что в скобках осталась арифметическая прогрессия, а нам необходимо найти ее сумму. Подробнее про арифметические прогрессии можно прочитать в статье «Арифметическая прогрессия». 

Сразу применим формулу суммы арифметической прогрессии:

\(kS(\frac{\frac{n}{n}+\frac{1}{n}}{2}*n)+S=22,5\)
\(kS((\frac{n+1}{n}*\frac{1}{2})*n)+S=22,5\)
\(kS*\frac{n+1}{2}+S=22,5\)

5. Заменим переменные на известные величины:

\(0,1*15*\frac{n+1}{2}+15=22,5\)
\(1,5*\frac{n+1}{2}=7,5\)
\(1,5(n+1)=15\)
\(n+1=10\)
\(n=9\)

Ответ: 9 лет. 

Сравнение видов платежей по кредиту

Мы рассмотрели задачи на аннуитетные и дифференцированные платежи. Подведем небольшой итог и сравним эти платежи. 

	Аннуитетные платежи	Дифференцированные платежи
Выплаты	Выплаты равны между собой	Выплаты со временем уменьшаются
Как уменьшается долг	Неравномерно	Равномерно
Из чего складывается выплата	Начисленные на остаток проценты и часть от долга.  В первое время выплачиваются в основном проценты, а долг лишь малой частью. Со временем в основном будет выплачиваться долг.	Начисленные на остаток проценты и часть от долга. Долг выплачивается равными частями.
График выплат

Чек-лист: как правильно решать экономические задачи? Чтобы решение задач было удобным и быстрым, необходимо следовать алгоритму: 1. Определить, какая схема выплат представлена в задаче. 2. Ввести все нужные переменные. Обязательно указать, что обозначает каждая переменная. 3. Составить таблицу или схему выплат. В таблице необходимо отразить все условия, которые приведены в задаче. 4. Составить итоговое уравнение или неравенство на основе таблицы или схемы. 5. Решить полученное уравнение или неравенство и найти ответ.

Если придерживаться приведенного выше чек-листа, можно решить экономическую задачу на любую схему выплат. 

В задачах может попасться и смешанная схема выплат, то есть схема, при которой есть разные виды выплат. Рассмотрим такую задачу на примере №15 ЕГЭ по профильной математике.

В феврале планируется взять кредит на некоторую сумму S рублей, где S – целое число. В начале месяца банк начисляет 5% на долг по кредиту, после чего производится выплата. Кредит взят на 6 месяцев. Первые два месяца выплачиваются только проценты по кредиту, при этом сам долг не меняется. В следующие четыре месяца долг после выплаты должен быть меньше на одну и ту же сумму, чем до выплаты. Какую сумму взяли в кредит, если общая сумма выплат равна 490 тысяч рублей?

Решение. 
1. Пусть \(k=1+\frac{5}{100}=1,05\). 
2. Составим таблицу. Заметим, что в первые два месяца сумма долга не меняется, то есть выплачиваются только проценты. Заполним эти ячейки:

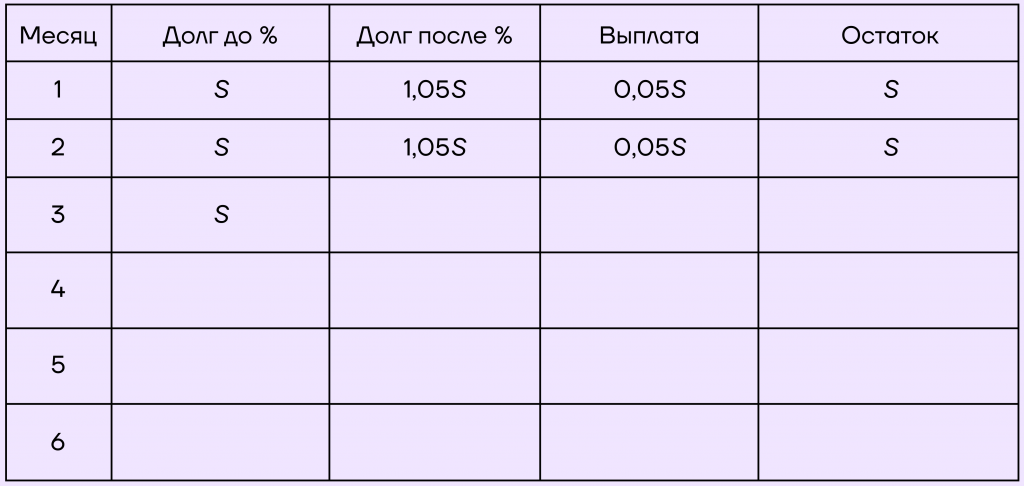
Следующий четыре месяца долг будет уменьшаться на одну и ту же сумму, то есть на \(\frac{S}{4}\). Закончим заполнять таблицу:

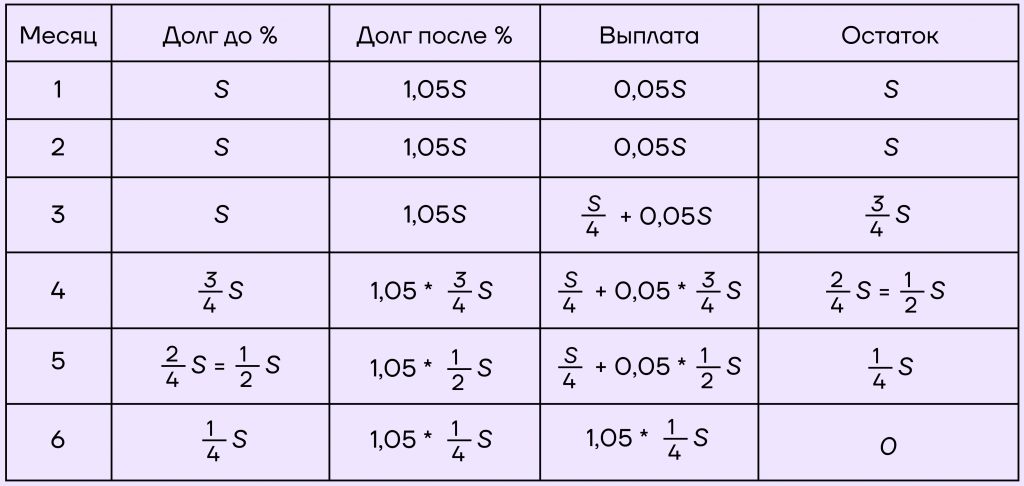
3. Заметим, что \(1,05*\frac{1}{4}S=\frac{S}{4}+0,05*\frac{1}{4}S\). 

По условию нам дана сумма выплат. Составим уравнение:

\(0,05S+0,05S+\frac{S}{4}+0,05S+\frac{S}{4}+0,05*\frac{3}{4}S+\frac{S}{4}+0,05*\frac{1}{2}S+\frac{S}{4}+0,05*\frac{1}{4}S=490\)

Преобразуем левую часть уравнения: 

\(0,05S+0,05S+\frac{S}{4}+0,05S+\frac{S}{4}+0,05*\frac{3}{4}S+\frac{S}{4}+0,05*\frac{1}{2}S+\frac{S}{4}+0,05*\frac{1}{4}S=\)
\(=0,1S+4*\frac{S}{4}+0,05S(1+\frac{3}{4}+\frac{1}{2}+\frac{1}{4})=0,1S+S+0,05S*2,5=1,1S+0,125S=1,225S\)

Получаем уравнение:

\(1,225S=490\)
\(S=\frac{490}{1,225}\)
\(S=400\) тысяч рублей

Это и будет ответ! 

Ответ: 400 тыс. рублей. 

Мы разобрались в основных видах платежей по кредиту, а также в том, как решать финансовые задачи. Теперь нам не страшны никакие условия, поскольку мы с легкостью можем рассчитать что угодно, связанное с кредитом.

Однако финансовые задачи бывают не только с кредитами и вкладами. Что делать, если нам нужно будет рассчитать наиболее прибыльную модель бизнеса? В этом нам помогут «Задачи на оптимальный выбор».

Фактчек

• С кредитами мы встречаемся не только в математике, но и в реальной жизни. Для их выплат существуют две основные схемы: аннуитетная и дифференцированная. 
• Аннуитетные платежи — такая система выплат, при которых кредит выплачивается раз в год (или в другой период времени в зависимости от договора) равными платежами. Аннуитетные платежи фиксированны и равны между собой. А долг уменьшается неравномерно. 
• Дифференцированные платежи — такая система выплат, при которой сумма долга уменьшается равномерно. В этом случае долг будет уменьшаться равномерно, а вот платежи будут различными. Каждый новый платеж будет меньше предыдущего. 
• Схема выплат может быть составлена по-разному, и не всегда это чисто аннуитетные и дифференцированные платежи. Если схема отличается от них, то перед нами смешанная схема выплат. 
• Для решения задач необходимо научиться составлять таблицы и уравнения на основе данных в условии. Также для решения можно пользоваться чек-листом, чтобы точно ничего не упустить.

Проверь себя

Задание 1.
Как уменьшается долг при аннуитетных платежах?

1. равномерно
2. неравномерно
3. на одинаковую величину каждый расчетный период
4. долг не уменьшается

Задание 2.
Как уменьшается долг при дифференцированных платежах? 

1. равномерно
2. неравномерно
3. на различную величину каждый расчетный период
4. долг не уменьшается

Задание 3.
Из чего складывается выплата?

1. Выплачивается только долг.
2. Выплачиваются только проценты.
3. Выплата складывается из части долга и процентов, начисленных на остаток.
4. Выплата всегда складывается из части долга и процентов, начисленных на весь долг. 

Задание 4.
Что такое сумма выплат?

1. Это сумма всех процентов, начисленных на кредит.
2. Это сумма долга.
3. Это последний платеж, который был внесен за кредит.
4. Это сумма всех платежей, внесенных за кредит. 

Задание 5.
Для какой системы выплат характерны равные платежи?

1. дифференцированная
2. аннуитетная
3. и дифференцированная, и аннуитетная
4. ничего из перечисленного выше 

Ответы: 1. — 2; 2. — 1; 3. — 3; 4. — 4; 5. — 2.