Многочлены и действия с ними

На этой странице вы узнаете 

• Много – это сколько?
• Какой многочлен может трансформироваться в одночлен?
• Что такое полином?

Девизом этой статьи станет выражение «Одночлен в поле не воин».

В статье «Одночлены и действия с ними» мы уже познакомились с тем, что из себя представляет одночлен и где он применяется в математике. Поэтому перед началом рекомендуем освежить в памяти этот материал.

На самом же деле одночлены являются лишь кирпичиками для создания более серьезных конструкций – многочленов. Именно о них сегодня и пойдет речь.

Понятие многочлена

Из названия «одночлен» можно задаться вопросом: существует ли двучлен, трехчлен, четырехчлен и так далее? Конечно, да, и для этого придумали общее название – многочлен.

Многочлен – это сумма двух и более одночленов.

Много – это сколько? В жизни мы не раз сталкиваемся со словом «много», и, в зависимости от ситуации, привыкли понимать под этим словом разные числовые значения. Например, много учеников в классе – это 40, много жителей города – 1000000, много «пятерок» в четверти – это 10. Так же и в математике: никогда нельзя точно сказать, что значит «много». При этом, когда речь идет о многочленах, «много» – значит два и более. То есть, вне зависимости от того, из двух одночленов состоит многочлен или из 52, мы можем назвать его многочленом.

Можем представить, что одночлен – это кирпичик, а многочлен – это стена, которая из этих кирпичиков строится.

Одночлены, из которых состоит многочлен, называются членами многочлена. 

Несмотря на то что в определении многочлена указана именно сумма, в записи многочлена может встречаться знак «-», ведь от вычитания мы всегда можем перейти к сложению по правилу: \(a-b=a+(-b)\)

Приведем пример многочлена: \(7ab+8x^2+15k^5kx^9+2x*4x-8ba\).
Так же, как и у одночлена, у любого многочлена существует свой стандартный вид. Для того чтобы привести многочлен к стандартному виду, для начала необходимо все одночлены, входящие в состав данного многочлена, привести к стандартному виду. Сделаем это с нашим многочленом: 

Одночлен \(7ab\) уже стоит в стандартном виде, так же, как и одночлены \(8x^2\) и \(-8ba\).
\(15k^5kx^9=15k^6x^9\)
\(2x*4x=8x^2\)

Получаем:
\(7ab+8x^2+15k^5kx^9+2x*4x+8ba=7ab+8x^2+15k^6x^9+8x^2-8ba\)

Далее приведем подобные слагаемые в этом одночлене. Подобными тут являются слагаемые \(7ab\) и \(-8ba\), а также слагаемые \(8x^2\) и \(8x^2\):
\(7ab-8ba=-ab\)
\(8x^2+ 8x^2= 16x^2\)

Таким образом:
\((7ab-8ba)+(8x^2+8x^2)+15k^6x^9 = -ab+16x^2+15k^6x^9\)

Мы получили многочлен стандартного вида \(-ab+16x^2+15k^6x^9\), который является наиболее простой формой записи данного многочлена.

После рассмотренного примера мы можем выделить алгоритм для приведения многочлена к стандартному виду.

Чтобы привести многочлен к стандартному виду, необходимо:
1. Привести все одночлены, из которых состоит данный многочлен, к стандартному виду

2. В полученном многочлене привести подобные слагаемые

Стандартный вид многочлена – вид многочлена, при котором все его члены представлены в стандартном виде, а также приведены все подобные слагаемые.

Именно по стандартному виду, в зависимости от того, из скольких слагаемых состоит многочлен, этому многочлену дают название. В данном случае в стандартном виде многочлена \(-ab+16x^2+15k^6x^9\) три слагаемых, значит, и называться он будет трехчленом.

Какой многочлен может трансформироваться в одночлен? Рассмотрим многочлен \(2xy+xy-5xy\). Все члены этого многочлена – подобные слагаемые. Значит, мы можем привести эти подобные слагаемые: \(2xy+xy-5xy=-2xy\) Видим, что получился одночлен \(-2xy\). Как же так: был многочленом, а стал одночленом? Все верно, такая «трансформация» может произойти, если изначально многочлен не был приведен к стандартному виду и все члены этого многочлена – подобные слагаемые.

Степень многочлена – это старшая (наибольшая) среди степеней всех членов многочлена.

В нашем случае, многочлен \(-ab+16x^2+15k^6x^9\) в его стандартном виде состоит из трех членов: \(-ab\) (степень 2), \(16x^2\) (степень 2), \(15k^6x^9\) (степень 15). Наибольшая среди степеней этих членов – 15. Поэтому и степень многочлена будет равна 15. В таком случае, говорят, что многочлен \(-ab+16x^2+15k^6x^9\) – трехчлен пятнадцатой степени.

Многочлен первой степени называют линейным многочленоном (линейный двучлен, линейный трехчлен).

Многочлены второй степени также называют квадратными (например, квадратный трехчлен, квадратный двучлен).

Член с наибольшей степенью среди всех членов многочлена называется старшим членом.

В данном случае старшим членом многочлена \(-ab+16x^2+15k^6x^9\) является член \(15k^6x^9\).

Старший коэффициент многочлена – коэффициент старшего члена данного многочлена.

В нашем случае, коэффициент \(15k^6x^9\) равен \(15\), что и будет являться старшим коэффициентом многочлена \(-ab+16x^2+15k^6x^9\).

Что такое полином? Помимо классического и привычного названия  «многочлен», смысл которого довольно понятен – «много членов», в математике многочлен также называют полиномом. Произошло это название от греческих слов poly, что в переводе означает  «много», и nomos, что переводится как «часть». В таком случае названия многочленов в зависимости от количества членов: двучлены, трехчлены, четырехчлены и так далее, также носят свои названия. В греческом языке существуют числительные приставки, которые и будут меняться. Например: бином (двучлен), трином (трехчлен).Не забыли и про приставку числительного 1, поэтому одночлен будет также называться  «моном».

Итак, мы разобрались с понятием многочлена, а значит, самое время перейти к действиям с многочленами.

Сложение и вычитание многочленов

Многочлен – это в первую очередь сумма одночленов. 

Когда речь заходит о суммах, легче всего представлять себе что-то в денежном эквиваленте. Представим, у нас есть две суммы: первая – пять золотых монет и шесть серебряных, вторая – одна золотая монета и две серебряных. Что будет, если мы их сложим? Конечно, у нас получится одна большая сумма, состоящая из шести золотых монет и восьми серебряных. 

Так же работает и с многочленами – сумма двух многочленов образует новую сумму, то есть многочлен.

Итак, сумма двух или нескольких многочленов также является многочленом.

При вычитании же одного многочлена из другого может получиться как многочлен, так и одночлен. 

Для сложения и вычитания многочленов мы будем пользоваться следующими правилами:

1. \(a+(b+c)=a+b+c\)
   Если перед скобками стоит знак «+», то скобки раскрываются без изменения знаков слагаемых, стоящих внутри.

2. \(a-(b+c)=a-b-c\)
   Если перед скобками стоит знак «-», то скобки раскрываются с изменением знаков слагаемых, стоящих внутри, на противоположные.

Пользуясь первым правилом, сложим два многочлена: \(5x*7pk+8x^2y-2z и 6z-2xyx*2\):

\(5x*7pk+8x^2y-2z+(6z-2xyx*2)=5x*7pk+8x^2y-2z+6z-2xyx*2\)

Мы получили многочлен \(5x*7pk+8x^2y-2z+6z-2xyx*2\), осталось только привести его к стандартному виду. Для этого сначала приведем к стандартному виду все члены этого многочлена:

\(5x*7pk+8x^2y-2z+6z-2xyx*2=35xpk+8x^2y-2z+6z-4x^2y\)

Теперь приведем подобные слагаемые:

\(35xpk+8x^2y-2z+6z-4x^2y=35xpk+8x^2y-4x^2y-2z+6z=35xpk+4x^2y+4z\)

Получили многочлен стандартного вида \(35xpk+4x^2y+4z\), а именно – трехчлен третьей степени.

Пользуясь вторым правилом, вычтем из многочлена \(w^2q^5-5c^4+17sps*2\) многочлен \(c^3c+25s^2p-8\):

\(w^2q^5-5c^4+17sps*2-( c^3c+25s^2p-8)=w^2q^5-5c^4+17sps*2- c^3c-25s^2p+8\)

Далее аналогично приведем все члены получившегося многочлена к стандартному виду:

\(w^2q^5-5c^4+17sps*2- c^3c-25s^2p+8=w^2q^5-5c^4+34s^2p- c^4-25s^2p+8\)

И, наконец, осталось привести подобные слагаемые: 

\(w^2q^5-5c^4+34s^2p- c^4-25s^2p+8=w^2q^5-5c^4- c^4+34s^2p-25s^2p+8=\)
\(=w^2q^5-6c^4+9s^2p+8\)

Получили одночлен стандартного вида \(w^2q^5-6c^4+9s^2p+8\), а именно – четырехчлен седьмой степени.

Таким образом, чтобы произвести сложение/вычитание многочленов, необходимо:

1) раскрыть скобки по одному из правил выше;

2) при необходимости, привести получившийся многочлен к стандартному виду.

Со сложением и вычитанием мы разобрались, поэтому переходим к умножению. Для начала рассмотрим умножение многочлена на одночлен.

Умножение многочлена на одночлен

Для того чтобы умножить многочлен на одночлен, вспомним одно очень важное свойство в математике – распределительное свойство:

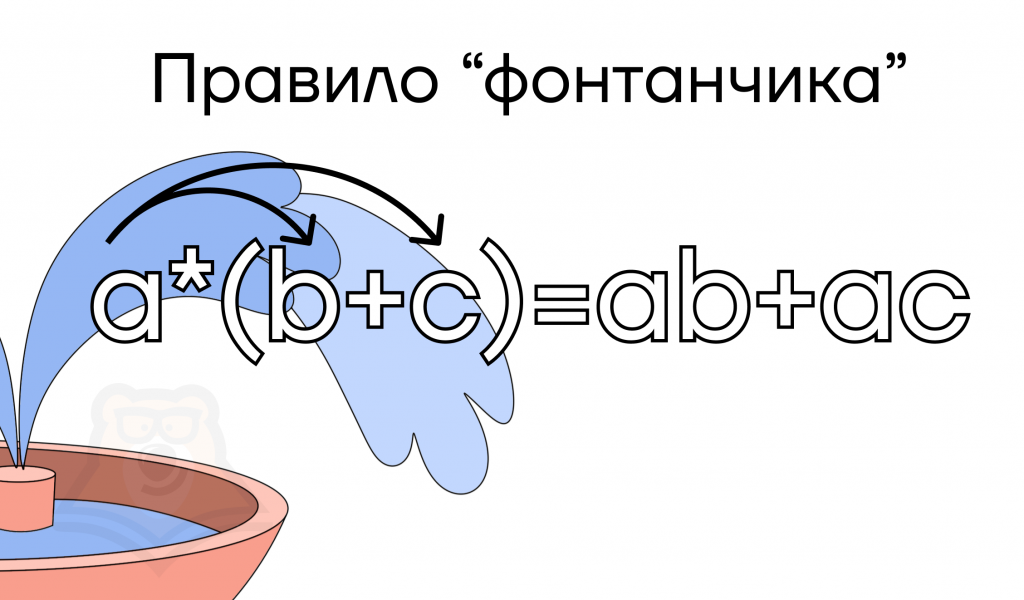
\(a*(b+c)=ab+ac\)

Чтобы умножить многочлен на одночлен, необходимо этот одночлен умножить на каждый член данного многочлена и полученные произведения сложить. 

Это правило также называют правилом «фонтанчика», так как схема раскрытия скобок визуально напоминает фонтан:

Пользуясь этим свойством, рассмотрим пример: умножим многочлен \(2a+xy-7axa^3\) на одночлен \(3a^2xy^3\):

\((2a+xy-7axa^3)*3a^2xy^3=2a*3a^2xy^3+xy*3a^2xy^3+7axa^3*3a^2xy^3\)

Получили многочлен, который теперь можем привести к стандартному виду:

\(2a*3a^2xy^3+xy*3a^2xy^3+7axa^3*3a^2xy^3=6a^3xy^3+3a^2x^2y^4+21a^6x^2y^3\)

В полученном многочлене нет подобных слагаемых, значит, можно считать, что он приведен к своему стандартному виду.

Разберем пример задания №20 из ОГЭ по математике.

Задание. Сократить дробь \(\frac{(6x)^2*(2y)^3}{144x^2y^3}\).

Решение. Начнем с преобразования числителя: возведем в степени одночлены \((6x)^2\) и \((2y)^3\), а затем выполним умножение получившихся одночленов:

\(\frac{(6x)^2*(2y)^3}{144x^2y^3}=\frac{(6^2*x^2)*(2^3*y^3)}{144x^2y^3}=\frac{36x^2*8y^3}{144x^2y^3}=\frac{36*8*x^2*y^3}{144x^2y^3}=\frac{288x^2y^3}{144x^2y^3}\)

Теперь осталось всего лишь выполнить деление двух одночленов:

\(\frac{288x^2y^3}{144x^2y^3}=\frac{288}{144}=2\)

Ответ: 2

Усложним задачу и попробуем разобраться в умножении многочлена на многочлен.

Умножение многочлена на многочлен

Снова обратимся к распределительному свойству умножения:

\(a*(b+c)=ab+ac\)

Что произойдет, если вместо переменной a в этой формуле поставить сумму двух переменных \((d+e)\)? Получим:

\((d+e)*(b+c)=(d+e)*b+(d+e)*c=db+eb+bc+ce\)

Таким образом: 

\((d+e)*(b+c)=db+eb+bc+ce\)

Чтобы умножить многочлен на многочлен, необходимо каждый член первого многочлена умножить на каждый из членов второго многочлена и полученные произведения сложить.

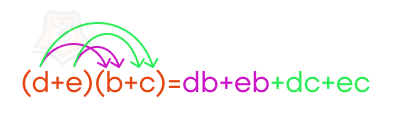
Очень важно при таком  «перемножении» не забывать учитывать знаки множителей.

Приведем пример. Умножим многочлен \(-7d+8m^2-1\) на многочлен \(5+8d\):

\((-7d+8m^2-1)*(5+8d)=-7d*5+8m^2*5-1*5-7d*8d+8m^2*8d-1*8d\)

Полученный многочлен приведем к стандартному виду:

\(-7d*5+8m^2*5-1*5-7d*8d+8m^2*8d-1*8d=\)
\(= -35d+40m^2-5-56d^2+64m^2d-8d=64m^2d+40m^2-56d^2-43d-5\)

Получили многочлен стандартного вида \(64m^2d+40m^2-56d^2-43d-5\).

Итак, осталось последнее действие с многочленами – деление многочлена на многочлен.

Деление многочлена на одночлен

Перед тем как перейти к разбору примера, опять же обратимся к важному свойству, которое понадобится нам для того чтобы мы смогли разделить многочлен на одночлен:

\(\frac{a+b}{c}=\frac{a}{c}+\frac{b}{c}\)

Чтобы разделить сумму на число, можно каждое слагаемое разделить на это число и полученные результаты сложить. 

Чтобы разделить многочлен на одночлен, можно каждый член данного многочлена разделить на этот одночлен и сложить полученные результаты.

Разберем пример: разделим многочлен \(6d^9oa^2-2dax^3\) на одночлен \(2da\):

\(\frac{6d^9oa^2-2dax^3}{2da}=\frac{6d^9oa^2}{2da}-\frac{2dax^3}{2da}=3d^8oa-x^3\)

В этом случае мы получили многочлен стандартного вида \(3d^8oa-x^3\).

При делении многочлена на одночлен результатом может быть выражение, не являющееся многочленом. Например:

\(\frac{4pv+9p^2vy-1}{2p^2v^2}=\frac{4pv}{2p^2v^2}+\frac{9p^2vy}{2p^2v^2}-\frac{1}{2p^2v^2}=\frac{2}{pv}+\frac{9y}{2v}-\frac{1}{2p^2v^2}\)

Как видим, выражение \(\frac{2}{pv}+\frac{9y}{2v}-\frac{1}{2p^2v^2}\) многочленом не является.

Рассмотрим пример задания №8 из ОГЭ по математике.

Задание. Найти значение выражения \(\frac{3a^2b-3ab^2}{3ab}\) при \(a=1059, b=1058\).

Решение. Для начала выполним деление многочлена \(3a^2b-3ab^2\) на одночлен \(3ab\):

\(\frac{3a^2b-3ab^2}{3ab}=\frac{3a^2b}{3ab}-\frac{3ab^2}{3ab}=\frac{3}{3}*\frac{a^2}{a}*\frac{b}{b}-\frac{3}{3}*\frac{a}{a}*\frac{b}{b^2}=a-b\)

При \(a=1059, b=1058\) получаем:

\(a-b=1059-1058=1\)

Ответ: 1

После того, как мы познакомились с действиями над многочленами, важно дать ответ еще на один вопрос: существуют ли равные многочлены? И как можно определить это равенство?

Тождественно равные многочлены

Выражения называют тождественно равными, если их значения равны при любых значениях переменных, входящих в эти выражения.

Например, рассмотрим два многочлена: \(5x+10y и 5(x+y)+5y\). Какие бы значения x и y мы ни взяли, значения этих выражений всегда будут получаться равными.

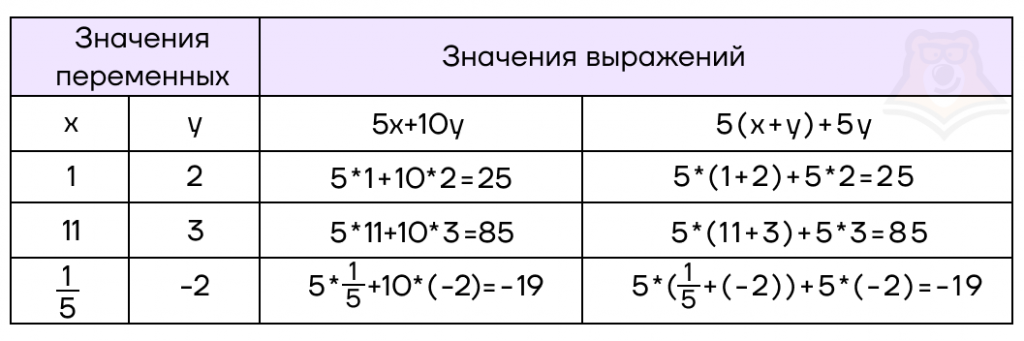
Можно и дальше продолжать подставлять различные значения переменных, значения выражений всегда будут получаться равными. Тогда можно сказать, что выражения \(5x+10y\) и \(5(x+y)+5y\) являются тождественно равными. Обозначается такое равенство знаком «=», то есть \(5x+10y=5(x+y)+5y\). 

Казалось бы, на первый взгляд и не скажешь, что два этих выражения равны друг другу, ведь выглядят они по-разному. При этом важно помнить, что многочлены могут принимать разные «облики», поэтому не нужно судить о равенстве сразу по внешнему виду.

Как же тогда определить тождественно равные выражения? Представим, что нам нужно доказать равенство выражений \(5x+10y\) и \(5(x+y)+5y\). То есть, доказать, что:

\(5x+10y=5(x+y)+5y\)

Для начала раскроем скобки в левой части этого равенства:

\(5x+10y=5x+5y+5y\)

Далее можно привести подобные слагаемые в левой и правой частях равенства. 

\(5x+10y=5x+10y\)

С левой и правой сторон равенства мы получили два одинаковых выражения. На самом деле, этого уже достаточно для того чтобы сказать, что выражения \(5x+10y\) и \(5(x+y)+5y\) являются тождественно равными. 

Если же мы хотим более точно показать это равенство, можно все слагаемые этого равенства перенести в одну сторону. Как переносить слагаемые из одной стороны равенства в другую, можно вспомнить из статьи «Линейные, квадратные и кубические уравнения».

\(5x+10y=5x+10y\)
\(5x+10y-5x-10y=0\)

Если теперь привести подобные слагаемые, то получим верное равенство:

\(0=0\)

Из этого следует и тождественное равенство двух исходных выражений \(5x+10y\) и \(5(x+y)+5y\). 

Таким образом, два выражения A и B тождественно равны друг другу, если A-B=0.  

Чтобы доказать, что выражения тождественно равны друг другу, необходимо в обоих выражениях раскрыть скобки и привести подобные слагаемые. Если в результате этих преобразований получились два одинаковых выражения, то равенство доказано.

Приведем еще один пример: докажем, что \(12a^2-4(a-1)=12a(a-1)+4(1+2a)\). Для начала раскроем скобки:

\(12a^2-4a+4=12a^2-12a+4+8a\)

Далее приведем подобные слагаемые:

\(12a^2-4a+4=12a^2-4a+4\)

Получили верное равенство, следовательно, выражения \(12a^2-4(a-1)\) и \(12a(a-1)+4(1+2a)\) тождественно равны друг другу, что нам и требовалось доказать.

На этом наше знакомство с многочленами закончилось. В этой статье мы разобрались с тем, что из себя представляет многочлен, а также посмотрели, как выполнять различные арифметические действия над многочленами.

В статье «Преобразования алгебраических выражений. Часть 1» речь пойдет о преобразованиях многочленов, что также играет большую роль при работе с различными выражениями. Так что очень рекомендуем сразу перейти и ознакомится с ней.

Термины

Одночлен – это алгебраическое выражение, представляющее собой произведение чисел и переменных, взятых в определенных степенях с натуральным показателем.

Фактчек

• Многочлен – это сумма двух и более одночленов. Одночлены, из которых состоит многочлен, называются членами многочлена. 
• Многочлен также имеет свой стандартный вид, с помощью которого можно определить степень, старший член и старший коэффициент многочлена. 
• Над многочленами можно совершать следующие операции: сложение и вычитание многочленов, умножение многочлена на одночлен, умножение многочлена на многочлен.

Проверь себя

Задание 1.
Многочлен – это:

1. сумма одночленов;
2. разность одночленов;
3. произведение одночленов;
4. множество одночленов.

Задание 2.
Многочлен \(5x^2-10xy+xx-2yx\):

1. представлен в стандартном виде;
2. представлен в нестандартном виде;
3. представлен в обычном виде;
4. ни один из вариантов.

Задание 3.
Чему равна степень многочлена \(ac^3+5k^7-2x^2y^6\)?

1. 4
2. 5
3. 7
4. 8

Задание 4.
Многочлен \(2x^2+3x-1\) является:

1. квадратным двучленом;
2. трехчленом третьей степени;
3. квадратным трехчленом;
4. двучленом третьей степени.

Ответы: 1. – 1; 2. – 2; 3. – 4; 4. – 3