Одночлены и действия с ними

На этой странице вы узнаете 

• На каком языке говорят математики?
• Почему любое число тоже многочлен?
• Какую неопределенность смог внести 0?

Практически каждый человек, когда речь заходит о математике, в первую очередь представляет себе числа и арифметические действия с этими числами: сложение, вычитание, умножение и деление. Поэтому и на вопрос «Где математика может пригодиться в жизни?‎» часто возникают ответы из рода «‎Посчитать сдачу в магазине/сколько птиц на небе/калории в порции обеда».

На самом же деле, в математике и других точных науках ключевую роль играют именно буквы, а не числа. Сегодня мы разберемся, что из себя представляют эти самые буквы в математике, где и в каких случаях они применяются, а также как с ними работать при решении тех или иных задач, разобрав тему «Одночлены‎». 

Числовые и алгебраические выражения

Представим ситуацию: кот Борис выловил из аквариума 10 рыб, а затем еще 2 рыбы. Тогда запись 10+2 обозначает математическое действие, которое нужно совершить, чтобы посчитать, сколько всего рыб Борис выловил из аквариума. 

Запись 10+2 называют числовым выражением. Число, которое мы получим в результате выполнения этого действия, называется значением числового выражения: 10+2=12, то есть 12 – значение выражения (10+2).

В данном случае необходимо выполнить только одно действие – сложение. При решении других задач действий может быть больше. 

Например, если кот Василий выловил из аквариума в два раза больше рыб, чем Борис, то, чтобы посчитать, сколько рыб выловил Василий, необходимо проделать следующие действия: (10+2)*2. Эта запись также будет называться числовым выражением. Аналогично посчитаем значение этого числового выражения: (10+2)*2=24.

Числовое выражение – это запись, состоящая из чисел, арифметических действий между этими числами (сложения, вычитания, умножения, деления), а также, при необходимости, скобок.

Значение числового выражения – это число, получаемое после выполнения всех действий данного числового выражения.

Числовые выражения отражают действия, которые необходимо совершить, чтобы прийти к необходимому результату, а значение числового выражения – сам результат.

Примеры числовых выражений и их значений приведены в таблице ниже:

Числовое выражение	Значение числового выражения
\(\frac{1}{4}+\frac{3}{4}\)	\(1\)
\(3*(5+8)-3\)	\(36\)
\(\frac{(13-5):4}{16}\)	\(\frac{1}{8}\)

Чтобы описать действия для более общих ситуаций, где величины могут принимать разные числовые значения, эти величины обозначают буквами. Буквы в математике также называют переменными, так как они могут менять свои числовые значения.

Например, вычисление периметра прямоугольника со сторонами a и b запишем следующим образом: (a+b)*2. 

Запись (a+b)*2 называют алгебраическим или буквенным выражением. 

Тогда, чтобы найти периметр прямоугольника со сторонами 2 и 5, необходимо проделать следующие действия: (2+5)*2. Получим результат 14. Это число называется значением алгебраического выражения  (a+b)*2 при a=2 и b=5. Чтобы найти значение алгебраического выражения, необходимо задать числовые значения всех переменных, входящих в это выражение.

Алгебраическое (буквенное) выражение – это запись, состоящая из чисел и переменных (букв), арифметических действий между ними (сложения, вычитания, умножения, деления), а также, при необходимости, скобок.

Значение алгебраического выражения при заданных значениях переменных – это число, получаемое при заданных значениях всех переменных, входящих в алгебраическое выражение, после выполнения всех действий данного алгебраического выражения. 

Важное замечание: при записи алгебраических выражений знак умножения между переменными ставить не принято. Например, запись ab означает a*b. 

Если в произведении числа и переменной число стоит перед переменной, то знак умножения тоже можно опустить. Например: 5x означает 5*x. 

Если же числовой множитель стоит после переменной, то убрать знак умножения нельзя. То есть, мы можем записать x*5 и никак иначе.

Разберем №12 из ОГЭ по математике.

Задание. Расстояние x, пройденное человеком, определяется по формуле x=nk, где n – число шагов, пройденных человеком, k – длина одного шага. Пользуясь этой формулой, определите расстояние в метрах, которое прошел Миша шагом в 0,6 м, сделав 10 шагов.

Решение. Длина шага Миши равна 0,6 м, то есть k=0,6 м, а также Миша сделал 10 шагов, то есть n=10. Необходимо найти расстояние x=nk. 

То есть нам нужно найти значение алгебраического выражения nk при k=0,6 и n=10. Сделаем это, подставив числовые значения переменных n и k в выражение.

nk=10*0,6=6

Выходит, что Миша прошел 6 м.

Ответ: 6

Приведем несколько примеров: 

Алгебраическое выражение	Заданные значения переменных	Значение выражения
\(2a+8\)	\(a=5\)	\(18\)
\((3+x)*2-y\)	\(x=3, y=1\)	\(11\)
\(\frac{k+p}{23}\)	\(k=2, p=14\)	\(\frac{16}{23}\)

Числовые и алгебраические выражения должны иметь смысл. То есть, записи 

• \(2+-17\)
• \(109:((3\)
• \(a∶0\)

не являются числовыми/алгебраическими выражениями.

На каком языке говорят математики? Как мы уже выяснили, в математике переменные обозначаются буквами. Тогда может возникнуть вопрос: буквами какого алфавита мы можем обозначать переменные?  Ответ прост – буквами латинского или греческого алфавита.  С латинским алфавитом мы уже не раз сталкивались. Точнее сказать, не с самим латинским алфавитом, а его братом-близнецом – английским алфавитом. Английский язык произошел от латинского, поэтому состоит из тех же букв, что и латинский. Но произносятся эти одинаковые буквы в разных алфавитах по-разному. От латинского алфавита произошло много других алфавитов и языков, которые мы сейчас знаем: итальянский, французский, испанский и так далее. С греческим алфавитом мы сталкиваемся не так часто в школьной программе, но, тем не менее, он активно используется в математике, ведь история математики начинается прямиком из Древней Греции. Из букв греческого алфавита, которые часто используются в математике, можно выделить известное число («Пи»), а также («альфа»). Последней буквой обычно обозначают углы в геометрических  фигурах.

В дальнейших разделах речь пойдет об алгебраических выражениях, а именно об одночленах и многочленах. Давайте разберемся, что они из себя представляют.

Понятие одночлена

Одночлен – это алгебраическое выражение, представляющее собой произведение чисел и переменных, взятых в определенных степенях с натуральным показателем. Напомним, что натуральные числа – это числа, используемые при счете (1; 2; 3; 4 и так далее).

Далее в ходе статьи мы не раз будем сталкиваться со степенями, поэтому рекомендуем вспомнить свойства степеней, которые описаны в статье «Действия с натуральными числами». 

Приведем несколько примеров одночленов: 

• \(2x^2yx\) 
• \(-a*9b^5z*5\)
• \(12\)

Почему любое число тоже одночлен? Да-да, обычные числа тоже являются одночленом. Очевидно, что в записи чисел нет ни одной переменной, однако мы помним, что любое число в степени с показателем 0 равно 1. Используем это: \(5=5*1=5*x^0=5*a^0b^0\) То есть, любое число можно представить как произведение этого же числа и переменных, взятых в нулевых степенях. А эта запись соответствует всем требованиям для одночлена.

Из статьи «Действия с натуральными числами» мы также помним, что деление – это действие, обратное умножению. То есть, от деления легко можно перейти к умножению. Поэтому выражения 

• \(\frac{5k}{3}=\frac{5}{3}k\)
• \(\frac{12z^5n^4}{7}=\frac{12}{7}z^6n^4\)

также являются одночленами.

А вот, например, выражение \(\frac{с}{7l}\) и другие выражения, где переменные стоят в знаменателе, одночленами не являются. Чтобы разобраться, почему так, перейдем в этом выражении от деления к умножению:

\(\frac{с}{7l}=с*\frac{1}{7l}=c*\frac{1}{7}*\frac{1}{l}=\frac{1}{7}cl^{-1}\)

Из определения одночлена помним, что переменные должны стоять  в степенях с натуральными показателями. В этом же случае показатель степени одной из переменных – отрицательное число, поэтому данное выражение одночленом являться не будет.

Наверняка практически каждый не раз слышал фразы  «Не накручивай себя»,  «Не усложняй». Вот и одночлены зачастую любят усложнять себя и свой внешний вид. 

Например, посмотрим на следующий одночлен: \(13*d^2*v^4*\frac{2}{13}*d^3*k^5*k*8\).

Согласитесь, выглядит слишком сложно? Так и хочется  здесь что-то  упростить. Если выполнить пару простых преобразований, то мы придем к другому, более «простому» виду:

\(13*d^2*v^4*\frac{2}{13}*d^3*k^5*k*8 = 13*\frac{2}{13}*8*d^2*d^3*v^4*k^5*k=16d^5v^4k^6\)

Мы преобразовали наш одночлен и свели его к максимально упрощенному виду: \(16d^5v^4k^6\). Его будет гораздо удобнее использовать в дальнейшем для решения различных задач. 

Такой максимально упрощенный вид одночлена называют стандартным видом одночлена. Он есть у абсолютно каждого одночлена. 

Как видим, стандартный вид одночлена получается путем перемножения всех числовых множителей, включенных в состав одночлена (в нашем случае \(13*\frac{2}{13}*8\)), а также степеней с одинаковым буквенным основанием (в нашем случае \(d^2*d^3, k^5*k, v^4\)).

В стандартном виде одночлена числовой множитель также называют коэффициентом одночлена. В произведении его записывают перед всеми буквами. В нашем случае \((16d^5v^4k^6)\) коэффициент одночлена равен 16.

Чтобы определить коэффициент одночлена, этот одночлен необходимо привести к стандартному виду.

Стандартный вид одночлена – это вид одночлена, представляющий собой произведение чисел и переменных, взятых в натуральных степенях, притом что каждая переменная встречается в этом произведении только один раз.

Коэффициент одночлена – это числовой множитель в стандартном виде записи данного одночлена.

Разберем пример задания №8 из ОГЭ по математике.

Задание. Упростить выражение \(5y^2*6y^3\) и найти его значение при \(y=2\).

Решение. Для упрощения выражения приведем одночлен \(5y^2*6y^3\) к стандартному виду:

\(5y^2*6y^3=5*6*x^2*x^3=30x^5\)

Осталось найти значение этого выражения при \(x=2\).

\(30x^2=30*2^5=30*32=960\)

Ответ: 960

Посмотрим еще пример приведения одночлена к стандартному виду:

\(a^2*\frac{2}{3}*a*z^{11}*z^6*\frac{3}{2}=\frac{2}{3}*\frac{3}{2}*a^2*a*z^{11}*z^6=a^3z^{17}\)

Таким образом, мы свели одночлен \(a^2*\frac{2}{3}*a*z^{11}*z^6*\frac{3}{2}\)  к его стандартному виду: \(a^3z^{17}\). Несмотря на то, что в стандартном виде \(a^3z^{17}\) мы напрямую не видим числового множителя, коэффициент здесь будет равен 1, потому что \(a^3z^{17}=1a^3z^{17}\).

Помимо коэффициента, ключевую роль при работе с одночленами играет степень одночлена. 

Степень одночлена – это сумма показателей степеней всех переменных, входящих в данный одночлен.

Например, у одночлена \(2k^4n^5l\) степень равна \(4+5+1=10\). Говорят, что одночлен \(2k^4n^5l\) – одночлен десятой степени. Обращаем внимание, что учитываются здесь показатели степеней всех переменных, входящих в одночлен, в том числе переменной \(l\), которая стоит в первой степени \((l=l^1)\).

Какую неопределенность смог внести 0? Нуль так же, как и все числа, является одночленом. При этом если говорить о всех числах, кроме 0, то степень таких одночленов равна 0. Действительно, ведь, как говорилось ранее, любое число, кроме 0, можно представить как произведение этого же числа на любую переменную в нулевой степени (напомним, что любое число/переменная в нулевой степени равняется 1): \(12=12a^0\) Сам же 0 считается одночленом неопределенной степени, ведь его можно представить, как произведение 0 на какую-либо переменную в любой натуральной степени: \(0=0*a^0=0*a^{15}=0*a^{1000}\) Таким образом, 0 – единственный одночлен, степень которого нельзя определить.

Итак, мы разобрались с понятием одночлена и его основными характеристиками: коэффициентом и степенью. Самое время перейти к действиям с одночленами. Ну а начнем мы со сложения и вычитания.

Сложение и вычитание одночленов

Что будет, если сложить пять мешков картошки с шестью мешками картошки? Правильно, получится одиннадцать мешков картошки.

А теперь обозначим мешок с картошкой какой-нибудь переменной, например, a. Тогда, 5a+6a=11a. Таким образом, сумма одночленов 5a и 6a есть одночлен 11a. 

Таким же образом мешок картошки можно было бы обозначить любым другим набором переменных в различных степенях. Например:

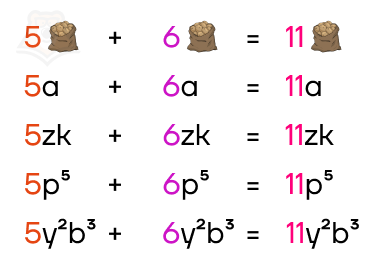
Как видим, вне зависимости от того, каким набором переменных и в каких степенях мы обозначим мешок картошки, в итоге все равно получится одночлен, коэффициент которого равен сумме коэффициентов складываемых одночленов (складываются количества мешков с картошкой), а набор степеней в соответствующих степенях останется таким же (если складываем мешки с картошкой, получаем мешки с картошкой).

Слагаемые одночлены с одинаковым набором переменных с одинаковыми показателями степеней называются подобными одночленами. 

Сумма подобных одночленов есть одночлен, коэффициент которого равен сумме коэффициентов складываемых одночленов, а набор переменных в соответствующих степенях равен этому же набору в складываемых одночленах.

Проще говоря, чтобы сложить подобные одночлены, необходимо сложить их коэффициенты, а набор переменных в соответствующих степенях оставить тем же. 

Приведем примеры:

\(29c+11c=40c\)
\(-5vj+7vj=2vj\)
\(\frac{8}{15}f^4k^2+\frac{7}{15}f^4k^2=\frac{15}{15}f^4k^2=f^4k^2\)

Обращаем внимание: у подобных одночленов должен быть не только одинаковый набор переменных, но и одинаковый набор показателей этих переменных. То есть, одночлены \(a\) и \(a^2\) подобными являться не будут. Сложить их по этому правилу не получится.

Что же касается вычитания? Из уже упомянутой статьи «Действия с натуральными числами» мы помним, что вычитание – это действие, обратное сложению. То есть, от вычитания легко можно перейти к сложению по принципу \(a-b=a+(-b)\). Пользуясь этим, вычтем из одночлена \(91aw\) одночлен \(85aw\).

\(91aw-85aw=91aw+(-85aw)=(91+(-85))aw=(91-85)aw=6aw\)

Как видим, вычитание подобных одночленов выполняется таким же образом, как и сложение. Только коэффициенты уже не складываются, а из коэффициента первого одночлена вычитается коэффициент второго одночлена.

А можем ли мы сложить пять мешков картошки с шестью мешками моркови? Разумеется, нет. Картошка и морковь – овощи разные, поэтому мешки картошки и мешки моркови будут обозначаться уже разными наборами переменных или одинаковым набором переменных, но взятых в разных степенях, то есть слагаемые одночлены не будут являться подобными. 

Отсюда вывод: выполнять действия сложения и вычитания можно только с подобными одночленами.

Процесс выполнения сложения и вычитания подобных одночленов также называют приведением подобных одночленов или приведением подобных слагаемых.

Таким образом, мы разобрались со сложением и вычитанием одночленов. Самое время перейти к следующему действию – умножению.

Умножение одночленов

Если коротко, то одночлен – это произведение чисел и переменных. Что же будет, если умножить одно произведение на другое? Конечно, получится одно большое произведение. Получается, что произведение двух одночленов также является одночленом.

Например, рассмотрим произведение одночленов \((5xy)\) и \((-12y^2x^3z)\):

\((5xy)*(-12y^2x^3z)=5xy*(-12)y^2x^3z\)

Мы получили одночлен \(5xy*(-12)y^2x^3z\), который теперь можно свести к стандартному виду:

\(5xy*(-12)y^2x^3z=5*(-12)*x*x^3*y*y^2*z=-60x^4y^3z\)

Получили одночлен восьмой степени \(-60x^4y^3z\) с коэффициентом \(-60\).

С умножением одночленов мы разобрались, а там, где есть умножение, есть и возведение в степень.

Возведение одночлена в степень

Как же быть с возведением одночлена в степень? Из свойств степеней мы помним, что \((ab)^n=a^nb^n\). По этому свойству и выполняется возведение одночлена в степень: чтобы возвести одночлен в степень, необходимо каждый множитель этого многочлена возвести в данную степень. Например, возведем многочлен \(3u^7bo^3\) в третью степень:

\((3u^7bo^3)^3=3^3*(u^7)^3*b^3*(o^3)^3=27u^{21}b^3o^9\)

Получили одночлен 33 степени \(27u^{21}b^3o^9\) с коэффициентом 27.

Мы уже выяснили, как выполнять целых три операции с одночленами: сложение, вычитание, умножение, а также разобрались, как возводить одночлен в натуральную степень. Осталось понять, как выполняется деление одночленов.

Деление одночленов

Предлагаем сразу рассмотреть пример: разделим одночлен \(13k^3i^7z\) на одночлен \(26k^9zx^4\). Для удобства, запишем деление в виде дроби с числителем \(13k^3i^7z\) и знаменателем \(26k^9zx^4\):

\(\frac{13k^3i^7z}{26k^9zx^4}=\frac{13}{26}*\frac{k^3}{k^9}*\frac{i^7}{1}*\frac{z}{z}*\frac{1}{x^4}=\frac{1}{2}*\frac{1}{k^6}*\frac{i^7}{1}*1*\frac{1}{x^4}=\frac{i^7}{2k^6x^4}\)

В ходе вычисления мы разложили наше деление таким образом, чтобы отдельно поделить числовые коэффициенты двух одночленов, а также переменные, которые входят в состав сразу обоих одночленов. Переменные \(i\) и \(x\) в их степенях  встречаются только в одном из одночленов, участвующих в делении, поэтому \(i^7\) остается без изменений в числителе, \(x^4\) – в знаменателе дроби.

Таким образом и выполняется деление одночленов: отдельно выполняется деление числовых коэффициентов, отдельно – переменных, которые входят в состав обоих одночленов. 

Приведем еще несколько примеров:

1. \(\frac{7x^5y^8}{9x^2y^6}=\frac{7}{9}*\frac{x^5}{x^2}*\frac{y^8}{y^6}=\frac{7}{9}x^3y^2\)

2. \(\frac{c^9u^2k}{9k^9u^2c}=\frac{1}{9}*\frac{c^9}{c}*\frac{u^2}{u^2}*\frac{k}{k^9}=\frac{1}{9}*\frac{c^8}{1}*1*\frac{1}{k^8}=\frac{c^8}{9k^8}\)

Как видим, при делении одночлена на одночлен может получиться как одночлен (в первом примере), так и выражение, не являющееся одночленом (второй пример).

Что же, с одночленами на этом покончено. На самом деле, одночлены – это лишь частички чего-то большего, а именно частички многочленов, с которыми мы и познакомимся в статье «Многочлены и действия с ними».

Термины

Периметр –  сумма длин всех сторон геометрической фигуры.

Прямоугольник – четырехугольник, у которого противоположные стороны равны и все углы прямые (90°).

Фактчек

• В математике различают числовые и алгебраические (буквенные) выражения.
• Одночлен – это алгебраическое выражение, представляющее собой произведение чисел и переменных, взятых в определенных степенях с натуральным показателем. У одночлена есть свой стандартный вид, коэффициент и степень.
• Слагаемые одночлены с одинаковым набором переменных с одинаковыми показателями степеней называются подобными одночленами. 
• Складывать и вычитать можно только подобные одночлены, умножать и делить – все одночлены.

Проверь себя

Задание 1.
Запись \(\frac{6ab}{7}\) является:

1. числовым выражением;
2. алгебраическим выражением;
3. оба варианта верны;
4. ни один из вариантов.

Задание 2.
Среди предложенных вариантов выбрать тот, где указаны подобные одночлены:

1. \(5ac^2\) и \(ac^2\)
2. \(m^3k^3\) и \(mk\)
3. \(7h\) и \(7y\)
4. \(-2f^5\) и \(2f\)

Задание 3.
Чему равна степень одночлена \(3xy^2z^5\)?

1. 1
2. 5
3. 7
4. 8

Задание 4.
Произведение одночлена \(5x^2\) и одночлена \(7xy\) равно:

1. \(35x^2y\);
2. \(35xy\);
3. \(35x^3y\);
4. невозможно определить.

Ответы: 1. – 2; 2. – 1; 3. – 4; 4. – 3