Модуль

На этой странице вы узнаете

• Как перевернуть график модуля?
• Одной ногой тут, другой там: к какому промежутку относить граничные точки?
• Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0? 

Модуль числа — это великая математическая мудрость, которая показывает дружбу и соперничество противоположных знаков: минуса и плюса. О том, что держит число в рамках, узнаем в статье.  

Модуль 

Мы легко можем найти расстояние от точки до точки, достаточно просто измерить его линейкой. Но можно ли найти расстояние от 0 до любого числа? 

Представим, что наш дом находится посередине между школой и магазином. И до школы, и до магазина 500 метров, но они стоят по разные стороны от дома. 

Расположим их на координатной прямой. Поскольку и школа, и магазин располагаются на одинаковом расстоянии, то от дома до них мы будем идти 500 метров. Но на координатной прямой до школы мы пройдем −500 метров, поскольку движемся против направления оси, а до магазина 500 метров. 

Будет ли являться полученный результат противоречием? Нет, поскольку когда мы ищем расстояние, нам неважно направление движения и знак. В математике существует специальное определение — это модуль, или абсолютная величина. 

Модуль — расстояние от любой точки на координатной прямой до начала координат. 

Поскольку на координатной прямой мы можем отложить расстояние в две стороны, то такое расстояние можно найти и с отрицательными точками, и с положительными. Расстояние измеряет длину отрезка, то есть оно всегда будет положительно. 

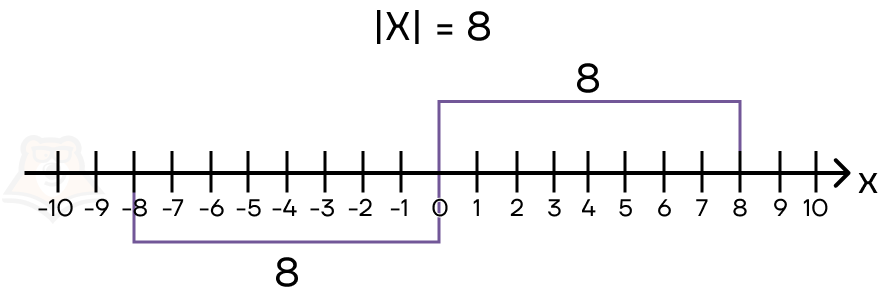
Можно сказать, что от любого числа модуль берет только цифры, а на знаки не обращает внимания. Например, |−8| = 8 и |8| = 8. 

Может возникнуть вопрос: куда исчезает минус? Чтобы избавиться от минуса, достаточно умножить число на −1: (-8) * (-1) = 8. Значит, модуль просто умножает число на -1. 

Отсюда получается, что модулем числа а называют выражение:

Возьмем два случая: a = 8 и a = -8. Для первого получаем |8| = 8, а для второго |-8| = -(-8) = 8, то есть определение выполняется. 

Можно ли взять модуль функции? Да. Модулем произвольной функции называют выражение:

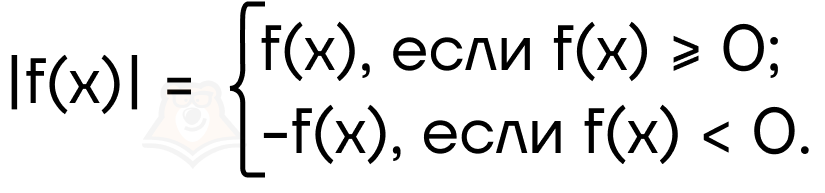
Изучить весь материал для ЕГЭ и ОГЭ и разобраться с темами любой сложности вы можете на курсах в онлайн-школе «Умскул»! Запишитесь на бесплатную консультацию и узнайте подробности про вебинары, платформу с домашками и пробниками и скидки:

Свойства модуля

Модуль, как и все понятия в математике, обладает своими свойствами. 

Свойство 1. |a| >= 0. 

Как мы уже говорили, модуль всегда будет положительным числом, поскольку он не обращает внимания на знак числа. 

Свойство 2. |a| = |-a|. 

Это свойство также подтверждает рассуждения выше. Модули противоположных чисел, то есть чисел с разными знаками, равны. 

Свойство 3. |a| >= a. 

Если число а будет положительным, например, 5, то неравенство |5| >= 5 \(\rightarrow\) 5 >= 5  выполняется, поскольку знак неравенства нестрогий. 

Если число а будет отрицательным, например, -5, то неравенство |-5| >= -5 \(\rightarrow\) 5 >= -5  выполняется, поскольку положительное число всегда больше отрицательного. 

Свойство 4. |a * b| = |a| * |b|. 

Пусть a = 5, b = -2, тогда |5 * (-2) | = |-10| = 10, и |5| * |-2| = 5 * 2 = 10, то есть выражения равны между собой. 

Свойство 5. \(|\frac{a}{b}| = \frac{|a|}{|b|}\). 

Рассуждения такие же, как и в предыдущем свойстве. Пусть a = 10, b = -5, тогда \(|\frac{10}{(-5)}| = |-2| = 2 и \frac{|10|}{|-5|} = \frac{10}{5} = 2\). 

Свойство 6. |a + b| <= |a| + |b|.

Почему появилось неравенство, а не уравнение, как в предыдущих двух свойствах? Разберем два примера. 

Пусть a = 1, b = 2, тогда |1 + 2| = |3| = 3 и |1| + |2| = 1 + 2 = 3 — неравенство выполняется, поскольку знак нестрогий.

Но если a = -1, b = 2, тогда |-1 +2| = |1| = 1 и |-1| + |2| = 1 + 2 = 3, откуда получаем 1 < 3. 

Свойство 7. \(\sqrt{a^2} = |a|\). 

Докажем это свойство. Пусть \(\sqrt{a^2} = x\), тогда x₀, поскольку квадратный «Корень» не может быть отрицательным. Возведем полученное уравнение в квадрат: a² = x² 
a² — x² = 0
(a — x)(a + x) = 0

Из уравнения x = a,  из-за ограничений на x получаем a >= 0.

И x = -a,  из-за ограничений на x получаем a < 0. 

То есть получается выражение модуля. 

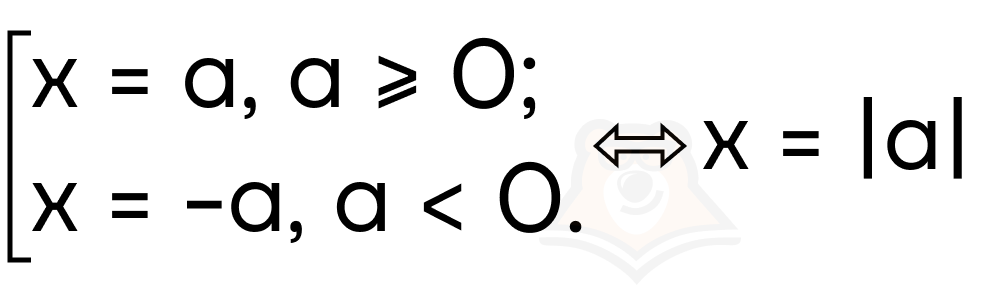
Свойство 8. |a|² = a².

Поскольку и модуль, и квадрат числа дают положительный результат, модуль в квадрате можно заменить просто квадратом числа. 

График модуля

Как изобразить функцию с модулем? Для начала разберемся, что делает модуль с графиком функции. 

Рассмотрим функцию y = x — это прямая. При этом у может быть и положительным, и отрицательным. 

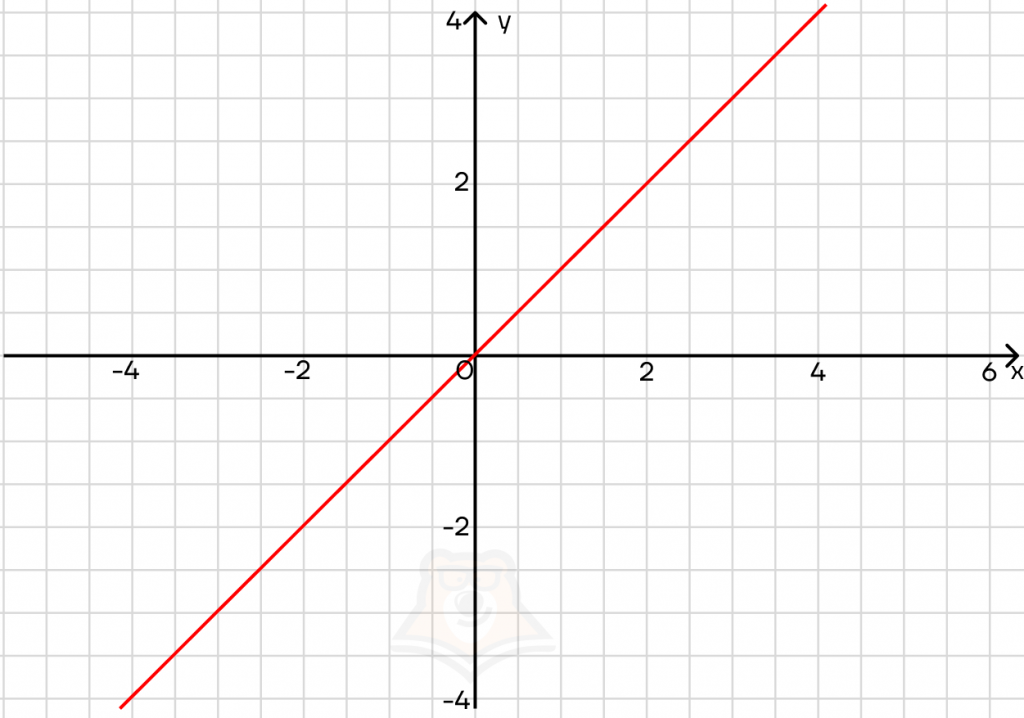
Занесем х под знак модуля: y = |x|. Теперь у может быть только положительным. Что происходит с частью графика, которая лежит ниже оси х? Она зеркально отражается. В итоге мы получаем галочку: 

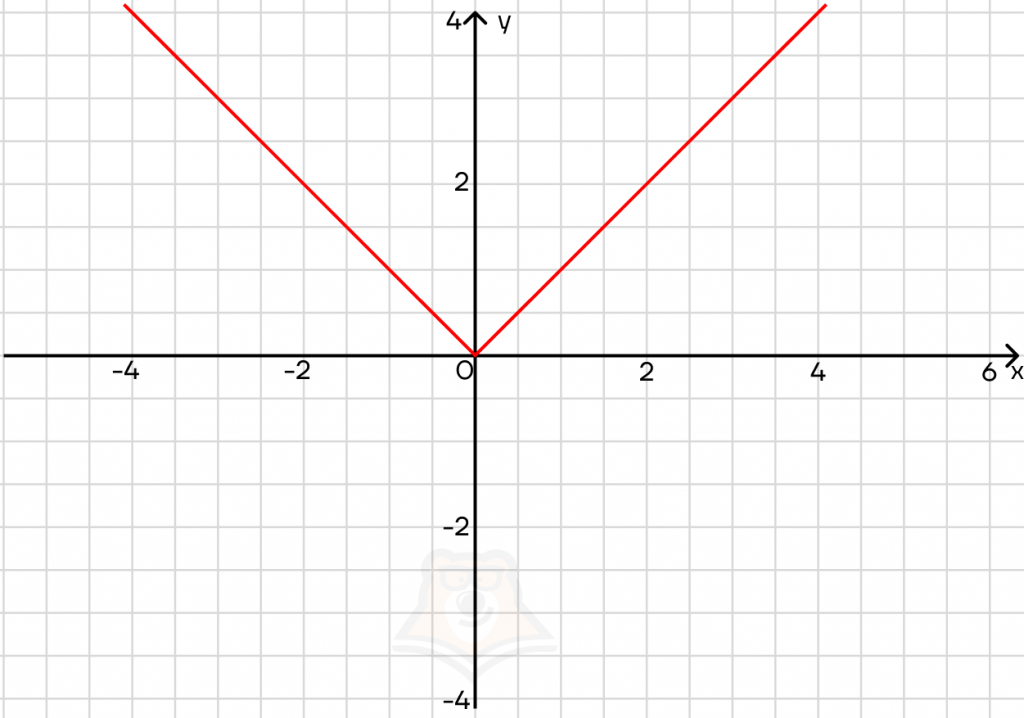
Модуль отражает любой график относительно оси х. 

Что будет, если перед х будет стоять коэффициент? Построим графики: 

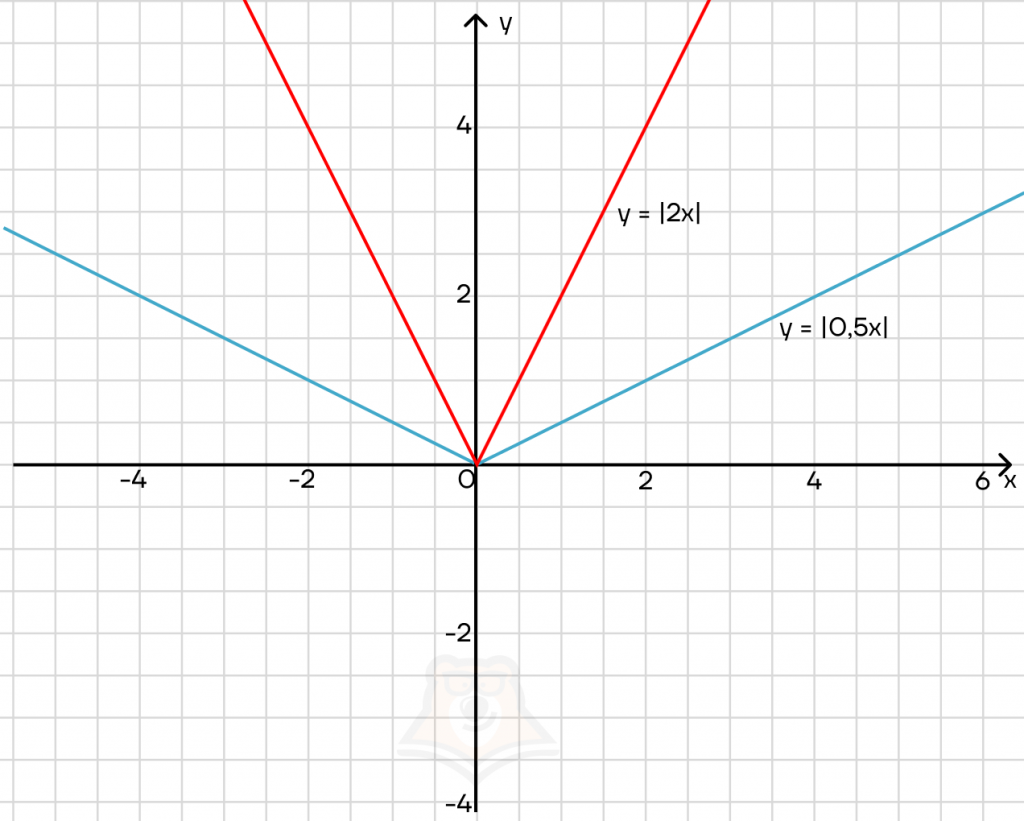
Галочка будет сужаться и расширяться. Причем чем больше коэффициент перед х, тем ýже будет галочка. 

Попробуем добавить слагаемое к подмодульному выражению. 

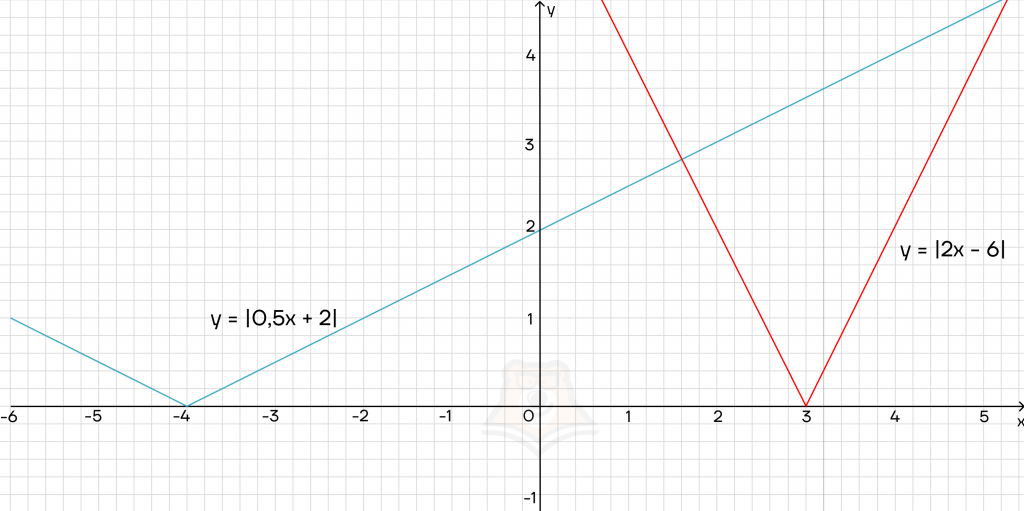
График модуля будет двигаться вдоль оси х. Причем:

• если мы прибавляем число, то график сдвигается влево;
• если мы вычитаем число, то график сдвигается вправо. 

Добавим число к модулю, а не подмодульному выражению:

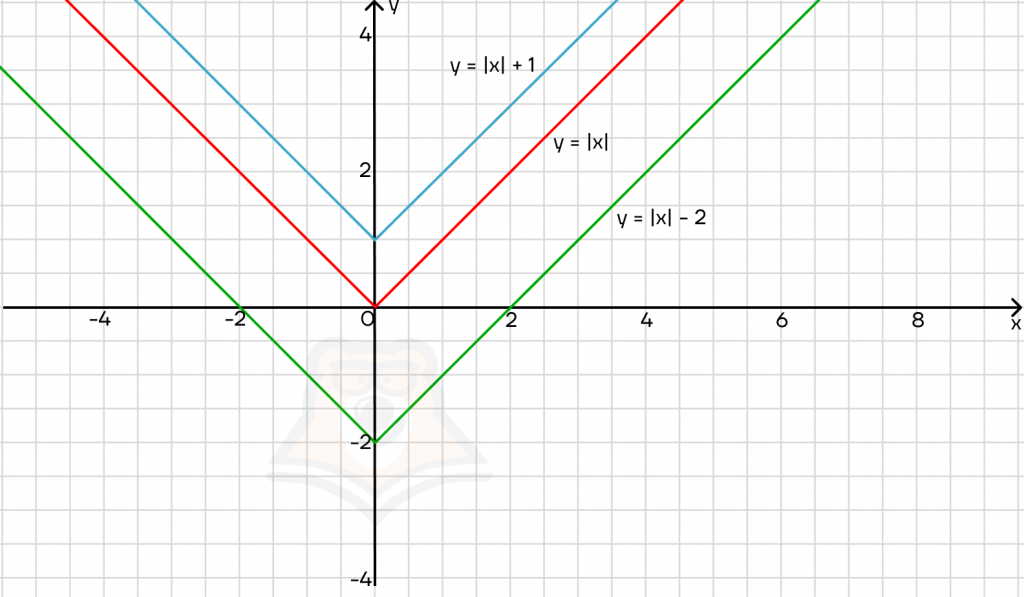
График будет двигаться вдоль оси у. 

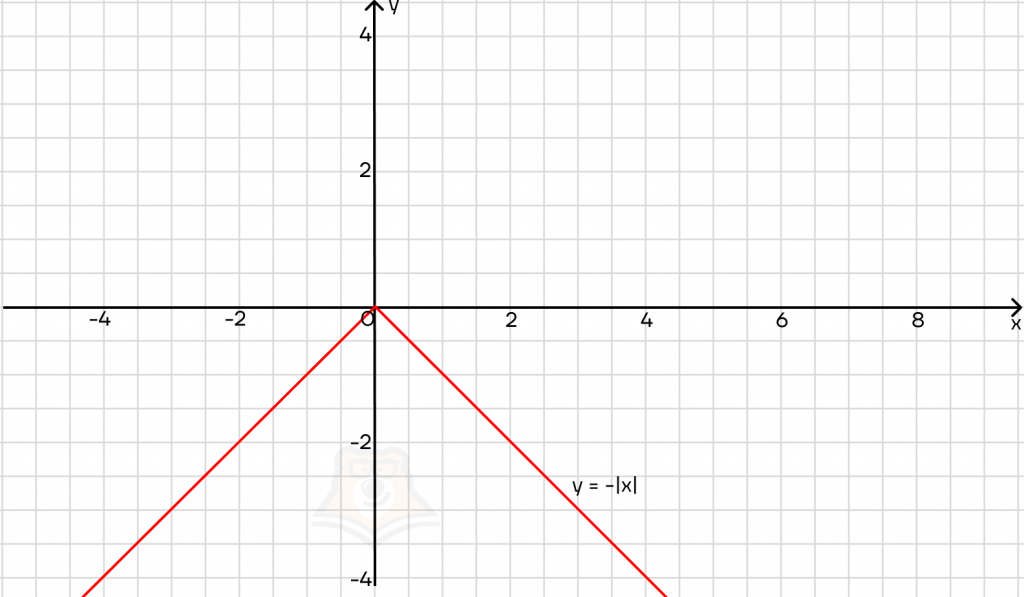
Как перевернуть график модуля? Для этого достаточно добавить перед модулем минус. Важно, чтобы минус стоял именно перед модулем, а не внутри него. Тогда график будет отзеркален относительно оси х и лежать только ниже нее.  Это легко проследить с помощью уравнений: если y = -|x|, то, при x = 3 получаем: y = -|3| = -3

Уравнения с модулем

1. Возьмем уравнение вида |f(x)| = a. Поскольку модуль не может быть отрицательным, то и а  не может быть отрицательным. Получаем следующий переход:

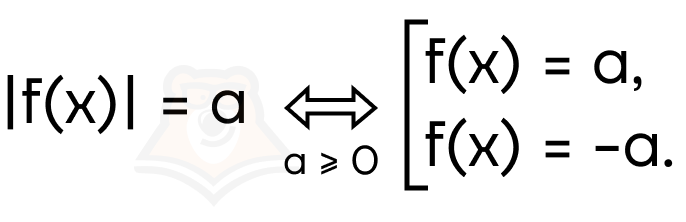
Пример 1. Решите уравнение |4x + 5| = 7. 

Решение. В уравнении f(x) = 4x + 5, a = 7. Воспользуемся переходом:

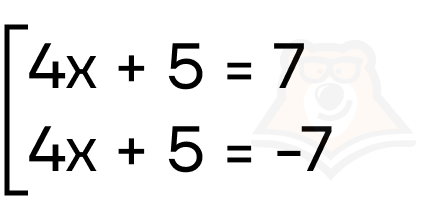
Из первого уравнения x = 0,5, а из второго уравнения x = -3. 

Ответ: 0,5: -3. 

2. В уравнениях и неравенствах можно встретить два разных модуля. Как быть в этом случае? 

Алгоритм решения уравнений с несколькими модулями  Шаг 1. Находим нули подмодульных выражений.  Шаг 2. Чертим числовую прямую и ищем знаки на промежутках для каждого модуля. Если подмодульное выражение отрицательно на промежутке, то ставится минус, если положительно — ставится плюс.  Шаг 3. Для каждого промежутка раскрываем модули. Если подмодульное выражение на промежутке отрицательно, то модуль раскрывается со знаком минус. Если положительно — модуль раскрывается со знаком плюс. Важно: полученные корни должны принадлежать промежуткам, на которых раскрывается модуль, иначе они не будут решениями уравнения.  Шаг 4. Записать все полученные корни в ответ.

Пример 2. Решите уравнение |x — 2| — |x + 2| = 4x — 5.

Решение. Найдем, в каких точках модули будут равны 0. Для этого подмодульное выражение также должно быть равно 0:

x — 2 = 0 \(\rightarrow\) x = 2
x + 2 = 0 \(\rightarrow\) x = -2

Нарисуем числовую прямую с этими точками: 

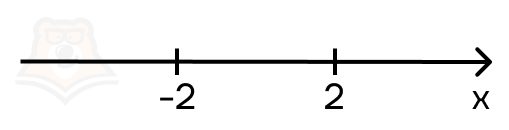
У нас получилось три промежутка: 

• (-\(\infty\);-2)
• [-2;2)
• [2;+\(\infty\))

Обратим внимание, какие знаки имеет первый модуль на промежутках: x — 2 > 0 при x > 2. Следовательно, на первых двух промежутках модуль будет отрицательным, а на третьем положительным. Расставим его знаки красным цветом. 

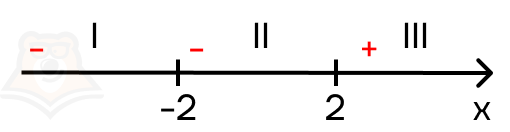
Проанализируем второй модуль: x + 2 > 0 \(\rightarrow\) x>-2. Получается, подмодульное выражение будет положительно на втором и третьем промежутке, и отрицательным на первом промежутке. Расставим его знаки синим цветом. 

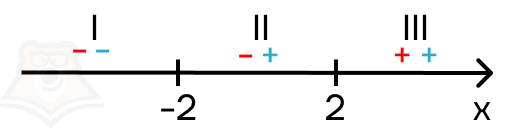
Теперь мы можем рассмотреть уравнение на всех трех промежутках. Однако для этого обязательно ввести ограничения: полученные точки должны принадлежать только этому промежутку, поскольку на следующем модули будут раскрываться уже по-другому. 

2. Рассмотрим первый промежуток: x<-2. Оба модуля раскрываются с отрицательным знаком, и мы получаем следующее уравнение:

-(x — 2) — (-(x + 2)) = 4x — 5
-x + 2 + x + 2 = 4x — 5
4 = 4x — 5
4x = 9
x = 2,25

Точка не удовлетворяет ограничению, поскольку не лежит в промежутке (-\(\infty\);-2):

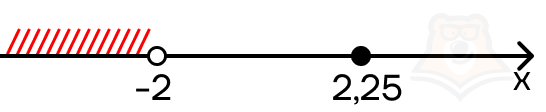
Рассмотрим второй промежуток: [-2;2). Первый модуль раскрывается с минусом, а второй с плюсом:

-(x — 2) — (x + 2) = 4x — 5
-x + 2 — x — 2 = 4x — 5
-2x = 4x — 5
6x = 5
\(x = \frac{5}{6}\)

Эта точка лежит в заданном промежутке и является решением уравнения. 

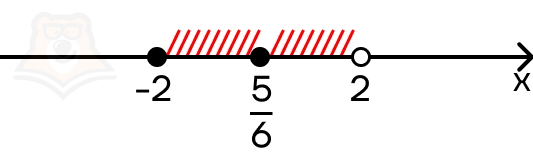
Рассмотрим третий промежуток [2;+\(\infty\)). Оба модуля раскрываются со знаком плюс, мы получаем уравнение:

(x — 2) — (x + 2) = 4x — 5
x — 2 — x — 2 = 4x — 5
-4 = 4x — 5
4x = 1

x = 0,25 — эта точка не лежит в промежутке, то есть не является решением уравнения. 

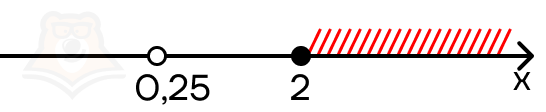
Решением уравнения будет только \(x = \frac{5}{6}\). 

Ответ: \(\frac{5}{6}\)

Одной ногой тут, другой там: к какому промежутку относить граничные точки? Разбивая прямую на промежутки, может возникнуть вопрос: а что делать с точками, в которых модуль равен 0? Их обязательно нужно проверять. Можно сделать это как отдельно, подставив точки в уравнение, так и сразу включить их в условие раскрытия модуля.  Если точки включаются в условие раскрытия модуля, то достаточно включить их только в один из двух промежутков. Включать их в два промежутка нецелесообразно: одна и та же точка будет проверяться дважды.

3. Уравнения вида |f(x)| = g(x)

Поскольку вместо функций могут стоять любые выражения, раскрыть модуль можно двумя способами. Выбор одного из них зависит от того, какая функция проще: f(x) или g(x). 

Как можно раскрыть модуль?

• Можно раскрыть его в зависимости от знаков подмодульного выражения: если подмодульное выражение отрицательное, то модуль раскрывается с минусом, если положительное, то с плюсом. 
• Можно возвести уравнение в квадрат. Но здесь необходимо ввести ограничения на g(x) — поскольку функция равна модулю, она не может быть отрицательной. 

Для удобства можно пользоваться следующей схемой: 

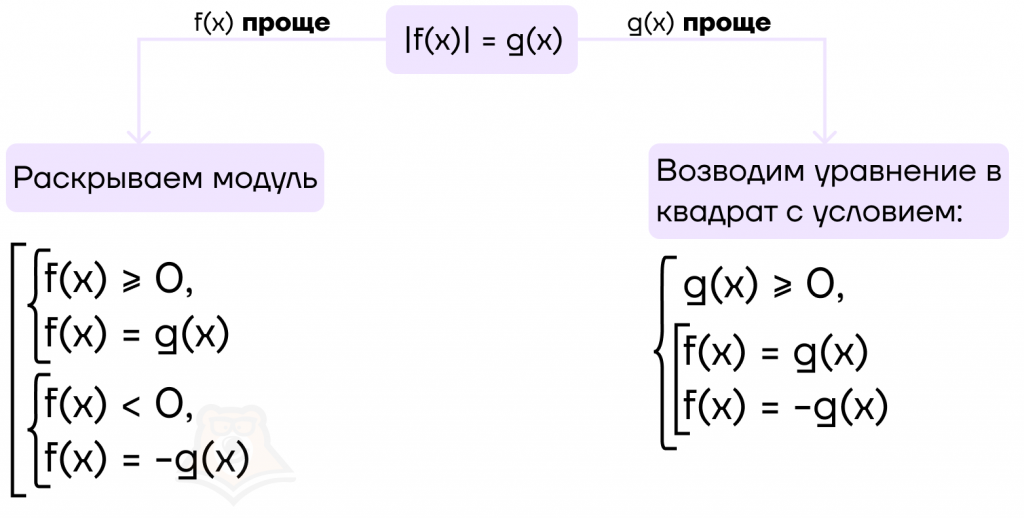
Пример 3. Решите уравнение |8 — x| = x² — 5x + 11.

Решение. Заметим, что подмодульное выражение значительно проще функции справа, в этом случае удобнее будет раскрыть модуль. Получаем совокупность двух систем: 

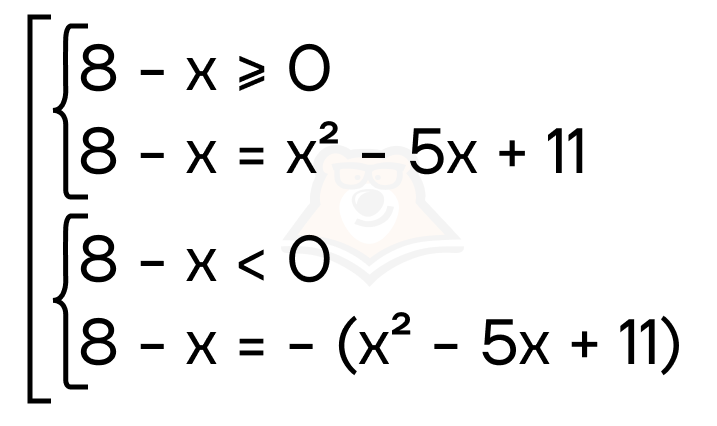
Рассмотрим первую систему.

8 — x >= 0 \(\rightarrow\) x <= 8

Решим уравнение:

8 — x = x² — 5x + 11
x² — 4x + 3 = 0
D = 16 — 12 = 4
\(x_1 = \frac{4 + 2}{2} = 3\)
\(x_2 = \frac{4 — 2}{2} = 1\)

Оба корня уравнения удовлетворяют условию x <= 8, значит, решением системы будут 1 и 3. 

Рассмотрим вторую систему. 

8 — x < 0 \(\rightarrow\) x > 8

Решим уравнение: 

8 — x = -x² + 5x — 11
x² — 6x + 19 = 0
D = 36 — 76 = -40 — при отрицательном дискриминанте решения уравнений нет. 

Решением всего уравнения будут x = 1 и x = 3. 

Ответ: 1, 3

4. Разберем еще один тип уравнений, когда модуль равен модулю. Неужели придется рассматривать целых 4 случая раскрытия модуля? Нет, достаточно будет возвести в квадрат обе части уравнения. Таким образом, мы получаем следующий переход: 

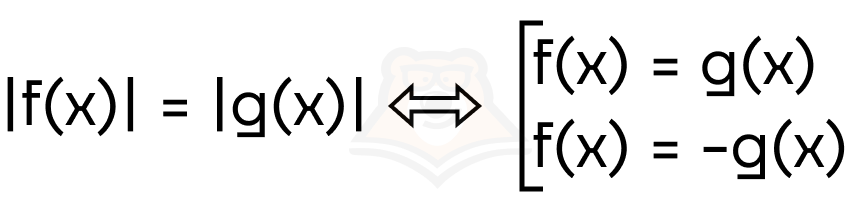
Пример 4. Решите уравнение |x — 2| = |2x + 8|.

Решение. Возведем обе части уравнения в квадрат. Для этого воспользуемся свойством 8.

(x — 2)² = (2x + 8)²
(x — 2)² — (2x + 8)² = 0

Воспользуемся формулой сокращенного умножения:

((x — 2) — (2x + 8))((x — 2) + (2x + 8) = 0

Если произведение множителей равно 0, то каждый множитель равен 0. Тогда:

x — 2 — (2x + 8) = 0 \(\rightarrow\) x — 2 = 2x + 8
x — 2 + (2x + 8) = 0 \(\rightarrow\) x — 2 = -(2x + 8)

Получаем совокупность: 

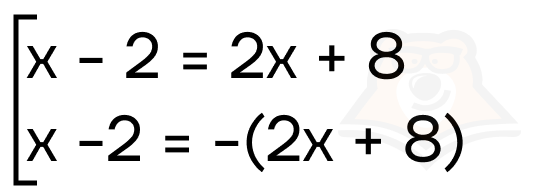
Решим первое уравнение совокупности:

x — 2 = 2x + 8
x = -10

Решим второе уравнение совокупности:

x — 2 = -2x — 8
3x = -6
x = -2

Решением уравнения будут x = -10 и x = -2

Ответ: -2, -10

Неравенства с модулем

Разобравшись, как решаются уравнения с модулем, можно приступать к неравенствам. 

Пример 5. Решите неравенство x² — |3x — 7| + 7 >= 0. 

Решение. Найдем, при каких значениях х модуль равен 0. Получаем 3x = 7 \(\rightarrow\) \(x = \frac{7}{3}\). 

Определим, с какими знаками модуль будет раскрываться на каждом промежутке. 

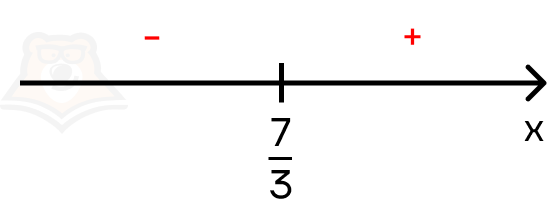
Осталось рассмотреть неравенство на двух промежутках. 

1. \(x \leq \frac{7}{3}\), тогда
x² — (-(3x — 7)) + 7 >= 0
x² + 3x — 7 + 7 >= 0
x² + 3x >= 0
x(x + 3) >= 0

Решим это неравенство «Методом интервалов». Сразу учтем ограничение \(x \leq \frac{7}{3}\). 

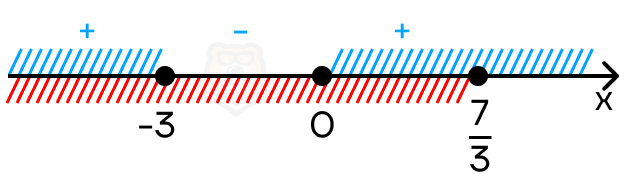
Получаем, что решением неравенства на заданном промежутке будет \(x \in (-\infty; -3] U[0; \frac{7}{3}]\). 

2. \(x > \frac{7}{3}\), тогда 
x² — 3x + 7 + 7 >= 0
x² — 3x + 14 >= 0
x² — 3x + 14 = 0
D = 9 — 56 = -47 — корней на заданном отрезке не будет. 

Может ли решением квадратного неравенства быть любое число, если дискриминант меньше 0?  Вспомним, что корни квадратного уравнения — это точки пересечения параболы и оси х. Если парабола не пересекает ось х, то неизбежно лежит выше или ниже ее. Поскольку в нашем случае ветви параболы направлены вверх, мы можем нарисовать ее примерный график.  Так как парабола задается функцией y = x2 — 3x + 14, то неравенство будет выполняться при всех y >= 0. Парабола целиком попадает в эту область, а решением неравенства будет любое х.

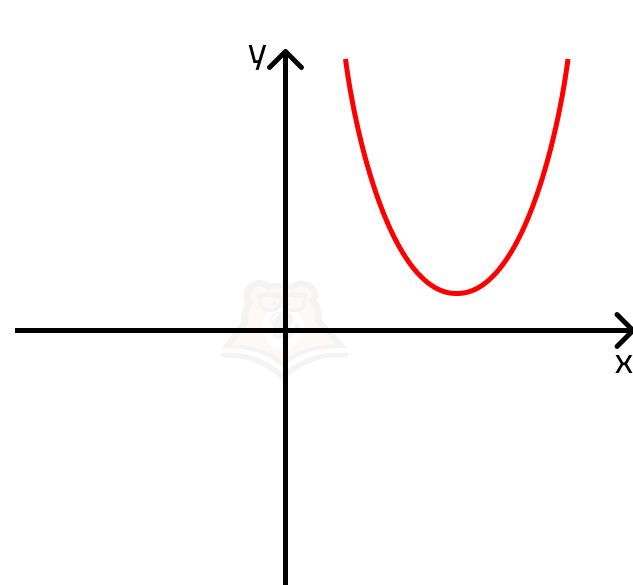
Однако не стоит забывать про ограничение \(x > \frac{7}{3}\). Накладывая его, получаем решение \((\frac{7}{3}; + \infty)\). 

Осталось только объединить полученные на промежутках решения: 

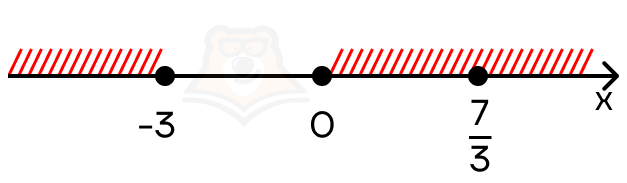
Получаем, что \(x \in (-\infty;- 3] U [0; +\infty)\).

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

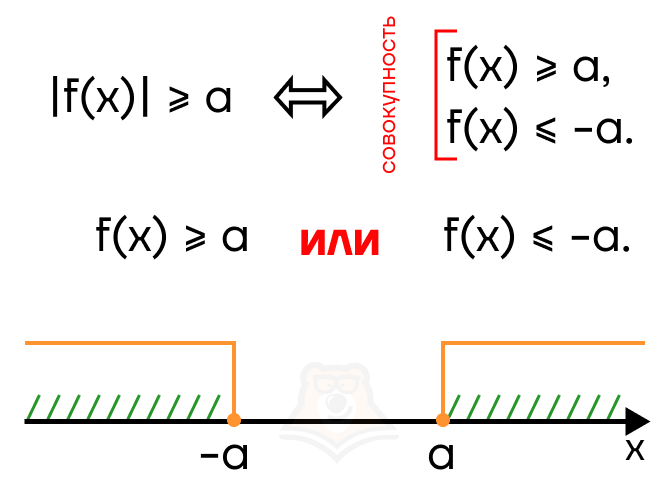
Рассмотрим неравенства вида |f(x)| > a и |f(x)| < a, где а — некоторое число и a >= 0. Модуль можно раскрыть двумя способами и получить два неравенства. Но будет это совокупность или система?

Это зависит от знака. Разберем случай |f(x)| > a. Заметим, что строгость знака может быть любой. Тогда модуль раскрывается как: 

f(x) > a и -f(x) > a \(\rightarrow\) f(x) < -a. 

Отметим эти промежутки на числовой прямой:

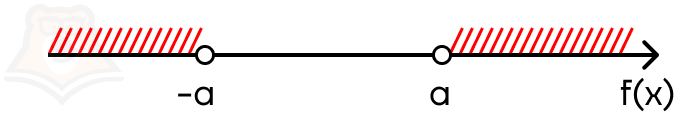
В ответе должны оказаться оба промежутка — их нужно объединить. В этом случае модуль раскрывается в совокупности. 

Рассмотрим случай |f(x)| < a, здесь строгость знака также может быть любой. Раскроем модуль: f(x) < 0 и -f(x) < a \(\rightarrow\) f(x) > -a. На числовой прямой это будет выглядеть следующим образом: 

В в ответе должен оказаться промежуток от —а до а. Следовательно, необходимо воспользоваться системой, чтобы “отсечь” лишние промежутки. 

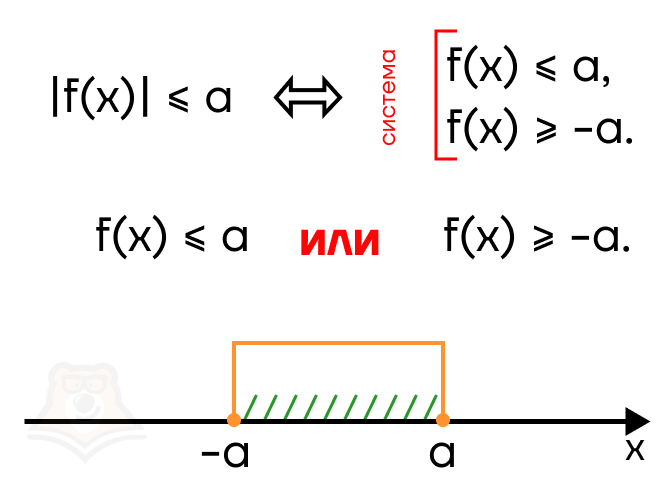
Можно ли обойтись в этом случае без раскрытия модуля? Да, но необходимо возвести неравенство в квадрат. 

|f(x)| ⋁ a | \(\uparrow\) 2 — вместо ⋁ может стоять любой знак неравенства. 
f²(x) ⋁ a²
f²(x) — a² ⋁ 0

Воспользуемся формулой сокращенного умножения:

(f(x) — a)(f(x) + a) ⋁ 0

Однако стоит помнить, что обе части неравенства можно возвести в квадрат только в том случае, если они неотрицательны. То есть обязательно должно выполняться условие a0. 

Мы получили равносильный переход. Но существуют ли равносильные переходы, если вместо числа а стоит другая функция или даже модуль? Да. Они выводятся таким же способом, как и переход для неравенства с числом. Получаем еще два равносильных перехода:

• |f(x)| ⋁ g(x) \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0  

g(x) обязательно должно быть неотрицательным, чтобы можно было возвести неравенства в квадрат. 

• |f(x)| ⋁ |g(x)| \(\rightarrow\) (f(x) — g(x))(f(x) + g(x)) ⋁ 0

Разберем на примере, как можно использовать равносильный переход. Для этого возьмем то же неравенство, что и в примере 5, но решим его по-другому. 

Пример 6. Решите неравенство x² — |3x — 7| + 7 >= 0. 

Решение. Перенесем модуль в другую часть неравенства:

|3x — 7| <= x² + 7. Модуль всегда неотрицателен. Правая часть неравенства неотрицательна, поскольку число в квадрате всегда положительно. 

Повторим действия, чтобы прийти к равносильному переходу:

(3x — 7)² <= (x²+7)²
(3x-7)² — (x² + 7)² <= 0
(3x — 7 — (x² + 7))(3x — 7 + x² + 7) <= 0
(3x — 7 — x² — 7)(3x + x²) <= 0
(-x² + 3x — 14) * x(3 + x) <= 0
-(x² — 3x + 14) * x(3 + x) <= 0
(x² — 3x + 14) * x(3 + x) <= 0

Рассмотрим первую скобку:

x² — 3x + 14 = 0

D = 9 — 56 = -47 — корней нет. Выражение всегда будет положительно, то есть на него можно разделить все неравенство. Получаем:

x(3 + x) <= 0

Тогда \(x \in (-\infty;- 3] U [0; +\infty)\)

Ответ: \(x \in (-\infty;- 3] U [0; +\infty)\)

При решении можно сразу использовать равносильный переход, не расписывая его. 

Итак, неравенства с модулем можно решить двумя способами: раскрывать модуль и воспользоваться равносильным переходом. Выбор способа зависит от личных предпочтений и удобства решения.

Фактчек

• Модуль — расстояние от любой точки на координатной прямой до начала координат. Модуль обозначается двумя вертикальными черточками: |a| = a и |-a| = a. 
• Модулем числа называют выражение: 

• График модуля представляет собой “галочку”, которая лежит выше оси х. Модуль отражает график любой функции зеркально оси х так, что значения у всегда больше 0. 
• Модуль можно раскрыть двумя способами. Этим свойством можно пользоваться при решении уравнений с модулем. 
• При решении неравенств с модулем можно раскрывать его, либо воспользоваться равносильным переходом, если в неравенстве выполняются все условия для него. 

Проверь себя

Задание 1. 
Чему равно выражение |-16 * 2|?

1. 32
2. −32
3. −16
4. 16

Задание 2. 
Какой график имеет функция y = |x|?

1. Парабола
2. Гипербола
3. Прямая
4. Галочка

Задание 3. 
Решите уравнение |x| = -3. 

1. 3
2. −3
3. Решений нет
4. 3 и −3 

Задание 4. 
Решите уравнение |x + 2| = 15. 

1. −13
2. 17
3. 13 и -17
4. Решений нет 

Задание 5.
Какой равносильный переход можно использовать для неравенства вида |f(x) |⋁ |g(x)|?

1. f(x) ⋁ g(x)
2. f(x) ⋀ g(x)
3. f²(x) — 2 * f(x) * g(x) + g²(x) ⋁ 0
4. (f(x) — g(x))(f(x) + g(x)) ⋁ 0 

Ответы: 1. — 1 2. — 4 3. — 3 4. — 3 5. — 4