Свойства чисел

На этой странице вы узнаете

• От чего пошло название Google? 
• Где в подсолнухе находятся числа?
• Как представить число π в виде дроби?

Числа представляют собой основу математики и позволяют понимать мир вокруг нас, описывая количество, порядок, структуру и многое другое. Возможно покажется, что свойства чисел представляют из себя скучные и ненужные факты, но это не так. Они помогают нам решать задачи, анализировать данные, принимать решения и даже понимать поведение окружающей нас среды. Именно об этом мы поговорим в этой статье. 

Советуем перед изучением данной статьи ознакомиться со статьей «Дроби», так вам будет намного легче понять тему.

В повседневной жизни свойства чисел помогают нам считать, измерять, планировать бюджеты, строить графики, анализировать тенденции, разрабатывать алгоритмы, и даже делать прогнозы. Понимание свойств чисел позволяет нам улучшать навыки решения проблем, расширять понимание мира и принимать лучшие решения на основе числовых данных.

Понятия числа и числовые множества

Числа – это абстрактные математические объекты, которые используются для измерения, подсчета, оценки и многих других математических операций. 

В математике и повседневной жизни используются различные типы чисел для различных целей.

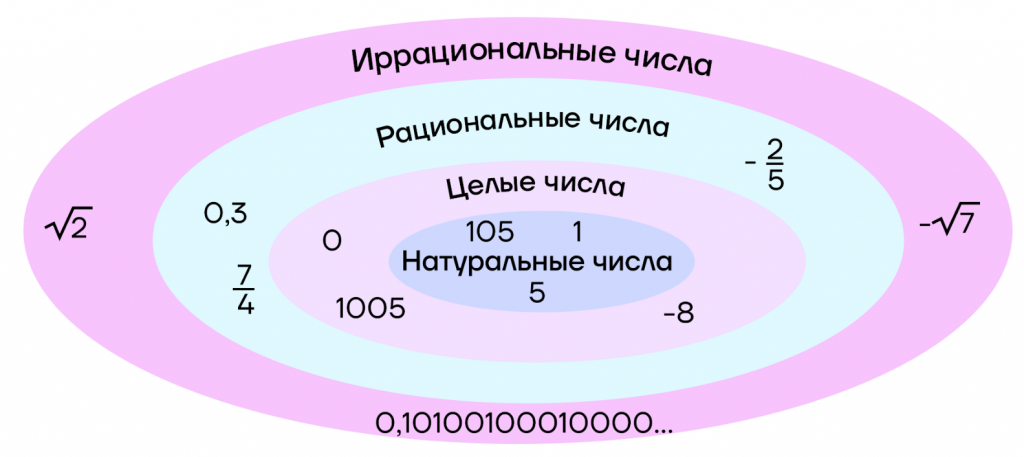
• Натуральные числа (1, 2, 3, 4, …) используются для подсчета объектов и представляют количество элементов в конечном множестве.

• Целые числа (…, -3, -2, -1, 0, 1, 2, 3, …) расширяют натуральные числа так, чтобы они включали отрицательные числа и ноль. 

• Рациональные числа (например, -4, 2,7) представляются в виде дробей или конечных/периодических десятичных дробей. 

• Иррациональные числа (например, √2, π (число Пи), e (экспонента)) не могут быть представлены в виде дроби и имеют бесконечное непериодическое разложение. 

Так, каждое множество включает в себя предыдущее и расширяет его.

Любое целое число можно записать в виде суммы. Это важно помнить, так как это может сильно помочь при решении 19 задания ЕГЭ по профильной математике.

Например, \(321 = 3*100+2*10+1*1\) или
\(12345 = 1*10000+2*1000+3*100+4*10+5*1\). 

От чего пошло название Google? Название Google является искаженным написанием слова «гугол». Когда создатели поисковика хотели использовать «googol», оказалось, что такой домен уже занят.  А вот сам гугол означает число \(10^{100}\). Казалось бы, что это много, но факториал 70 превышает гугол на 20%. Но видели бы вы число гуголплекс, который является числом 10 в степени гугол…

Каждый тип чисел имеет свои уникальные свойства и применения в математике и реальном мире. Давайте же поговорим о понятиях, которые чаще всего используются в математике. 

Целая и дробная части чисел

Давайте представим, что числа – это пироги. Целая часть пирога –  это то, что у нас есть целиком, без каких-либо кусочков, а дробная часть –  это та маленькая часть, которую мы можем отделить от целого пирога.

Например, представим, что у нас есть пирог, но мы должны поделить его поровну между тремя друзьями. В таком случае, мы порежем пирог на три равные части, и каждая часть пирога будет равна \(\frac{1}{3}\).

Целая часть числа – это часть числа, которая находится перед десятичной точкой или запятой в его десятичном представлении.

Дробная часть числа – это часть числа, которая находится после десятичной точки или запятой в его десятичном представлении. 

Например, для числа 25,36:

• 25 – целая часть числа;
• 0,36 – дробная часть числа. 

Часто в заданиях необходимо найти различные части числа. Как же это сделать? Например, найти у числа 15,25 дробную его часть легко. Нам нужно просто исключить целую часть, и останется 0,25. Найти целую часть тоже легко, просто убираем дробную: в нашем случае от 15,25 останется 15. 

Иногда нужно найти число по его дроби. Как это сделать, можно подробнее узнать в этой статье. Приведем наглядный пример.

\(15\frac{1}{4}=\frac{15*4+1}{4}=\frac{61}{4}=15,25\) или \(15 \frac{1}{4}=15+0,25=15,25\)

То есть можно сделать дробь неправильной, а далее перевести ее в привычный десятичный вид. Либо же перевести только дробь, а затем сложить с целой частью.

Где в подсолнухе находятся числа? Слышали про числа Фибоначчи? Это такая последовательность чисел, в которой первые два числа равны 0 и 1, а все последующие числа равны сумме двух предыдущих. Первые 11 чисел Фибоначчи выглядят так: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. С помощью этой последовательности была создана спираль Фибоначчи, которая встречается в природе. Например, в подсолнухах, сосновых шишках, раковинах улиток и так далее.

Мы рассмотрели определения, связанные с числами. Теперь можем ввести понятия и свойства четности чисел, которые часто требуются для быстрого счета или решения задач и упрощают математические действия. Давайте поговорим о них.

Четность чисел

Все числа в математике делятся на четные и нечетные. Какие же это числа?

Четное число – это число, которое делится на 2 без остатка.

Например, 4, 10, и 18 являются четными числами.

Нечетное число – это число, которое не делится на 2 без остатка. 

Например, 3, 7 и 11 являются нечетными числами.

Из этих понятий вытекают некоторые математические свойства, которые бывают очень полезны.

• Сумма или разность двух четных чисел всегда является четным числом.
• Сумма или разность четного и нечетного числа всегда является нечетным числом.
• Произведение двух четных чисел всегда является четным числом.
• Произведение четного числа на нечетное число всегда является четным числом.

Рассмотрим это на примерах.

Четное число в общем виде записывается как 2n, так как четные делятся на 2, соответственно в общей записи должен быть этот множитель. А нечетное записывается как \(2n+1\). 

• Сумма или разность двух четных чисел: \(2n+2n=4n\), то есть число четное. 
• Сумма или разность четного и нечетного чисел: \(2n+2n+1=4n+1\), получилось нечетное число.
• Произведение двух четных чисел: \(2n*2n=4n\), и опять четное число.
• Произведение четного числа на нечетное число: \(2n*(2n+1)=4n^2+2n\), четное.

Как представить число π в виде дроби? Число π — иррациональное, поэтому представить в виде обыкновенной дроби его невозможно. Но в древности этого не знали. Примерно в 1900 году до нашей эры было первое из более точных, чем 3, приближений: \(\frac{25}{8}=3,125\) и \(\frac{256}{81}\approx 3,16\). Во втором веке китайский ученый Чжан Хэн предложил два эквивалента числа \(π: \frac{92}{29}\approx 3,1724\) и \(\sqrt{10}\approx 3,1622\). Архимед получил такую оценку: \(3\frac{10}{71}<π<3\frac{1}{7}\).  Позднее еще были варианты \(\frac{377}{120}, \frac{864}{275}\) и \(\frac{355}{113}\).

Мы рассмотрели все понятия, определения и свойства. Давайте же скорее перейдем к практике и посмотрим, как можно применять полученные знания.

Решение задач

Решение задач позволяет развивать навыки работы с арифметическими операциями. При этом задачи не только помогают понять особенности различных типов чисел, но и развивают логическое мышление, аналитические способности и умение применять полученные знания на практике. А уже далее от простых задач перейти к более сложным!

Задачи на целые числа

Задачи на целые числа предполагают решение задач, включающих операции над целыми числами, такие как сложение, вычитание, умножение, деление, а также решение уравнений и неравенств с использованием целых чисел. Примерами задач могут быть задачи на арифметические действия с целыми числами, задачи на нахождение делителей, простых чисел, кратности и другие.

Задача. На школьной ярмарке было продано 315 билетов. Если в первый день было продано 86 билетов, а во второй – 147 билетов, то сколько билетов было продано на третий день?

Чтобы найти количество билетов, проданных на третий день, нужно из общего количества билетов вычесть количество билетов, проданных в первый и второй дни:

\(315 — 86 — 147 = 82\)

Ответ: на третий день было продано 82 билета.

Такая простая задача является типичной для обучения арифметическим операциям с целыми числами. По сути большинство задач, которые решаются нами, относятся к задачам этого типа.

Решим задание, которое может встретиться на ОГЭ по математике в задании №8.

Задание. Найдите значение выражения \((8b-8)(8b+8)-8b(8b+8)\) при \(b=2\)

Решение. Можно сразу заметить, что у выражения есть похожие скобки \((8b+8)\). Вспомним свойства:

\(ab+ac=a(b+c)\)

Тогда получим: 

\((8b+8)((8b-8)-8b)=(8b+8)(8b-8-8b)=(8b+8)*(-8)\)

Теперь можно подставить \(b=2\):

\((8*2+8)*(-8)=(16+8)*(-8)= -192\)

Ответ: \(-192\)

Задачи с целой и дробной частью числа

Задачи с целой и дробной частью числа представляют собой разнообразные математические задачи, требующие работу с целыми числами и их дробными частями.  Эта тема помогает  развить навыки работы с дробями, понимание их операций, а также применение математических концепций в повседневных ситуациях.

Задачи включают различные типы, такие как операции с дробями, решение уравнений и неравенств с дробными числами, а также практические применения дробей.

Давайте для начала рассмотрим самую простую задачу, требующую знания работы с обыкновенными дробями.

Задача. Вычислить \(\frac{4}{25}+\frac{15}{4}\).

Здесь нужно привести дроби к общему знаменателю, получим:

\(\frac{4}{25}+\frac{15}{4}=\frac{4*4}{25*4}+\frac{15*25}{4*25}=\frac{16}{100}+\frac{375}{100}=\frac{391}{100}\)

Теперь можем привести дробь к десятичной:

\(\frac{391}{100}=3\frac{91}{100}=3,91\)

Ответ: \(3,91\)

Задача:  У Лизы было \(\frac{3}{4}\) пачки муки. Она использовала \(\frac{1}{2}\) этой части для выпечки пирога. Сколько частей пачки муки осталось у Лизы?

Согласно условию, часть пачки, которая была использована Лизой, составляет:

\(\frac{3}{4}*\frac{1}{2}=\frac{3}{8}\) пачки муки

Чтобы найти сколько частей пачки муки осталось у Лизы, вычитаем использованную часть из начальной: 

\(\frac{3}{4}-\frac{3}{8} =\frac{6}{8} — \frac{3}{8} =\frac{3}{8}\)

Ответ: у Лизы осталось \(\frac{3}{8}\) пачки муки.

Такая задача демонстрирует применение дробей в повседневной ситуации.

Решим задание, которое может встретиться на ОГЭ по математике в задании №6.

Задание. Найдите значение выражения \(\frac{2,4}{2,9 — 1,4}\)

Решение. Последовательно найдем значение выражения:
\(\frac{2,4}{2,9 — 1,4}=\frac{2,4}{1,5}=\frac{24}{15}=\frac{8}{5}=1\frac{3}{5}=1,6\)

Ответ: \(1,6\)

Но на самом деле задач такого типа очень много. В рамках данной статьи мы показали лишь базовые примеры. Нам пора двигаться дальше и изучить другой тип задач.

Задачи на перебор всех возможных вариантов

Задачи на перебор всех возможных вариантов включают в себя разнообразные математические задачи, которые требуют перебора всех возможных комбинаций или вариантов решения для достижения оптимального результата. Эти задачи способствуют развитию навыков логического мышления.

Задача. У вас есть 3 различных цвета LEGO кубиков: красный, синий и зеленый. Сколькими различными способами вы можете сложить эти кубики в ряд? Необходимо использовать все кубики.

Для решения этой задачи мы можем использовать прямой метод перебора. Мы можем начать с одного цвета, затем двух и, наконец, всех трех цветов. Таким образом, возможные варианты для укладки цветов в ряд будут:

1. красный, синий, зеленый;
2. красный, зеленый, синий;
3. синий, красный, зеленый;
4. синий, зеленый, красный;
5. зеленый, синий, красный;
6. зеленый, красный, синий. 

Итак, всего у нас получилось 6 вариантов. Эту же задачу можно решить с помощью формулы перестановок, о которой мы говорили в этой статье. 

Ответ:  6

Этот пример иллюстрирует, как мы можем применить принцип перебора всех возможных вариантов для нахождения количества комбинаций в данной задаче. То есть для больших и сложных задач это долгий процесс, требующий внимания и концентрации.

Теперь сделаем то, к чему мы готовились всю эту статью, — решим задачу из ЕГЭ по профильной математике.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №19. 

Задание. Есть трехзначное натуральное число, которое не может начинаться с 0 и не кратное 100.
а)  Может ли частное этого числа и суммы его цифр равняться 90?
б)  Может ли частное этого числа и суммы его цифр равняться 88?
в)  Какое наибольшее натуральное значение у частного данного числа и суммы его цифр?

Решение. Представим наше число как \(100a+10b+c\). 

Пусть \(k\) — частное числа и суммы его цифр, то есть \(k=\frac{100a+10b+c}{a+b+c}\). Запишем иначе: \(100a+10b+c=ka+kb+kc\).

Нужно отметить, что в пунктах а и б
в ответе нужно лишь подобрать пример, который подтверждает или опровергает вопрос из задания.

а) Нужно, чтобы частное было равно \(90\), тогда:

\(100a+10b+c=90a+90b+90c\)
\(10a=80b+89c\)

Это уравнение выполняется при таком наборе чисел:

\({a, b, c} = {8, 1, 0}.\)

Проверим это, подставив в уравнение:

\(10*8=80*1+89*0\)
\(80=80\)

Соответственно, частное числа и суммы его цифр может быть равным \(90\).

б) По аналогии с пунктом а:

\(100a+10b+c=88a+88b+88c\)
\(12a=78b+87c\)

Если \(a\geq 10\), то число будет уже четырехзначное, поэтому \(a<10\). То есть максимальные значения \(b\) и \(с\) — \(0\) и \(1\) или \(1\) и \(0\) соответственно. Причем, при \(b=c=1\) получаем \(78b+87c=78+87=165>12*9=108\), (\(108\) будет являться наибольшим числом, которое мы можем получить слева). Значит какое-то из чисел (\(b\) или \(c\)) нужно обнулить. Но при этих значениях уравнение не выполняется. Проверим это:

— Если \(a = 7\), то слева будет \(84\).
— Если \(a = 8\), то слева будет \(96\).
— Если \(a = 9\), то слева будет \(108\).

Такие значения не получаются ни при каких \(b\) и \(c\), поэтому и не может частное трехзначного числа и суммы его цифр быть равным \(88\).

в) Выведем общую формулу из \(100a+10b+c=ka+kb+kc\):

\((100-k)a=(k-10)b+(k-1)c\)

Так как \(b+c>0\), потому что число не может быть кратно \(100\), а \((100-k)a\) должно быть меньше \(10\), то:

\(9(100-k)\geq (100-k)a=(k-10)b+(k-1)c\geq (k-10)(b+c)\geq k-10\)

То есть:

\(9(100-k)\geq k-10\)
\(900-9k\geq k-10\)
\(910\geq 10k\)
\(91\geq k\)

Соответственно, наибольшее число \(k\), а то есть частное числа и суммы его цифр, равно \(91\). 

Рассмотрим число \(910\). Сумма его цифр равна \(10\). \(\frac{910}{10}=91\).
Ответ: а) да, например \(810\); б) нет; в) \(91\).

Не нужно бояться последних заданий! Как вы могли заметить, первые два пункта вообще решаются с помощью логики и много теории для них знать не нужно.

Итак, мы рассмотрели определения, свойства, а также ознакомились с основными практическими задачами по данным темам. Надеемся, что вам было интересно! Приглашаем вас познакомиться и с другими не менее интересными темами и продолжить изучение математики в статье «Действия с натуральными числами».

Термины

Факториал — произведение всех натуральных чисел от 1 до данного числа, обозначается знаком «!». Например, \(5!=1*2*3*4*5\).

Фактчек

• Число – это абстрактный математический объект, используемый для измерения количества или подсчета. Числа могут быть классифицированы по различным критериям, например, натуральные числа, целые числа, рациональные числа и действительные числа.
• Целая часть числа – это часть числа без дробной части или остатка.
• Дробная часть числа – это часть числа, которая находится после десятичной точки. 
• Четное число – это такое число, которое делится на 2 без остатка. Например, 2, 4, 6, и т.д. являются четными числами.  

Проверь себя

Задание 1.
Какое из следующих чисел является четным?

1. 17
2. 23
3. 42
4. 3

Задание 2.
Что из следующего является целой частью числа 5,78?

1. 5
2. 78
3. 5,78
4. 0,78

Задание 3.
Пусть a – четное число, тогда каким числом является выражение \(3a\)?

1. Четным
2. Нечетным
3. Простым
4. Максимальным

Задание 4.
В гараже стоит 15 автомобилей. \(\frac{3}{5}\) из них – черные. Сколько автомобилей красного цвета?

1. 3
2. 10
3. 9
4. 5

Ответы: 1. — 3; 2. — 1; 3. — 1; 4. — 3.