Тригонометрическая окружность. Часть 2

На этой странице вы узнаете

• Как еще больше закрутить окружность?
• Как связаны треугольник и окружность?
• Где на окружности оси тангенса и котангенса?

Тригонометрическая окружность — один из способов работы с тригонометрическими функциями. В статье «Тригонометрическая окружность. Часть 1» мы обсудили: что такое тригонометрическая окружность, как ее построить и как отложить на окружности углы в градусах или радианах. Сейчас мы продолжим изучение тригонометрической окружности и разберемся, как с ней связаны тригонометрические функции. 

В предыдущих сериях…

На окружности можно отложить любой угол. Для этого необходимо отложить от 0 необходимую величину и отметить точку на окружности. 

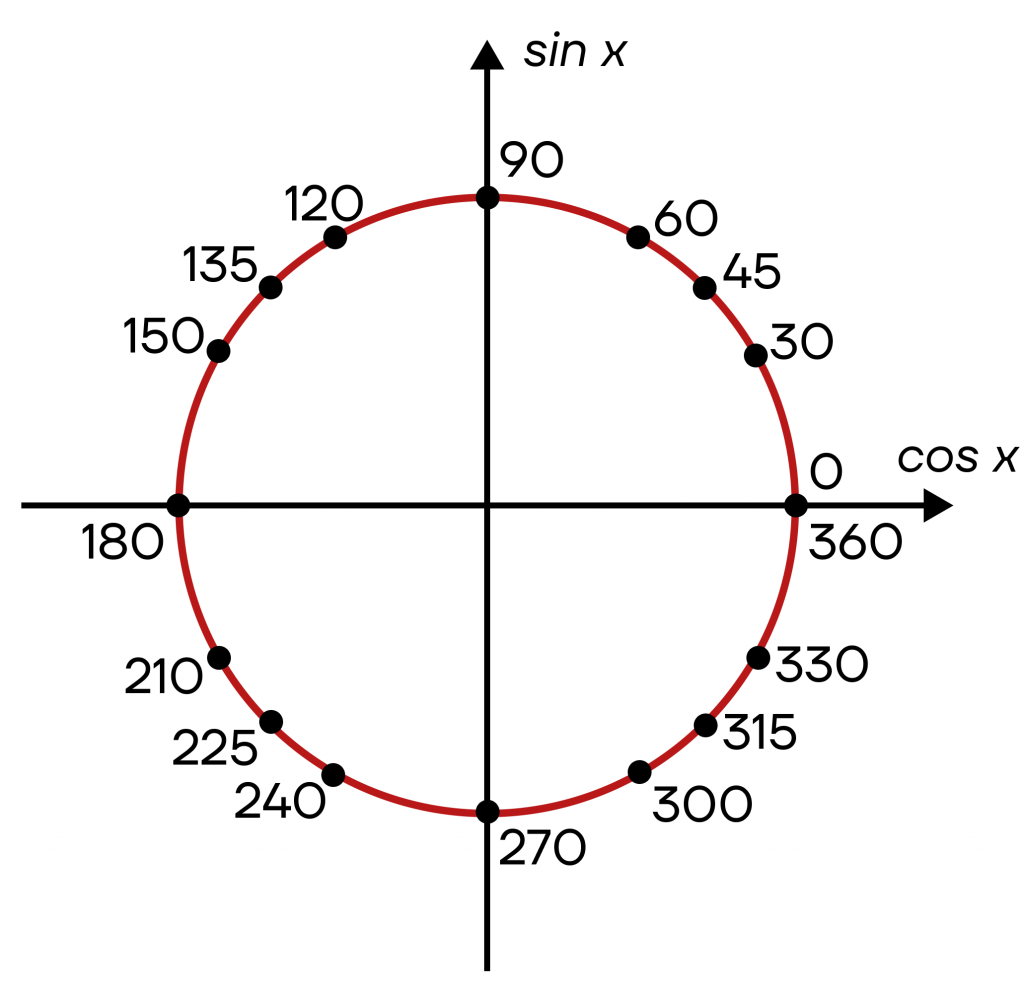
При этом углы можно откладывать как в градусах, так и в радианах. Радианы обозначаются числом , которое примерно равно 3,14. На окружности π=180°. 

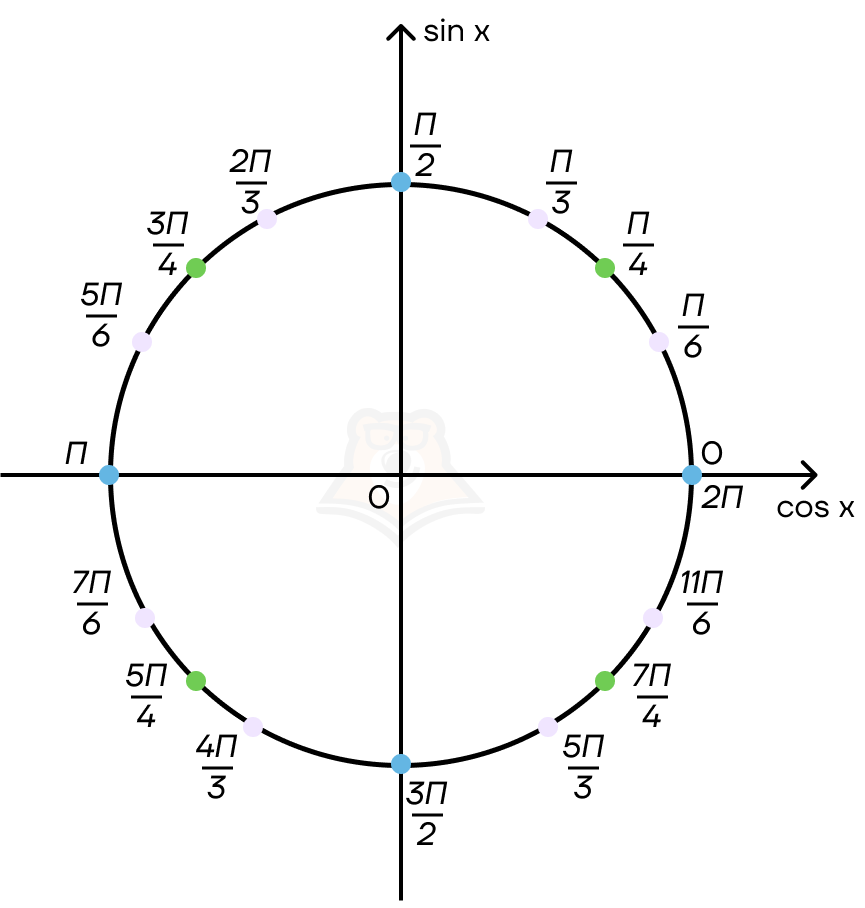
Движение по тригонометрической окружности в «положительную» сторону идет против часовой стрелки, в «отрицательную» сторону — по часовой стрелке. 

Как еще больше закрутить окружность? Движение по тригонометрической окружности можно сравнить с движением по числовой прямой, закрученной в спираль. Каждый новый оборот будет прибавлять к данному углу 360 градусов (или 2π). Зная это свойство, можно отложить любой угол на окружности, а также несколько углов, которые лежат в «одной» точке.

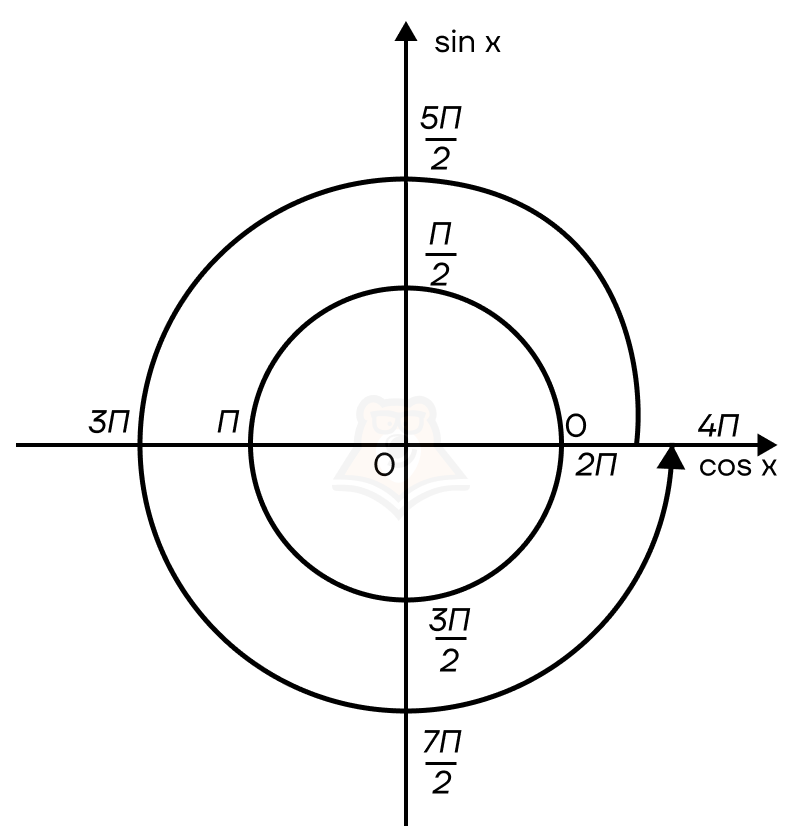
Множество точек на окружности

Если мы будем делать один оборот по окружности, то будем попадать в одну и ту же точку. Но значения этих точек будут разные. Как записать множество точек, находящихся в одной точке окружности, но на разных витках спирали?

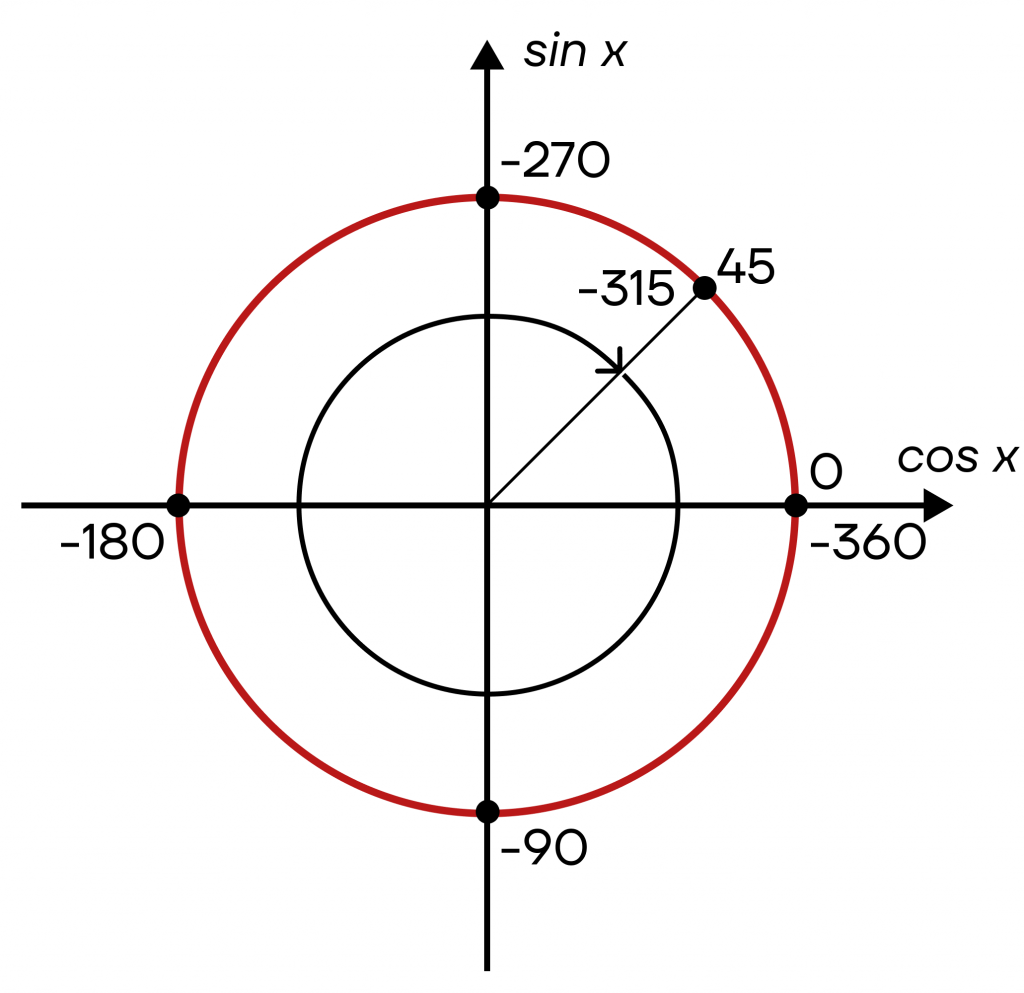
Сделаем оборот в отрицательную сторону из точки \(\frac{π}{4}\), то есть из точки 45°. 

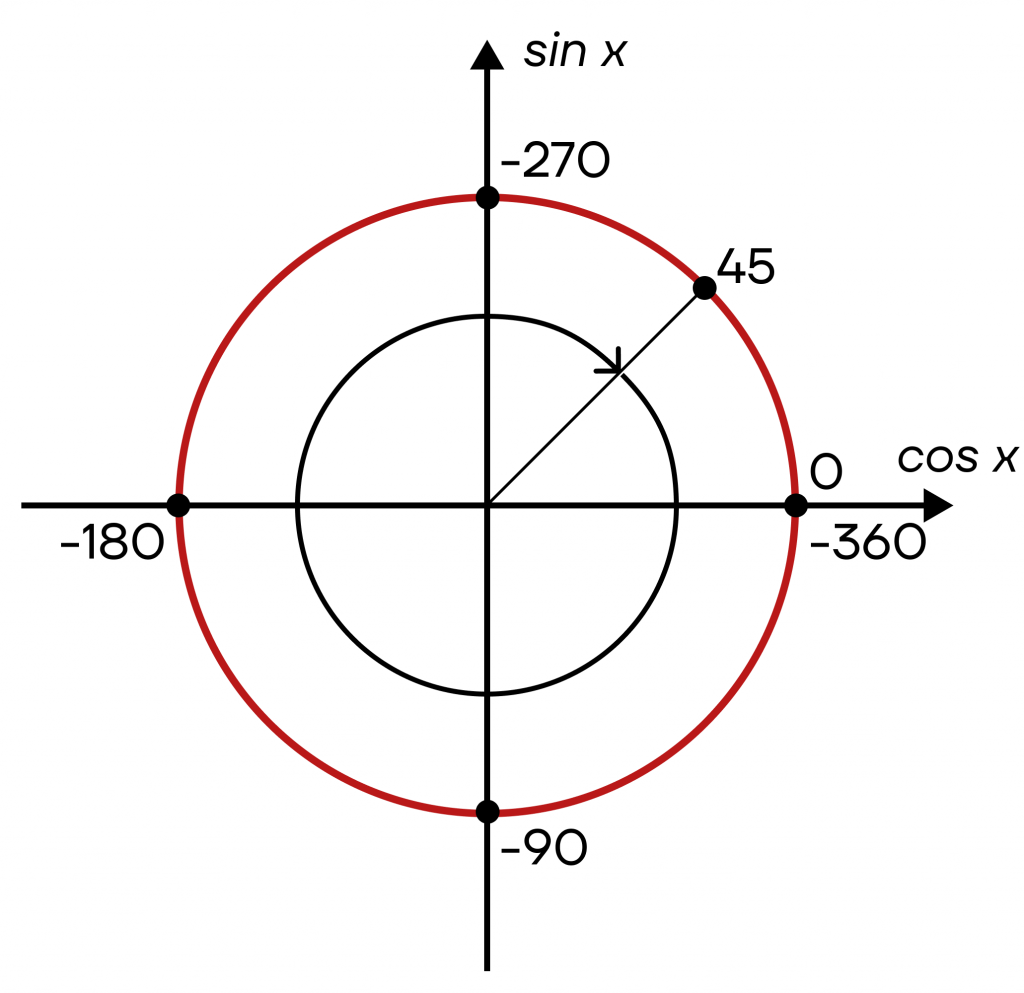
Поскольку мы сделали оборот на один круг, то прошли 360 градусов. Тогда мы попадем в точку 45°-360°=-315°. Точки 45° и -315° будут лежать в одном и том же месте, но при этом иметь разные значения.

Отбор по тригонометрической окружности является одним из способов решения №12(б) в ЕГЭ по профильной математике. Рассмотрим, как решать этот пункт.

а) Решите уравнение \(sin x * cos x -cos x =0\).
б) Найдите корни этого уравнения, принадлежащие отрезку \([6\pi;\frac{15\pi}{2}]\).

Решение.

Решение пункта а вы можете посмотреть в статье «Тригонометрические уравнения и неравенства».
Ответом к этому пункту будет \(x=\frac{\pi}{2}+\pi k, k \in Z\).

А сейчас начнем подробно рассматривать пункт б.

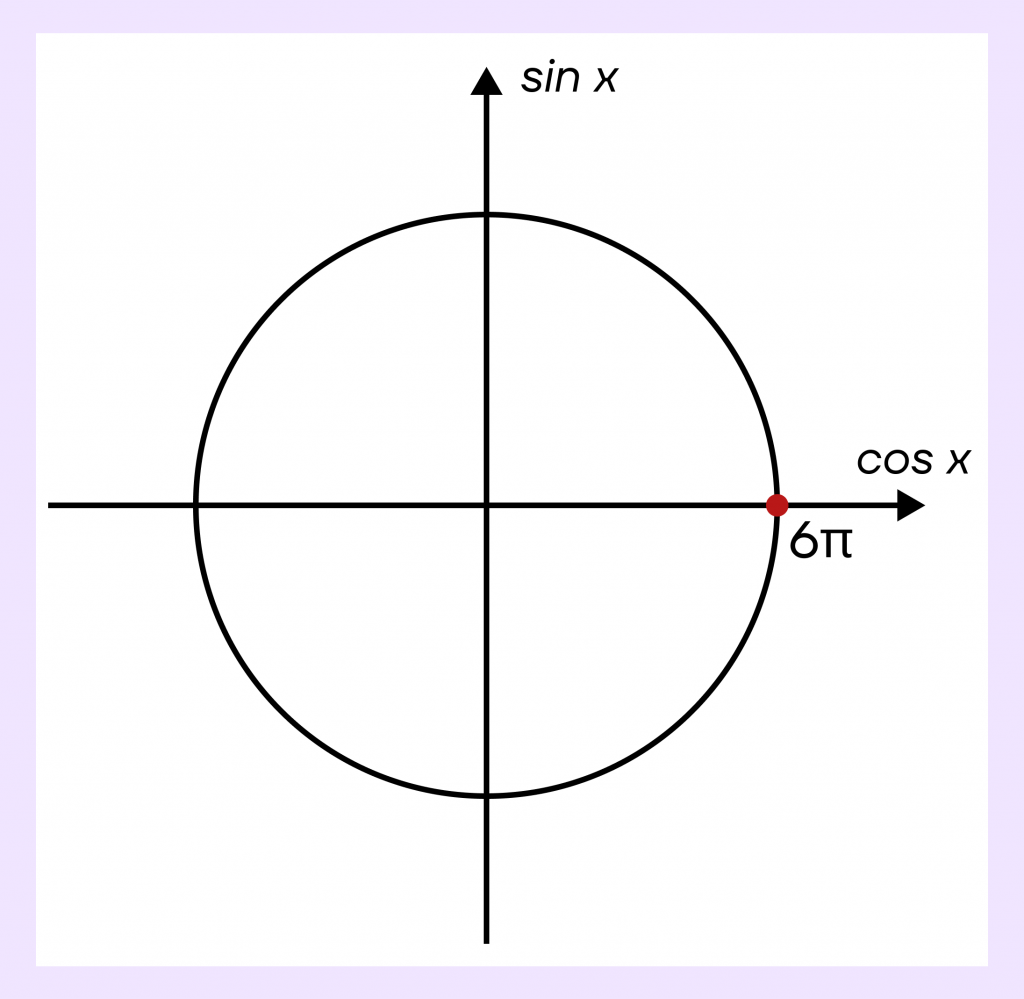
Шаг 1. Первым делом, нам необходимо начертить тригонометрическую окружность и отметить начало заданного отрезка. По условию, у нас это \(6\pi\).

Для того чтобы попасть в точку \(6\pi\), необходимо сделать три круга от начала отсчета.

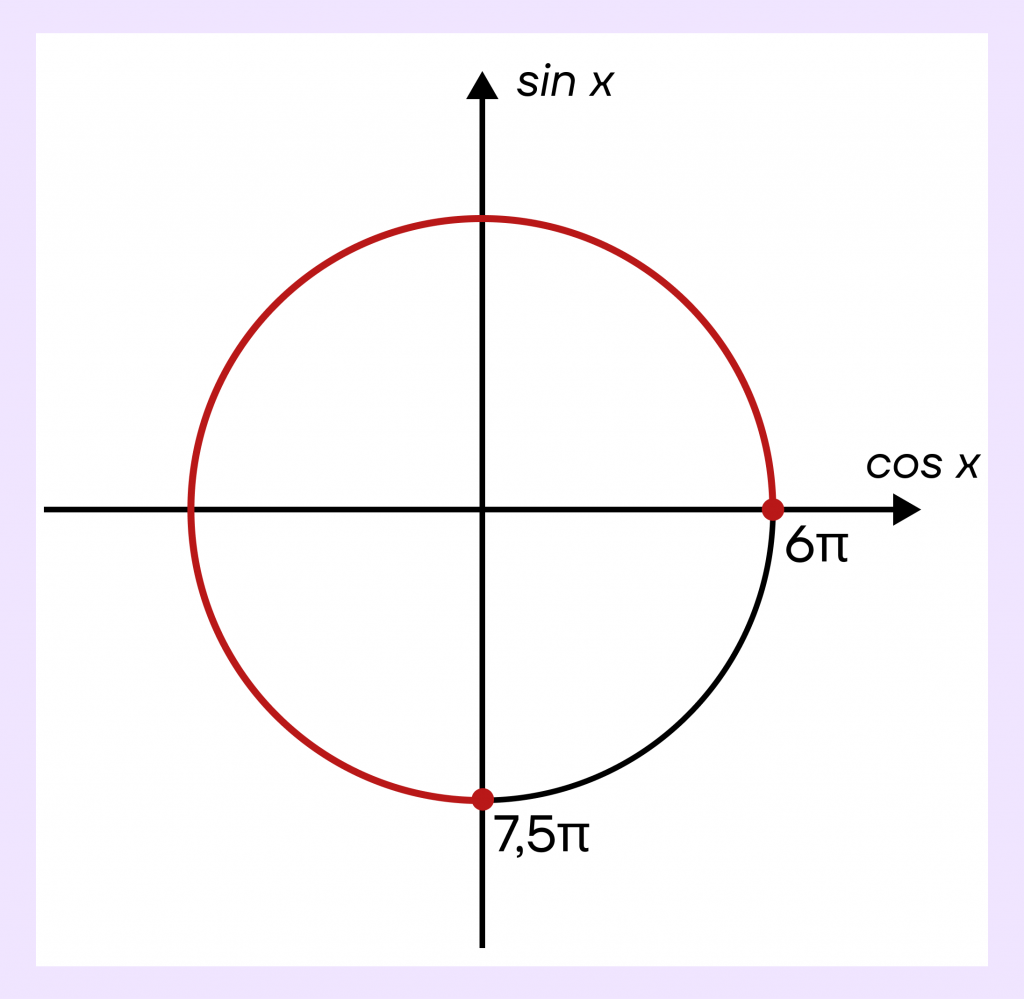
Шаг 2. Поскольку \(\frac{15\pi}{2}=7,5\pi\), что больше 6, мы движемся по окружности в «положительную» сторону, то есть против часовой стрелки. Чтобы попасть в точку \(7,5\pi\), нужно пройти еще \(\frac{3}{4}\) оборота по окружности.

После того как мы обозначили границы промежутка, нужно обязательно заштриховать дугу, которая лежит «внутри» него. Таким образом, мы показываем все значения, которые принадлежат этому отрезку. 

Шаг 3. Теперь на этом промежутке нам необходимо определить расположение точек, принадлежащих \(x=\frac{\pi}{2}+\pi k, k \in z\). Такие точки будут лежать на пересечении оси синуса и окружности.

Поскольку скобочки у отрезка квадратные (то есть заданные точки включаются в итоговый промежуток), то одну из точек мы уже нашли: это \(7,5\pi=\frac{15\pi}{2}\).

Вторая точка будет лежать сверху окружности и нам необходимо посчитать ее значение.

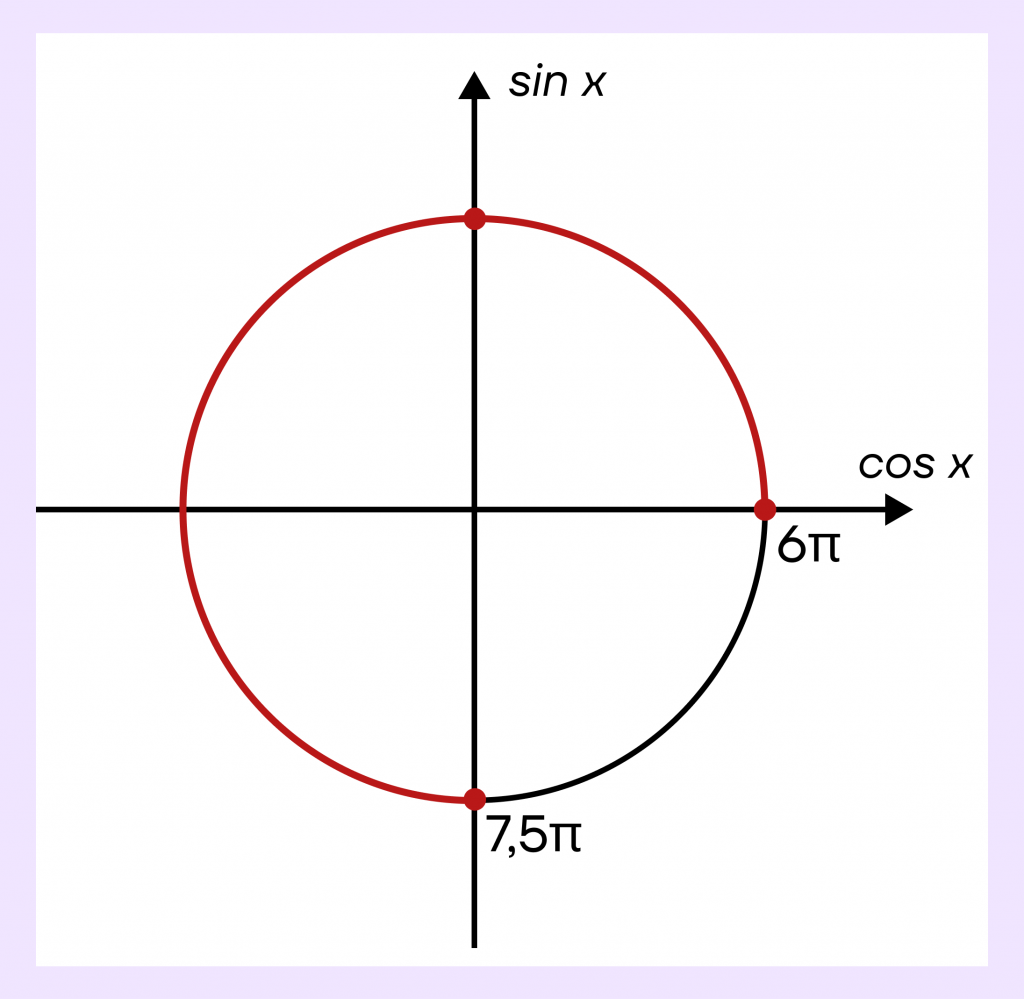
Заметим, что эта точка лежит через четверть окружности от \(6\pi\). Следовательно, нам необходимо прибавить 2 к границе отрезка:

\(6\pi+\frac{\pi}{2}=6,5\pi=\frac{13\pi}{2}\)

Шаг 4. Полученные точки нужно обязательно подписать на окружности.

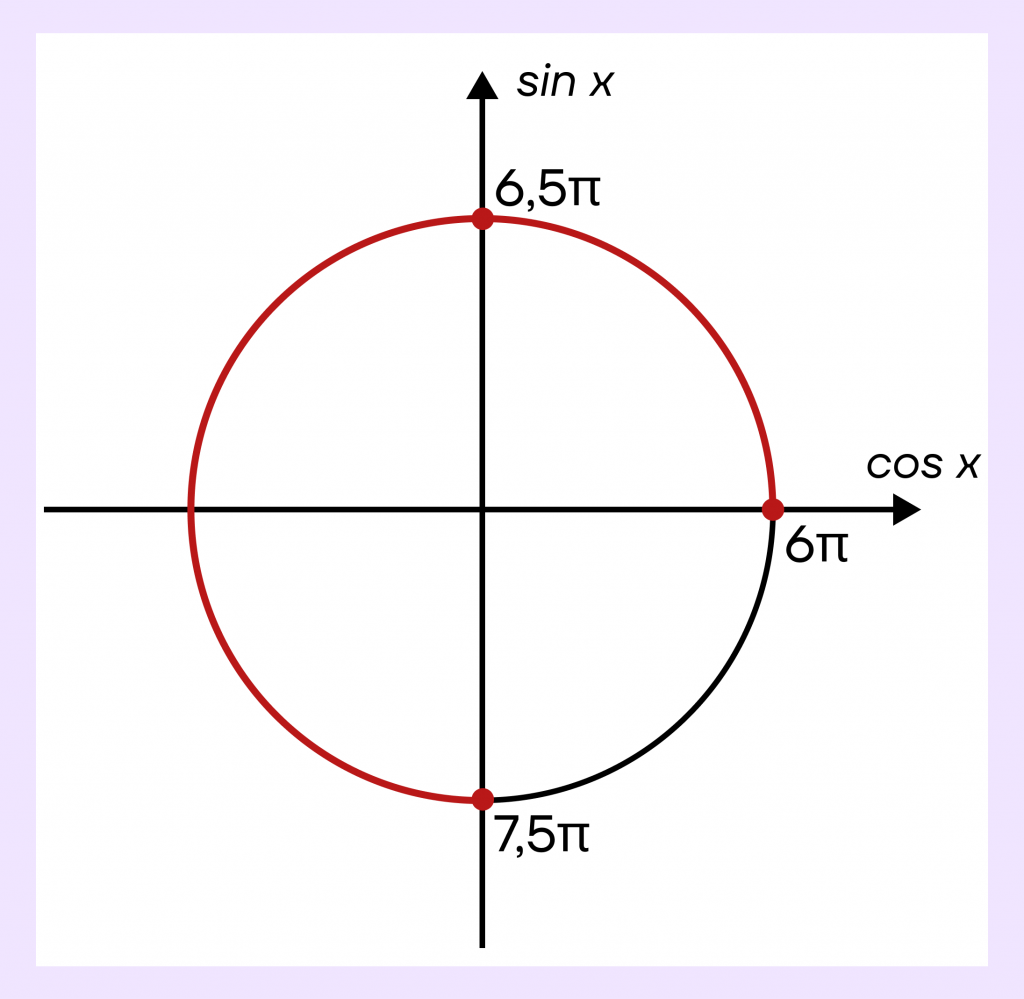
В итоге мы получили ответ на оба пункта задания.

Ответ: а) \(x=\frac{\pi}{2}+\pi k, k \in z\); б) \(\frac{13\pi}{2}, \frac{15\pi}{2}\). 

Определение значений синуса и косинуса

Поскольку окружность — это в том числе и график, значит, мы можем определить и значения функций с ее помощью. Разберем чуть подробнее, как это сделать. 

Вспомним, что окружность построена с помощью осей синуса и косинуса. Значит, чтобы откладывать значения этих функций, мы будем пользоваться именно этими осями. В точке пересечения осей будет лежать значение 0. 

Первым делом вспомним, что окружность у нас единичная, следовательно, точки пересечения осей и окружностей можно с легкостью вычислить. Они будут равны 1 или -1. 

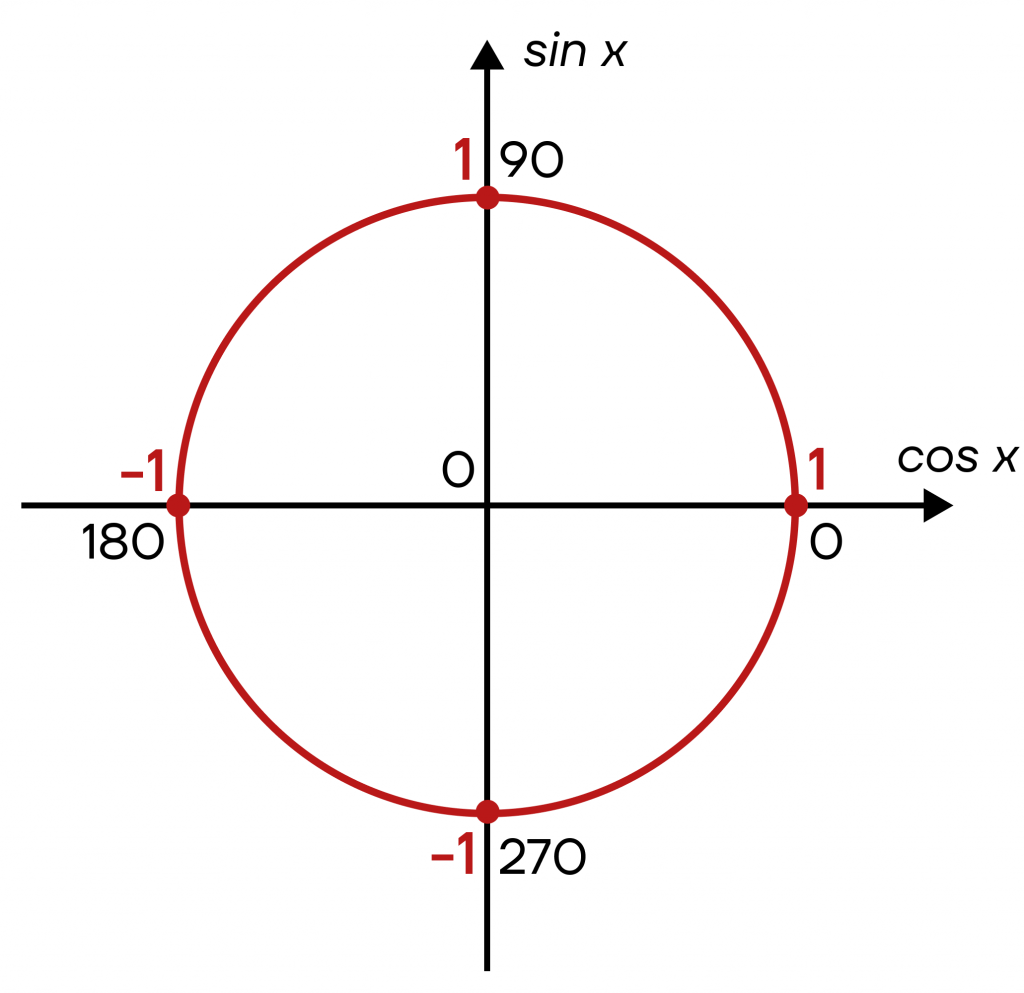
Значения косинусов

Для начала рассмотрим ось косинусов. Чтобы определить, чему равен косинус в той или иной точке, нам понадобятся углы и значения на прямой. 

Начнем рассматривать с точки -1. Поскольку на оси мы откладываем значения косинуса, то получаем уравнение \(cos x=-1\), где \(x\) — угол. 

Теперь смотрим, какой угол отложен в данной точке. Поскольку это опорная точка, мы можем с точностью определить, что это угол 180°. Следовательно, \(x=180\). 

Получаем уравнение \(cos 180°=-1\) или \(cosπ=-1\). 

Однако, если мы сделаем оборот по окружности и попадем в ту же точку, косинус до сих пор будет равен -1, но сам угол меняется. В этом выражается периодичность тригонометрической функции. 

Периодическая функция — это функция, значения которой повторяются через определенный период.

Для косинуса периодом будет 2π — именно через столько оборотов по окружности мы будем попадать в точки с равным значением. 

Следовательно, если \(cos x=-1\), то \(x=π+2πn, n\in Z\). Такая запись будет правильной, поскольку отражает все точки, в которых косинус будет равен -1. 

Аналогичная ситуация и с cos X = 1. На окружности в этой точке лежит 0. Добавляя периодичность косинуса, получаем:

\(cos x=1 => x=0+2πn=2πn, n\in Z\). 

Теперь рассмотрим случай cos X = 0. На оси косинусов точка 0 не пересекается с окружностью. Как тогда определить значения в этой точке?

Все просто: нужно провести перпендикуляр к оси косинусов из этой точки. Поскольку 0 — точка пересечения осей, то нашим перпендикуляром будет ось синусов. Этот перпендикуляр пересечет окружность в точках 90 и 270 (или \(\frac{π}{2}\) и \(\frac{3π}{2}\)). 

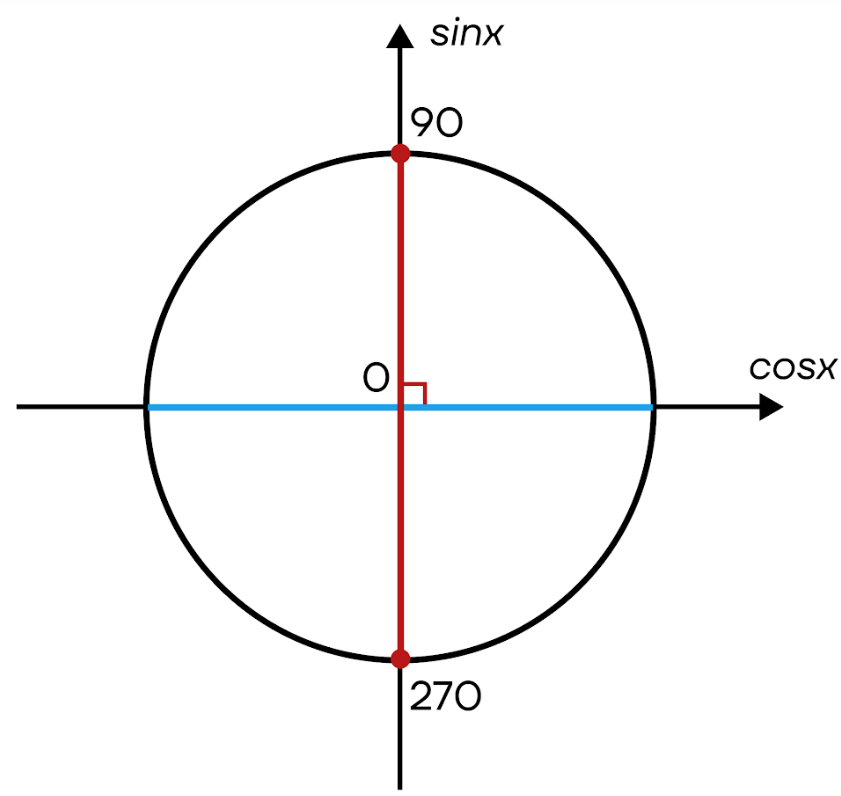
Итак, пользуясь предыдущими рассуждениями и вводя период, у нас получаются два значения:

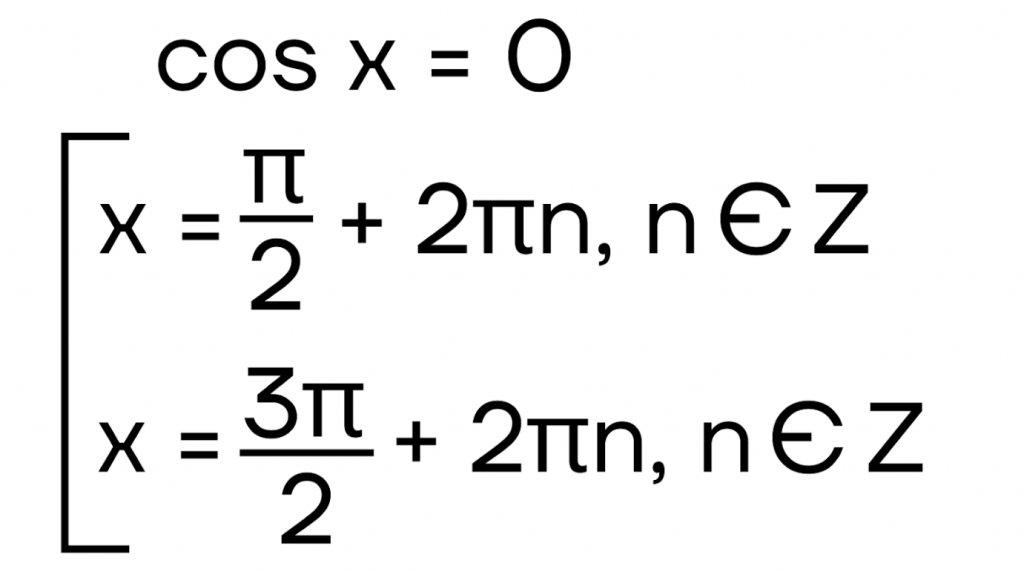
Уточним, что запись \(2\pi n, n \in Z\) обозначает именно наши «шаги» по окружности: мы каждый раз продвигаемся на круг (то есть на \(\pi2\)), начиная с точки \(\frac{\pi}{2}\). Важно отметить, что условие \(n \in Z\) необходимо, поскольку подсказывает, что вместо n мы можем подставить только целые числа. Тогда мы будем попадать в нужную нам точку. 

Однако если внимательно посмотреть на окружность, то можно заметить, что точки лежат через каждые полкруга (то есть через \(\pi\)). Значит, мы можем сократить запись и записать их с периодом :

\(x=\frac{\pi}{2}+\pi n, n \in Z\). 

В этом случае мы будем «останавливаться» на окружности каждые полкруга: 90°, 270°, 450°, 630° и т.д.

Значения синусов

Если мы будем рассматривать значения синусов, то действовать нужно аналогично, но в этот раз двигаться по вертикальной оси. Тогда мы получим следующую картину:

\(sin x=-1 => x=-\frac{\pi}{2}+2\pi n, n \in Z\)
\(sin x=0 => x=\pi n, n \in Z\)
\(sin x=1 => x=\frac{\pi}{2}+2\pi n, n \in Z\)

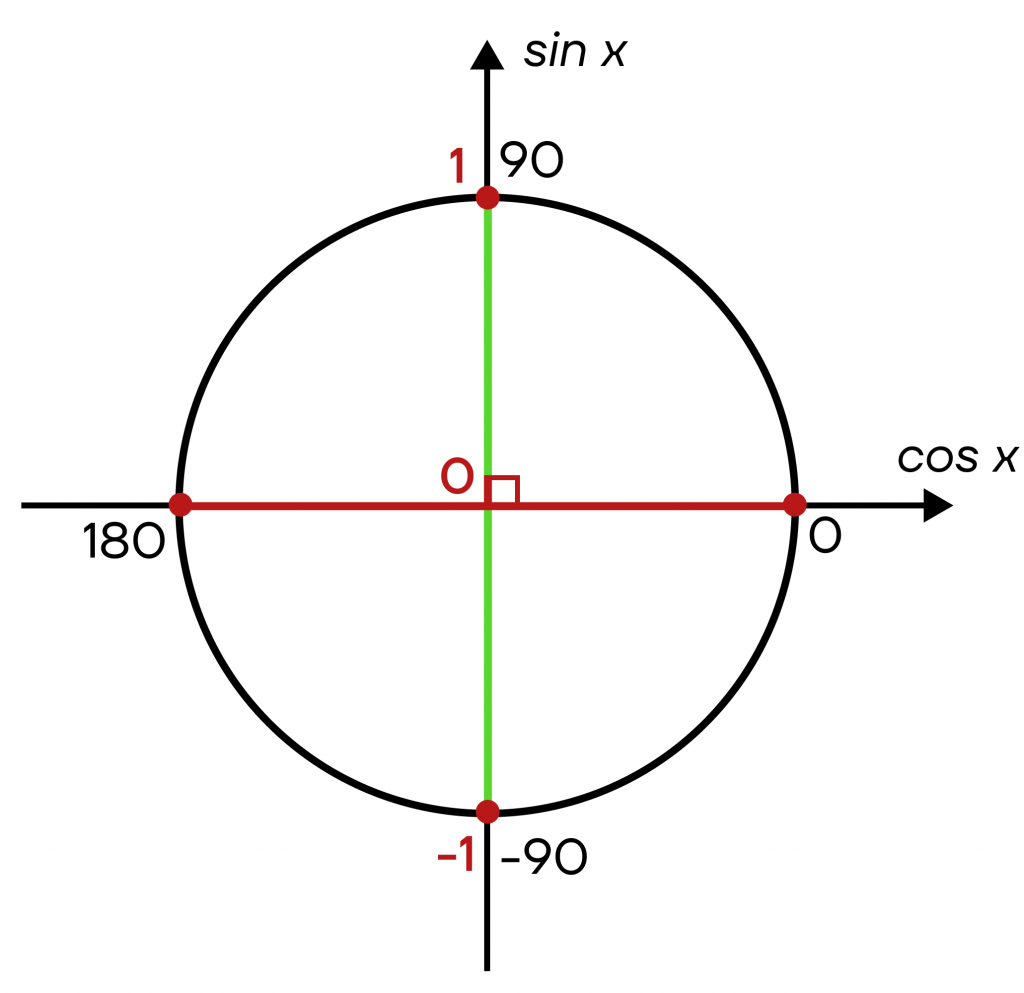
Здесь мы тоже можем отложить любой угол и найти его значение для синуса или косинуса. Например, рассмотрим угол 45° (\(\frac{\pi}{4}\)). Проведем из этой точки перпендикуляры к осям синуса и косинуса:

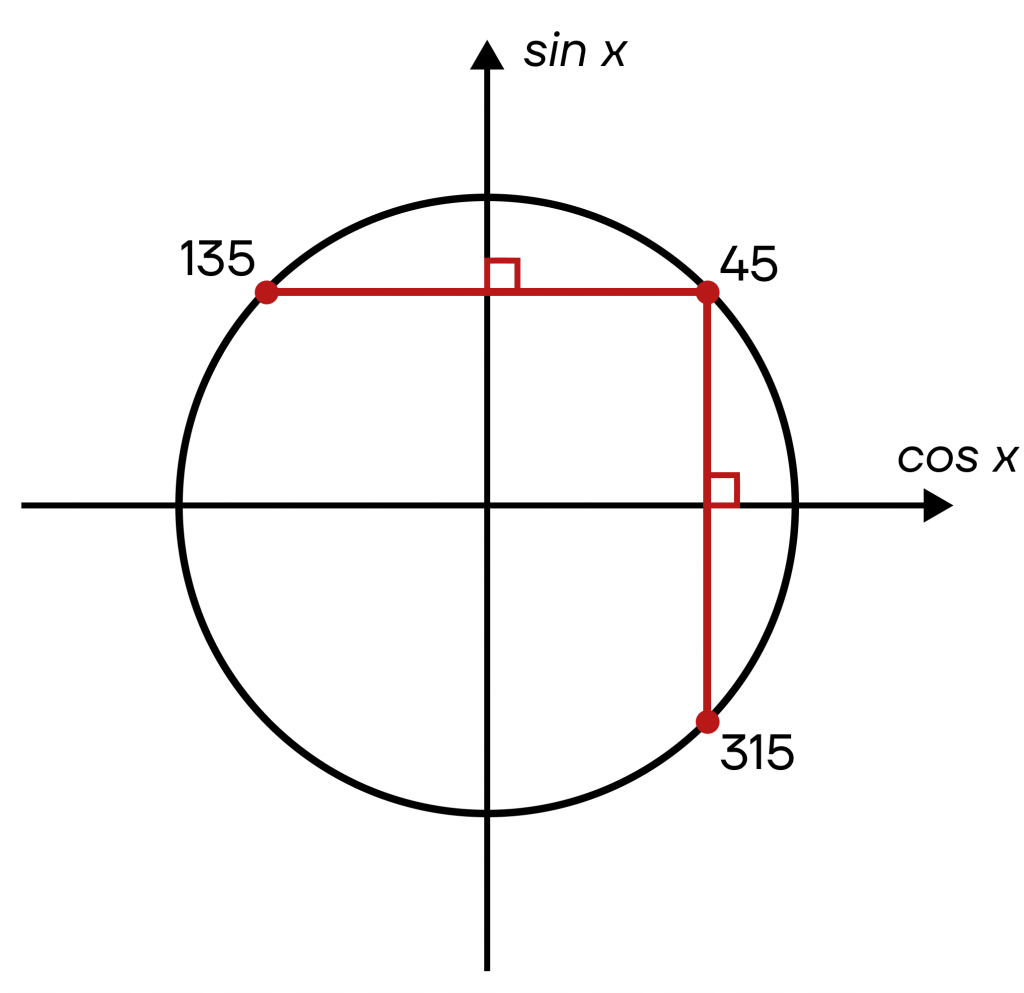
Заметим, что эти перпендикуляры мы ведем до повторного их пересечения с окружностью. Таким образом, мы попадем в точки 135° и 315° (или \(\frac{3\pi}{4}\) и \(\frac{7\pi}{4}\)). 

Теперь внимательнее посмотрим на перпендикуляры: они пересекают оси синуса и косинуса в какой-то определенной точке. Если угол табличный, значение этой точки можно узнать с помощью таблицы. 

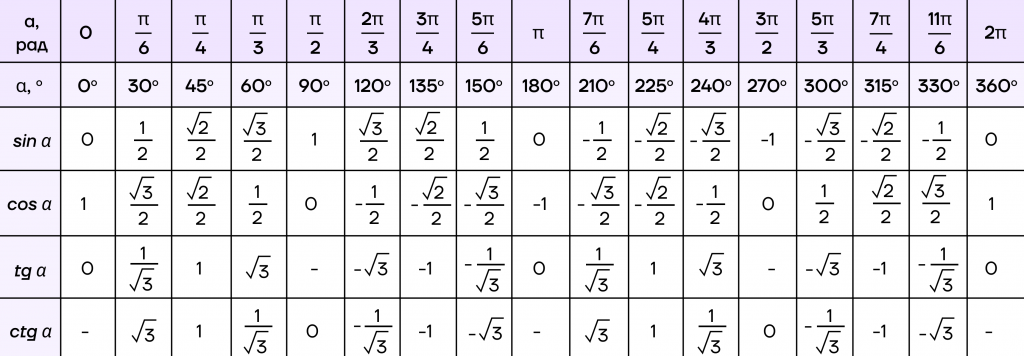
Поскольку мы взяли табличный угол, то с легкостью можем определить, чему равны точки на осях. На обеих осях мы попадем в точку \(\frac{\sqrt2}{2}\).

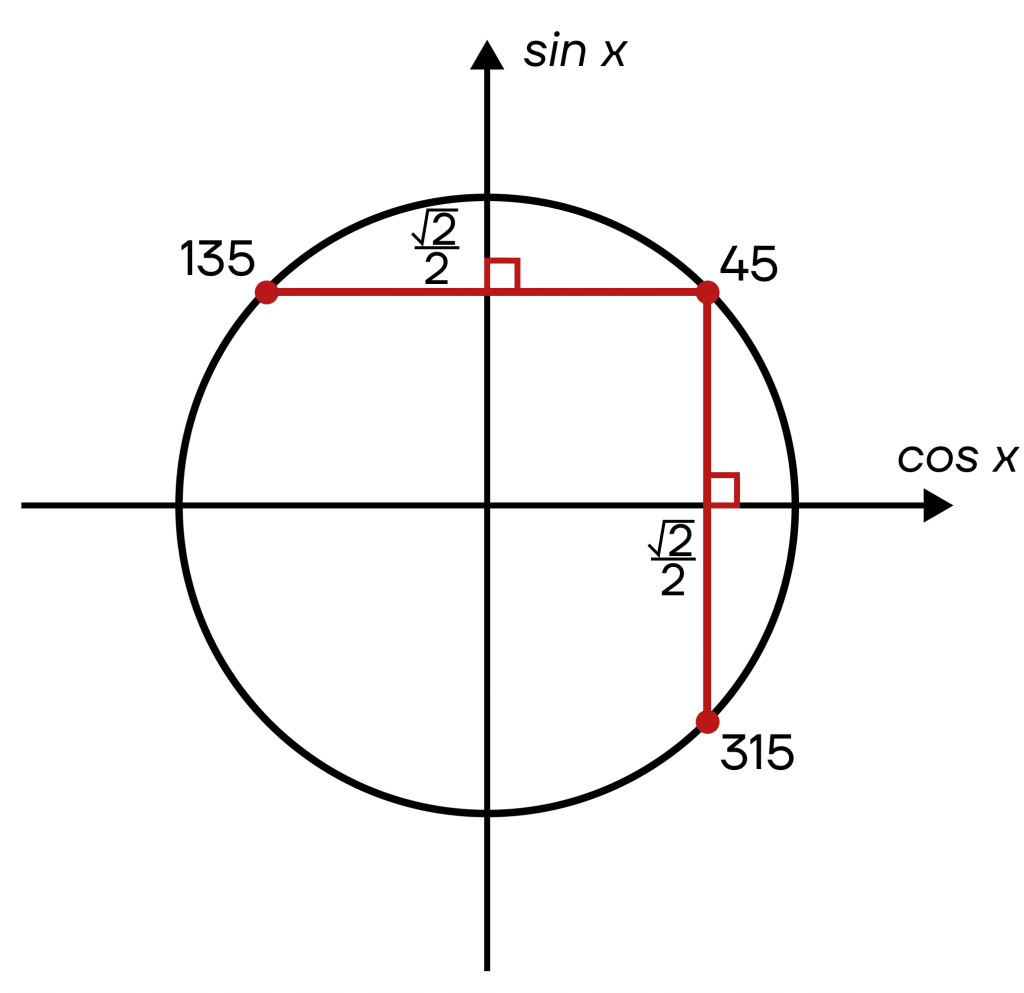
Отметим также, что в этом случае мы не можем объединить корни: они лежат не через равные промежутки. Записать их значение можно будет с помощью совокупности:

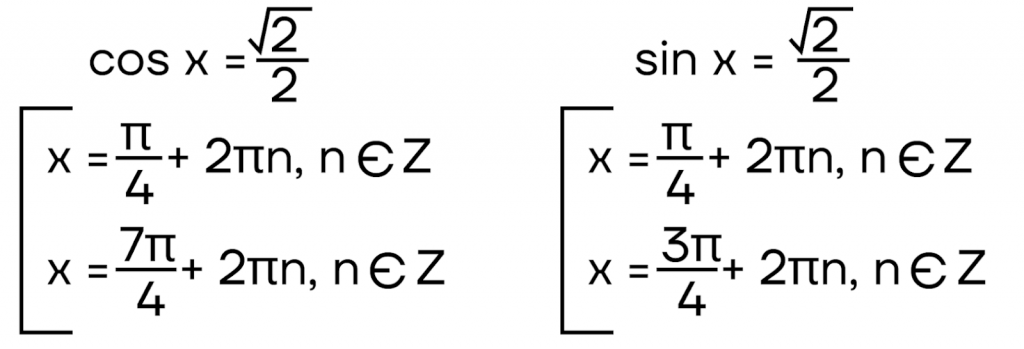
Таким способом можно отложить любое значение для синуса или косинуса, или узнать, чему они равны для любого угла. Этот навык очень нужен для решения тригонометрических уравнений и неравенств.

Как связаны треугольник и окружность? В статье «Тригонометрическая окружность. Часть 1» мы уже разбирали, что выразить тригонометрические функции можно с помощью прямоугольного треугольника. В этом случае тригонометрические функции будут равны отношению сторон треугольника. Теперь мы разобрали, как искать значения функций с помощью окружности. Но можно ли это объяснить с помощью треугольника? Да! Разберем на примере sin 30° и cos 30°. Для начала отметим на окружности угол 30 градусов и построим прямоугольный треугольник так, чтобы одним из катетов он «опирался» на ось синусов.  Как найти, чему равна точка В на оси синусов? Посчитать с помощью свойств треугольника! Для расчета нам понадобится два свойства: — Свойство 1: В прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы. — Теорема Пифагора: Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. Подробнее про эти и другие свойства прямоугольных треугольников можно прочесть в статье «Равнобедренный, равносторонний и прямоугольный треугольник». Итак, какие стороны нам известны? В первую очередь — гипотенуза. Поскольку в данном случае гипотенуза совпадает с радиусом окружности, то она равна 1. Дальше, пользуясь свойством 1, находим сторону АВ. Она равна половине гипотенузы, то есть \(\frac{1}{2}\). Таким образом, мы получаем, что \(sin 30°=\frac{1}{2}\). А теперь проделаем то же самое для косинуса. Но в этот раз точка В будет лежать на оси косинусов. Применяя аналогичные рассуждения, получаем: AC=1, BC=\(\frac{1}{2}\)=0,5. В этот раз нам нужно найти АВ. Для этого воспользуемся теоремой Пифагора: \(AB^2+BC^2=AC^2\) \(AB^2=AC^2-BC^2\) \(AB^2=1^2-(\frac{1}{2})^2=1-\frac{1}{4}=\frac{3}{4}\) \(AB=\sqrt{\frac{3}{4}}=\frac{\sqrt3}{2}\) Так мы получаем \(cos 30°=\frac{\sqrt3}{2}\). Рассчитанные нами с помощью прямоугольного треугольника значения синуса и косинуса соответствуют табличным значениям. Это означает, что мы все сделали верно!

Вернемся к нашей окружности и отметим табличные значения для синуса и косинуса: 

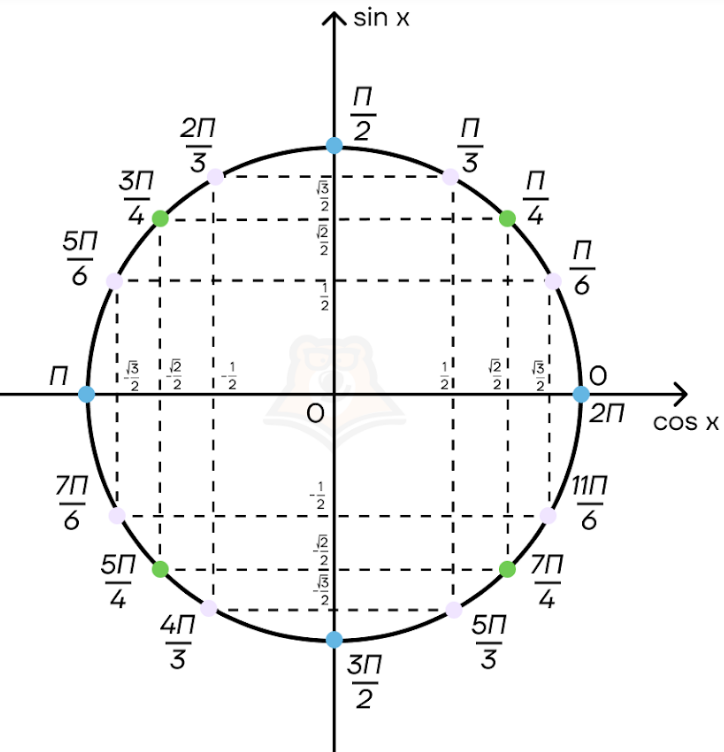
Пример 1. Нужно узнать чему равно \(sin\frac{\pi}{3}\).

Сначала найдем \(\frac{\pi}{3}\) на окружности, затем проведем перпендикулярную прямую к прямой синусов. Ответом является значение в точки пересечения.

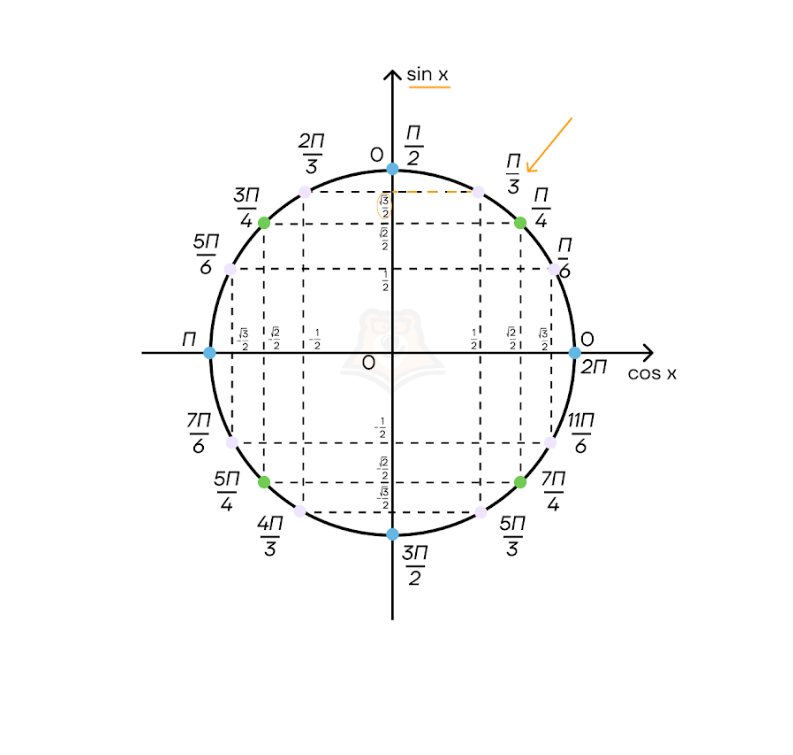
Ответ: \(sin\frac{\pi}{3}=\frac{\sqrt3}{2}\).

Определение значений тангенса и котангенса

Мы разобрались с синусами и косинусами. Но как с помощью окружности находить тангенс или котангенс? 

Где на окружности оси тангенса и котангенса? На самом деле, у них тоже существуют свои оси, отличные от осей синуса и косинуса. — Ось тангенса проходит вертикально через точку 1 на оси косинусов. Оси тангенса и синуса параллельны. — Ось котангенса проходит горизонтально через точку 1 на оси синусов. Оси котангенса и косинуса параллельны.

Поиск значений функций тоже отличается. В отличие от синуса и косинуса, мы не будем проводить перпендикуляры. В случае с тангенсом и котангенсом необходимо соединить центр окружности и точку на ней, а после продолжить эту прямую до нужной оси. 

Посмотрим, как это выглядит на окружности: 

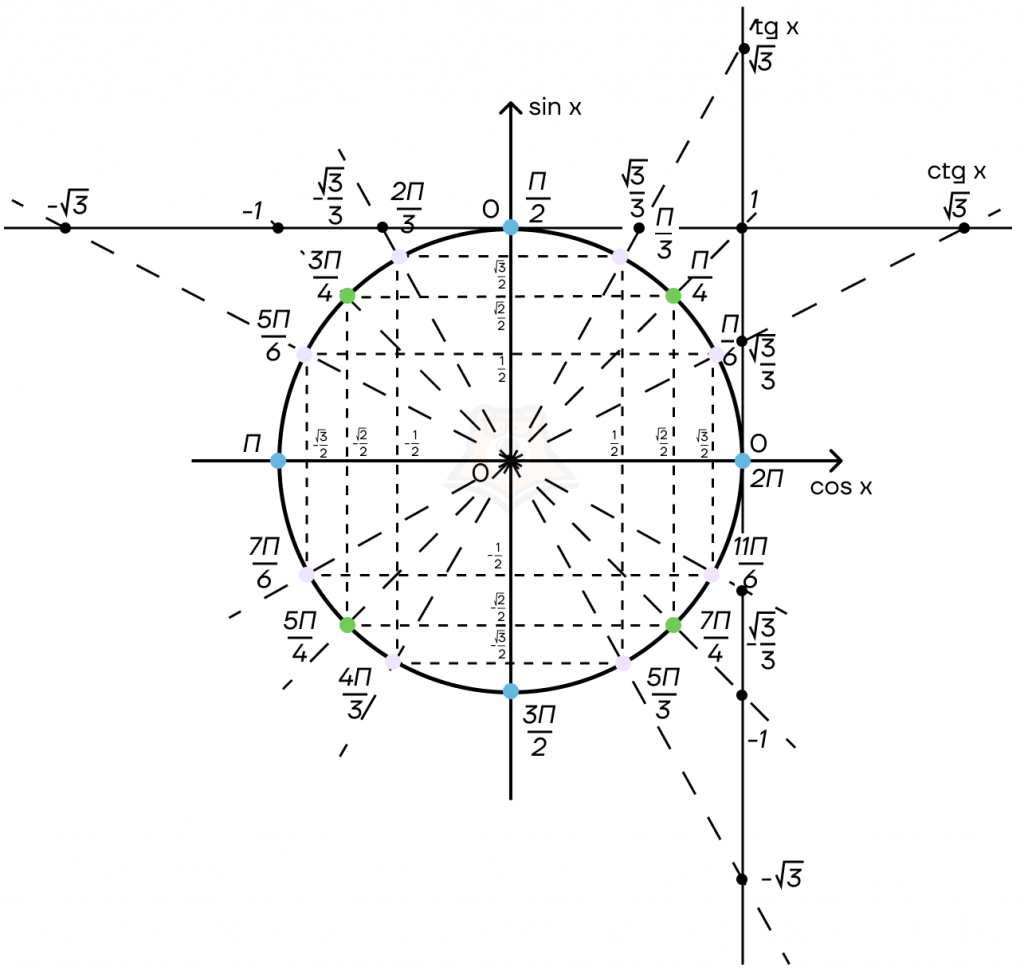
Для нахождения значения тангенса или котангенса известного угла нужно провести прямую через точку (0; 0) и это число на окружности. Значение, в котором она пересечет прямую данной функции, будет являться значением этой тригонометрической функции от известного числа.

Пример 2. Нужно узнать чему равно \(ctg\frac{2\pi}{3}\).

Сначала найдем \(\frac{2\pi}{3}\) на окружности, затем проведем прямую через (0; 0) и эту точку на окружности. Ответом является значение в точке пересечения проведенной прямой и прямой котангенсов. 

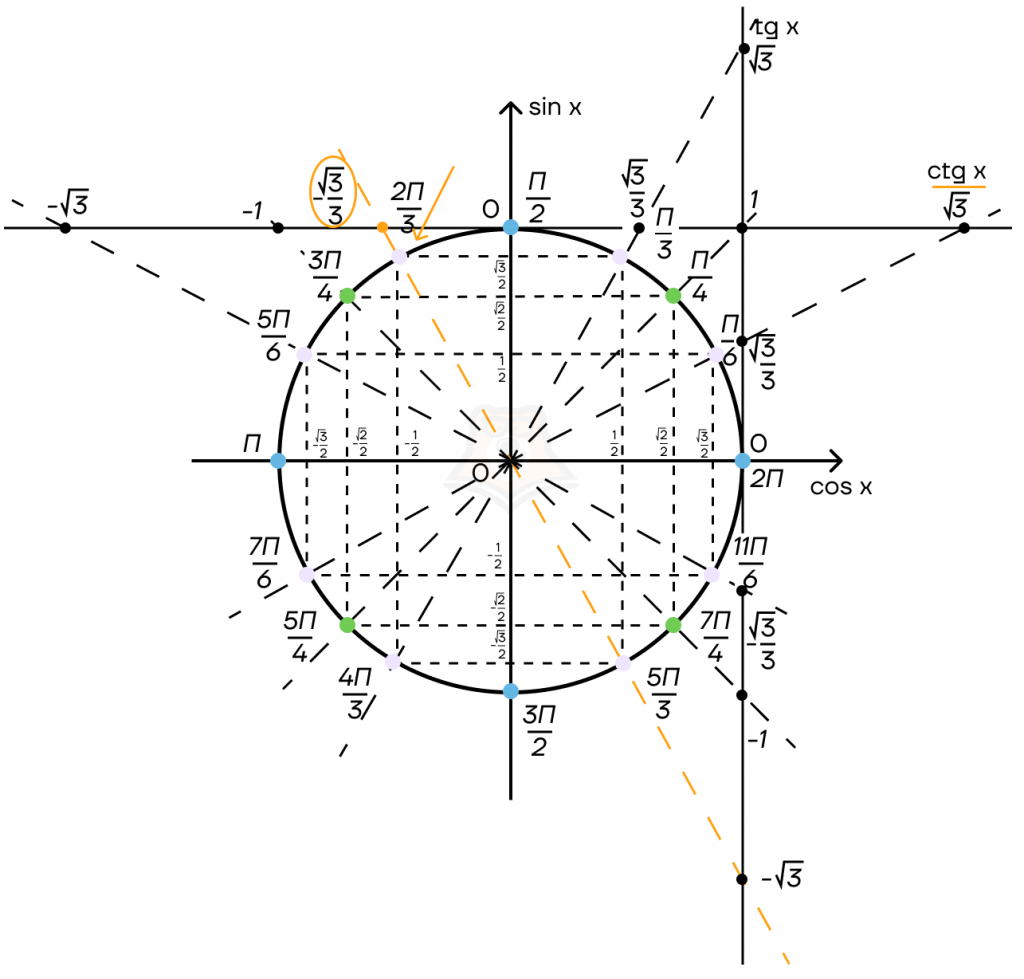
Ответ: \(ctg\frac{2\pi}{3}=-\frac{\sqrt3}{3}\).

Заметим, что период тангенса и котангенса будет уже \(\pi\). Это связано с тем, что точки повторяются через каждые полкруга. То есть «кружить» по окружности будет уже не одна точка, как в случае с синусом или косинусом, а сразу пара. 

Окружность — очень удобный инструмент для решения тригонометрических уравнений или неравенств, а также для выборки корней. Движение по окружности встретится нам и в дальнейшем изучении тригонометрии, например, в формулах приведения.

Необходимо уметь правильно и быстро находить значения функций. Например, такое задание может встретиться в №16 ЕГЭ по базовой математике:

Найдите значение выражения \(19\sqrt3*sin60°*ctg45°\).

Решение. 
С помощью окружности найдем, чему равны \(sin 60°\) и \(ctg45°\)

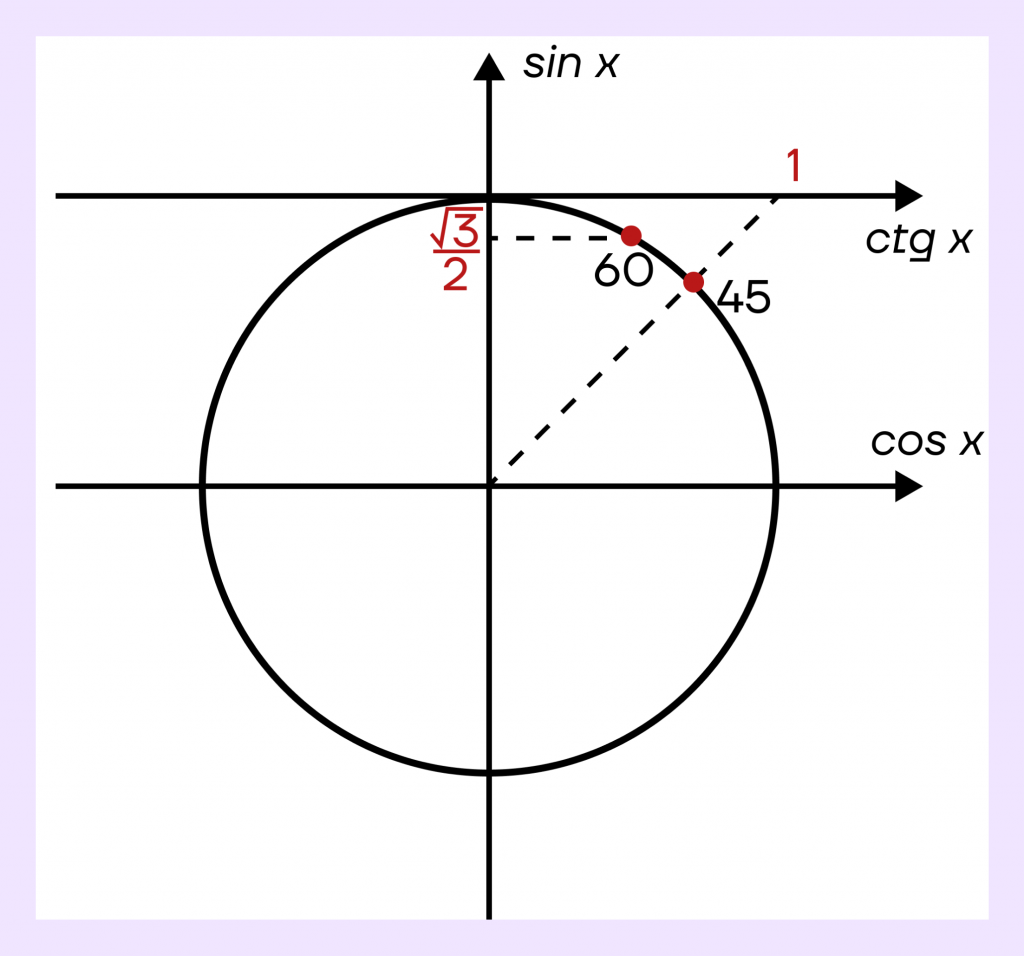
Получаем значения:
\(sin 60°=\frac{\sqrt3}{2}\)
\(ctg45°=1\)

Подставляем полученные значения в данное выражение и считаем ответ:
\(19\sqrt3*sin 60°*ctg45°=19\sqrt3*\frac{\sqrt3}{2}*1=19*\sqrt3*\sqrt3*\frac{1}{2}=19*3*\frac{1}{2}=28,5\).

Ответ: 28,5

Однако окружность — не единственный способ представить тригонометрические функции графически. А как выглядят графики синуса, косинуса, тангенса и котангенса в привычном нам понимании, вы сможете узнать в статье «Графики тригонометрических функций». 

Термины

Гипотенуза — это сторона прямоугольного треугольника, лежащая против прямого угла.

Катет — это одна из двух сторон, образующих прямой угол в прямоугольном треугольнике.

Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.

Перпендикуляр — это линия, составляющая прямой угол с другой прямой линией или плоскостью.

Прямоугольный треугольник — это треугольник, один из углов которого прямой, то есть равен 90°. Подробнее о нем можно прочитать в статье «Равнобедренный, равносторонний и прямоугольный треугольник».

Радиус окружности — это отрезок, построенный от центра окружности до любой точки на окружности. 

Целые числа — это натуральные числа, нуль, а также противоположные натуральным числам (то есть со знаком минус). 

Опорная точка — это точки, лежащие на пересечении окружности и осей синуса и косинуса. Такие точки равны 90, 180, 270 и 360 градусов (а также всем остальным значениям, которые можно получить при движении по окружности). 

Фактчек

• С помощью тригонометрической окружности можно найти значение любой тригонометрической функции для заданного угла.
• Чтобы найти значение синуса или косинуса, необходимо провести перпендикуляр из точки на окружности к оси функции. Осью синуса будет вертикальная ось (она совпадает с осью у), осью косинуса — горизонтальная ось (совпадает с осью х). 
• Оси тангенса и котангенса касаются окружности в точках 1. Так, ось тангенса проходит параллельно оси синуса и касается окружности справа. Ось котангенса проходит параллельно оси косинуса и касается окружности сверху. 
• Чтобы найти значение тангенса или котангенса, необходимо соединить центр окружности с точкой на ней, а после продолжить прямую до пересечения с осью функции.

Проверь себя

Задание 1.
Как на окружности лежат точки \(\frac{\pi}{2}\) и \(\frac{3\pi}{2}\)?

1. Они лежат в одной и той же точке.
2. Они лежат напротив друг друга.
3. Они лежат в первой и третьей четверти соответственно.
4. Они лежат на оси косинусов.

Задание 2.
Как на окружности лежат точки \(\frac{\pi}{4}\) и \(\frac{9\pi}{4}\)?

1. Они лежат в одной и той же точке.
2. Они лежат напротив друг друга.
3. Они лежат в первой и второй четверти соответственно.
4. Они лежат на оси синусов.

Задание 3.
Выберите верное утверждение для оси котангенса:

1. Ось котангенса проходит вертикально через центр окружности.
2. Ось котангенса проходит горизонтально через центр окружности.
3. Ось котангенса вертикальна и касается окружности слева.
4. Ось котангенса горизонтальна и касается окружности сверху. 

Задание 4.
Чему равна функция \(sin\frac{\pi}{3}\)?

1. \(\frac{\sqrt2}{2}\)
2. \(\frac{\sqrt3}{2}\)
3. \(\frac{1}{2}\)
4. \(1\)

Задание 5.
Чему равна функция \(tg\frac{\pi}{2}\)?

1. \(\sqrt3\)
2. \(\frac{\sqrt3}{3}\)
3. \(0\)
4. тангенс не существует в точке \(\frac{\pi}{2}\)

Ответы: 1. — 2; 2. — 1; 3. — 4; 4. — 2; 5. — 4.