Формулы приведения

На этой странице вы узнаете

• Кто и когда вывел формулы приведения?
• Как лошадь помогает приведениям? 
• Какие знаки имеют тригонометрические функции в четвертях? 

Любите ли вы квесты, загадки и секретные пароли? А игры? Надеемся, что ответ утвердительный, так как мы приготовили для вас очень необычную статью. С ней вы не только освоите новые способы решения заданий тригонометрии, но и немного отдохнете от однообразных учебных будней.

Глава 1. Знакомство

– Ты снимаешь?

– Сейчас, только настрою камеру. 

– Мы нашли старый заброшенный замок! И сегодня мы проверим, что там внутри.

– Безумно страшно!

– Неужели ты веришь в привидений? Просто побродим по комнатам и чуть-чуть попугаемся. Воспринимай это как страшный квест! Вперед!

– Фух! Еле-еле открыли двери!

– И правда, кто вообще додумался их заколотить на столько досок? 

– Может, было что прятать? Или кого удержать внутри?

– Не нагнетай атмосферу! 

– Не слышал песню «Проклятый старый дом»? Может, уйдем, пока не повторили ее сюжет?

– А ты попробуй меньше страшных песен слушать!

– Ты слышал это?..

– Что именно? Это ты и шуршишь!

– Это не я! Замри! Послушай!

– Хватит меня разыгрывать!

– …

– Кто вы и что вам нужно в моем замке?!

– Ты это видишь?..

– Конечно, вижу…

– Кто вы?

– Мы… мы не хотели вас потревожить, уважаемый… а… а кт-т-то вы?

– Мое имя слишком древнее, вы не запомните. Можете обращаться просто Формула Приведения. 

– Как в математике, что ли?

– Цыц! Не зли его! Или ее…

– Я заточен тут слишком давно, и вы первые, кто догадался потревожить мой покой!

– А как давно?

– Уже почти три века.

Кто и когда вывел формулы приведения? В XVIII веке член Петербургской академии наук Леонард Эйлер придал тригонометрии современный вид. К его достижениям также можно отнести вывод формул приведения.

– Почему вас тут заточили?

– Я слишком важен для тригонометрии. Без Формул Приведения будет почти невозможно решать тригонометрические уравнения и неравенства. 

– Получается, вы оберегаете какой-то секрет?

– Да. И сегодня я расскажу вам, как решать Формулы Приведения без запоминания множества других формул. Идите за мной!

Глава 2. Определение 

– Мы в самом сердце моего замка – в библиотеке. Начнем с…

– А что такое Формула Приведения?

– Не перебивай! Формула Приведения – это тригонометрическая функция, в которой угол отложен от одной из осей, например, \(sin(\frac{\pi}{2}+x)\) или \(cos(\pi-x)\). 

Формулы приведения – формулы, позволяющие привести аргумент, в котором угол отложен от одной из осей на окружности, к обычному аргументу с углом. 

Формулы приведения используются для упрощения вычислений. Например, с их помощью можно превратить \(sin(\frac{\pi}{2}+x)\) в \(cos x\). 

– Так вот. С помощью Формул Приведения можно перейти к новой функции. Для этого первым делом нужно определить, заменится ли тригонометрическая функция на противоположную.

– То есть синус на косинус или тангенс на котангенс?

– А также косинус на синус или котангенс на тангенс. Именно так. Для этого нам понадобится мой помощник. Сейчас он сюда подойдет. 

– Лошадь?.. Что? Причем тут лошадь?

– Она помогает определять, меняется ли тригонометрическая функция на противоположную.

– Да как?!

– Слушайте… 

Глава 3. Правило лошади

Как лошадь помогает приведениям? В тригонометрии существует правило лошади. Рассмотрим, как с его помощью определять, меняется ли функция на противоположную. Первым делом нужно представить голову лошади, которая располагается ровно посередине тригонометрической окружности.  Дальнейшие рассуждения зависят от оси, от которой отложен угол. Главное – запомнить, что голова лошади будет двигаться только по той оси, которая дана в формуле приведения.  — Если в формуле приведения угол отложен от вертикальной оси, например, от точек \(\frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}\), то лошадь как бы кивает головой и говорит «Да». В этом случае функция меняется на противоположную. Например, для формулы \(tg(\frac{\pi}{2}+x)\) лошадь будет кивать головой, а значит, функция поменяется с тангенса на котангенс. — Если в формуле приведения угол отложен от горизонтальной оси, например, от точек \(0,\pi, 2\pi\), то лошадь как бы мотает головой и говорит «Нет». В этом случае функция не меняется.  Для формулы \(tg(\pi+x)\) лошадь будет мотать головой, то есть функция не поменяется и в ответе останется тангенс.

– А как понять, от какой оси отложена точка, если она, например, равна 10?

– Для этого нужно хорошо ориентироваться на тригонометрической окружности. Сейчас, я найду вам рукопись, в которой рассказано все об окружности. Вот она: «Тригонометрическая окружность. Часть 1».

– Звучит достаточно просто. Это все, что нужно для решения Формул?

– Разумеется, нет. Дальше мы должны определить, какой знак будет у новой функции.

– И как это сделать?

– Узнаем, какие знаки принимают тригонометрические функции в разных четвертях. Подойдите к вон той стене. На ней висит картина с памяткой. 

Какие знаки имеют тригонометрические функции в четвертях?  Знак каждой функции в четверти легко определить по ее оси на окружности. Расположение осей на окружности мы разбирали в статье «Тригонометрическая окружность. Часть 2».  Разберем на примере синусов. Ось синусов – вертикальная ось, проходящая через центр окружности. По ней легко определяем значения синусов – синус положителен, если его значение лежит над осью косинусов (этот промежуток выделен красным), и отрицателен, если его значение лежит под осью косинусов (этот промежуток выделен синим).  Следовательно, синус будет принимать положительные значения в I и II четвертях и отрицательное в III и IV четвертях.  Аналогично можно вывести знаки для остальных тригонометрических функций: — Косинус будет положителен в I и IV четвертях и отрицателен в II и III четвертях. — Тангенс и котангенс будут положительны в I и III четвертях и отрицательны в II и IV четвертях.

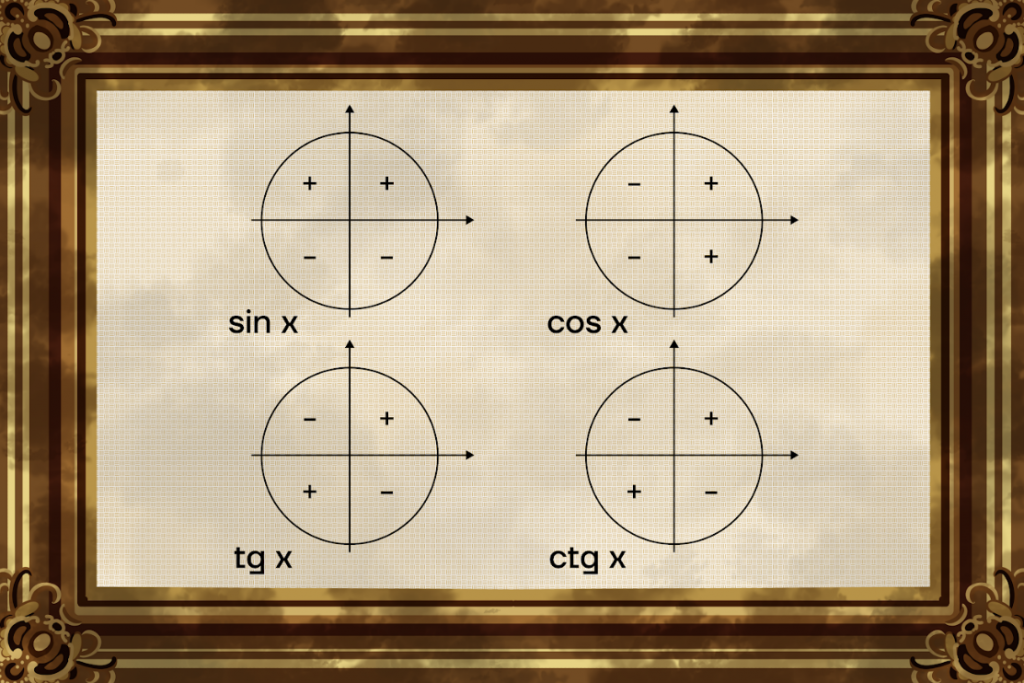
– По какой функции нам нужно определять знак? По той, которая была в начале, или по той, которая будет в ответе?

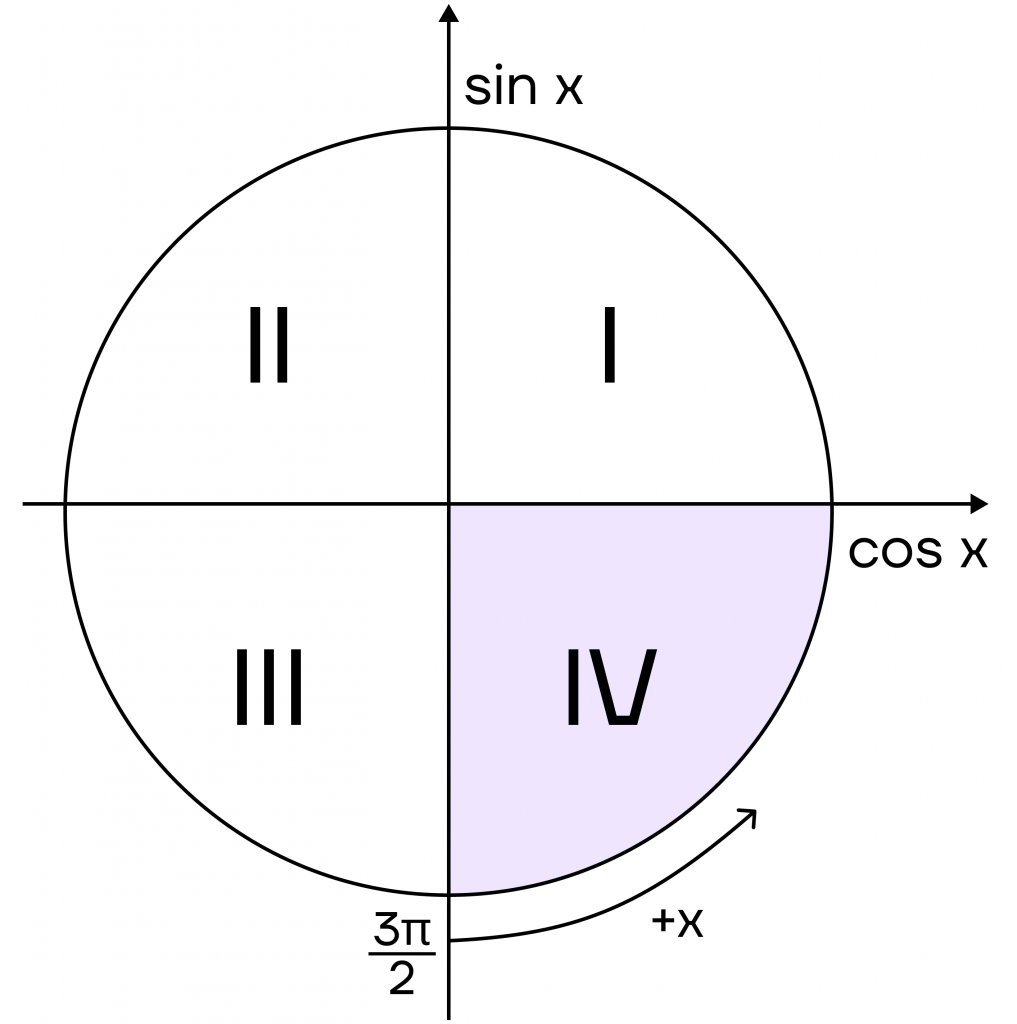
– Обязательно по той, которая была в начале. Например, в формуле \(ctg(\frac{3\pi}{2}+x)\) угол будет лежать в четвертой четверти, а значит, знак функции в ответе будет отрицательный. 

Глава 4. Заключительная

– Теперь-то все? 

– Нет, остался самый важный шаг: записать ответ.

– Есть ли у вас памятка, как решать Формулы Приведения? 

– Конечно! 

– Однако вам обязательно закрепить знания на практике! Если вы решите мое задание, то, так уж и быть, я отпущу вас из замка на волю.

Эпилог. Практика

Формулы приведения могут встретиться в любом задании с тригонометрией, поэтому очень важно знать, как с ними работать. Например, они встречаются в №6 ЕГЭ по профильной математике.

Найдите значение выражения \(sin(x-\frac{15\pi}{2})\), если \(sin x=\frac{\sqrt3}{2}\) и \(x\in (\frac{3\pi}{2};2\pi)\).

Решение.
Шаг 1.
Важно, чтобы в формуле приведения на первом месте стояла точка, от которой мы откладываем угол. Следовательно, нам нужно преобразовать выражение \(sin(x-\frac{15\pi}{2})\). Для этого вынесем минус из аргумента. Подробнее про формулы, с помощью которых мы можем преобразовывать тригонометрические выражения, можно прочесть в статье «Формулы тригонометрии и простейшие тригонометрические уравнения». Вынесем минус с помощью формулы \(sin(-x)=-sin(x)\):

\(sin(x-\frac{15\pi}{2})\)=\(sin(\frac{15\pi}{2}-x)\)

Шаг 2.
Теперь мы можем применить алгоритм для решения формул приведения. 

Проверим правило лошади: угол отложен от вертикальной оси, то есть лошадь кивает, следовательно, синус меняется на косинус. 

Далее определяем знак. Угол попадет в III четверть, в которой синус отрицательный. Значит, знак поменяется на противоположный:

\(-sin(\frac{15\pi}{2}-x)=cos x\)

Шаг 3.
Чтобы найти значение косинуса, необходимо воспользоваться основным тригонометрическим тождеством:  

\(sin^2x+cos^2x=1\)
\(cos^2x=1-sin^2x\)
\(cos x=\pm\sqrt{1-sin^2x}\)

Основное тригонометрическое тождество  мы также подробно обсуждали в статье «Формулы тригонометрии и простейшие тригонометрические уравнения».

Шаг 4.
По условию угол х лежит в четвертой четверти, в которой косинус положителен. Следовательно, получаем:

\(cos x=\sqrt{1-sin^2x}\)

Подставим значение синуса:

\(cos x=\sqrt{1-(\frac{\sqrt3}{2})^2}=\sqrt{1-\frac{3}{4}}=\sqrt{\frac{1}{4}}=\frac{1}{2}\)

Ответ: \(\frac{1}{2}\).

– Больше в страшные замки ни ногой! 

– Зато узнали что-то новое. Оказалось, Формулы Приведения не такие страшные, как казалось на первый взгляд. Интересно, сможем ли мы теперь решать «Тригонометрические уравнения»?

– Думаю, сможем. Давай проверим! 

Надеемся, что вам понравилось небольшое путешествие в замок к призракам. Давайте подведем небольшой итог.

Формулы приведения применяются для преобразования аргумента тригонометрической функции в том случае, если угол отложен от одной из осей. 

Формулы приведения могут выглядеть так: \(sin(\frac{\pi}{2}+x), cos(\pi-x), tg(\frac{13\pi}{2}-x), ctg(x-15\pi)\) и т.д. Поскольку невозможно решать уравнения и неравенства с таким аргументом, его нужно преобразовывать. 

Именно в этом случае на помощь приходят формулы приведения. Их можно попробовать выучить, для этого необходимо воспользоваться таблицей:

Однако учить их все совсем необязательно! Решить любую формулу приведения можно с помощью простого алгоритма: 

Шаг 1. Записать формулу приведения.

Шаг 2. По правилу лошади определить, меняется ли функция на противоположную.

Правило лошади опирается на представление головы лошади на тригонометрической окружности. При этом лошадь двигает головой по той оси, от которой отложен угол.
— Если угол отложен от вертикальной оси, например, \(sin(\frac{\pi}{2}+x)\), то лошадь кивает (говорит «да»), и функция меняется на противоположную, то есть синус на косинус или тангенс на котангенс (и наоборот).
— Если угол отложен от горизонтальной оси, например, \(sin(\pi-x)\), то лошадь мотает головой (говорит «нет»), и функция не меняется. 

Шаг 3. Определить знак новой функции.

Для этого нужно опираться на функцию, которая была дана изначально. Задача: установить, в какую четверть попадает угол и какой знак имеет функция в этой четверти.

Шаг 4. Записываем результат.

Термины

Аргумент функции – это независимая переменная, обычно ее обозначают через x.

Тригонометрические функции – это синус, косинус, тангенс и котангенс. С их помощью выражается величина угла в численном значении. 

Фактчек

• Формулы приведения – формулы, позволяющие привести аргумент, в котором угол отложен от одной из осей на окружности, к обычному аргументу с углом. 
• Примерами формул приведения могут служить \(sin(\frac{\pi}{2}+x), cos(\pi-x), tg(x+\frac{3\pi}{2}), ctg(x-\pi)\).
• Чтобы решить формулы приведения, нужно следователь алгоритму. По нему определяется, меняется ли функция на противоположную (синус на косинус или тангенс на котангенс и наоборот). Это делается с помощью правила лошади.
• Дальше определяется знак. Знак определяется по изначальной функции с помощью четвертей на окружности. 

Проверь себя

Задание 1.
Чему равно \(sin x+\pi\) ?

1. \(sin x\)
2. \(-sin x\)
3. \(1\)
4. \(cos x\)

Задание 2.
Чему равно \(ctg x+\frac{\pi}{2}\)?

1. \(tg x\)
2. \(ctg x\)
3. \(- ctg x\)
4. \(- tg x\)

Задание 3.
Чему равно \(tg-2x-\pi\)?

1. \(2x\)
2. \(0\)
3. \(-tg2x\)
4. \(tg2x\)

Задание 4.
Решите уравнение \(sin x+\frac{3\pi}{2} =1\)

1. \(x=π+2πk, k∈z\)
2. \(x=π+πk, k∈z\)
3. \(x=2πk, k∈z\)
4. \(x=-π+2πk, k∈z\)

Задание 5.
В каких четвертях тангенс положителен?

1. I и II
2. I и III
3. II и IV
4. I и IV

Ответы: 1. — 2; 2. — 4; 3. — 3; 4. — 1; 5. — 2.