Касание к окружности

На этой странице вы узнаете

• Сколько вариантов “окружность + прямая” можно начертить на листе бумаги?
• Что такое сопряжение и с чем его едят?
• Какие окружности изображены на олимпийском флаге? 

В жизни мы ежедневно сталкиваемся с касаниями. Касаемся предметов или друг друга. А может ли окружность, подобно человеку, чего-то касаться?  Давайте узнаем в этой статье.

Взаимное расположение прямой и окружности

Перед нами стоит задача начертить прямую и окружность на бумаге. Задумайтесь на секунду: как бы вы сейчас выполнили эту задачу? 

Поскольку их взаимное расположение не уточнено, то есть несколько вариантов, как их начертить. 

1 случай. Прямая и окружность будут лежать в разных местах на листе и никак не пересекутся друг с другом. 

2 случай. Прямая будет только касаться окружности. 

3 случай. Прямая пересечет окружность. 

Сколько вариантов “окружность + прямая” можно начертить на листе бумаги? Каждый человек изобразит эти элементы в разных положениях относительно друг друга. Но так ли много разнообразия будет? На самом деле, существует всего три варианта расположения фигур:  — Они не касаются и не пересекаются; — Прямая касается окружности; — Прямая пересекает окружность.

Оказывается, в математике существуют термины для второго и третьего случая. Начнем их рассматривать с касательной к окружности. 

Касательная

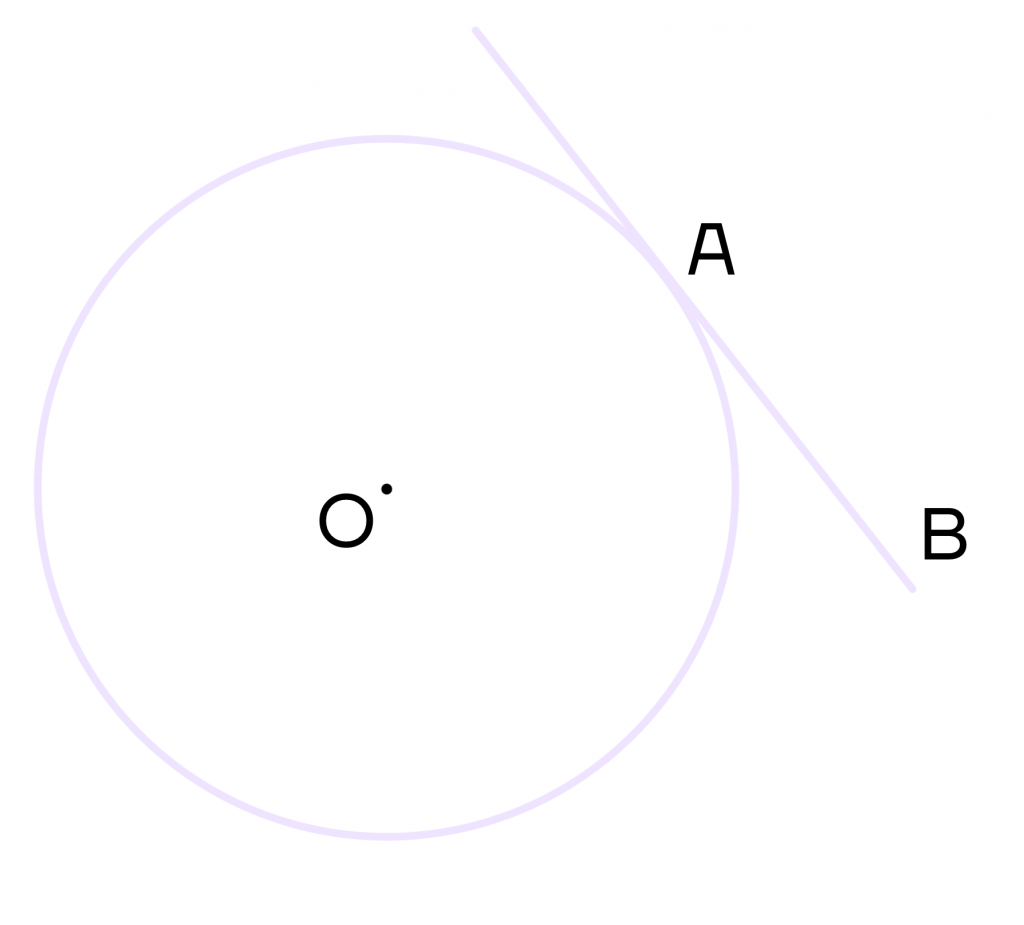
Касательная – это прямая, которая имеет с окружностью только одну общую точку. 

На рисунке АВ – касательная, которая касается окружности в точке А. 

Что такое сопряжение и с чем его едят? Многие вещи, которые нас окружают, имеют плавные формы. Например, если мы посмотрим на цепь велосипеда, она имеет изогнутую форму.  Все такие детали можно вычертить, а называться эти чертежи будут сопряжениями. Сопряжение в черчении – это плавный переход линии в окружность или окружности до окружности. Чтобы построить сопряжения, есть целые законы, которые основаны на касании к окружности.

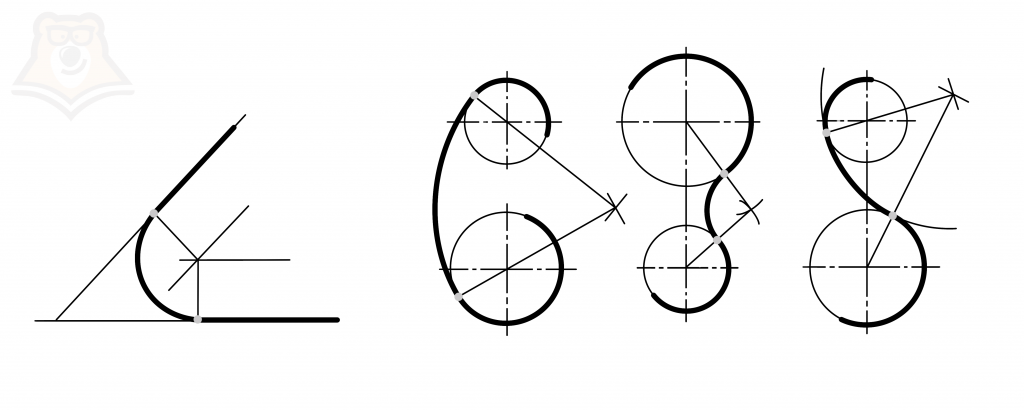
Свойства касательной

1 свойство. Касательная перпендикулярна радиусу, проведенному из центра окружности в точку касания. 

Проведем радиус ОА, тогда ОА ⟂ АВ. 

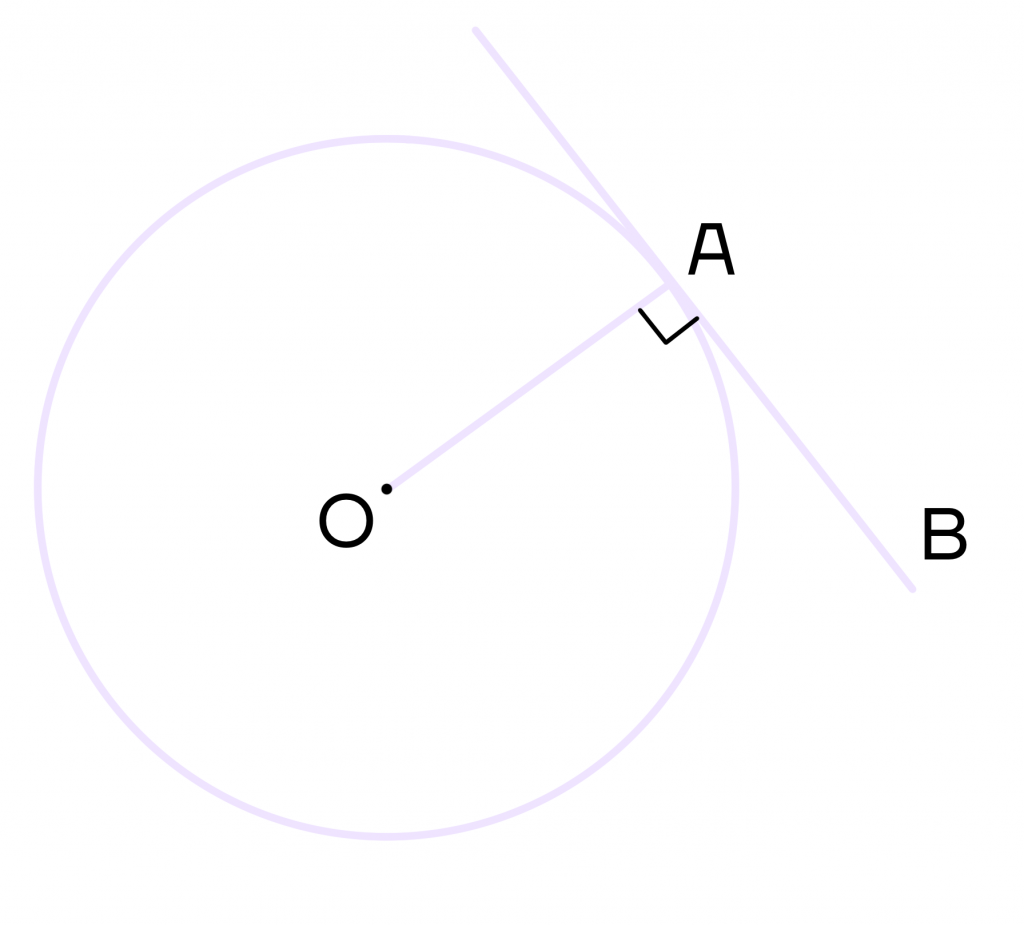
2 свойство. Если провести две касательных из одной точки, то их отрезки будут равны.

Проведем из точки В еще одну касательную ВС, тогда АВ = ВС. 

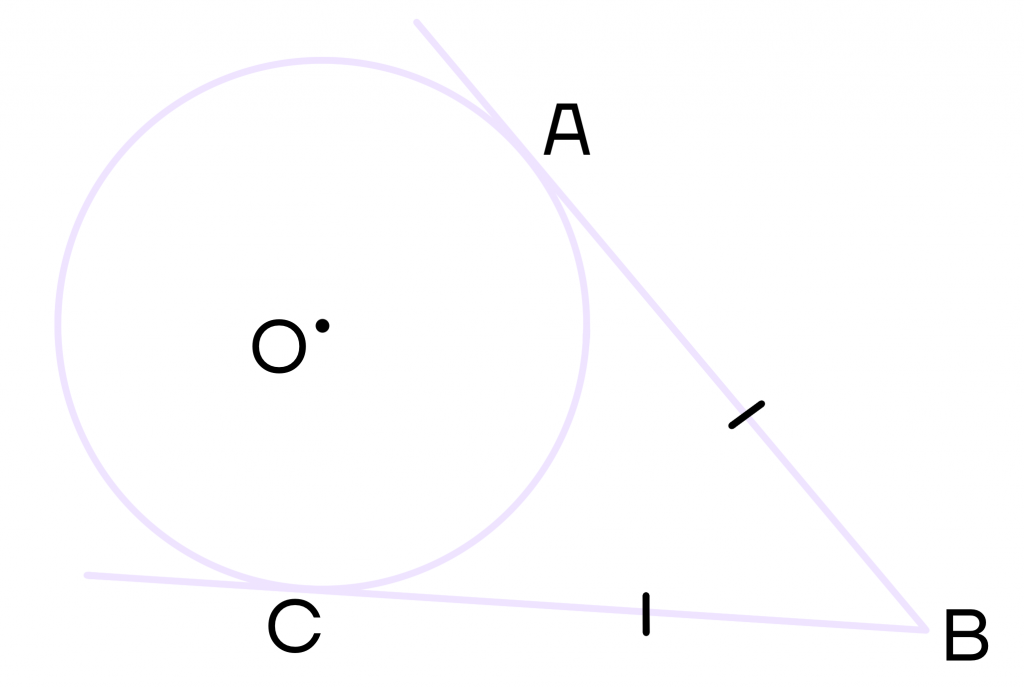
Если перевернуть рисунок, то можно заметить, что он отдаленно напоминает воздушный шар. А в воздушных шарах, также как и в свойстве касательных, используются равные по длине веревки. 

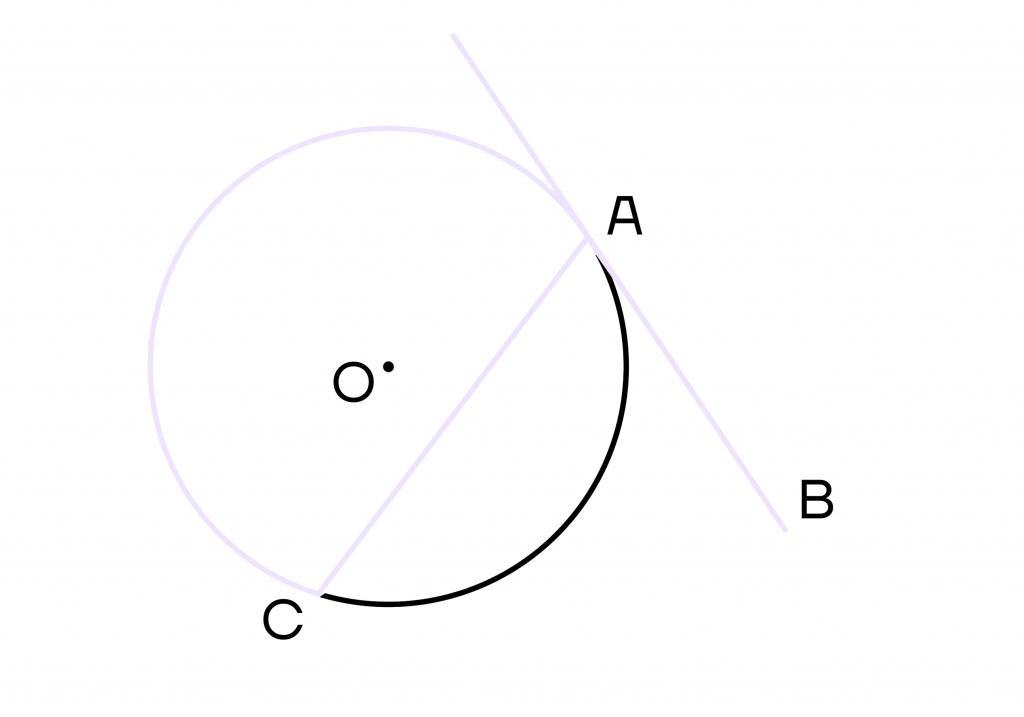
3 свойство. Угол между хордой и касательной равен половине дуги, которая заключена между этими касательной и хордой. 

Проведем хорду АС, тогда угол САВ равен \(\frac{1}{2}⋃АС\). 

Секущая

Теперь обратим внимание на третий случай, когда прямая пересекает окружность. Такая прямая называется секущей.

Секущая – это прямая, которая пересекает окружность в двух точках. 

Пусть на рисунке АВ – секущая, тогда точки А и В – точки пересечения окружности и секущей. 

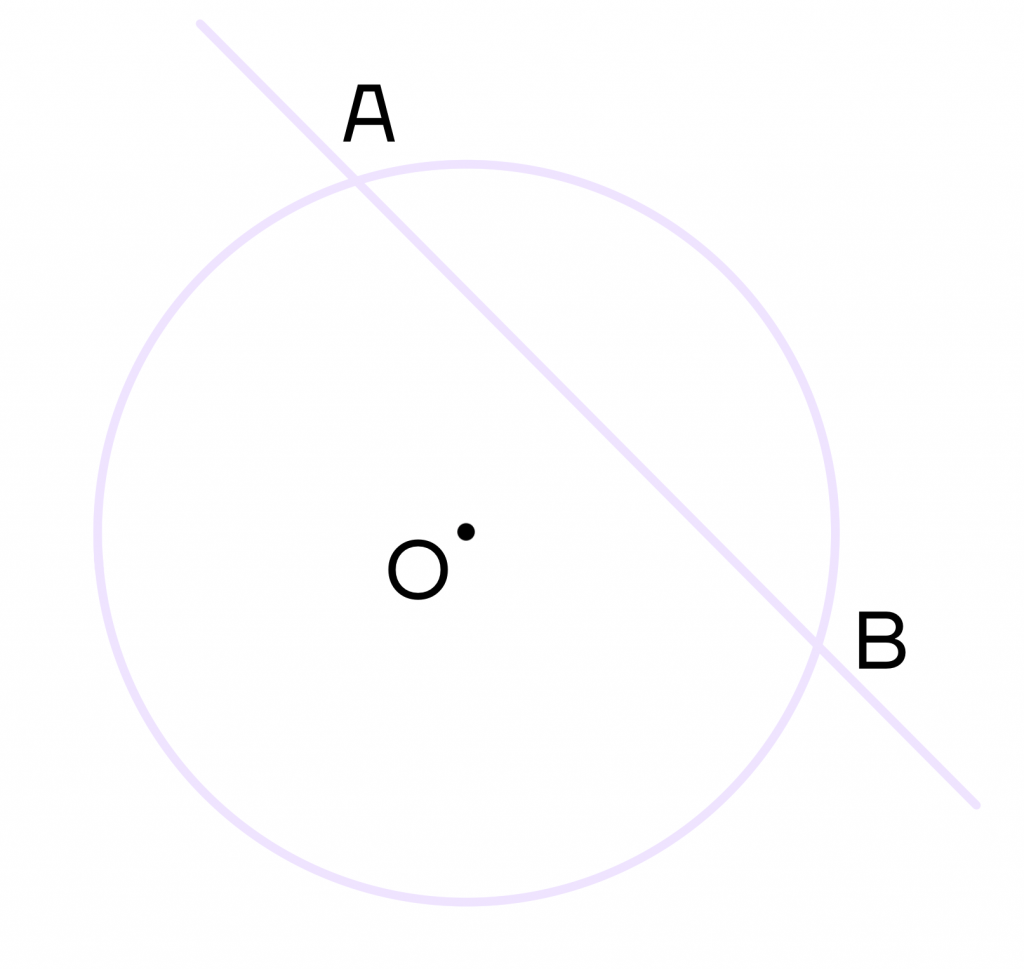
Вспомни, как мы нарезаем пиццу или пирог. Каждый разрез будет секущей, то есть будет разделять круг на несколько частей. 

Свойства секущей 

1 свойство. Если из одной точки провести секущую и касательную к окружности, то квадрат касательной равен произведению секущей на ее внешнюю часть. 

Проведем из точки А касательную АВ и секущую АС. Пусть секущая будет пересекать окружность в точках С и Е. Тогда выполняется равенство АВ² = АС * АЕ. 

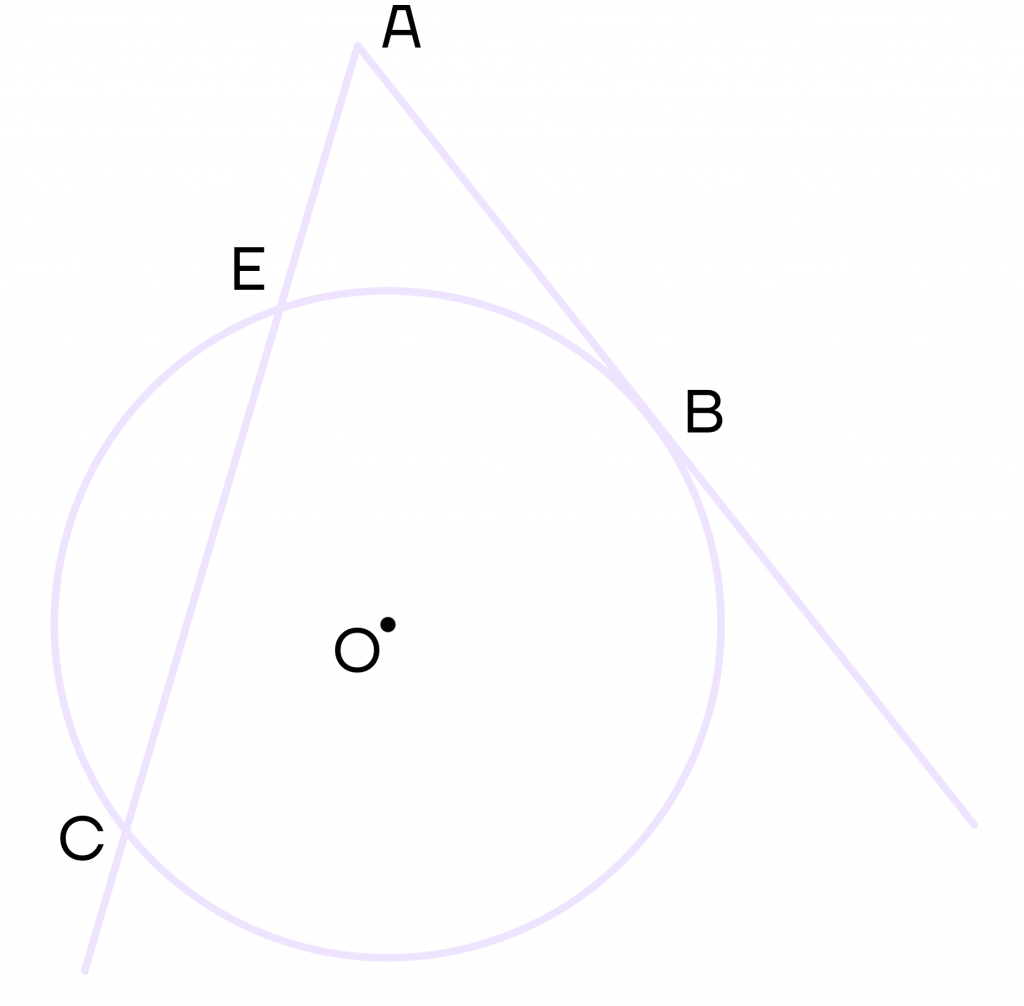
2 свойство. Если из одной точки провести две секущих к окружности, то произведение первой секущей на ее внешнюю часть равняется произведению второй секущей на ее внешнюю часть. 

Проведем секущие АВ (пересекает окружность в точках Е и В) и АС (пересекает окружность в точках С и D). Тогда выполняется равенство АС * AD = АВ * АЕ. 

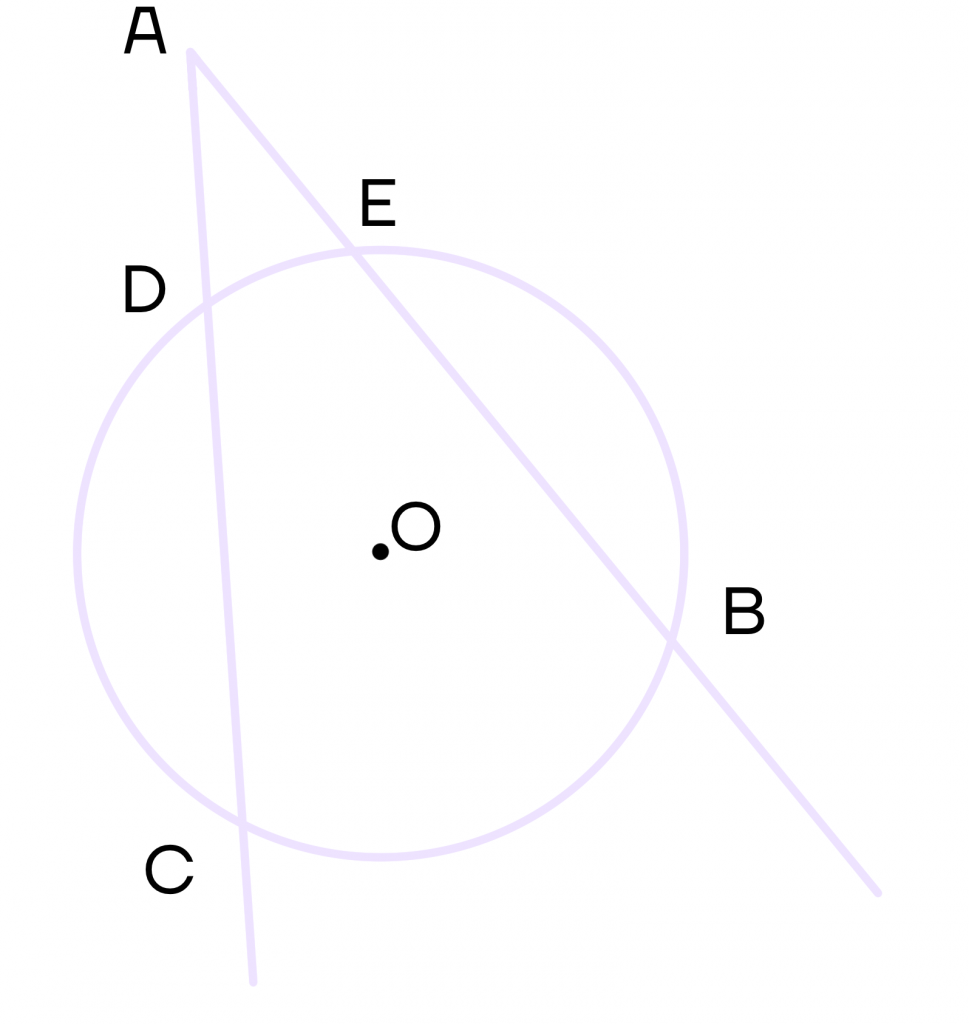
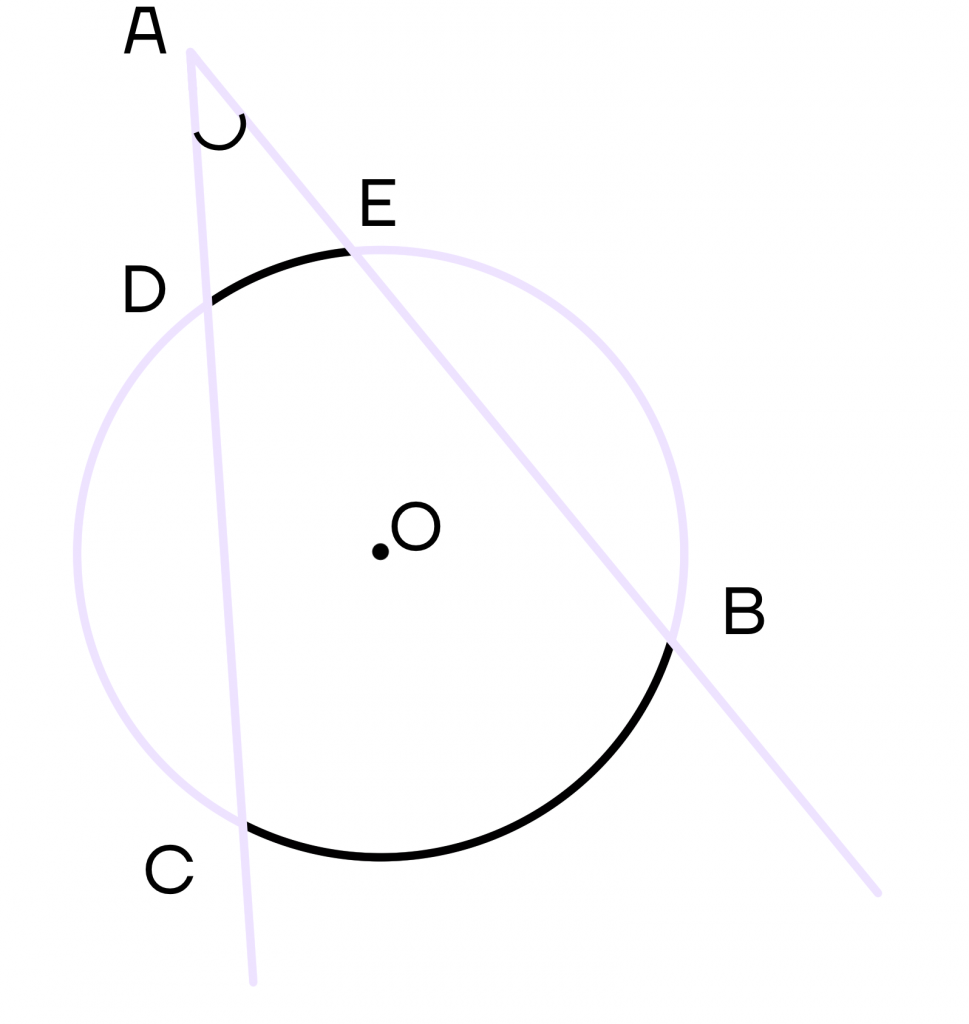
3 свойство. Угол между двумя секущими равен половине разности градусных мер большей и меньшей дуг, которые заключены между секущими. 

Допустим, необходимо найти угол САВ. Тогда угол \(CAB = \frac{1}{2}(⋃CB-⋃DE)\). 

Не стоит пугаться знака “⋃” – в математике таким образом обозначают дугу окружности. 

Касание окружностей

Мы рассмотрели касание прямой и окружности, но могут ли две окружности касаться друг друга? Если у окружностей одна общая точка, то они являются касающимися друг к другу. 

И есть даже несколько вариантов такого касания: 

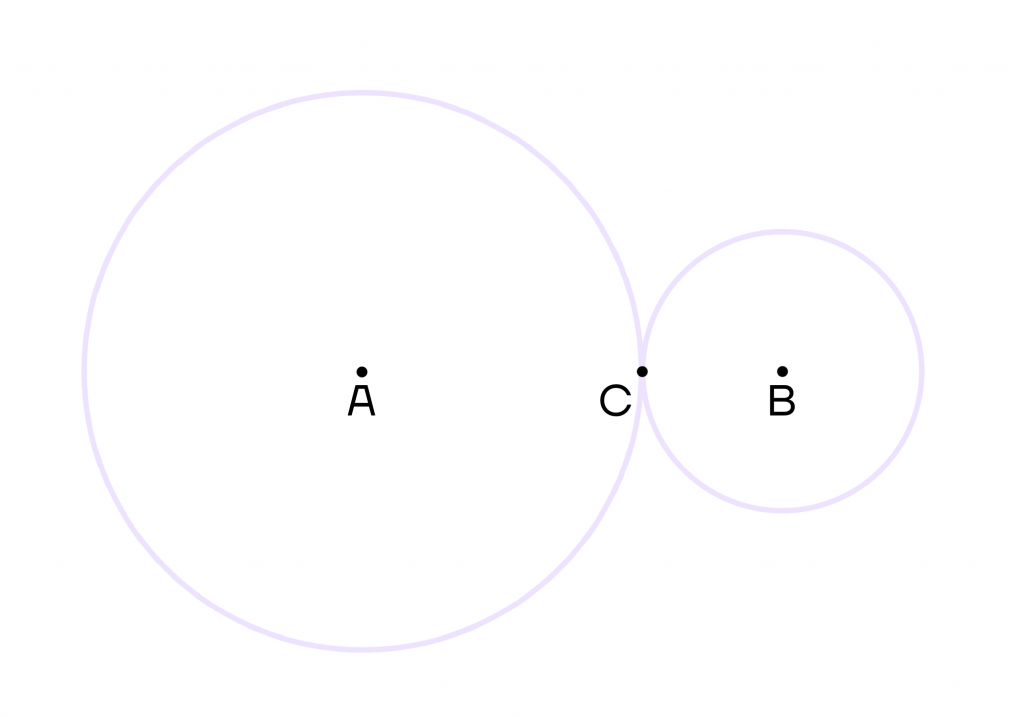
• Внешнее, когда окружности лежат по разные стороны от точки касания. 

В данном случае точка С – точка касания. 

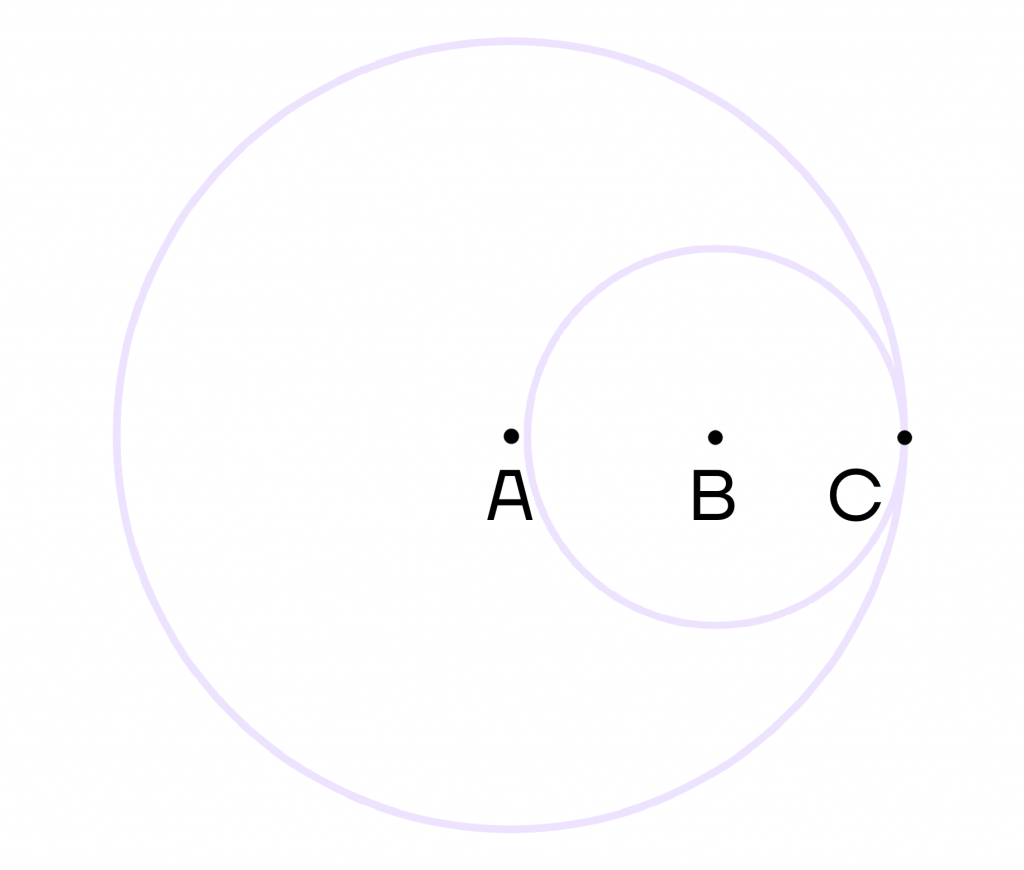
• Внутреннее, когда одна окружность как бы “лежит” в другой. 

В данном случае точка С также является точкой касания. 

Касание окружностей нередко применяется при создании ювелирных украшений. Такое решение создает неповторимые и очень красивые образы. 

Какие окружности изображены на олимпийском флаге?  Как мы уже определили, окружности могут касаться друг друга. Но есть еще один вариант их взаимного расположения: окружности пересекаются друг с другом. В этом случае они будут иметь две общие точки.  Пересекающиеся окружности изображены на олимпийском флаге, их там целых 5. По одной из версий, они обозначают 5 частей света.

Рассмотрим свойство касающихся окружностей: 

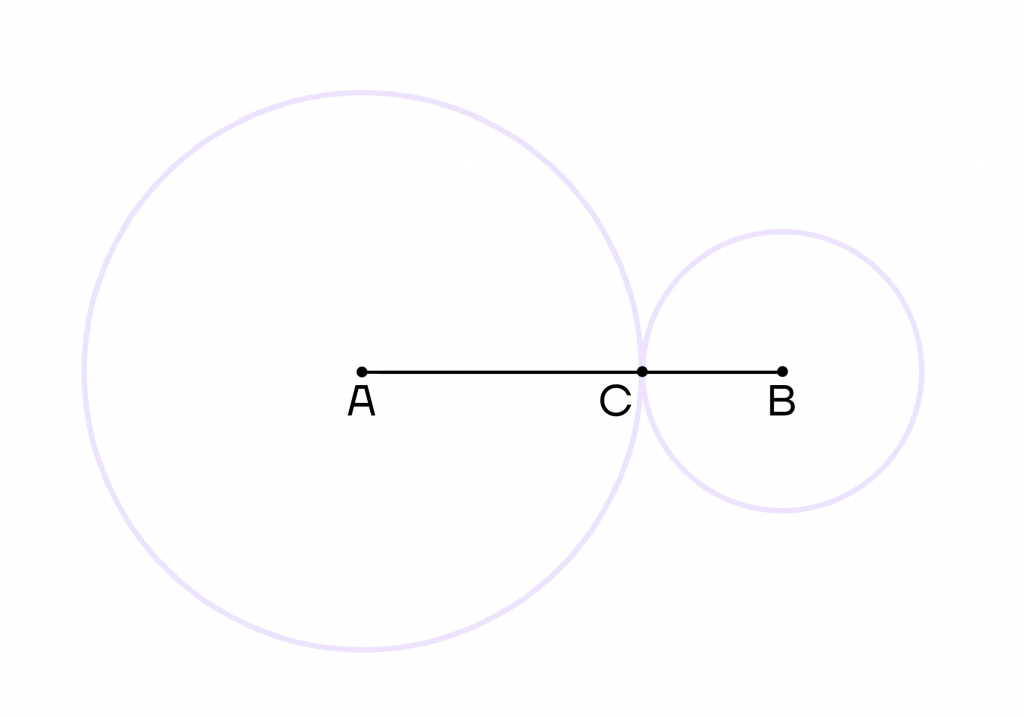
•  Прямая, построенная через центры таких окружностей, включает точку касания. 

Если мы построим прямую через центры окружностей А и В, то на этой же прямой будет лежать точка касания С. 

Фактчек

• Прямая и окружность имеют три варианта взаимного расположения: не пересекаться, касаться или пересекать друг друга. 
• Касательная – это прямая, которая проведена к окружности и имеет с ней только одну общую точку. Касательная перпендикулярна радиусу, который проведен в точку касания. 
• Секущая – это прямая, которая проходит через окружность и имеет с ней две точки пересечения. 
• Если провести из одной точки касательную и секущую, то квадрат касательной будет равен произведению секущей на ее внешнюю часть. 
• Две окружности также могут касаться друг друга. Касание может быть как внешним, так и внутренним. При этом если соединить центры окружности прямой, то на этой же прямой будет лежать точка касания. 

Проверь себя

Задание 1.
Как называется прямая, которая проведена к окружности и имеет с ней одну общую точку?

1. Секущая;
2. Хорда;
3. Касательная;
4. Диаметр.

Задание 2. 
Дуга, заключенная между касательной и хордой, равняется 50^\(\circ\). Чему равен угол между касательной и хордой?

1. 25^\(\circ\);
2. 50^\(\circ\);
3. 100^\(\circ\);
4. 180\^(\circ\).

Задание 3. 
Длина секущей равна 9, а ее внешняя часть равняется 4. Чему равна касательная к окружности, проведенная из той же точки, что и секущая?

1. 36;
2. 6;
3. 9;
4. 5.

Задание 4. 
Между секущими заключены дуги окружности, которые равняются 70 и 30 градусам. Чему равен угол между секущими?

1. 40;
2. 10;
3. 80;
4. 20. 

Задание 5. 
Каким бывает касание двух окружностей?

1. Только внешним;
2. Только внутренним;
3. Внешним и внутренним;
4. Две окружности не могут касаться друг друга. 

Ответы: 1. – 3 2. – 1 3. – 2 4. – 4 5. – 3