Показательная и логарифмическая функции

На этой странице вы узнаете

• В какой песне поется про математические функции? 
• Где прячется аргумент в показательной функции? 
• Как изменить логарифмическую функцию?

Оценка за тест зависит от набранных баллов, а они зависят от количества и качества ответов. Цена билета в развлекательный центр может меняться от времени суток или дня недели. Погода в городе напрямую связана со временем года, географическим положением, температурой воздуха, влажностью, осадками и многими другими факторами. Функция в математике показывает нам зависимость одной переменной от другой. Что нам дает знание о характере этой зависимости? Об этом подробнее поговорим в статье.

Что такое показательная функция?

Для начала вспомним, что же такое функция. 

Функция — это зависимость одной переменной от другой.

Обычно функция обозначается через переменные у и х. Общепринятая запись y = f(x) как раз показывает нам идею функции: величина у изменяется в зависимости от значения неизвестной величины х, а процесс этого изменения подчинен определенному правилу f. 

В этом случае у и есть сама функция. Но иногда применяется и другая запись, когда функцию обозначают только как f(x) или g(x) (или любой другой зависимостью от х) — эта информация пригодится нам в дальнейшем. 

Так же как и в «жизненных» примерах во вступлении нашей статьи, на «ответ» (на y) будет влиять значение неизвестной x, которую мы подставим. 

В какой песне поется про математическую функцию? Математика может быть лиричной. Например, про зависимость между у и х можно услышать в припеве песни Pyrokinesis: А ты в себе разберись, и Каждый от чего-то зависим Будто игрек по иксу Коли смерть заносит, хитрая, косу То важно не терять равновесие… А песня так и называется: «Зависимость».

Что меняется, когда мы говорим про показательную функцию? 

В первую очередь стоит запомнить, что показательная функция напрямую связана со степенями. Вспомним, как можно представить возведение в степень. 

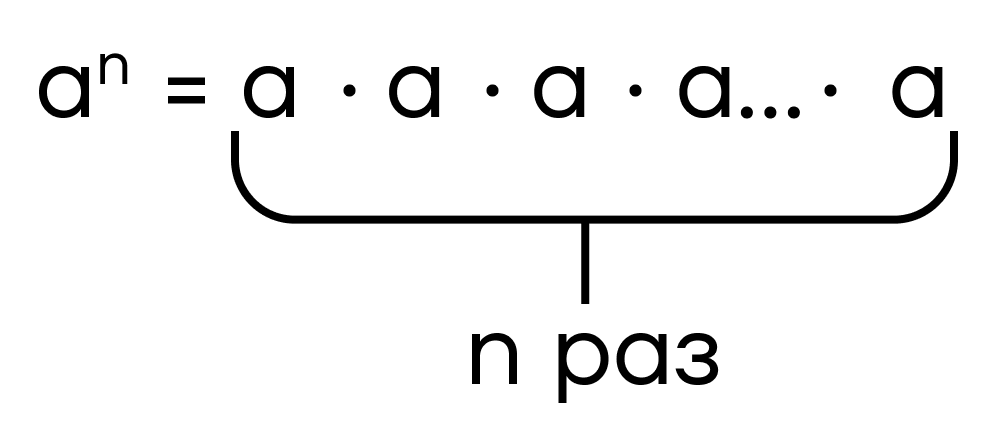
Со степенями мы уже сталкивались при решении линейных, квадратичных и других элементарных функций. Тогда у нас была неизвестная величина x в какой-то конкретной, заранее указанной степени. Например, в функции y=x². Здесь значение нашей функции менялось в зависимости от того, какое число x мы возводим в квадрат. Если x = 2, то y будет равен 4, а при x = 3, получим у = 9.

Что могло пойти «не так» в показательной функции?

Показательная функция — это функция, у которой неизвестная находится в показателе степени.

Записывается показательная функция так:

Такая функция также называется экспонентой (как и кривая, которая задает ее график). 

При этом существует понятие экспоненциальной зависимости. Она описывает процесс, при котором быстро увеличивается или быстро уменьшается количество некоторых элементов.

Если мы посмотрим на показательную функцию, то заметим, что это так и есть: количество элементов (а) многократно умножается на само себя при изменении показателя степени. Экспоненциальной зависимостью, например, можно описать рост населения планеты. 

Где прячется аргумент в показательной функции? Аргумент функции — это независимая переменная, то есть значение, которое мы можем менять по нашему усмотрению. От аргумента всегда зависит значение функции. В показательной функции значение y зависит от выражения a x. Рассмотрим его чуть подробнее: — Основание степени а — неизменное выражение (за исключением некоторых случаев, которые мы рассмотрим в статье «Показательные уравнения и неравенства»). То есть поменять мы его не сможем. — Показатель степени х — переменная, которую мы можем сами назначать. Вместо нее мы можем подставить любое число и уже в зависимости от него найти значение функции. Следовательно, аргументом показательной функции будет показатель степени (х).

Таким образом, в отличие от ранее известных нам функций, некая величина a будет задавать функцию. И находится эта величина в неизвестной степени x.

Примеры показательной функции: y = 2 ^x, y = (12) ^x и т. д.

Заметили разницу? В основных элементарных функциях мы знали показатель степени (квадрат, куб и т.д.), но не знали, какое число в эту степень возводится. Теперь мы знаем, какое число является основанием степени, но не знаем, в какую степень его возвели. 

Какие ограничения имеет показательная функция? 

\(y=a^x\), где \(a > 0\) и \(a ≠ 1\)

Такие ограничения появляются из-за того, что для а < 0 (для отрицательного основания степени) данное выражение будет иметь смысл не для всех а. 

Посмотрим:

• Если \(a=0\) значение функции меняться не будет. В какую бы степень мы ни возвели 0, он всегда останется 0. 
• Если a<0, то мы можем получить противоречие. Допустим, \(a=-4\), тогда мы получаем функцию \(y=(-4)^x\). Поскольку вместо х мы можем подставить любое число, то возьмем \(x=\frac{1}{2}\). Попробуем вычислить. Для этого воспользуемся свойством степеней и перейдем к корню: \((-4)^{\frac{1}{2}}=\sqrt{-4}\). И здесь нам стоит вспомнить, что под корнем положительной степени не может стоять отрицательное число. Во избежание подобных парадоксов, на основание степени введено ограничение. 

Аналогично с ограничением а ≠ 1. Если \(a=1\), как бы мы ни меняли степени, все равно получим единицу.

Поэтому под показательной функцией понимают то выражение, в основании степени которого стоит положительное и не равное 1 число. 

Свойства показательной функции

Как и любая функция, показательная обладает своими свойствами, которые мы рассмотрим дальше. А чтобы вспомнить, какими свойствами может обладать функция и на что они влияют, обязательно загляните в статью «Определение и график функции». 

Как мы выяснили чуть выше, основание функции должно быть строго больше 0 и не равняться 1. По факту у нас получается два отдельных случая: 

1. когда a больше единицы; 
2. когда а больше нуля, но меньше единицы. 

Рассмотрим эти случаи по отдельности.

Случай 1: a > 1. 

Для примера возьмем за a число 2 и попробуем построить график. Подставляем это значение в основание функции и получаем \(y=2^x\). 

Построим таблицу. В строке со значениями х пропишем числа, которые будем подставлять в функцию. Во второй строке укажем значения, которые получаются при вычислении. 

Например, пусть \(x=-2\), тогда \(y=2^{-2}=\frac{1}{2^2}=\frac{1}{4}\). 

Аналогично заполняем все оставшиеся ячейки:

Отметим эти точки на координатной плоскости и соединим их плавной линией. Таким образом, мы получим следующий график:

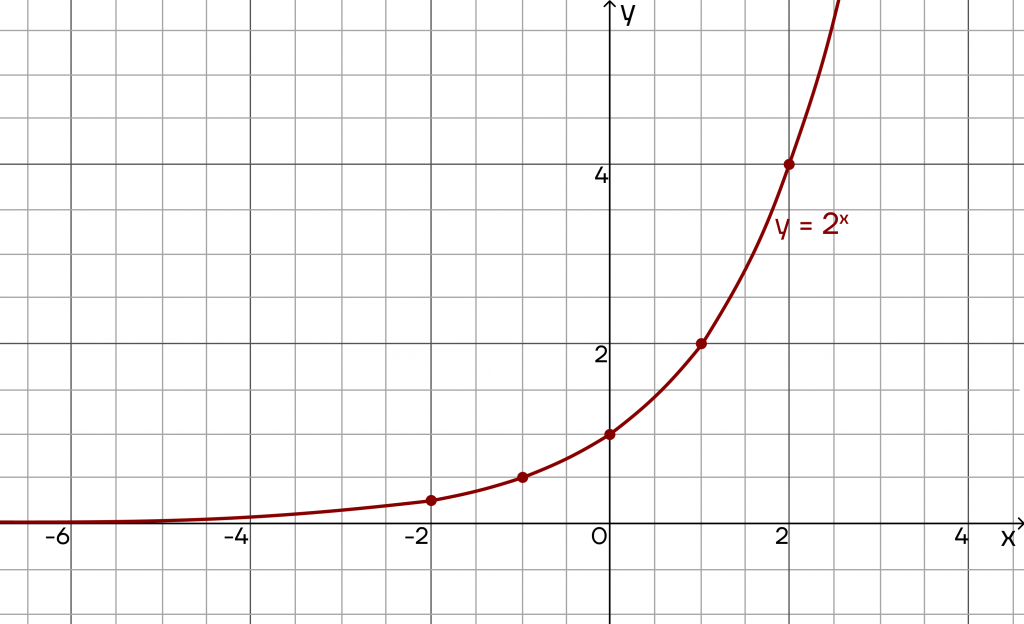
Что мы можем сказать про этот график? 

Во-первых, график любой показательной функции называется экспонентой

Мы можем подставить любое значение х и при этом сможем найти значение функции. Это свойство называется областью определения. 

Область определения функции — это все допустимые значения аргумента функции (х), при которых функция будет определена. Область определения обозначается как D(y).  

Получаем, что \(D(y)=(-\infty;+\infty)\). 

А что мы можем сказать про значения у, то есть про область значений? 

Область значений функции — это все значения, которые может принимать функция. Область значений обозначается как Е(у). 

По графику видно, что функция лежит выше оси х, то есть все значения функции строго положительны. Чем меньше будет значение у, тем ближе будет график к горизонтальной оси, но никогда ее не пересечет. Это связано с тем, что не существует степени, в которую можно возвести положительное число и получить 0. 

Получаем, что \(E(y)=(0;+\infty)\).

Что мы еще можем сказать про график? Если мы представим, что идем по кривой слева направо, то заметим, что нам придется подниматься в горку. Следовательно, функция возрастает (чем правее, тем выше точка). Также мы можем не бояться идти: ни на одном участке функция не прервется, то есть она монотонна и непрерывна.

А теперь рассмотрим второй случай. 

Случай 2: 0 < a < 1. 

Для примера возьмем \(a=\frac{1}{2}\).

Заполним таблицу для этой функции: 

Отметим точки на графике и построим кривую:

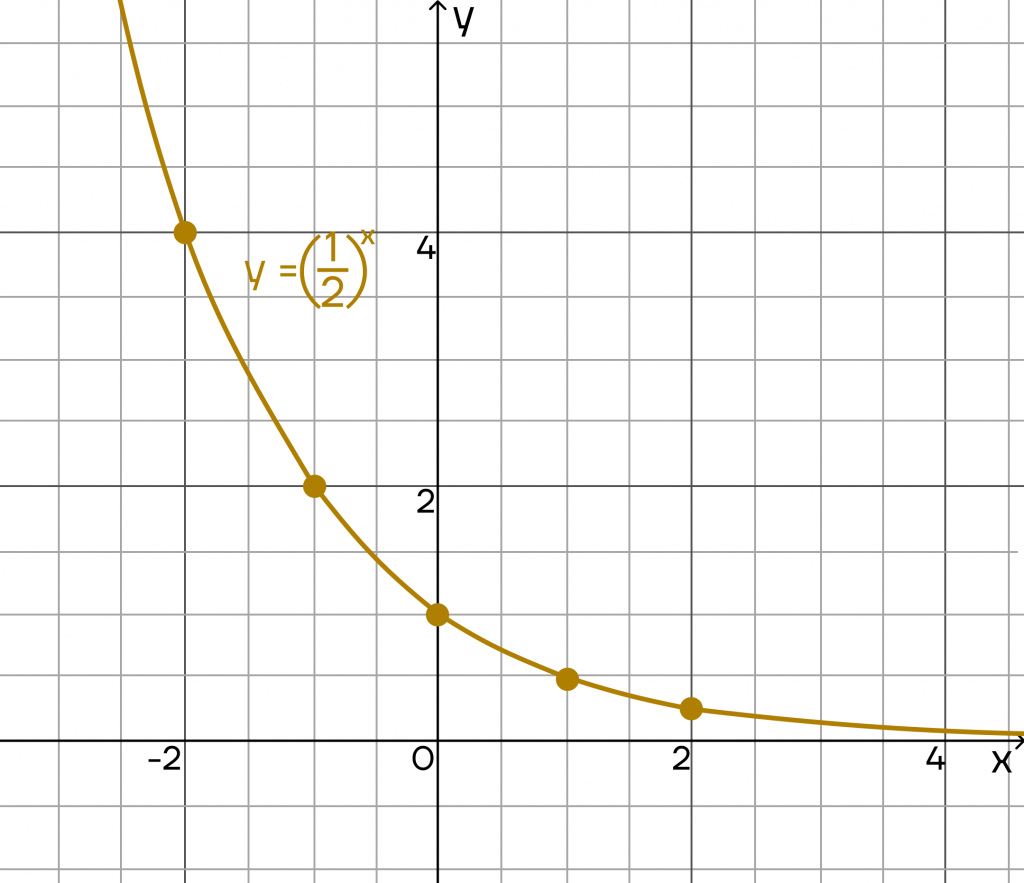
Теперь рассмотрим график. Аналогично со случаем 1, мы можем взять любое значение х, при этом у будет принимать только положительные значения. Получаем:
\(D(y)=(-\infty;+\infty)\)
\(E(y)=(0;+\infty)\)

Если мы попробуем пройтись по графику слева направо, то увидим, что будем спускаться с горки. Следовательно, функция монотонно убывает и при этом непрерывна. 

Заметим, что в обоих графиках нет экстремумов, то есть точек, в которых функция перестает убывать и начинает возрастать (или наоборот). Таким образом, нет ни наименьшего, ни наибольшего значения. 

Как мы уже определили, в обоих случаях графики не пересекают ось х. Но при этом у графиков и оси у есть общие точки. Как найти их координаты?

Все достаточно просто: все точки, которые лежат на оси у имеют координату \(x=0\). Тогда для нахождения у достаточно подставить \(x=0\) в уравнение функции. 

Например, для функции \(y=2^x\) мы получим: 

\(y=2^0=1\)

То есть координата ее пересечения с осью у будет равна (0;1). 

Но что интересно, это справедливо для любой показательной функции! Ведь по свойству степеней: \(a^0=1\), то есть какое бы число ни стояло в основании степени, при его возведении в степень 0 мы получим 1. 

Рассмотрим промежутки, которым может принадлежать a.
При 0 < a < 1 и a > 1 показательные функции отличаются. Графики функций выглядят «зеркально» (или симметрично) друг другу, если основание степени одной из них b, а второй — \(\frac{1}{b}\) .

Например:

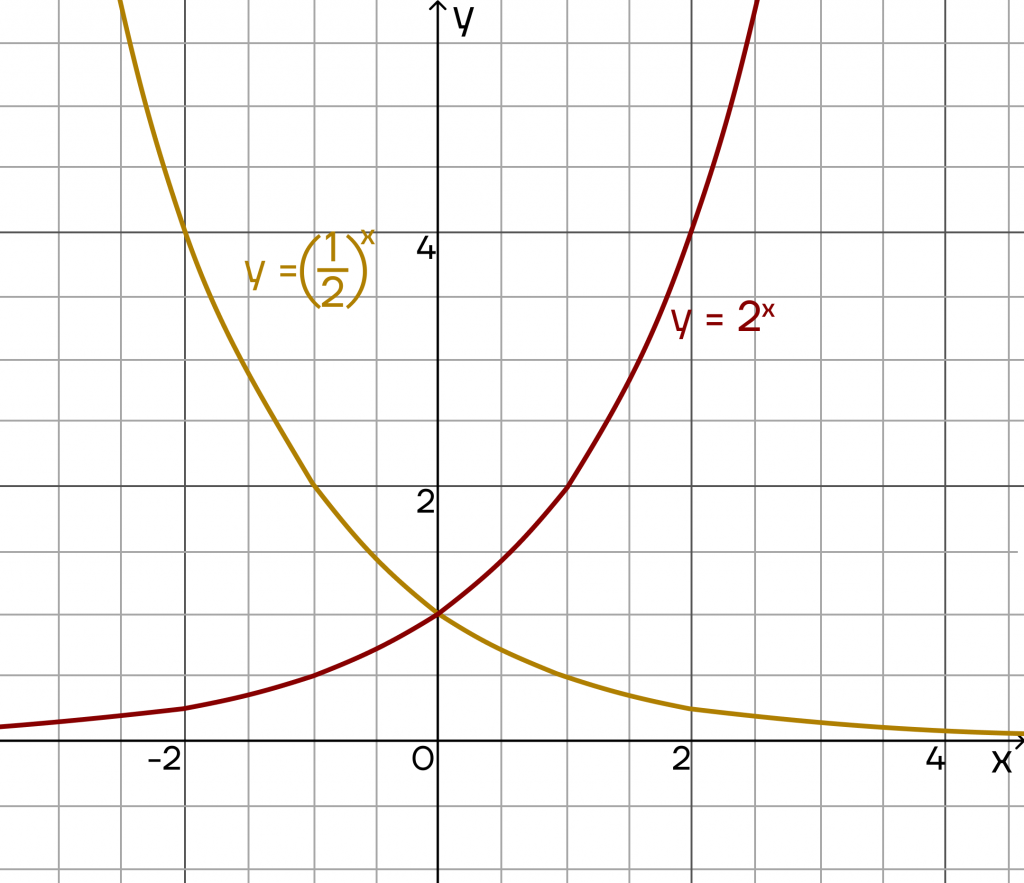
Составим сравнительную таблицу для двух рассмотренных нами случаев, чтобы зафиксировать свойства показательной функции. 

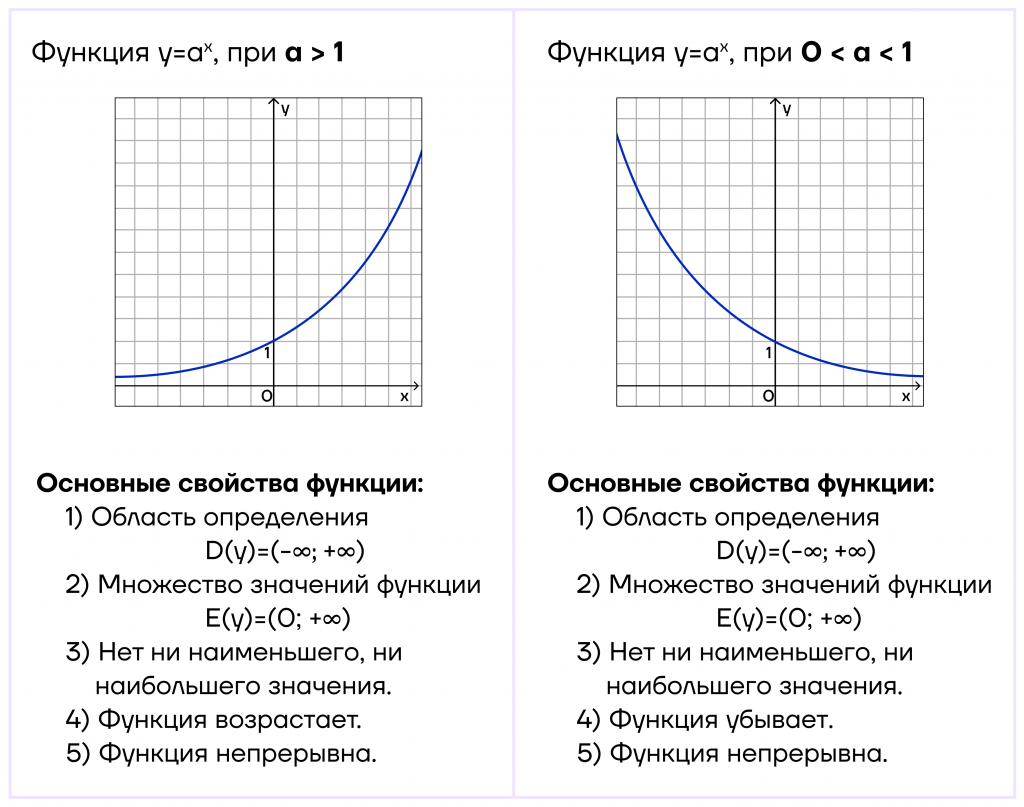
Графики показательных функций могут встретиться и на экзамене. Для примера разберем №10 из ЕГЭ по профильной математике.

На рисунке изображен график функции \(g(x)=a^{x-b}\). Найдите g(5). 

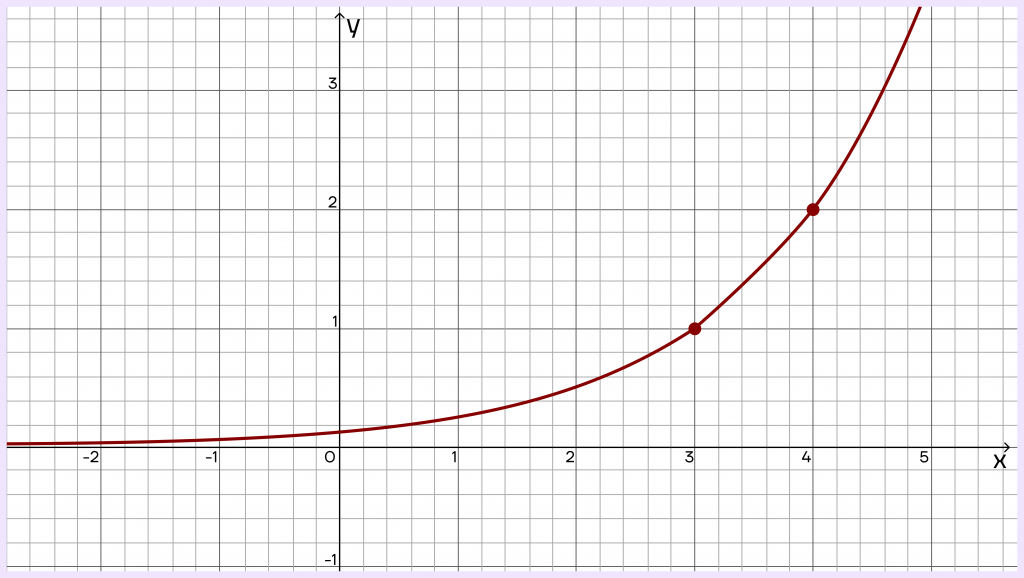
Решение.
Посмотрим на график функции внимательнее. Первое, что бросается в глаза — он возрастает, то есть a>1.

У нас есть две точки, в которых мы имеем точные значения. Координаты первой будут (4;2), а второй — (3;1). Следовательно, мы можем подставить эти координаты в уравнение функции вместо g(x) и х. Вспомним, что координаты указываются в таком порядке: (x;y), а запись g(x) равнозначна записи у. 

Получаем два уравнения:
\(2=a^{4-b}\) и \(1=a^{3-b}\). 

Рассмотрим второе уравнение. В каких случаях мы можем получить 1 при возведении числа в степень? Всего их два:
1) Мы возводим в степень число 1. Однако этот вариант нам не подходит, поскольку мы уже определили, что \(a>1\).
2) Мы возводим любое число в степень 0. Этот вариант нам подходит. 

Из рассуждений выше получаем, что \(3-b=0\). Тогда \(b=3\).
 
Подставим полученное значение в первое уравнение:
\(2=a^{4-b}\)
\(2=a^{4-3}\)
\(2=a^1\)
\(a=2\).

Мы нашли все неизвестные переменные. Теперь у нас есть функция вида \(g(x)=2^{x-3}\). Чтобы найти \(g(5)\), необходимо подставить \(x=5\) в уравнение функции.

\(g(5)=2^{5-3}\)
\(g(5)=2^2\)
\(g(5)=4\)

Ответ: 4

Логарифмическая функция

Когда мы говорим про степени, невозможно не вспомнить про логарифмы. Мы максимально подробно обсуждаем их в статье «Логарифмические уравнения и неравенства». А сейчас кратко вспомним все важные моменты.

Взятие логарифма – это обратная операция возведению в степень. Иными словами, с помощью логарифма мы ищем, в какую степень нужно возвести число а, чтобы получить число b. 

Логарифм — это число, в которое нужно возвести основание a, чтобы получить число b.

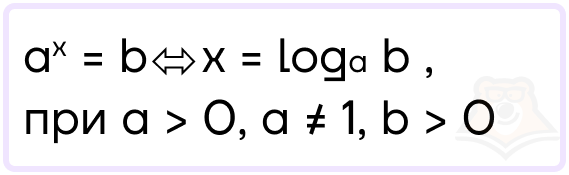
В этой записи а – основание логарифма, b – его аргумент. 

Вспомним также и про ограничения логарифмов. В первую очередь они касаются основания: основание логарифма должно быть строго положительным и не равняться единице. 

В свою очередь, аргумент логарифма должен быть строго положительным.

Итак, мы немного разобрались в логарифмах. А как же выглядит логарифмическая функция? 

Логарифмическая функция – это функция, в которой неизвестная находится в аргументе логарифма. 

Такая функция имеет вид \(y=log_ax\). Вместо а может стоять почти любое число.

Почему почти? Для логарифмической функции действуют те же ограничения, как и для логарифма:

• \(a>0\);
• \(a\neq 1\);
• \(x>0\).

Итак, попробуем построить графики двух логарифмических функций. Как и для показательной функции, рассмотрим случаи:

• когда основание a>1,
• когда 0<a<1.

Случай 1: \(y=log_2x\).

Построим таблицу:

Отметим точки на координатной плоскости и соединим их плавной линией. 

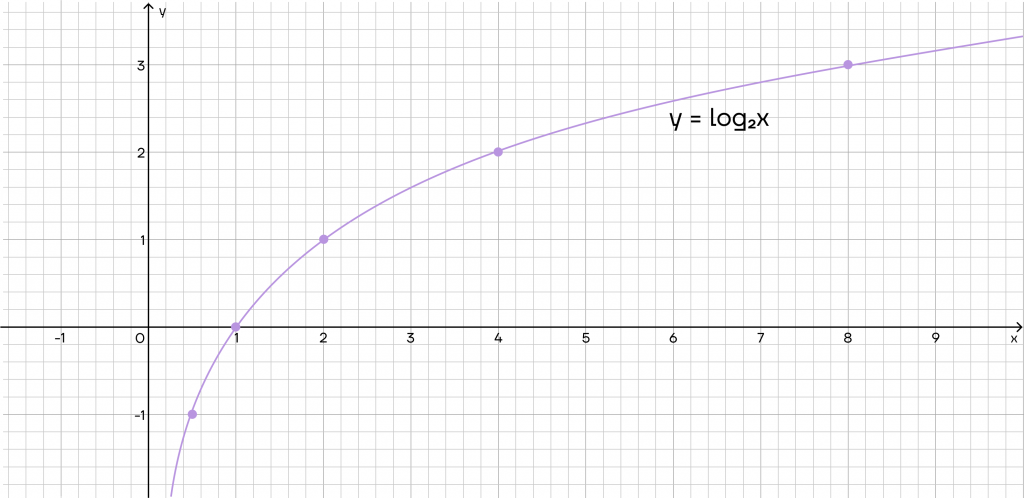
Что мы можем сказать про этот график? 

1. Область определения:

\(D(y)=(0;+∞)\).

2. Множество значений функции:

\(Е(y)=(-∞;+∞)\).

3. Нет ни наименьшего, ни наибольшего значения.
4. Функция возрастает.
5. Функция непрерывна.

Заметим, что любая логарифмическая функция, у которой a>1, будет возрастать. Это связано с тем, что чем больше мы подставим х, тем в большую степень нам нужно будет возвести основание:

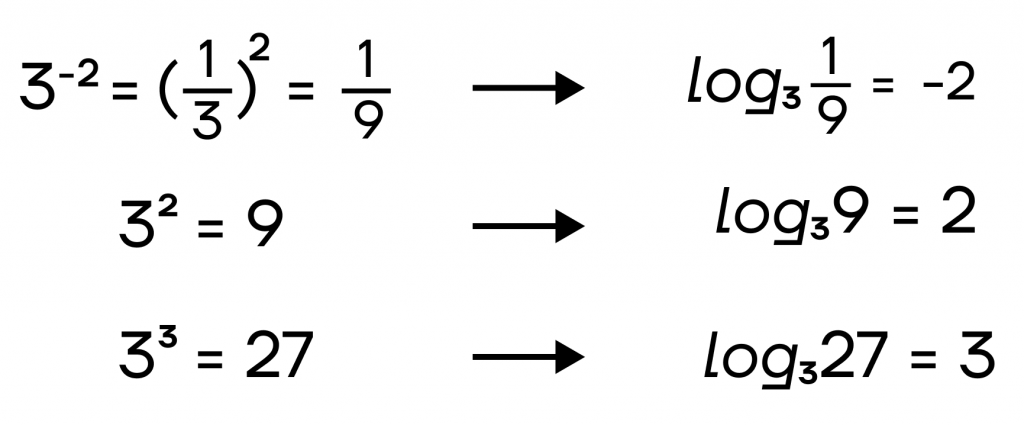
Обратную ситуацию мы видим для функций, у которых 0<a<1. В этом случае чем в большую степень мы возводим число, тем меньшее значение получаем. Это связано со свойствами дроби. 

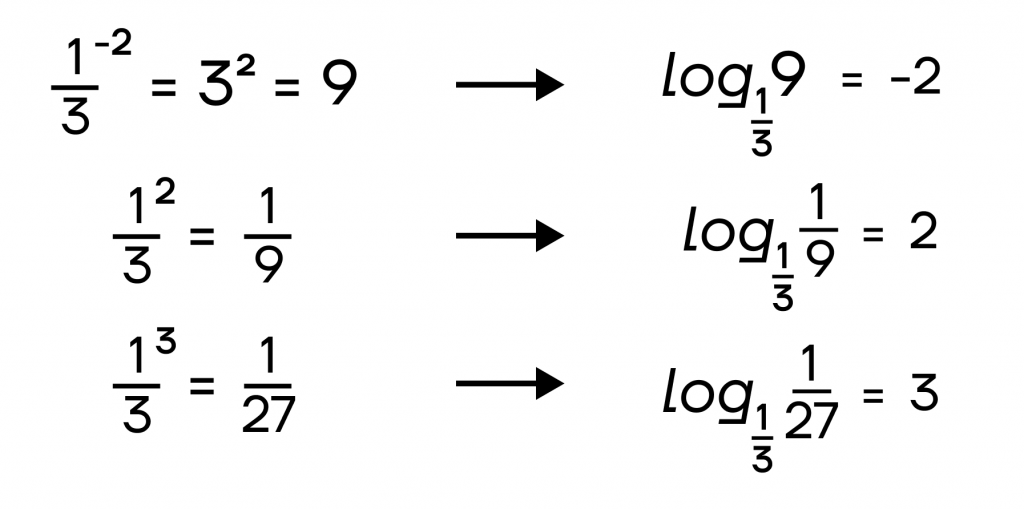
Случай 2: \(y=log_{\frac{1}{2}}x\).

Построим таблицу и график:

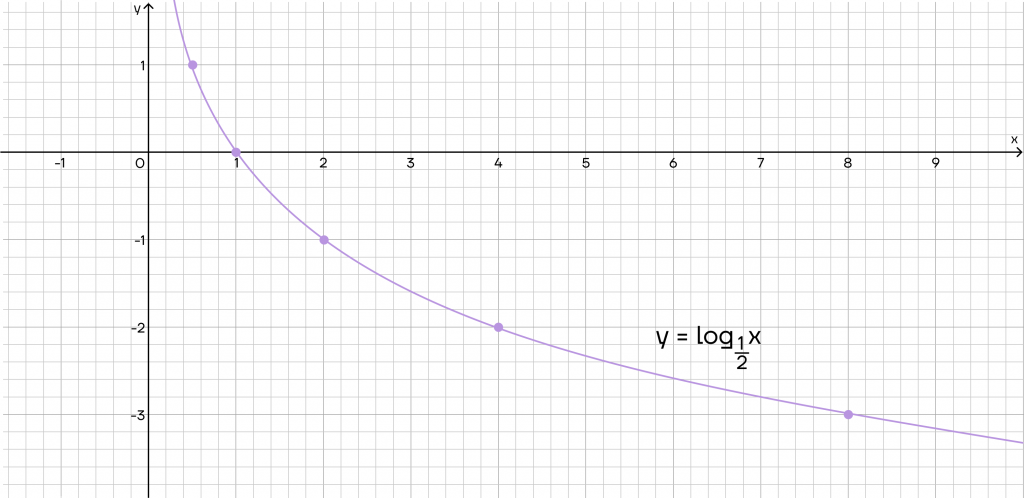
Что мы можем сказать про этот график?

1. Область определения:

\(D(y)=(0;+∞)\).

2. Множество значений функции:

\(Е(y)=(-∞;+∞)\).

3. Нет ни наименьшего, ни наибольшего значения.
4. Функция убывает.
5. Функция непрерывна.

В отличие от показательной функции, логарифмическая не пересекает ось у, но мы можем найти координаты ее пересечения с осью х. То есть нам нужно в уравнение такой функции подставить \(у=0\). 

Тогда функция примет вид: \(log_ax=0\). По свойству логарифма \(log_a1=0\), следовательно, \(x=1\). 

Из-за свойств логарифма любая логарифмическая функция будет проходить через точку (1;0). 

Как изменить логарифмическую функцию? Как и любая другая функция, логарифмическая меняется в зависимости от коэффициентов. Если мы добавим коэффициент к логарифму, то функция сдвинется вдоль оси у. Например, \(y=log_2x+3\) будет лежать на 3 единицы выше, чем уже рассмотренная функция \(y=log_2x\).  Значение коэффициента b легко определить по значению функции в точке x=1. Поскольку по свойству логарифма \(log_a1=0\), то смещение этой точки от оси х будет равно b. Если мы добавим коэффициент к аргументу логарифма, то функция сдвинется вдоль оси х. Причем, если мы прибавляем число, то функция двигается влево, а если отнимаем – вправо. Например, функция \(y=log_2(x+3)\) сдвинется влево на три единицы. Это также можно определить по точке пересечения графика функции и оси х. А вот функция \(y=log_2(x-3)\) сдвинется на 3 единицы вправо:

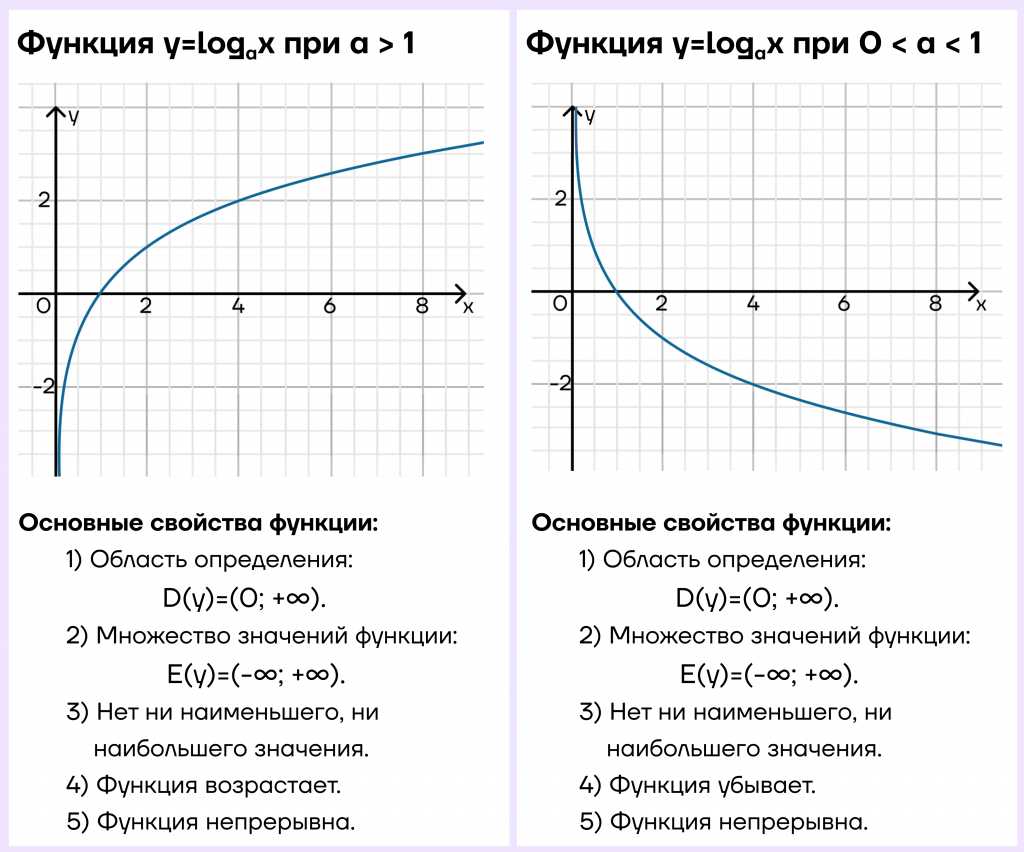
Подведем итог и составим сравнительную таблицу для двух рассмотренных случаев. 

Разберем еще один вариант №10 ЕГЭ по профильной математике.

На рисунке изображен график функции \(f(x)=log_ax+b\). Найдите f(64). 

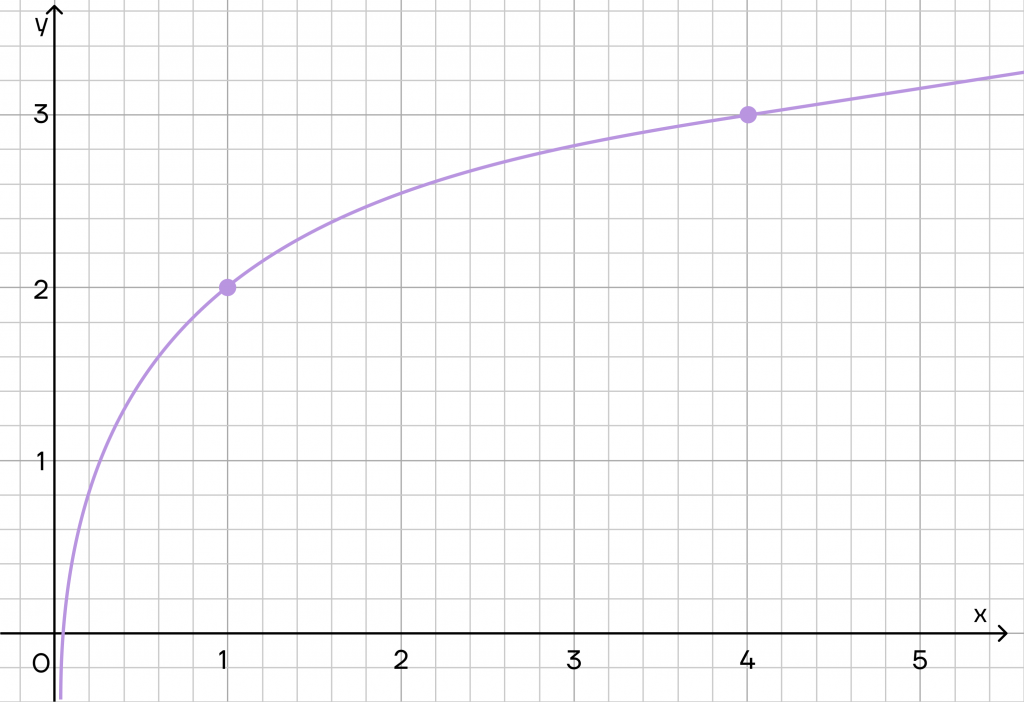
Решение. 

Шаг 1. Внимательно смотрим на график. Мы сразу можем назвать координаты у двух точек: (1;2) и (4;3). Вспомним, что координаты записываются как (x:y). 

Шаг 2. Подставим в уравнение значения из первой координаты \(x=1, y=2\):

\(2=log_a1+b\)

Вспомним одно важное свойство логарифма: \(log_a1=0\). Тогда получаем уравнение:

\(2=0+b => b=2\)

Теперь подставим значения из второй координаты, уже зная b:

\(3=log_a4+2\)
\(log_a4=3-2\)
\(log_a4=1\)

Следовательно, \(a=4\). 

Шаг 3. Мы нашли все неизвестные коэффициенты. Осталось посчитать f(64):

\(f(64)=log_464+2=3+2=5\)

Ответ: 5

Связь показательной и логарифмической функций

И показательная, и логарифмическая функция связаны со степенями. 

Когда мы работаем с показательной функцией, мы ищем результат, который получается при возведении числа в ту или иную степень. При работе с логарифмической же функцией, мы ищем степень, в которую возвели число, получив тот или иной результат. Иными словами, эти две функции – противоположные друг другу действия.

Показательная функция	\(y=a^x\)	Ищем результат возведения числа в степень.
Логарифмическая функция	\(y=log_ax\)	Ищем степень, в которую было возведено число.

Заметим: если в обеих функциях основания степени и логарифма будут равны, то мы будем совершать примерно одно и то же действие. 

Например, \(y=2^x\) и \(y=log_2x\). 

Если в первом случае мы подставим \(x=3\), то получим \(y=2^3=8\). 

А теперь подставим полученный результат вместо х во вторую функцию: \(y=log_28=3\). Мы вернулись к той же степени, в которую возводили число в первой функции. 

Как это отражается на графиках функций? Графики будут обратны друг другу. Иными словами, один график будет как бы «отзеркален» относительно линии \(y=x\). То есть графики будут симметричны. 

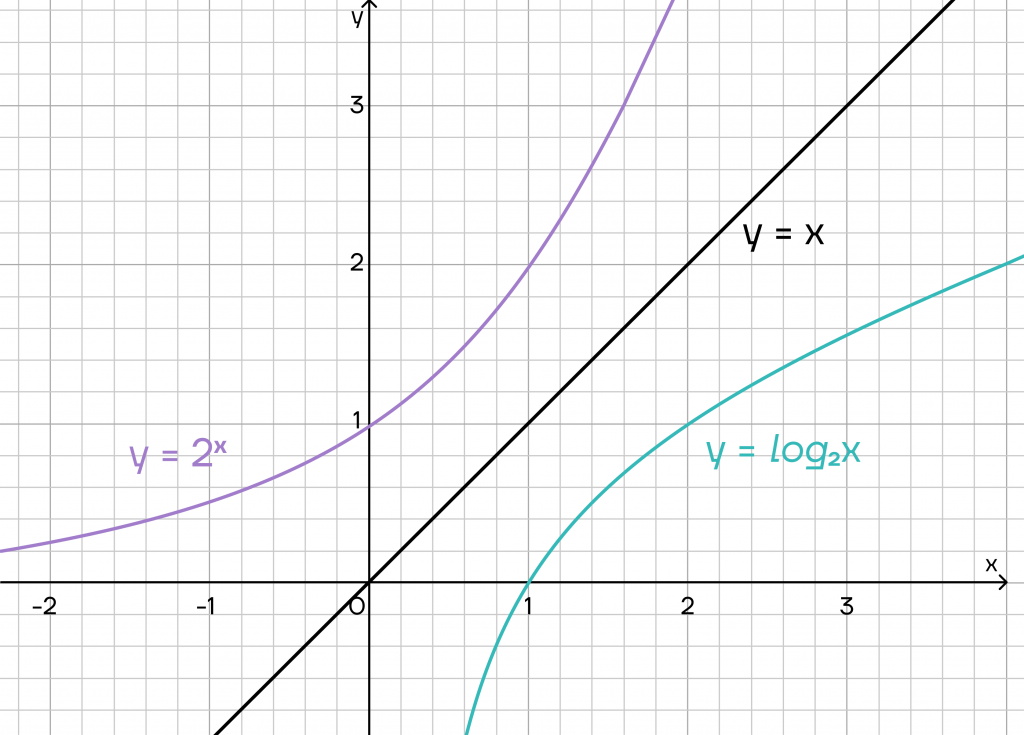
Аналогичную ситуацию мы увидим и в случае, когда \(0<a<1\).

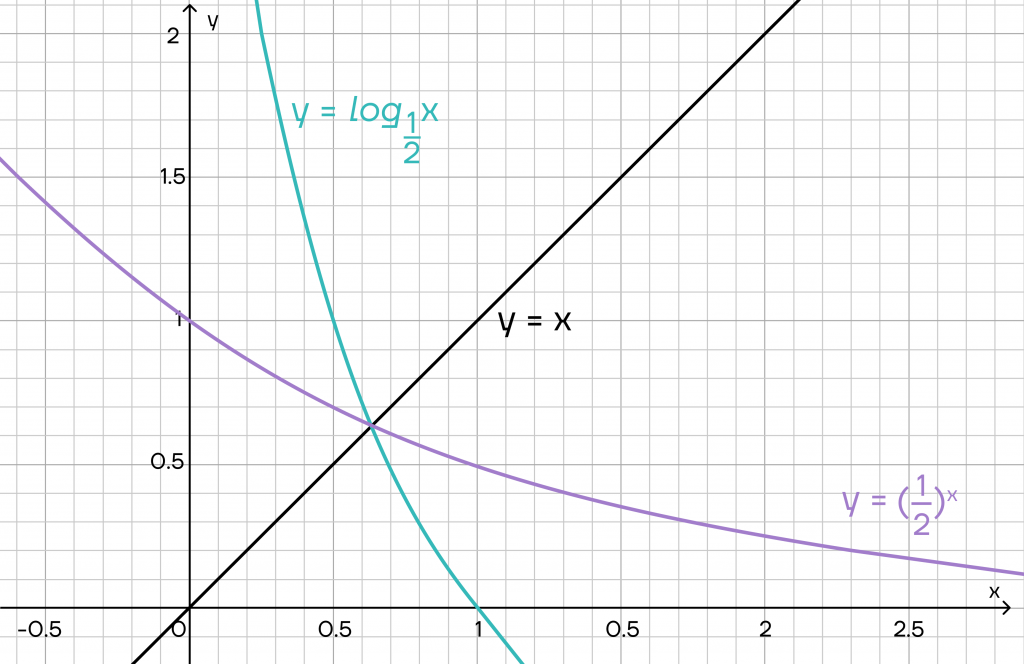
Мы разобрались в показательной и логарифмической функциях, узнали об их применении и как решать задания с ними. Однако показательная функция может нам встретиться и в уравнениях, и в неравенствах. А чтобы узнать, как их решать, приглашаем вас в статью «Показательные уравнения и неравенства».

Термины

Свойства степеней — это формулы или правила, которые могут быть использованы для упрощения вычислений и преобразования выражений, содержащих число или переменную в степени. С полной таблицей свойств степеней вы можете ознакомиться в статье «Действия с натуральными числами».

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.

Симметрия – свойство фигур, заключающееся в том, что части повторяют друг друга относительно центральной оси. 

Фактчек

• Показательная функция — это функция, у которой неизвестная находится в показателе степени. Ее можно записать как \(y=a^x\), где \(a > 0\) и \(a ≠ 1\).
• На график показательной функции влияет значение основания степени (то есть а). 
• Если a>1, то функция монотонно возрастает, \(D(y)=(-∞;+∞), Е(y)=(0;+∞)\), нет ни наименьшего, ни наибольшего значения. 
• Если 0<a<1, то функция монотонно убывает, \(D(y)=(-∞;+∞), Е(y)=(0;+∞)\), нет ни наименьшего, ни наибольшего значения. 
• Логарифмическая функция – это функция, в которой неизвестная находится в аргументе логарифма. Ее можно записать как \(y=log_ax\), где \(a>0, a\neq 1, x>0\). 
• Если в логарифмической функции \(a>1\), то функция монотонно возрастает, \(D(y)=(0;+∞), E(y)=(-∞;+∞)\), нет ни наименьшего, ни наибольшего значения. 
• Если в логарифмической функции \(0<a<1\), то функция монотонно убывает, \(D(y)=(0;+∞), E(y)=(-∞;+∞)\), нет ни наименьшего, ни наибольшего значения. 

Проверь себя

Задание 1.
Какая из функций является показательной?

1. \(f(x)=2x^2+x\)
2. \(g(x)=\frac{1}{x^2}\)
3. \(y=3^x\)
4. \(y=x^2+1\)

Задание 2.
Что в записи \(y=a^x\) является аргументом функции?

1. \(y\)
2. \(a\)
3. \(x\)
4. \(a^x\)

Задание 3.
Какие ограничения имеет показательная функция? 

1. \(x\geq 0\)
2. \(a<0\) и \(a\neq 1\)
3. \(x>0\) и \(x\neq 1\)
4. \(a>0\) и \(a\neq 1\)

Задание 4.
Какие ограничения имеет логарифмическая функция?

1. \(a>0, x>0\)
2. \(a<0, a\neq 1\)
3. \(a>0, a\neq 1, x>0\)
4. \(a>0, a\neq 1, x\geq 0\)

Задание 5.
Какой из вариантов ответа верен для функции \(y=(\frac{1}{3})^x\)?

1. Функция монотонна и непрерывна.
2. Существует значение х, при котором \(y=0\).
3. Область значений функции \((-∞;+∞)\).
4. График функции возрастает. 

Ответы: 1. — 3; 2. — 3; 3. — 4; 4. — 3; 5. — 1.