Понятие корня
На этой странице вы узнаете
- Где в корнях спрятан куб?
- Как не запутаться в корнях?
- Как найти значение выражения, если ответов получается два?
Без корня погибнет растение, а слово потеряет свой смысл. В математике корень — тоже очень важное понятие. Давайте разберемся, что такое корень n-ой степени и какие действия с ним можно совершить.

Понятие корня
Мы уже изучали, как возводить числа в степень в статье «Действия с натуральными числами». А как узнать, в какой степени находится то или иное число, если мы имеем только результат? Для этого и нужен корень! Итак, взятие корня является обратным действием возведению в степень.
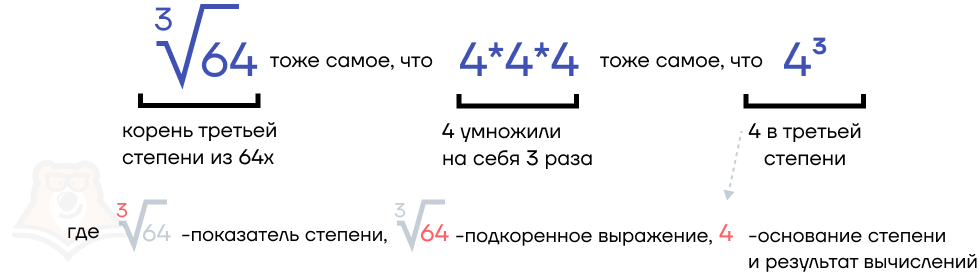
Корнем n-ой степени числа х называют такое число, при возведении которого в степень n получается х.
| \(\sqrt[n]{x}=y, y^n=x\), где n — степень корня, которая является натуральным числом; x — подкоренное выражение; y — результат вычисления. |

| Где в корнях спрятан куб? У некоторых корней есть особые названия в зависимости от их степени: Если \(n = 2\), такой корень называют квадратным корнем, часто его записывают без указания степени \(\sqrt{x}\). Если \(n = 3\), корень называется кубическим и записывается следующим образом \(\sqrt[3]{x}\). |

В некоторых источниках можно столкнуться с понятием «радикал». На самом деле, это тот же корень, просто названный по-другому.
Заметим, что любое число можно внести под знак корня, если проделать «обратную» операцию. Например, нам нужно представить число 7 в виде корня. Как это сделать?
Нам просто нужно возвести число в степень корня (и соответственно записать полученный результат под корнем):
- Если мы хотим представить число 7 в виде квадратного корня, то получим: \(\sqrt{7^2}=\sqrt{49}\)
- Если мы хотим представить число 7 в виде корня пятой степени, то получим: \(\sqrt[5]{7^5}=\sqrt[5]{16807}\)
Такие преобразования могут очень пригодиться при упрощении математических выражений.
Например, попробуем найти значение выражения \(2\sqrt[4]{5,0625}\). Извлечь корень тут будет проблематично, поскольку число “сложное”. А теперь попробуем внести 2 под знак корня, при этом в подкоренном выражении мы получим произведение чисел:
\(2\sqrt[4]{5,0625}=\sqrt[4]{2^4*5,0625}=\sqrt[4]{16*5,0625}=481\)
Теперь мы с легкостью можем найти ответ:
\(\sqrt[4]{81}=3\)
При решении этого примера мы применили одно из свойств корней, о котором обязательно поговорим дальше.
А пока давайте разберем работу с четными (кратными 2) и нечетными (не кратными 2, соответственно) степенями, и чем они отличаются.
Посмотрим на примеры:
- \(\sqrt[3]{125}=5\), потому что \(5^3=125\).
- \(\sqrt[3]{-125}=-5\), потому что \((-5)^3=-125\).
- \(\sqrt[2]{-9}=\)?
Допустим, ответ 3. Проверим: \(3*3=9\) — не подходит.
Пробуем -3. Проверяем: \((-3)*(-3)= 9\), так как минус на минус дает плюс.
Получается, что \(\sqrt[2]{-9}\) не имеет смысла, так как степень — четная, а подкоренное выражение — отрицательное.
Любое число в квадрате будет больше или равно нулю, а значит, и под знаком корня с четной степенью не может появиться отрицательного числа.
| Как не запутаться в корнях? При работе с четными и нечетными степенями корней важно помнить, что: — корень нечетной степени можно взять из любого числа; — корень четной степени из отрицательных чисел не существует, его можно брать только из положительного числа. |
Могут ли получиться разные результаты, если степень корня и подкоренное выражение одинаковые?
Да, такое возможно. Число, извлеченное из корня четной степени, может быть и положительным, и отрицательным, потому что любое число в четной степени будет больше или равно нулю. Такое число следует записывать в модульных скобках.
\(\sqrt[2]{9}=|3|\), потому что \(3^2=(-3)^2=9\)
Это одно из свойств корней, которые мы будем рассматривать дальше. А зачем нужны модульные скобки можно прочитать в статье «Модуль».
Корень можно представить в виде математической функции, которая будет соответственно называться коренной или радикальной. Подробнее про нее можно узнать в статье “Основные элементарные функции. Часть 2”.
Свойства корней
Мы уже узнали, что такое корень. Теперь самое время узнать, как совершать логичные и правильные преобразования с ними.
Основные свойства корней:
- Степень числа а под корнем выносится в числитель, а степень корня в знаменатель.
\(\sqrt[n]{a^k}= a^{\frac{k}{n}}\)
Таким образом, можно представить любой корень в виде степени, что очень удобно при решении некоторых примеров.
Например, найдем значение выражения \(2^{\frac{2}{3}}*\sqrt[3]{2}\).
Преобразуем корень по свойству. При этом заметим, что число 2 под корнем находится в первой степени. Получаем:
\(2^{\frac{2}{3}}*2^{\frac{1}{3}}\)
А дальше по свойству степеней, про которые можно узнать в статье «Действия с натуральными числами», находим ответ:
\(2^{\frac{2}{3}}*2^{\frac{1}{3}}=2^{\frac{2}{3}+\frac{1}{3}}=2\frac{3}{3}=2^1=2\)
- Если под корнем находится число а в степени корня, то от корня можно избавиться, используя первое свойство корней, так как ann=a1.
При этом нельзя забывать про четность степени.
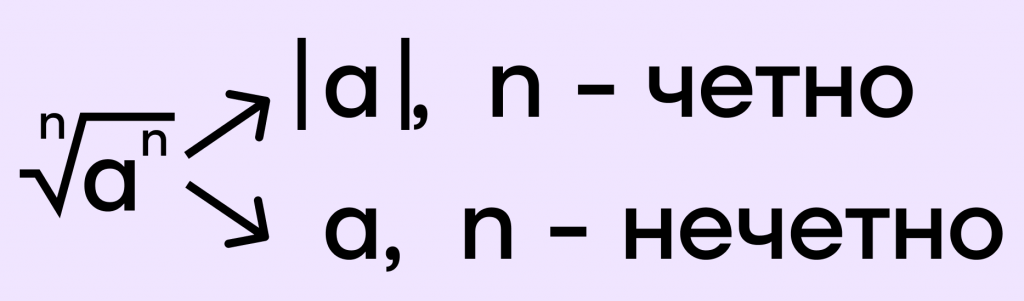
Например, \(\sqrt[3]{4^3}=4\), поскольку 3 — нечетно.
Но при этом \(\sqrt[4]{4^4}=|4|\), поскольку 4 — четно. Проверим, действительно ли нужно ставить модуль.
Если возвести 4 в четвертую степень, то мы получим 256. Следовательно:
\(\sqrt[4]{4^4}=\sqrt[4]{256}\).
Для последнего выражения будут справедливы два уравнения:
\(4^4=256\) и \((-4)^4=256\).
Следовательно, в данном случае обязательно нужно поставить модуль.
| Как найти значение выражения, если ответов получается два? В заданиях будут часто встречаться корни с четной степенью, у которых необходимо будет найти значение. Какой из двух ответов — положительный или отрицательный — записывать в этом случае? На самом деле, существуют алгебраический и арифметический корень. До этого мы рассматривали алгебраический корень числа. Обычно в заданиях просят найти арифметический корень числа. Что это за зверь такой? Арифметический корень n из числа a — это неотрицательный корень n из числа а. Так, если мы будем искать значение выражения \(\sqrt{81}\), то получим два корня: \(\pm9\). При этом арифметическим корнем из них будет только число 9. Заметим, что в экзаменационных заданиях с развернутым ответом необходимо записывать все полученные корни. |
- Если степень корня нечетная, а подкоренное выражение отрицательное, можно вынести минус перед корнем, тогда под корнем останется положительное число.
\(\sqrt[n]{-a}= -\sqrt[n]{a}\), где n — нечетно.
Например, \(\sqrt[7]{-20}=-\sqrt[7]{20}\).
Это свойство связано с тем, что при возведении отрицательного числа в нечетную степень мы всегда получим отрицательное число:
\((-2)*(-2)=4\), но \((-2)*(-2)*(-2)=-8\).
- Произведение чисел а и b в подкоренном выражении можно записать как произведение корней.
\(\sqrt[n]{a*b}=\sqrt[n]{a}*\sqrt[n]{b}\)
Например, \(\sqrt{144}=\sqrt{16*9}=\sqrt{16}*\sqrt{9}=|4*3|=|12|\).
- Частное чисел а и b в подкоренном выражении можно записать как частное корней.
\(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}, b\neq0\)
Например, \(\sqrt[4]{\frac{625}{16}}=\frac{\sqrt[4]{625}}{\sqrt[4]{16}}=|52|=|2,5|\).
Давайте немного попрактикуемся и решим пример, который может встретиться в номере 8 ОГЭ.
Найдите значение выражения \(\frac{\sqrt{15}*\sqrt{30}}{\sqrt{18}}\).
Решение.
Воспользуемся свойствами №4 и №5 и представим выражение под одним знаком корня:
\(\frac{\sqrt{15}*\sqrt{30}}{\sqrt{18}}=\frac{\sqrt{15*30}}{\sqrt{18}}=\sqrt{\frac{15*30}{18}}\)
Сократим дробь (то есть разделим ее числитель и знаменатель на их общий делитель) и найдем ее значение:
\(\sqrt{\frac{15*30}{18}}=\sqrt{\frac{15*30}{6}}=\sqrt{\frac{5*5}{1}}=\sqrt{25}=5\)
Ответ: 5
- Если в подкоренном выражении находится еще один корень, от такой вложенности можно избавиться путем перемножения степеней.
\(\sqrt[n]{\sqrt[m]{a}}=\sqrt[n*m]{a}\)
Вывести это свойство можно с помощью первого свойства корней, а также свойства степеней.
Представим выражение \(\sqrt[n]{\sqrt[m]{a}}\) в виде степени:
\(\sqrt[n]{\sqrt[m]{a}}=\sqrt[n]{a^{\frac{1}{m}}}={(a^{\frac{1}{m}})}^{\frac{1}{n}}\)
По свойству степеней \({(x^n)}^m=x^{nm}\) получаем:
\({(a^{\frac{1}{m}})}^{\frac{1}{n}}=a^{\frac{1}{m}*\frac{1}{n}}=a^{\frac{1}{mn}}\)
Теперь совершим обратное преобразование и представим степень в виде корня:
\(a^{\frac{1}{mn}}=\sqrt[mn]{a^1}=\sqrt[mn]{a}\)
Например, \(\sqrt[3]{\sqrt{729}}=\sqrt[6]{729}=|3|\).
- Степень подкоренного выражения можно выносить из-под корня, тогда корень будет возводиться в эту степень.
\(\sqrt[n]{a^m}={(\sqrt[n]{a})}^m\)
Рассмотрим это свойство чуть подробнее с помощью уже известных свойств корней и степеней:
\(\sqrt[n]{a^m}=a^{\frac{m}{n}}=a^{m*\frac{1}{n}}={(a^{\frac{1}{n}})^m} ={(\sqrt[n]{a^1})}^m={(\sqrt[n]{a})}^m\)
Например, \(\sqrt[3]{8^7}={(\sqrt[3]{8})}^7=2^7=128\).
- Если степень корня и степень подкоренного выражения имеют общий делитель k, тогда обе степени можно разделить на k, и значение выражения не изменится.
\(\sqrt[n*k]{a^{m*k}}=\sqrt[n]{a^m}\)
Рассмотрим выведение этого свойства:
\(\sqrt[n*k]{a^{m*k}}=a^{\frac{mk}{nk}}\)
Вспомним, что общие множители в числителе и знаменателе сокращаются, а значит, получаем:
\(a^{\frac{mk}{nk}}=a^{\frac{m}{n}}=\sqrt[n]{a^{m}}\)
Стоит отметить, что свойства работаю в обе стороны.
Например:
\(\sqrt[n]{a^k}= a^{\frac{k}{n}} \Leftrightarrow a^{\frac{k}{n}}= \sqrt[n]{a^k}\)
Для удобства мы собрали все свойства корней в одну таблицу. Можете распечатать ее себе или сохранить как изображение.

Возведение числа в дробную степень
Мы знаем про обычные степени, например \(5^2=25\) и \(3^3=27\). А что, если в степени дробное число?
В таком случае, число попадает под корень, причем по такому правилу:
\(a^{\frac{q}{p}}=\sqrt[p]{a^q}\)
На самом деле, это и есть одно из свойств корней, которые мы рассматривали выше. Просто сейчас стоит запомнить: любой корень можно представить в виде числа, возведенного в дробную степень.
Посмотрим, как это работает, на паре примеров:
\(25^{\frac{1}{2}}=\sqrt[2]{25^1}=5\)
\(27^{\frac{2}{3}}=\sqrt[3]{27^2}=\sqrt[3]{(3^3)^2}=3^2=9\)
Произведение квадратных корней
В основном произведение выполняется по этому правилу, которое мы уже рассмотрели выше:
\(\sqrt{a}*\sqrt{b}=\sqrt{ab}\)
Посмотрим, как это работает, на примерах:
\(\sqrt{5}*\sqrt{5}=\sqrt{5*5}=\sqrt{25}=5\)
\(\sqrt{18}*\sqrt{8}=\sqrt{18*8}=\sqrt{144}=12\)
Но бывают и случаи, когда корни имеют множители. Например:
\(9\sqrt{2}*2\sqrt{6}\)
В таком случае множители мы умножаем отдельно от корней:
\(9\sqrt{2}*2\sqrt{6}=9*2*\sqrt{2*6}=18\sqrt{12}\)
Аналогично работает и деление.
Деление квадратных корней
Деление происходит по свойству корней:
\(\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}\)
Разберем на примерах:
\(\frac{\sqrt{50}}{\sqrt{2}}=\sqrt{\frac{50}{2}}=\sqrt{25}=5\)
\(\frac{\sqrt{60}}{\sqrt{12}}=\sqrt{\frac{60}{12}}=\sqrt{5}\)
Ну и, конечно, могут быть множители. Как и в случае с умножением, множители делятся отдельно от корней.
\(\frac{21\sqrt{48}}{7\sqrt{3}}=\frac{21}{7}*\sqrt{\frac{48}{3}}=3*\sqrt{16}=3*4=12\)
Теперь попрактикуемся с преобразованиями.
Практика преобразований
Теперь давайте рассмотрим применение свойств корней на практике.
Пример 1: \(\sqrt[3]{-216}\)
1 способ:
\(\sqrt[3]{-216}=-\sqrt[3]{6^3}=-6\)
В этом выражении мы сначала выносим минус перед корнем (свойство под номером 3). Затем представляем число 216 в виде 6 в степени 3 и избавляемся от корня нечетной степени (свойство под номером 2).
Чтобы прийти к этому результату, можно было использовать и другие преобразования.
2 способ:
\(\sqrt[3]{-216}=(-216)^{\frac{1}{3}}=(-6)^{3*\frac{1}{3}}=-6\)
В этом варианте сначала воспользуемся свойством под номером 1, чтобы уйти от знака корня. Далее число -216 представим в виде числа в степени 3, после чего перемножаем степени по свойству степеней и получаем -6.

Давайте рассмотрим другой пример.
Пример 2: \(\sqrt{9+16}\)
\(\sqrt{9+16}=\sqrt{25}=5\)
В данном случае ни одно из свойств корней не подходит, поэтому складываем слагаемые подкоренного выражения и уже после находим результат.
| Важно: нельзя путать сумму в подкоренном выражении с произведением в подкоренном выражении, потому что свойство корней есть только для произведения. То есть \(\sqrt{a+b}\pm \sqrt{a}+\sqrt{b}\), аналогично и с разностью \(\sqrt{a-b} \pm \sqrt{a}-\sqrt{b}\). |
Можно ли как-то складывать или вычитать квадратные корни? Да, но есть одно условие: подкоренное выражение должно быть одинаковым для всех слагаемых.
Например, попробуем решить \(\sqrt{11}+\sqrt3\). Под знаком корня находятся разные числа, а значит, сложить мы их не можем. Более того, эти числа иррациональны, то есть извлечь корень будет проблематично. В таком случае запись лучше оставить как есть.
А вот пример \(2\sqrt{11}+3\sqrt{11}\) мы уже можем решить. Для этого нужно сложить коэффициенты перед знаком корня:
\(2\sqrt{11}+3\sqrt{11}=5\sqrt{11}\)
Аналогично и с вычитанием корней. Если подкоренные выражения одинаковые, то мы можем вычитать корни, при этом работаем только с коэффициентами:
\(11\sqrt{17}-7\sqrt{17}=4\sqrt{17}\)
Но что делать, если нам все-таки попались иррациональные числа и необходимо определить их значение? В этом случае нам на помощь придет сравнение чисел.
Допустим, нам нужно определить, чему примерно равен \(\sqrt{11}\). Проще всего это сделать, если найти целые числа, между которыми он “лежит”. Для этого записываем неравенство:
\(\sqrt*<\sqrt{11}<\sqrt{**}\)
Теперь вместо звездочек нужно подставить ближайшие значения, которые будут давать целое число при извлечении корня. В нашем случае это будут 9 и 16:
\(\sqrt9<\sqrt{11}<\sqrt{16}\)
Теперь просто извлекаем корни:
\(3<\sqrt{11}<4\)
Следовательно, \(\sqrt{11}\) лежит в промежутке между 3 и 4.
Выражения с корнями могут встретиться и в текстовых задачах. Например, в №8 ЕГЭ по профильной математике.
Мотоцикл разгоняется по прямолинейному участку гоночной трассы с постоянным ускорением а км/ч2. Скорость \(\theta\) (км/ч) в конце пути вычисляется по формуле \(\theta=\sqrt{2la}\), где l – расстояние, которое проехал мотоцикл (в км). Найдите расстояние l, если мотоцикл достиг скорости 90 км/ч при ускорении 810 км/ч2.
Решение.
Выразим из формулы расстояние. Для этого нам нужно будет избавиться от корня. Следовательно, нужно возвести все выражение в квадрат:
\(\theta=\sqrt{2la}|\uparrow^2\)
\(\theta^2=2la\)
Теперь выражаем расстояние l:
\(l=\frac{\theta^2}{2a}\)
Осталось подставить данные в условии значения:
\(l=\frac{\theta^2}{2a}=\frac{90^2}{2*810}=\frac{8100}{2*810}=\frac{10}{2}=5\)
Ответ: 5
Рассмотрим еще одну распространенную ситуацию, когда нужно вынести множитель из-под знака корня.
Пример 3: 480
\(\sqrt[4]{80}=\sqrt[4]{2*2*2*2*5}=\sqrt[4]{2^4}*\sqrt[4]{5}=2\sqrt[4]{5}\)
Сначала 80 нужно разложить на множители. Далее используем свойство под номером 4 и раскладываем произведение подкоренного выражения на произведение корней, а затем к первому множителю применяем свойство под номером 2 и избавляемся от корня.
Важно хорошо ориентироваться в свойствах корней, поскольку задания с ними могут встретиться как отдельным номером, так и в качестве части решения более сложного примера.
Рассмотрим задание №6 из ЕГЭ по профильной математике.
Найдите значение выражения: \(\frac{\sqrt[5]11*\sqrt[13]11}{\sqrt[65]{11^{18}}}\)
Решение.
Воспользуемся свойством №1 и преобразуем выражение:
\(\frac{\sqrt[5]11*\sqrt[13]11}{\sqrt[65]{11^{18}}}=\frac{11^{\frac{1}{5}}*11^{\frac{1}{13}}}{11^{\frac{18}{65}}}\)
Далее нам понадобится следующее свойство степеней: \(a^n*a^m=a^{n+m}\). Применим его для числителя:
\(\frac{11^{\frac{1}{5}}*11^{\frac{1}{13}}}{11^{\frac{18}{65}}}=\frac{11^{\frac{1}{5}+\frac{1}{13}}}{11^{\frac{18}{65}}}\)
Приведем выражение в числителе к общему знаменателю и обратно вернемся к записи с помощью корня:
\(\frac{11^{\frac{1}{5}+\frac{1}{13}}}{11^{\frac{18}{65}}}=\frac{11^{\frac{13+5}{65}}}{11^{\frac{18}{65}}}=\frac{11^{\frac{18}{65}}}{11^{\frac{18}{65}}}=\frac{\sqrt[65]{11^{18}}}{\sqrt[65]{11^{18}}}\)
Заметим, что в числителе и знаменателе одинаковые выражения, а значит, их можно сократить:
\(\frac{\sqrt[65]{11^{18}}}{\sqrt[65]{11^{18}}}=1\)
Ответ: 1
Мы рассмотрели корни и их свойства, таким образом, преодолели еще одну ступеньку в изучении математики. Корни будут нередко нам попадаться в решении уравнений, неравенств или задач, поэтому необходимо досконально разобраться в их свойствах. А если вам интересно начать изучать решение уравнений и неравенств, приглашаем вас в статью «Метод интервалов».
Термины
Знаменатель — нижнее число в дроби.
Иррациональные числа — это числа, которые не могут быть представлены в виде обыкновенной дроби. Иными словами, у них нет точного значения.
Натуральные числа — это числа, используемые при счете предметов (например: 1, 2, 3, 4, …).
Произведение чисел — это результат их умножения.
Частное чисел — это результат деления одного числа на другое.
Числитель — верхнее число в дроби.
Фактчек
- Взятие корня — это противоположное действие возведению в степень.
- Корень нечетной степени берется из любого числа, а корень четной степени только из положительных чисел.
- Извлеченное из корня четной степени число записывается в модульных скобках.
- Существую специальные правила работы с корнями, они называются свойствами корней.
- Преобразования корней на практике могут состоять из нескольких действий.
Проверь себя
Задание 1.
Чему равно выражение \(\sqrt[15]{3^{12}}\) ?
- \(\sqrt[3]{3^4}\)
- \(3^{\frac{4}{5}}\)
- \(3^{\frac{15}{12}}\)
- \(\sqrt[15]{1^4}\)
Задание 2.
Чему равно выражение \(\sqrt[4]{625}\)?
- 5
- \(\sqrt{15}\)
- \(\sqrt5\)
- \(|5|\)
Задание 3.
Чему равно выражение \(\sqrt[5]{\sqrt[2]{1}}\)?
- 1
- \(\sqrt[7]{1}\)
- 10
- 7
Задание 4.
Чему равно выражение \(\sqrt[5]{2^3*7^5}*\sqrt[5]{4}\)?
- 9
- 12
- 14
- 1
Задание 5.
Чему равно выражение \(\sqrt{13^2-5^2}\)?
- 144
- 4
- 12
- 8
Ответы: 1. — 2; 2. — 4; 3. — 1; 4. — 3; 5. — 3.


 к списку статей
к списку статей