Целые рациональные, дробно-рациональные и иррациональные уравнения

На этой странице вы узнаете

• Как не перепутать целое рациональное с дробно-рациональным уравнением?
• Чудо-метод: как легко решить любое иррациональное уравнение?
• Без каких трех букв не справиться с ЕГЭ?

Сравнить зарплату и расходы, рассчитать количество продуктов в блюде или решить, сколько плитки взять для ремонта в ванной — мы встречаем уравнения гораздо чаще, чем кажется. В этой статье мы продолжим наше знакомство с многообразием уравнений и научимся решать некоторые из видов. 

Виды уравнений

Вспомним, что такое уравнения? 

Уравнение — это равенство, содержащее неизвестное, обозначенное буквой. 

Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством. 

Уравнения можно представить в виде весов: на каждой чаше должно быть что-то одинаковое по значению. Если же весы не находятся в равновесии, то перед нами будет уже не уравнение. 

В статье «Линейные, квадратные и кубические уравнения» мы уже начали разбираться в них. Настало время немного усложнить задачу. 

Какие еще уравнения бывают? 

Уравнения могут быть рациональными и иррациональными. Вспомним, что рациональность и иррациональность мы встречали в числах. 

• Рациональные числа — это числа, которые можно представить в виде обыкновенной дроби. Например,  12.
• Иррациональные числа — это числа, которые не являются рациональными. Это бесконечные непериодические десятичные дроби. Например, 2,2360679775. Именно в иррациональных числах мы сталкиваемся с корнями или нецелыми степенями. 

Минутка русского языка! Как проще запомнить отличие рациональных и иррациональных чисел? Вспомним, что слово рациональный образовано от «рацио» — разумный. Иными словами, рациональные числа — это «логичные» и «правильные» числа, которые мы можем точно представить. Иррациональные числа же, в свою очередь, «нелогичные», представить их намного тяжелее (например, чему точно равен \(\sqrt3\)?). 

Рациональные уравнения делятся на:

• целые рациональные и
• дробно-рациональные.

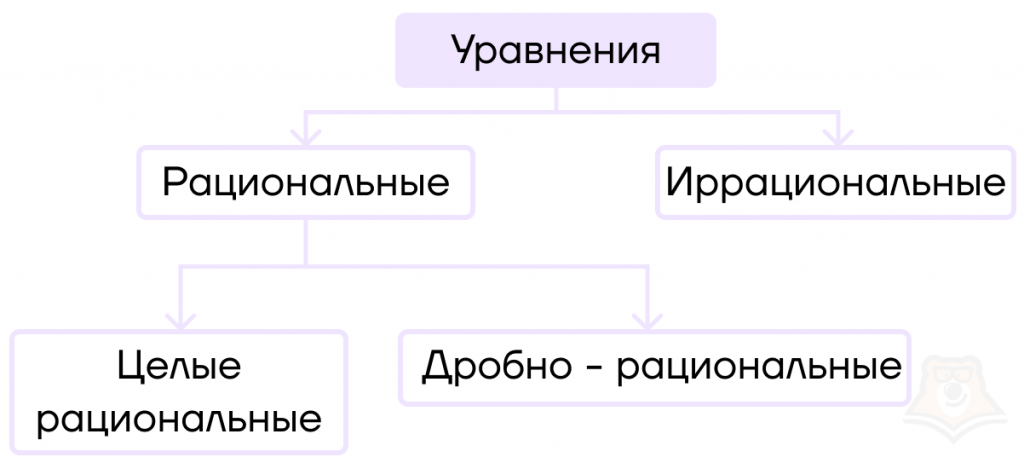
Итак, теперь, когда мы определились с видами уравнений, настало время рассмотреть каждый из них чуть подробнее. 

Целые рациональные уравнения

Целое рациональное уравнение — это уравнение, в котором есть только сложение, вычитание, умножение, деление и возведение в целую степень.

Такое уравнение может являться линейным, квадратным или другим алгебраическим уравнением. Для тех, кто еще не успел с ними разобраться, мы написали статью «Линейные, квадратные и кубические уравнения».

Вид рационального уравнения:

f(x) = 0, где f(x) — рациональное выражение.

Заметим, что вместо f(x) может стоять любое выражение с переменной. Например, целыми рациональными уравнениями являются:

\(32x-15=0\);
\(3x-2=2x+3\);
\(57x(x+8)(33x-11)=10x\).

Как мы будем решать такие уравнения?

Алгоритм решения рационального уравнения

1. Перенести все слагаемые из правой части в левую, чтобы справа был только ноль.
2. Совершить преобразования для приведения к обычному алгебраическому уравнению (линейное, квадратное, кубическое и т.д.).
3. Решить полученное уравнение и найти корни.

А теперь приступим к самому интересному: решению уравнений. Рассмотрим решение рационального уравнения на следующем примере:

\(\frac{x^2-1}{8}=10\)

1. Перенесем 10 в левую часть. Обязательно поменяем знак на противоположный: если мы отнимаем что-то от одной части уравнения, то обязаны отнять такое же число и от другой. 

\(\frac{x^2-1}{8}-10=0\)

2. Домножим обе части уравнения на 8, чтобы избавиться от дроби.

\(8*(\frac{x^2-1}{8}-10)=0*8\)

3. Раскроем скобки и приведем подобные слагаемые, то есть сложим слагаемые с одинаковой буквенной частью.

\(x^2-1-80=0\)

\(x^2-81=0\)

4. Решим неполное квадратное уравнение. 

\(x^2=81\)

Извлечем корень и получим x=±9. Мы получили два числа, поскольку при возведении в квадрат и положительные, и отрицательные числа становятся положительными: \(9^2=9*9=81\) и \((-9)^2=(-9)*(-9)=81\).

Как мы уже сказали, есть целые и дробно-рациональные уравнения. Так в чем особенность вторых? 

Дробно-рациональные уравнения

Дробно-рациональное уравнение — это уравнение, у которого хотя бы в одной дроби в знаменателе есть неизвестная.

Вид дробно-рационального уравнения:

\(\frac{f(x)}{g(x)}=0\), где \(f(x)\) и \(g(x)\) — выражения с неизвестной х.

Как понятно из определения, в дробно-рациональном уравнении мы должны не просто иметь дробь, в знаменателе обязательно должна быть переменная. Иными словами, это уравнения, в которых мы делим что-либо на буквенное выражение. 

Как не перепутать целое рациональное с дробно-рациональным уравнением? Если х находится только в числителе дроби, то такое уравнение — целое рациональное. Если х есть в знаменателе дроби, то такое уравнение — дробно-рациональное. В этом их основное отличие.   Например: \(\frac{12}{7-x}=x\) — дробно-рациональное уравнение, а вот \(\frac{12-x}{7}=x\) — целое рациональное. Аналогично \(\frac{x}{2}=\frac{1+x}{5}\) — целое рациональное уравнение, а \(\frac{x^{-1}}{2}=\frac{1+x}{5}\) — дробно-рациональное уравнение. Заметим, что второе уравнение мы можем переписать в виде \(\frac{1}{2x}=\frac{1+x}{5}\). Может возникнуть вопрос: а как мы перевернули дробь? В случае если данное преобразование непонятно для вас, стоит ознакомиться со статьей «Действия с натуральными числами».

Составим алгоритм решения. В этот раз нам потребуется чуть больше шагов, чем в предыдущем случае. 

Алгоритм решения дробно-рационального уравнения

1. Перенести все слагаемые из правой части в левую, если они есть, чтобы справа был только ноль.
2. Слева сделать преобразования, если нужно.
3. Привести все слагаемые слева к общему знаменателю и записать в виде дроби.
4. Записать систему, где числитель этой дроби равен нулю, а знаменатель не равен нулю.
5. Решить систему.

Давайте рассмотрим решение дробно-рационального уравнения на данном примере:

\(\frac{x^2+2x-9}{x-2}-1=\frac{x+4}{2}\).

1. Перенесем все слагаемые в левую часть. Не забываем менять знаки при переносе слагаемых через знак равно. 

\(\frac{x^2+2x-9}{x-2}-1-\frac{x+4}{2}=0\)

2. Приведем к общему знаменателю. Для этого каждую дробь домножим на то выражение, которого ей «не хватает» в знаменателе.

В нашем случае общий знаменатель будет \(2(x-2)\):

\(\frac{x^2+2x-9}{x-2}*2-1*2(x-2)-\frac{x+4}{2}*(x-2)=0\)

\(\frac{2(x^2+2x-9)-2(x-2)-(x+4)(x-2)}{2(x-2)}=0\)

3. Раскроем скобки в числителе:

\(\frac{2x^2+4x-18-2x+4-x^2+2x-4x+8}{2(x-2)}=0\).

4. Сложим подобные слагаемые:

\(\frac{(2x^2-x^2)+(4x-2x+2x-4x)+(-18+4+8)}{2(x-2)}=0\)

\(\frac{x^2-6}{2(x-2)}=0\)

5. Вспомним, что числитель должен быть равен 0, а знаменатель не равен. Знаменатель никогда не будет равен 0, поскольку на 0 делить нельзя. Запишем систему уравнений:

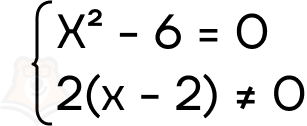
Решим каждое уравнение. 

\(x^2-6=0 => x^2=6 => x=\pm\sqrt6\)

\(2(x-2)\neq0\), следовательно, каждый множитель не равен 0. Тогда получаем, что \(x-2\neq0 => x\neq2\). 

Решением системе будет \(x=\pm\sqrt6\), это и есть решение уравнения.

Иррациональные уравнения

Мы уже рассмотрели два вида рациональных уравнений, перейдем к иррациональным.

Иррациональное уравнение — это уравнение, которое содержит неизвестную под корнем или она возведена в дробную степень.

Именно наличием корня или дробной степени иррациональные уравнения похожи на иррациональные числа. 

Например: \(\sqrt{10 -x}=x-4; x^{\frac{2}{3}}=4\) — это иррациональные уравнения.

Иррациональные уравнения могут быть нескольких видов:

1) \(\sqrt{f(x)}=g(x)\) 2) \(\sqrt{f(x)}=\sqrt{g(x)}\) Разные комбинации корней.

Не стоит пугаться, что виды иррациональных уравнений записаны через функции. Вместо \(f(x)\) и \(g(x)\) может стоять любое выражение! 

Чудо-метод: как легко решить любое иррациональное уравнение? Такие уравнения решаются методом возведения в квадрат. Он заключается в трех простых действиях: Шаг 1. Изолируем корень с одной стороны от знака равенства, то есть слева мы оставляем только корень. Шаг 2. Переносим остальные слагаемые в другую сторону.  Шаг 3. Далее нужно возвести обе части уравнения (и правую, и левую) в квадрат, чтобы избавиться от знака корня.  Такой метод можно использовать столько раз, сколько потребуется, чтобы избавиться от всех корней в уравнении.

Что нужно учитывать при решении иррационального уравнения методом возведения в квадрат? Корень не может быть отрицательным, поэтому обязательно нужно добавлять условие на выражение, к которому приравнивается корень. Такое выражение всегда больше или равно нулю.

Алгоритм решения иррационального уравнения

1. Поместить выражение с корнем в одну часть уравнения, а все остальное в другую.
2. Возвести в нужную степень обе части уравнения.
3. Первые два пункта можно повторять, пока не избавитесь от всех корней.
4. Решить полученное рациональное уравнение.

А теперь практика.

1. Решение уравнения вида \(\sqrt{f(x)}=g(x)\):

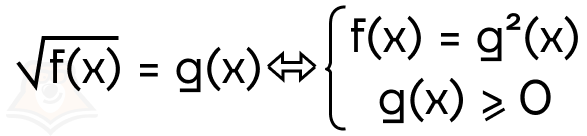
Пример:  

\(\sqrt{x^2-5}=x+1\)

1. Перейдем к системе. В нашем случае \(f(x)=x^2-5, g(x)=x+1\). 

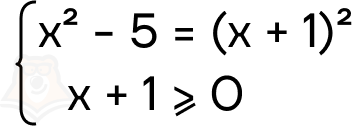
2. Решим первое уравнение \(x^2-5=(x+1)^2\).

Раскроем скобки. Для этого воспользуемся формулой сокращенного умножения для квадрата суммы \((a+b)^2=a^2+2ab+b^2\):

\(x^2-5=x^2+2x+1\).

Перенесем все слагаемые влево:

\(x^2-5-x^2-2x-1=0\)
\(-2x-6=0\)
\(2x=-6\)

Получим \(x=-3\), но данный корень не подходит под второе условие, поэтому уравнение не имеет корней.

2. Решение уравнения вида \(\sqrt{f(x)}=\sqrt{g(x)}\):

Пример: 

\(\sqrt{x^2+2}={2x+2}\)

В этом случае \(f(x)=x^2+2, g(x)=2x+2\).

1. Перейдем к системе: 

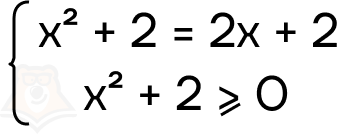
2. Заметим, что второе условие выполняется при любом х:

\(x^2\geq-2\).

Поскольку квадрат числа — это всегда неотрицательное число, тогда квадрат числа всегда будет больше отрицательного числа. Значит, все корни первого уравнения будут являться решениями. 

3. Решим неполное квадратное уравнение:

\(x^2+2-2x-2=0\)
\(x^2-2x=0\)
\(x(x-2)=0\)
\(x=0\) и \(x-2=0\). 

Получим корни 0 и 2.

3. Решение уравнения с тремя корнями:

Пример: 

\(\sqrt{1+x}-\sqrt{1-x}=\sqrt{x}\)

1. Найдем область допустимых значений (ОДЗ), то есть все значения, которые x может принимать в уравнении или неравенстве.

Для этого составим систему условий на подкоренные выражения, а после найдем решения этой системы:

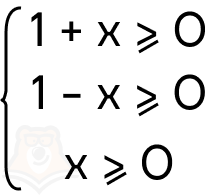
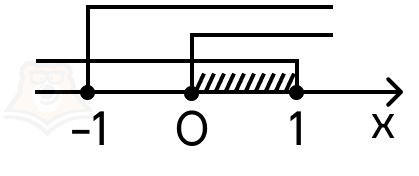
\(0≤x≤1\)

Без каких трех букв не справиться с ЕГЭ? Таким тремя буквами является аббревиатура ОДЗ. В базовом ЕГЭ и первой части профильной математики можно обойтись и без ОДЗ. Но решить некоторые задания второй части профиля без ОДЗ не получится. Чтобы получить верный ответ, последним действием нужно пересечь ОДЗ уравнения с его решениями. Промежутки, которые будут принадлежать и ОДЗ, и решению, пойдут в ответ.

2. Перенесем одно слагаемое в правую часть:

\(\sqrt{1+x}=\sqrt{x}+\sqrt{1-x}\).

3. Возведем обе части уравнения в квадрат:

\((\sqrt{1+x})^2=(\sqrt{x}+\sqrt{1-x})^2\)

Справа от знака равно воспользуемся формулой сокращенного умножения \((a+b)^2=a^2+2ab+b^2\): 

\(1+x=x+2*\sqrt{x-1}*\sqrt{x}+1-x\).

4. Перенесем все слагаемые в одну сторону и сложим подобные:

\(1+x-x-2\sqrt{x-1}*\sqrt{x}-1+x=0\)
\(x-\sqrt{x-1}*\sqrt{x}=0\)

Перенесем второе слагаемое вправо и получим систему вида \(2\sqrt{f(x)}=g(x)\)

\(x=2\sqrt{1-x}*\sqrt{x}\).

5. Снова перейдем к системе уравнений:

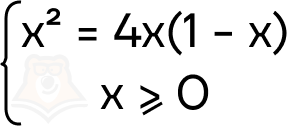
6. Решим первое уравнение. Для этого необходимо раскрыть скобки, перенести все слагаемые в одну сторону, сложить подобные и найти значения х: 

\(x^2=4x(1-x)\)
\(x^2=4x-4x^2\)
\(x^2-4x+4x^2=0\)
\(5x^2-4x=0\)
\(x(5x-4)=0\)

Если произведение множителей равно 0, то каждый множитель равен 0. Следовательно, получаем:

\(x=0\)
\(5x-4=0 => x=\frac{4}{5}\). 

Оба корня подходят и под условие \(x ≥ 0\), и под найденное ранее ОДЗ, значит, корни данного уравнения 0 и \(\frac{4}{5}\).

Уравнения встречаются почти во всех заданиях экзамена, поскольку с их помощью составляются математические модели, решаются геометрические и стереометрические задачи, находятся нули неравенств и многое-многое другое. Поэтому для успешной сдачи экзамена необходимо уметь решать любой вид уравнений.

Кроме того, существуют отдельные задания, в которых необходимо только правильно решить уравнение. Например, в профильной математике это номера 5 и 12, в базовой математике — №17, а в ОГЭ — №9 и №20. 

Для примера разберем №12 из ЕГЭ по профильной математике. 

Задание. 

а) Решите уравнение: \(y-\sqrt{78-2y}+1=0\).

б) Найдите корни этого уравнения, принадлежащие отрезку \((\sqrt{37};\sqrt{53})\).

Решение. 

а) Оставим корень слева, а остальные слагаемые перенесем вправо:

\(\sqrt{78-2y}=y+1\)

Теперь мы можем воспользоваться системой:

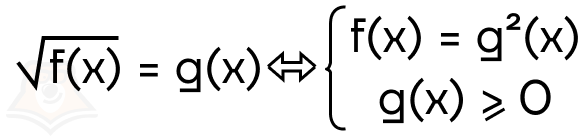
, где \(f(x)=\sqrt{78-2y}, g(x)=y+1\)

Решим второе неравенство из системы:
\(y+1\geq 0\)
\(y\geq -1\) — это ограничение на полученные корни, которое обязательно нужно будет учесть в конце. 

А теперь решим само уравнение:

\(78-2y=(y+1)^2\)

Раскроем скобки, для этого воспользуемся формулой сокращенного умножения \((a+b)^2=a^2+2ab+b^2\). Получаем:

\(78-2y=y^2+2y+1\)

Перенесем все слагаемые в одну сторону и приведем подобные:

\(y^2+2y+1-78+2y=0\)
\(y^2+4y-77=0\)

Решим квадратное уравнение с помощью дискриминанта, который мы подробно разобрали в статье «Линейные, квадратные и кубические уравнения»:

\(D=b^2-4ac=4^2-4*(-77)=16+308=324\)
\(y_1=\frac{-b+\sqrt{D}}{2a}=\frac{-4+18}{2}=7\)
\(y_2=\frac{-b-\sqrt{D}}{2a}=\frac{-4-18}{2}=-11\)

Вспомним, что у нас есть ограничение \(y\geq -1\). Следовательно, нам подходит только корень \(y=7\). 

б) Представим \(7\) в виде корня, получаем \(\sqrt{49}\). 

Заметим, что \(\sqrt{37}<\sqrt{49}<\sqrt{53}\), следовательно, \(y=7\) принадлежит отрезку \((\sqrt{37};\sqrt{53})\). 

Ответ: а) 7; б) 7.  

В этой статье мы изучили целых три вида уравнений. Но на самом деле их значительно больше! И следующий этап — показательные уравнения. 

Термины

Подобные слагаемые — это слагаемые, которые имеют одинаковую буквенную часть, а также слагаемые, которые не имеют буквенной части.

Система уравнений — это два и более равенства, объединенных фигурной скобкой, имеющих несколько решений, которые одновременно являются решениями для всей системы.

Фактчек

• Рациональное уравнение — это уравнение, в котором есть только сложение, вычитание, умножение, деление и возведение в целую степень. Решается такое уравнения путем сведения к алгебраическому уравнению, то есть уравнению, в котором есть только сложение, вычитание, умножение, деление или возведение в целую степень.
• Дробно-рациональное уравнение — это уравнение, у которого хотя бы в одной дроби в знаменателе есть неизвестная. Для решения нужно привести уравнение к виду, когда дробь равна нулю, и перейти к системе уравнений, где числитель равен нулю, а знаменатель — нет.
• В иррациональном уравнении неизвестная содержится под корнем или возведена в дробную степень. Для решения используются следующие равносильные переходы:

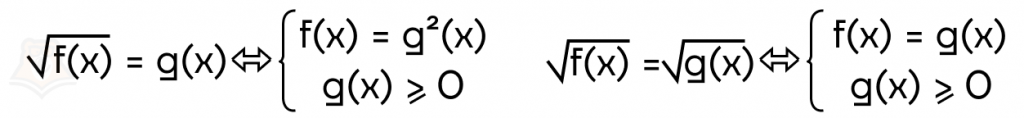
•  Если уравнение состоит из комбинации корней, то можно каждый раз возводить обе части в степень, пока не избавитесь от корней. Также не стоит забывать про ОДЗ.

Проверь себя

Задание 1.
Выберите дробно-рациональное уравнение:

1. \(\frac{x^2+2x+3}{3}=2x+1\)
2. \(x^3+2x=0\)
3. \(\frac{x^2+1}{x-3}=0\)
4. \(\sqrt{x-2}=\sqrt{x^3-8}\)

Задание 2.
Выберите иррациональное уравнение:

1. \((x-2)(3x+1)=0\)
2. \(\sqrt{x}-2=-x\)
3. \(5x^2+8x-1=3^2\)
4. \(\frac{x+7}{2x}=5\)

Задание 3.
Решите уравнение \(\frac{5x+2}{3}=x\).

1. -1
2. 2
3. -2
4. 3

Задание 4.
Решите уравнение \(\frac{9x-15}{x-5}=\frac{1}{x-3}\).

1. \(2\) и \(\frac{25}{9}\)
2. \(-2\) и \(\frac{9}{25}\)
3. \(9\) и \(25\)
4. \(\frac{25}{9}\) и \(-2\)

Задание 5.
Решите уравнение \(\sqrt{x^2+3x}=\sqrt{5x-1}\).

1. 1 и 2
2. 1
3. 0 и 2
4. 2

Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 1; 5. — 2.