Тригонометрическая окружность. Часть 1

На этой странице вы узнаете

• Почему радиус тригонометрической окружности обязательно должен быть равен 1?
• Как посчитать радианы?
• Как не запутаться, в какую сторону «крутить» окружность?

Слово «тригонометрия» звучит пугающе, не так ли? На самом деле, она встречается почти везде. Вы используете ее в повседневной жизни, даже не задумываясь. Так ли страшна «Та-Кого-Нельзя-Называть»? 

Допустим, вы захотели сфотографировать красивый пейзаж. Достали телефон, навели камеру, но решили чуть-чуть отмасштабировать картинку. А приближая или удаляя объекты на камере телефона, мы тем самым меняем угол обзора камеры! И вот она тригонометрия во всей красе.

Сегодня мы познакомимся с этим разделом математики поближе. И начнем наш разбор с тригонометрической окружности.

Немного про тригонометрические функции

В тригонометрии мы в первую очередь будем сталкиваться с углами. Но как их выразить? Как посчитать их значение? Использовать в расчетах градусы у нас не получится, поскольку это не та характеристика угла, которая поможет в вычислениях. 

Чтобы выразить величину угла в численном значении, используют тригонометрические функции: синусы, косинусы, тангенсы, котангенсы. А для их подсчета можно пользоваться обычным прямоугольным треугольником. 

Вспомним, что в прямоугольном треугольнике стороны называются по-особенному. Так, стороны, которые примыкают к прямому углу, называются катетами, а вот третья сторона — гипотенузой. 

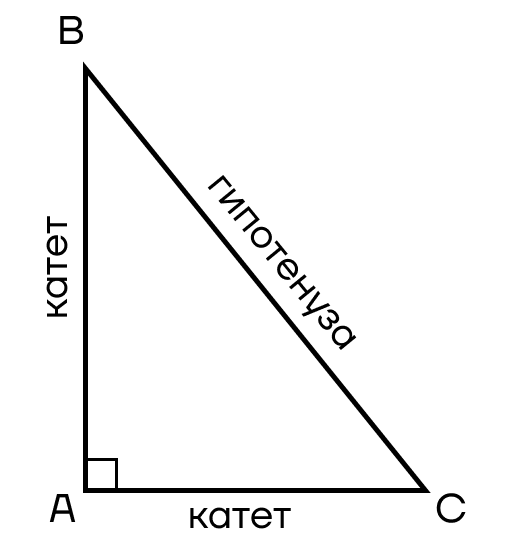
Но как связаны тригонометрические функции и треугольники, и как использовать треугольник для расчетов? Все просто: синус, косинус, тангенс и котангенс выражаются с помощью отношения сторон прямоугольного треугольника. Рассмотрим на примере угла С. 

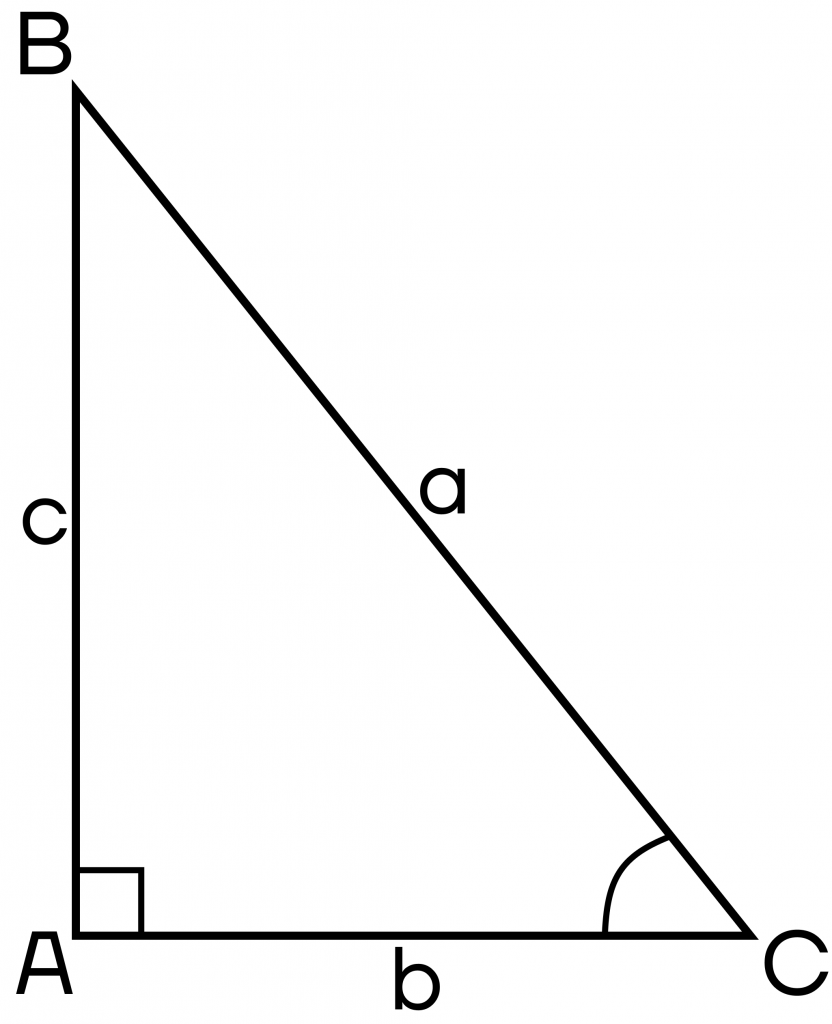
Синус — это отношение противолежащего катета к гипотенузе.

\(sinC=\frac{c}{a}\)

Косинус — это отношение прилежащего катета к гипотенузе. 

\(cosC=\frac{b}{a}\)

Тангенс — это отношение противолежащего катета к прилежащему катету.

\(tgC=\frac{c}{b}\)

Котангенс — это отношение прилежащего катета к противолежащему катету. 

\(ctgC=\frac{b}{c}\)

Например, пусть у нас будет треугольник со сторонами a=41, b=19, c=40. Тогда мы можем рассчитать значения тригонометрических функций, например:

\(sinC=\frac{c}{a}=\frac{40}{41} \approx 0,976\)

\(ctgC=\frac{b}{c}=\frac{19}{40}=0,475\)

При этом, если мы пропорционально поменяем длины сторон (то есть увеличим или уменьшим треугольник в несколько раз, не меняя его формы), то значение тригонометрических функций не изменится, поскольку сам угол не меняется. 

Разумеется, считать углы с помощью прямоугольного треугольника не всегда возможно. Например, когда нам дан не прямоугольный треугольник или когда мы знаем только размер угла в градусах. Для этого существуют специальные таблицы, в которых можно быстро узнать значение угла. Называются они таблицами Брадиса. Вы можете ознакомиться с ними по ссылкам ниже: 

• Таблица Брадиса для синуса и косинуса
• Таблица Брадиса для тангенса и котангенса

Итак, угол можно изобразить с помощью треугольника. Но есть еще один способ графически изобразить и посчитать угол. Для этого нам нужно познакомиться с понятием единичной окружности. 

Как построить единичную тригонометрическую окружность

К этому моменту изучения математики, многие уже, скорее всего, привыкли, что любую функцию можно изобразить с помощью графика. Одним из способов исследовать тригонометрические функции является единичная тригонометрическая окружность. 

Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1.

Почему радиус тригонометрической окружности обязательно должен быть равен 1? Это связано с ограничениями, которые есть для синуса и косинуса. Как мы уже знаем, синус и косинус — это отношение катета к гипотенузе. По одному из свойств треугольника — о них вы можете подробнее узнать в статье «Треугольник» — напротив большей стороны лежит больший угол. В прямоугольном треугольнике наибольшим углом будет прямой угол: поскольку сумма углов треугольника 180°, а один из них равен 90°, то на два других остается еще 90° градусов. При этом угол не может быть равен 0, иначе треугольник «схлопнется» и превратится в линию. Следовательно, наибольшей стороной будет гипотенуза. А отношение меньшего числа (длина катета) к большему (длина гипотенузы) не может быть больше 1. Например, пусть длина гипотенузы равна у, а длина катета равна х. Тогда их отношение можно записать в виде дроби: \(\frac{x}{y}\) У нас получается следующая закономерность: числитель всегда меньше знаменателя, а значит, число меньше 1. Таким образом, синус и косинус имеют ограничение в значениях: они не могут быть меньше -1 и больше 1. Отметив эти точки на осях, мы получаем окружность с радиусом 1.

А как же начертить единичную окружность? 

1. Для начала мы чертим обычные оси, перпендикулярные друг другу, а также рисуем окружность с единичным радиусом.

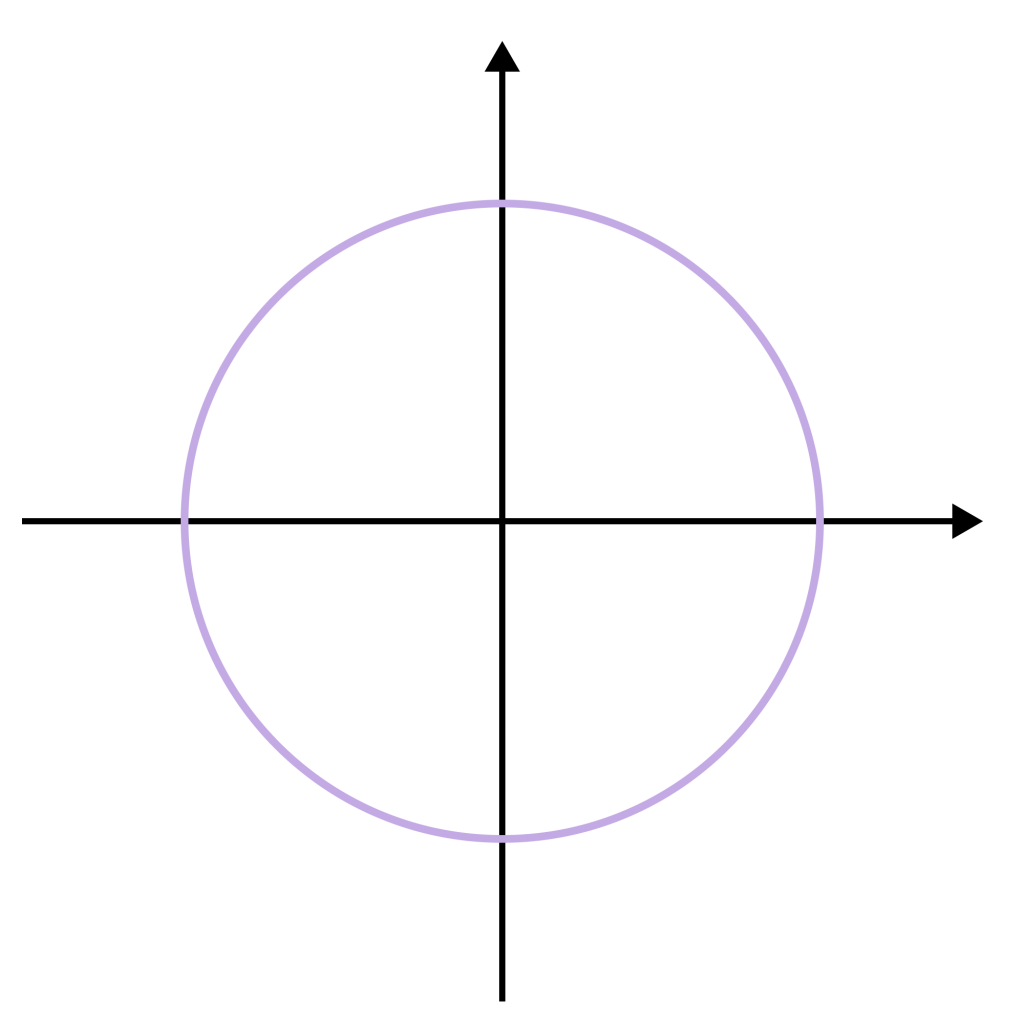
2. После этого оси нужно назвать. Если вы уже сталкивались с графиками, то первым порывом будет назвать их х и у. Однако здесь не все так просто! Горизонтальная ось — это ось косинуса, а вертикальная — ось синуса. Называются они соответственно.

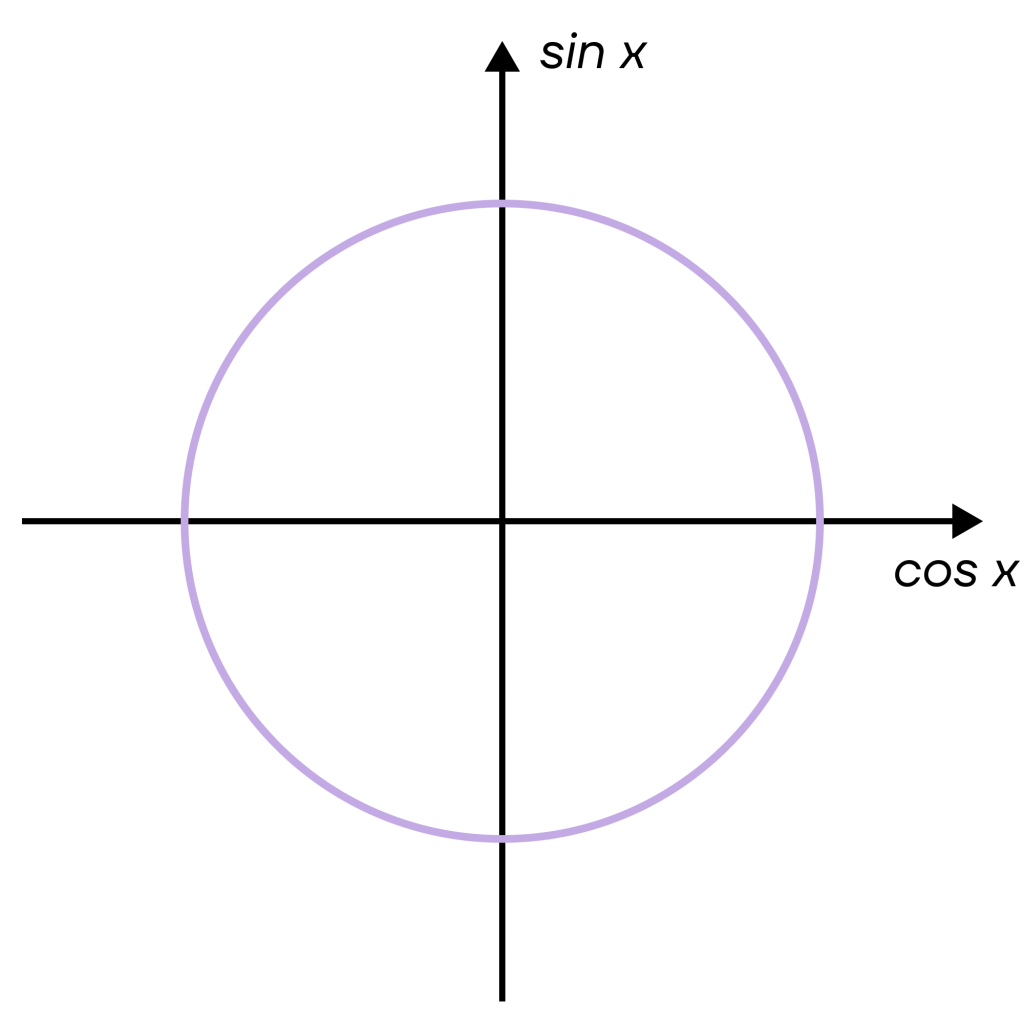
3. Теперь мы можем отметить начало отсчета. Оно будет лежать на оси косинуса справа. При этом движение в «положительную» сторону по окружности будет совершаться против часовой стрелки.

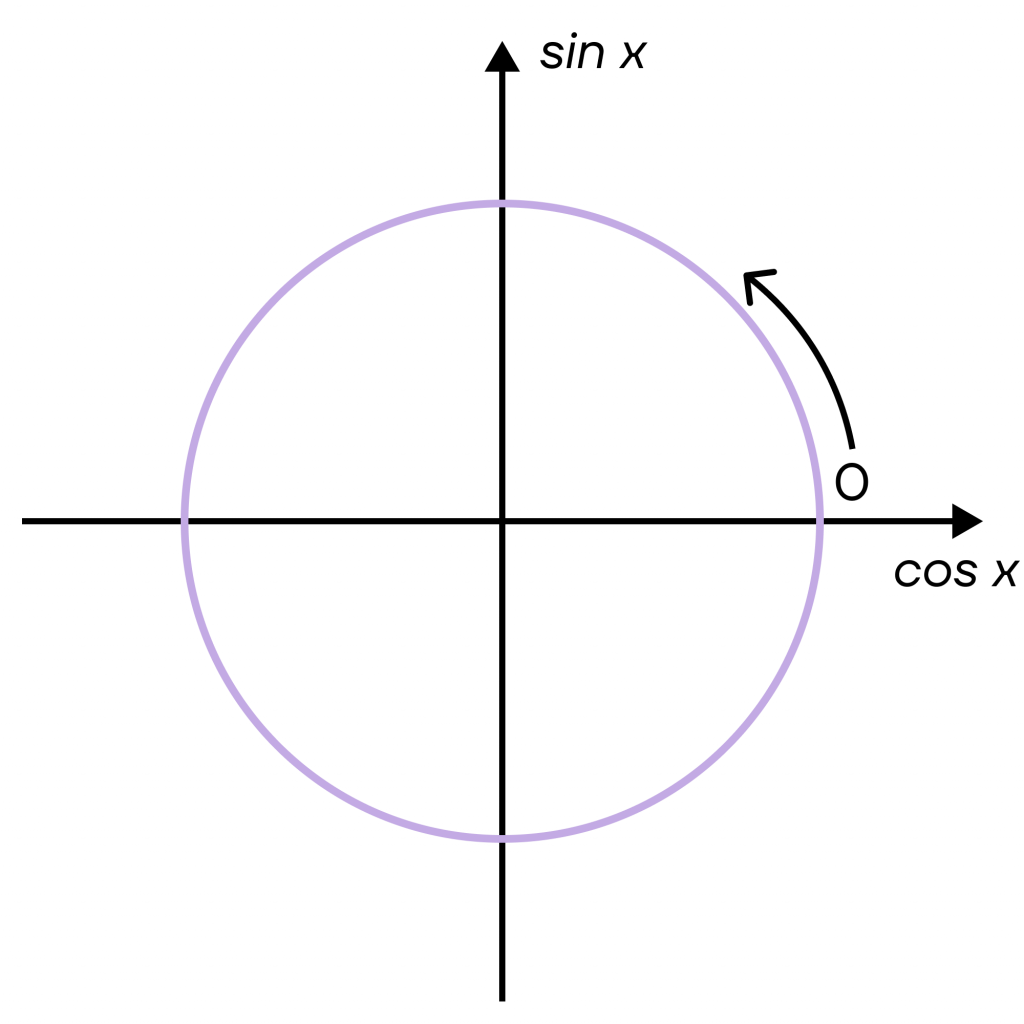
Итак, осталось подписать «знаковые» точки, то есть наиболее характерные точки для отсчета. Они будут лежать на пересечении осей и окружности, и всего их 4: 90°, 180°, 270° и 360° с начала отсчета. 

Но тригонометрия не была бы тригонометрией, если бы все было так просто. Мы знаем, что угол можно выразить с помощью градусов, знаем, что его даже можно посчитать. Но оказывается, есть еще один способ указать на величину угла — это радианы. 

Как посчитать радианы? Радианы измеряются с помощью числа пи. Оно записывается как \(\pi\) и примерно равно 3,14.  Чтобы считать углы в радианах, нужно запомнить, что \(\pi=180°\). Отсюда просто посчитать, что \(90°=\frac{\pi}{2}\), \(270°=\frac{3\pi}{2}\), \(360°=2\pi\).  Аналогично можно посчитать любой угол, например, \(30°=\frac{180°}{6}=\frac{\pi}{6}\).

Теперь мы можем подписать на нашей окружности углы. 

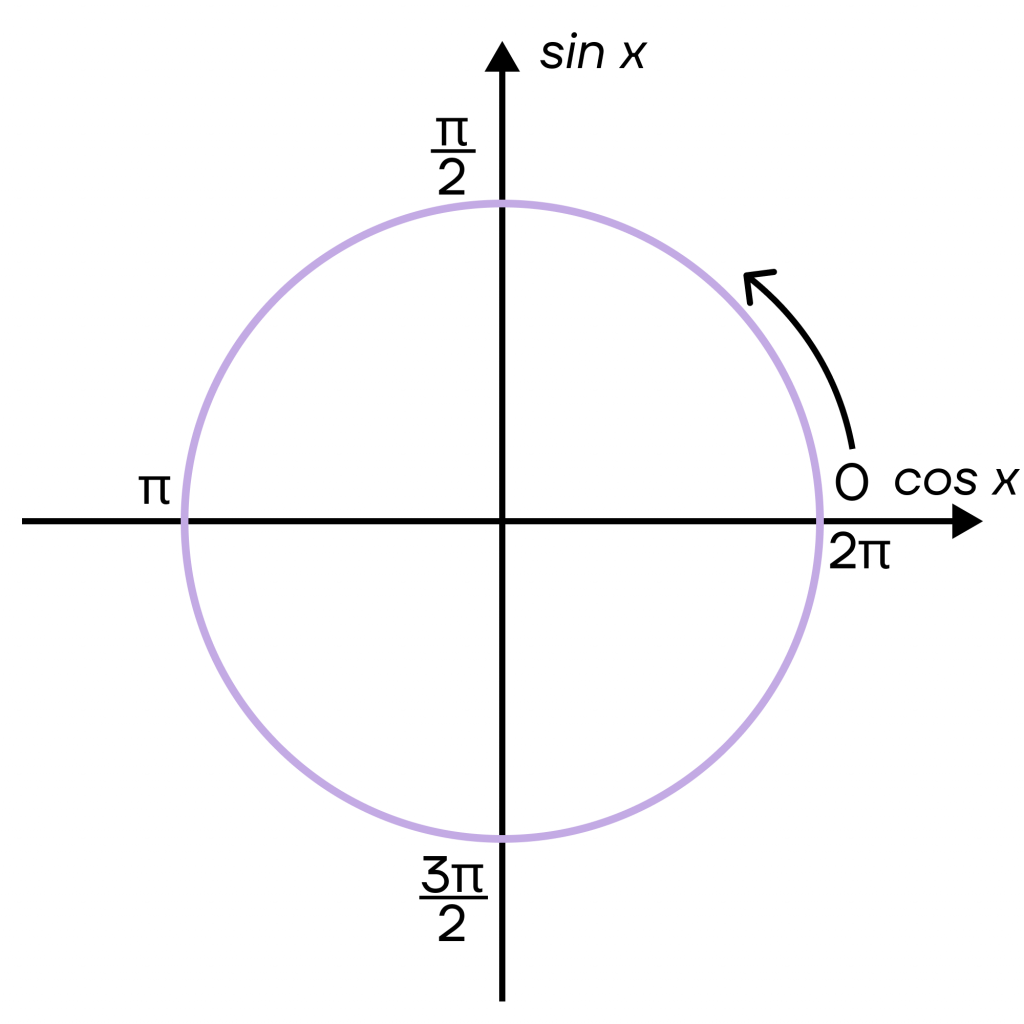
Заметим, что длина всей окружности равна 2π. То есть от точки 0 мы сделали ровно один круг. При этом 0 и 2π лежат в одной точке. Если мы сделаем еще один круг, то окажемся в точке 2π+2π=4π, и снова окажемся в той же точке. Так можно двигаться по окружности бесконечно долго, причем в обе стороны.

Условно, окружность можно представить в виде детской игрушки — спирали. Если посмотреть на нее сверху, то это будет обычная окружность. А вот если растянуть, то можно заметить, как одна окружность перетекает в другую. Когда мы «идем» по окружности, мы двигаемся по такой спирали. 

В какую сторону «крутить» окружность? В задачах нередко будут встречаться промежутки на окружности, которые необходимо правильно определить. Неправильное определение промежутка влечет за собой и неправильный ответ. Чтобы точно не ошибиться, нужно запомнить, в какую сторону идет положительное направление, а в какую отрицательную. Для этого представим, что наша окружность — это гоночная трасса. При этом машина будет ехать против часовой стрелки. Если машина едет «передом», то она движется в «положительном» направлении. Сделав один круг, она проедет расстояние 2π, два круга — 4π, а через пять кругов она окажется в точке 10π.  А вот если машина будет ехать «задом», то отсчет будет идти в отрицательную сторону. Так, через круг она окажется в точке -2π, через два круга — в точке -4π и так далее. То есть она будет проезжать то же самое расстояние, но со знаком минус.

Как откладывать углы на тригонометрической окружности

Итак, мы узнали четыре важные точки. А как отметить на окружности другие углы? Например, 30 или 150 градусов? 

Стоит упомянуть, что на окружности можно отметить угол с любым градусом. Но самыми важными будут углы 30°, 45°, 60°, 120°, 135°, 150°, 210°, 225°, 240°, 300°, 315°, 330°. 

Все эти точки можно условно разделить на две части. Первая будет лежать «наверху» окружности — это точки от 0 до 180 градусов. Вторая часть будет лежать «внизу» окружности — это точки от 180 до 360 градусов. 

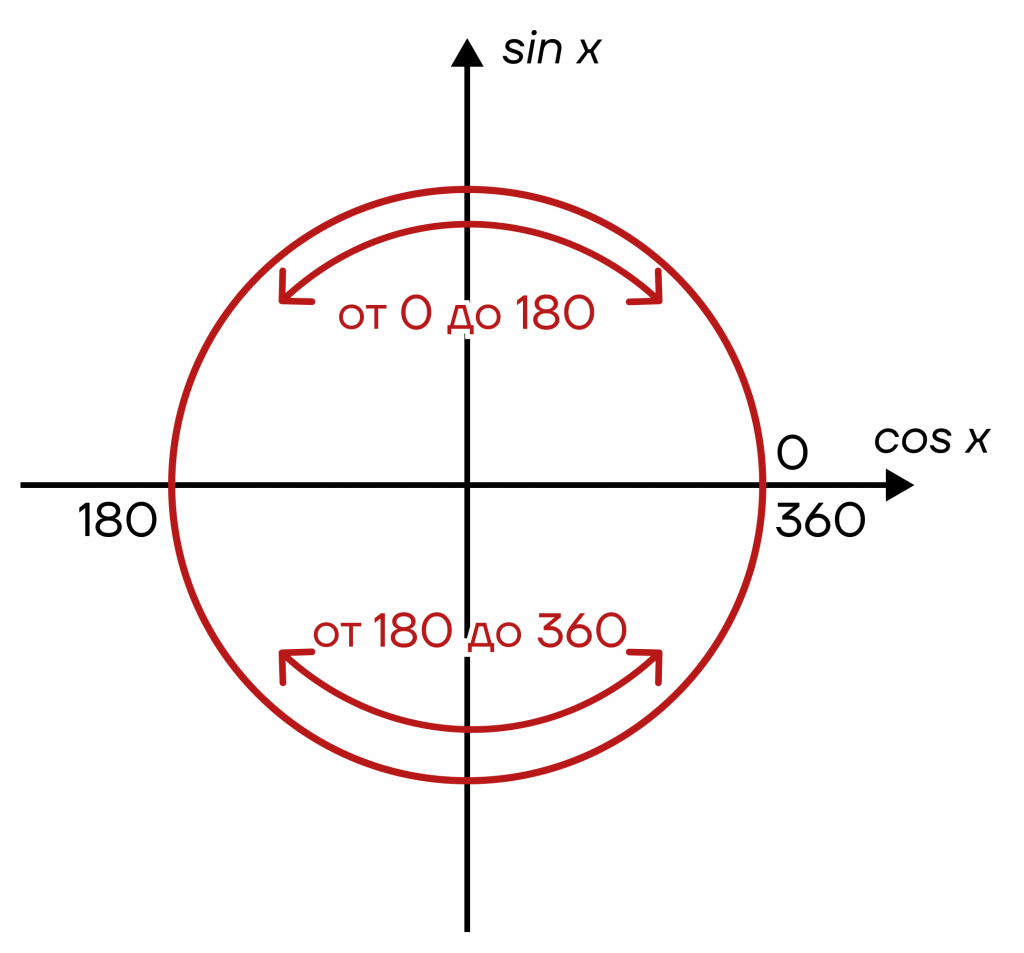
Далее заметим, что каждую половину можно разделить еще на две части — у нас получатся четвертинки окружности.

• В первой четверти будут лежать углы со значением от 0° до 90°, 
• во второй — от 90° до 180°,
• в третьей — от 180° до 270°, 
• в четвертой — от 270° до 360°. 

Точки 0°, 90°, 180° и 270° — точки, от которых мы будем вести отсчет остальных углов. Такие точки называются опорными.

Также обозначим, что четверти в окружности имеют свой номер, который необходимо запомнить. 

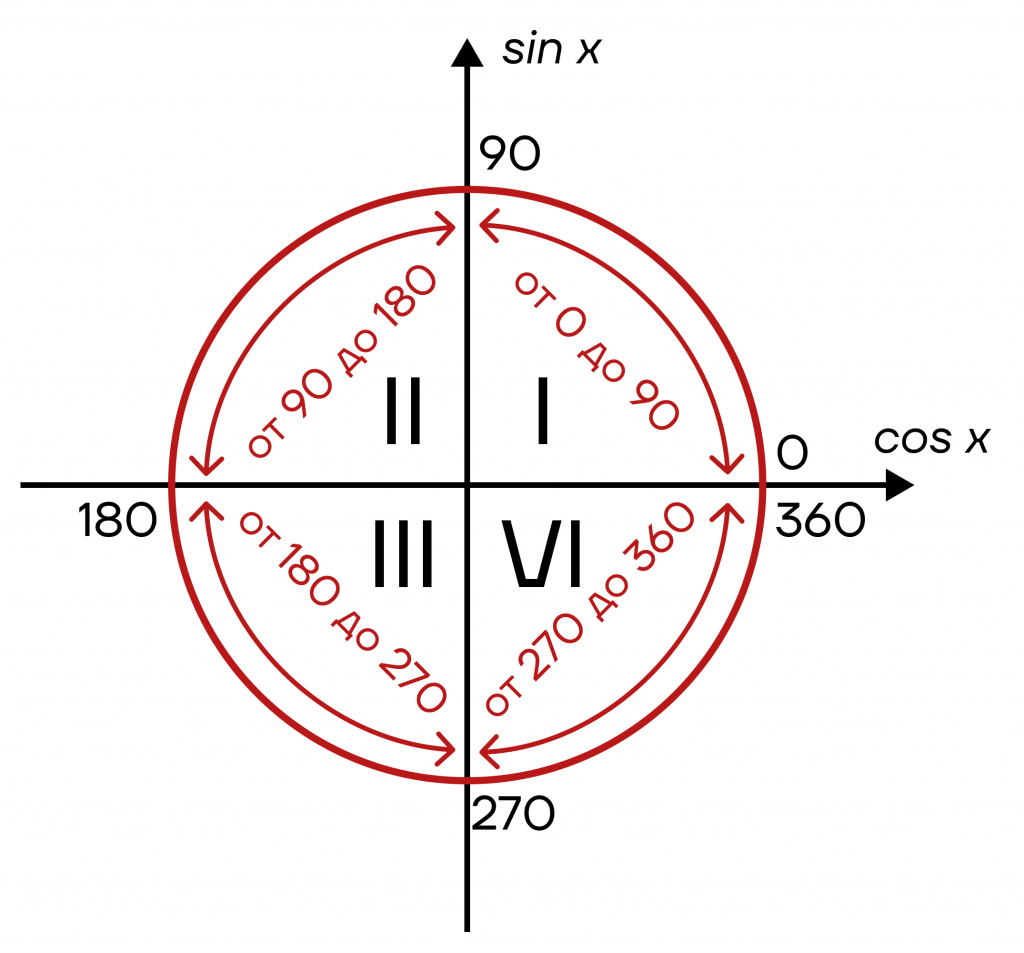
А теперь начнем откладывать наши углы. Чтобы отложить нужный угол, нужно от 0 «поднять» линию по окружности на нужное количество градусов. Это будет схоже с прокручиванием стрелки часов в обратном направлении. Для примера отложим угол 30°. 

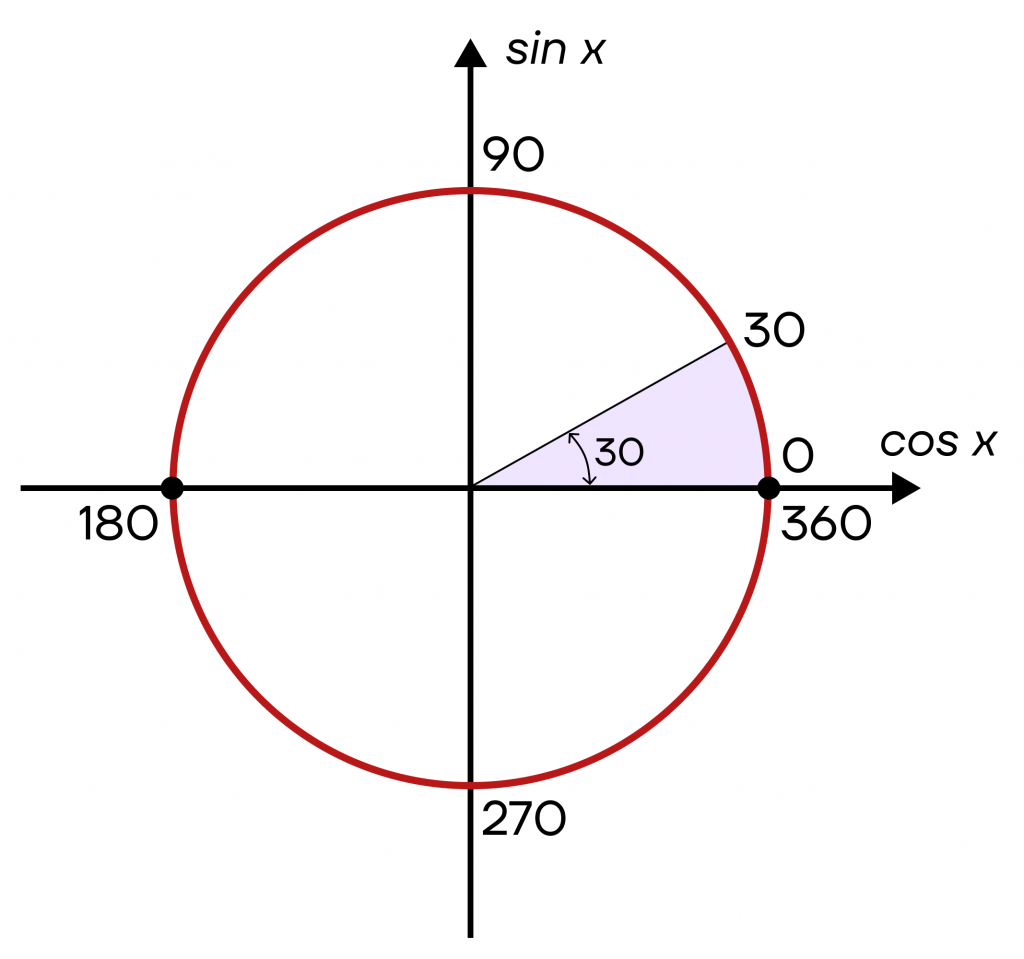
А теперь отложим такой же угол в каждой четверти. При этом во второй четверти мы попадем в точку 90°+30°=120°, в третьей четверти в точку 180°+30°=210°, а в четвертой в точку 270°+30°=300°. Таким образом, у нас получится уже четыре угла из категории «важных». 

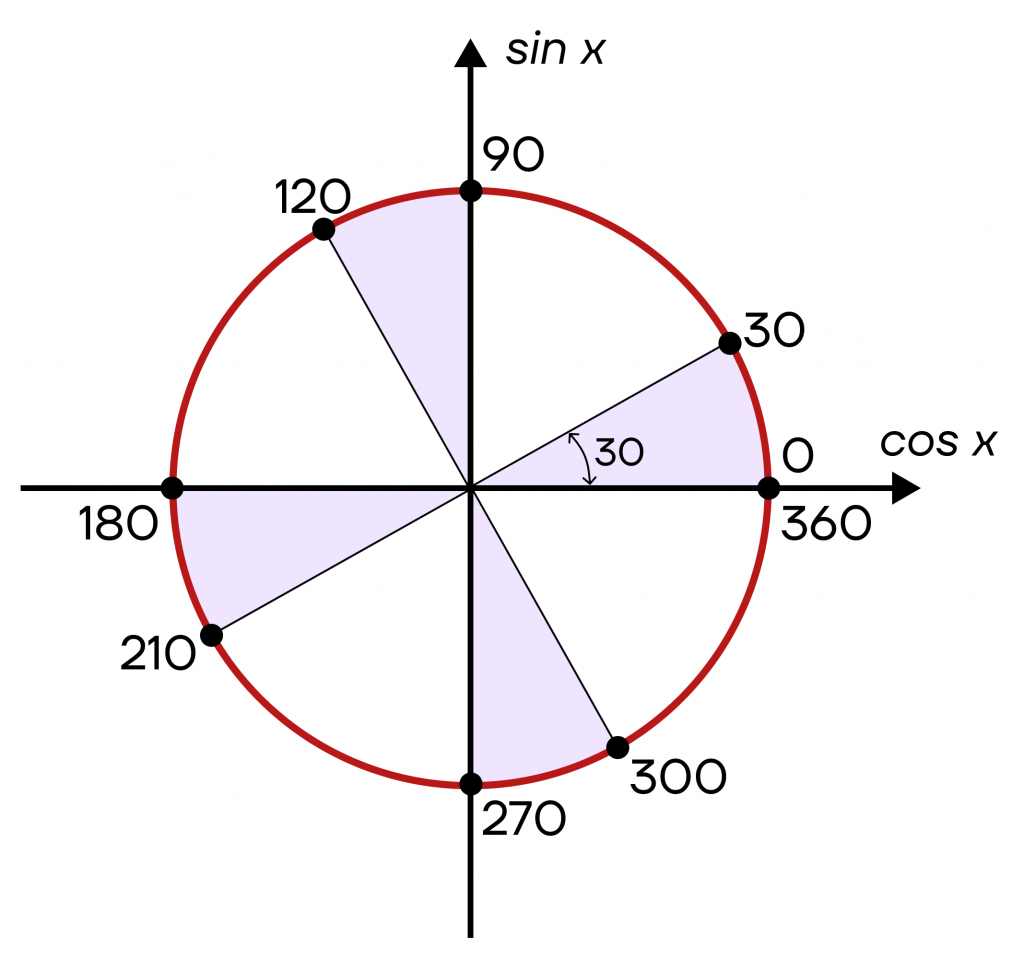
Теперь аналогично отложим угол в 45 градусов от каждой опорной точки. Мы получим точки 45°, 135°, 225° и 315°. 

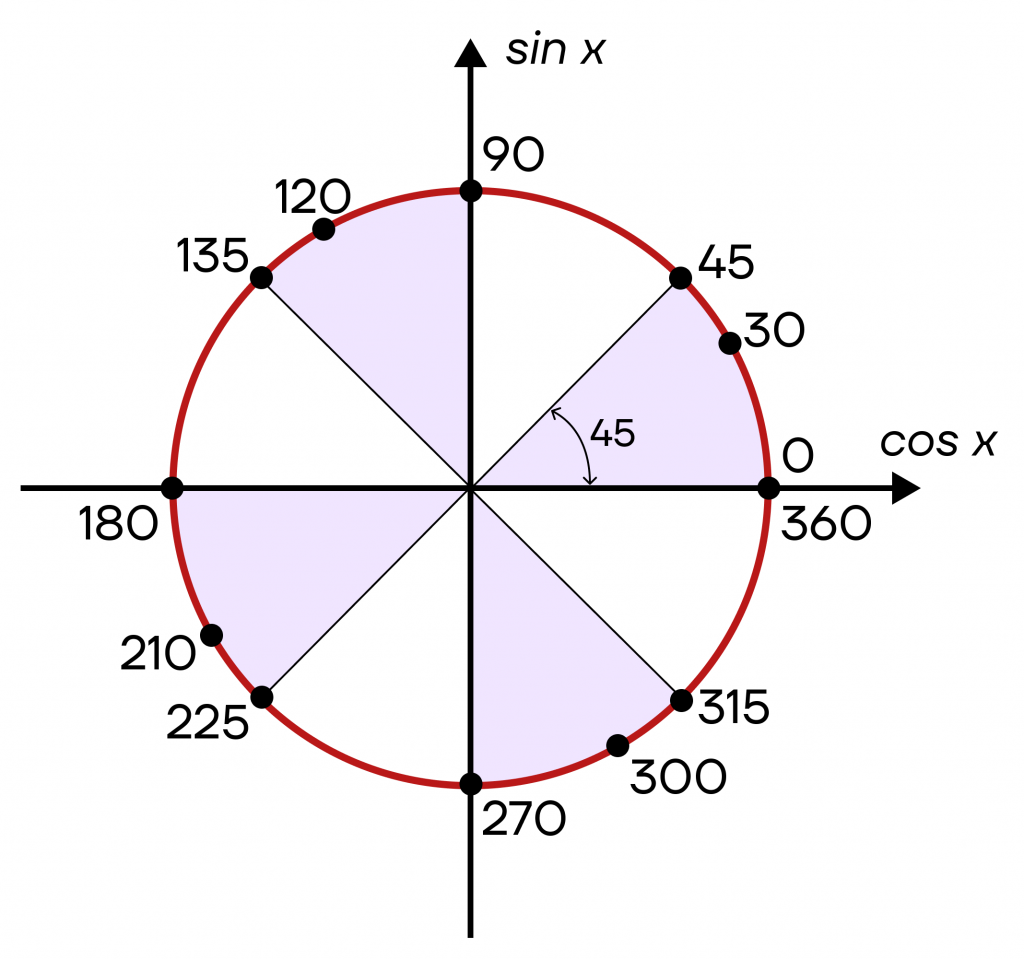
Осталось распределить точки 60°, 150°, 240° и 330°. В этот раз нам нужно будет отложить по 60 градусов от опорных точек. 

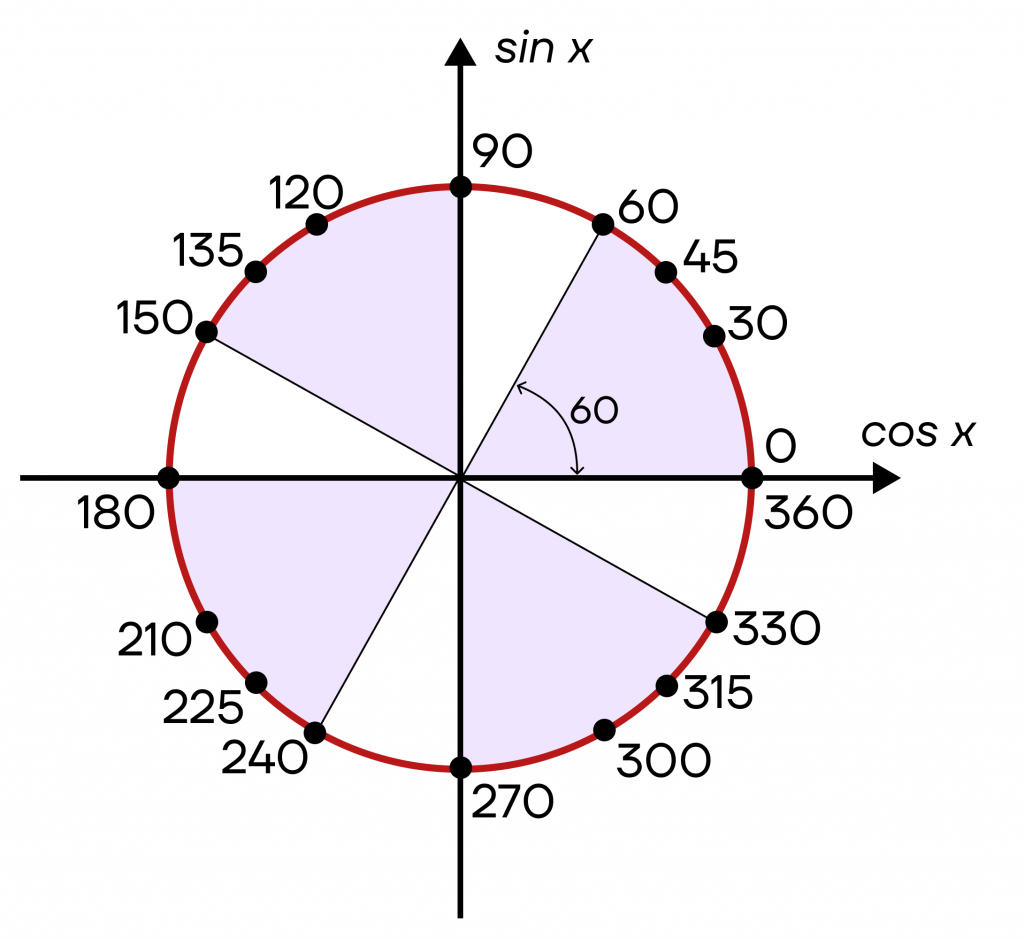
Точно таким же способом можно отложить любой угол на окружности, даже если он больше 360°. Например, возьмем угол 418° и начнем двигаться от 0. Первый круг мы пройдем полностью, отложив таким образом 360 градусов из данного угла. 

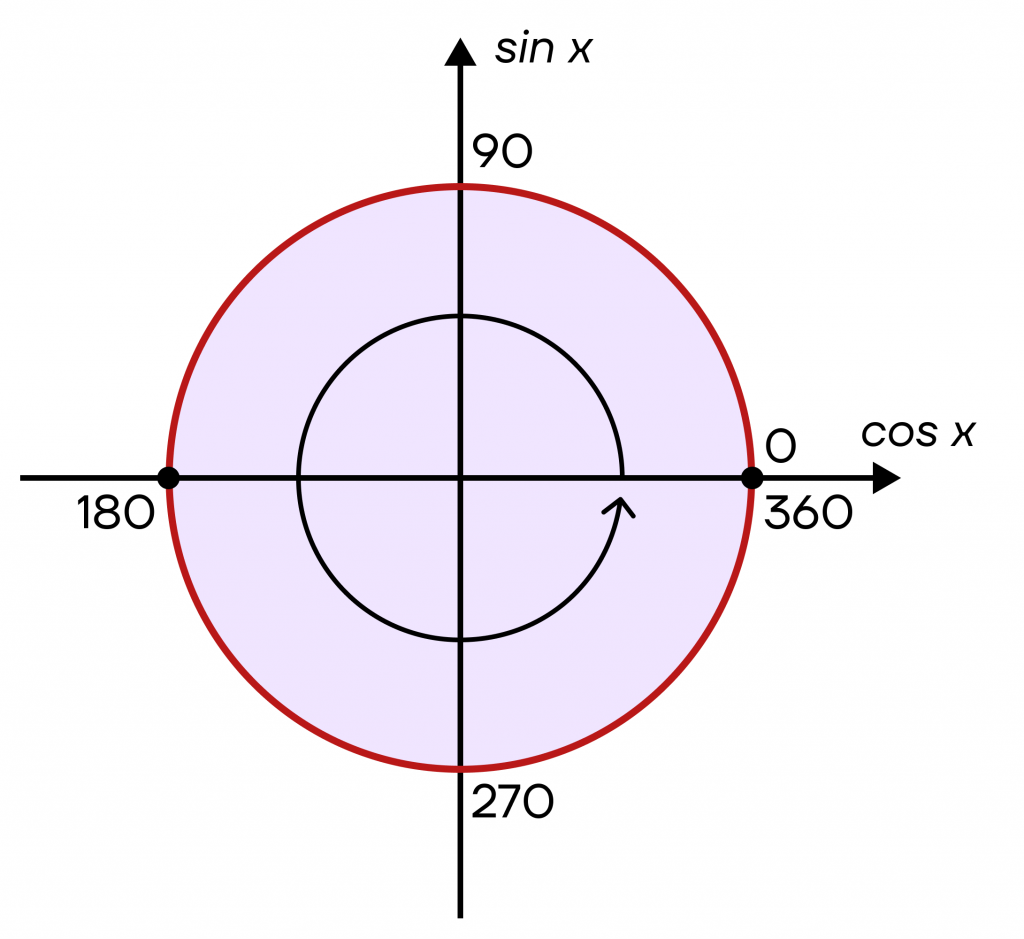
На втором круге нам останется отложить 418°-360°=58°. Заметим, что этот угол будет лежать в первой четверти. Осталось «прокрутить» его от точки 360° (уже не 0, поскольку круг не первый), и получить необходимую точку.

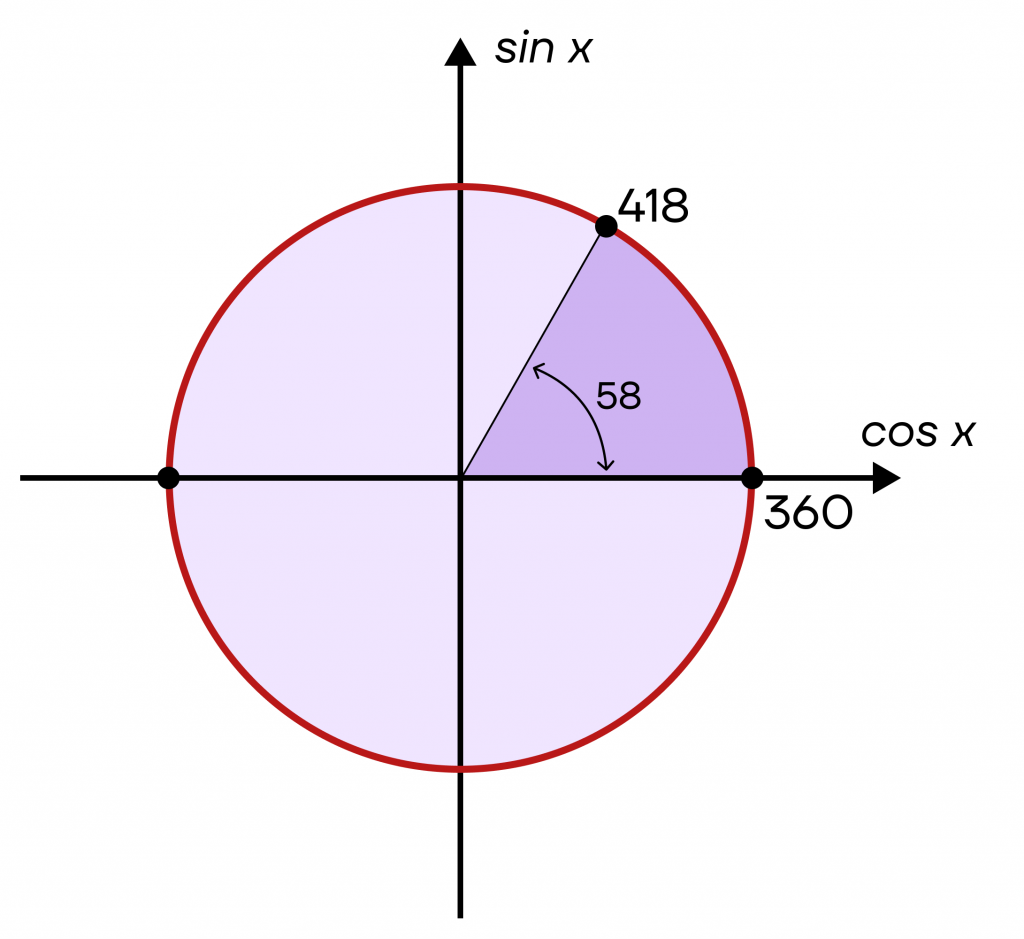
Подобным образом мы можем «кружиться» на любой угол, который только сможем придумать. Аналогично нужно действовать и с отрицательными углами, но двигаться не против часовой, а по часовой стрелке. 

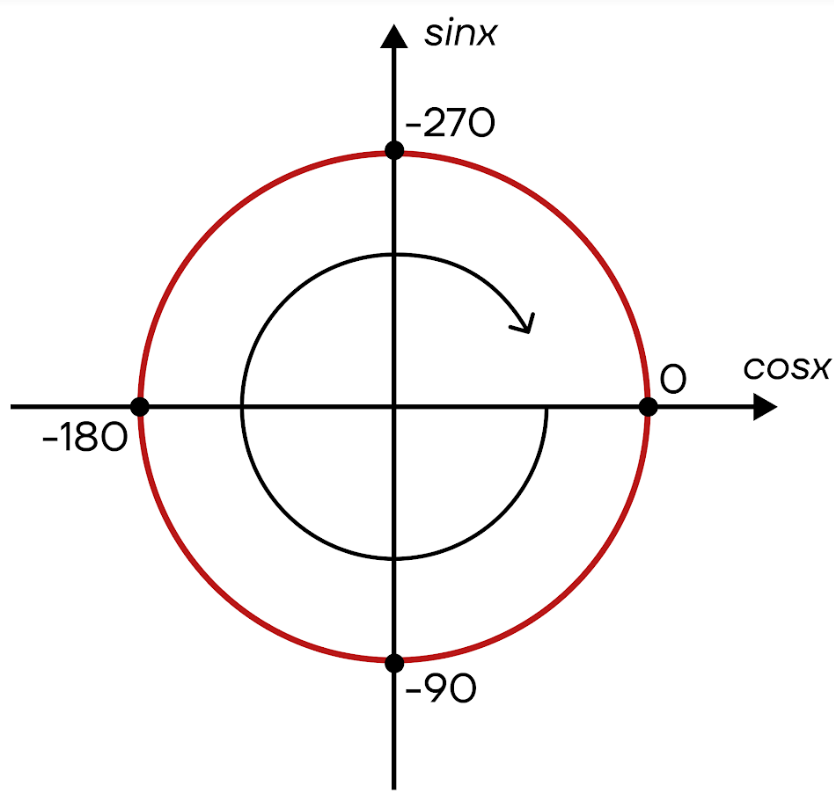
Но вернемся к нашим «важным» точкам. Почему мы на окружности откладывали именно их? На самом деле, значения этих углов — табличные, то есть они уже заранее определены. В задачах такие точки встречаются чаще всего, поэтому с легкостью можно перейти от угла к его значению. Значения углов приведены в таблице ниже. 

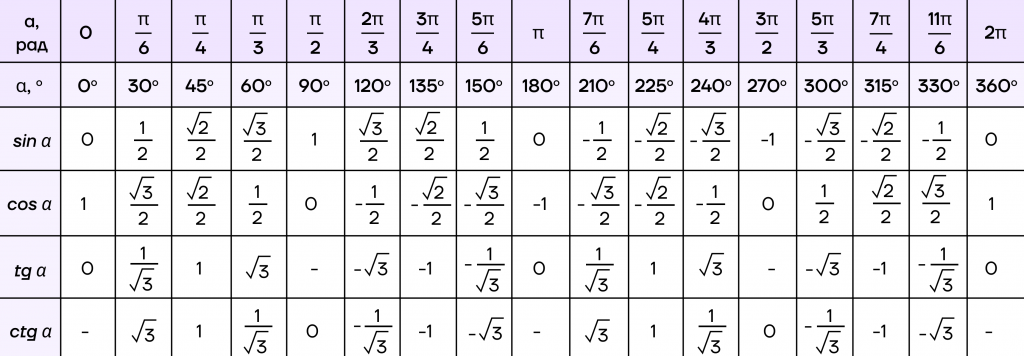
Нахождение значений функций может встретиться как отдельным заданием, так и составной частью большого решения, поэтому важно хорошо ориентироваться в таблице выше. Для примера разберем задание №16 из ЕГЭ по базовой математике:

Найдите значение выражения \(36\sqrt{6}tg\frac{\pi}{6}sin\frac{\pi}{4}\).

Решение. С помощью таблицы найдем значения \(tg\frac{\pi}{6}\) и \(sin\frac{\pi}{4}\):
\(tg\frac{\pi}{6}=\frac{1}{\sqrt3}=\frac{\sqrt3}{3}\)
\(sin\frac{\pi}{4}=\frac{\sqrt2}{2}\)

Теперь осталось подставить эти значения в данное выражение:
\(36\sqrt{6}tg\frac{\pi}{6}sin\frac{\pi}{4}=36\sqrt6*\frac{\sqrt3}{3}*\frac{\sqrt2}{2}\)

Умножим дроби друг на друга, для этого необходимо будет воспользоваться одним из свойств корней. Подробнее про это и другие свойства корней можно узнать в статье «Понятие корня». 
\(\frac{\sqrt3}{3}*\frac{\sqrt2}{2}=\frac{\sqrt{3*2}}{6}=\frac{\sqrt6}{6}\)

Найдем ответ:
\(36\sqrt6*\frac{\sqrt6}{6}=\frac{36\sqrt6*\sqrt6}{6}=\frac{36*6}{6}=36\)

Ответ: 36

Как мы знаем, углы могут быть выражены не только градусами, но и радианами. Отметим наши точки с помощью радиан. Например, \(30°=\frac{180°}{6}=\frac{\pi}{6}\). Перевод из градусов в радианы и обратно очень пригодится нам в дальнейших вычислениях. 

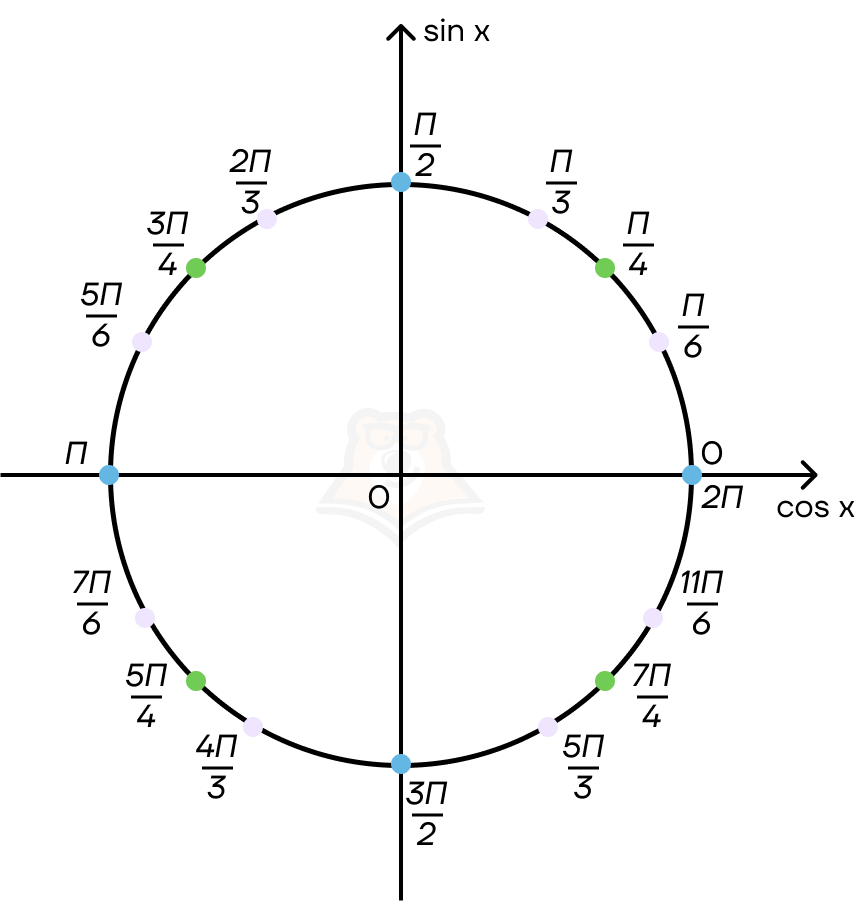
Еще раз обратим внимание: точка 0 совпадает с точкой 2π. Это означает, что мы сделали один оборот по окружности. Но мы можем продолжать идти так и дальше, тогда эта же точка будет принимать значения 4π, 6π, 8π. 

И тригонометрические функции, и окружность могут встретиться и на ЕГЭ по профильной математике, например, в задании №6.

Найдите значение выражения 153*sin(1140°)

Решение. Угол 1140° очень сложно вычислить без преобразований. В таких случаях нужно вспомнить, что по окружности можно делать несколько оборотов, каждый из которых равен 360°. Попробуем сделать несколько «оборотов» обратно, чтобы понять, из какого угла мы пришли к такому значению:
1140°-360°=780°
780°-360°=420°
420°-360°=60°

Следовательно, 1140°=60°+3*360°.

В тригонометрической окружности есть одна особенность: значения тригонометрической функции в одной и той же точке равны. Подробнее об этом мы ведем в разговор в продолжении этой статьи — «Тригонометрическая окружность. Часть 2» — а сейчас просто применим эту особенность. 

Следовательно, \(sin(1140°)=sin(60°)=\frac{\sqrt3}{2}\).

Подставим это значение в данное выражение и найдем ответ:
\(15\sqrt3*sin(1140°)=15\sqrt3*\frac{\sqrt3}{2}=\frac{15*\sqrt3*\sqrt3}{2}=\frac{15*3}{2}=22,5\).

Ответ: 22,5 

Мы разобрали основные понятия, связанные с тригонометрической окружностью. Но с ее помощью можно также находить значения тригонометрических функций и делать выборку корней для заданного промежутка. Об этом и многом другом вы можете узнать в статье «Тригонометрическая окружность. Часть 2». 

Термины

Координатная плоскость — плоскость, на которой изображена система координат, имеющая начало координат, оси координат и координатные углы (то есть углы, образованные при пересечении осей координат). 

Окружность — это замкнутая кривая, все точки которой равноудалены от центра. 

Прямоугольный треугольник — это треугольник, один из углов которого прямой, то есть равен 90°. Подробнее о нем можно прочитать в статье «Равнобедренный, равносторонний и прямоугольный треугольник».

Фактчек

• Тригонометрические функции нужны для исследования углов. С их помощью можно не только определить угол в градусах или радианах, но и найти его значение. 
• К тригонометрическим функциям относятся синус, косинус, тангенс и котангенс. Один из способов их нахождения тесно связан с прямоугольным треугольником. Так, синус — это отношение противолежащего катета к гипотенузе, косинус — отношение прилежащего катета к гипотенузе, тангенс — отношение противолежащего катета к прилежащему катету и котангенс — отношение прилежащего катета к противолежащему. 
• Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1. 
• Единичная тригонометрическая окружность используется для графического изображения тригонометрических функций.

Проверь себя

Задание 1.
Что такое тангенс?

1. Отношение противолежащего катета к гипотенузе.
2. Отношение прилежащего катета к гипотенузе.
3. Отношение противолежащего катета к прилежащему катету.
4. Отношение прилежащего катета к противолежащему катету. 

Задание 2.
Выберите верное утверждение для оси косинуса:

1. Ось косинуса проходит вертикально через центр окружности.
2. Ось косинуса проходит горизонтально через центр окружности.
3. Ось косинуса вертикальна и касается окружности справа.
4. Ось косинуса горизонтальна и касается окружности сверху.

Задание 3.
Чему равен угол 40° в радианах?

1. \(\frac{\pi}{9}\)
2. \(\frac{9\pi}{2}\)
3. \(\frac{2\pi}{9}\)
4. \(\frac{\pi}{40}\)

Задание 4.
В какой четверти лежит угол 238°?

1. 1.
2. 2. 
3. 3.
4. 4.

Задание 5.
В какой четверти лежит угол 995°?

1. 1.
2. 2. 
3. 3.
4. 4.

Ответы: 1. — 3; 2. — 2; 3. — 3; 4. — 3; 5. — 4.