Метод рационализации

На этой странице вы узнаете

• Почему рационализация важна не только в математике?
• Почему важно соблюдать диету?
• Что метод рационализации украл у логарифма?

В одной далекой математической стране под названием «Неравнус» много лет люди занимались решением разнообразных сложных неравенств. Жизнь этих людей была полна боли и страданий, пока однажды не пришел в страну некий волшебник, который принес с собой магическую палочку под названием «Метод рационализации». С ней людям на Неравнусе жить стало гораздо легче и спокойнее, ведь любое неравенство теперь не представляло из себя никакой проблемы. 

Что же это за палочка такая и как ей пользоваться? Предлагаем разобраться в этом вместе.

Суть метода рационализации

При решении любого неравенства мы определяем, при каких значениях переменных некоторая функция f(x) принимает положительные, отрицательные, неположительные или неотрицательные значения. 

То есть, нас интересуют не сами значения этой функции, а их знаки. Например, в неравенстве \(5x\geq 0\) необходимо определить значения x, при которых функция \(5x\) принимает неотрицательные (то есть больше 0 или равные 0) значения. 

В некоторых случаях функцию можно заменить другой, более «удобной» функцией, знак которой будет определяться точно так же. Например, функцию 5x можно таким образом заменить на функцию x. Действительно:

• если \(x\geq 0\), то и \(5x\geq 0\); 
• если \(x\leq 0\), то и \(5x\leq 0\); 
• если \(x<0\), то и \(5x<0\);
• если \(x>0\), то и \(5x>0\). 

Знак функции x определяется так же, как и знак функции 5x. Поэтому в неравенстве мы можем 5x заменить на x.

В этом и заключается суть метода рационализации – заменить функцию более «удобной» равносильной функцией, знак которой определяется так же.

Почему рационализация важна не только в математике? Одно из определений рационализации – способ наиболее эффективных и оптимальных способов достижения цели, усовершенствование чего-либо. В математике с помощью метода рационализации мы можем упрощать неравенства. На промышленном производстве рационализация помогает повышать эффективность этого производства, совершенствовать технологический процесс. Даже если взять в пример наш распорядок дня: чем более рациональным будет распорядок дня, тем больше полезных дел можно будет успеть сделать и тем лучше от этого будет наше настроение и состояние. Получается, что уметь рационализировать что-либо важно каждому человеку, ведь именно это умение позволяет упрощать жизнь и повышать ее качество.

Выше был разобран пример лишь для того, чтобы показать эту суть. На практике метод рационализации используется для решения более сложных неравенств: логарифмических, показательных, иррациональных неравенств, а также неравенств, содержащих знак модуля.

Разберемся подробнее с каждым из перечисленных видов неравенств.

Метод рационализации для логарифмических неравенств

Для начала рекомендуем вспомнить общие сведения о функции логарифма. Речь об этом шла в статье «Показательная и логарифмическая функция».

Мы помним, что при решении уравнений или неравенств очень важно учитывать область допустимых значений – ОДЗ. 

Почему важно соблюдать диету? Представим: Маше необходимо составить рацион питания так, чтобы за день получить 2500 килокалорий. При этом Маше также необходимо соблюдать диету, согласно которой нельзя включать в рацион ничего сладкого и мучного.  В понедельник Маша выполнила план по килокалориям, при этом рацион ее состоял только из мучного. Похвалит ли Машу диетолог? Ответ очевиден – нет, ведь Маша не учла ограничения в рационе. Так же и с методом рационализации: при решении неравенств методом рационализации важно учитывать все ограничения, то есть ОДЗ, для того чтобы получить верный ответ.

Вспомним ОДЗ для функции логарифма:

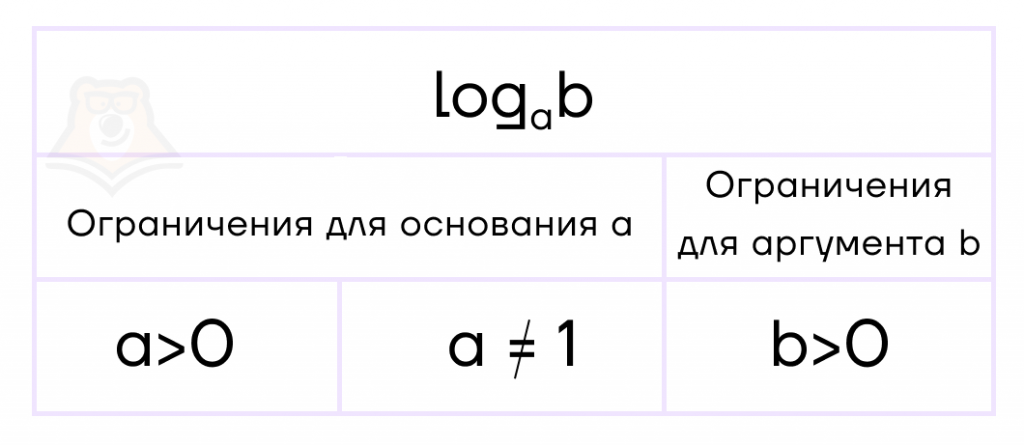
Как видим, ограничения здесь накладываются как на аргумент (больше 0), так и на основания (больше 0 и не равно 1).

Теперь вернемся к самому методу рационализации. Выделим несколько типов логарифмических неравенств.

1. Если логарифм сравнивается с нулем (например, \(log_ba>0\)), то функцию логарифма в таком неравенстве можно заменить функцией \((b-1)(a-1)\), где \(a\) – аргумент логарифма, \(b\) – основание логарифма.

Например, решим неравенство \(log_3x>0\). 

Для начала укажем ОДЗ данного логарифма:

\(x>0\)

Идем далее: согласно методу рационализации, неравенство \(log_3x>0\) можно преобразовать в неравенство \((3-1)(x-1)>0\), которое теперь можно легко решить привычным способом:

\(log_3x>0\)
\((3-1)(x-1)>0\)
\(2*(x-1)>0\)
\(x-1>0\)
\(x>1\)

Получили промежуток \((1;+\infty)\), который полностью удовлетворяет ОДЗ \((x>0\)). 

Как видим, метод рационализации здесь помог нам полностью «избавиться» от логарифма в неравенстве, что, безусловно, облегчает решение.

2. Если разность двух логарифмов с одинаковым основанием сравнивается с нулем (например, \(log_ba-log_bc>0)\), то функцию разности таких логарифмов можно заменить функцией \((b-1)(a-c)\), где \(b\) – основание логарифмов, \(a\) и \(c\) – аргументы первого и второго логарифмов соответственно.

Например, решим неравенство \(log_97x-log_96\geq 0\).  Начнем, как обычно, с ОДЗ. Для функции \(log_97x-log_96\):

\(7x>0\)
\(x>0\)

Функцию \(log_97x-log_96\) по методу рационализации можно заменить функцией \((9-1)(7x-6)\) и решить получившееся неравенство:

\(log_97x-log_96\geq 0\)
\((9-1)(7x-6)\geq 0\)
\(8*(7x-6)\geq 0\)
\(7x-6\geq 0\)
\(7x\geq 6\)
\(x\geq \frac{6}{7}\)

Промежуток \([\frac{6}{7}; +\infty)\) полностью удовлетворяет ОДЗ \((x>0)\), поэтому решением данного неравенства будет: \([\frac{6}{7}; +\infty)\).

3. Если разность логарифма и единицы сравнивается с нулем (например, \(log_ba-1>0\)), то функцию такой разности можно заменить функцией \((b-1)(a-b)\). 

Это можно легко доказать, воспользовавшись методом рационализации для разности двух логарифмов с одинаковым основанием. Представим единицу в виде логарифма с основанием \(b\):

\(1=log_bb\)
Тогда:
\(log_ba-1=log_ba-log_bb\)

Функцию \(log_ba-log_bb\), в свою очередь, согласно методу рационализации можно заменить на функцию \((b-1)(a-b)\). 

Рассмотрим пример: решим неравенство \(log_{x+1}(x^2+2x+1)-1>0\). 

Определим ОДЗ для логарифма \(log_{x+1}(x^2+2x+1)\). Заметим, что \(x^2+2x+1\) представляет из себя полный квадрат \((a^2+2ab+b^2=(a+b)^2)\), то есть \(x^2+2x+1=x^2+2*x*1+1^2=(x+1)^2\).

Далее воспользуемся методом рационализации: функцию \(log_{x+1}(x^2+2x+1)-1\) в неравенстве можно заменить функцией \((x+1-1)(x^2+2x+1-(x+1))\):

\(log_{x+1}(x^2+2x+1)-1>0\)
\((x+1-1)(x^2+2x+1-(x+1))>0\)
\(x(x^2+2x+1-x-1)>0\)

Во второй скобке приведем подобные слагаемые \((2x\) и \(-x; 1\) и \(-1)\):

\(x(x^2+x)>0\)

В множителе \(x^2+x\) можно вынести общий множитель за скобки:

\(x^2+x=x(x+1)\)

Подставим получившееся выражение в наше неравенство:

\(x*x(x+1)>0\)
\(x^2(x+1)>0\)

Полученное неравенство решим методом интервалов. Для начала найдем нули каждого множителя:

1. \(x^2=0\)
   \(x_1=0\)

2. \(x+1=0\)
   \(x_2=-1\)

Подставим полученные значения на числовую прямую и определим знаки               каждого интервала:

Неравенство строгое (знак \(>\)), поэтому все точки на координатной прямой выколотые (незакрашенные). 

В неравенстве \(x^2(x+1)>0\) стоит знак «\(>\)», поэтому выделим те интервалы, где функция принимает положительные значения:

Получили два промежутка: \((-1;0)\cup (0;+\infty)\).

Не забываем и про учет ОДЗ \((x>-1; x\neq 0)\). Оба промежутка полностью удовлетворяют этим ограничением. Поэтому решением неравенства будет: \((-1;0)\cup (0;+\infty)\).

4. Если разность двух логарифмов с одинаковым аргументом сравнивается с нулем (например, \(log_ba-log_ca>0\)), то функцию разности таких логарифмов можно заменить функцией \((b-1)(c-1)(a-1)(c-b)\), где \(a\) – аргумент логарифмов, \(b\) и \(c\) – основания первого и второго логарифмов соответственно.

Приведем пример: решим неравенство \(log_{2x}(9x^2)-log_{3x}(9x^2)<0\). Сначала отметим ОДЗ для логарифмов:

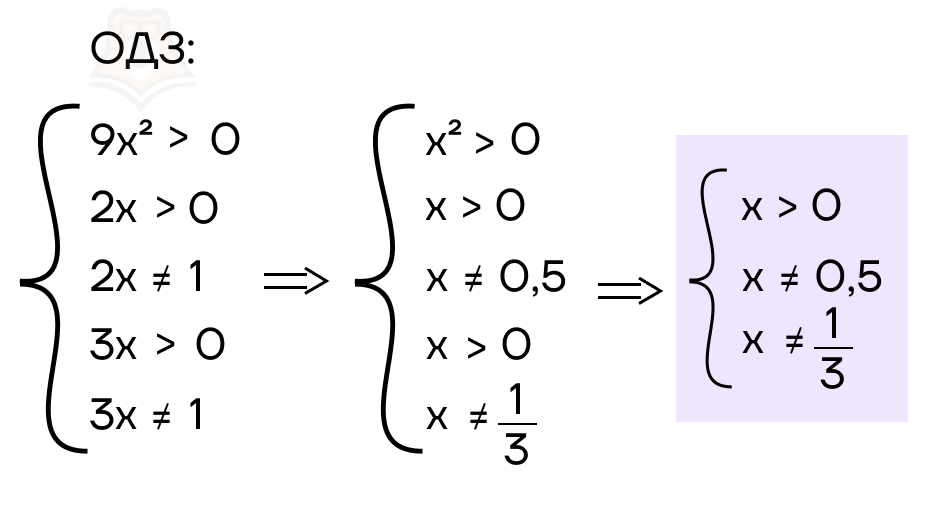
Далее, согласно методу рационализации, заменим функцию \(log_{2x}(9x^2)-log_{3x}(9x^2)\) функцией \((2x-1)(3x-1)(9x^2-1)(3x-2x)\):

\(log_{2x}(9x^2)-log_{3x}4<0\)
\((2x-1)(3x-1)(9x^2-1)(3x-2x)<0\)

Выражение \(9x^2-1\) можно разложить на множители, воспользовавшись формулой разности квадратов \(a^2-b^2=(a-b)(a+b)\): 

\(9x^2-1=(3x)^2-1^2=(3x-1)(3x+1)\)

Подставим получившееся выражение в неравенство:

\((2x-1)(3x-1)(3x-1)(3x+1)(3x-2x)<0\)
\((2x-1)(3x-1)^2(3x+1)x<0\)

Далее для решения получившегося неравенства воспользуемся методом интервалов. Для начала найдем нули каждого множителя:

1. \(2x-1=0\)
   \(2x=1\)
   \(x_1=0,5\)

2. \((3x-1)^2=0\)
   \(3x-1=0\)
   \(3x=1\)
   \(x^2=\frac{1}{3}\)

3. \(3x+1=0\)
   \(3x=-1\)
   \(x_3=-\frac{1}{3}\)

4. \(x_4=0\)

Поставим полученные нули множителей на координатную прямую и отметим знаки полученных интервалов:                    

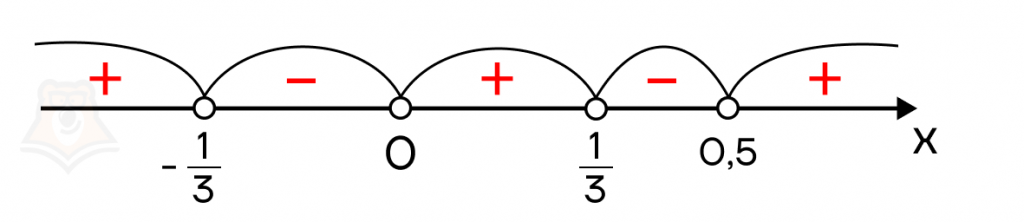
Неравенство строгое (знак \(<\)), поэтому все точки – выколотые (незакрашенные). Вернемся к неравенству \((2x-1)(3x-1)^2(3x+1)x<0\). Так как нас интересуют отрицательные значения функции \((2x-1)(3x-1)^2(3x+1)x\), выделим соответствующие интервалы:

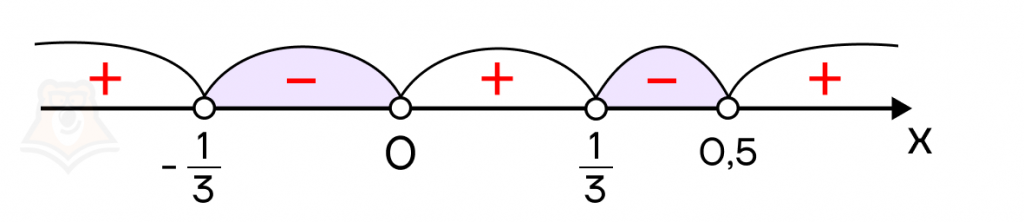
Получили промежутки \((-\frac{1}{3};0)\cup (\frac{1}{3};0,5)\). При этом не забываем учесть здесь ОДЗ \((x>0;x\neq 0,5;x\neq \frac{1}{3}\)), согласно которому x может принимать только положительные значения. 

По этому критерию не подходит промежуток \((-\frac{1}{3};0)\). Тогда решением данного неравенства является промежуток \((\frac{1}{3};0,5)\).

Что метод рационализации украл у логарифма? Как видим, при решении логарифмических неравенств метод рационализации украл у логарифма сам логарифм. Действительно, в ходе решения мы полностью «избавились» от логарифма и смогли получить обычное неравенство, которое решается методом интервалов, что значительно облегчает решение.

При этом метод рационализации может применяться не только для логарифмов, но и для степеней.

Метод рационализации для показательных неравенств

Для начала рекомендуем повторить общие сведения о степенях, с которыми мы уже знакомились в статье «Действия с натуральными числами».

С показательной функцией мы уже познакомились в статье «Показательная и логарифмическая функции». Напомним, что в такой функции переменная находится в показателе степени.

В общем виде показательная функция не имеет ограничений, так как показатель x степени \(a^x\) может принимать любые числовые значения при условии, что основание степени больше 0 и не равно 1, то есть \(a>0\) и \(a\neq 1\).

Однако про ОДЗ таких функций также не стоит забывать. Например, в функции \(3^{\frac{1}{x}}\) ограничения накладываются на показатель степени \(\frac{1}{x}\): знаменатель дроби не может быть равен 0, то есть, \(x\neq 0\). Тогда ОДЗ для  функции \(3^{\frac{1}{x}}\) будет являться промежуток \((-\infty;0)\cup (0;+\infty)\).

Самое время перейти к методу рационализации для показательных неравенств. Так же, как и с логарифмами, рассмотрим несколько видов таких неравенств. 

1. Если разность двух степеней с одинаковым основанием сравнивается с нулем (например, \(a^b-a^c>0\)), то функцию такой разности можно заменить функцией \((a-1)(b-c)\), где \(a\) – основание степеней, \(b\) и \(c\) – показатели первой и второй степеней соответственно.

Приведем пример: решим неравенство \(2^{3x}-2^{5x}>0\). В функции \(2^{3x}-2^{5x}\) переменная не обладает никакими ограничениями, поэтому ОДЗ здесь: \((-\infty; +\infty)\).

Далее, согласно методу рационализации, заменим функцию \(2^{3x}-2^{5x}\) функцией \((2-1)(3x-5x)\) и решим полученное неравенство методом интервалов:

\((2-1)(3x-5x)>0\)
\(1*(-2x)>0\)
\(-2x>0\)
\(x<0\)

Получили промежуток \((-\infty;0)\). Не забываем учесть и ОДЗ \((-\infty;+\infty)\), которая в данном случае никак не ограничивает полученный промежуток.

Ответ: \((-\infty;0)\)

2. Если разность степени и 1 сравнивается с нулем (например, \(a^b-1>0\)), то функцию такой разности можно заменить функцией \((a-1)b\), где \(a\) – основание степени, \(b\) – показатель степени.

Это можно легко доказать: представим единицу как степень с основанием a: 

\(1=a^0\)

Тогда:

\(a^b-1=a^b-a^0\)

По методу рационализации функцию \(a^b-a^0\) можно заменить функцией \((a-1)(b-0)=(a-1)b\). Значит, и функцию \(a^b-1\) в неравенстве можно заменить функцией \((a-1)b\). Что и требовалось доказать.

Приведем пример: решим неравенство \((-5)^{x^2}-1\leq 0\). 

ОДЗ функции: \((-\infty;+\infty)\).

По методу рационализации заменим функцию \((-5)^{x^2}-1\) функцией \((-5-1)x^2\), после чего решим полученное неравенство методом интервалов:

\((-5)^{x^2}-10\)
\((-5-1)x^2\leq 0\)
\((-6)*x^2\leq 0\)
\(-6x^2\leq 0\)
\(x^2\geq 0\)

Получили неравенство \(x^2\geq 0\). Воспользовавшись методом интервалов, найдем нули функции \(x^2\). 

\(x^2=0\)
\(x=0\)

Отметим полученное значение на координатной прямой и определим знаки получившихся интервалов: 

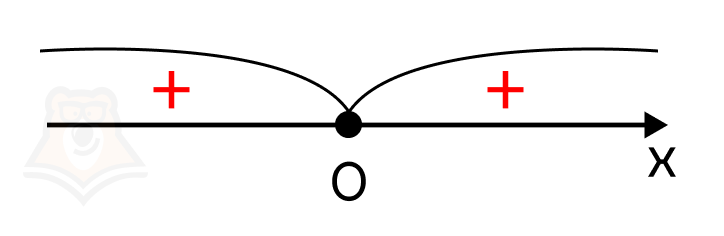
Неравенство нестрогое (знак \(\geq\)), поэтому точка не выколотая (закрашенная). Из неравенства \(x^2\geq 0\) следует, что необходимо найти значения переменной, при которых функция \(x^2\) принимает неотрицательные значения:

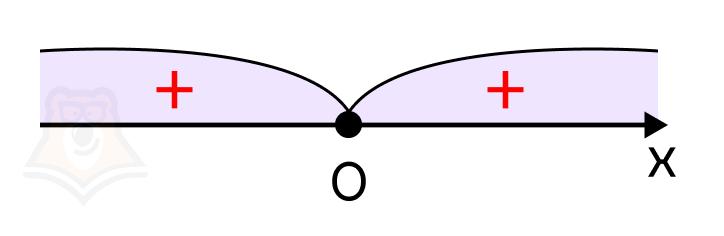
Получили промежуток \((-\infty; +\infty)\), которое полностью удовлетворяет ОДЗ \((-\infty; +\infty)\).

Ответ: \((-\infty; +\infty)\)

3. Если разность степеней с одинаковым показателем степени сравнивается с нулем (например, \(a^c-b^c>0)\), то функцию такой разности можно заменить функцией \((a-b)c\), где \(a\) и \(b\) – основания степеней, \(с\) – показатель степеней. 

В качестве примера рассмотрим неравенство \((\frac{1}{2})^{x^2+2x+1}-(\frac{5}{2})^{x^2+2x+1}\geq 0\).

На данную функцию также не накладываются никакие ограничения, поэтому ОДЗ функции \((\frac{1}{2})^{x^2+2x+1}-(\frac{5}{2})^{x^2+2x+1}\) является промежуток \((-\infty; +\infty)\).

Теперь воспользуемся методом рационализации, заменим функцию \((\frac{1}{2})^{x^2+2x+1}-(\frac{5}{2})^{x^2+2x+1}\) на функцию \((\frac{1}{2}-\frac{5}{2})(x^2+2x+1)\) и решим получившееся неравенство методом интервалов:

\((\frac{1}{2})^{x^2+2x+1}-(\frac{5}{2})^{x^2+2x+1}\geq 0\)
\((\frac{1}{2}-\frac{5}{2})(x^2+2x+1)\geq \)
\(-2*(x^2+2x+1)\geq 0\)

Обе части неравенства разделим на \((-2)\). В таком случае знак неравенства меняется на противоположный:

\(\frac{-2*(x^2+2x+1)}{-2}\leq \frac{0}{-2}\)
\(x^2+2x+1\leq 0\)

Обратим внимание на второе выражение \(x^2+2x+1\). Здесь можно заметить полный квадрат суммы \(a^2+2ab+b^2=(a+b)^2\).

\(x^2+2x+1=x^2+2*x*1+1^2=(x+1)^2\)

Теперь вернемся к нашему неравенству:

\(x^2+2x+1\leq 0\)
\((x+1)^2\leq 0\)

Решим получившееся неравенство методом интервалов. Для этого найдем нули функции \((x+1)^2\).

\((x+1)^2=0\)
\(x+1=0\)
\(x=-1\)

Полученное значение поставим на координатную прямую и определим знаки образованных интервалов:

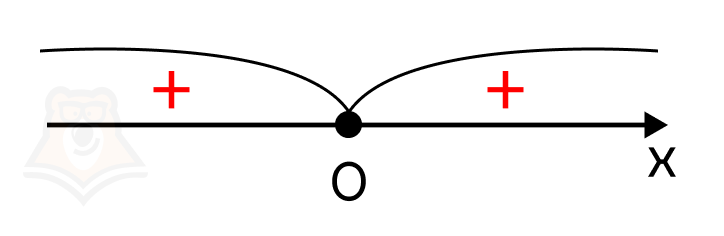
Точка 1 здесь не выколотая (закрашенная), так как неравенство нестрогое (знак ).

Нас интересуют значения переменной, при которой функция принимает неположительные значения: \((x+1)^2\leq 0\). В данном случае нам подойдет только одно значение переменной: \(x=1\), при котором значение функции равно 0. При любых других значениях x функция будет принимать положительные значения.

Ответ: 1.

Как видим из разобранных примеров, метод рационализации для степеней позволяет полностью «избавиться» от степеней в неравенствах и перейти к обычным неравенствам, решаемым с помощью метода интервалов.

Ну а мы двигаемся дальше, ведь возможности нашей волшебной палочки на этом не останавливаются. На этот раз направим ее иррациональные неравенства.

Метод рационализации для иррациональных неравенств

Иррациональное неравенство – это неравенство, содержащее переменные под знаком корня.

Например: 

• \(\sqrt{x} \leq 0\)
• \(\sqrt{x-2}+8\geq 0\)
• \(-1+\sqrt[3]{-x^2-8+x}+3x^3<0\)

Сейчас же мы коснемся иррациональных неравенств, содержащих знак квадратного корня. Для некоторых таких неравенств мы можем применить метод рационализации.

Если разность двух функций квадратных корней сравнивается с нулем (например, \(\sqrt{a}-\sqrt{b}>0)\), то такую разность можно заменить равносильной функцией \((a-b)\), где \(a\) и \(b\) – подкоренные выражения первого и второго квадратных корней соответственно. 

При этом не стоит забывать про ОДЗ для квадратного корня: подкоренное выражение не может принимать отрицательные значения:

\(\sqrt{x}\Rightarrow x\geq 0\)

Приведем пример: решим неравенство \(\sqrt{3x}-\sqrt{2x} \geq 0

Начнем с ОДЗ для функции \(\sqrt{3x}-\sqrt{2x})\):

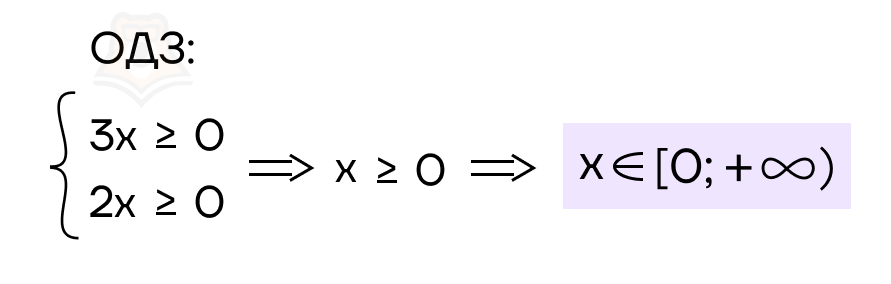
Далее заменим функцию \(\sqrt{3x}-\sqrt{2x})\), согласно методу рационализации, равносильной функцией \((3x-2x)\) и решим получившееся неравенство:

\(\sqrt{3x}-\sqrt{2x} \geq 0\)
\(3x-2x\geq 0\)
\(x\geq 0\)

Получили промежуток \([0;+\infty)\), который полностью удовлетворяет ОДЗ: \([0;+\infty)\).

Ответ: \([0;+\infty)\)

Таким образом, метод рационализации может применяться и для иррациональных неравенства: в них он позволяет нам «избавиться» от знака корня.

Тем временем наша волшебная палочка уже помогла нам избавиться от логарифмов, степеней и даже квадратных корней в неравенствах. А сможет ли она справиться с модулем?

Метод рационализации для неравенств, содержащих знак модуля

В статье «Модуль» было разобрано, как решаются неравенства с модулем. Сейчас же мы посмотрим, как к некоторым таким неравенствам можно применить метод рационализации.

Если разность двух модулей сравнивается с нулем \((|a|-|b|\geq 0; |a|-|b|\leq 0; |a|-|b|>0; |a|-|b|<0)\), то функцию такой разности можно заменить функцией \((a-b)(a+b)\), где \(a\) и \(b\) – выражения, стоящие под знаком модуля.

Например, в неравенстве \(|x^2|-|9x|>0\) функцию \(|x^2|-|9x|\) можно заменить функцией \((x^2-9x)(x^2+9x)\). В данном случае никаких ограничений нет, поэтому областью допустимых значений будет являться промежуток \((-\infty ;+\infty)\).

\(|x^2|-|9x|>0\)
\((x^2-9x)(x^2+9x)>0\)

В обоих множителях вынесем общий множитель \(x\) за скобки:

\(x(x-9)x(x+9)>0\)
\(x^2(x-9)(x+9)>0\)

В левой части неравенства получили выражение, разложенное на множители. Значит, решим данное неравенство методом интервалов. Для этого найдем нули каждого множителя функции \(x(x-9)\):

1. \(x^2=0\)
   \(x_1=0\)
   
2. \(x-9=0\)
   \(x_2=9\)
   
3. \(x+9=0\)
   \(x_3=-9\)

Подставим полученные значения на числовую прямую и определим знаки образовавшихся интервалов:

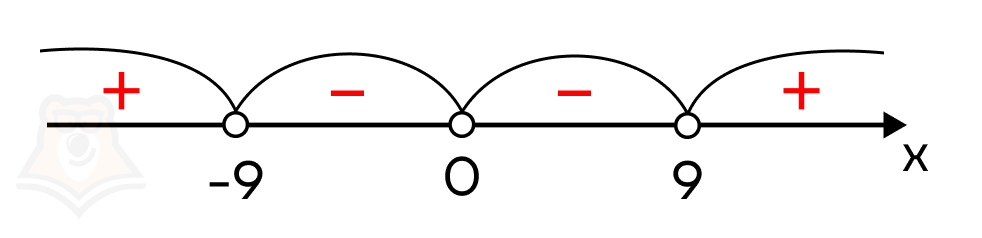
Неравенство строгое (знак \(>\)), поэтому все три точки выколотые (незакрашенные). Выделим промежутки, на которых функция \(x^2(x-9)(x+9)\) принимает положительные значения, то есть \(x(x-9)>0\):

Получили промежутки \((-\infty;-9)\cup (9;+\infty)\), которые никак не противоречат ОДЗ: \((-\infty; +\infty)\).
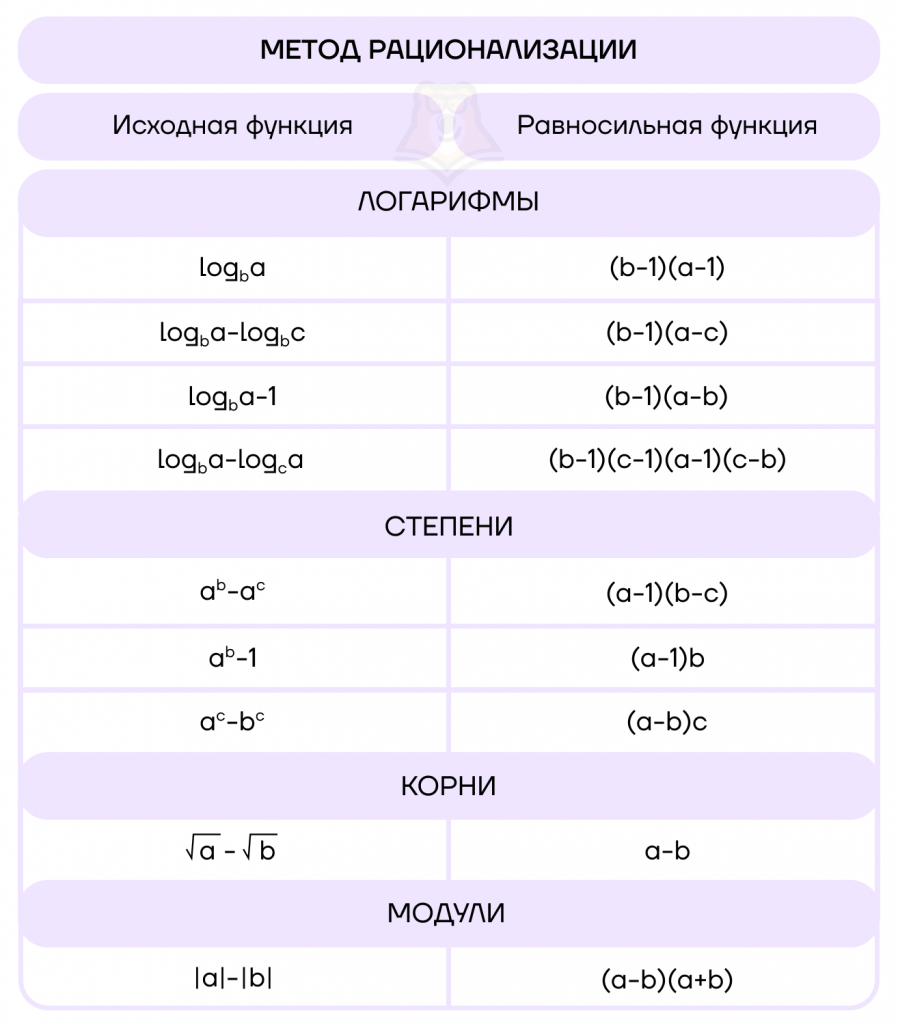
Представим общую таблицу данных приемов метода рационализации:
Ответ: \((-\infty;-9)\cup (9;+\infty)\)

На этом мы разобрали основные способы применения метода рационализации. На самом деле, их гораздо больше, мы же остановились на тех, которые наиболее часто встречаются в неравенствах. 

При этом часто в учебнике алгебры можно увидеть «страшные» неравенства, в состав которых включены и логарифмы, и степени, и корни одновременно. Можно ли в таком случае комбинировать несколько «видов» метода рационализации в одном неравенстве?

Неравенства на комбинацию приемов метода рационализации

В ходе статьи мы рассмотрели неравенства, в которых применили метод рационализации. В этих неравенствах мы всю функцию заменяли на равносильную ей функцию.

На самом деле, метод рационализации можно применять не только для всей функции, но и для отдельных ее множителей. Разберемся в этом, разобрав пример из ЕГЭ.

Решим пример задания №15 из ЕГЭ по профильной математике

Задание. Решите неравенство \(\frac{log_3(5x)*log_4(x)}{|x|-x^2}\geq 0\).

Решение. Начнем с ОДЗ функции \(\frac{log_3(5x)*log_4(x)}{|x|-x^2}\): ограничения здесь будут накладываться на логарифмы, аргумент которых должен быть больше \(0\): \(5x>0\) и \(x>0 \Rightarrow x\in (0;+\infty)\).

Также знаменатель функции не может быть равен нулю: \(|x|-x^2\neq 0 \Rightarrow x\neq 0\) и \(x\neq 1\).

Если учесть все эти ограничения, получим, что областью допустимых значений данной функции является промежуток \((0;1)\cup (1;+\infty)\)

Далее обратим внимание на множители в числителе и знаменателе.
1. Множитель \(log_3(5x)\), согласно методу рационализации, можно заменить равносильной функцией \((3-1)(5x-1)=2(5x-1)\).
2. Множитель \(log_4(x)\), согласно методу рационализации, можно заменить равносильной функцией \((4-1)(x-1)=3(x-1)\).
3. Знаменатель \(|x|-x^2\) можно представить в виде \(|x|-|x^2|\). Тогда знаменатель также можно заменить равносильной функцией \((x-x^2)\)

Подставим получившееся выражение в неравенство:

\(\frac{log_3(5x)*log_4(x)}{|x|-x^2}\geq 0\)
\((\frac{2(5x-1)*3(x-1)}{x-x^2}\geq 0\)
\((\frac{6(5x-1)(x-1)}{x-x^2}\geq 0\)

В знаменателе \(x-x^2\) вынесем общий множитель за скобки:

\(\frac{6(5x-1)(x-1)}{x(x-1)}\geq 0\)

Осталось воспользоваться методом интервалов: найдем нули числителя и знаменателя, поставим их на числовую прямую и определим знаки получившихся интервалов.
1) \(5x-1=0\)
\(5x=1\)
\(x_1=\frac{1}{5}\)

2) \(x-1=0\)
\(x_2=1\)

3) \(x_3\neq 0\)

Выделим те интервалы, на которых функция принимает неотрицательные значения \((\frac{6(5x-1)(x-1)}{x(x-1)}\geq 0)\):

Неравенство нестрогое (знак \(\geq \) ), поэтому нули числителя выделим не выколотыми точками, а нули знаменателя – выколотыми. Получили интервалы \((-\infty ;0]\cup [\frac{1}{5};1)\cup(1;+\infty)\). 
При этом ОДЗ функции: \((0;1)\cup(1;+\infty)\). Тогда с учетом ОДЗ, решением неравенства будут два промежутка: \([\frac{1}{5};1)\cup(1;+\infty)\).

Ответ: \([\frac{1}{5};1)\cup(1;+\infty)\)

Чтобы еще больше закрепить метод рационализации, разберем еще одно задание ЕГЭ, на этот раз со степенью и логарифмом.

Решим пример задания №15 из ЕГЭ по профильной математике

Задание. Решите неравенство \((10^{x^2-3x-4}-1)*log_{0,5}(4x^2)\geq 0\).

Решение.
Начнем, как обычно, с ОДЗ. Ограничения здесь накладываются только на логарифм \(log_{0,5}(4x^2)\), аргумент которого должен быть больше \(0\):

\(4x^2>0\Rightarrow x\neq 0\)

В таком случае областью допустимых значений функции \((10^{x^2-3x-4}-1)*log_{0,5}(4x^2)\) является промежуток \((-\infty;0)\cup (0;+\infty)\).

Теперь рассмотрим подробнее каждый множитель неравенства:

1)Множитель \((10^{x^2-3x-4}-1)\) по методу рационализации можно заменить равносильной функцией \((10-1)(x^2-3x-4)=9(x^2-3x-4)\).
Множитель \((x^2-3x-4)\) здесь можно разложить на множители как квадратный трехчлен:

\(x^2-3x-4=(x-4)(x+1)\)

Тогда получим: \(9(x^2-3x-4)=9(x-4)(x+1)\)

2) Множитель \(log_{0,5}(4x^2)\) также можно заменить равносильной функцией \((0,5-1)(4x^2-1)=-0,5(4x^2-1)\). Множитель \(4x^2-1\) здесь можно разложить на множители, воспользовавшись формулой разности квадратов \((a^2-b^2=(a-b)(a+b))\):

\(4x^2-1=(2x)^2-1^2=(2x-1)(2x+1)\)

Тогда \(-0,5(4x^2-1)=-0,5(2x-1)(2x+1)\)

Подставим полученные выражение в наше неравенство:

\((10^{x^2-3x-4}-1)*log_{0,5}(4x^2)\geq 0\)
\(9(x-4)(x+1)*(-0,5)*(2x-1)(2x+1)\geq 0\)
\(-4,5*(x-4)(x+1)(2x-1)(2x+1)\geq 0\)

Далее воспользуемся методом интервалов. Найдем нули каждого множителя:

1) \(x-4=0\)
\(x_1=4\)

2) \(x+1=0\)
\(x_2=-1\)

3) \(2x-1=0\)
\(2x=1\)
\(x_3=0,5\)

4) \(2x+1=0\)
\(2x=-1\)
\(x_4=-0,5\)

Полученные нули поставим на числовую прямую. Неравенство нестрогое (знак ), поэтому все точки будут не выколотыми. Обозначим знаки полученных интервалов и выделим те из них, на которых функция принимает неотрицательные значения \((-4,5*(x-4)(x+1)(2x-1)(2x+1)\geq 0)\):

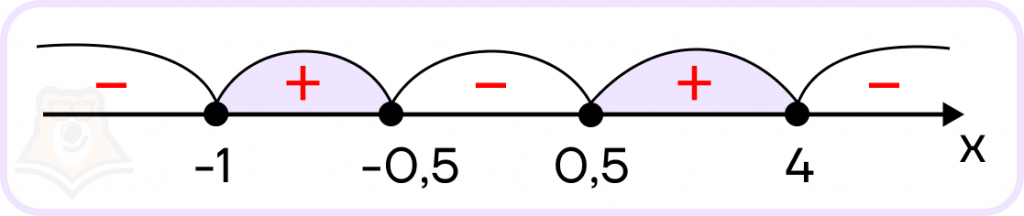
Получили два промежутка: \([-1;-0,5]\cup [0,5;4]\), которые полностью удовлетворяют ОДЗ: \((-\infty;0)\cup(0;+\infty)\). 

Ответ: \([-1;-0,5]\cup [0,5;4]\)

Удивительная вещь все-таки – метод рационализации. Несмотря на то что его нельзя применять ко всем неравенствам, часто он может сильно помочь. Теперь и мы можем без проблем пользоваться этой волшебной палочкой, а значит – цель данной статьи достигнута.

Предлагаем не останавливаться на достигнутом и сразу перейти к статье «Тригонометрические неравенства», где речь пойдет о еще одном, немаловажном, виде неравенств.

Термины

Неотрицательные числа – все положительные числа и 0.

Неположительные числа – все отрицательные числа и 0.

Фактчек

• Метод рационализации – это метод решения неравенств, который позволяет заменить функцию более «удобной» равносильной функцией, знак которой определяется так же.
• Метод рационализации применяется во многих видах неравенств, основные из них – логарифмические, показательные, показательно-степенные, иррациональные неравенства а также неравенства, содержащие знак модуля.
• Метод рационализации можно применять не только для всей функции, но и для отдельных ее множителей.

Проверь себя

Задание 1.
Метод рационализации применяется для:

1. решения уравнений;
2. преобразования числовых выражений;
3. решения неравенств;
4. преобразования алгебраических выражений.

Задание 2.
Согласно методу рационализации, функцию \(log_ba\) в неравенстве можно заменить на равносильную функцию:

1. \((a-1)(b-1)\);
2. \((a-1)b\);
3. \(a(b-1)\);
4. \(ab\).

Задание 3.
Согласно методу рационализации, функцию \(a^b-a^c\) в неравенстве можно заменить на равносильную функцию:

1. \(a(b-c)\);
2. \((a-1)(b-1)\);
3. \(ab-ac\);
4. \((a-1)(b-c)\).

Задание 4.
Согласно методу рационализации, функцию \(\sqrt{a}-\sqrt{b}\) в неравенстве можно заменить на равносильную функцию:

1. \(a-b\);
2. \(b-a\);
3. \(\sqrt{a-b}\);
4. \(\sqrt{b-a}\).

Ответы: 1. – 3; 2. – 1; 3. – 4; 4. – 1