Графический метод в задачах с параметром

На этой странице вы узнаете

• Где найти параметры в спорте? 
• Лайфхак: как учесть все варианты расположения прямой? 
• Как рисовать окружности с нецелым радиусом? 

О человеке можно многое сказать по его внешнему виду, поведению, речи. Существует вид арт-терапии, в котором по рисункам можно понять характер человека. А если мы скажем, что по графику можно узнать абсолютно все о функции?

Графический метод в решении задач с параметром

Решая задачи с параметрами, можно пойти двумя разными путями:

• Мы можем проанализировать функцию, понять ее поведение, и на основании этих выводов найти значения параметров. 
• Можно построить график функции, и, опираясь на него, решить задачу. 

Чтобы использовать графический метод в решении задач с параметром, необходимо свободно ориентироваться в «Основных элементарных функциях» и их свойствах. 

Немного освежим в памяти линейную функцию. На графике это прямая, которая задается уравнением y = kx + b, где k — коэффициент наклона функции, а b отвечает за ее смещение вдоль оси у. 

Могут встречаться задания, в которых параметр стоит вместо коэффициентов прямой. Как быть с такими заданиями?

Рассмотрим уравнение, в котором вместо коэффициента b стоит параметр а. Мы получим уравнение y = kx + a. Как оно будет выглядеть на графике? 

Это уравнение будет задавать семейство прямых с одинаковым углом наклона, но смещенных по вертикали. 

Например, если k = 3, то получим следующий график. 

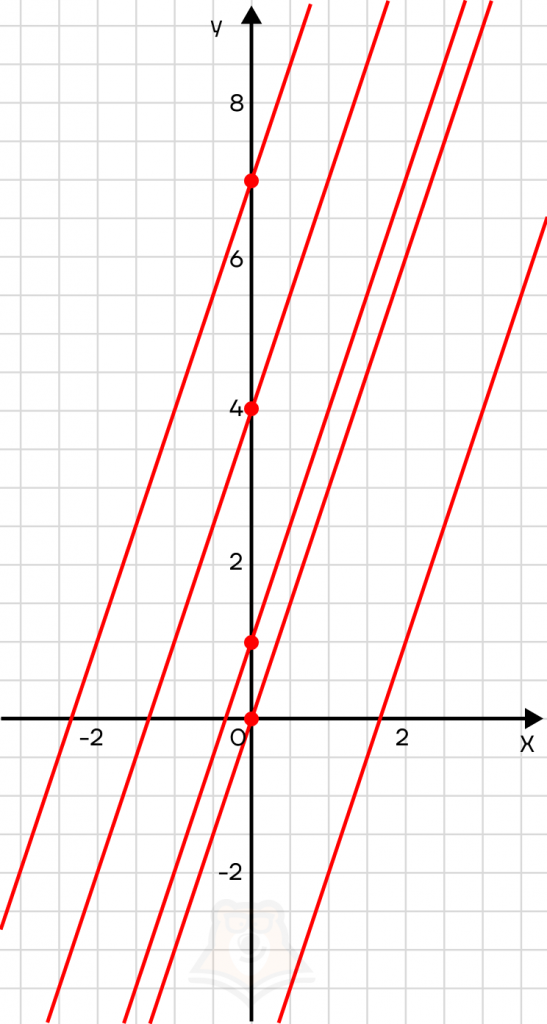
На самом деле, прямых будет намного больше, а именно бесконечное множество. Значение параметра а  будет влиять на точку, в которой прямая пересекает ось у, при этом параметр может принять любое значение. 

Рассмотрим уравнение, в котором параметр будет стоять вместо коэффициента угла наклона. Мы получим уравнение y = ax + b. Поскольку коэффициент b может принимать только одно значение, то прямые не будут смещаться относительно оси у. Но будут менять угол своего наклона. 

На графике они примут вид «пучка», то есть из одной точки будет выходить множество лучей. Пусть b = 0, тогда получаем следующий график. 

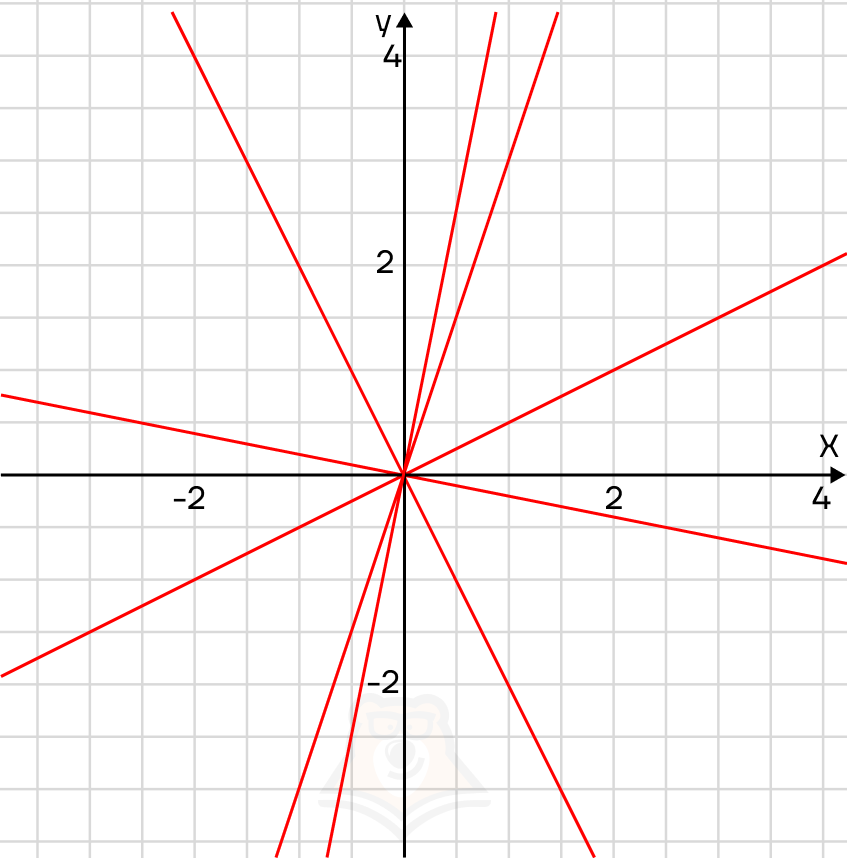
Еще немного усложним задачу. Что, если параметр будет стоять вместо обоих коэффициентов? Получаем уравнение y = ax + a. 

В предыдущих случаях мы знали либо коэффициент наклона, либо точку пересечения графиков с осью у. Но как быть, когда мы не знаем ничего из этого? 

Необходимо понять, вокруг какой точки вращаются все прямые данного семейства. Для этого достаточно найти, при каких значениях х множитель перед параметром равен 0. 

Немного преобразуем уравнение. Вынесем общий множитель за скобки:

y = ax + a \(\Rightarrow\) y = a(x + 1). 

Множитель перед параметром будет равен х + 1, значит, должно выполняться уравнение:

x + 1 = 0 \(\Rightarrow\) x = -1. 

Найдем значение y при данном значении х:

y = a(-1 + 1) = a * 0 = 0

При x = -1 и y = 0, все прямые этого семейства будут вращаться вокруг точки (-1; 0).

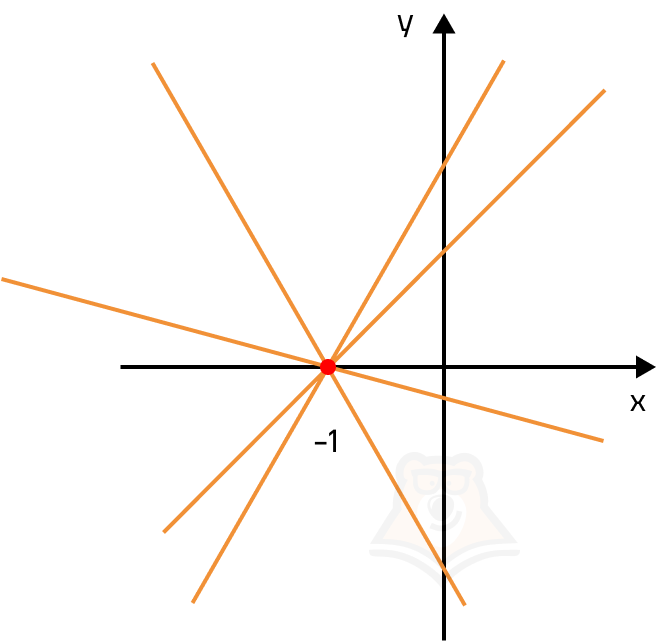
Семейство вращающихся прямых, проходящих через точку (–1; 0)

Где найти параметры в спорте? В математике, как и в жизни, есть вещи, на которые мы можем повлиять своим поведением, и есть независящие от нас обстоятельства. Параметры задаем мы. В спорте это: количество и интенсивность тренировок, регулярность их посещения, здоровый сон и пища — все, что определяется только нашей силой воли и дисциплиной. А переменные — это то, на что мы повлиять не можем. Уровень подготовки соперников на соревнованиях, компетентность тренера, отсутствие простуды — это данность, которую нельзя изменить по своему желанию.  В графиках функций все точно так же: параметры меняют график, двигают его вдоль оси или поворачивают, а переменные задают точные точки, которые невозможно изменить.

Вспомним, как прямые могут располагаться относительно друг друга:

• прямые будут параллельны;
• прямые будут перпендикулярны;
• прямые будут пересекаться под углом. 

Нам интересны первые два случая. Параллельность и перпендикулярность прямых можно задать с помощью коэффициента угла наклона. 

Представим, что на берегу рыбачат два человека с абсолютно одинаковыми удочками. Чтобы не держать их постоянно в руках, они поставили удочки на одинаковые рогатки. Что можно сказать про удочки в этом случае? 

Удочки будут иметь одинаковый угол наклона относительно земли. Если бы мы захотели их задать с помощью уравнения, то коэффициенты k были бы равны. 

Если нам даны прямые y = k₁x + b₁ и y = k₂x + b₂, то они будут параллельны при условии: 

k₁ = k₂

Если есть условие параллельности, то есть и условие перпендикулярности. 

Рассмотрим на графике прямые y = x и y = -x. Они как раз будут перпендикулярны. Угол наклона прямой y = x равен 45°, угол наклона прямой y = -x равен 135°, тогда угол между прямыми равен  135°-45°=90°. 

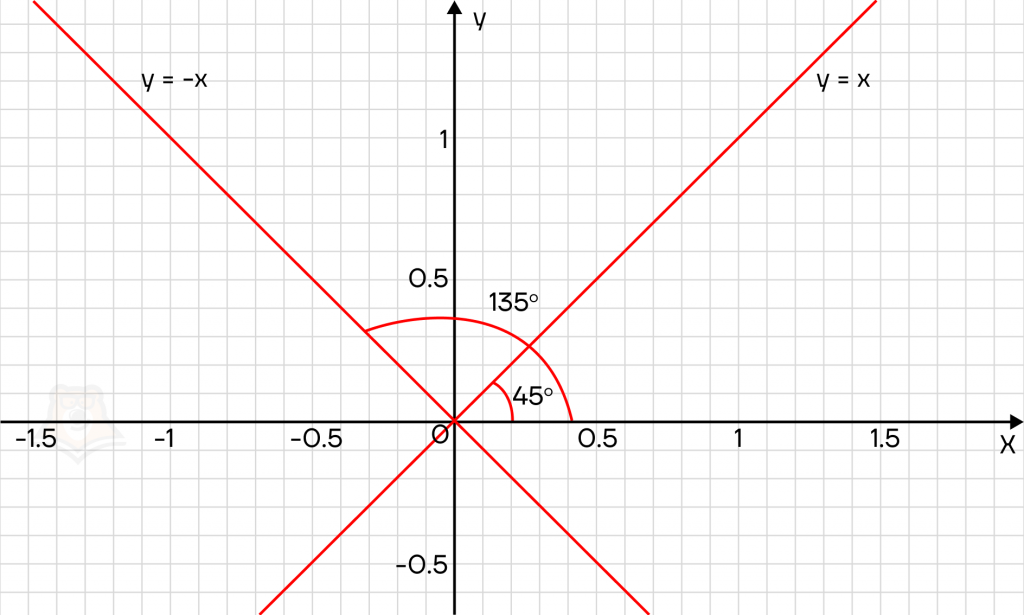
Обратим внимание на коэффициенты уравнений перед x. Их произведение равно –1. Это и есть условие перпендикулярности прямых. 

k₁ * k₂ = -1

Пример 1. Найдите все значения параметра а, при каждом из которых система уравнений имеет ровно три различных решения. 

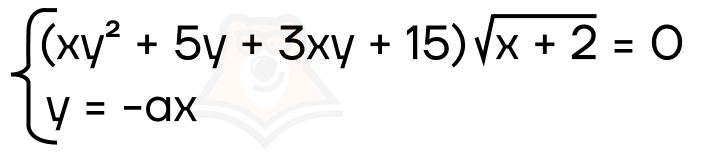
Решение.
Шаг 1. Система подсказывает нам ограничение: подкоренное выражение не может быть отрицательным, так как корня четной степени из отрицательных чисел не существует. 

Отсюда:

x+2 >= 0
x >= -2

Как показать это неравенство графически? Необходимо задать полуплоскость. Это неравенство задает все точки, которые лежат правее линии x = -2. Вся полученная область называется полуплоскостью. 

На графике полуплоскость будет выглядеть следующим образом: 

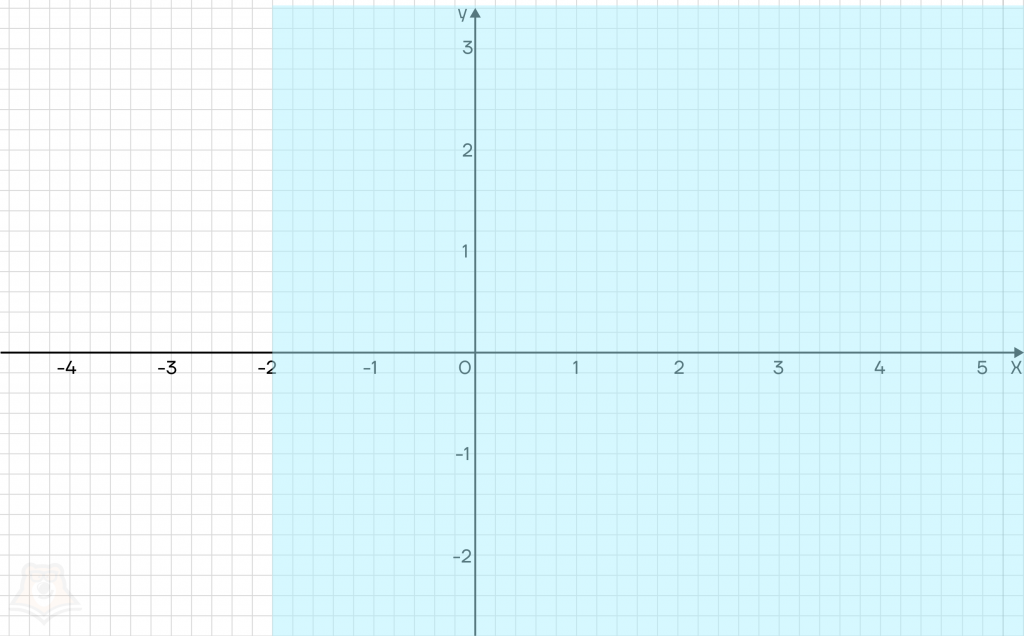
Все точки, которые попадут в голубую зону, будут удовлетворять системе. Но если точка окажется в белой зоне, она уже точно не сможет быть решением системы. 

Шаг 2. Рассмотрим первое уравнение системы и преобразуем его. 

\((xy^2 + 5y + 3xy + 15)\sqrt{x + 2} = 0\)

Если произведение множителей равно 0, то каждый множитель равен 0. Упростим выражение в скобках.

\(xy^2 + 5y + 3xy + 15 =0\)
\(y(xy + 5) + 3(xy + 5)=0\)
\((xy + 5)(y + 3)=0\)

\(xy + 5=0\)
\(xy = -5\)
\(y = -\frac{5}{x}\) — гипербола. 
\(y + 3=0\)
\(y = -3\) — прямая, параллельная оси х. 

Рассмотрим корень. 
\(\sqrt{x + 2} = 0\)
\(x = -2\) — прямая, параллельная оси у. 

Построим три графика, которые получились при решении первого уравнения. 

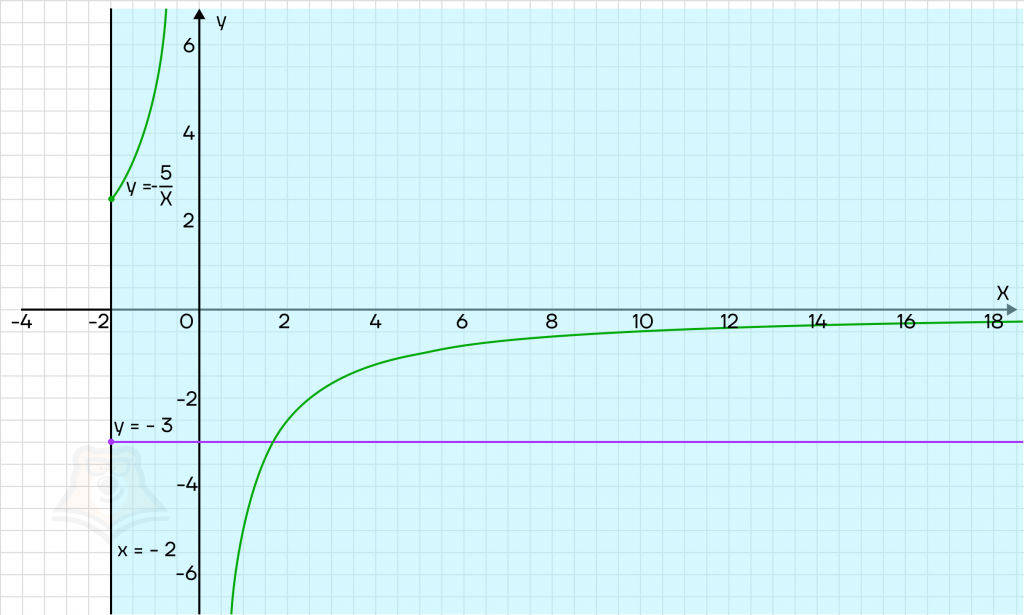
Мы обрезали части гиперболы и прямой, которые не попадают в синюю область. Поскольку уравнение системы не может существовать в белой области, то и графики в ней чертить нельзя. 

Шаг 3. Разберем второе уравнение системы y = -ax. Это семейство прямых, где коэффициент b отсутствует, то есть b = 0. Значит, эти прямые будут пересекать ось у в точке 0. 

Поскольку у = 0 получаем уравнение 0 = -ax \(\Rightarrow\) x = 0. Все прямые семейства будут проходить через точку (0; 0). 

Шаг 4. Как определить с помощью графика, сколько решений будет в системе? Решений будет ровно столько же, сколько будет общих точек у двух уравнений. 

То есть три решения возможны, когда прямая y = -ax пересечет график \((xy^2 + 5y + 3xy + 15)\sqrt{x + 2} = 0\) трижды. 

Начертим семейство прямых на графике. На графике достаточно изобразить только те прямые, которые иллюстрируют изменение количества решений. Рисовать бесконечное множество прямых не нужно.

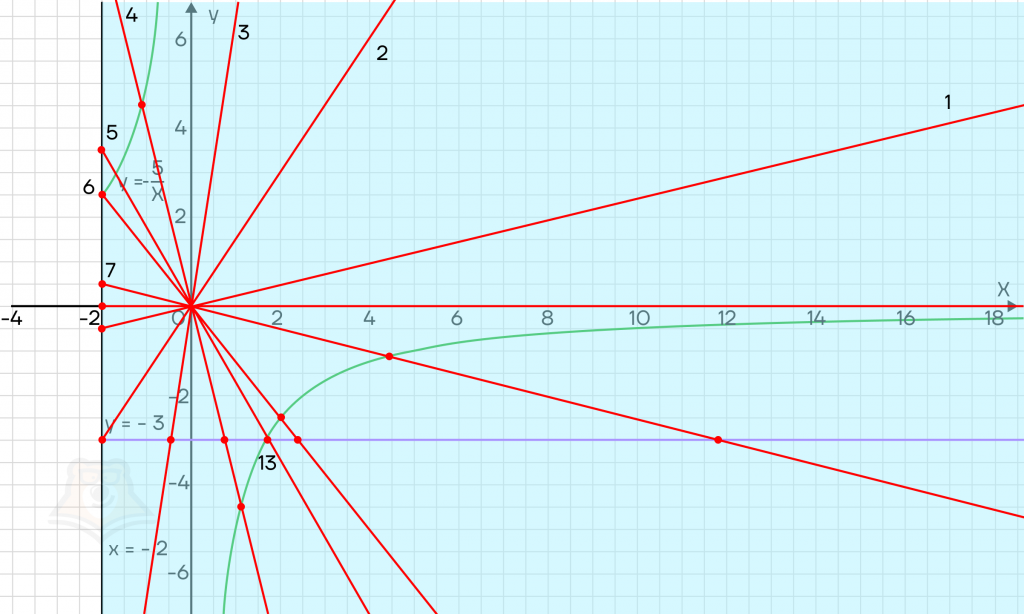
Рассмотрим каждую из прямых:

• Прямая 1 имеет с графиком одну общую точку, то есть решение будет только одно.
• Прямая 2 имеет с графиком только одну общую точку с координатами (-2; -3). Решение будет одно.
• Прямая 3 имеет с графиком две общие точки: пересекает прямые y = -3 и x = -2. Вторая точка пересечения лежит за пределами чертежа, поэтому ее не видно. 
• Прямая 4 пересечет график четыре раза: прямые y = -3, x = -2 и дважды пересечет гиперболу. 
• Прямая 5 пересечет график трижды: прямую x = -2, гиперболу и точку В. Точка В является точкой пересечение гиперболы и прямой y = -3. 
• Прямая 6 пересечет график трижды: точку А, гиперболу и прямую y = -3. Точка А является точкой пересечения гиперболы и прямой x = -2. 
• Прямая 7 пересечет график трижды.
• Прямая 8 пересечет график только один раз.

По условию необходимо, чтобы система имела три решения. Получается, что подходят все прямые, которые лежат между прямыми 6 и 8, а также прямая 5. 

5. Найдем значения параметра для каждой из отобранных прямых. 

Прямая 5 проходит через точку В. Определим ее координаты. 

Поскольку это точка пересечения \(y = -\frac{5}{x}\) и y = -3, подставим значение y =-3 в первое уравнение:

\(-3 = -\frac{5}{x}\)
\(3x = 5\)
\(x = \frac{5}{3}\). 

Подставим координаты точки в уравнение с параметром y = -ax. 

\(-3 = -a * \frac{5}{3}\)
\(a = 3 * \frac{3}{5} = \frac{9}{5} = 1,8\)

Прямая 6 проходит через точку А, то есть точку пересечения \(y = -\frac{5}{x}\) и x = -2. Подставим х в первое уравнение:

\(y = -\frac{5}{-2} = 2,5\)

Подставим координаты точки в уравнении с параметром y = -ax. 

2,5 = -a * (-2)
-a = -1,25
a = 1,25

Прямая 8 имеет уравнение у = 0 и проходит через точку (– 2; 0). 
Подставим координаты точки в уравнении с параметром y=-ax.

0 = -a * (-2)
a = 0.

Поскольку прямая 8 имеет одно решение, ее включать в итоговый промежуток нельзя. 

6. Получаем, что система будет иметь три решения при \(a \in (0; 1,25) \cup {1,8}\)

Ответ: \(a \in (0; 1,25) \cup {1,8}\)

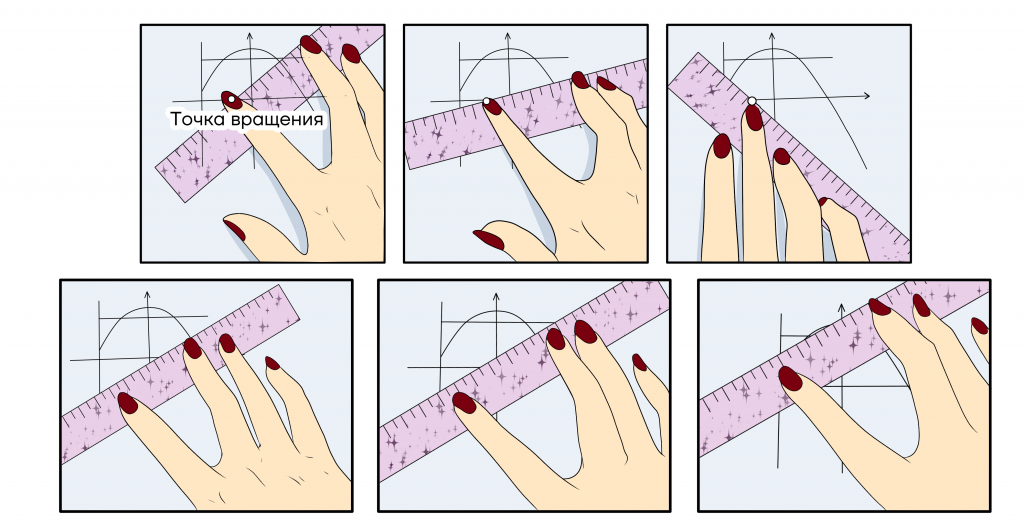
Лайфхак: как учесть все варианты расположения прямой? Поскольку вариантов расположения прямой бесконечное множество, нужно решить задачу и не запутаться. На помощь приходит линейка.  Для начала нужно начертить графики всех функций, которые не имеют параметра, а следовательно, их графики меняться не будут. Если параметр стоит вместо коэффициента k, то есть прямые вращаются вокруг точки — прикладываем линейку к этой точке и вращаем ее, зажимая пальцем. Точки, в которых линейка пересечет график функции, будут решениями системы. Если параметр стоит вместо коэффициента b, то есть прямые двигаются вдоль оси у, — находим их наклон и фиксируем с таким же наклоном линейку. Теперь ее можно двигать вдоль оси и искать количество решений.

Уравнение окружности 

Окружность встречается в задачах с параметром намного чаще, чем может показаться на первый взгляд. Каким уравнением она задается? 

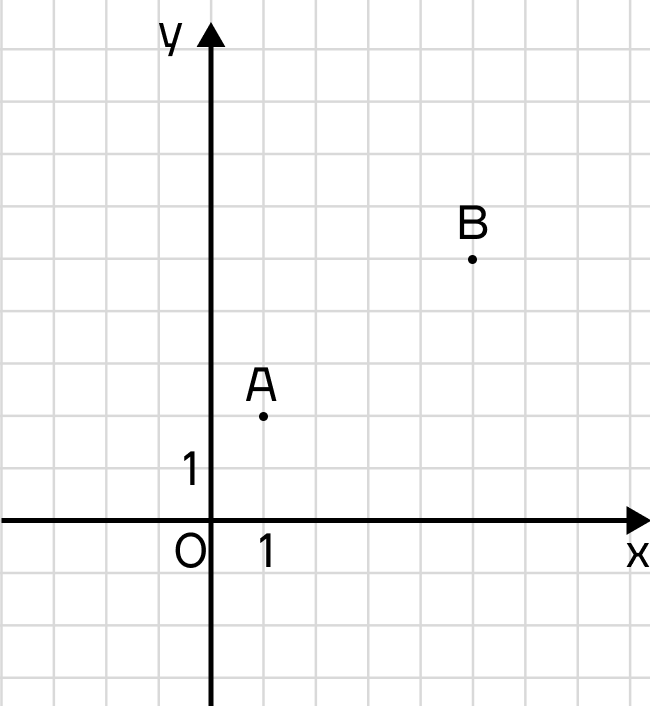
Будем подходить к уравнению окружности последовательно. Для начала попробуем найти расстояние между двумя точками на координатной плоскости. Пусть точка А имеет координаты (х₁; у₁), а точка В координаты (х₂; у₂). 

Как найти длину прямой АВ? Построим прямоугольный треугольник АВС и найдем длину АВ по теореме Пифагора. Подробнее про теорему Пифагора можно прочесть в статье «Равнобедренный, равносторонний и прямоугольный треугольник». 

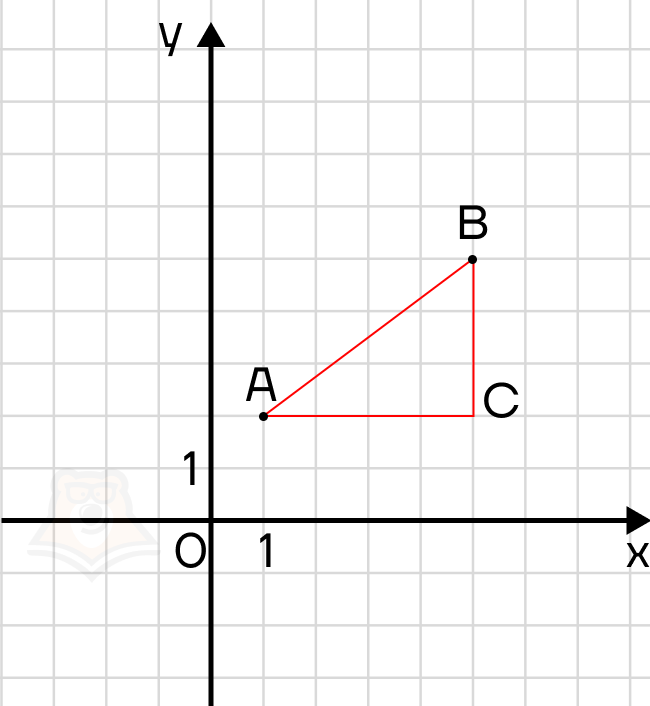
По теореме Пифагора получаем:

AB² = AC² + BC²

Заметим, что AC = x₂ — x₁, BC = y₂ — y₁, следовательно,

AB² = (x₂ — x₁)² + (y₂ — y₁)²

Пусть расстояние между точками будет равно d. Значит, его можно найти по следующей формуле: 

\(d = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}\)

Но при чем здесь окружность? Вспомним, что окружность — это кривая, все точки которой равноудалены от центра. Если мы закрепим точку А, а точку В начнем вращать вокруг — получится окружность. 

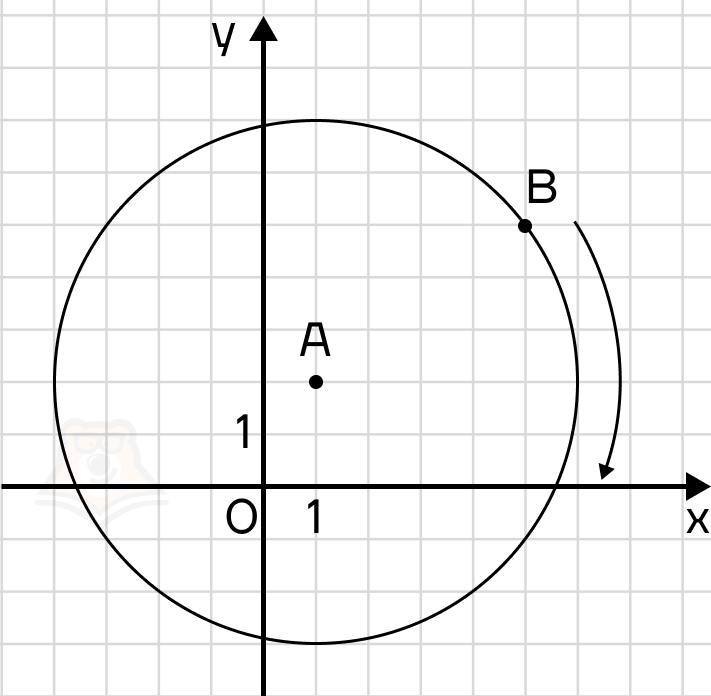
Все ее точки будут удалены от центра А на расстояние d. Это расстояние будет радиусом окружности. 

Таким образом, мы можем представить радиус окружности как расстояние между точками: 

\(r = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}\)

Если возвести выражение в квадрат, мы получим уравнение окружности. 

(x — x₀)² + (y — y₀)² = r²

В этом уравнении r — радиус, а (х₀; у₀) — центр окружности. 

Как рисовать окружности с нецелым радиусом? В уравнении окружности не всегда дан целый радиус. Например, в уравнении (x — 3)2 + (y — 5)2 = 34 радиус будет равен \(\sqrt{34}\). Точно отложить его по клеточкам не получится.  Воспользуемся прямоугольными треугольниками. Заметим, что 32 + 52 = 9 + 25 = 34. Тогда от центра окружности достаточно отложить несколько прямоугольных треугольников с катетами 3 и 5, после чего соединить полученные точки окружностью.

Также при решении задач может пригодиться формула расстояния от точки до прямой. 

Возьмем прямую l, которую зададим уравнением ax + by + c = 0. Это один из способов задать прямую с помощью уравнения. Если перенести слагаемые в другую сторону уравнения и разделить его на b, то получится обычное уравнение прямой. 

Точку зададим как А(х₀, у₀). 

Расстояние от точки А до прямой будет \(\rho\)(A; l)

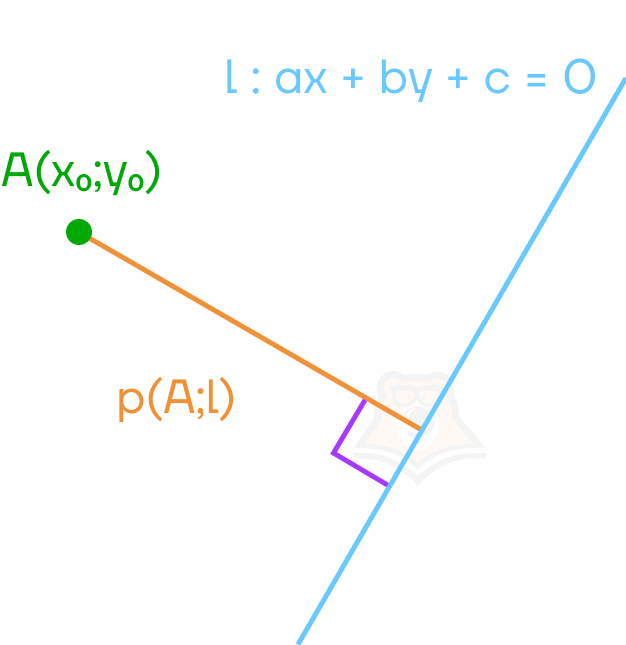
Чтобы найти расстояние, достаточно будет воспользоваться следующей формулой. 

\(\rho (A; l) = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}\)

На экзамене вам может попасться задание с параметром, которое будет проще и быстрее решить графическим способом.

Обратите внимание: если вы видите в одном из уравнений системы, что оно задает окружность, то с большей вероятностью это задание будет легче решить графическим способом.

Теперь давайте попробуем применить эти знания на практике при решении заданий с параметром.

Пример 2. Найдите все значения параметра а, при каждом из которых система имеет единственное решение. 

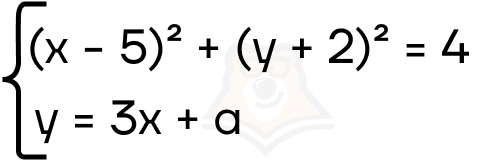
Решение. 1. Первое уравнение системы задает окружность. Ее центр будет лежать в точке (5; -2), а радиус будет равен 2. 

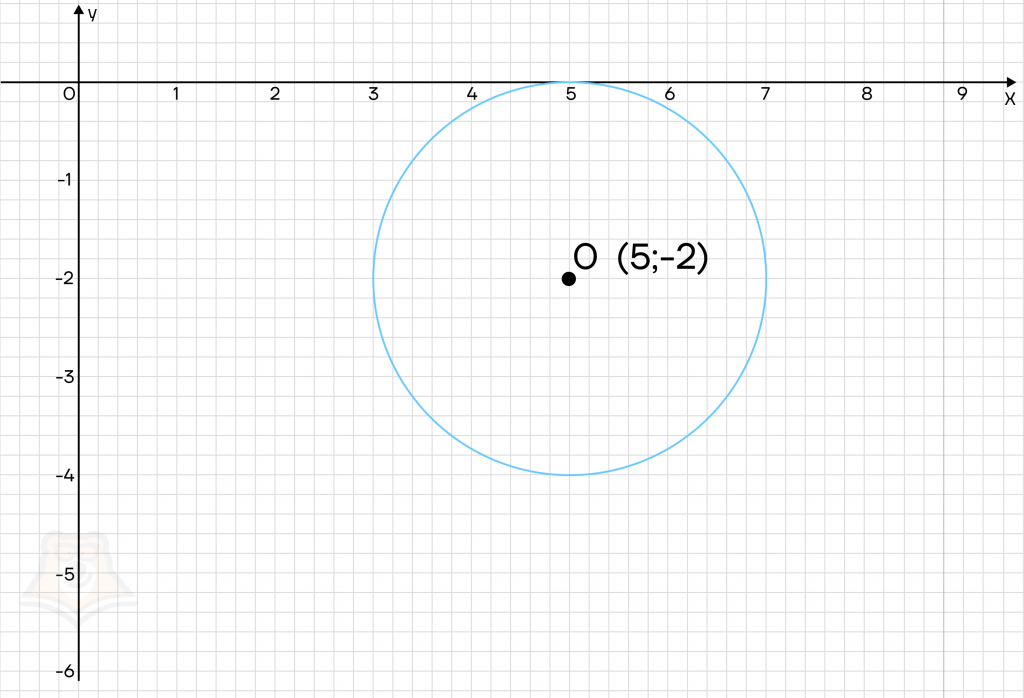
Второе уравнение системы задает семейство прямых y = 3x + a с коэффициентом угла наклона k = 3. Параметр а будет отвечать за сдвиг прямой вдоль оси у. 

2. Система будет иметь единственное решение только в том случае, если прямая касается окружности. Касание может произойти в двух случаях:

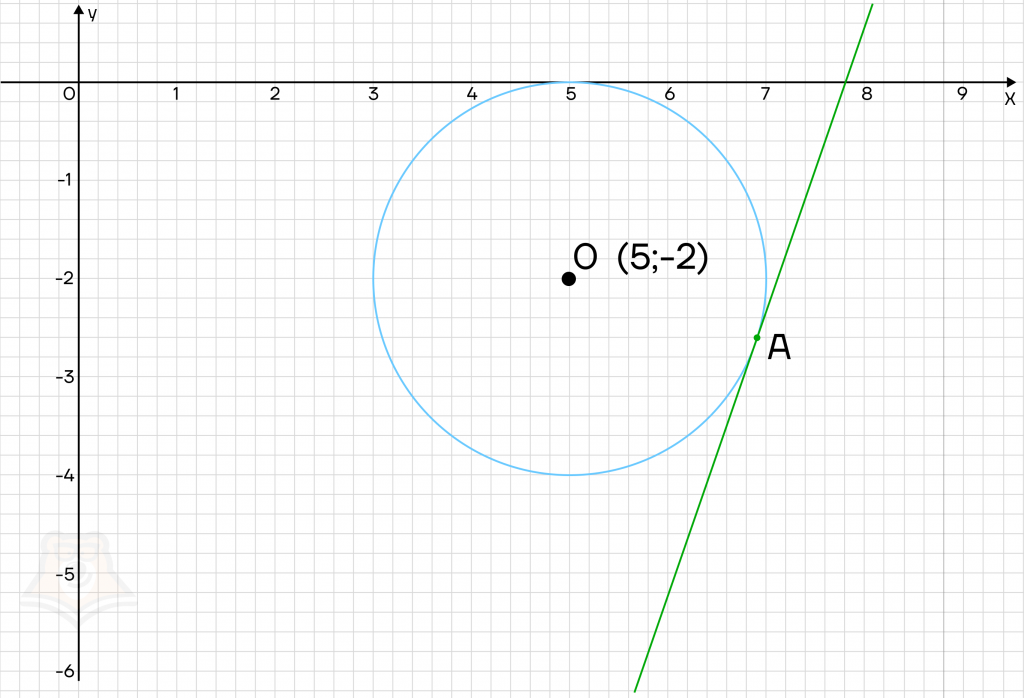
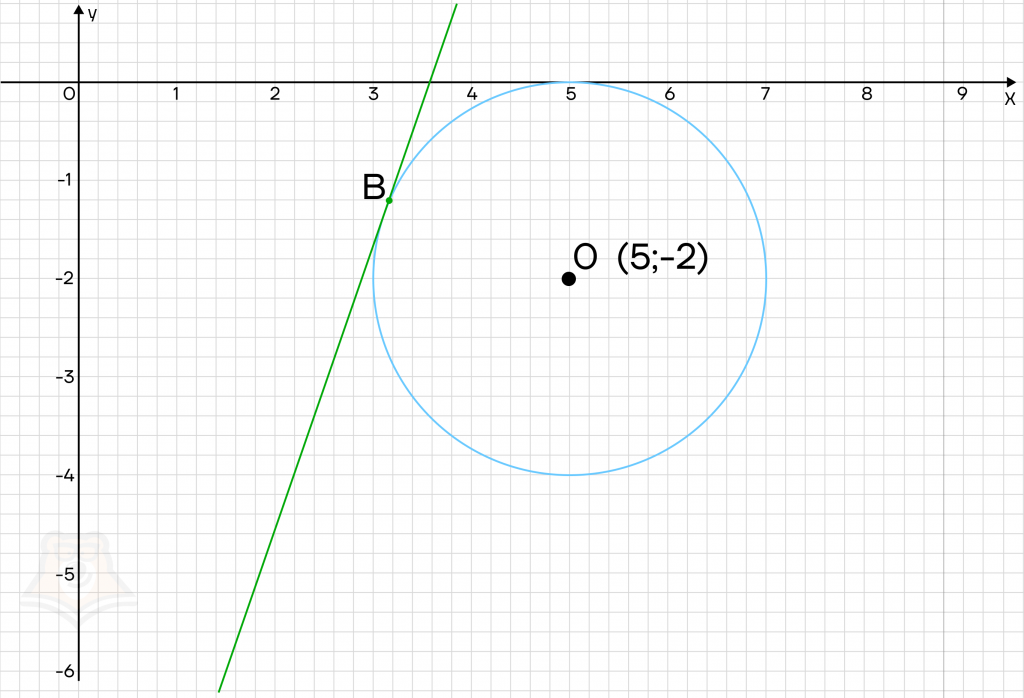
3. Радиусы, проведенные к точке касания, перпендикулярны касательным к окружностям. Это будет расстояние от центра окружности до касательных. 

Центр окружности лежит в точке О(5; -2), а касательные заданы прямыми y = 3x + a \(\Rightarrow\) -y + 3x + a = 0. 

Воспользуемся формулой расстояния от точки до прямой: 

\(\rho (O; l) = \frac{|3 * 5 + (-1) * (-2) + a|}{\sqrt{3^2 + (-1)^2}}\)

Поскольку расстояние равно радиусу, имеем:

\(2 = \frac{|15 + 2 + a|}{\sqrt{10}}\)
\(|17 + a| = 2 \sqrt{10}\)

4. Раскроем модуль двумя способами. Подробнее про уравнения с модулем можно прочесть в статье «Модуль». 

Получаем совокупность:

Следовательно, \(a = 2 \sqrt{10} — 17\) — для прямой, проходящей через точку В, \(a = -2 \sqrt{10} — 17\) — для прямой, проходящей через точку А. 

Ответ: \(a = 2 \sqrt{10} — 17, a = -2 \sqrt{10} — 17\).

На этом наша статья подошла к концу, пришло время подводить итоги.

Сегодня мы узнали:
— как определить, каким способом легче решить систему уравнений с параметром;
— как ведет себя линейная функция, если один из коэффициентов выступает в виде параметра;
— как графически решать задания с параметром из второй части экзамена по профильной математике №17.
— Мы уже вместе немного попрактиковались в решении заданий. Но для закрепления такой непростой темы предлагаем вам самостоятельно продолжить практику в рубрике «Проверь себя».

Фактчек

• Прямая задается функцией y = kx + b, где k — коэффициент угла наклона прямой, b — ее сдвиг вдоль оси у. Если заменить один из коэффициентов на параметр, получится семейство прямых. 
• Если вместо обоих коэффициентов стоит параметр, то необходимо найти точку, через которую пройдут все прямые семейства. Для этого необходимо найти, при каких значениях х множитель перед параметром равен 0. 
• Если прямые параллельны, коэффициенты их наклона равны. Если прямые перпендикулярны, выполняется равенство k₁ * k₂ = -1. 
• Чтобы найти расстояние между точками, достаточно воспользоваться формулой \(d = \sqrt{(x_2 — x_1)^2 + (y_2 — y_1)^2}\).
• Чтобы найти расстояние между точкой и прямой, достаточно воспользоваться формулой \(\rho (A; l) = \frac{|a * x_0 + b * y_0 + c|}{\sqrt{a^2 + b^2}}\).
• Окружность задается уравнением (x — x₀)² + (y — y₀)² = r², где r — радиус окружности (х₀; у₀) — ее центр.

Проверь себя

Задание 1. 
За что отвечает коэффициент k в уравнении прямой y = kx + b?

1. угол наклона прямой
2. точка ее пересечения с осью х
3. точка ее пересечения с осью у
4. длина прямой 

Задание 2. 
За что отвечает коэффициент b в уравнении прямой y = kx + b?

1. угол наклона прямой
2. точка ее пересечения с осью х
3. точка ее пересечения с осью у
4. длина прямой 

Задание 3. 
Какое равенство выполняется, если прямые перпендикулярны?

1. k₁ * k₂ = 1
2. k₁ * k₂ = -1
3. k₁ * k₂ = 0
4. b₁ * b₂ = -1

Задание 4. 
Каким уравнением задается окружность?

1. y = kx + b
2. x + y = r
3. r² = x² — y²
4. (x — x₀)² + (y — y₀)² = r²

Задание 5. 
Чему равен радиус в окружности, заданной уравнением (x — 3)² + (y + 7)² = 16?

1. 3
2. –7
3. 16
4. 4 

Ответы: 1. — 1; 2. — 3; 3. — 2; 4. — 4; 5. — 4.