Основы математической статистики
На этой странице вы узнаете
- 9 из 10 стоматологов рекомендуют: как реклама использует статистику в своих целях?
- Что модно в математике?
- В чем секрет идеальной презентации?
Удивительный факт: на Земле больше деревьев, чем звезд в нашей галактике. Деревьев насчитывается примерно 3 триллиона, а вот звезд всего 400 миллиардов. О том, как в принципе возможно посчитать все деревья на планете, расскажет наша статья.
Основы математической статистики
Еще немного интересных фактов из цифр: население Земли выросло в 22 раза за последнюю тысячу лет.
Люди в среднем проходят 7500 шагов в день. Этого достаточно, чтобы за всю жизнь обойти Землю по экватору 4,5 раза, то есть пройти 180000 км.
Разумеется, эти данные не выявлялись напрямую: никто не ходил по лесам и не считал каждое дерево. И никто не подсчитывал каждого человека на Земле целую тысячу лет назад. Да и не все люди проходят в день 7500 шагов: кто-то больше, а кто-то меньше. Все эти факты возможно было вывести только благодаря статистике.
Статистика — раздел математики, в котором изучаются методы сбора, систематизации, обработки результатов наблюдений для выявления закономерностей.
Простыми словами, с помощью статистики можно сделать вывод, что характерно для той или иной отрасли нашей жизни. Эти выводы не будут на сто процентов соответствовать для каждого человека, но для большинства они будут приближены к правде.
| 9 из 10 стоматологов рекомендуют: как реклама использует статистику в своих целях? В рекламе нередко используют высокие статистические данные. «99% покупателей довольны» или «Четыре из пяти девушек подтвердили результат». Считается, что так покупатель охотнее поверит в пользу продукта. Стоит ли полагаться на такие данные — решать вам, но только после прочтения этой статьи. |

Решим небольшую задачу.
Аня живет недалеко от школы, ей нужно пройти всего 100 метров от подъезда. Саша живет чуть дальше: ей нужно проехать два километра. А Даша живет на другом конце города: каждое утро она ездит по шесть километров. Насколько далеко в среднем живут девочки от школы?
Подобные задачи можно решить, если найти среднее арифметическое.
Среднее арифметическое чисел — это отношение суммы всех данных чисел к их количеству.
Чтобы найти среднее арифметическое чисел, нужно воспользоваться следующей формулой.
m=\frac{a_1+a_2+...+a_n}{n}Поэтому чтобы найти среднее расстояние до школы, нужно сложить все значения расстояния и разделить их на три. Для удобства счета переведем километры в метры: в одном километре 1000 метров.
\frac{100+2000+6000}{3}=\frac{8100}{3}=2700Мы и нашли ответ: в среднем девочки живут на расстоянии 2700 метров от школы. Это не будет справедливо ни для одной из них, но если бы им пришлось каждое утро проходить равное расстояние, то они должны были бы жить именно в таком отдалении от школы.
А если бы девочки жили на равном расстоянии от школы, например, 500 метров, то и их среднее расстояние до школы было бы равно 500 метрам.
Убедимся в этом. Для этого снова найдем среднее арифметическое:
\frac{500+500+500}{3}=\frac{1500}{3}=500Мы вычислили среднее расстояние, на котором живут ученики от школы. Однако мы рассмотрели только трех человек, а в школе наверняка учится намного больше. Поэтому считать наши данные полностью достоверными нельзя.
Для того чтобы сделать данные более достоверными, нужно увеличить выборку. Желательно приблизить ее ко всем ученикам школы.
Выборка — часть всего множества объектов, событий или наблюдений.
В нашем случае все ученики школы, пусть их будет 1000 — это все множество. А 3 человека, которых мы рассмотрели, будут являться частью этого множества, то есть выборкой.
А если мы рассмотрим уже не 3 людей, а 500, то что произойдет? Мы увеличим выборку. Но в математике правильнее будет сказать — «увеличим объем выборки».
Объем выборки — количество элементов, которые попали в выборку.
В первом случае объем нашей выборки был 3, а сейчас уже 500. Это существенная разница.
Поскольку 500 человек — это большой объем выборки, для удобства дальнейших рассуждений сократим до 8 человек.
Представим данные о них в таблице.
| Саша | Аня | Лия | Миша | Леша | Илья | Никита | Даша | |
| Расстояние до школы | 500 м | 1000 м | 5500 м | 1500 м | 250 м | 600 м | 1700 м | 4500 м |
Сейчас мы расставили сведения в произвольном порядке. Немного поменяем колонки местами так, чтобы ребята расположились в порядке увеличения расстояния до школы.
| Леша | Саша | Илья | Аня | Миша | Никита | Даша | Лия | |
| Расстояние до школы | 250 м | 500 м | 600 м | 1000 м | 1500 м | 1700 м | 4500 м | 5500 м |
Можем сделать вывод, что Леша живет ближе всех остальных ребят из выборки, а Лия — дальше всех.
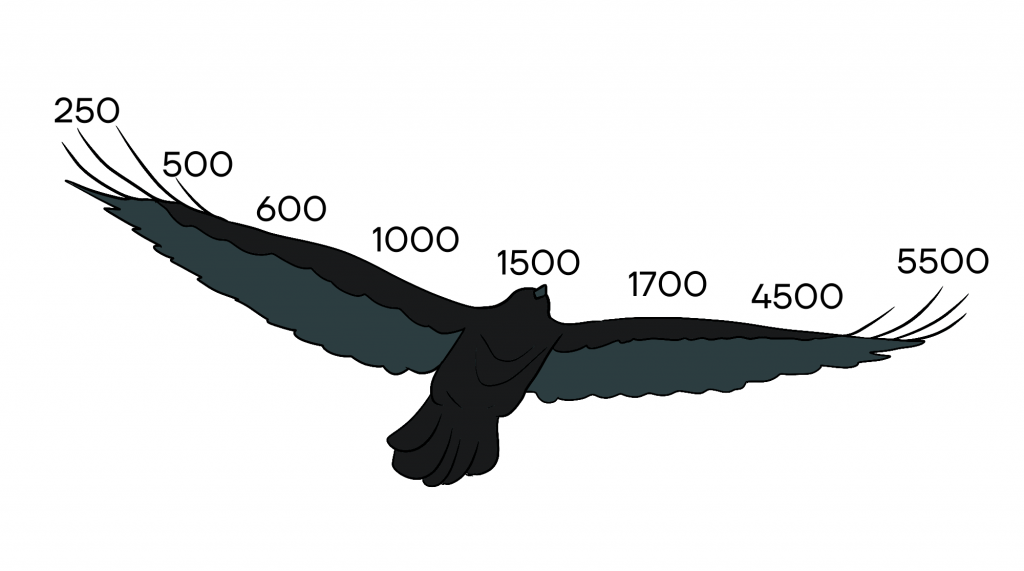
Пока мы составляли таблицу, мимо окна пролетела огромная птица. Удивительно: «Какой у нее размах крыльев!»
Что такое размах?
Для птицы это будет расстояние между крайними точками перьев. Что если мы представим таблицу в виде размаха крыльев? Мы получим такой же размах, но уже математический.
Размах выборки — разность между максимальными и минимальными значениями выборки.
В нашем случае это будет разность между крайними значениями, то есть 5500 — 250 = 5250.
Чтобы узнать, как далеко в среднем живут эти 8 учеников от школы, нужно найти среднее арифметическое.
\frac{250+500+600+1000+1500+1700+4500+5500}{8}=1943,75м.Рассмотрим еще один пример. Восемь девочек покупают одни и те же кексики в столовой, но в разных количествах.
Приведем данные в таблице:
| Аня | Даша | Маша | Полина | Алина | Вика | Алена | Настя | |
| Количество кексиков | 5 | 5 | 7 | 2 | 2 | 2 | 3 | 4 |
Заметим, что некоторые из девочек покупают одно и то же количество кексиков: две девочки покупают по 5 кексиков, и три девочки по два кексика.
Если одно и то же значение в выборке повторяется несколько раз, то количество его повторений будет называться частотой. Например, два кексика покупают с частотой 3. Пять кексиков покупают с частотой 2. А семь кексиков покупают с частотой 1.
При этом сумма частот всегда должна равняться объему выборки.
Составим таблицу частот. Она будет отличаться от предыдущей, поскольку количество купленных кексиков мы запишем в первой строчке без повторений. Во второй строке запишем, частоту покупки кексиков.
| Количество купленных кексиков (без повторений) | 2 | 3 | 4 | 5 | 7 |
| Частота | 3 | 1 | 1 | 2 | 1 |
Если мы выразим частоту в процентах, то найдем относительную частоту выборки.
Относительная частота выборки — отношение частоты к общему числу данных в ряду. Относительная частота обычно выражается в процентах.
Найдем все относительные частоты в нашей таблице. Для этого нам понадобится воспользоваться процентами. Прежде чем приступать к дальнейшим рассуждениям, советуем посмотреть статью «Финансовые задачи. Проценты».
Всего у нас 8 элементов в выборке.
Относительная частота покупки двух кексиков:
\frac{3}{8}*100=37,5\%Относительная частота покупки пяти кексиков:
\frac{2}{8}*100=25\%Относительные частоты покупки семи, трех и четырех кексиков:
\frac{1}{8}*100=12,5\%Составим отдельную таблицу относительных частот. В этой таблице, так же как и в предыдущей, количество купленных кексиков мы записываем без повторений.
| Количество купленных кексиков (без повторений) | 2 | 3 | 4 | 5 | 7 |
| Относительная частота | 37,5% | 12,5% | 12,5% | 25% | 12,5% |
Проведем небольшую проверку и сложим относительные частоты. Если мы правы, их сумма должна равняться 100%.
37,5 + 12,5 + 12,5 + 25 + 12,5 = 100%, значит, все верно.
Мы с легкостью можем найти значение с наибольшей частотой повторений. Это явление тоже учитывается в статистике. Называется оно модой.
Мода — выборочное данное с наибольшей частотой повторений.
Для нашей выборки модой будет число 2.
| Что модно в математике? У слова «мода» несколько значений, и более привычное для нас относится к одежде. Между этими понятиями можно провести параллели. Когда приходит мода на какую-то вещь, она будет встречаться достаточно часто, возможно, чаще, чем другие. В этом сходство с модой в математике, которая присутствует в выборке чаще, чем остальные значения. |
Распределим наших девочек по возрастанию количества купленных ими кексиков. Оказалось, что на прошедшей перемене еще одна девочка по имени Карина купила 2 кексика.
Запишем новую таблицу:
| Полина | Алина | Вика | Карина | Алена | Настя | Аня | Даша | Маша | |
| Количество кексиков | 2 | 2 | 2 | 2 | 3 | 4 | 5 | 5 | 7 |
Посередине нашего упорядоченного списка окажется Алена. Середина списка называется медианой. Если в выборке нечетное количество элементов, то медиану легко найти.
Медиана ряда чисел с нечетным количеством членов — число, которое стоит в середине упорядоченного ряда.
Упорядоченным называют ряд, в котором все члены расставлены в определенном порядке, например, по возрастанию. Такую операцию еще называют ранжированием.
А что делать, если в ряду четное количество членов? Тогда числа посередине просто не будет существовать. В этом случае нужно найти среднее арифметическое двух чисел, которые стоят в середине.
Медиана ряда чисел с четным показателем — среднее арифметическое двух чисел, которые стоят в середине упорядоченного ряда.
Рассмотрим таблицу до того, как кексики купила Карина. У нас будет четное количество девочек.
| Полина | Алина | Вика | Алена | Настя | Аня | Даша | Маша | |
| Количество кексиков | 2 | 2 | 2 | 3 | 4 | 5 | 5 | 7 |
Две девочки, которые стоят в середине, это Алена и Настя. Тогда, чтобы найти медиану этого ряда, необходимо найти среднее арифметическое 3 и 4:
\frac{3+4}{2}=\frac{7}{2}=3,5Диаграммы в статистике
Все рассмотренные ранее выборки достаточно маленькие, поэтому их легко можно было представить в виде таблицы. Но если в выборке тысячи элементов или миллионы? Как быстро и наглядно узнать результат исследований?
Можно использовать диаграммы. Они бывают разных видов.
Данные можно представить в виде обычного графика. Примерно такой же график мы чертим, когда работаем с функциями, но в этом случае переменные будут приближены к жизни, а не абстрактные х и у.
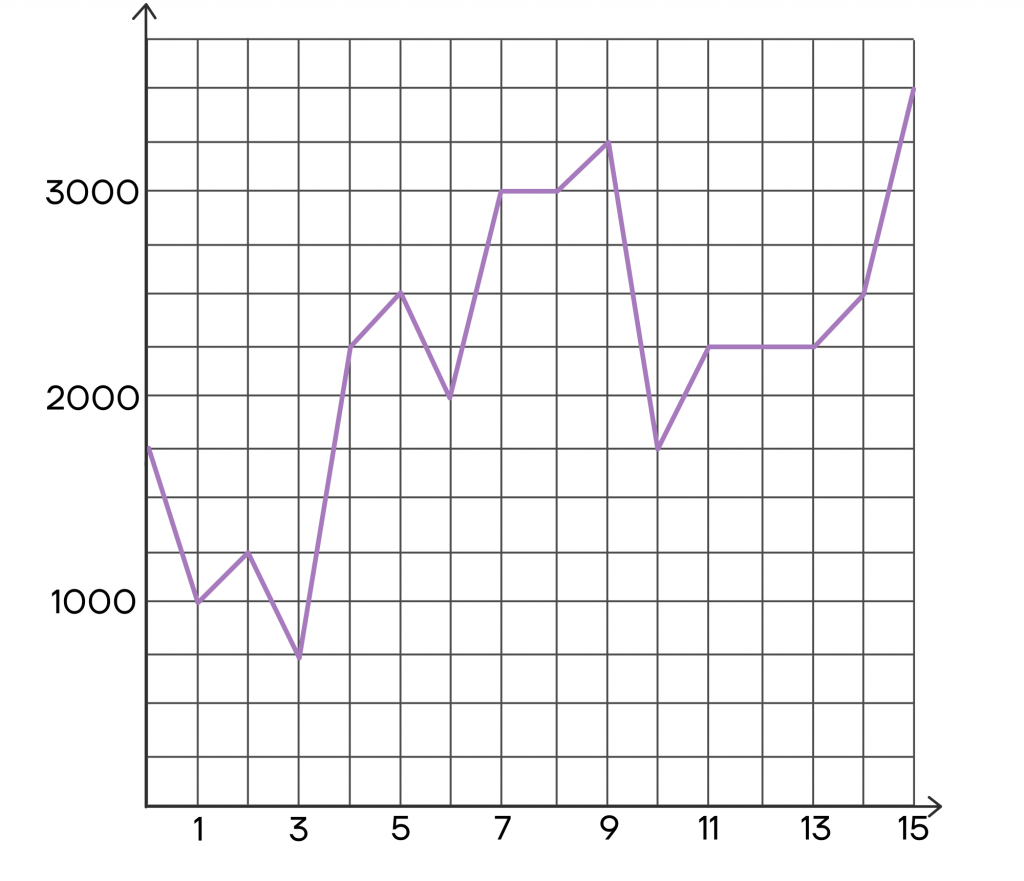
Такой график называют полигоном. Его удобно применять в случаях, когда одна переменная зависит от другой. С помощью полигона можно отобразить изменение температуры в течение дня, месяца или года. Или, к примеру, количество выпавших осадков, температуру нагрева двигателя в зависимости от времени работы.
Вот его пример. По вертикали отложена стоимость ценной бумаги, а по горизонтали дни месяца. Легко отследить, как менялась стоимость со временем. Например, шестого числа ценная бумага стоила 2000.
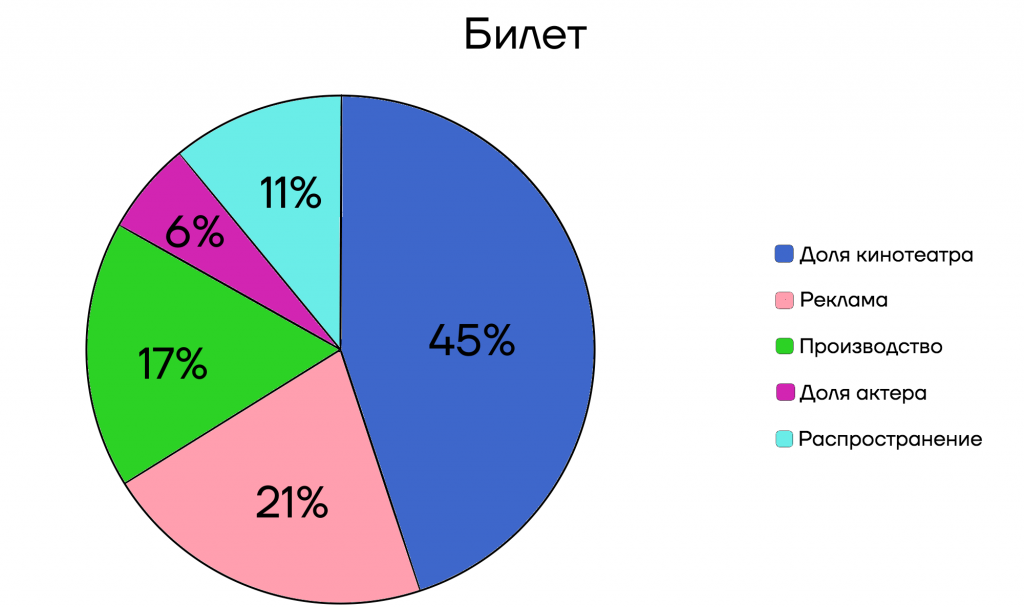
С помощью диаграмм можно показать распределение данных. Рассмотрим с помощью круговой диаграммы, из чего складывается цена билета в кино.
Известно, что 45% берут кинотеатры, 21% уходит на рекламу, 17% на производство, 11% на распространение и 6% актерам. В виде круговой диаграммы это будет выглядеть наглядно.
Подобным образом мы можем представить данные на столбчатой диаграмме. На примере ниже мы можем узнать предпочтения читателей по выбору жанра книги.
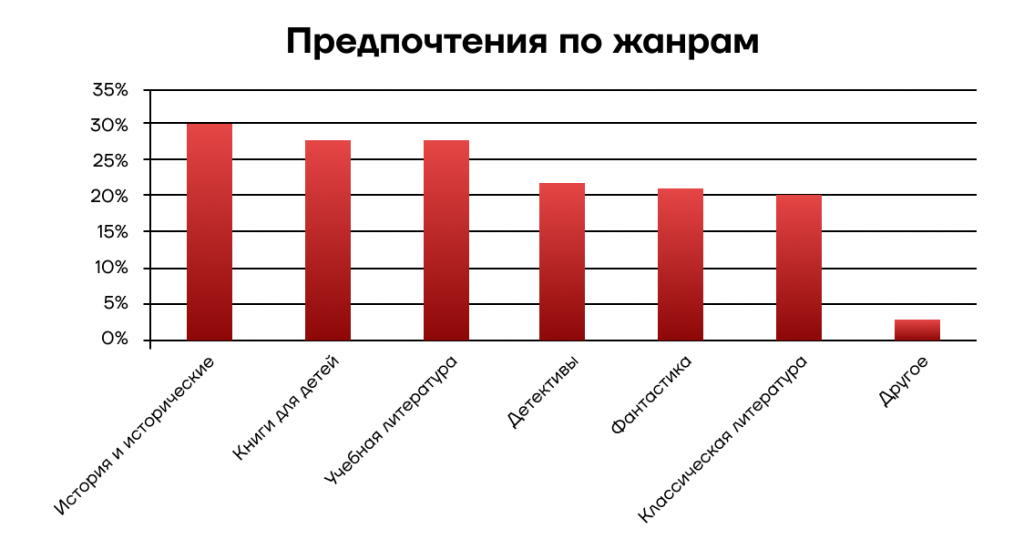
Любые статистические данные можно изобразить с помощью графиков или диаграмм. Выбор их вида напрямую зависит от типа информации, которая должна быть отражена.
| В чем секрет идеальной презентации? В течение дня человек больше воспринимает именно визуальную информацию. Поэтому при составлении презентации важно придерживаться простого правила: с первого взгляда должно быть понятно, о чем слайд. Для слушателя удобнее, когда информация отражена не в текстовом виде — это отвлекает от выступления самого докладчика, — а в виде изображений, диаграмм, схем. Навык оформления последних ценится современными фирмами. |
Фактчек
- Статистика — раздел математики, в котором изучаются методы сбора, систематизации, обработки результатов наблюдений для выявления закономерностей. С помощью статистики можно обработать любые данные и сделать по ним вывод.
- Среднее арифметическое чисел — это отношение суммы всех данных чисел к их количеству.
- Выборка — часть всего множества объектов, событий или наблюдений. Объем выборки — количество элементов, которые попали в выборку. Размах выборки — разность между максимальными и минимальными значениями выборки.
- Если одно и то же значение в выборке повторяется несколько раз, то количество его повторений будет называться частотой. Относительная частота выборки — отношение частоты к общему числу данных в ряду. Относительная частота обычно выражается в процентах.
- Мода — выборочное данное с наибольшей частотой повторений. Медиана ряда чисел с нечетным количеством членов — число, которое стоит в середине упорядоченного ряда. Медиана ряда чисел с четным показателем — среднее арифметическое двух чисел, которые стоят в середине упорядоченного ряда.
- Любые статистические данные можно отобразить графически с помощью графиков и диаграмм.
Проверь себя
Задание 1.
Найдите среднее арифметическое чисел 20 и 40.
- 25
- 20
- 40
- 30
Задание 2.
Найдите среднее арифметическое чисел 6, 7, 9, 20, 34 и 14.
- 15
- 6
- 45
- 50
Задание 3.
Дана выборка: 1, 1, 3, 5, 4, 6, 9, 9, 3, 9, 8. Чему будет равна мода?
- 1
- 9
- 3
- 6
Задание 4.
Дана упорядоченная выборка: 1, 1, 3, 4, 5, 6, 7, 9, 10, 11. Чему равна медиана?
- 5
- 6
- 5,5
- 1
Задание 5.
Дана упорядоченная выборка: 1, 1, 3, 4, 6, 7, 9, 10, 11, 13, 28. Чему равна медиана?
- 1
- 7
- 93
- 8,5
Ответы: 1. — 4; 2. — 1; 3. — 2; 4. — 3; 5. — 2.


 к списку статей
к списку статей





