Тригонометрические неравенства

На этой странице вы узнаете

• Какие точки опасны для тангенса и котангенса?
• Есть ли универсальные решения в тригонометрии?
• Как промежутку попасть в цель? 

С неравенствами мы встречаемся и в жизни. Когда делаем выбор между двумя сортами яблок, сравниваем две модели джинсов или, например, выбираем сериал. Обычно у каждого варианта свои достоинства и недостатки, исходя из которых мы приходим к решению.

Математические неравенства почти ничем не отличаются от примеров выше. Обычно одна их часть больше или меньше другой, и необходимо найти все значения неизвестного, которые удовлетворяют данному условию. Но что же такое тригонометрическое неравенство? Это такое же неравенство, как и обычное, однако теперь в нем будут присутствовать тригонометрические функции. 

Коротко о важном

С тригонометрией мы встречаемся уже не в первый раз. Например, мы уже научились решать тригонометрические уравнения и узнали про область допустимых значений (ОДЗ) тригонометрических функций.

Вспомним, что тригонометрические функции — это синус, косинус, тангенс и котангенс. С их помощью мы можем выразить численное значение заданного угла.

Также нам важно всегда держать в голове ограничения на допустимые значения тригонометрических функций:

• ОДЗ синуса и косинуса от -1 до 1 включительно: \(-1\leq cos x\leq 1\) и \(-1\leq sin x\leq 1\).
• ОДЗ тангенса: \(tg x=\frac{sin x}{cos x}, cos x\neq 0\), тогда \(x\neq \frac{\pi}{2}+\pi n, n\in Z\).
• ОДЗ котангенса: \(ctg x=\frac{cos x}{sin x}, sin x\neq 0\), следовательно, \(x\neq \pi n, n\in Z\).

Чтобы вспомнить, как преобразовывать тригонометрические функции и решать простейшие уравнения с ними, можно заглянуть в статью «Формулы тригонометрии и простейшие уравнения». Такие преобразования могут встретиться и в неравенствах, о которых мы будем говорить в этой статье. 

Простейшие тригонометрические неравенства

Тригонометрическое неравенство — это неравенство, в котором переменная содержится под знаком тригонометрической функции.

Как решаются тригонометрические неравенства?
Для их решения нужно хорошо ориентироваться в тригонометрической окружности. Этот навык очень пригодится нам в нахождении угла или значения угла заданной тригонометрической функции. 

Рассмотрим решение на примерах простейших тригонометрических неравенств.

Пример 1: \(cos x > \frac{1}{2}\).

Вспомним, что на тригонометрической окружности значения синуса лежат на оси ординат, а значения косинуса – на оси абсцисс. 

Отметим значение \(\frac{1}{2}\) на оси косинусов и выделим промежуток, на котором значения больше \(\frac{1}{2}\). 

Далее выделим промежуток, для точек которого неравенство верно. Для этого через точку \(\frac{1}{2}\) проведем перпендикуляр до пересечения с единичной окружностью. Точки на окружности будут выколотыми, поскольку знак неравенства строгий. По таблице получаем точки \(-\frac{\pi}{3}\) и \(\frac{\pi}{3}\). 

Какую часть окружности нужно закрасить? Заметим, что проведенный перпендикуляр делит окружность на две части. Заштриховать нужно именно ту часть, со стороны которой закрашена часть оси косинуса. В этом случае ось косинуса заштрихована справа, следовательно, заштриховываем правую часть окружности. 

Важно: точки называем в соответствии с тригонометрической окружностью так, чтобы между ними можно было определить непрерывный промежуток. Для этого важно, чтобы в записи промежутка левая точка была меньше, чем правая.

Ответ: \((-\frac{\pi}{3}+2\pi k, k\in z; \frac{\pi}{3}+2\pi k, k\in z )\).

Пример 2: \(cos x < \frac{1}{2}\).

Заметим, что это неравенство обратное предыдущему. То есть мы совершаем такие же шаги:

1. Отмечаем на оси косинуса точку \(\frac{1}{2}\).
2. Заштриховываем нужную часть оси, а именно левую. 
3. Проводим через точку \(\frac{1}{2}\) перпендикуляр до точек пересечения с единичной окружностью. Попадаем в точки \(\frac{\pi}{3}\) и \(\frac{5\pi}{3}\). Значения поменялись, поскольку начальная точка должна быть меньше, чем конечная. 
4. Заштриховываем левую часть окружности (то есть с той же стороны, с которой заштрихована ось косинуса). 

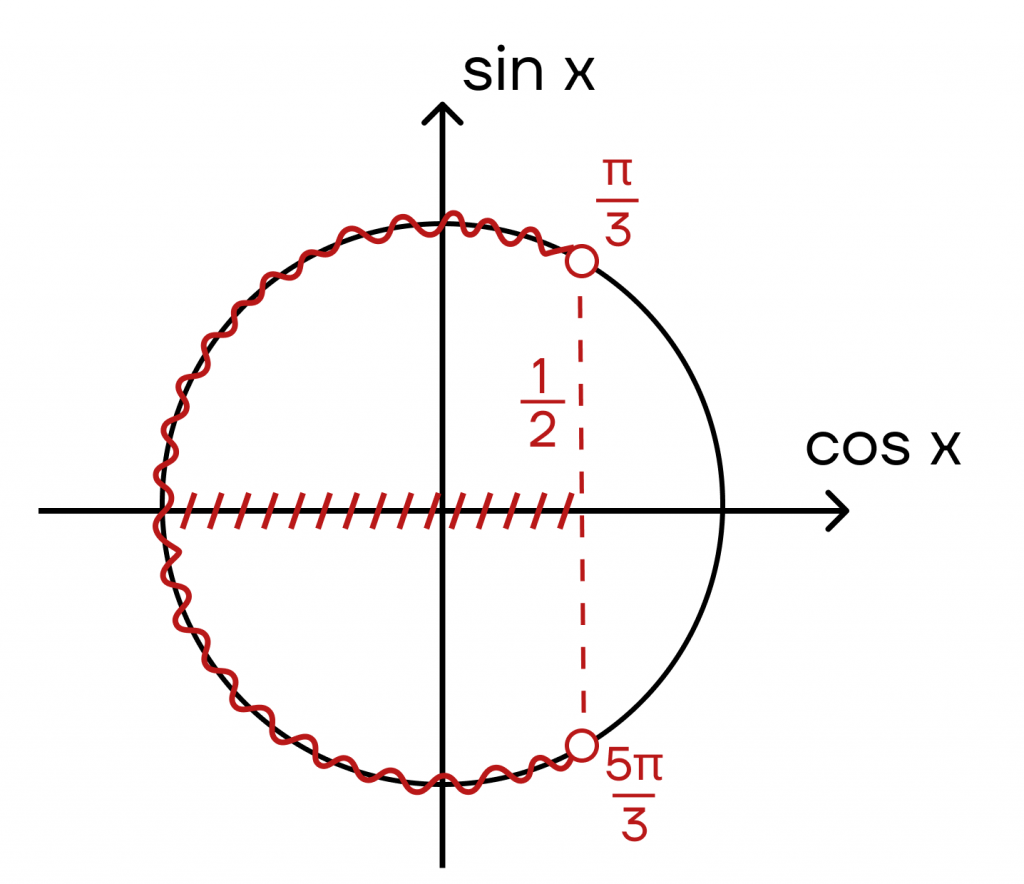
Ответ: \((\frac{\pi}{3}+2\pi k, k\in z; \frac{5\pi}{3}+2\pi k, k\in z)\).

Тригонометрические неравенства могут встретиться в решении ОДЗ. В свою очередь, правильное решение ОДЗ позволит не потерять баллы, например, в №12 ЕГЭ по профильной математике. 

Предположим, мы имеем уравнение вида \(\sqrt{2sin x-1}=sin x\). Попробуем составить для него ОДЗ.

Решение.
Вспомним, что подкоренное выражение не может быть меньше 0. Получаем неравенство:

\(2sin x-1 \geq 0\)

Перенесем единицу вправо и разделим все неравенство на 2:

\(2sin x\geq 1\)
\(sin x\geq \frac{1}{2}\)

Теперь решим это неравенство.
1. Отметим на оси синуса точку \(\frac{1}{2}\). Поскольку знак неравенства нестрогий, точку закрашиваем. 
2. Нам нужны значения больше, чем \(\frac{1}{2}\), то есть заштриховываем верхнюю часть оси. 
3. Проводим через точку \(\frac{1}{2}\) перпендикуляр до точек пересечения с окружностью. По таблице значений функций видим, что попадаем в точки \(\frac{\pi}{6}\) и \(\frac{5\pi}{6}\). 
4. Заштриховываем верхнюю часть окружности (то есть с той же стороны, с которой заштрихована ось синуса. 

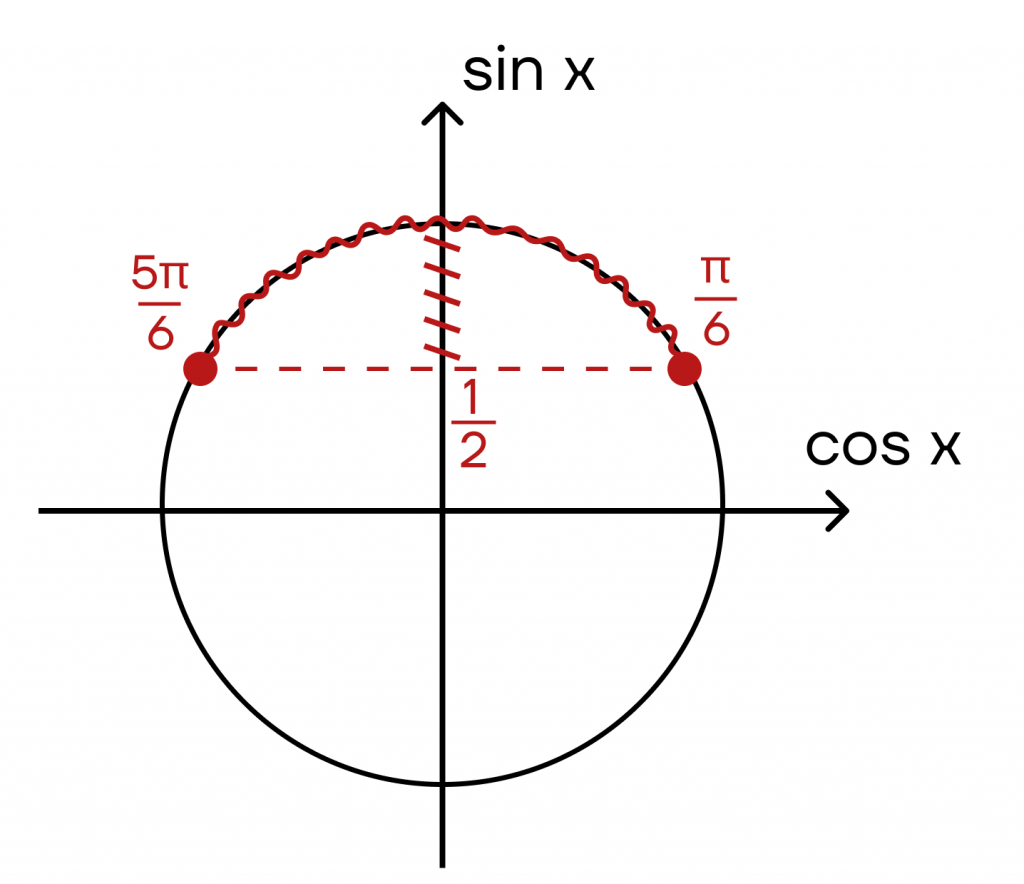
5. Получаем промежуток \([\frac{\pi}{6}+2\pi k, k\in z; \frac{5\pi}{6}+2\pi k, k\in z]\). Это и будет ОДЗ. 

Ответ: \([\frac{\pi}{6}+2\pi k, k\in z; \frac{5\pi}{6}+2\pi k, k\in z]\)

Пример 3: \(sin x <\frac{1}{2}\).

Это неравенство решается аналогично предыдущему, только заштриховывается уже нижняя часть оси, а следовательно, и нужная часть окружности. 

Также не забываем, что первая точка должна быть меньше, чем вторая, а значит, у нас получаются значения \(-\frac{7}{6}\) и \(\frac{\pi}{6}\). 

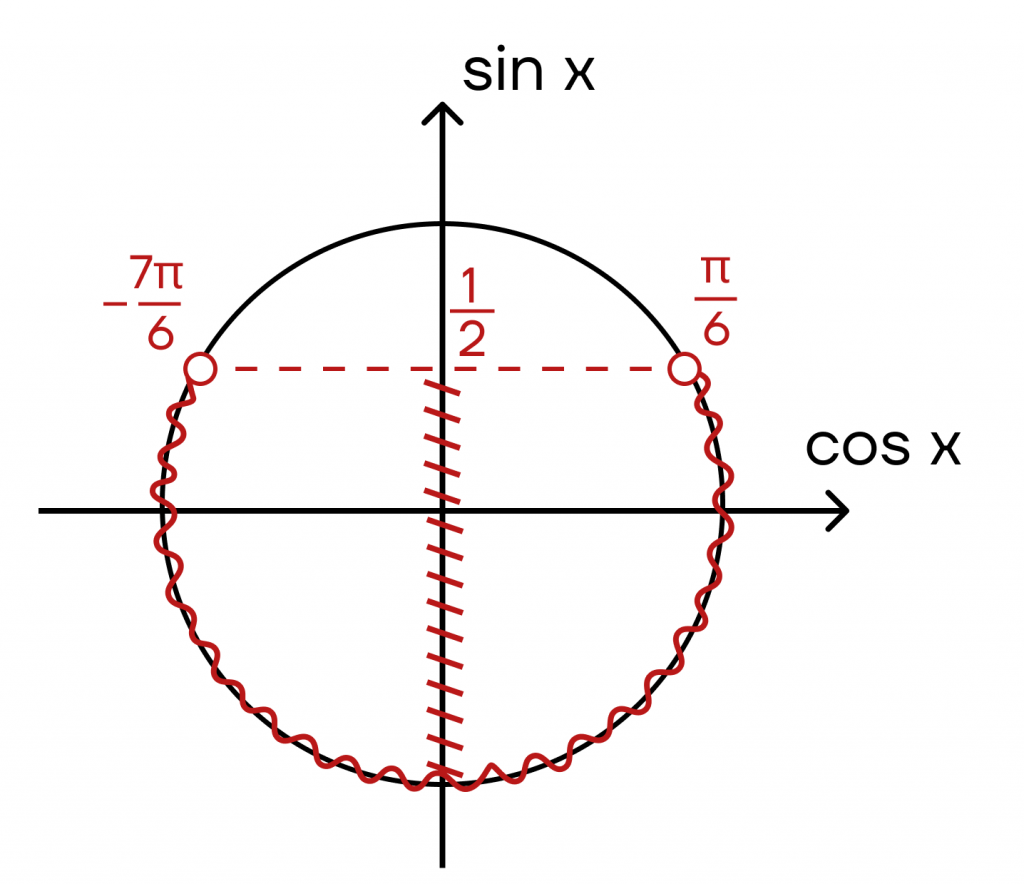
Здесь, как и в примере 1, называем точки так, чтобы в итоге можно было записать непрерывный промежуток.

Ответ: \((\frac{7\pi}{6}+2\pi k, k\in z; \frac{\pi}{6}+2\pi k, k\in z)\).

Пример 4: \(tg x >1\).

По таблице получаем точки \(\frac{\pi}{4}\) и \(\frac{5\pi}{4}\). На оси тангенсов отмечаем точку 1 и заштриховываем верхнюю часть оси. 

В этом случае мы уже не можем провести перпендикуляр. Что делать? Мы проводим прямую через точку на оси тангенсов и центр окружности и продолжаем ее до пересечения с самой окружностью. 

Вспомним, что тангенс положителен в 1 и 3 четвертях и отрицателен во 2 и 4. Поскольку по неравенству он может принимать только положительные значения, то и заштриховывать мы можем только часть окружности в 1 и 3 четвертях. Подробнее про знаки функций в четвертях можно узнать в статье «Формулы приведения». 

Осталось определить, в какую сторону от отмеченных точек необходимо заштриховать дугу. Поскольку мы ищем значения, больше 1 (то есть идем на увеличение значений), то и дугу заштриховываем в большую сторону. 

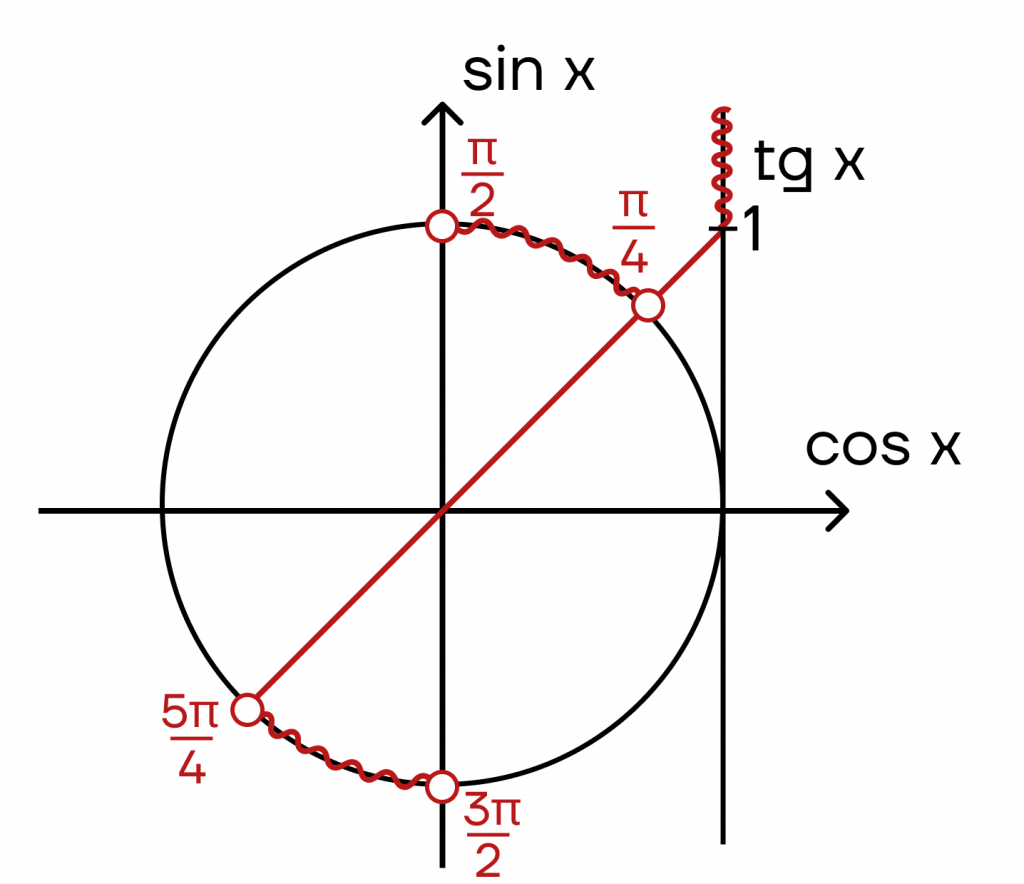
Какие точки опасны для тангенса и котангенса? Если мы вспомним ОДЗ этих функций, то в случае тангенса \(cos x\neq 0\), а в случае котангенса \(sin x\neq 0\). Именно из-за наличия ОДЗ появляются «опасные» точки. Разберем на примере тангенса. Если \(cos x\neq 0\), то \(x\neq \frac{\pi}{2}+\pi n, n\in Z\). То есть для тангенса опасными точками будут \(\frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}\) и так далее. При решении неравенств с тангенсом эти точки должны быть выколоты на окружности.   Аналогично и с котангенсом. Если \(sin x\neq 0 => x\neq \pi n, n\in Z\), значит, эти точки нужно будет выкалывать на окружности при решении неравенств с котангенсом.

В данном примере у нас получились диаметрально противоположные промежутки, таким образом, можно записать только первый, но с периодом в половину окружности.

Ответ: \((\frac{\pi}{4}+\pi k, k\in z; \frac{\pi}{2}+\pi k, k\in z )\).

Пример 5: \(tg x < 1\).

Заметим, что точки на окружности сохраняются, а на оси тангенсов заштриховывается уже нижняя часть. 

В чем особенность этого неравенства? По неравенству нам необходимы все значения, которые меньше 1, а значит, тангенс может в этом случае быть отрицательным (ведь \(-1<1\)). Тогда 2 и 4 четверти, в которых тангенс отрицателен, так же нам подходят. Осталось только заштриховать дугу на окружности в сторону уменьшения значений. 

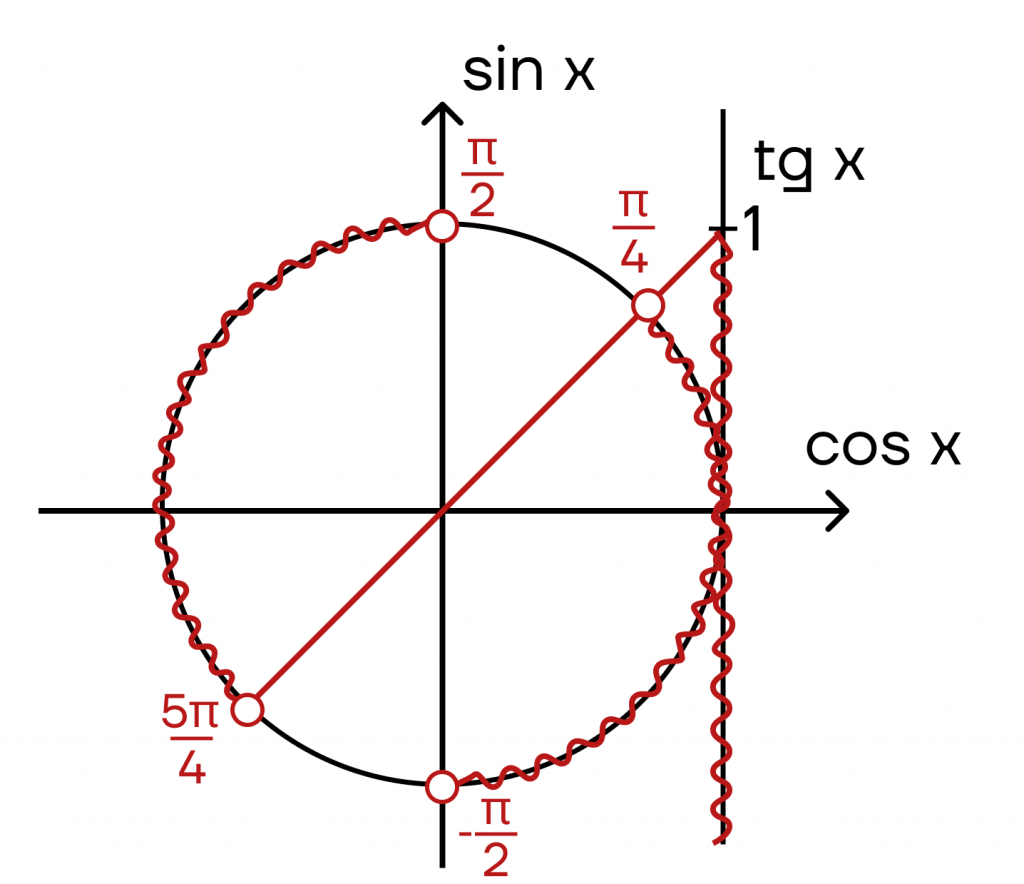
Ответ: \((-\frac{\pi}{2}+\pi k, k\in z; \frac{\pi}{4}+\pi k, k\in z )\). 

Пример 6: \(ctg x < 1\).

Аналогично с решением предыдущего неравенства: нам подойдут все значения котангенса, которые меньше 1, то есть отрицательные значения также нужно учесть. 

Котангенс отрицателен во 2 и 4 четвертях и положителен в 1 и 3. Дальше действуем по уже отработанной схеме:

1. Отмечаем на оси котангенсов точку 1. 
2. Заштриховываем левую часть оси. 
3. Соединяем точку на оси котангенсов и центр окружности, продолжаем прямую до пересечения. Не забываем, что точки на окружности должны быть выколотыми из-за строгости знака. 
4. Заштриховываем нужную часть дуги. 

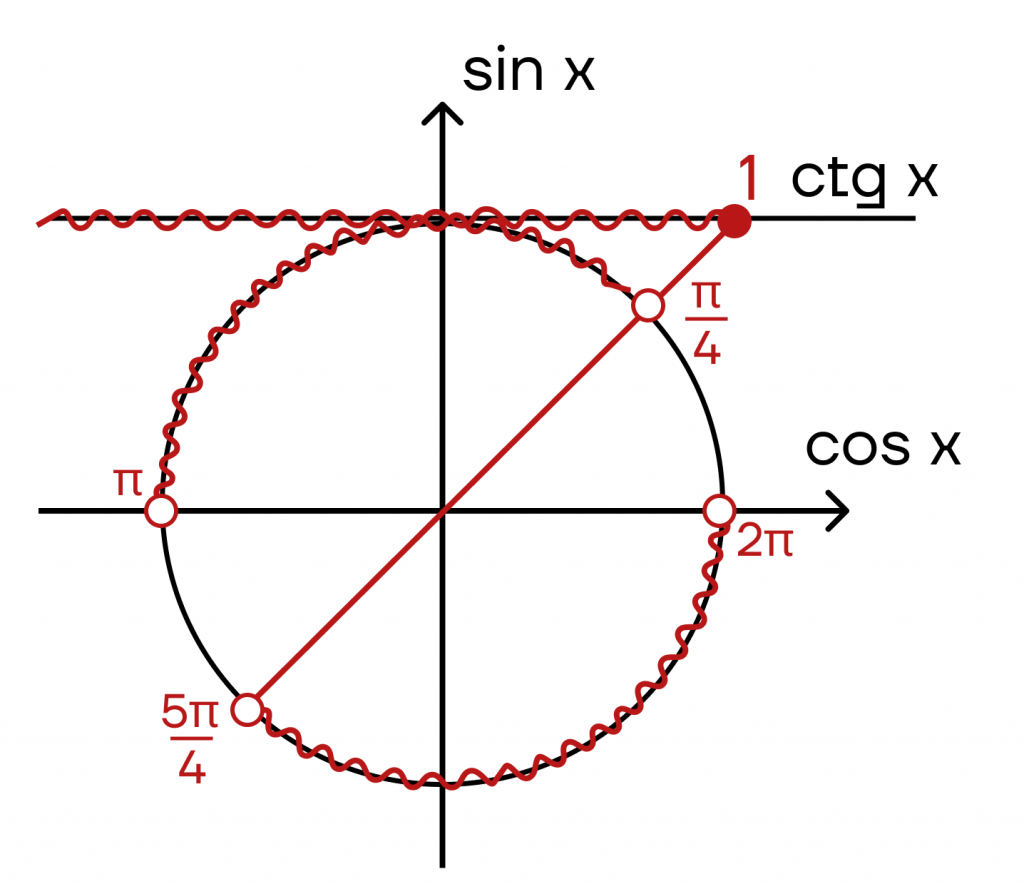
Важно: у котангенса не существуют точки 0 и , поэтому они тоже выкалываются.

Ответ: \((\frac{\pi}{4}+\pi k, k\in z;\pi +k, k\in z)\).

Пример 7: \(ctg x > 1\).

Решаем аналогично предыдущим неравенствам, но теперь отмечаем точки и промежутки с помощью оси котангенсов. 

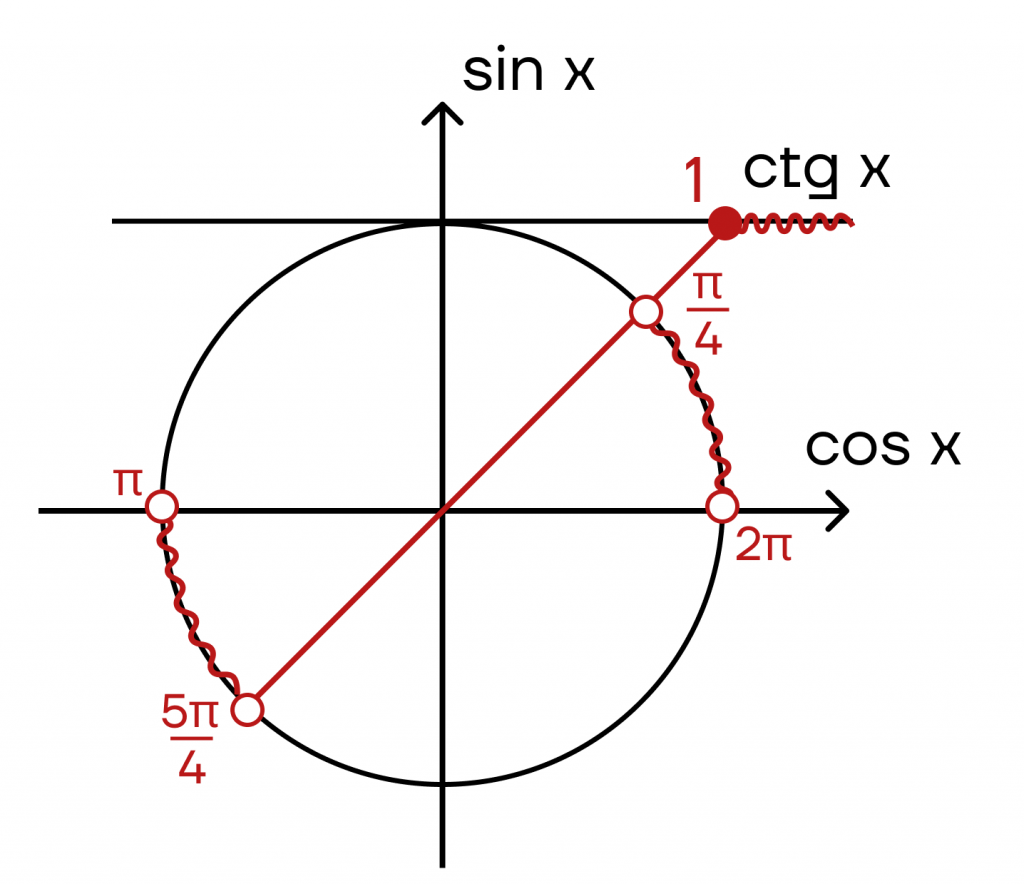
Ответ: \((\pi k, k\in z; \frac{\pi}{4}+\pi k, k\in z )\).

Алгоритм решения простейшего тригонометрического неравенства:

1. Отметить промежуток на прямой тригонометрической функции.
2. Найти граничные точки.
3. Отметить дугу или дуги и записать в ответ промежуток.

Еще раз рассмотрим решение простейшего неравенства более детально:

\(sin x>-\frac{1}{2}\)

Шаг 1. Нарисуем тригонометрическую окружность и отметим на ней промежуток, где синус больше \(-\frac{1}{2}\).

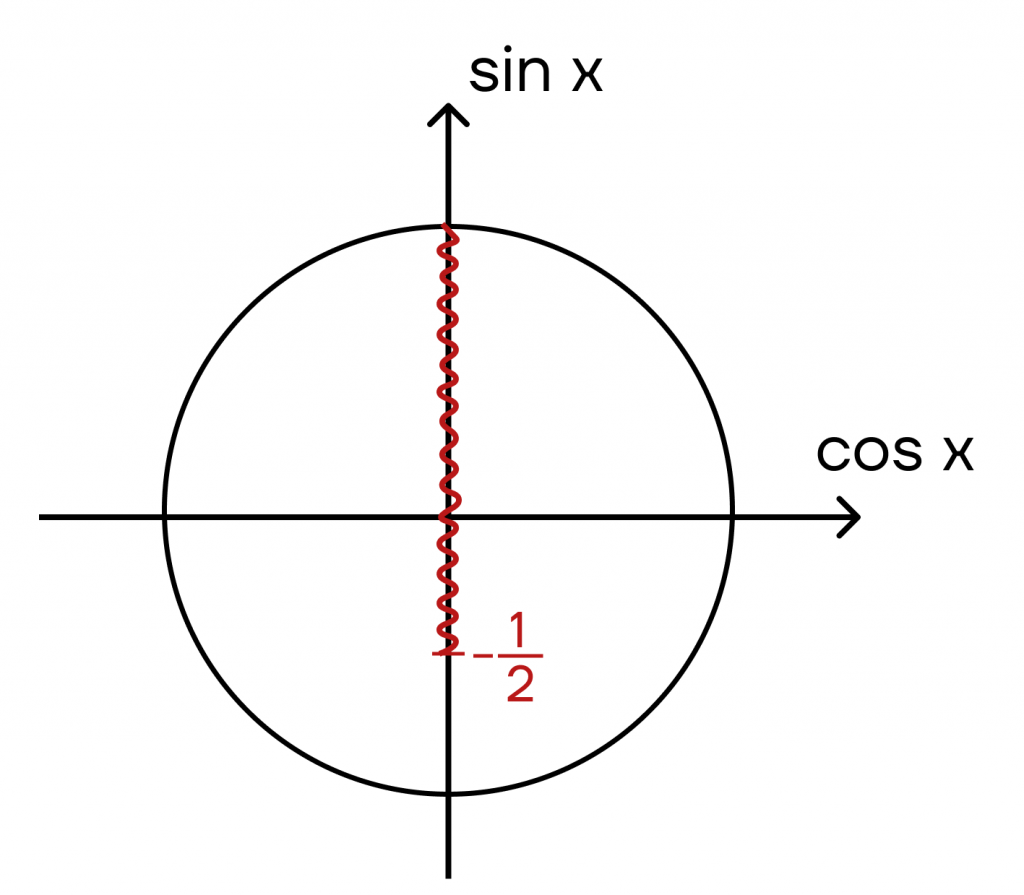
Шаг 2. Теперь найдем значения х, при которых синус х равен \(-\frac{1}{2}\), используя тригонометрический круг, знак неравенства строгий — точки выколоты.

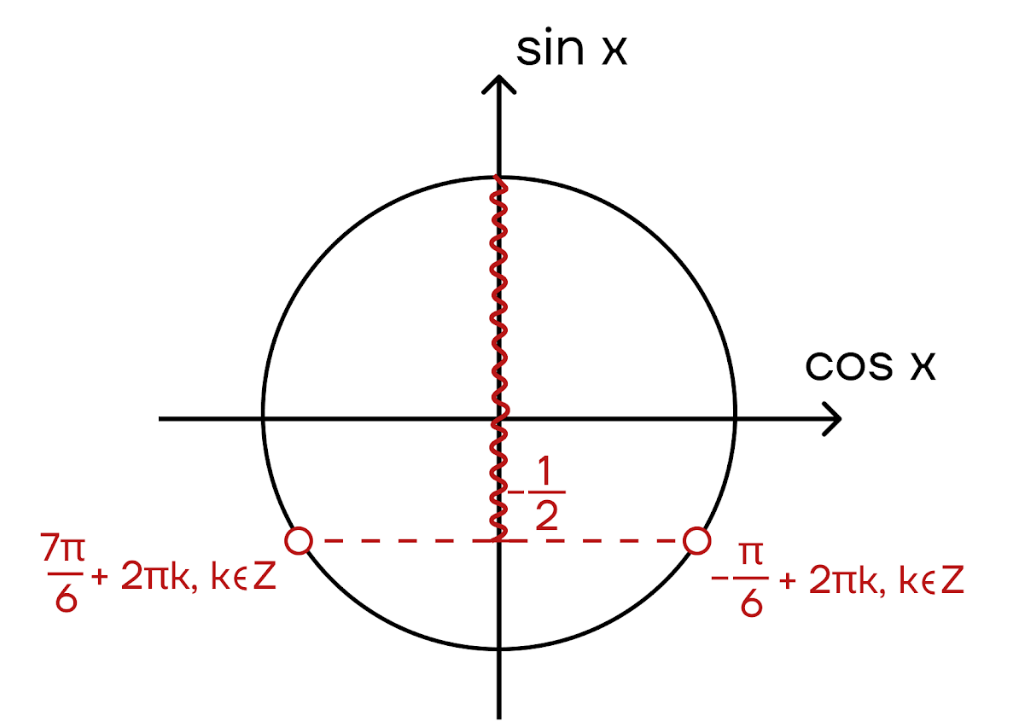
Шаг 3. Отметим промежуток, который должен идти в ответ. Поскольку заштрихована верхняя часть оси синуса, то необходимо выделить верхнюю часть дуги. 

Ответ: \((-\frac{\pi}{6}+2\pi k, k\in z; \frac{7\pi}{6}+2\pi k, k\in z)\).

Решение тригонометрических неравенств

Тригонометрические неравенства отличаются от тригонометрических уравнений только одним пунктом. В уравнениях ищутся отдельные решения, а в неравенствах — множество решений, которое чаще всего является промежутком(ами). 

Есть ли универсальные решения в тригонометрии? Для решения тригонометрических неравенств можно применять те же методы, что и для решения тригонометрических уравнений: — Введение новой переменной. — Разложение на множители.

Основные способы решения тригонометрических неравенств

1. Введение новой переменной.

В статье «Тригонометрические уравнения» мы уже подробно разобрали этот способ. Как мы уже упомянули, разница между решением уравнений и неравенств не слишком большая. В данном случае процесс отличается лишь тем, что после замены переменной нужно решать обычное неравенство и далее рассматривать промежуток. Давайте сейчас вспомним основные шаги наших действий.

Алгоритм решения тригонометрического неравенства путем введение новой переменной:

1. Введя новую переменную t, привести неравенство к простейшему виду.
2. Решить полученное неравенство для переменной t.
3. Затем вернуться к переменной x и найти ее значение.
4. Записать ответ в виде промежутка.

Рассмотрим неравенство \(3cos^2x-5cosx-2<0\):

1. Введем новую переменную. Не забудем указать, что по ОДЗ cos x может принимать значения только от -1 до 1:

\(cos x =t, -1 ≤ t ≤ 1\)
\(3t^2-5t-2<0\)

2. С помощью метода интервалов решим неравенство и получим:

\(-\frac{1}{3}<t<2\)

3. Так как по ОДЗ нашего неравенства \(-1 ≤ t ≤ 1\), неравенство \(t<2\) будет выполняться всегда. Опустим эту часть и сделаем обратную замену:

\(cos x > -\frac{1}{3}\)

А теперь решим простейшее тригонометрическое неравенство: 

Здесь нам пришлось встретиться с аркфункцией. Мы подробно разбирали ее суть в статье «Формулы тригонометрии и простейшие уравнения». Обратитесь к ней, если вам нужно вспомнить для чего применяются функции, обратные тригонометрическим. А сейчас мы запишем ответ.

Ответ: \((-arccos(-\frac{1}{3})+2\pi k, k\in z; arccos(-\frac{1}{3})+2\pi k, k\in z )\).

2. Разложение на множители.

Если вы уже уверенно решаете тригонометрические уравнения, этот способ также вам знаком. 

Алгоритм решения тригонометрического неравенства путем разложения на множители:

1. Разложить выражение на множители.
Сделать это можно путем вынесения общего множителя за скобку, методом группировки или иными способами, о которых мы рассказывали в статье «Линейные, квадратные и кубические уравнения». Важно условие: вместо сложения или вычитания должно появиться произведение.
2. Решить полученное неравенство методом интервалов или совокупностью систем.
3. Записать полученный промежуток. 

В качестве примера рассмотрим неравенство:

\(sin x cos x -cos x >0\)

Шаг 1. Вынесем общий множитель за скобку:

\(cos x sin x -1>0\)

В каких случаях произведение двух множителей будет больше 0? Если они оба будут положительны (плюс на плюс дадут плюс) или оба будут отрицательны (минус на минус будет плюс). Если один из множителей будет отрицательным, а второй положителен, то их произведение будет отрицательным. 

Шаг 2. Запишем совокупность:

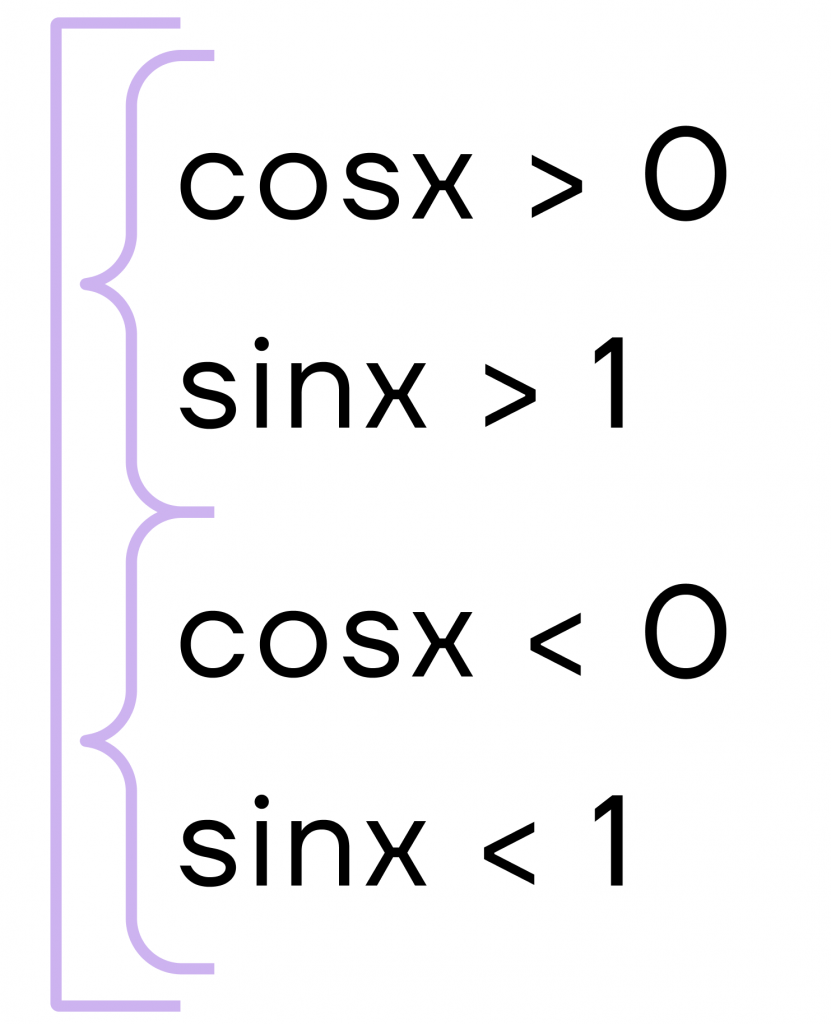
У первой системы нет решений, так как синус не может быть больше 1. 

Шаг 3. Решим вторую систему. 

Решением системы будут те промежутки, которые справедливы для каждого неравенства в системе. Отметим на окружности решение первого неравенства красным цветом, а решение второго — синим. 

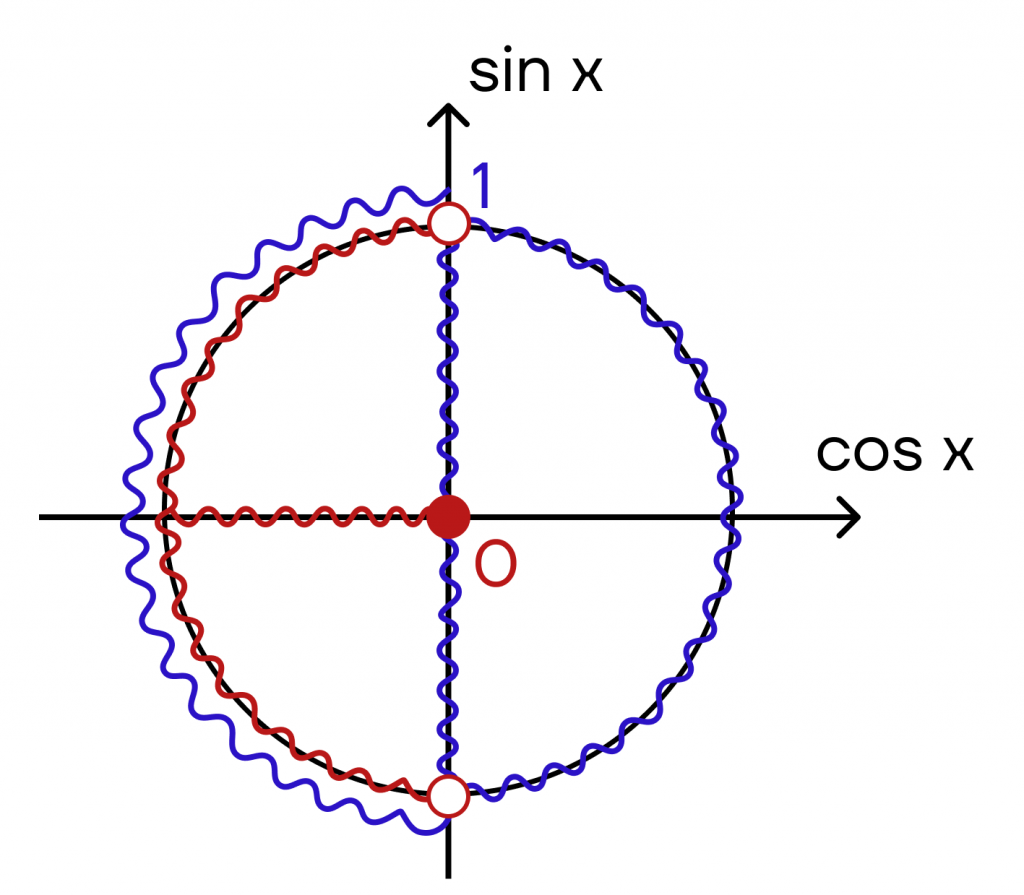
Нам нужны промежутки, которые заштрихованы и красным, и синим. Тогда из второй системы получим: \((\frac{\pi}{2}+2\pi k, k\in z; \frac{3\pi}{2}+2\pi k, k\in z)\).

Это и будет ответом.

3. Решение квадратных, рациональных, дробно-рациональных и иррациональных тригонометрических неравенств. 

Возможно, это и звучит немного устрашающе, но на самом деле ничем не отличается от решения обычных неравенств такого типа. Поскольку нам нужно будет упростить задачу, придется снова сделать замену.

Алгоритм решения квадратных, рациональных, дробно-рациональных и иррациональных неравенств:

1. Сделать замену для тригонометрических функций.
2. Решить полученное неравенство любым наиболее удобным способом.
3. Сделать обратную замену.
4. Найти значение переменной, стоящей в аргументе тригонометрических функций.

Рассмотрим решение таких неравенств на примере дробно-рационального неравенства:

\(\frac{1}{sin x}-20\)

Шаг 1. Сделаем замену. Также сразу вспомним ОДЗ синуса: \(-1\leq sin x\leq 1\). 

Тогда пусть \(t=sin x, -1\leq t\leq 1\). 

Получаем неравенство:

\(\frac{1}{t}-2\geq 0\)

Шаг 2. Данное неравенство удобно решать методом интервалов. Но для этого нам сначала нужно привести левую его часть к общему знаменателю:

\(\frac{1}{t}-\frac{2t}{t}\geq 0=>\frac{1-2t}{t}\geq 0\)

Приравняем выражение к 0 и найдем нули функций:

\(\frac{1-2t}{t}=0\)
\(1-2t=0 =>2t=1=>t=\frac{1}{2}\)
\(t\neq 0\)

Заметим, что в последнем случае мы использовали знак “не равно”, поскольку переменная стоит в знаменателе, а знаменатель никогда не равен 0. Эта точка на числовой прямой будет выколота.

Начертим числовую прямую, расставим знаки и закрасим нужный промежуток. В нашем случае это промежуток со знаком “плюс”. 

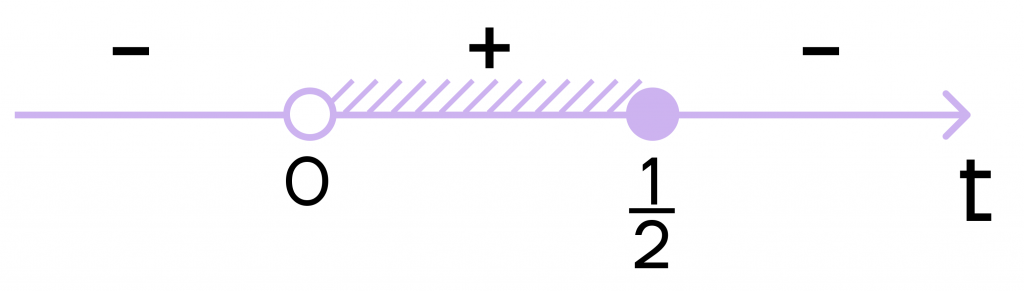
Получаем: \(0<t\leq \frac{1}{2}\).

Сделаем обратную замену:

\(0<sin x\leq \frac{1}{2}\)

Дальше действуем по уже известному нам алгоритму, однако теперь перед нами будет система неравенств: 

Для ее решения должны выполняться оба неравенства одновременно. 

Обратим внимание на первое неравенство: синус должен быть строго положителен. Определить это можно по четвертям: синус положителен в первой и второй четвертях. Следовательно, все значения, полученные при решении второго неравенства должны лежать именно в этом промежутке.

Второе неравенство мы уже решали. Осталось пересечь его с решением первого неравенства системы. 

Пусть промежуток для первого неравенства будет отмечен синим, а для второго красным. Получаем:

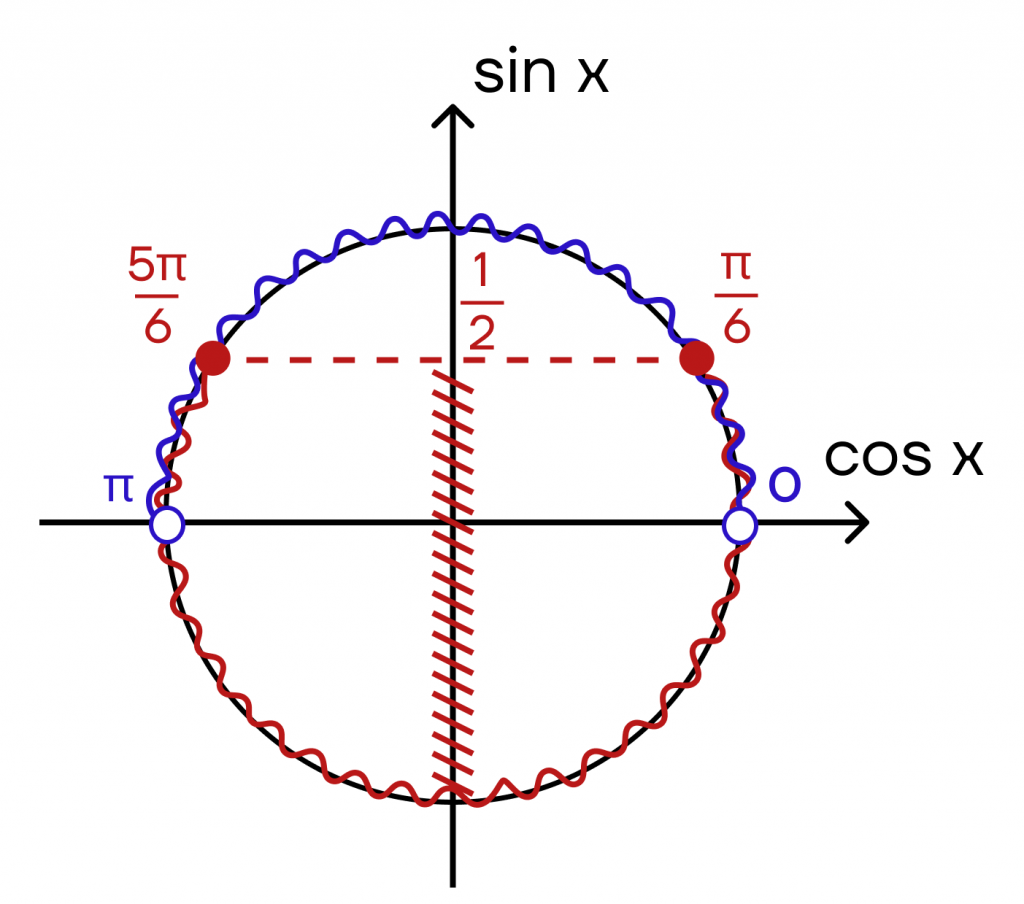
Условиям неравенства удовлетворяют два промежутка, которые закрашены обоими цветами. В этом случае удобнее будет начать запись ответа от 0. 

Ответ: \((2\pi n, n\in Z;\frac{\pi}{6}+2\pi n, n\in Z][\frac{5\pi}{6}+2\pi n, n\in Z;\pi +2\pi n, n\in Z)\).

Мы уже несколько раз сталкивались с системами при решении неравенств. Давайте чуть подробнее разберемся, что это такое и как с ними работать. 

Системы тригонометрических неравенств

Чтобы найти значение системы тригонометрических неравенств, нужно решить каждое неравенство отдельно и найти пресечение их решений.

Как промежутку попасть в цель?.. …то есть в ответ системы тригонометрических неравенств. Решение системы неравенств можно сравнить с двумя реками, впадающими в море на определенном участке. У них в устьях стоят сетки, не пропускающие мусор в море.  Так и в системе неравенств: сначала решается каждое уравнение отдельно, а после пересекают найденные промежутки. В ответ идет промежуток, принадлежащий обоим неравенствам.

Рассмотрим следующий пример:

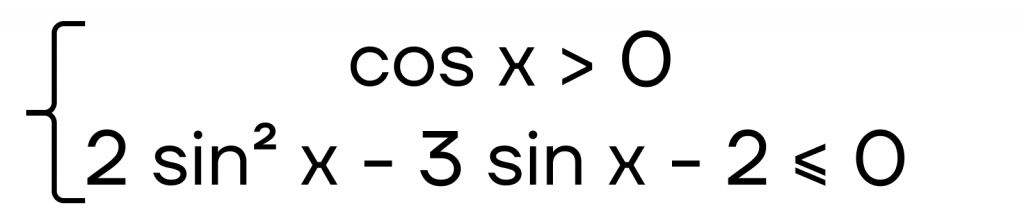
Решим каждое уравнение отдельно.

Шаг 1: \(cos x >0\) 

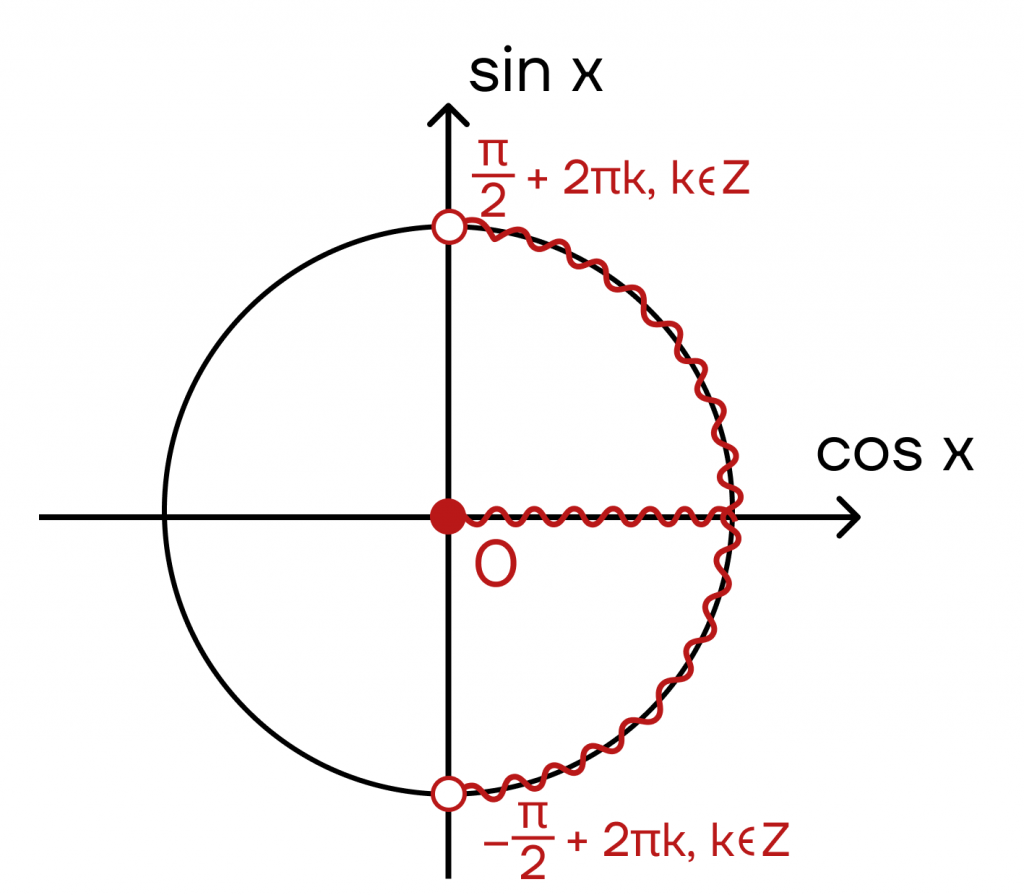
Получим промежуток: \((-\frac{\pi}{2}+2\pi k, k\in z;\frac{\pi}{2}+2\pi k, k\in z )\)

Шаг 2: \(2sin^2x-3sin x -2\leq 0\)

Сделаем замену \(sin x =t, -1 \leq t  \leq  1\)

\(2t^2-3t-2 \leq 0\)

Найдем нули функции. 

\(2t^2-3t-2=0\)
\(D=9+16=25\)
\(t_1=\frac{3+5}{4}=2\)
\(t_2=\frac{3-5}{4}=-\frac{1}{2}\)

С помощью метода интервалов определяем промежуток. 

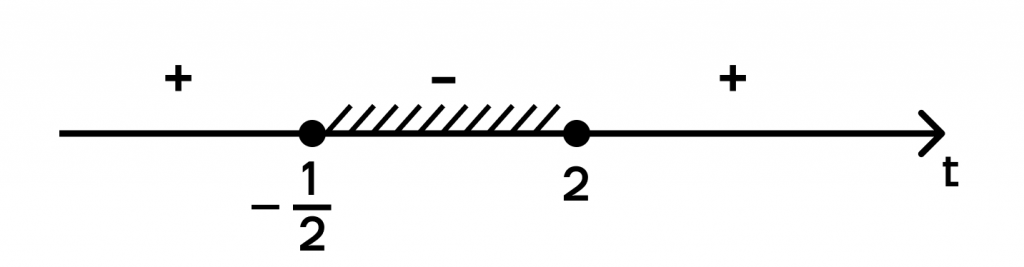
\(-\frac{1}{2} \leq  t \leq 2\)

 Сделаем обратную замену:

\(-\frac{1}{2}\leq sin x \leq 2\)

Так как sin x всегда меньше двух, опустим правую часть и решим простейшее тригонометрическое неравенство.

\(-\frac{1}{2} \leq sin x\)

Получим промежуток \([-\frac{\pi}{6}+2\pi k, k\in z; \frac{7\pi}{6}+2\pi k, k\in z]\). Заметим, что поскольку знак неравенства нестрогий, точки на окружности закрашены, а скобочки в записи промежутка квадратные. 

Шаг 3. Отметим оба промежутка и найдем их пересечение. То есть нам нужна та часть дуги, которая заштрихована и красным, и синим цветом. Для удобства она отдельно помечена зеленым.

Запишем найденный промежуток.

Ответ: \([-\frac{\pi}{6}+2\pi k, k\in z; \frac{\pi}{2}+2\pi k, k\in z )\).

Мы разобрали одну из самых сложных, но в то же время и интересных тем по тригонометрии. Если вы прочитали все наши статьи по тригонометрии, вам не страшны ни тригонометрические функции, ни уравнения, ни неравенства с ними. А значит, одна из важных частей теории для подготовки к экзамену уже освоена. Но если вдруг сложилось так, что тригонометрия все еще щекочет вам нервы, очень советуем повторить эту тему от начала и до конца, а помогут сам в этом наши предыдущие статьи:

• Тригонометрическая окружность. Часть 1
• Тригонометрическая окружность. Часть 2
• Графики тригонометрических функций
• Формулы тригонометрии и простейшие уравнения
• Формулы приведения
• Тригонометрические уравнения

Желаем вам успехов в изучении математики и высоких баллов на экзамене! 

Термины

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.

Перпендикуляр — линия, составляющая прямой угол с другой прямой линией, плоскостью.

Фактчек

• Чтобы решить простейшее тригонометрическое неравенство, необходимо выделить на оси функции точку, которая дана в неравенстве, заштриховать ось в нужном направлении, а после определить по окружности, какие углы попадают в нужный промежуток. 
• Квадратные, рациональные, дробно-рациональные и иррациональные тригонометрические неравенства решаются совершением замены. Затем используются методы решения неравенств данного типа, совершается переход к изначальной переменной, и решается простейшее тригонометрическое неравенство.
• Для решения системы неравенств сначала решается каждое неравенство отдельно, а потом находится пересечение.

Проверь себя

Задание 1.
Решите неравенство \(cos x ≤-1\).

1. нет решений 
2. \((-∞; +∞)\)
3. \(π+2πk, k∈z\)
4. \(2πk, k∈z\)

Задание 2.
Решите неравенство \(ctg x  ≥-1\).

1. \((\pi k, k\in z; \frac{3\pi}{4}+\pi k, k\in z ]\)
2. \((\pi k, k\in z; \frac{\pi}{4}+\pi k, k\in z ]\)
3. нет решений
4. \((\pi+\pi k, k\in z; \frac{7\pi}{6}+\pi k, k\in z )\)

Задание 3.
Решите неравенство \(sin x>0\).

1. нет решений
2. \((-\frac{\pi}{2}+2\pi k;\frac{\pi}{2}+2\pi k, k\in Z)\)
3. \((2k;+2k, kZ)\)
4. \([2k;+2k, kZ]\)

Задание 4.
Решите неравенство \(2sin^2x -3sin x <0\).

1. \((2\pi k, k\in z;\pi +2\pi k, k\in z )\)
2. \((\pi k, k\in z;\pi +\pi k, k\in z )\)
3. \(\pi k, k\in z\)
4. \(\pi +2\pi k, k\in z\)

Задание 5.
Решите систему неравенств:

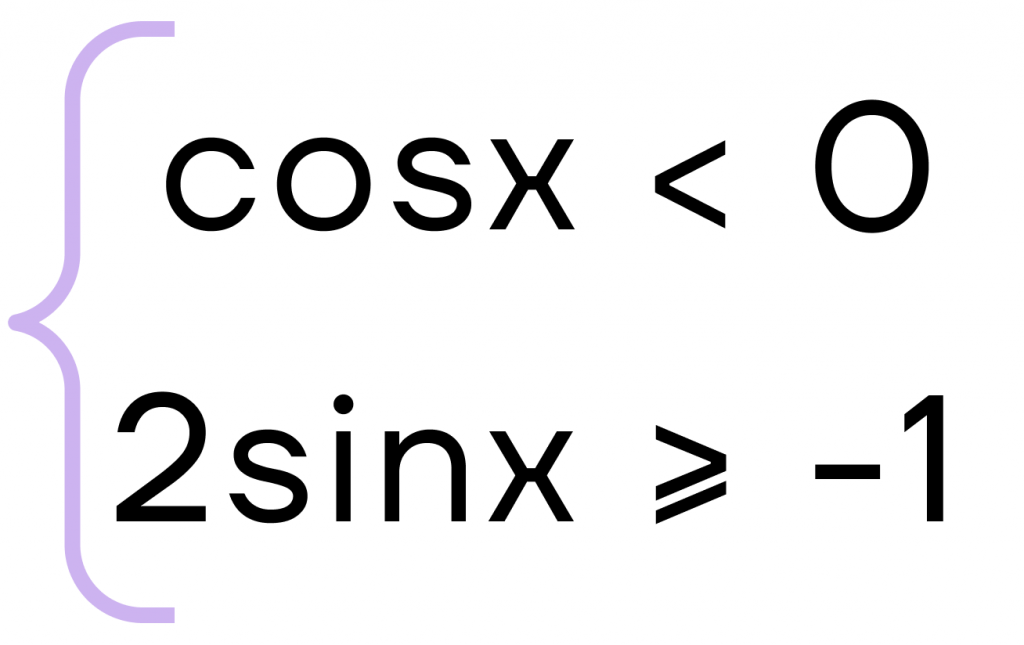
1. \([\frac{\pi}{2}+2\pi k, k\in z; \frac{5\pi}{4}+2\pi k, k\in z ]\)
2. нет решений
3. \([\frac{\pi}{2}+2\pi k, k\in z; \pi+2\pi k, k\in z ]\)
4. \([\frac{\pi}{2}+2\pi k, k\in z; \frac{7\pi}{6}+2\pi k, k\in z ]\)

Ответы: 1. — 3; 2. — 1; 3. — 3; 4. — 1; 5. — 4.