Окружность и круг

На этой странице вы узнаете

• Где в ловце снов спрятана хорда?
• В чем отличие окружности от пиццы? 
• Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360? 

Оглянитесь вокруг: геометрические фигуры окружают нас повсюду, а в математике и вовсе встречаются почти в каждом задании. Не стали исключением и окружность и круг, которые попадают в задачки чаще, чем может показаться. Поэтому эта статья будет полезна: овладеете всеми премудростями, необходимыми для жизни и экзаменов.

Обруч и окружность

Давайте вспомним один из предметов инвентаря художественной гимнастики  – обруч. Это узкое кольцо большого диаметра, внутри которого ничего нет. Обруч состоит только из “контура”, то есть из того самого кольца.  Именно с помощью обруча мы приближаемся к термину “окружность”. 

Окружность – это замкнутая кривая, все точки которой равноудалены от центра. 

Разберем чуть подробнее, что значит фраза “равноудалены от центра”. Допустим, мы точно знаем, где центр нашего обруча, и через этот центр натянем много-много ленточек. Тогда окажется, что длина каждой ленточки от центра до обруча будет одинаковой. 

То есть окружность состоит из бесконечного множества точек, которые располагаются на равном расстоянии от центра. 

Элементы окружности

Радиус – это отрезок, построенный от центра окружности до любой точки на окружности. 

Если вспомнить обруч с ленточками, то одна ленточка – это радиус. Радиус обозначается буквой R. В окружности можно построить множество радиусов, и все они будут равны между собой.

Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности. 

Можно сразу заметить, что диаметр будет состоять из двух радиусов, которые проведены по разные стороны от центра окружности. 

Диаметр обозначается буквой D и равняется двум радиусам.

D = 2R

Хорда – это отрезок, соединяющий две любые точки на окружности. При этом хорда не обязательно проходит через центр окружности. 

Где в ловце снов спрятана хорда? Представим ловец снов. Когда его изготавливают, натягивают нитку от точки на ободе до точки на другом конце обода. Чтобы получился красивый узор, нитки должны быть разной длины и проходить через разные точки – не обязательно через центр.  Получается, каждая ниточка внутри ловца слов будет хордой.

Таким образом, хорда может иметь любой размер и любое направление, главное, чтобы ее начало и конец лежали на окружности. 

Рассмотрим свойства хорды. 

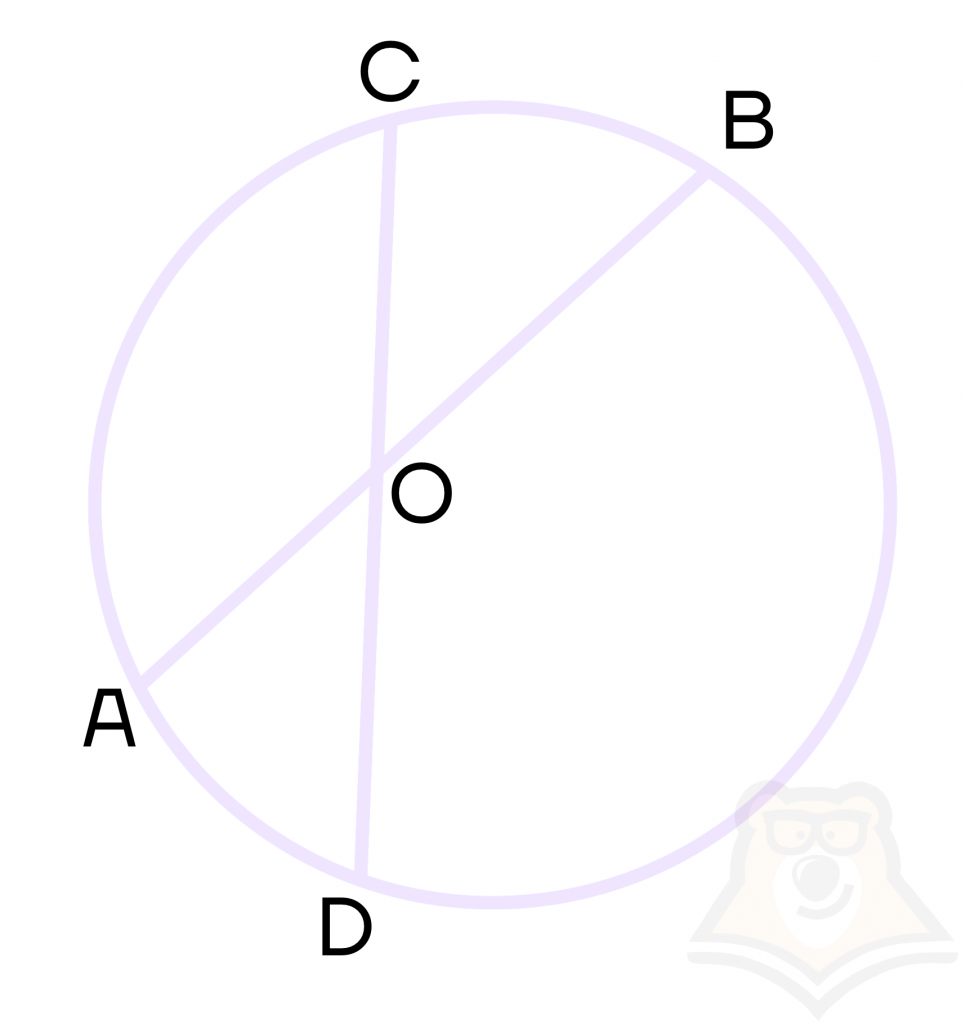
1 свойство. При пересечении двух хорд произведения их отрезков равны. 

Пусть в окружности проведены хорды АВ и CD, которые пересекаются в точке О. Тогда выполняется равенство АО * ОВ = СО * OD.  

2 свойство. Равные хорды стягивают равные дуги. 

3 свойство. Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ей дуги пополам. 

Если диаметр CD перпендикулярен хорде АВ, то АЕ = ЕВ. 

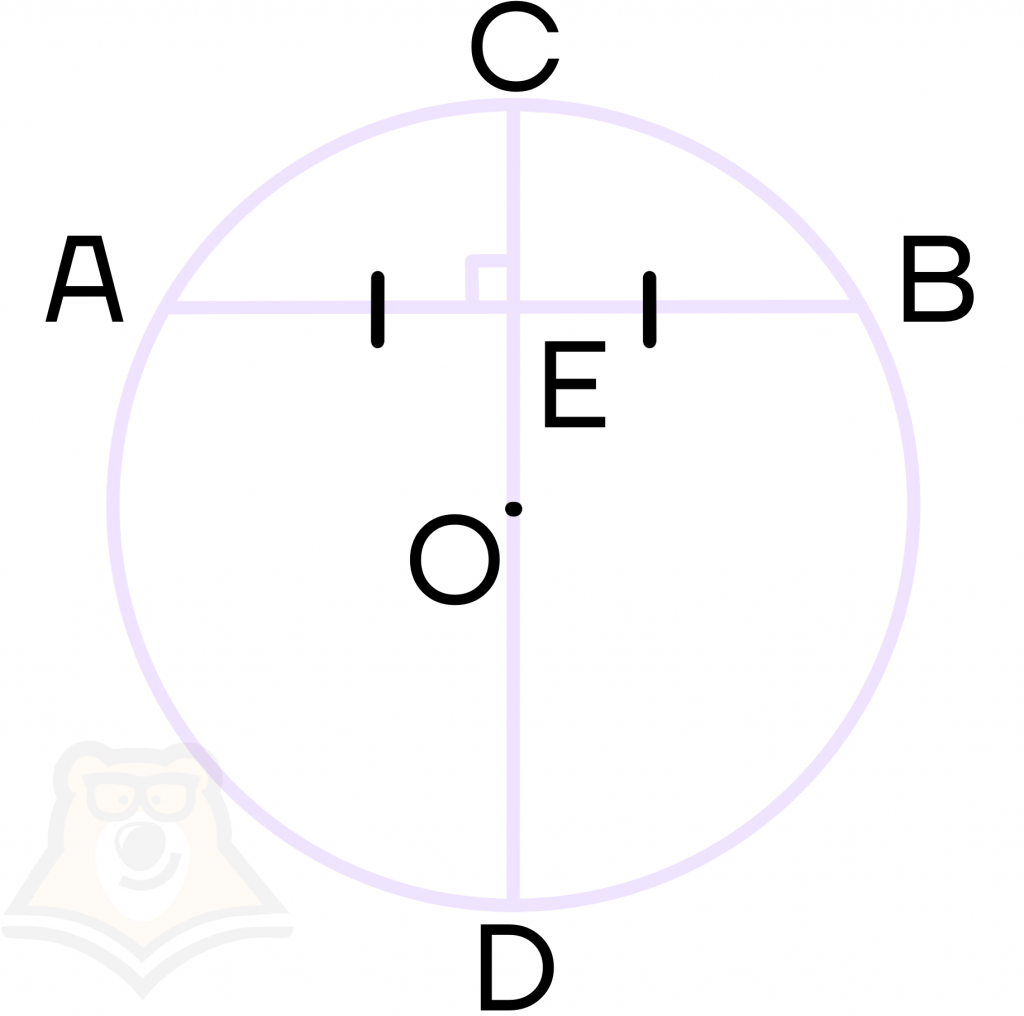
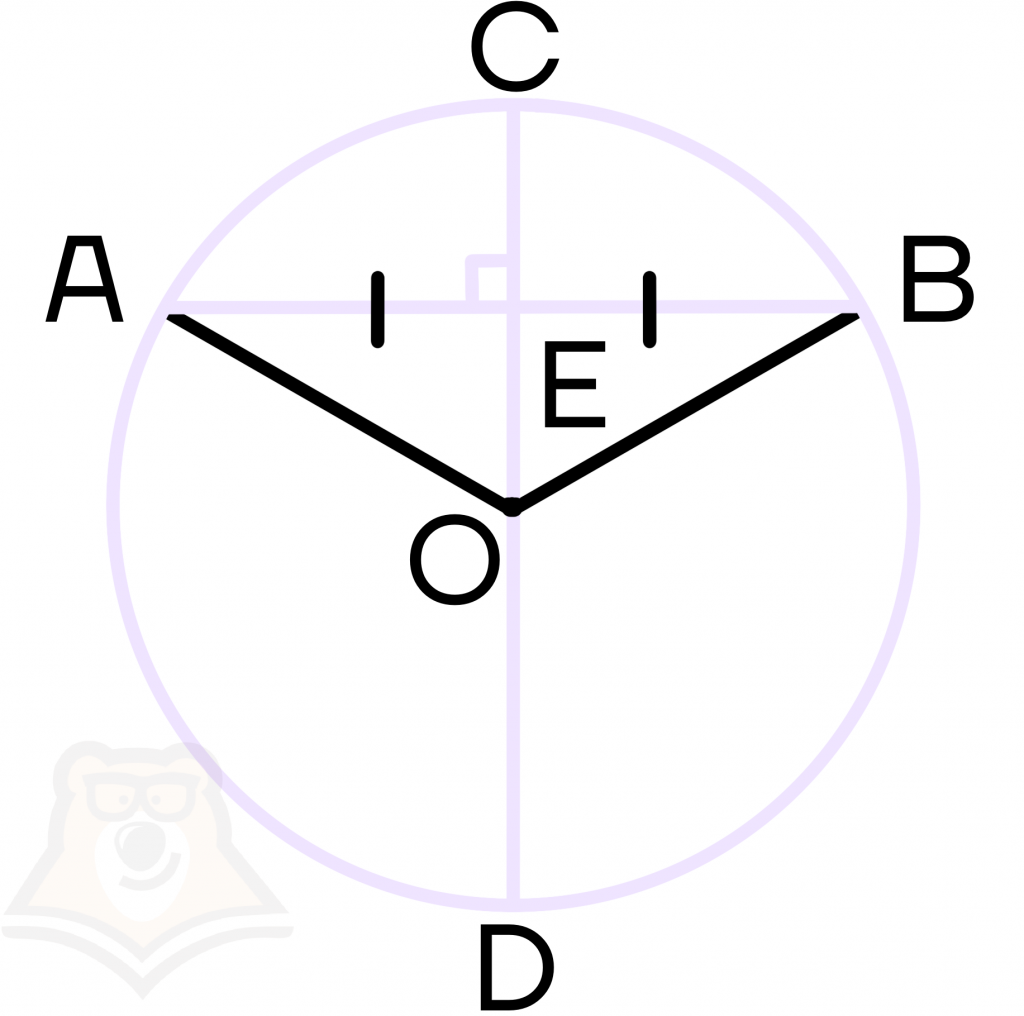
Рассмотрим, почему выполняется это свойство. Достроим треугольник АОВ, в котором АО и ОВ – радиусы. Радиусы в окружности равны, следовательно, треугольник равнобедренный. 

Рассмотрим ОЕ – высота в равнобедренном треугольнике, проведенная к основанию. 

Высота в равнобедренном треугольнике, проведенная к основанию, совпадает с медианой и биссектрисой, следовательно, ОЕ – медиана, а значит АЕ = ЕВ. 

Свойство 4. Угол между пересекающимися хордами окружности равен половине суммы дуг, заключенных между ними. 

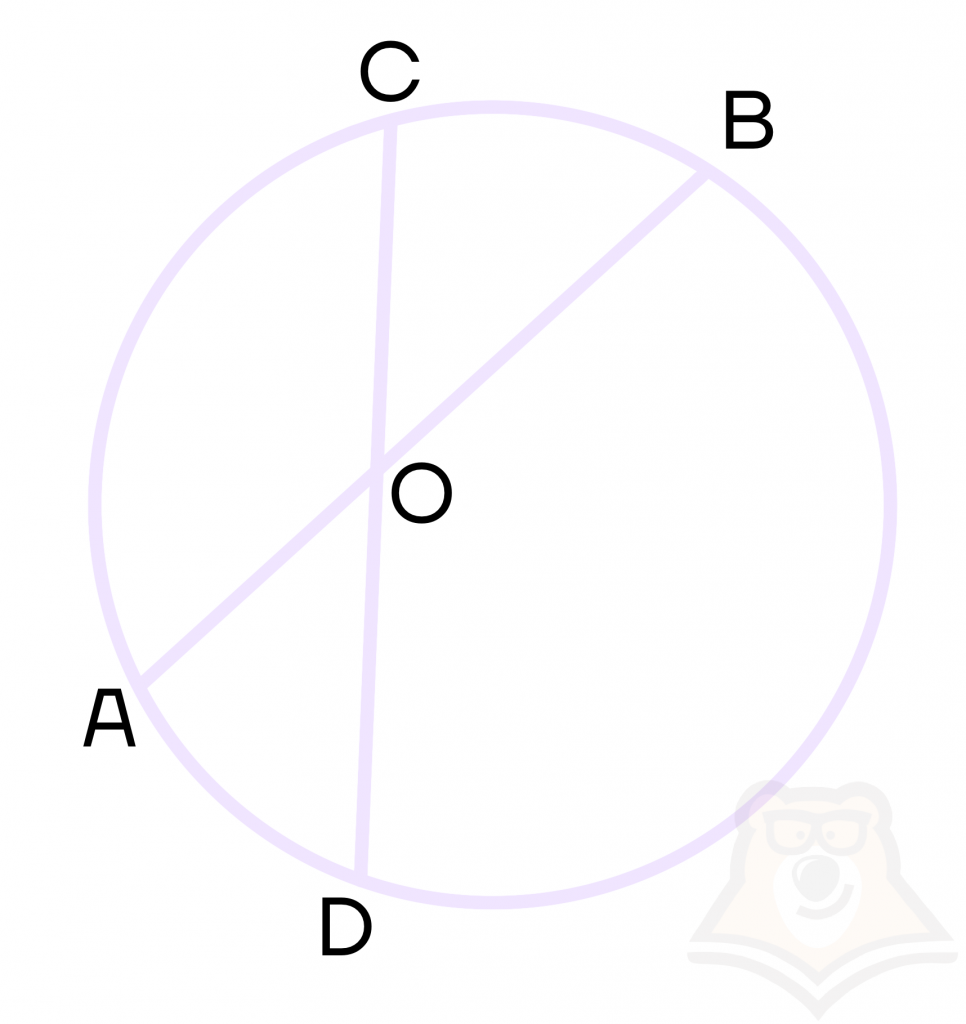
\(∠COB=∠AOD=\frac{1}{2}(\cup BC+ \cup AD)\)

Заметим, что углы COB и AOD равны между собой, поскольку являются вертикальными.

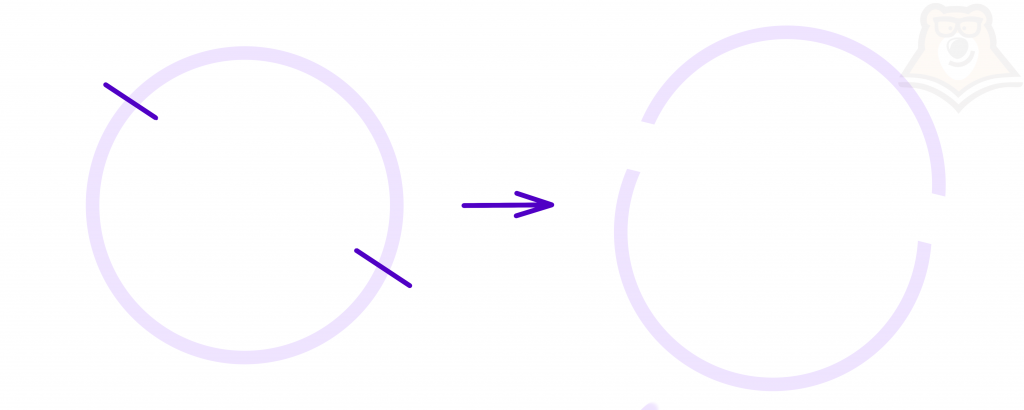
Дуга – это часть окружности, началом и концом которой являются две произвольные точки. 

Допустим, из нашего обруча вырежут какую-то часть. Тогда и вырезанная часть, и оставшаяся часть будут дугами.

Пицца и круг

Мы рассмотрели окружность. Тут уже может возникнуть вопрос: чем круг отличается от окружности? 

В чем отличие окружности от пиццы? Представим пиццу. Она круглой формы? Да. Похожа она на обруч? Нет. И пицца, и обруч имеют форму круга. Разница в том, что обруч внутри полый, а пицца полностью состоит из теста и начинки. Иными словами, в пицце есть не только контур в виде корочки, но и все, что лежит внутри него.  Когда окружность внутри заполнена “начинкой” – это уже круг.

Круг – это геометрическая фигура, которая ограничена окружностью. 

Элементы круга

Рассмотрим элементы круга. 

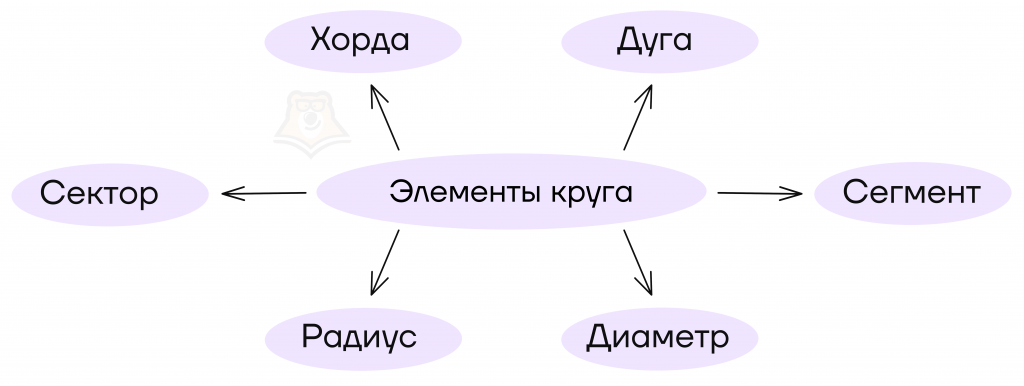
Радиус, диаметр хорды в круге имеют такие же определения, как и в окружности. Поскольку мы теперь рассматриваем не только контур, а всю фигуру, то появляются новые элементы. 

Предположим, к нам в гости пришли друзья, и теперь нужно разделить пиццу между всеми. Разумеется, мы разрежем ее на несколько кусочков. 

Форма кусочков пиццы очень напоминает сектор круга. 

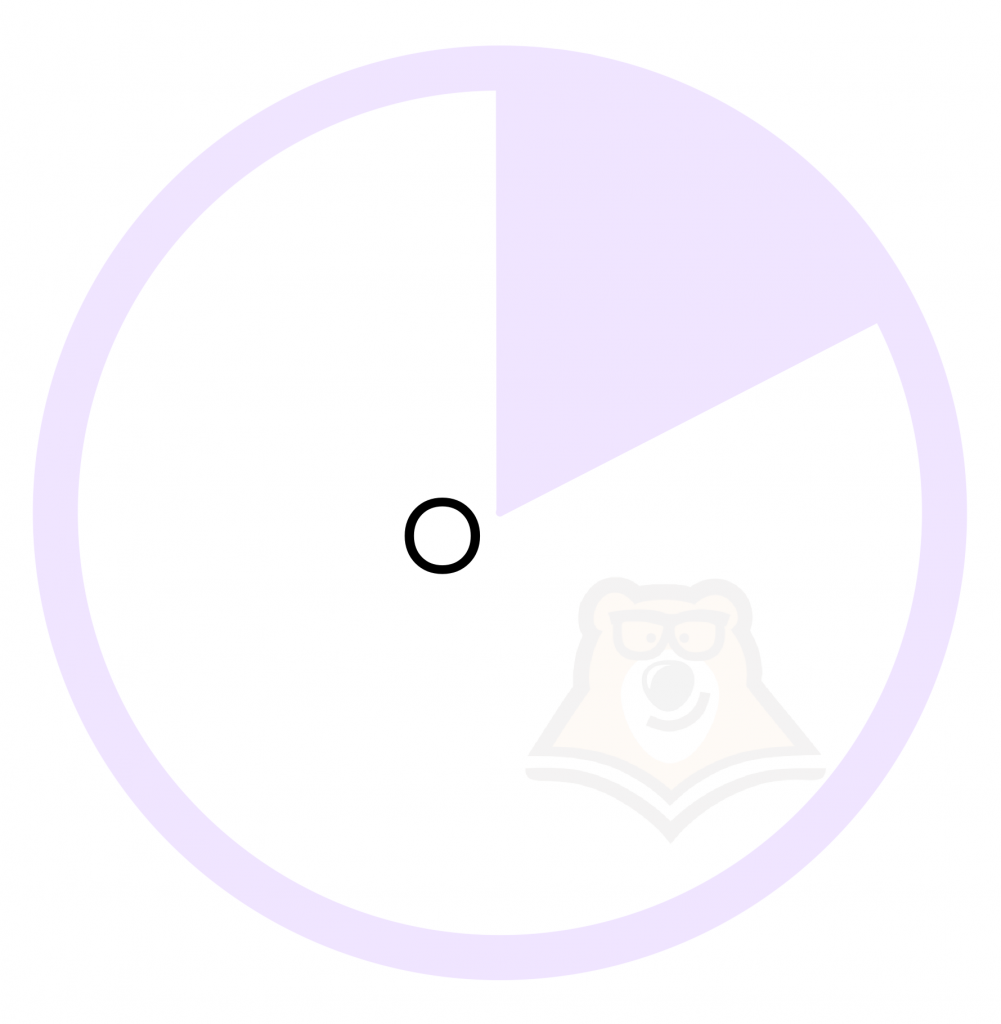
Сектор – это часть круга, которую ограничивают радиусы и дуга. 

При этом два радиуса делят круг на два сектора: один больший, а другой меньший. На рисунке один из них закрашен фиолетовым, а другой белым. 

Если мы захотим отрезать только один кусочек пиццы, то и отрезанный кусочек, и оставшаяся пицца будут секторами круга. 

Теперь разрежем пиццу иначе. Отрежем кусочек по прямой, не проходя через ее середину: 

Таким образом, мы отрежем уже не сектор, а сегмент от пиццы. 

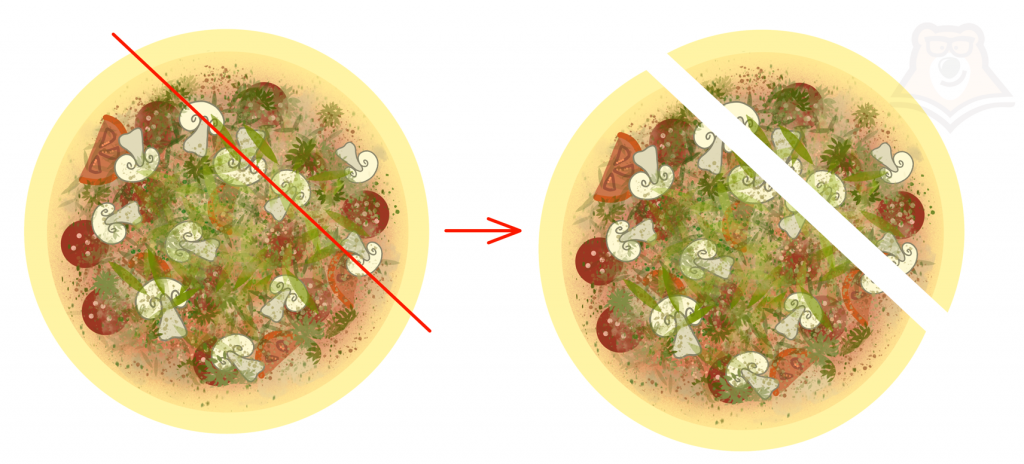
Сегмент – это часть круга, которая ограничена хордой и дугой. 

Причем одна хорда является границей для двух сегментов: и отрезанный кусочек пиццы, и оставшаяся часть будут сегментами. На рисунке ниже один сегмент закрашен фиолетовым, а другой белым. 

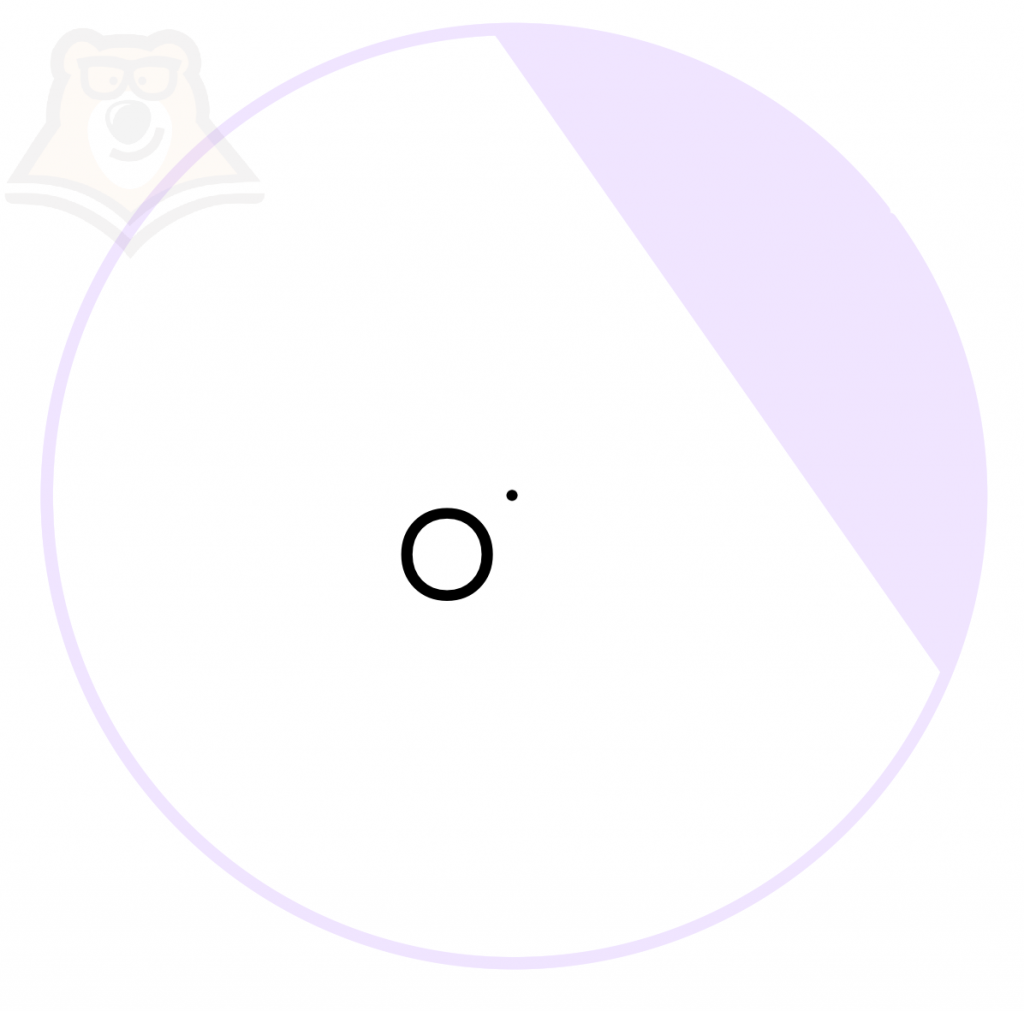
Подведем итог: И в окружности, и в круге можно встретить радиус, диаметр, хорду и дугу. В круге дополнительно появляются сектор и сегмент.

Формулы для окружности и круга

Мы рассмотрели окружности и круг, а также их элементы, однако ни одну задачу не получится решить без формул. Давайте рассмотрим их. 

Однако перед этим необходимо ввести еще несколько терминов. 

Длина окружности – это длина кривой, которая образует окружности. 

Если мы с помощью сантиметровой ленты измерим длину нашего обруча, то как раз получим длину окружности. 

Длина дуги – это длина части кривой, которая образует окружность. 

Отличие от длины окружности только в том, что тут измеряется не вся кривая, а только ее часть. 

В таблице ниже приведены основные формулы, которые могут встретиться при решении задач. 

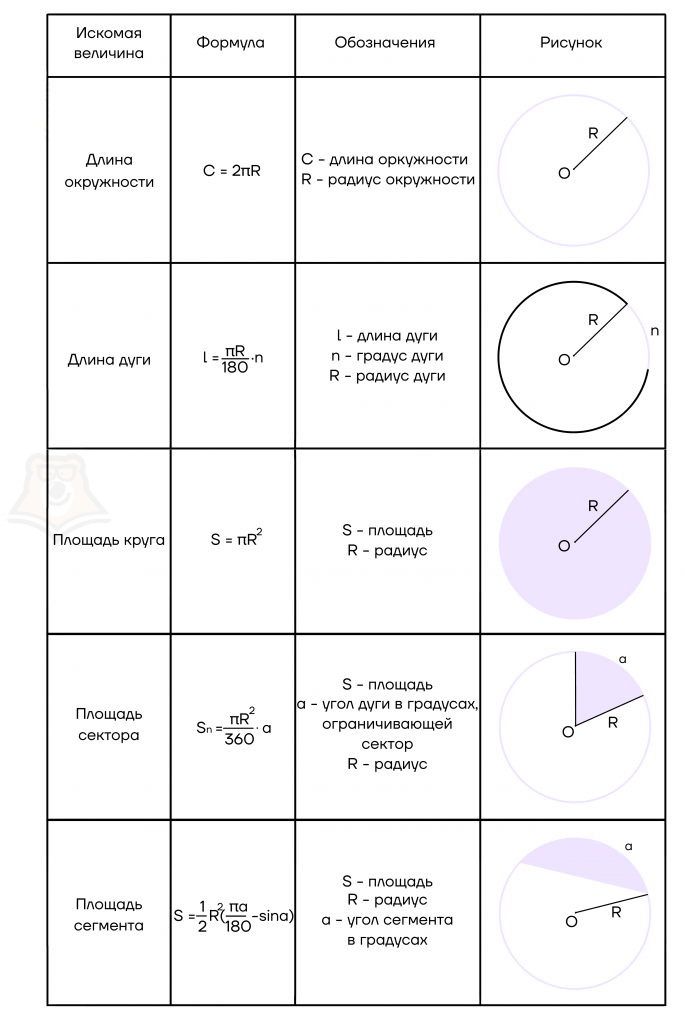
Дуга окружности

Дугу можно измерять не только в единицах измерения длины, но и в градусах. Вся дуга окружности имеет градусную меру 360^\(\circ\). Тогда половина дуги окружности будет равняться 180. 

При этом дуга, равная 180^\(\circ\), называется полуокружностью. Полуокружность ограничивается двумя концами диаметра.  

Думаем, хоть раз в жизни вы слышали  фразу “повернуться на 180^\(\circ\) градусов” или “поменять свое мнение на 180^\(\circ\) градусов”. Это означает, что человек меняет свое мнение буквально на противоположное. Рассмотрим на примере окружности: пусть человек стоит в точке А. Ему нужно пройти по окружности ровно 180^\(\circ\). 

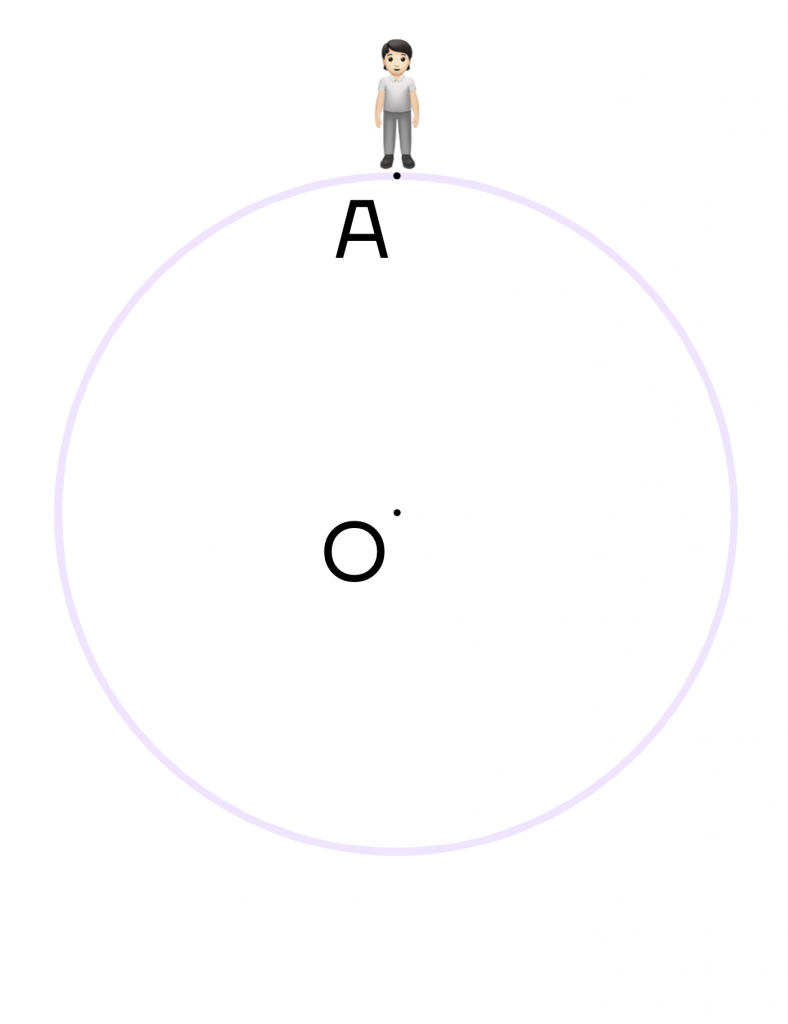
Поскольку человеку нужно пройти полуокружность, то она ограничивается диаметром. Достроим диаметр АВ, тогда наш человек окажется в точке В, то есть на противоположной стороне окружности. 

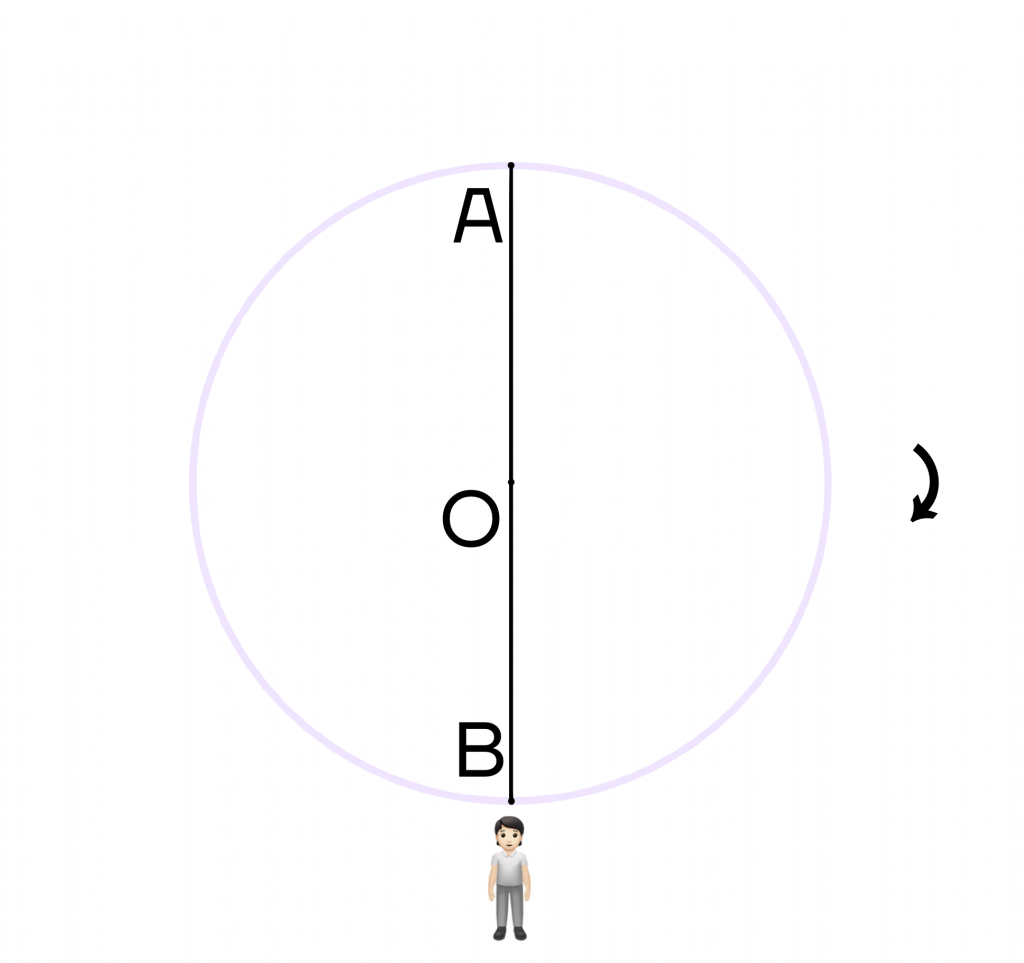
А если он дважды пройдет полуокружность, то снова окажется в точке А, то есть пройдет дугу в 2 * 180 = 360 градусов.

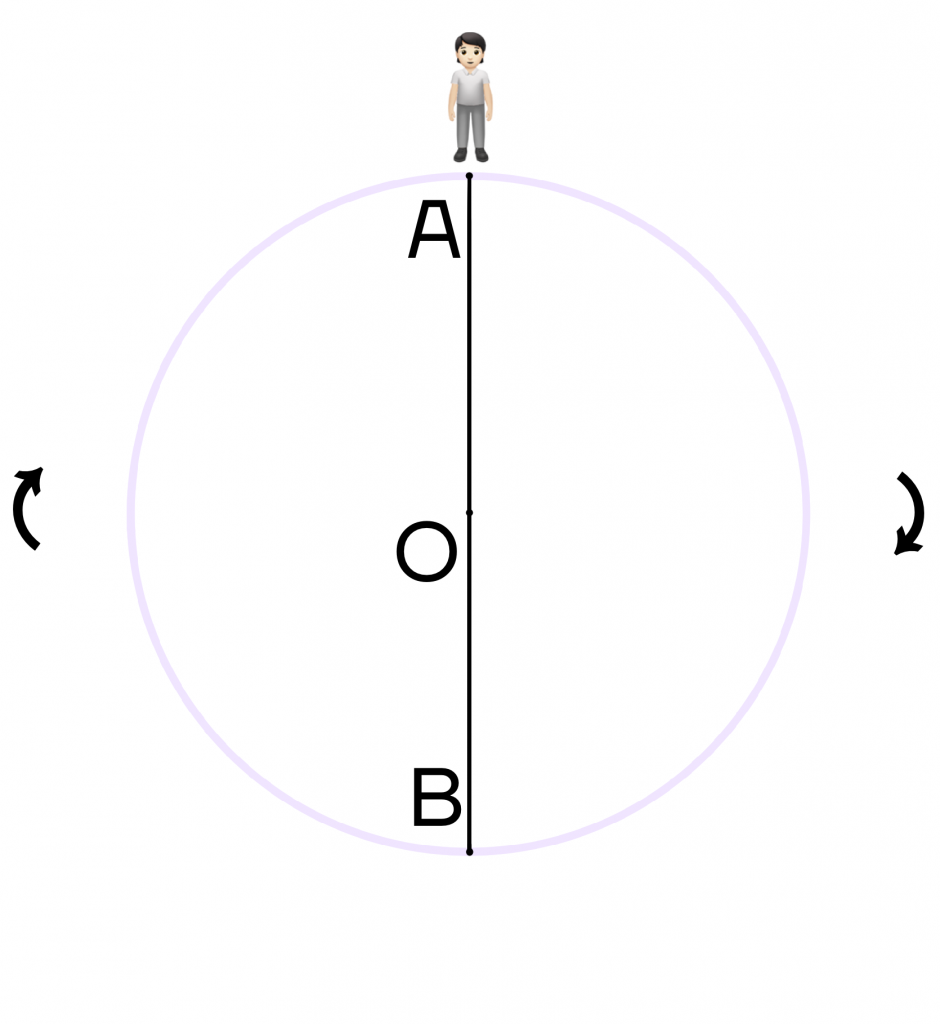
Поэтому если человек будет находиться в точке О и захочет повернуться на 180 градусов, то вместо точки А он будет смотреть на точку В. При повороте на 360 градусов, человек снова будет смотреть на точку А. 

Почему если мы хотим что-то сильно поменять, то лучше разворачивать жизнь на 180 градусов, а не на 360?  При повороте на 180 градусов, мы смотрим на что-то с совершенно противоположной стороны. А вот если повернуться на 360 градусов, то мы будем смотреть на ту же точку, на которую смотрели изначально.

Углы в окружности

Центральный угол – это угол, вершина которого лежит в центре окружности. При этом угол опирается на дугу окружности. 

На рисунке угол АОВ будет центральным. 

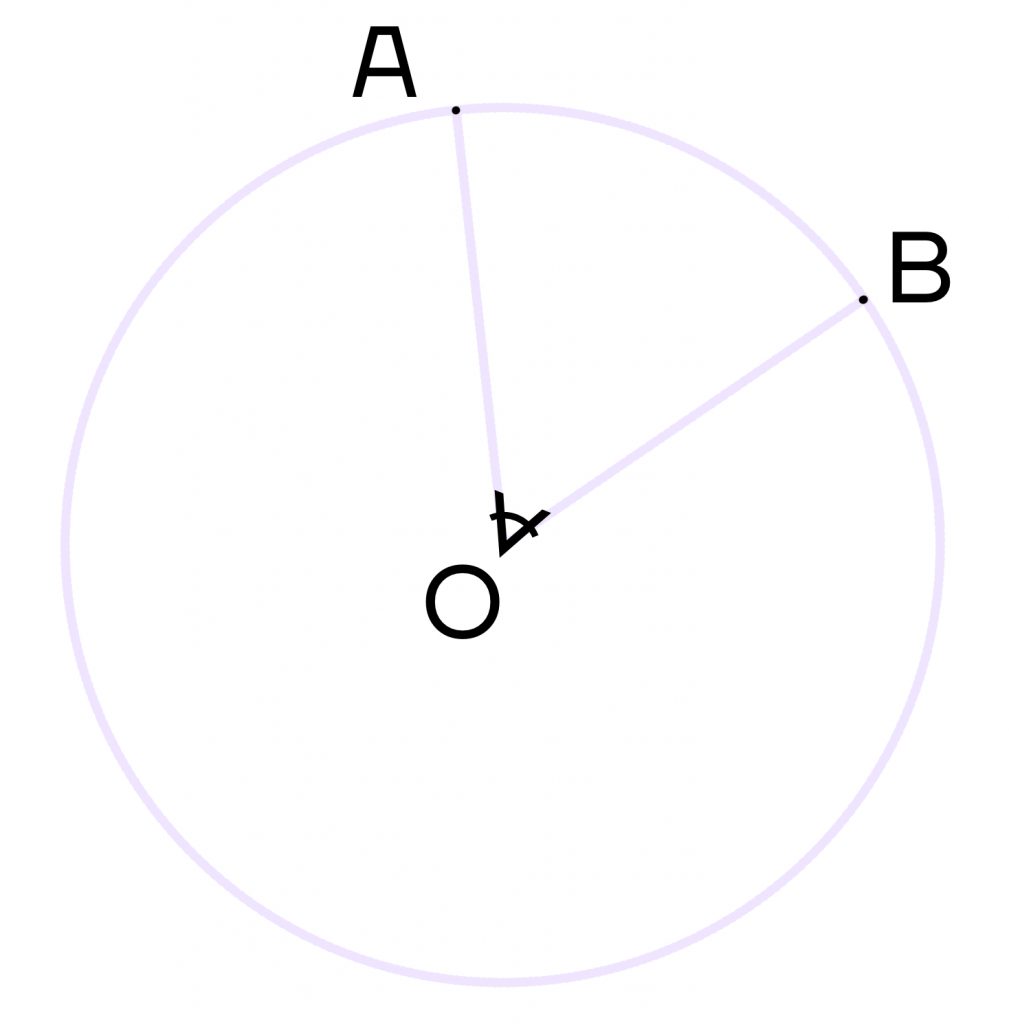
Свойство центрального угла: 

• Центральный угол равен градусной мере дуги, на которую он опирается. 

Например, дуга АВ равна 36^\(\circ\), тогда угол АОВ также равен 36^\(\circ\). 

Вписанный угол – это угол, вершина которого лежит на окружности. Вписанный угол также должен опираться на дугу окружности. 

На рисунке угол АСВ – вписанный. 

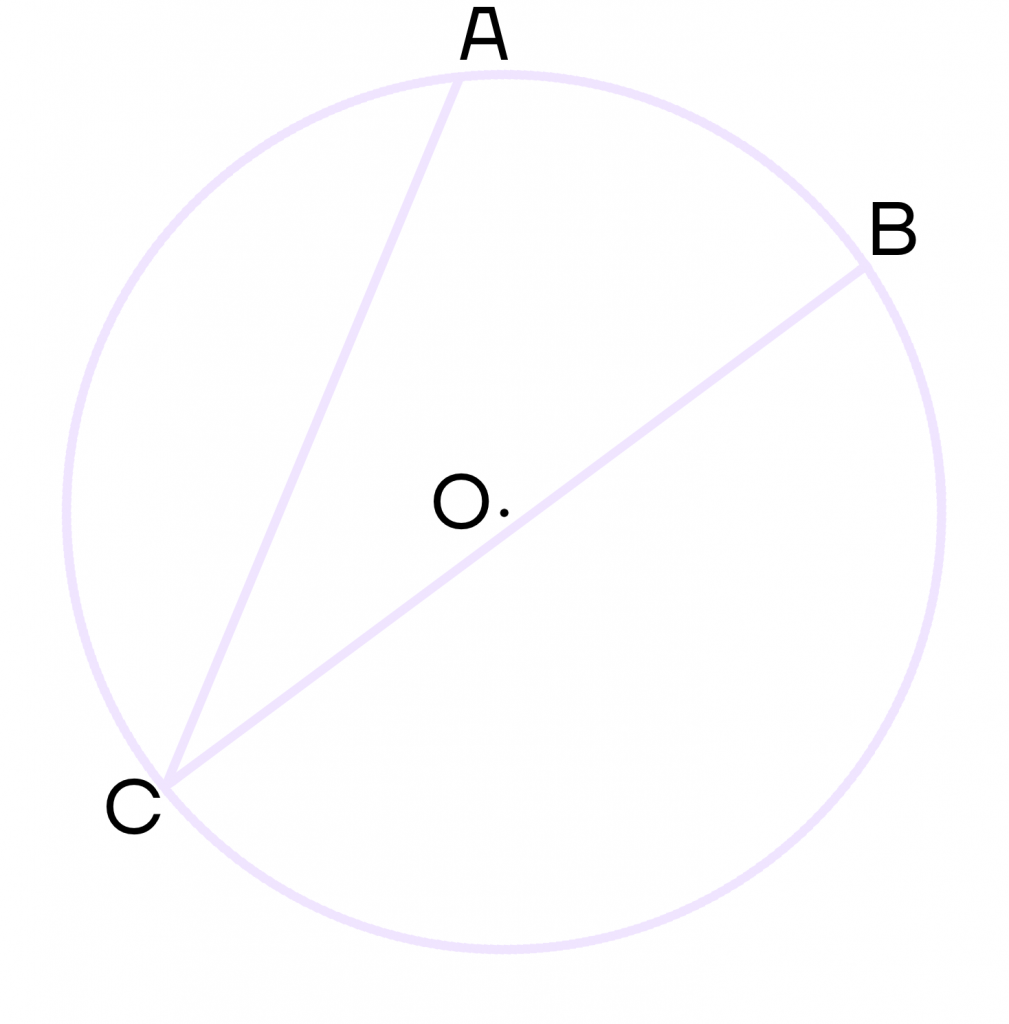
Свойства вписанного угла окружности:

• Вписанный угол равен половине градусной меры дуги, на которую он опирается. 

Например, дуга АВ равна 50^\(\circ\), тогда угол АСВ равен 25^\(\circ\).  

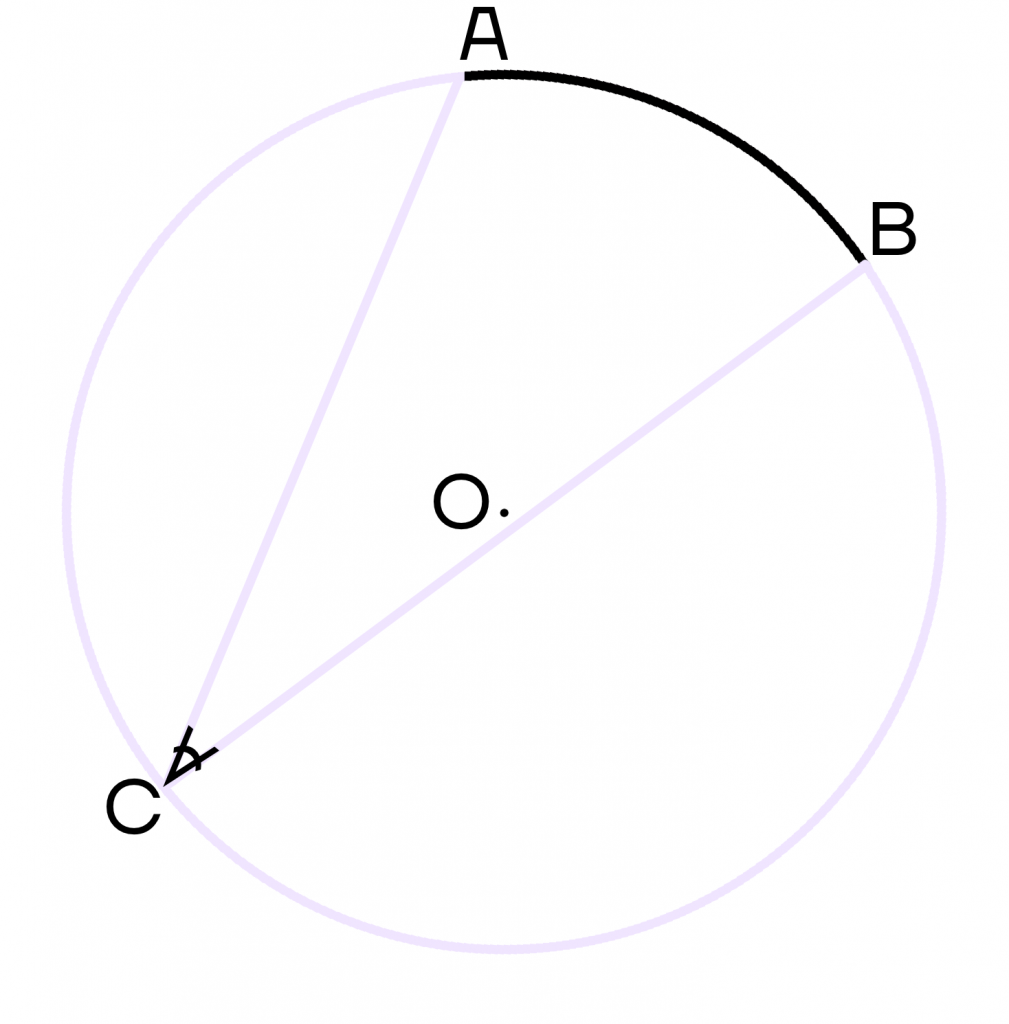
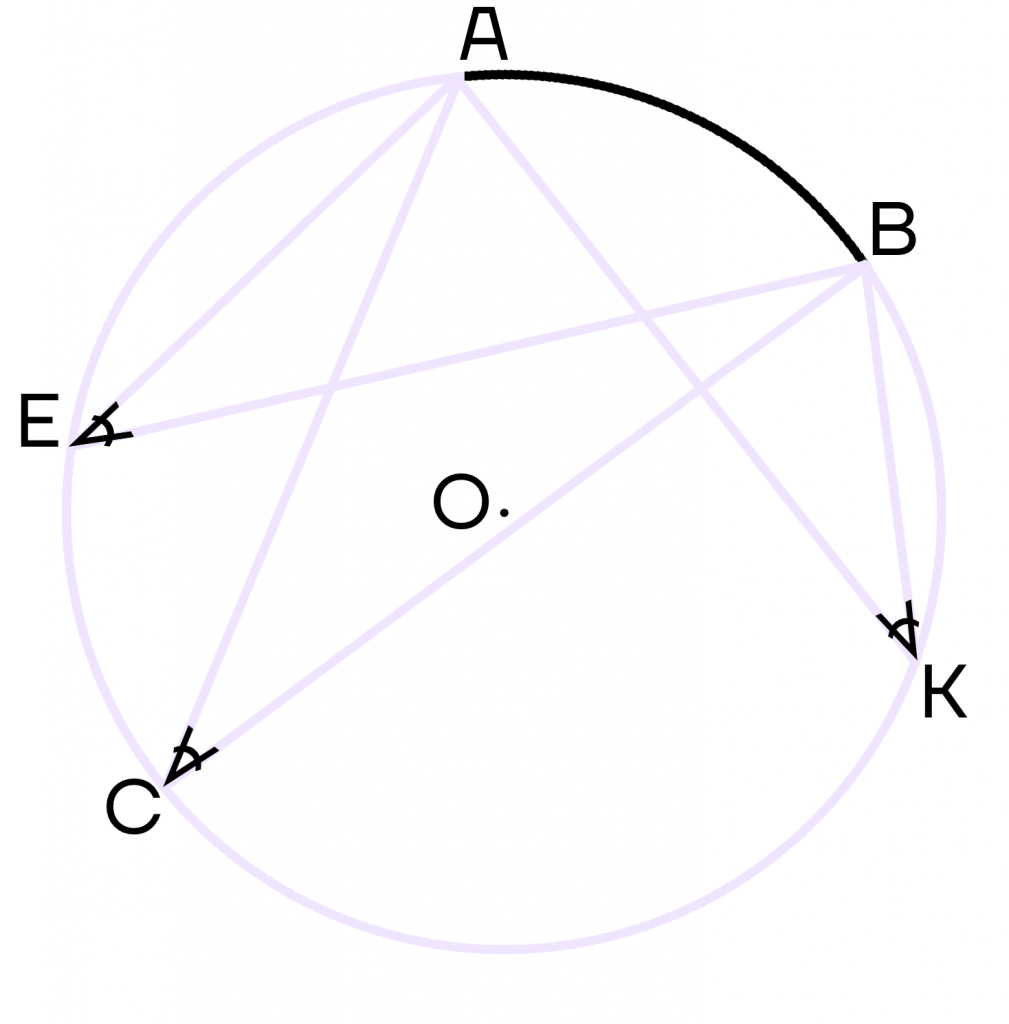
• Вписанные углы, опирающиеся на одну и ту же дугу, равны. 

Пусть углы АСВ, АЕВ и АКВ опираются на душу АВ. Тогда эти углы будут равны между собой. 

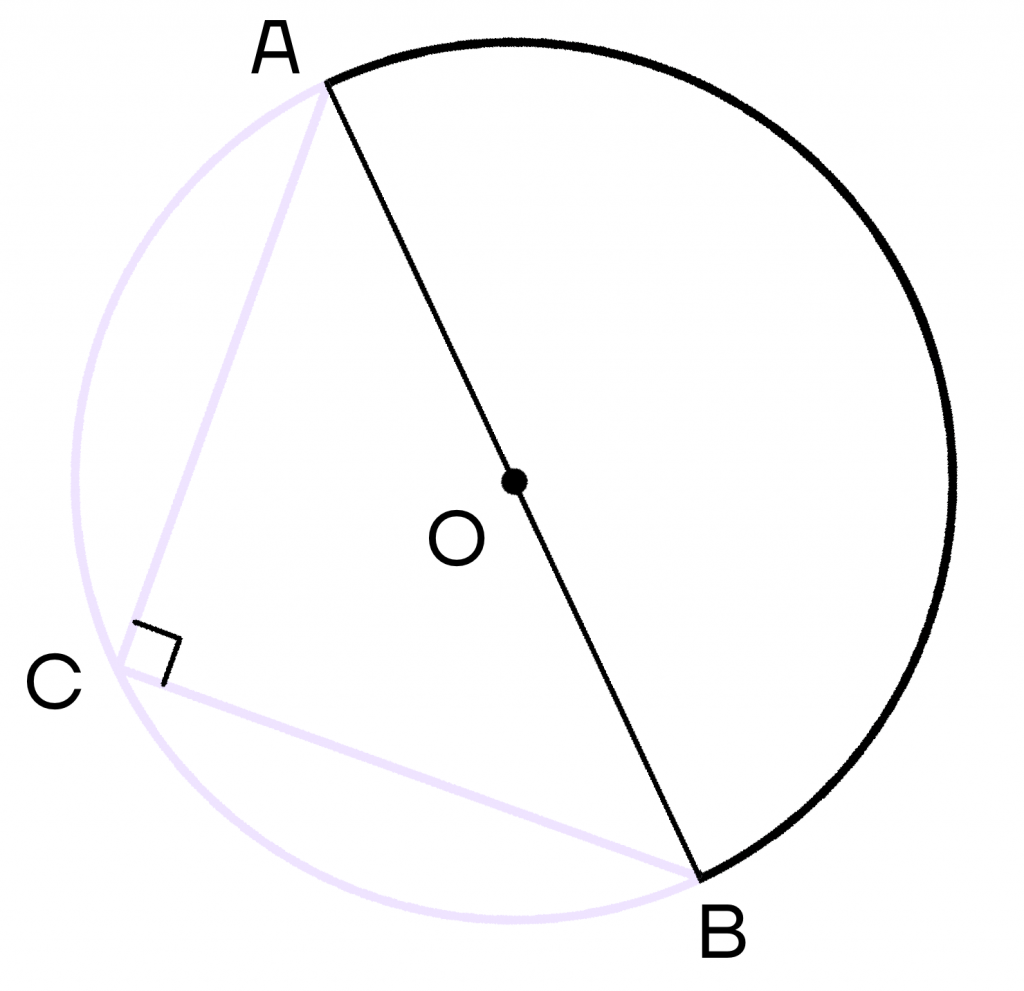
• Вписанный угол, опирающийся на диаметр, равен 90^\(\circ\). 

Вспомним, что диаметр делит окружность на две полуокружности, градусные меры которых равны 180^\(\circ\). Тогда вписанный угол будет равняться 180^\(\circ\) : 2 = 90^\(\circ\). 

Также важно заметить, что вписанный угол равен половине центрального угла. При этом данные углы обязательно должны опираться на одну дугу. 

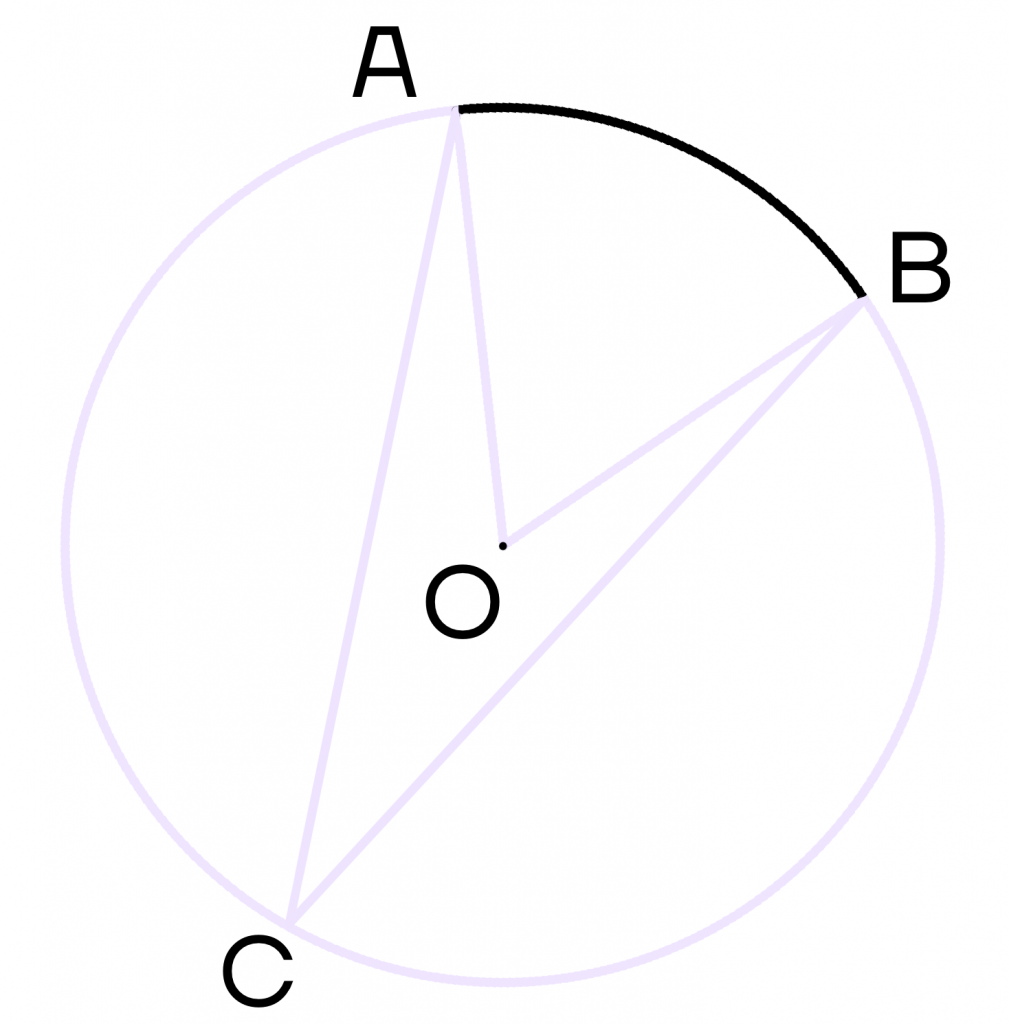
Это легко доказать, если вспомнить, что:

• центральный угол равен градусной мере дуги, на которую он опирается, 
• вписанный угол равен половине градусной меры дуги, на которую он опирается. 

Следовательно, \(∠ACB = \frac{1}{2}∠AOB\).

Термины

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого такого угла.

Фактчек

• Окружность – это замкнутая кривая, все точки которой равноудалены от центра. Элементами окружности являются радиус, диаметр, хорда, дуга. 
• Круг – это геометрическая фигура, которая ограничена окружностью. Помимо радиуса, диаметра и хорды, в круге может встретиться сегмент и сектор. 
• Вся дуга окружности имеет величину 360 градусов. Тогда половина дуги будет равняться 180 градусам. 
• В окружности встречаются центральные и вписанные углы. При этом вписанный угол равен половине дуги, на которую он опирается, а центральный угол равен градусной мере дуги, на которую он опирается. Как следствие, если центральный и вписанный углы опираются на одну дугу, то центральный угол равен двум вписанным углам. 

Проверь себя

Задание 1. 
Что такое окружность? 

1. Замкнутая кривая, все точки которой равноудалены от центра;
2. Геометрическая фигура, которая ограничена замкнутой кривой, все точки которой равноудалены от центра;
3. Геометрическая фигура, которая имеет круглую форму;
4. Часть плоскости, ограниченная замкнутой кривой, все точки которой равноудалены от центра. 

Задание 2. 
Что такое диаметр окружности?

1. Это отрезок, соединяющий центр окружности и любую точку на окружности;
2. Это отрезок, соединяющий две произвольные точки на окружности;
3. Это отрезок, соединяющий две точки на окружности и проведенный через центр окружности;
4. Это половина дуги окружности.

Задание 3.
По какой формуле можно найти длину окружности?

1. \(l = \frac{R}{180} * n\) 
2. \(C=2 \pi R\)
3. C=2R
4. \(l = \pi R\)

Задание 4. 
На окружности выделили дугу в 60 градусов. Какую часть от всей окружности занимает эта дуга?

1. \(\frac{1}{2}\)
2. \(\frac{1}{3}\)
3. \(\frac{1}{6}\)
4. \(\frac{1}{4}\)

Задание 5. 
Вписанный угол равен 50 градусов. Чему равен центральный угол, опирающийся на ту же дугу?

1. 200
2. 50
3. 100
4. 150

Ответы: 1. – 1 2. – 3 3. – 2 4. – 3 5. – 3