Математика

Основы комбинаторики

1.12.2022

2284

На этой странице вы узнаете

Чем удобен капсульный гардероб и зачем здесь математика?
Сколько существует способов перемешать игральные карты?
Сколько различных сэндвичей можно получить из одинакового набора продуктов?

Решить задачу по комбинаторике не сложнее, чем применить комбинацию “горячих клавиш” на компьютере. О том, как именно это сделать мы расскажем в статье.

Комбинаторика

Вы когда-нибудь ездили в короткие поездки? Представим, что мы поехали в одну из таких и взяли с собой совсем немного вещей. Пусть у нас будут одни джинсы и два свитера.

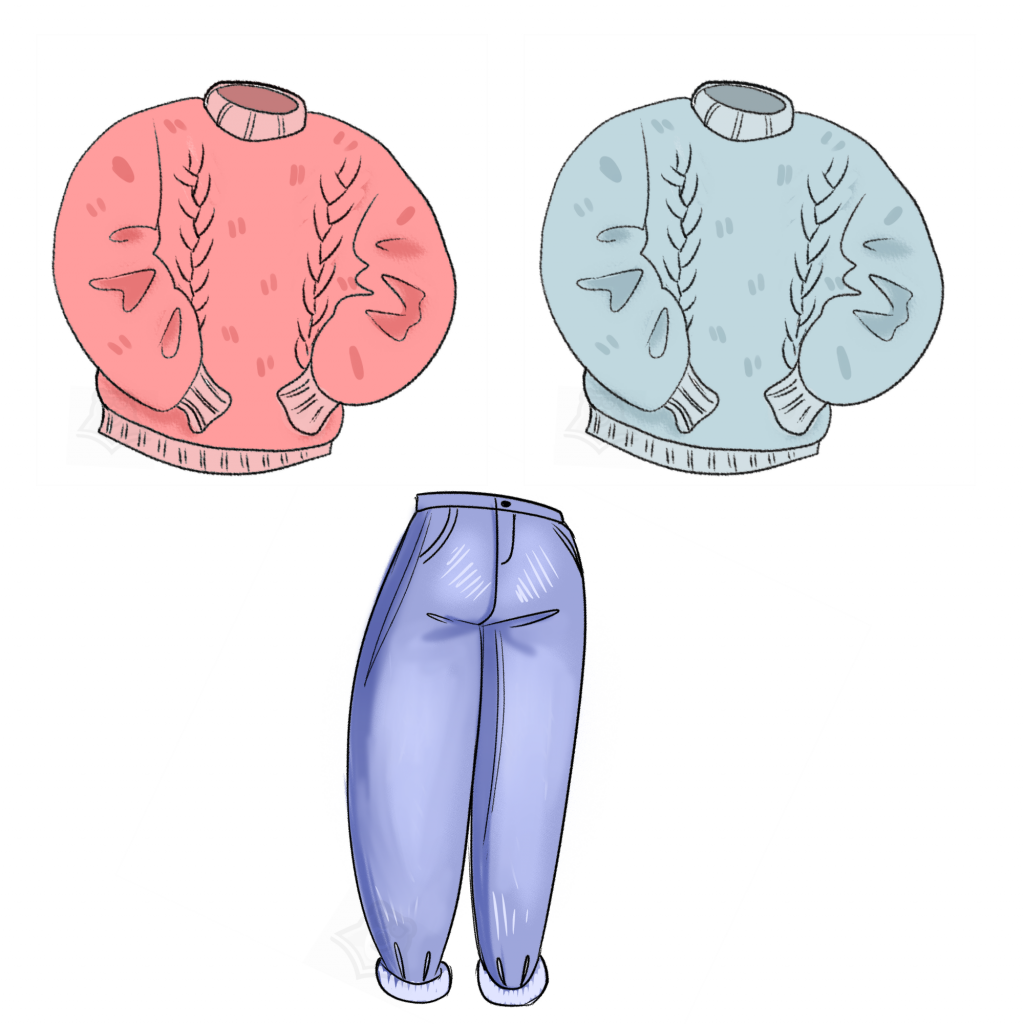
Сколькими комбинациями мы можем их совместить? Ответ очевиден: двумя.

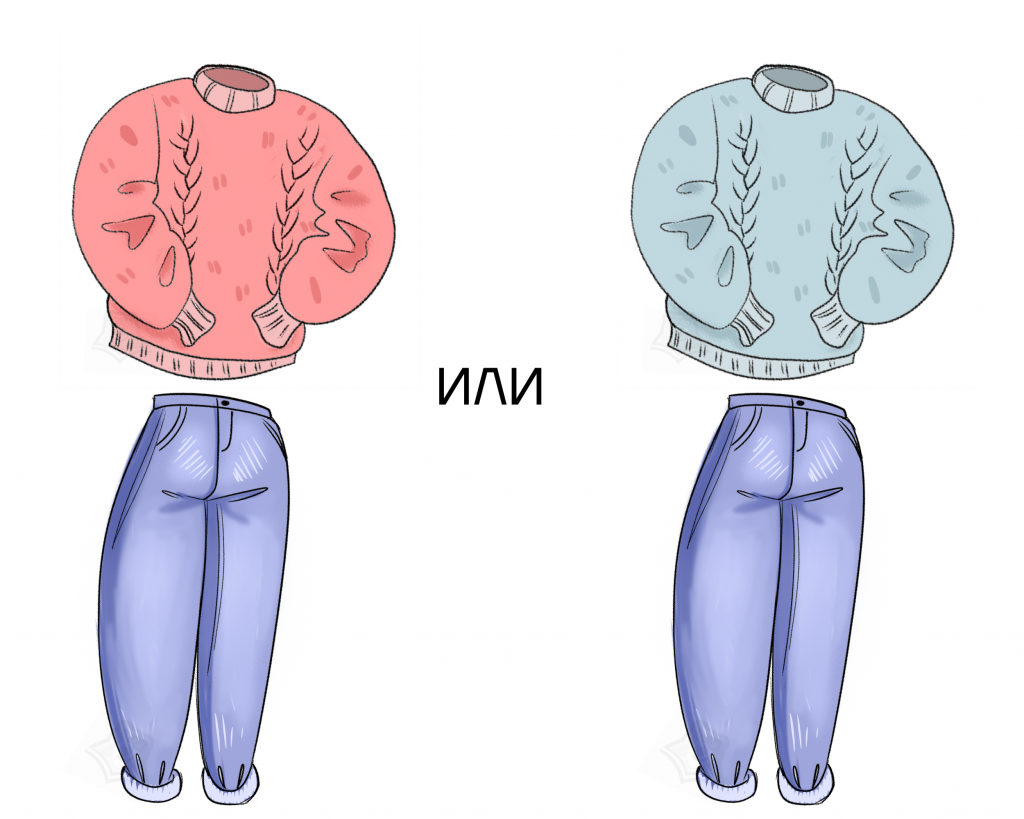
Теперь предположим, что мы взяли джинсы, брюки и два свитера. Сколько получится комбинаций? Четыре.

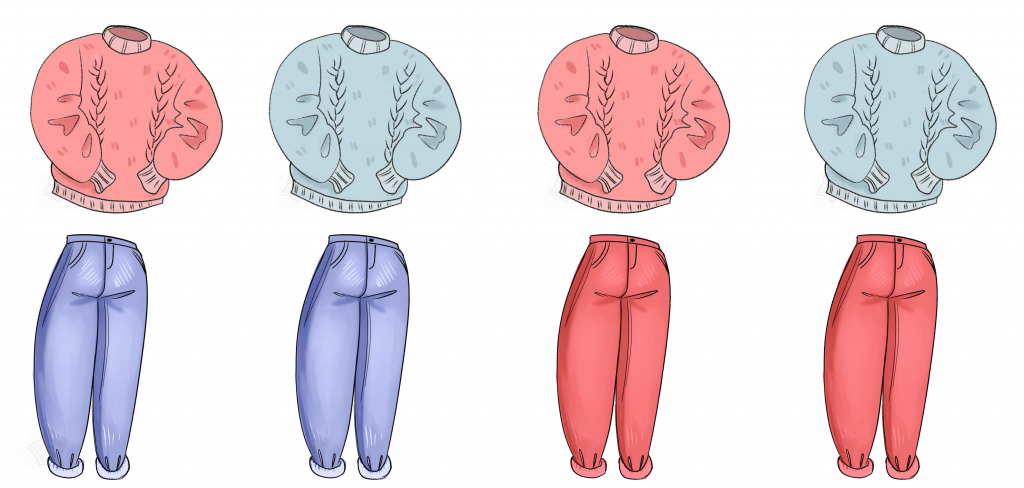
Эти простые процессы иллюстрируют нам очень интересный раздел математики: комбинаторику.

Комбинаторика — раздел математики, изучающий сочетания, перемещения, перестановки элементов, цифр, переменных, данных и т.д.

Комбинаторика встречается в нашей жизни чаще, чем может показаться на первый взгляд. От выбора одежды до выбора маршрута до магазина.

Чем удобен капсульный гардероб и зачем здесь математика?

Капсульный гардероб — это набор из нескольких сочетающихся вещей, которые закрывают все потребности в повседневной одежде. Он удобен, поскольку все вещи сочетаются между собой, не нужно ломать голову над их комбинацией.

Составление комплектов из вещей такого гардероба отлично иллюстрирует комбинаторику. Из ограниченного количества элементов (вещей в гардеробе) мы составляем различные комбинации — образ на день.

Факториал

Но прежде чем знакомиться с комбинаторикой чуть глубже, узнаем про факториал.

Чему будет равно произведение 1 * 2 * 3 * 4? Ответ: 24.

Факториал числа — это произведение натуральных чисел от 1 до а.

То есть 1 * 2 * 3 * 4 — это факториал числа 4.

Факториал обозначается с помощью восклицательного знака, вот так: 4!

Еще немного примеров:
3! = 1 * 2 * 3 = 6
6! = 1 * 2 * 3 * 4 * 5 * 6 = 720
10! = 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9 * 10 = 3628800

Ничего сложного, верно? Но зачем нам может пригодиться факториал? Он очень часто применяется в комбинаторике. Прямо сейчас начнем в нее углубляться.

Перестановки

Как мы можем комбинировать элементы во множестве? Сперва мы можем сделать это логически, если задача несложная.

Пример 1. Монету подкинули 3 раза. Найдите все возможные комбинации.

Решение. Пусть О — выпал орел, а Р — выпала решка. Перечислим все возможные комбинации:

ООО
ООР
ОРО
РОО
РОР
РРО
ОРР
РРР

Всего 8 комбинаций.

Ответ: 8

Но такой способ удобно применять только в простых задачах. Если монетку подкинут 4 раза, то количество комбинаций вырастет до 24. Что делать в более сложных примерах?

Пример 2. Представим, что перед нами лежит список сериалов, которые мы хотим посмотреть. Допустим, их всего 4, назовем их А, Б, В и Г. Теперь вопрос: в каком порядке мы будем смотреть сериалы?

Возможно, мы посмотрим их в порядке АБВГ. Или вдруг захотим посмотреть в порядке АВГБ. Или даже в порядке ГВБА.

Мы только что переставляли местами буквы, за которыми скрываются сериалы. В комбинаторике такая операция так и будет называться: перестановка.

Перестановки — комбинации, состоящие из n объектов и отличающиеся только их расположением.

Заметим, что в перестановках участвуют все элементы множества, то есть все n объектов.

Выведем формулу для перестановок. Вернемся к сериалу.

Сколько сериалов можно посмотреть первым делом? Всего 4.

Дальше мы выбрали один из них. Сколько сериалов могут оказаться на втором месте? 4 — 1 = 3. То есть у нас четыре варианта сериала, который может оказаться на первом месте. Для каждого из этих вариантов еще по три того, какой сериал может оказаться на втором месте. Всего получаем 4 * 3 комбинаций.

Применим аналогичные рассуждения. Сколько сериалов может оказаться на третьем месте? 3 — 1 = 2. Получаем 4 * 3 * 2 комбинаций.

Остался последний сериал. Значит, на четвертом месте может оказаться только один из сериалов. Получаем 4 * 3 * 2 * 1 комбинаций. Ничего не напоминает? Все верно, это факториал.

Следовательно, чтобы найти количество перестановок для n элементов, нужно найти n!

Перестановки обозначаются буквой Р.

P_n = n!

Для наглядности воспользуемся схемой. По какой бы ветке мы ни пошли, мы получим разные комбинации сериалов. В первой строчке будут сериалы, которые мы смотрим в первую очередь, во второй — вторым номером и так далее.

Уже по схеме можно заметить, что вручную считать комбинации очень тяжело, поэтому лучше пользоваться формулой.

Сколько существует способов перемешать игральные карты?

Перемешивание колоды является той же перестановкой: мы просто меняем местами карты. Чтобы найти количество комбинаций, которые могут получиться при перемешивании обычной игральной колоды, нужно вычислить значение 36!

Получаем, что карты можно перемешать 36! = 371993326789901217467999448150835200000000 способами.

Сочетания

А если нам не важен порядок, в котором мы выбираем элементы? Как посчитать, сколько всего комбинаций можно составить с учетом, что в каждой из них будет разный набор элементов?

Представим, что на полке стоит 7 учебников и мы наугад берем три из них. Сколькими способами можно взять эти три учебника?

Пронумеруем учебники, пусть они называются 1, 2, 3, 4, 5, 6 и 7.

Допустим, мы вытащим сначала учебник №1. Для второго места останется 6 учебников. А для третьего — 5. Для данного случая получаем 1 * 5 * 6 = 30 комбинаций.

Первым учебником можно взять и 2, и 3, и 4 и так далее. Следовательно, всего мы получаем 7 * 6 * 5 = 210 комбинаций.

Однако по такой логике некоторые комбинации будут повторяться. Например, 1,2,3,7 и 3,7,2,1 — это одни и те же учебники. А нам необходимо, чтобы в каждом наборе были разные элементы.

Вручную не избавиться от всех “лишних” комбинаций. Воспользуемся формулой сочетаний из комбинаторики.

Чтобы ее понять, введем термин сочетаний.

Сочетания — комбинации из m элементов, которые выбраны из n различных элементов и отличаются только составом элементов.

Разберем термин на примере. У нас было 7 учебников – это n различных элементов. Из них мы берем только 3 учебника – то есть m элементов.

Формула сочетания выглядит так:

\(C_n^m = \frac{n!}{(n — m)! * m!}\)

Вспоминаем, что у нас m = 3, n = 7. Подставляем в формулу:

\(С_7^3 = \frac{7!}{(7 — 3)! * 3!} = \frac{7!}{4! * 3!}\)

Немного преобразуем формулу, чтобы не считать большие числа. Для этого раскроем 7! как 1 * 2 * 3 * 4 * 5 * 6 * 7 и 4 как 1 * 2 * 3 * 4, а после сократим дробь:

\(\frac{7!}{4! * 3!} = \frac{1 * 2 * 3 * 4 * 5 * 6 * 7}{1 * 2 * 3 * 4 * 3!} = \frac{5 * 6 * 7}{3!}\)

Дальше раскрываем 3! как 1 * 2 * 3 и считаем ответ:

\(\frac{5 * 6 * 7}{3!} = \frac{5 * 6 * 7}{1* 2 * 3} = \frac{210}{6} = 35\)

Всего 35 способов вытянуть разные учебники.

Теперь представим, что к нам в гости на день рождения должны прийти трое друзей. Они решили принести по шарику из ближайшего цветочного магазина. В этом магазине 5 видов шариков, а наши друзья покупают их независимо друг от друга — не видят, что купили двое других. Сколько способов у наших друзей купить шарики так, чтобы они не повторялись?

Всего у нас 5 шариков – это n. Друзей трое, то есть они принесут на праздник только три шарика – это m. По формуле получаем:

\(С_5^3 = \frac{5!}{(5 — 3)! * 3!} = \frac{5!}{2! * 3!} = \frac{1 * 2 * 3 * 4 * 5}{1 * 2 * 1 * 2 * 3} = \frac{4 * 5}{1 * 2} = \frac{20}{2} = 10\) способов.

Изобразим графически. Пусть в магазине продаются красные, зеленые, голубые, оранжевые и фиолетовые шарики. Значит, они могут распределиться между друзьями так:

В этом случае нам неважно, кто из друзей какой шарик принесет. Нам просто нужно найти количество комбинаций шариков так, чтобы они не повторялись между собой.

Размещения

Сколько всего вариантов у наших друзей принести шарики? То есть сейчас нас интересует не только комбинация, но и порядок элементов в ней.

Рассмотрим одно из сочетаний. Сейчас нам важен порядок шариков. Пусть верхний шарик принесет первый друг, средний – второй, а нижний – третий.

Для первой комбинации имеем еще шесть комбинаций:

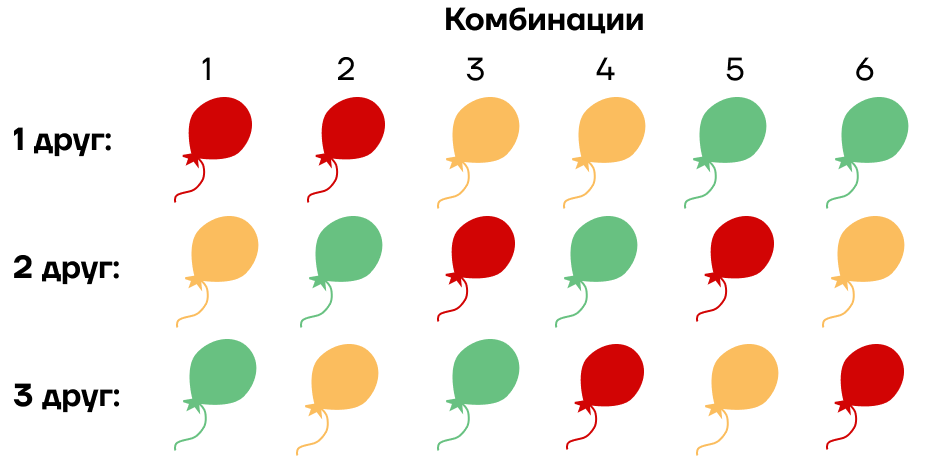
То есть для каждой из десяти комбинаций у нас есть по шесть вариантов размещения шариков в них. Всего получаем 10 * 6 = 60 комбинаций.

В этом случае у нас был достаточно простой счет. А если каждая комбинация будет состоять из 10 элементов? Найти все варианты вручную у нас не получится. Но в комбинаторике есть решение и для этого случая.

Когда важны и порядок, и комбинация элементов, мы имеем дело с размещениями.

Размещения — комбинации, составленные из m элементов, которые выбраны из n различных элементов и отличаются составом и порядком элементов.

В нашем случае n = 5 — виды шариков в магазине, а m = 3 — сколько всего шариков окажется на дне рождения.

Формула для размещений выглядит следующим образом:

\(A_n^m = \frac{n!}{(n-m)!}\)

В нашем случае получаем:

\(A_5^3 = \frac{5!}{(5 — 3)!} = \frac{5!}{2!} = \frac{1 * 2 * 3 * 4 * 5}{1 * 2} = 3 * 4 * 5 = 60\), как мы и нашли ранее.

В рассуждениях выше можно заметить, что мы сочетания умножили на перестановки. Выразим это в формулах:

\(\frac{n!}{(n — m)! * m!} * m! = \frac{n!}{(n — m)!}\)

Таким образом, мы можем вывести зависимость между перестановками, сочетаниями и размещениями.

\(A_n^m = C_n^m * P_m\)

Правила сложения и умножения

Один из наших друзей решил принести нам в подарок еще и цветы. Он знает, что мы любим розы, пионы и кактусы. К сожалению, денег у него хватит только на один цветок. Сколько у него способов купить цветы?

Три: или роза, или пион, или кактус.

Важно обратить внимание на “или”. Это слово-маркер, которое показывает, что нужно применить правило сложения.

Правило сложения — одно из правил комбинаторики, которое утверждает, что если элемент в первом множестве можно выбрать n способами, а элемент во втором множестве можно выбрать m способами, и при этом множества не имеют общих элементов, то выбор одного из элементов множества осуществляется по формуле m+n.

Рассмотрим это правило на примере.

Допустим, в коробке 15 шариков: 7 из них фиолетовые и 8 оранжевые. Сколько существует способов вытянуть три шарика одинакового цвета?

Чтобы решить эту задачу, нам необходимо вытянуть три фиолетовых или три оранжевых шарика. Значит, можно воспользоваться правилом сложения.

Нам нужно сложить все комбинации троек фиолетовых шариков и троек оранжевых шариков. Воспользуемся формулой сочетания, поскольку нам важно, какие именно шарики мы вытягиваем, а не в каком порядке.

Для фиолетовых шариков: \(C_7^3 = \frac{7!}{(7 — 3)! * 3!} = \frac{7!}{4! * 3!} = \frac{1 * 2 * 3 * 4 * 5 * 6 * 7}{1 * 2 * 3 * 4 * 1 * 2 * 3} = \frac{5 * 6 * 7}{1 * 2 * 3} =35\) комбинаций.

Для оранжевых шариков: \(C_8^3 = \frac{8!}{(8 — 3)! * 3!} = \frac{8!}{5! * 3!} = \frac{1 * 2 * 3 * 4 * 5 * 6 * 7 * 8}{1 * 2 * 3 * 4 * 5 * 1 * 2 * 3} = \frac{6 * 7 * 8}{1 * 2 * 3} = 56\) комбинаций.

По правилу сложения мы получаем всего 35 + 56 = 91 комбинацию.

Предположим, мы захотели сделать горячий шоколад. Для этого нам нужно молоко и шоколад. В магазине у дома 3 вида молока и 4 вида шоколада. Сколько способов купить ингредиенты для напитка?

К каждому виду молока мы можем взять один из четырех видов шоколада. Для одного вида молока у нас есть 4 вида шоколада.

Всего таких комбинаций 3: по одной на каждый вид молока.

Всего мы получаем 3 * 4 = 12 комбинаций ингредиентов. Здесь мы видим в действии правило умножения.

Правило умножения — правило комбинаторики, согласно которому, если элемент из первого множества может быть выбран n раз и элемент из второго множества может быть выбран m раз, то их пара может быть составлена m * n способами.

Правило умножения можно заменить союзом и. Нам нужно взять и молоко, и шоколад.

Следует заметить, что элементов может быть не только пара, а три, четыре, пять и так до бесконечности.

Например, мы решили купить к горячему шоколаду еще и зефирки. Их в магазине два вида. Тогда в нашей корзине может оказаться 2 * 3 * 4 = 24 комбинаций продуктов.

Если мы захотим еще докупить одну из десяти кружек в магазине , то получим 2 * 3 * 4 * 10 = 240 комбинаций покупок.

Сколько различных сэндвичей можно получить из одинакового набора продуктов?

Предположим, мы захотели купить сэндвич и зашли за ним в одно из кафе. На выбор нам предоставили:
— три вида хлеба — белый, зерновой, ржаной;
— два вида огурчиков — свежие и малосольные;
— помидоры;
— два вида мяса — курица и говядина;
— два вида моркови — свежая и по-корейски;
— четыре соуса — майонез, кетчуп, сырный, грибной.

Нам захотелось все и сразу. Попросим сделать сэндвичи так, чтобы они отличались хотя бы одним ингредиентом. Повара очень долго готовили нам заказ, но справились с задачей. В итоге у нас получилось 3 * 2 * 1 * 2 * 2 * 4 = 96 сэндвичей.

Фактчек

Комбинаторика — раздел математики, изучающий сочетания, перемещения, перестановки элементов, цифр, переменных, данных и другие.
Факториал числа а —это произведение натуральных чисел от 1 до а. Факториал обозначается с помощью восклицательного знака и ищется по формуле а! = 1 * 2 * 3 * … * а.
Перестановки — комбинации, состоящие из n объектов и отличающиеся только их расположением. Перестановки обозначаются буквой Р и находятся по формуле P_n = n!
Сочетания — комбинации из m элементов, которые выбраны из n различных элементов и отличаются только составом элементов. Сочетания обозначаются с помощью буквы С и находятся по формуле \(C_n^m = \frac{n!}{(n — m)! * m!}\)
Размещения — комбинации, составленные из m элементов, которые выбраны из n различных элементов и отличаются составом и порядком элементов. Размещения обозначаются буквой А и находятся по формуле \(A_n^m = \frac{n!}{(n — m)!}\).
Правила сложения и умножения позволяют найти количество сочетаний объектов из нескольких множеств. Правило сложения можно заменить союзом или, а правило умножения — союзом и.

Проверь себя

Задание 1.
В пенале лежит три черных ручки, две красных и пять синих. Сколько способов взять ручку из пенала?

Задание 2.
На конкурсе Алине необходимо вытянуть жребий из двух мешочков. Жребий представляет собой шарики разных цветов. В первом мешочке лежит 5 различных шариков, а во втором мешочке 7 различных шариков. Сколько способов у Алины вытянуть жребий?

Задание 3.
Сколько сочетаний из пяти букв можно составить из А, Б, Е, Г, Д?

Задание 4.
Маша в магазине выбирает помаду из пяти оттенков. Она решила купить два из них. Сколько способов у Маши купить помаду?

Задание 5.
Перед Костей лежит 6 билетов. Он наугад тянет 3 из них и отвечает на вопросы. Учитывая порядок вопросов, cколько способов у Кости ответить на билеты?

Ответы: 1. – 4 2. – 4 3. – 3 4. – 2 5. – 3

Комбинаторика Математика

Понравилась статья? Оцени: