Текстовые задачи

На этой странице вы узнаете

• В каком задании ЕГЭ по профильной математике можно получить легчайший 1 балл?
• ОДЗ: встречается ли она в реальной жизни или же это особенность функций?
• Как сложное домашнее задание сделало одного студента всемирно известным?

Сегодня мы попробуем себя в разных профессиях, будем и химиками, и токарями, отправимся в поход и, конечно же, порешаем текстовые задачки! 

Единицы измерения

Сначала вспомним единицы измерения, которые используются в текстовых задачах на ЕГЭ:

• 1 метр = 100 сантиметров = 1000 миллиметров = 0,001 километра
• 1 килограмм = 1000 грамм = 0,001 тонны
• 1 литр = 1000 грамм
• 1 минута = 60 секунд = \(\frac{1}{60}\) часа

Это обязательно пригодится нам дальше! А теперь узнаем, что такое масштаб.

Масштаб

Масштаб — отношение двух величин, отношение расстояния на изображении или карте к реальной местности. 

Например, посмотрим на карту Москвы:

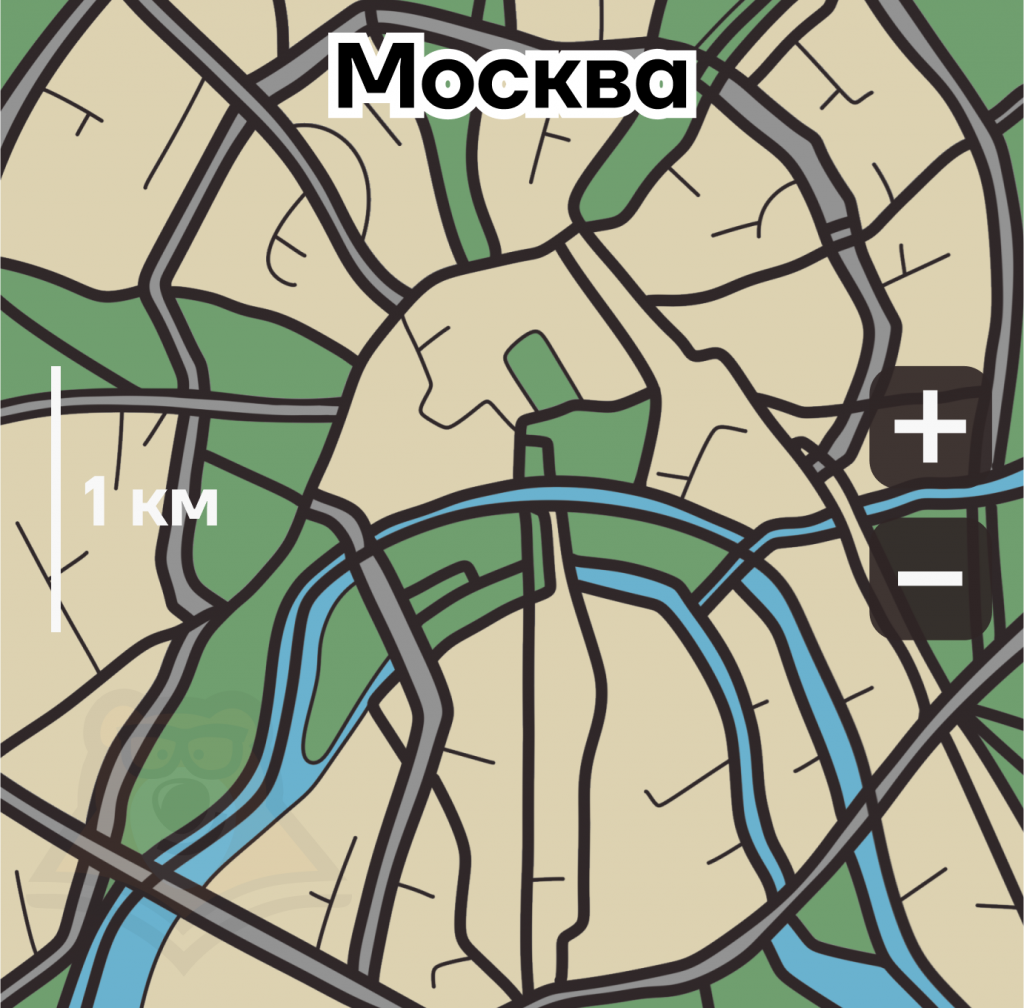
Масштаб — 1:100 000, то есть одному сантиметру на карте соответствует 100 000 см (1 км) в реальности. Это пример численного масштаба. 

Есть еще именованный масштаб. Например, пишут так: «В 1 сантиметре 1 километр». Существуют и другие виды, которые используются реже. Все это — масштабы уменьшения.

Натуральная величина записывается как 1:1.

И есть еще масштабы увеличения. Например, 10:1, 100:1 и так далее. В таком случае, на чертеже размеры больше, чем реальные. В примере с 10:1 10 сантиметрам на чертеже соответствуют 1 сантиметру реальной местности. 

А теперь переходим к самим задачам!

Текстовые задачи с прикладным содержанием

Давайте представим, что сейчас уже лето: экзамены закончились, на улице тепло, птички поют свои песенки, а зеленую листву деревьев чуть колышет прохладный ветерок. Мы приехали в деревню к бабушке с дедушкой, и у них на участке стоит колодец. Мы кидали в него камешки, и вдруг пошел ливень. 

Нам стало интересно: на сколько должен повыситься уровень воды в колодце, чтобы время падения камешков изменилось с 0,8 секунд до 0,6? Поскольку мы только что сдали экзамены, то помним, что в данном случае расстояние, которое пролетает камушек, рассчитывается по формуле \(h = 5t^2\) и измеряется в метрах.  

Чтобы подсчитать, насколько должен подняться уровень воды, примем \(h_1\) как расстояние до воды до дождя, а \(h_2\) как расстояние до воды после дождя. Соответственно, получаем выражение:

\(h_1-h_2 = 5*0,8^2-5*0,6^2=1,4\)

Получилось, что уровень воды в колодце должен подняться на 1,4 метра. Это был пример текстовой задачи с прикладным содержанием. 

Решим еще одно задание, которое может попасться на ЕГЭ по профильной математике в задании №9. 

Задание. Некоторая компания продает свою продукцию по цене p=400 руб. за единицу, переменные затраты на производство одной единицы продукции составляют v=200 руб., постоянные расходы предприятия f = 700000 руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле (q)=q(p-v)-f. Определите месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет равна 300000 руб.

Решение. Подставим все данные числа из условия задачи в формулу:

\(300000 = q(400-200)-700000\)

Вся задача свелась к решению обычного линейного уравнения:

\(300000+700000 = q(400-200)\)
\(1000000 = 200q\)
\(q=\frac{1000000}{200}\)
\(q=5000\)

Ответ: 5000

В каком задании ЕГЭ по профильной математике можно получить легчайший 1 балл? Как вы можете заметить, задания №9 очень легкие: в них нужно просто подставить значения из условия в формулу и решить уравнения. Главное только не ошибиться в вычислениях.

Теперь перейдем к другому, более сложному, виду задач.

Задачи на совместную работу

Теперь давайте представим, что мы работаем на станке и делаем детали. Нам поступил заказ на 112 деталей. Мы выполним этот заказ на 1 час быстрее, чем другой работник. Мы хотим узнать, сколько деталей в час делает этот второй, другой работник, при условии, что мы делаем за час на 2 детали больше.

Все эти задачи решаются с использованием лишь одной формулы:

\(A = p * t\)

Здесь A — работа, p — производительность, t — время. За x принимаем количество деталей. Для этой задачи составим табличку и разберемся, что к чему относится:

	\(p\)	\(t\)	\(A\)
I рабочий	\(x + 2\)	\(\frac{112}{x+2}\)	\(112\)
II рабочий	\(x\)	\(\frac{112}{x}\)	\(112\)

Мы выполняем заказ быстрее на 1 час, значит:

\(t_2-t_1=1\)

Подставим вместо \(t_2\) и \(t_1\) то, что у нас получилось в табличке:

\(\frac{112}{x}-\frac{112}{x+2}=1\)

Такие уравнения легко сводятся к квадратному:

\(\frac{112(x+2)-112x-x(x+2)}{x(x+2)}=0\)
\(\frac{112x+224-112x-x^2-2x}{x(x+2)}=0\)

Приравняем числитель к \(0\). Перед этим запишем, что по ОДЗ \(x\neq 0\) и \(x\neq -2\), так как знаменатель не может быть равен нулю.

\(112x+224-112x-x^2-2x = 0\)
\(-x^2-2x+224=0\)
\(x^2+2x-224=0\)

Найдем дискриминант этого квадратного уравнения:

\(D = 4-4*1*(-224) = 900\)

Теперь найдем корни уравнения:

\(x_{1.2}=\frac{-2\pm \sqrt{900}}{2}\)
\(x_{1.2}=\frac{-2\pm 30}{2}\)

Получились такие корни:

\(x_1=\frac{-2+30}{2}=14\)
\(x_2=\frac{-2-30}{2}=-16\)

Напомним, что мы ищем производительность, а так как рабочие создают детали, а не разбирают их, значит, что ответ отрицательным быть не может. В качестве ответа получили 14 деталей.

ОДЗ: встречается ли она в реальной жизни, или же это особенность функций? Конечно же, ОДЗ встречается и в реальной жизни. Как мы уже заметили, в подобных жизненных задачах могут получиться отрицательные корни, но производительность, скорость или прочие величины не могут быть меньше нуля. Поэтому всегда важно думать перед тем, как записывать ответ.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №10. 

Задание. Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 180 литров она заполняет на 2 минуты дольше, чем вторая труба?

Решение. Пусть x — количество литров воды, которое пропускает первая труба в минуту. Тогда количество литров, пропускаемых второй трубой, равно \(x + 1\) литров в минуту. Резервуар объемом 180 литров первая труба заполняет на 2 минуты дольше, чем вторая, значит, по аналогии с предыдущей задачей, имеем:

\(\frac{180}{x}-\frac{180}{x+1}=2\)

Решим это уравнение:

\(\frac{180(x+1)-180x-2x(x+1)}{x(x+1)}=0\)
\(\frac{180x+180-180x-2x^2-2x}{x(x+1)}=0\)

ОДЗ: 

\(x\neq 0\)
\(x\neq -1\)

Приравняем числитель к нулю:

\(180x+180-180x-2x^2-2x=0\)
\(-2x^2-2x+180=0\)
\(2x^2+2x-180=0\)
\(x^2+x-90=0\)

Найдем дискриминант:

\(D = 1-4*1*(-90)=361\)

Теперь найдем корни уравнения:

\(x_{1.2}=\frac{-1\pm \sqrt{361}}{2}\)
\(x_{1.2}=\frac{-1\pm 19}{2}\)

Получились такие корни:

\(x_1=\frac{-1+19}{2}=9\)
\(x_2=\frac{-1-19}{2}=-10\)

Ответ должен быть положительным, значит отметаем второй корень.

Ответ: 9

Теперь рассмотрим задачи на смеси и сплавы.

Задачи на смеси и сплавы

Попробуем себя в роли химиков. Смешаем 30-процентный и 50-процентный растворы кислоты, а затем добавим 10 кг чистой воды. Получаем 36-процентный раствор кислоты. Но если бы вместо 10 кг воды мы добавили 10 кг 60-процентного раствора той же кислоты, то получили бы 40-процентный раствор. Давайте узнаем, сколько килограммов 30-процентного раствора мы использовали для получения смеси.

В задачах на смеси и сплавы мы используем эту формулу:

\(\frac{m_1p_1}{100}+\frac{m_2p_2}{100}=\frac{(m_1+m_2)p}{100}\)

где \(m_1\) и \(m_2\) — массы, \(p_1, p_2\) и \(p\) — проценты. Конечно же, формулу нужно будет видоизменять в зависимости от условий задачи.

Пусть масса 30-процентного раствора — \(m_1\), а 50-процентного — \(m_2\). Когда мы смешали 30-процентный и 50-процентный растворы кислоты, и затем добавили 10 кг воды, мы получили 36-процентный раствор: \(0,3m_1+0,5m_2= 0,36(m_1+m_2+10)\).
Если бы добавили 10 кг 60-процентного раствора, а не воды, то получили бы 40-процентный раствор: \(0,3m_1+0,5m_2+10*0,6= 0,4(m_1+m_2+10)\).
Получилась система уравнений:

Нас интересовало, сколько килограммов 30-процентного раствора мы использовали. В уравнении это \(m_1\). Соответственно, мы использовали 80 килограммов 30-процентного раствора. 

Решим еще одно задание, которое может попасться на ЕГЭ по профильной математике в задании №10. 

Задание. Имеется два сплава. Первый сплав содержит 20% меди, а второй  — 50%. Масса первого сплава меньше массы второго на 4 кг. Из этих двух сплавов получили третий, содержащий 40% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

Решение. Масса первого сплава m кг, масса второго — m + 4 кг, а значит масса третьего сплава — 2m + 4 кг. У первого сплава 20% содержания меди, у второго — 50% и 40% у третьего. Тогда:

\(0,2m+0,5(m+4)=0,4(2m+4)\)
\(0,2m+0,5m-0,8m=1,6-2\)
\(0,1m=0,4\)
\(m=4\)

Ответ: 4

Теперь порешаем задачи на смекалку!

Задачи на смекалку

В этот раз мы отправились с вами в поход. Во время нашего путешествия мы заметили улитку на дереве: она пыталась залезть до самого верха. В день она заползает вверх по дереву на 3 метра, а за ночь сползает на 2. Давайте посчитаем, через сколько дней она доползет до самого верха, если длина дерева 8 метров.

Так как улитка за день заползает на 3 метра, а за ночь сползает на 2, значит в сутки она проползает только 1 метр. За 5 суток она заберется на высоту 5 метров, а за 6 день проползет еще 3 и окажется на самом верху.

Решим еще одно задание, которое может попасться на ЕГЭ по базовой математике в задании №21. 

Задание. В магазине квас на разлив можно купить в бутылках, причем стоимость кваса в бутылке складывается из стоимости самой бутылки и кваса, налитого в нее. Цена бутылки не зависит от ее объема. Бутылка кваса объемом 1 литр стоит 28 рублей, объемом 2 литра  — 54 рубля. Сколько рублей будет стоить бутылка кваса объемом 2,5 литра?

Решение. Пусть бутылка стоит x рублей, а квас — y рублей за литр. Получаем систему уравнений:

Соответственно, бутылка кваса объемом 2,5 литра будет стоить \(2+26*2,5=67\) рублей

Ответ: 67

Переходим к самому сложному — задачам, которые решаются с использованием свойств чисел.

Задачи на свойства чисел

Это, на первый взгляд, самые сложные текстовые задачи на ЕГЭ. Сейчас мы решим одно из них, и вы поймете, что не такие уж они и страшные!

Решим первый пункт из задачи, которая может попасться на ЕГЭ по профильной математике в задании №19. 

Задание. Если в натуральном двузначном числе первую цифру поменять местами с последней, то число увеличится на 75%. Найдите все такие числа.

Решение. Пусть первая цифра — a, а вторая — b, тогда число — 10a+b. Если цифры поменять местами, то получится число 10b+a. Число увеличивается на 75% или на \(1+\frac{75}{100}=\frac{7}{4}\). Значит, справедливо равенство:

\(10b+a=\frac{7}{4}(10a+b)\)
\(10b+a=\frac{70}{4}a+\frac{7}{4}b\)
\(40b+4a=70a+7b\)
\(33b=66a\)
\(b=2a\)

Такие числа легко подобрать: 12, 24, 36, 48.

Ответ: а) 12, 24, 36, 48

Как сложное домашнее задание сделало одного студента всемирно известным? В 1939 году студент Джордж Бернард Данциг опоздал на занятие по статистике и увидел на доске две задачи, которые принял за домашнее задание. Через несколько дней он принес преподавателю решенные задания и сказал, что просрочил их из-за повышенной сложности, за что и извинился. Через 6 недель к нему домой влетел преподаватель, который что-то тараторил про научную статью. Оказалось, что Данциг решил совсем не домашнее задание, а две недоказанные статические теоремы, которые математики не могли доказать многие годы. Поэтому если вам говорят, что какое-то задание очень сложное, не нужно слушать это и создавать себе рамки. У вас обязательно все получится!

На этом наше путешествие закончилось. Мы много где побывали, много кем поработали и, самое главное, научились решать текстовые задачи. Теперь настало время познакомиться с задачами с параметром. 

Фактчек

• Задачи с прикладным содержанием решаются простой подстановкой чисел из условия в данную формулу.
• Задачи на совместную работу решаются по формуле \(A = p*t\).
• Задачи на смеси и сплавы чаще всего решаются с помощью формулы \(\frac{m_1p_1}{100}+\frac{m_2p_2}{100}=\frac{(m_1+m_2)p}{100}\), где p — процентное доля вещества, поделенная на \(100\), чтобы сразу избавиться от процентов; m — масса вещества. Также могут использоваться производные от этой формулы или система уравнений с этой формулой.
• Основные единицы измерения в текстовых задачах: метры, минуты, литры и килограммы.

Проверь себя

Задание 1.
Чему равна плотность жидкости , если ускорение свободного падения g равно 10 \(м/с^2\), давление p равно 17,04 Па и высота h равна 2,4 м? Формула: p=gh.

1. \(710,2 кг/м^3\)
2. \(71 кг/м^3\)
3. \(7,1 кг/м^3\)
4. \(710 кг/м^3\)

Задание 2.
По какой формуле можно найти время в задачах на совместную работу?

1. \(N=\frac{A}{t}\)
2. \(t = \frac{S}{v}\)
3. \(A = p * t\)
4. \(a = \frac{v}{t}\)

Задание 3.
Смешали два раствора кислоты концентрациями 14% и 30%. Получилось 32 литра раствора концентрацией 20%. Сколько килограмм первого раствора было взято?

1. 12
2. 8
3. 20
4. 24

Задание 4.
Каждую секунду бактерия делится на две новые. Через сколько секунд стакан будет заполнен бактериями наполовину, если весь объем стакана они заполняют за 1 минуту?

1. 59 секунд
2. 30 секунд
3. 29 секунд
4. 10 секунд

Ответы: 1. — 4; 2. — 3; 3. — 3; 4. — 1.