Преобразование алгебраических выражений. Часть 2

На этой странице вы узнаете 

• Как получить полный квадрат из неполного?
• Можно ли возвести двучлен в 100-ю степень?
• Кто сформулировал одну из основных теорем в алгебре?

Часто из математики мы можем получать навыки, которые помогают нам в повседневной жизни. 

«Упрощали, упрощаем и будем упрощать» – пожалуй, девиз всех математиков. Если подумать, то эта «суперспособность» полезна для каждого из нас. Именно через числа и буквы можно выделить для себя различные методы, с помощью которых можно выходить из тех или иных сложных ситуаций.

В статье «Преобразование алгебраических выражений. Часть 1» мы уже начали знакомиться со способами преобразования и упрощения алгебраических выражений. Самое время продолжить, изучив новые методы.

Разложение многочлена на множители с помощью формул сокращенного умножения

В статье «Преобразование алгебраических выражений. Часть 1» мы рассмотрели семь формул сокращенного умножения. В некоторых случаях их также можно использовать для разложения многочлена на множители. 

Разность квадратов

Запишем формулу разности квадратов «задом наперед»:

\(a^2-b^2=(a-b)*(a+b)\)

Если многочлен имеет вид \(a^2-b^2\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно разложить на множители \((a-b)*(a+b)\).

Приведем несколько примеров: 

\(64-y^2=82-y^2=(8-y)*(8+y)\)
\(81a^2-36c^2=(9a)^2-(6c)^2=(9a-6c)*(9a+6c)\)
\(4h^2e^4-25k^6=(2he^2)^2-(5k^3)^2=(2he^2-5k^3)*(2he^2-5k^3)\)

Итак, запомним: если видим разность двух квадратов, значит можем разложить ее на два множителя.

По такой же логике раскладывается на множители сумма и разность кубов.

Сумма и разность кубов

Для начала вспомним формулы суммы и разности кубов, записав их «задом наперед»:

\(a^3+b^3=(a+b)*(a^2-ab+b^2)\)
\(a^3-b^3=(a-b)*(a^2+ab+b^2)\)

• Если многочлен имеет вид \(a^3+b^3\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно разложить на множители \((a+b)(a^2-ab+b^2)\).

• Если многочлен имеет вид \(a^3-b^3\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно разложить на множители \((a-b)(a^2+ab+b^2)\).

Также приведем несколько примеров:

\(n^3+27=n^3+3^3=(n+3)*(n^2-3n+3^2)=(n+3)*(n^2-3n+9)\)

\(125x^3-8c^6=(5x)^3-(2c)^3=(5x-2c)*((5x)^2+5x*2c+(2c)^2)=\)
\(=(5x-2c)*(25x^2+10xc+4c^2)\)

Формулы разности квадратов, суммы и разности кубов позволяют разложить многочлен на два множителя, остальные формулы сокращенного умножения помогают выделить полный квадрат или куб из многочлена.

Выделение полного квадрата

Так же, как и рассматриваемые ранее формулы, напишем формулы для квадрата суммы и квадрата разности:

\(a^2+2ab+b^2=(a+b)^2\)
\(a^2-2ab+b^2=(a-b)^2\)

• Если многочлен имеет вид \(a^2+2ab+b^2\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно представить в виде \((a+b)^2\).

• Если многочлен имеет вид \(a^2-2ab+b^2\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно представить в виде \((a-b)^2\).

Чтобы выделить полный квадрат суммы или разности, в многочлене нужно увидеть два квадрата и их удвоенные произведения. Где-то это сделать можно сразу, а где-то для этого необходимо произвести некоторые преобразования. 

Разберем многочлен \(x^2+8xy+16y^2\). Сразу обращаем внимание, что два члена этого многочлена являются квадратами: \(x^2\) и \(16y^2=(4y)^2\), а \(8xy\) – удвоенным произведением: \(8xy=2*x*4y\). Значит, это выражение является полным квадратом суммы:

\(x^2+8xy+16y^2=x^2+2*x*4y+(4y)^2=(x+4y)^2\)

Также важно помнить, что слагаемые полного квадрата могут стоять «вразброс», а не только так, как стоят в формуле. Например, в выражении \(25p^4+16b^6-40p^2b^3\) вначале стоят два квадрата: \(25p^4=(5p^2)^2\) и \(16b^6=(4b^3)^2\), а затем – удвоенное произведение. Если поменять местами второй и третий член этого одночлена, получим классическую формулу полного квадрата разности:

\(25p^4+16b^6-40p^2b^3=(5p^2)^2+(4b^3)^2-2*5p^2*4b^3=\)
\(=(5p2)2-2*5p^2*4b^3+(4b^3)^2=(5p^2-4b^3)^2\)

Получается, что в подобных выражениях самое главное – найти этот квадрат суммы. На самом деле, из этого получается очень увлекательная игра, а самое приятное в этой «игре» – результат.

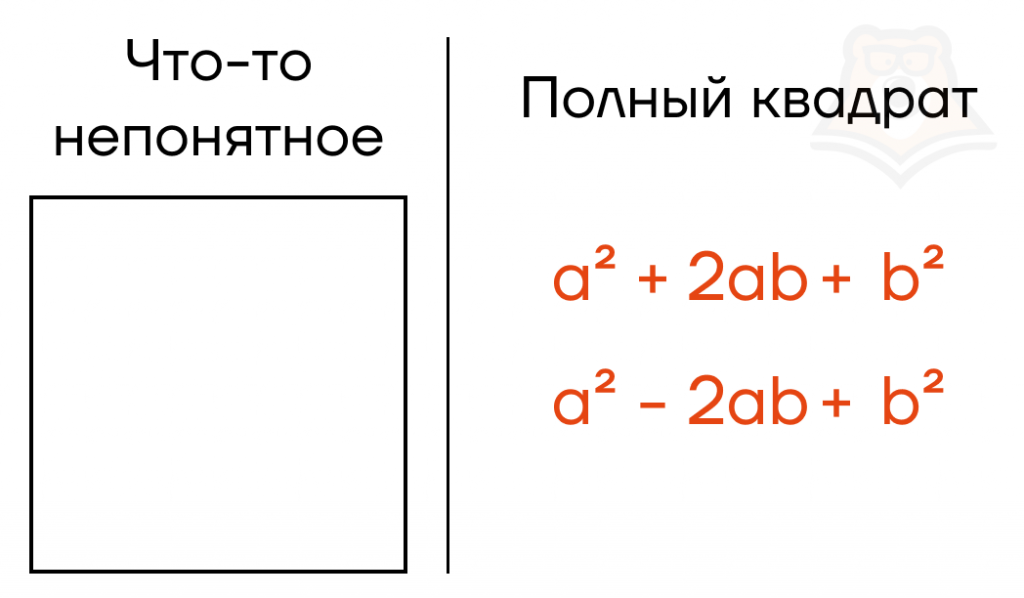
Как получить полный квадрат из неполного? К сожалению, далеко не каждый многочлен представляет из себя полный квадрат. Но многие многочлены можно представить в виде суммы или разности полного квадрата с определенным числовым коэффициентом и многочлена/одночлена. Например, рассмотрим выражение \(7x^2+56x+8\).  Чтобы избавиться от коэффициента перед \(x^2\), вынесем в этом выражении число \(7\) за скобки: \(7x^2+56x+140=7(\frac{7x^2}{7}+\frac{56x}{7}+\frac{140}{7})=7*(x^2+8x+20)\) Теперь обратим внимание на то, что осталось в скобках. Первое слагаемое \(x^2\) является квадратом, то есть первым слагаемым в нашем будущем квадрате суммы будет \(x\). Далее по формуле квадрата суммы должно идти удвоенное произведение первого слагаемого на второе. В данном случае это \(8x\), которое мы представим как \(8x=2*x*4\). Из этого удвоенного произведения можно заметить, что вторым слагаемым в квадрате суммы будет \(4\). Далее, по формуле, должно идти второе слагаемое в квадрате, то есть \(4^2=16\). Откуда же взять \(16\), если в скобках этого числа нет? Все просто: мы можем внутрь скобок добавить \(16\), и, чтобы выражение от этого не поменялось, сразу вычесть \(16\): \(7*(x^2+8x+20)=7*((x^2+2*x*4+4^2)-4^2+20)=\) \(=7*((x+4)^2-16+20)\) Таким образом, внутри скобок мы выделили полный квадрат \(x^2+2*x*4+4^2=(x+4)^2\). Теперь осталось раскрыть скобки, используя распределительное свойство: \(7*((x+4)2-16+20)=7*(x+4)2+7*4=7*(x+4)^2+28\) А теперь вернемся к самому началу. Мы получили что: \(7x^2+56x+8=7*(x+4)^2+28\) Данный способ выделения полного квадрата хоть и не является разложением полного многочлена на множители, но часто позволяет исследовать различные алгебраические выражения, а также решать уравнения. Например, зная, что \(7x^2+56x+8=7*(x+4)^2+28\), мы можем сказать, что это выражение принимает только положительные значения, ведь \(7*(x+4)^2\geq 0\), а \(28>0\), тогда \(7*(x+4)^2+28>0\).

Ну а теперь перейдем к последнему способу разложения многочлена на множители с помощью формул сокращенного умножения. 

Куб суммы и куб разности

Аналогично полному квадрату суммы или разности, в некоторых выражениях можно выделить куб суммы или разности, используя соответствующие формулы:

\(a^3+3a^2b+3ab^2+b^3=(a+b)^3\)
\(a^3-3a^2b+3ab^2-b^3=(a-b)^3\)

• Если многочлен имеет вид \(a^3+3a^2b+3ab^2+b^3\) , где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно представить в виде \((a+b)^3\).

• Если многочлен имеет вид \(a^3-3a^2b+3ab^2+b^3\), где \(a\) и \(b\) – некоторые одночлены, то этот многочлен можно представить в виде \((a-b)^3\).

Приведем несколько примеров:

\(1+6x+12x^2+8x^3=1^3+3*1^2*2x+3*1*(2x)^2+(2x)^3=(1+2x)^3\)

\(27k^9-108k^6y^4+144k^3y^8-64y^{12}=(3k^3)^3-3*(3k^3)^2*4y^4+3*3k^3*(4y^4)^2-(4y^4)^2=\)
\(=(3k^3-4y^4)^3\)

Так же, как и с полным квадратом, самое главное здесь – разглядеть в выражении эту самую формулу куба суммы или разности. 

Таким образом, мы разобрали способы разложения многочлена на множители с помощью вынесения общего множителя за скобки, метода группировки, а также формул сокращенного умножения. Самое время рассмотреть, как эти способы можно комбинировать между собой.

Можно ли возвести двучлен в 100-ю степень? Квадрат суммы и куб суммы – одни из ключевых формул в курсе алгебры. А можно ли возвести сумму двух одночленов, то есть двучлен, в четвертую, пятую и даже в сотую степень? Конечно можно. На самом деле, для всех таких формул есть своя закономерность. Чтобы в ней разобраться, напишем друг под другом двучлен \((a+b)^0, (a+b)^1, (a+b)^2, (a+b)^3\), используя соответствующие формулы: \(1\) \(a+b\) \(a^2+2ab+b^2\) \(a^3+3a^2b+3ab^2+b^3\) Образовался вот такой «треугольник». Что в этом треугольнике можно заметить? Во-первых, показатели переменной \(a\) во всех формулах убывают слева направо: начиная от степени, в которую мы возводим наш двучлен, заканчивая нулевой степенью, то есть единицей. Показатели степеней переменной \(b\), напротив, возрастают слева направо: от нулевой степени до степени, в которую возводится двучлен. Во-вторых, по краям этих формул коэффициенты членов равны единицам, а «внутри» формул каждый коэффициент равен сумме коэффициентов двух членов, написанных в этом треугольнике над ним. Например, над членом \(3a^2b\) с коэффициентом \(3\) в треугольнике стоят члены \(a^2\) с коэффициентом \(1\) и \(2ab\) с коэффициентом \(2\). Все сходится: \(3=2+1\). Если выписать эти коэффициенты в треугольник (без переменных), то такой треугольник будет называться треугольником Паскаля. Каждое число в нем равно сумме двух чисел, стоящих над ним, а по краям треугольника стоят единицы. По этой же логике можно продолжить такой треугольник, расписав формулы для четвертой, пятой, и даже сотой степени двучлена. Известный физик Исаак Ньютон даже вывел формулу для этого треугольника, которую назвали биномом Ньютона.

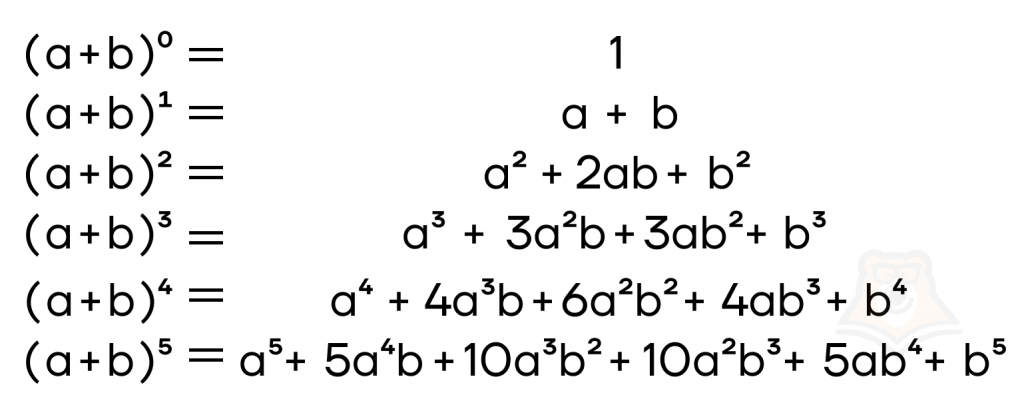
Разложение многочлена на множители комбинацией различных приемов

Часто для преобразования многочленов одного способа разложения на множители бывает недостаточно, вследствие чего приходится применять сразу несколько способов, комбинировать их.

Приведем несколько примеров, когда для полного разложения многочлена на множители необходимо скомбинировать несколько приемов.

Разберем пример задания№20 из ОГЭ по математике.

Задание. Сократить дробь \(\frac{y^3+5y^2-4y-20}{(y-2)(y+5)}\).

Решение. Чтобы сократить эту дробь, разложим ее числитель \(y^3+5y^2-4y-20\) на множители. Для начала, применим метод группировки:

\(y^3+5y^2-4y-20=y^2(y+5)-4(y+5)=(y+5)(y^2-4)\)

Заметим, что множитель \(y^2-4\) также можно разложить на множители, используя формулу для разности квадратов:

\((y+5)(y^2-4)=(y+5)(y^2-2^2)=(y+5)(y-2)(y+2)\)

Таким образом, мы разложили числитель дроби \(y^3+5y^2-4y-20\) на множители \((y+5)(y-2)(y+2)\). Подставим полученное разложение в нашу дробь и выполним соответствующие сокращения множителей в числителе и знаменателе:

\(\frac{y^3+5y^2-4y-20}{(y-2)(y+5)}=\frac{(y+5)(y-2)(y+2)}{(y-2)(y+5)}=y+2\)

Ответ: \(y+2\)

В рассмотренном выше примере для разложения многочлена на множители мы использовали комбинацию двух приемов: метода группировки и формулы разности квадратов. 

Можно использовать и комбинацию других способов. Рассмотрим еще один пример. 

Разберем пример задания №20 из ОГЭ по математике.

Задание. Решить уравнение \(x(x^2-8x+16)=3(x-4)\).

Решение. С основными моментами при решении уравнений можно ознакомиться в статье «Линейные, квадратные и кубические уравнения».

Для начала перенесем все слагаемые уравнения в одну сторону, оставив с другой только \(0\):

\(x^2-8x+16=3x(x-4)\)
\(x^2-8x+16-3x(x-4)=0\)

Далее мы будем работать выражением, получившимся в левой части этого уравнения. Разложим его на множители. Для этого сначала выделим полный квадрат в многочлене \(x^2-8x+16\), которое можно представить в виде \(x^2-2*x*4+4^2=(x-4)^2\).

\((x^2-8x+16)-3x(x-4)=0\)
\((x-4)^2-3x(x-4)=0\)

Видим, что в выражении появился общий множитель \(x-4\), который мы можем вынести за скобки:

\((x-4)^2-3x(x-4)=0\)
\((x-4)((x-4)-3x)=0\)
\((x-4)(x-4-3x)=0\)
\((x-4)(-2x-4)=0\)

Таким образом, мы разложили выражение \(x^2-8x+16-3x(x-4)\) на множители \((x-4)(-2x-4)\). 

Согласно получившемуся уравнению, произведение двух множителей равно \(0\). Так происходит только в тех случаях, когда один из множителей равен \(0\), то есть, \(x-4=0\) или \(-2x-4=0\). Осталось решить два этих уравнения:

1) \(x-4=0\)
\(x=4\)

2) \(-2x-4=0\)
\(-2x=4\)
\(x=-0,5\)

Эти значения и будут ответом.

Ответ: \(-0,5;4\)

При решении данного уравнения мы воспользовались двумя способами разложения многочлена на множители: вынесением общего множителя за скобки и выделением полного квадрата.

Таким образом, комбинируя различные способы разложения на множители, можно решать различные задачи по алгебре: от упрощения выражений до решения уравнений и неравенств.

На самом деле, есть еще один способ разложение многочлена на множители, о котором мы пока не сказали, а именно – разложение на множители делением «уголком». Давайте же разберемся с этим подробнее.

Разложение многочлена на множители делением. Теорема Безу

В статье «Многочлены и действия с ними» мы разобрались с тем, что многочлены можно делить на одночлены. А можно ли делить многочлен на многочлен? Оказывается, что можно. И об этом нам говорит теорема Безу:

Если \(a\) является корнем уравнения \(P(x)=0\), где \(P(x)\) – многочлен, в состав которого из переменных входит только переменная \(x\), то многочлен \(P(x)\) можно без остатка разделить на двучлен \(x-a\).

Кто сформулировал одну из основных теорем в алгебре? Теорема Безу – одна из главных теорем в мире алгебры. Она была сформулирована французским математиком Этьеном Безу в 1799 году и названа в его честь. Данная теорема позволяет решать уравнения высших степеней путем деления многочленов на двучлены. Теорема Безу вызвала много разногласий и споров среди математиков, так как в каких-то моментах условия для этой теоремы не были точно обозначены. Из-за чего кто-то до сих пор считает эту формулировку некорректной. Тем не менее теоремой Безу активно пользуются в алгебре в настоящее время, как и многими другими теоремами, которые сформулировал этот ученый. И можно с уверенностью сказать, что для математики 1799 года он совершил настоящий прорыв.

Разобраться в этом подробнее нам поможет не что иное, как пример. Чаще всего такое деление производится для решения кубических уравнений. Поэтому решим уравнение \(x^3-x^2+x+3=0\). 

Методом подбора находим что \(-1\) является одним из корней этого уравнения \(((-1)^3-(-1)^2+(-1)+3=-1-1-1+3=0)\). Значит, многочлен \(x^3-x^2+x+3\) можно разделить на двучлен \(x-(-1)\), то есть на \(x+1\). 

Деление будем производить тем самым «уголком», которым мы до этого делили обычные числа.

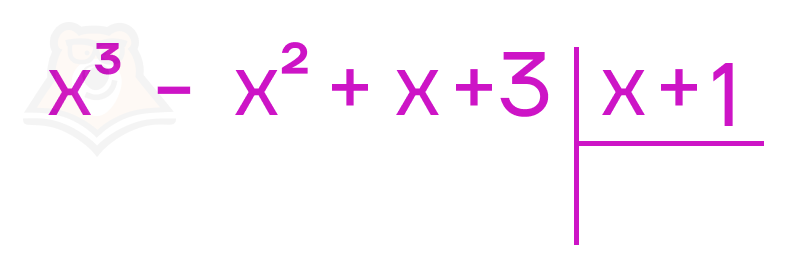
Для начала, разделим первый член многочлена \(x^3-x^2+x+3\) на переменную \(x\), то есть \(\frac{x^3}{x}=x^2\). Напишем получившийся результат \((x^2)\) в поле ответа, умножим на него двучлен \(x+1\), получим \((x+1)*x^2=x^3+x^2\). Далее спишем остаток от деления \((x^3-x^2-(x^3+x^2)=2x^2)\). К остатку от деления добавим следующий член многочлена \(+x\).

Далее продолжаем делить таким же способом: делим первый член двучлена \(-2x^2+x\) на переменную \(x\), то есть \(\frac{-2x^2}{x}=-2\), умножаем \(x+1\) на результат деления, «спускаем» остаток, к остатку добавляем следующую переменную.

Осталось выполнить последний шаг в этом делении, проделываем его таким же образом:

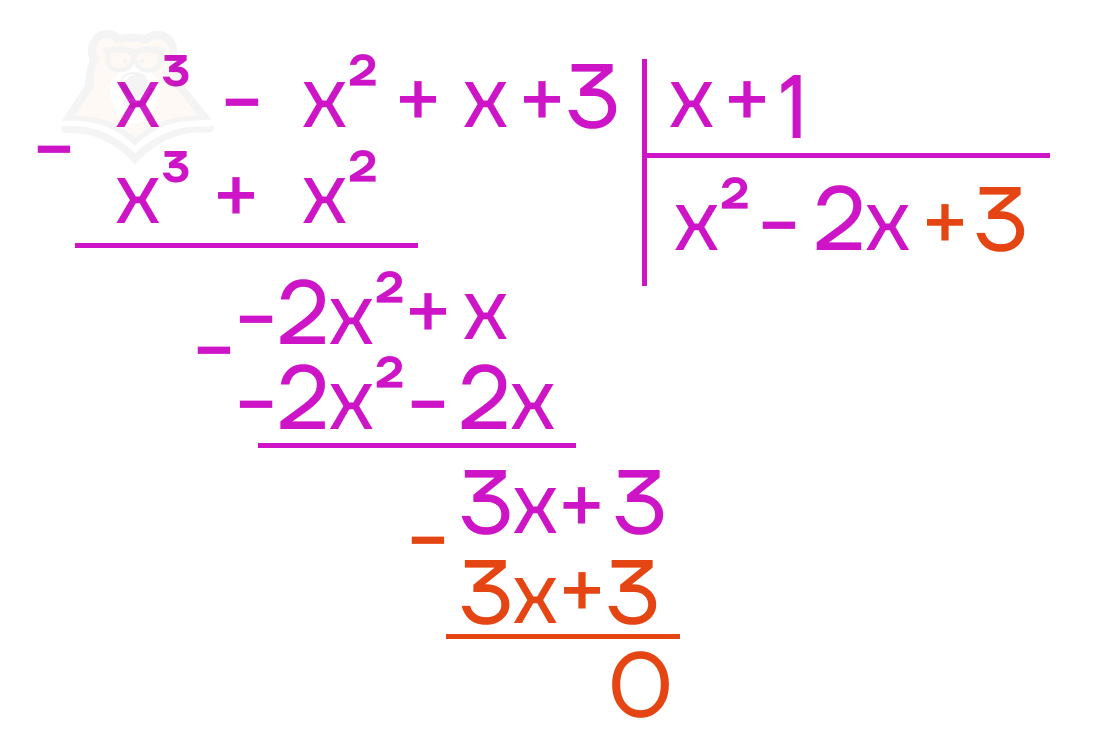
Получаем нулевой остаток, что говорит о том, что деление окончено. 

Мы разделили многочлен \(x^3-x^2+x+3\) на двучлен \(x+1\) и получили в результате многочлен \(x^2-2x+3\):

\((x^3-x^2+x+3):(x+1)=x^2-2x+3\)

Отсюда следует:

\(x^3-x^2+x+3=(x+1)(x^2-2x+3)\)

Многочлен, над которым выполнялось деление, можно представить в виде произведения двучлена-делителя на получившийся в результате деления многочлен.

Теперь вернемся к уравнению \(x^3-x^2+x+3=0\). Левую часть этого уравнения мы разложили на два множителя: 

\((x+1)(x^2-2x+3)=0\)

Множитель \(x^2-2x+3\) можно разложить на множители методом группировки:

\(x^2-2x+3=x^2+x-3x-3=x(x+1)-3(x+1)=(x+1)(x-3)\)

Подставим получившееся разложение в уравнение:

\((x+1)(x+1)(x-3)=0\)
\((x+1)^2(x+1)=0\)

Произведение двух множителей равно нулю в тех случаях, когда один из этих множителей равен нулю. Осталось приравнять два множителя к нулю и решить полученные уравнения:

1. \((x+1)^2=0\)
   \(x+1=0\)
   \(x=-1\)

2. \(x-3=0\)
   \(x=3\)

Тогда решением данного уравнения будут два числа: \(-1\) и \(3\).

Если в результате деления многочлена \(P(x)\) на двучлен \((x-a)\) получается ненулевой остаток \(b\), тогда этот многочлен можно представить в виде \(P(x)=B(x)*(x-a)+b\), где \(B(x)\) – многочлен, получившийся в результате деления. 

Приведем пример:

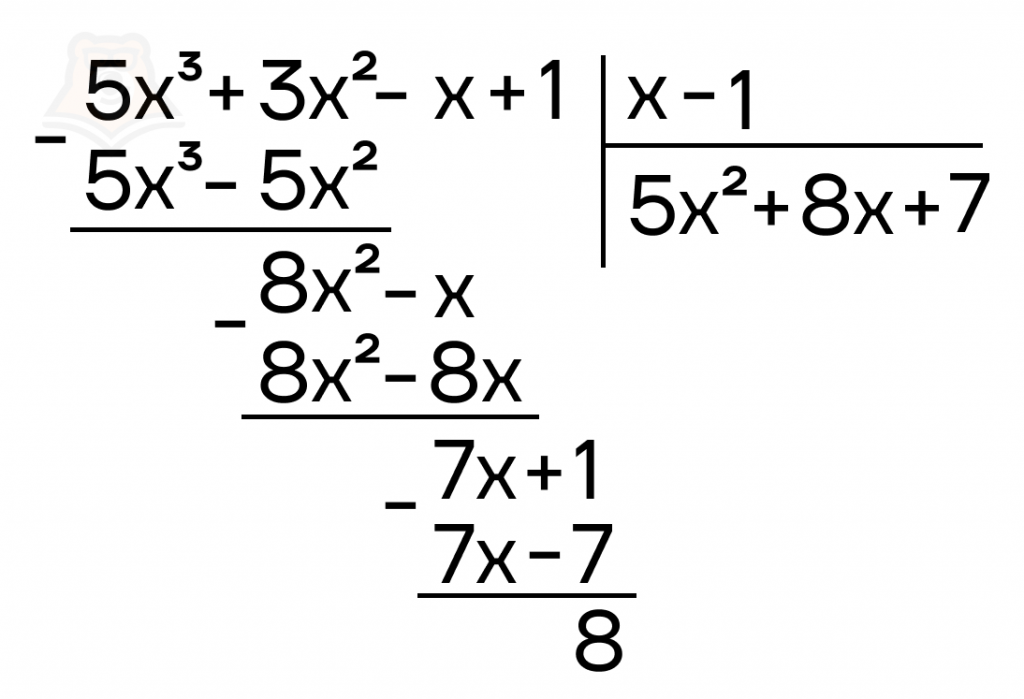
При делении многочлена \(5x^3+3x^2-x+1\) на двучлен \(x-1\) получаем многочлен \(5x^2+8x+7\) с остатком \(8\). Тогда:

\(5x^3+3x^2-x+1=(5x^2+8x+7)*(x-1)+8\)

Деление многочлена \(P(x)\) на двучлен \((x-a)\) можно выполнить не только «уголком», но и альтернативным способом – по схеме Горнера. При этом само деление выполняется точно так же, только другим способом. Выполним ранее рассмотренное деление \((x^3-x^2+x+3):(x+1)\). Для начала построим следующую таблицу:

Здесь числа \(1; -1; 1: 3\) обозначают коэффициенты многочлена \(x^3-x^2+x+3\), а число \(-1\) обозначает значение a в двучлене \((x-a)\), на который мы и делим наш многочлен. В нашем случае, мы делим многочлен на \((x+1)=(x-(-1))\). 

Под коэффициентами исходного многочлена в дальнейшем мы будем записывать коэффициенты многочлена, который должен получиться в результате деления.

Под первым коэффициентом запишем такое же число:

Дальнейшие коэффициенты будем определять следующим образом: \(n_2=k_2+a*n_1\), где \(n_2\) – определяемый коэффициент, \(k_2\) – соответствующий ему коэффициент исходного многочлена (число сверху), \(a=-1\) (по таблице), \(n_1\) – предыдущий коэффициент.

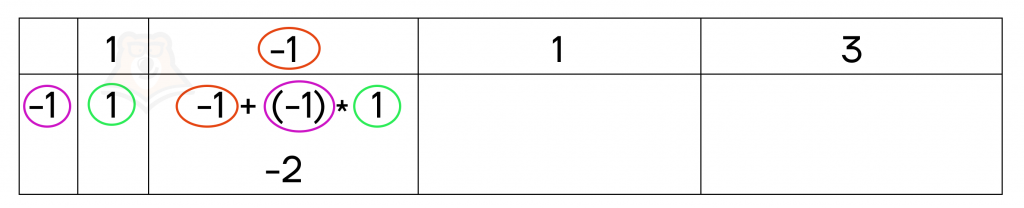
Выше приведен пример расчета второго коэффициента. Следующий коэффициент рассчитываем таким же  образом:

Ну и, наконец, остался последний коэффициент. 

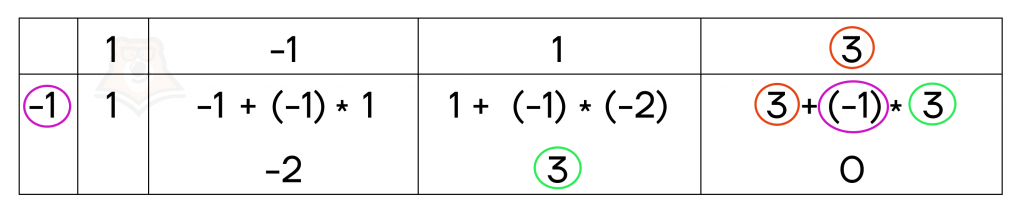
Мы получили 0, что говорит нам о том, что данное деление выполняется без остатка. Приведем полученную таблицу.

Теперь осталось записать получившийся после деления многочлен. Если изначально мы делили многочлен третьей степени \(x^3-x^2+x+3\), то в результате деления мы получим многочлен второй степени \(x^2-2x+3\), где коэффициенты этого многочлена мы определили по полученной таблице. Получаем:

\((x^3-x2+x+3):(x+1)=x^2-2x+3\)

Откуда:

\(x^3-x^2+x+3=(x^2-2x+3)*(x+1)\)

Как видим, получилось то же самое, что и при делении «уголком». Такой способ позволяет не запутаться в «столбике» и выполнить деление более быстрым, и, что самое главное, простым способом.

Конечно, кубические уравнения можно решить и без деления, используя способы разложения, рассмотренные выше. Но всегда лучше ознакомиться со всеми способами разложения, ведь в таком случае, если возникают трудности с одним способом, всегда можно воспользоваться другим.

В рассмотренном примере мы делили многочлен третьей степени. А что, если по теореме Безу разделить квадратный трехчлен? 

Рассмотрим квадратный трехчлен \(ax^2+bx+c\), где \(a, b\) и \(с\) – некоторые числа.
Квадратное уравнение \(ax^2+bx+c=0\), как мы помним из статьи «Линейные, квадратные и кубические уравнения» может либо иметь два решение, либо иметь одно решение, либо не иметь решений совсем. Остановимся подробнее на каждом случае:

1. \(ax^2+bx+c=0\) имеет два решения \(x_1\) и \(x_2\).

В таком случае, по теореме Безу, многочлен \(ax^2+bx+c\) можно поделить на двучлены \(x-x_1\) и \(x-x_2\). 

Сам же многочлен тогда можно разложить на множители следующим образом:

\(ax^2+bx+c=a(x-x_1)(x-x_2)\)

Если уравнение \(ax^2+bx+c=0\) имеет два решения \(x_1\) и \(x_2\), то многочлен \(ax^2+bx+c\) можно представить в виде \(a(x-x_1)(x-x_2)\).

2. \(ax^2+bx+c=0\) имеет одно решение \(x_0\).

По теореме Безу, в этом случае многочлен \(ax^2+bx+c\) можно поделить на двучлен \(x-x_0\).

Тогда многочлен можно следующим образом разложить на множители:

\(ax^2+bx+c=a(x-x_0)^2\)

Если уравнение \(ax^2+bx+c=0\) имеет единственное решение \(x_0\), то многочлен \(ax^2+bx+c\) можно представить в виде \(a(x-x_0)^2\).

3. \(ax^2+bx+c=0\) не имеет решений.

В этом случае многочлен \(ax^2+bx+c\) нельзя разложить на множители способами, указанными выше, так как, согласно теореме Безу, его нельзя без остатка разделить ни на один двучлен.

Таким способом, зная лишь корни квадратного уравнения, можно легко разложить квадратный трехчлен на множители, не используя способы, перечисленные выше. Часто это очень ускоряет процесс разложения. 

Например, рассмотрим многочлен \(x^2-5x+6\). Корнями уравнения \(x^2-5x+6=0\) являются числа \(3\) и \(2\), значит, данный многочлен можно представить в виде:

\(x^2-5x+6=(x-2)(x-3)\)

Можно считать, что на этом этапе мы окончательно разобрались с тем, как же преобразовывать многочлены, и теперь можем представлять их в совершенно различных образах: классический вид, полный квадрат, полный куб, разложение на множители различными способами. Определенно, это поможет нам при решении различных алгебраических задач, ведь работа с выражениями занимает значительную часть школьной программы.

Понравилась статья? В таком случае рекомендуем перейти к еще одной, не менее интересной – «Определение и график функции». 

Термины

Делитель – компонент деления, на который производится деление числа/выражения.

Множитель – компонент умножения, участвующий в самой операции умножения

Произведение – результат умножения.

Слагаемое – это число/выражение, которое складывается с другими числами/выражениями.

Фактчек

• Для разложения многочленов на множители можно использовать формулы сокращенного умножения.
• Выделить полный квадрат – значит выделить в выражении квадрат суммы или разности.
• В различных задачах способы разложения на множители приходится комбинировать, то есть использовать несколько способов одновременно.
• Некоторые многочлены можно без остатка разделить на двучлен, пользуясь теоремой Безу. В таком случае многочлен также раскладывается на множители путем деления «уголком».
• Зная корни квадратного уравнения, можно разложить квадратный трехчлен на множители по соответствующим формулам.

Проверь себя

Задание 1.
При разложении выражения \(a^2-36b^2\) на множители необходимо воспользоваться:

1. вынесением общего множителя за скобки;
2. способом группировки;
3. квадратом разности;
4. разностью квадратов. 

Задание 2.
Выделить полный квадрат из выражения \(y^2+16x^2+8xy\).

1. \((y+8x)^2\)
2. \((y+4x)^2\)
3. \((4x+8y)^2\)
4. \((x+y)^2\)

Задание 3.
Разложить многочлен \(25x-xy^2\) на множители. Выбрать результат разложения.

1. \(x(25-y^2)\)
2. \(x(5-y)^2\)
3. \((5-y)(5+y)\)
4. \(x(5-y)(5+y)\)

Задание 4.
Многочлен \(x^3-5x^2+3x+1\) можно разделить на:

1. \(x+1\);
2. \(x-1\);
3. \(x\);
4. нельзя ни на что разделить.

Ответы: 1. – 4; 2. – 2; 3. – 4; 4. – 2