Показательные уравнения и неравенства
На этой странице вы узнаете
- Чем отличается функция от уравнения?
- Как облегчить решение уравнения?
- Как поменять знак неравенства всего одним действием?
С уравнениями и неравенствами мы сталкиваемся постоянно. Когда сравниваем между собой товары перед покупкой или пытаемся посчитать, сколько нам придется заплатить за несколько чашек кофе в кофейне. Любое уравнение или неравенство можно описать языком математики.
Так и показательные уравнения или неравенства: их всегда можно представить в виде математической записи и, более того, без труда решить их! А как это сделать, разберем дальше.
Несколько слов о функциях и степенях
В основе показательных уравнений и неравенств лежит показательная функция. Что это такое?
Показательная функция — это функция, у которой неизвестная находится в показателе степени.
y=ax, где a > 0 и a ≠ 1
Важно помнить, что:
- Степень числа — это результат многократного умножения числа на само себя.
- Значение функции (y) зависит от выражения a x.
- Величина a — это основание степени (повторяющийся множитель). В показательной функции есть ограничения: a не может быть отрицательной и не может равняться единице или нулю.
- Величина a находится в неизвестной степени x, которая является показателем степени (число, показывающее количество повторений множителя).
Подробно эти и другие особенности данного вида функций мы обсуждаем в статье «Показательная и логарифмическая функции». Загляните в нее при необходимости.
Прежде чем переходить к показательным уравнениям, нам надо также вспомнить, что у степени числа есть свойства, которые можно применять для преобразований во время решения.

Теперь, вооружившись нужными знаниями, мы можем приступить к решению показательных уравнений и неравенств.
Методы решения показательных уравнений
Мы вспомнили, что такое показательная функция. Как же выглядит показательное уравнение?
Показательное уравнение — это уравнение, где неизвестная находится в показателе степени.
| Чем отличается функция от уравнения? Функция задает множество точек, при которых будет справедливо определенное выражение. Иными словами, функция ищет все возможные значения переменных. Когда же мы решаем уравнение, то ищем конкретное значение переменной, которое будет удовлетворять условию. |
Пример показательного уравнения: 5 4x-2=25.
Если неизвестная содержится и в показателе степени, и в основании, уравнение также считается показательным.
Пример такого показательного уравнения: (2x — 17)x+3 = 0.
В математике всегда есть множество способов, как решить тот или иной пример. Показательные уравнения не исключение. Рассмотрим несколько из них.
Методы решения показательных уравнений:
- графический метод;
- метод уравнивания показателей;
- метод введения новой переменной;
- метод вынесения общего множителя;
- метод группировки;
- метод умножения/деления на показательную функцию.
Графический метод
Название уже подсказывает, что мы будем строить графики.
Этот метод заключается в рассмотрении левой и правой частей уравнения как отдельных функций и изображении их на плоскости. Данный метод в некоторых случаях может оказаться неточным. Поэтому его лучше использовать для нахождения количества решений, а сами значения находить другим методом.
Для примера решим следующее уравнение:
0,5^x+2=x+5
Разделим его на отдельные функции:
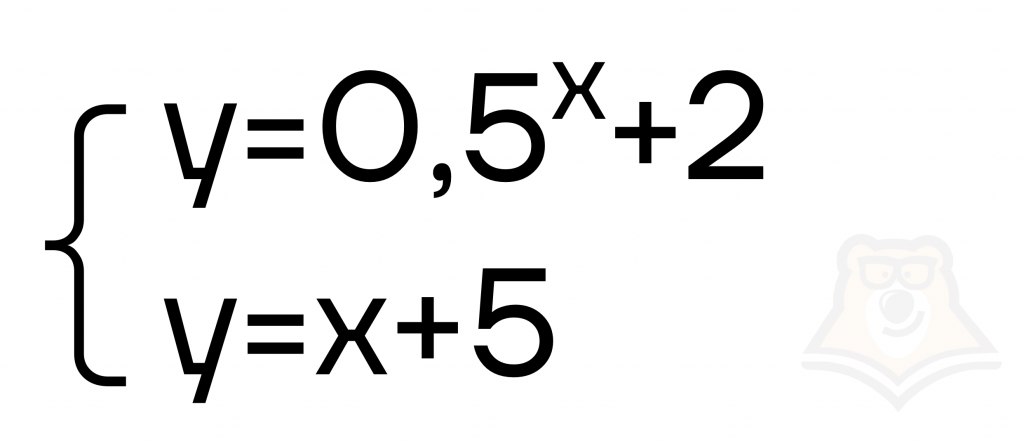
Построим таблицы для каждой функции:

Заметим, что вторая функция задает прямую, а значит, для ее построения достаточно найти только две точки.
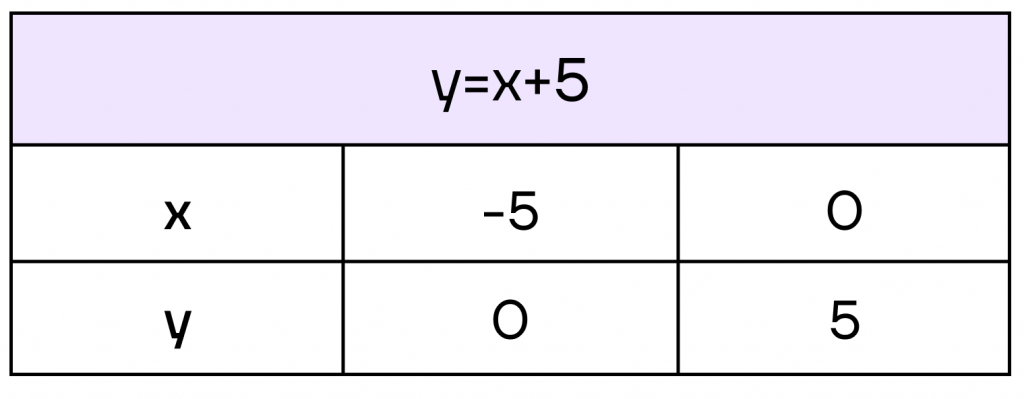
Отметим найденные точки и изобразим функции на плоскости. Найдем точку пересечения, именно она и будет решением данного уравнения.
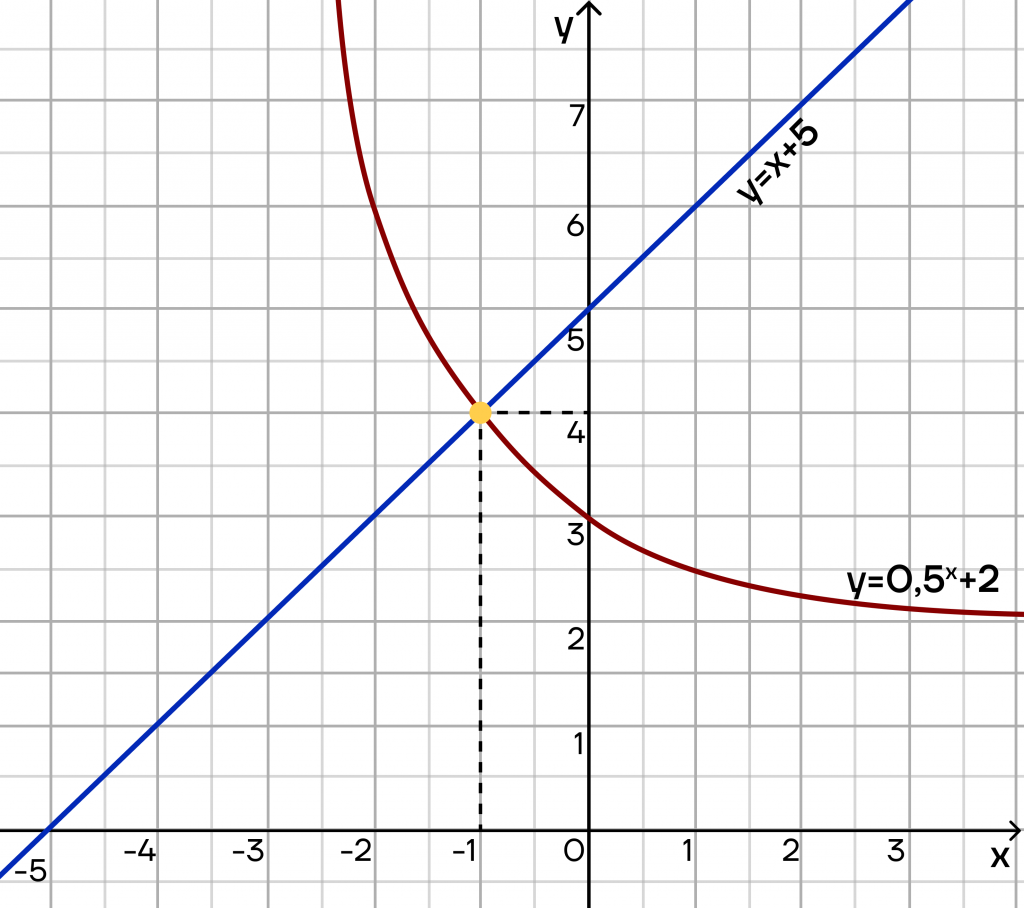
Точка пересечения имеет координаты (-1;4). Поскольку по условию нам нужно было найти только значение х, то в ответ выпишем x = — 1.
Метод уравнивания показателей
Этот метод заключается в представлении обеих частей уравнения в виде степени с одинаковыми основаниями и приравниванию показателей степеней.
Иными словами: если мы возводим одно и то же число в степень, то для получения одинаковых ответов степени должны быть равны.
af(x) = a g(x), где a > 0 и a ≠ 1 ⬄ f(x) = g(x)
Рассмотрим на примере:
2^x*3^x=36
Воспользуемся свойством степеней (свойство 3) для левой части и приведем к такому виду:
6^x=36
Запишем левую часть как степень с основанием 6:
6^x=6^2
Перейдем к равенству степеней и найдем х:
x=2
Метод введения новой переменной
| Как облегчить решение уравнения? Иногда перед нами предстает огромная запись уравнения, в которой разбегаются глаза. Чтобы упростить и решение, и запись, можно ввести замену. Под заменой мы понимаем новую переменную, которая «содержит» в себе какую-либо повторяющуюся часть в выражении. |
Суть метода: чтобы решить уравнение, нужно принять повторяющееся выражение за новую переменную и решить относительно нее, а после сделать обратную замену (то есть новую переменную опять представить в виде повторяющегося выражения).
Важно: нельзя забывать про обратную замену, потому что значение введенной переменной не равно значению изначальной переменной.
К примеру, мы имеем уравнение:
17^{2*(x^2-x+13)}-4*17^{x^2-x+13}+21=0Заметим, что у нас повторяется \(17^{x^2-x+13}\) следовательно, мы можем ввести замену.
Замена: пусть \(17^{x^2-x+13}=t\) тогда уравнение приобретает вид:
t^2-4t+21=0
А с таким уравнением уже намного приятнее и легче работать! Главное, после решения не забыть сделать обратную замену, поскольку в задании мы все же ищем х, а не t.

Решим следующее уравнение:
2^{2x}-2*2^x+6=5Соберем все слагаемые слева от знака равно:
2^{2x}-2*2^x+6-5=02^{2x}-2*2^x+1=0Разложим каждое слагаемое на множители:
2^x*2^x-2 * 2^x+1=0
Заметим, что 2x можно заменить. Пусть t = 2x, по ограничению показательной функции t > 0, тогда уравнение можно записать следующим образом:
t^2-2t+1=0
Решим уравнение относительно новой переменной. Заметим, что наше выражение очень похоже на формулу сокращенного умножения \((a-b)^2=a^2-2ab+b^2\).
Преобразуем выражение:
(t-1)^2=0
t=1
Найденное значение подходит под условие t > 0, сделаем обратную замену:
2^x=1
Представим правую часть в виде степени с основанием 2:
2^x=2^0
Приравняем показатели степеней и найдем х:
x=0
Метод вынесения общего множителя
Этот метод — как следует из его названия — заключается в вынесение общего множителя за скобку.
Рассмотрим подробнее на примере:
6^x-3^x=0
Разложим первое слагаемое на множители:
3^x*2^x-3x=0
Вынесем общий множитель за скобку:
3^x(2^x-1)=0
В скобках осталась единица, поскольку второе слагаемое мы можем представить как \(3^x=1*3^x\).
Произведение равно нулю, значит, один из множителей должен равняться нулю. Перейдем к системе уравнений:
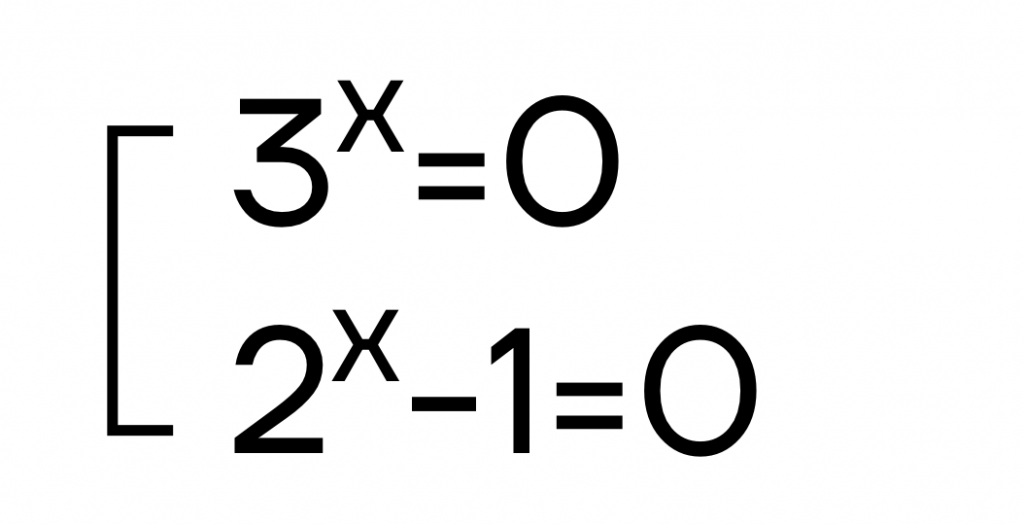
Так как показательная функция всегда больше 0, то у первого уравнения не будет решений.
Решим второе уравнение.
2^x-1=0
2^x=1
2^x=2^0
x=0
Единственным решением данного уравнения будет х = 0.
Метод группировки
Заключается этот метод во взятии слагаемых в скобки с последующим упрощением выражения.
Давайте решим такое уравнение:
x * 5^x-5x-3* 5^x+15=0
Заметим, что, сгруппировав 1‑е и 3‑е слагаемые и 2‑е и 4‑е слагаемые и вынося общий множитель за скобки, получаем одинаковые скобки:
(x*5^x-3*5^x)-(5x-15)=0
5^x(x-3)-5(x-3)=0
Вынесем за скобку общий множитель (x — 3):
(5^x-5)(x-3)=0
Если произведение множителей равно 0, то каждый множитель равен 0. Перейдем к совокупности уравнений:
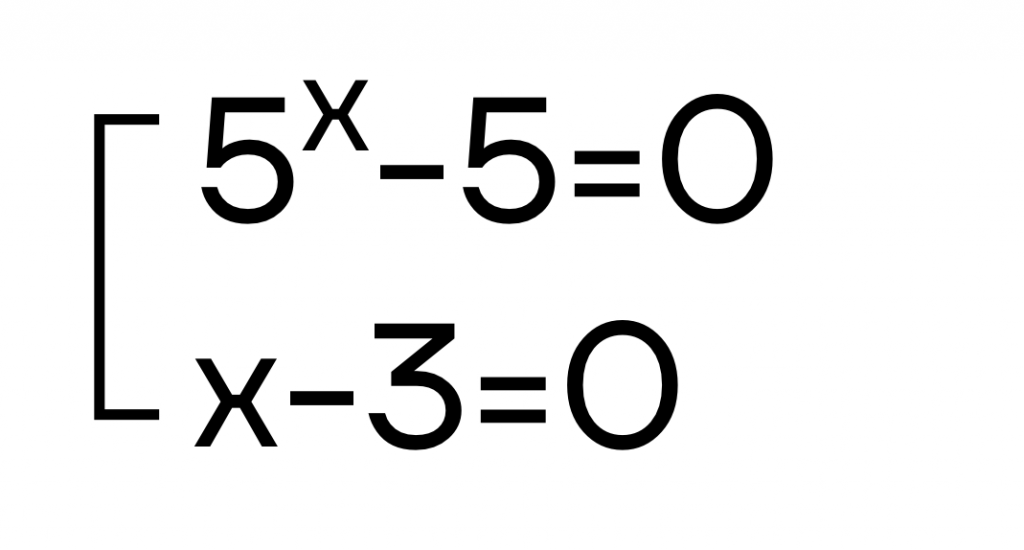
Решим первое уравнение:
5^x-5=0
5^x=5
5^x=5^1
x=1
Во втором уравнении перенесем -3 вправо и получим x = 3.
Таким образом, ответами будут 1 и 3.
Метод умножения/деления на показательную функцию
Данный метод заключается в умножении или делении каждого слагаемого уравнения на определенную показательную функцию.
Рассмотрим следующее уравнение:
2^x-\frac{1}{5^x}=0Для упрощения уравнения умножим каждое слагаемое на 5x и получим:
2^x*5^x-1=0
Заметим, что в данном случае мы можем умножать на показательную функцию без ограничений, поскольку она никогда не может быть равна 0. Напомним: в какую бы степень мы ни возводили положительное число, оно никогда не будет равняться 0. Если бы в знаменателе стояла другая показательная функция или просто переменная, то необходимо было бы указать область допустимых значений.

Воспользуемся свойством степеней для первого слагаемого, а второе перенесем вправо:
10^x-1=0
10^x=1
Представим справа степень с основанием 10:
10^x=10^0
Приравняем степени и получим ответ:
x=0
Также можно делить все слагаемые на показательную функцию для упрощения уравнения. Это допустимо, только если эта функция точно не равна нулю, так как на ноль делить нельзя.
Например, функция y = 2x — 1 будет равна 0 при x = 0.
Рассмотрим решение показательного уравнения на примере №12 из ЕГЭ по профильной математике.
а) Решите уравнение: \(49^x+\frac{48}{7}*7^{x+1}-49=0\).
б) Найдите корни, которые принадлежат промежутку (-\sqrt3;1).
Решение.
а) Представим \(49^x\) в виде степени с основанием 7:
\(7^{2x}+\frac{48}{7}*7^{x+1}-49=0\)
Преобразуем \(7^{x+1}\) по свойству степеней: \(7^{x+1}=7^x*7^1=7*7^x\).
Получаем выражение:
\(7^{2x}+\frac{48}{7}*7*7^x-49=0\)
\(7^{2x}+48*7^x-49=0\)
Заметим, что у нас есть повторяющаяся переменная, а значит, мы можем сделать замену.
Замена: \(t=7^x, t>0\) — ограничение показательной функции.
\(t^2+48t-49=0\)
Решим квадратное уравнение с помощью дискриминанта (за подробностями по этому шагу приглашаем вас в статью «Линейные, квадратные и кубические уравнения»):
\(D=b^2-4ac=2304+196=2500\)
\(t_1=\frac{-b+\sqrt{D}}{2a}=\frac{-48+50}{2}=1\)
\(t_2=\frac{-b-\sqrt{D}}{2a}=\frac{-48-50}{2}=-49\) — не подходит, поскольку \(t>0\).
Сделаем обратную замену:
\(t=7^x\)
\(1=7^x\)
\(7^x=7^0\)
\(x=0\)
б) Заметим, что \((-\sqrt3)\) — отрицательное число, а 1 — положительное. На числовой прямой 0 будет лежать между ними, следовательно, будет принадлежать данному промежутку.
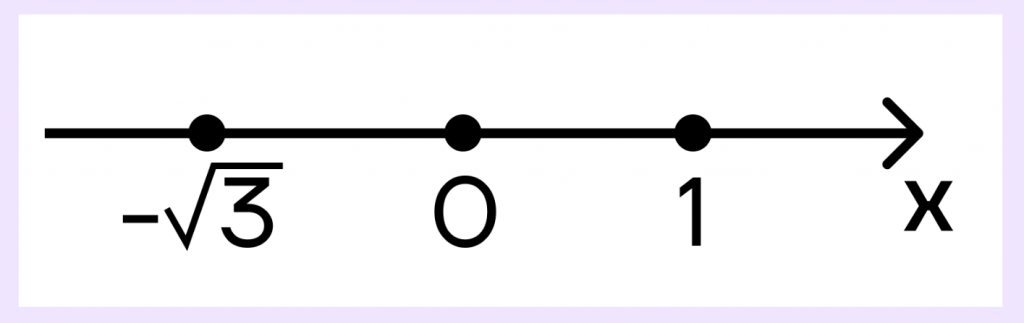
Ответ: а) 0; б) 0.
Показательные неравенства
Показательное неравенство — это неравенство, у которого переменная находится в показателе степени.
Самый простой вид показательного неравенства:
ax>y, где a и y — числа
Неравенства видов af(x) > y и af(x) > ag(x) называются простейшими показательными неравенствами.
Отметим, что вместо f(x) и g(x) может стоять любое выражение с переменной. То есть показательные неравенства могут выглядеть, например, так 2x > 8 или так 252x-4< (1/5)x+3 и т.п.
При решении неравенств можно облегчить себе задачу. Иногда встречаются неравенства, которые решаются «без решения». Это связано с логическими рассуждениями и ответ в таких неравенствах можно писать почти сразу.
Разберем такие особые случаи:
Случай № 1: af(x) < y при y ≤ 0 не имеет решений, так как положительное число в степени всегда больше 0.
Разберем на примере: 4x < — 1.
4x всегда будет положительным числом, поскольку при возведении положительного числа в любую степень всегда получится положительное число. Это наглядно видно на графиках показательных функций: кривая лежит выше оси x, то есть в какую бы степень (х) мы ни возвели число, оно будет положительным (у).
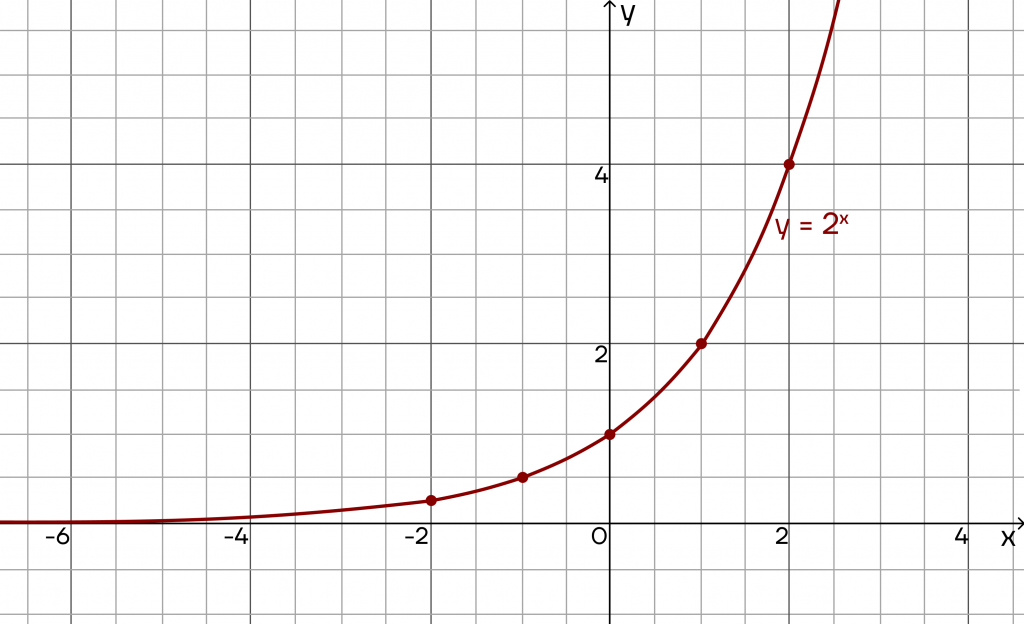
Тем временем (- 1) — отрицательное число.
Следовательно, мы получаем неравенство «положительное число» < «отрицательное число», что невозможно.
Случай №2: af(x)>y при y ≤ 0. В таком неравенстве множеством решений является множество действительных чисел.
Разберемся, почему так получается. Для примера возьмем аналогичное предыдущему неравенство: 4x > — 1.
Как мы уже определили, 4x всегда будет положительным числом.
В этом случае мы получаем неравенство «положительное число» > «отрицательное число», что выполняется при всех значениях х.
Как решать все остальные неравенства? Приступим к изучению.
Для начала давайте вспомним, как сравниваются показатели степеней с основаниями от 0 до 1 и основаниями больше 1.
| Если 0 < a < 1 ax < ay ⬄ x > y | Если a > 1 ax < ay ⬄ x < y |
Рассмотрим первый случай и попробуем сравнить выражения
\frac{1}{2}^3и \frac{1}{2}^{-1}Если рассуждать логически, то бóльшим будет первое число: чем больше степень, в которую возводится число, тем больше это число. Однако в данном случае все работает немного иначе.
Посчитаем:
\frac{1}{2}^3=\frac{1}{8}и (\frac{1}{2})^{-1}Оказывается, второе число больше!

Поэтому, если основание 0 < a < 1, то при переходе к неравенству степеней знак меняется на противоположный. В этом случае чем больше степень — тем меньше значение выражения.
Если 0 < a < 1
ax<ay ⬄ x>y
А вот если основание a > 1, то ничего не поменяется. Чем больше будет степень — тем больше будет значение выражения.
Например,
2^3=8
и
2^{-1}=\frac{1}{2}Таким образом, если основание больше 1, тогда при переходе знак остается прежним.
Если a > 1
ax < ay ⬄ x < y
| Как поменять знак неравенства всего одним действием? Поменять знак неравенства можно и «искусственно»! При делении или умножении каждой части неравенства на отрицательное число знак неравенства меняется на противоположный. Например: 2x — 1 > — 3 | :(- 1) — 2x + 1 < 3 |
Методы решения показательных неравенств
Для решения показательных неравенств можно использовать те же методы, что и для решения уравнений, но с некоторыми изменениями. Они коснутся графического метода, метода уравнивания показателей и метода умножения/деления на показательную функцию.
- Графический метод.
Теперь, используя этот метод, нужно закрашивать полученную область на графике функций.
Рассмотрим такое неравенство:
2^x≥-x+3
Запишем функции:
y=2^x
y=-x+3
Действуя аналогично с решением показательных уравнений, изобразим функции на графике:
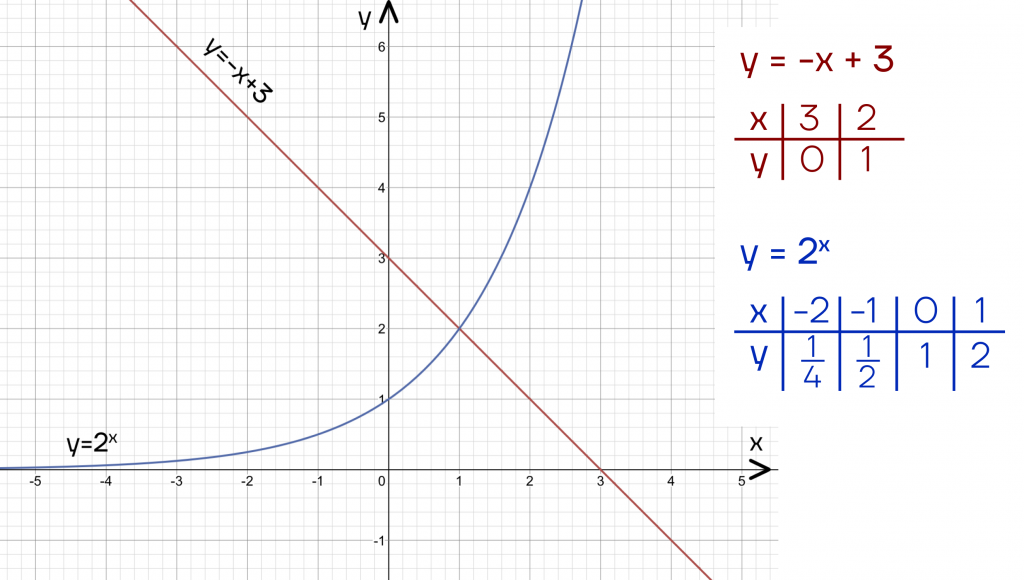
Так как первая функция больше или равна второй, выделим промежуток на графике, где график первой функции выше графика второй.
Поскольку нам нужно найти значения х, при которых один график больше второго, то закрашиваем всю область, лежащую правее точки пересечения графиков.
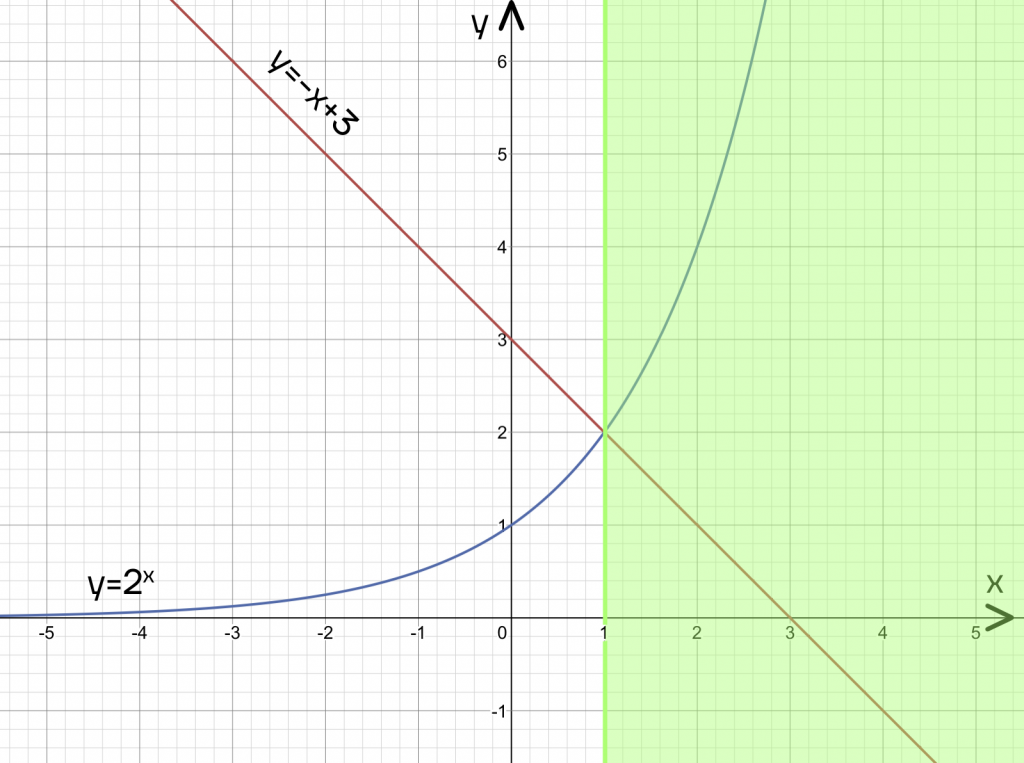
В ответ получим промежуток [1;+∞).
Заметим, что скобочка квадратная, поскольку в первоначальном выражении стоит нестрогий знак неравенства.
- Метод уравнивания показателей.
Данный метод будет записан по-разному для возрастающей и убывающей показательных функций. Это связано со сменой знака неравенства, которую мы рассмотрели выше.
af(x)<ag(x), где a > 1 ⬄ f(x) < g(x)
af(x)<ag(x), где 0 < a < 1 ⬄ f(x) > g(x)
Разберем пример из №15 ЕГЭ по профильной математике.
Решите неравенство
\(3^{x^2}<27*(\frac{1}{9})^x\)
Решение.
Представим все множители в виде степеней тройки:
\(3^{x^2}<27*(\frac{1}{9})^x\)
\(3^{x^2}<3^3*3^{-2x}\)
Воспользуемся свойством степеней \((a^n*a^m=a^{n+m})\):
\(3^{x^2}<3^{3-2x}\)
Теперь нам необходимо перейти к неравенству с показателями. Поскольку 3 > 1, то нам потребуется первое правило:
\(a^{f(x)}<a^{g(x)}\), где \(a > 1 \leftrightarrow f(x)<g(x)\)
В нашем случае \(f(x)=x^2, g(x)=3-2x\):
\(x^2<3-2x\)
Перенесем все слагаемые в одну сторону и приравняем выражение к 0, чтобы найти нули функции:
\(x^2+2x-3<0\)
\(x^2+2x-3=0\)
Решим уравнение с помощью дискриминанта:
\(D=b^2-4ac=4+12=16\)
\(x_{1}=\frac{-b+\sqrt D}{2a}=\frac{-2+4}{2}=1\)
\(x_{2}=\frac{-b+\sqrt D}{2a}=\frac{-2-4}{2}=-3\)
Отметим точки на прямой (заметим, что они будут выколотыми, поскольку знак неравенства строгий) и определим знаки на промежутках:
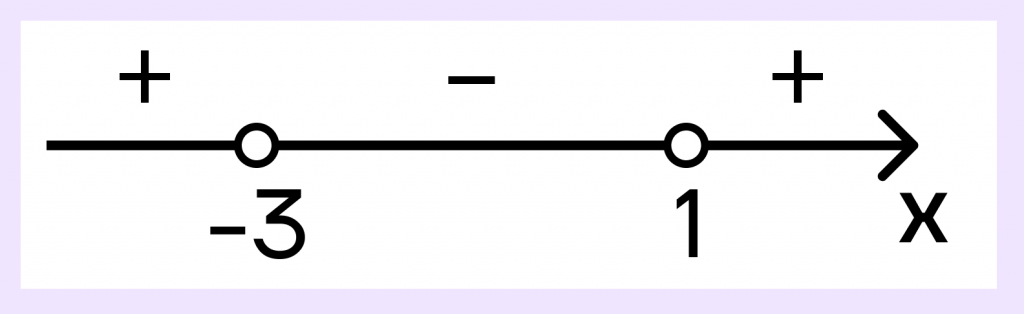
Поскольку нам нужны значения меньше 0, то нам подойдет промежуток (-3;1).
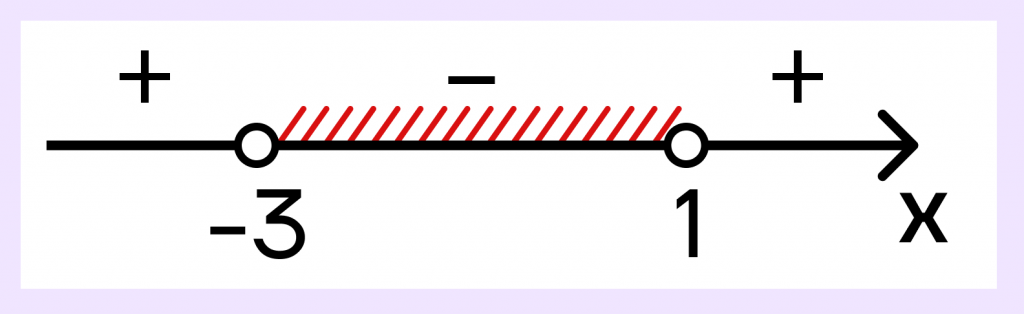
Этот промежуток и будет решением нашего неравенства.
Ответ: (-3;1)
Если бы основание было меньше 1, то необходимо бы было воспользоваться вторым правилом и поменять знак неравенства при переходе к выражению с показателями степеней.
Рассмотрим на примере того же неравенства, но вместо 3 возьмем \(\frac{1}{3}\):
(\frac{1}{3})^{x^2}<(\frac{1}{3})^{3-2x}Поскольку \(0 < \frac{1}{3} < 1\) нам необходимо воспользоваться вторым правилом:
(a^{f(x)}< a^{g(x)}, где 0 < a < 1\leftrightarrow f(x) > g(x)Тогда мы получим неравенство:
x^2 > 3- 2x
Заметим, что полученные неравенства отличаются только знаком.
3. Метод умножения/деления на показательную функцию.
Используя данный метод для неравенств, нужно учитывать, что при умножении/делении на отрицательное число знак неравенства меняется на противоположный.
Также нельзя делить на число или выражение, которое может быть корнем выражения. В противном случае можно потерять точку на прямой и найти неправильный промежуток. Иными словами, нельзя делить на выражение, «внутри» которого находится переменная.
Решим одно неравенство:
(\frac{1}{3})^{x+1}+(\frac{1}{3})^{x}≥ 12Воспользуемся свойством степеней и преобразуем:
(\frac{1}{3})^{x}*\frac{1}{3}+(\frac{1}{3})^{x}≥ 12Вынесем общий множитель:
(\frac{1}{3})^{x}*(\frac{1}{3}+1)≥ 12(\frac{1}{3})^{x}*\frac{4}{3}≥ 12Домножим обе части неравенства на \(\frac{3}{4}\). Поскольку это число без переменной, то корни мы не потеряем. Число положительное, значит, менять знак не нужно.
(\frac{1}{3})^{x}≥ 9Представим правую часть неравенства в виде степени с основанием \(\frac{1}{3}\):
(\frac{1}{3})^{x}≥(\frac{1}{3})^{-2}Перейдем к неравенству степеней, поменяем знак уравнения, так как \(0 < \frac{1}{3} < 1\):
x ≤-2
Ответ: (-∞; -2].
Методы введения новой переменной, вынесения общего множителя и группировки для показательных уравнений работают и с показательными неравенствами, причем без изменений.
Мы изучили один из видов уравнений и неравенств — показательные, но на этом они не закончились. Чтобы точно решить любой пример на экзамене, необходимо овладеть всеми видами уравнений и неравенств. Так что имеет смысл продолжить их изучение, например, узнать про «Логарифмические уравнения и неравенства».
Термины
Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле D = b2 — 4*a*c, где а, b и с берутся из уравнения.
Действительные числа — это все положительные и отрицательные числа, а также 0.
Нули функции — это значения аргумента, при которых функция равна нулю.
Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.
Фактчек
- Показательное уравнение или неравенство — это уравнение или неравенство, где неизвестная находится в показателе степени.
- Методы решения показательных уравнений и неравенств: графический метод; метод уравнивания показателей; метод введения новой переменной; метод вынесения общего множителя; метод группировки; метод умножения/деления на показательную функцию.
- Если основание степени в неравенстве от 0 до 1, то при переходе к неравенству степеней знак меняется на противоположный.
- При умножении/делении обеих частей неравенства на отрицательное число, знак неравенства меняется на противоположный.
Проверь себя
Задание 1.
Решите уравнение \(3^x*3^{x+2}=9\)
- 2
- -2
- 0
- 1
Задание 2.
Решите уравнение \(5^{\frac{x-5}{x}}-5^{\frac{1}{5}}=0\)
- 5
- 6
- 0
- 4
Задание 3.
Решите уравнение \(4^x* 2 = 256\)
- 3,5
- 0
- 1
- 2,8
Задание 4.
Решите неравенство \(\frac{1}{2}^x≤ 8\)
- -3
- (-3; 3)
- (-∞; -3]
- [-3; +∞)
Задание 5.
Решите неравенство \(3^{x+2}-9^x ≥ 0\)
- [2; +∞)
- (-∞; 2)
- (-∞; 2]
- 2
Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 4; 5. — 3.


 к списку статей
к списку статей