Преобразование алгебраических выражений. Часть 1

На этой странице вы узнаете

• Как не допустить самую популярную ошибку в математике?
• Что в алгебре произошло от геометрии?
• Куда можно вынести минус?

В жизни часто для тех или иных ситуаций мы можем подбирать себе разные образы: для школы или работы – что-то официальное, для дома – максимально удобное, для различных мероприятий – что-то, что соответствует тематике мероприятия, ну а для прогулок с друзьями – то, что нравится в первую очередь нам самим.

То же самое происходит и с многочленами, о которых шла речь в статье «Многочлены и действия с ними». Для решения различных задач нам будет удобно преображать многочлены так, чтобы с ними можно было совершать определенные действия. 

Давайте же разберемся, какими способами и как можно преобразовывать многочлены. Перед началом рекомендуем ознакомиться со статьей «Действия с натуральными числами», потому что в процессе мы не раз столкнемся со степенями.

Формулы сокращенного умножения 

Из статьи «Многочлены и действия с ними» мы помним, что многочлен можно умножить на другой многочлен. С некоторыми видами таких произведений мы часто сталкиваемся в алгебре, поэтому, чтобы каждый раз не перемножать такие многочлены, их выделили в отдельные формулы – формулы сокращенного умножения.

Далее мы рассмотрим основные формулы сокращенного умножения.

Разность квадратов

Умножим многочлен \(a-b\) на многочлен \(a+b\):

\((a-b)*(a+b)=a*a-b*a+a*b-b*b=a^2-ba+ba-b^2=a^2-b^2\)

Мы получили:

\((a-b)*(a+b)=a^2-b^2\)

Эту формулу сокращенного умножения называют формулой разности квадратов, ведь \(a^2-b^2\) – это разность квадратов (вторых степеней) одночленов a и b.

Как можно заметить, в формуле разности квадратов многочлены \(a-b\) и \(a+b\) отличаются лишь знаками между a и b: в первом случае – минус, во втором – плюс. В этом и заключается особенность этой формулы, по которой мы можем легко ее определить.

Вместо одночленов a и b, здесь могут стоять любые другие одночлены. Например:

\((m-k)*(m+k)=m^2-k^2\)
\((xy-t^3)*(xy+t^3)=(xy)^2-(t^3)^2=x^2y^2-t^6\)
\((5a+7zh)*(5a-7zh)=(5a)^2-(7zh)^2=25a^2-49z^2h^2\)

Что же будет, если в двух таких многочленах их члены стоят в разном порядке? Например, \((a-b)*(b+a)\). Что получится в таком случае: \(a^2-b^2\) или \(b^2-a^2\)?

Все просто, для этого достаточно вспомнить основное свойство сложения: от перемены мест слагаемых сумма не меняется. Поэтому в многочлене \(b+a\) мы можем поменять слагаемые местами: \(b+a=b+a\). Тогда многочлен примет вид 

\((a-b)*(a+b)=a^2-b^2\).

То есть, порядок, в котором стоят слагаемые в скобке со сложением, ничего не определяет, ведь эти слагаемые можно всегда поменять местами.

А вот от того, в каком порядке стоят слагаемые в скобке с вычитанием, зависит порядок, в котором будут идти квадраты одночленов в разности этих квадратов. Определяем этот порядок именно по скобке с вычитанием.

Приведем еще несколько примеров:

\((с+8)*(8-с)=8^2-c^2=64-c^2\)
\((h^2-2s)*(2s+o)=(h^2)^2-(2s)^2=h^4-4s^2\)

Из статьи «Понятие корня» мы помним, что вторая степень (квадрат) тесно связана с квадратным корнем, а именно \((\sqrt{a})^2=a\). Поэтому формулы сокращенного умножения часто используются для упрощения иррациональных выражений, то есть выражений, содержащих знак корня. Разберемся в этом на одном из примеров.

Разберем пример задания №6 из ЕГЭ по профильной математике.

Задание. Найти значение выражения \((\sqrt{39}-\sqrt{19})(\sqrt{39}+\sqrt{19})\).

Решение. В выражении \((\sqrt{39}-\sqrt{19})(\sqrt{39}+\sqrt{19})\) можно проследить формулу разности квадратов. Воспользуемся ей:

\((\sqrt{39}-\sqrt{19})(\sqrt{39}+\sqrt{19})=(\sqrt{39})^2-(\sqrt{19})^2=39-19=20\)

Таким образом, в одно действие мы смогли получить ответ 20.

Ответ: 20

Переходим к следующей формуле, которая тоже связана с квадратом, но имеющей совершенно другой вид.

Квадрат суммы

Умножим многочлен \(a+b\) на себя же, то есть, возведем этот многочлен во вторую степень:

\((a+b)^2=(a+b)*(a+b)=a*a+b*a+a*b+b*b=a^2+2ab+b^2\)

Получили формулу квадрата суммы: квадрат суммы двух одночленов равен сумме квадратов этих одночленов и их удвоенному произведению.

\((a+b)^2=a^2+2ab+b^2\)

Вместо a и b могут стоять любые другие одночлены. Например:

\((2+6x)=2^2+2*2*6x+(6x)^2=4+24x+36x^2\)
\((v^3+5km)=(v^3)^2+2*v^3*5km+(5km)^2=v^6+10v^3km+25k^2m^2\)
\((n^5y^{10}+2j^9n)=(n^5y^{10})^2+2*n^5y^{10}*2j^6n+(2j^6n)^2=n^{10}y^{20}+4n^6y^{10}j^6+4j^{12}n^2\)

Помимо квадрата суммы, выделяют также квадрат разности.

Квадрат разности

Точно так же умножим многочлен \(a-b\) на себя же, то есть, возведем этот многочлен во вторую степень:

\((a-b)^2=(a-b)*(a-b)=a*a-b*a-a*b+b*b=a^2-2ab+b^2\)

Получим формулу квадрата разности: квадрат разности двух одночленов равен сумме квадратов этих одночленов и их отрицательного удвоенного произведения.

\((a-b)^2=a^2-2ab+b^2\)

Как видим, выражения \(a^2-2ab+b^2\) и \(a^2+2ab+b^2\) отличаются только знаком удвоенного произведения. В дальнейшем эти выражения будем называть полным квадратом суммы или разности. 

Приведем несколько примеров:

\((y-12)^2=y^2-2*y*12+12^2=y^2-24y+144\)
\((s^4t-6k)^2=(s^4t)^2-2*s^4t*6k+(6k)^2=s^8t^2-12s^4tk+36k^2\)
\((8i^5-9i^3)^2=(8i^5)^2-2*8i^5*9i^3+(9i^3)^2=64i^{10}-144i^{15}+81i^6\)

Снова вернемся к иррациональным выражениям, только теперь для их преобразования применим формулы квадрата суммы и квадрата разности.

Разберем пример задания №8 из ОГЭ по математике.

Задание. Найти значение выражения \((\sqrt{11}+5)^2+(\sqrt{11}-5)^2\).

Решение. Раскроем скобки в этом уравнении, применив формулы для квадрата суммы и квадрата разности:

\((\sqrt{11}+5)^2+(\sqrt{11}-5)^2=\)
\(=(\sqrt{11})^2+2*\sqrt{11}*5+5^2+(\sqrt{11})^2-2*\sqrt{11}*5+5^2=\)
\(11+2\sqrt{11}+25+11-2\sqrt{11}+25=72\)

Получили значение данного выражения: 72.

Ответ: 72

Как не допустить самую популярную ошибку в математике? Наверно, практически каждый хотя бы раз при решении той или иной математической задачи пытался включить интуицию, особенно в тех моментах, где все кажется очевидным, как \(2+2=4\). Это абсолютно нормально, ведь любой человек склонен доверять своим чувствам и ощущениям. К сожалению, эта интуиция часто подводит нас как раз на самых очевидных местах. Пожалуй, самая популярная ошибка в математике – раскрытие скобок квадрата суммы или разности.  Квадрат суммы и квадрат разности раскрываются по формулам сокращенного умножения и никак иначе. Неправильно: \((a+b)^2=a^2+b^2\) \((a-b)^2=a^2-b^2\) Правильно: \((a+b)^2=a^2+2ab+b^2\) \((a-b)^2=a^2-2ab+b^2\) Поэтому, чтобы избежать самой популярной ошибки в математике, достаточно просто запомнить эти две формулы и, в данном случае, не доверять интуиции.

Таким образом, мы выделили три формулы для вторых степеней: разность квадратов, квадрат суммы и квадрат разности. 

Далее переходим к третьей степени, и начнем мы с куба суммы.

Куб суммы

Возведем многочлен \((a+b)\) в третью степень, то есть умножим его на самого себя три раза. Произведение первых двух многочленов распишем, как квадрат суммы:

\((a+b)^3=(a+b)*(a+b)*(a+b)=(a+b)^2*(a+b)=\)
\(=(a^2+2ab+b^2)*(a+b)=\)
\(=a^2*a+2ab*a+b^2*a+a^2*b+2ab*b+b^2*b=\)
\(a^3+2a^2b+b^2a+a^2b+2ab^2+b^3=a^3+3a^2b+3ab^2+b^3\)

Запишем получившуюся формулу куба суммы: куб суммы двух одночленов равен сумме кубов этих одночленов, утроенного произведения квадрата первого одночлена на второй одночлен и утроенного произведение первого одночлена на квадрат второго одночлена.

\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)

Приведем несколько примеров:

\((c+6a)^3=c^3+3*c^2*6a+3*c*(6a)^2+(6a)^3=c^3+18c^2a+108ca^2+216a^3\)
\((2he+3f^2)^3=(2he)^3+3*(2he)^2*3f^2+3*2he*(3f^2)^2+(3f^2)^3=\)
\(=8h^3e^3+36h^2e^2f^2+54hef^4+27f^6\)

От куба суммы переходим к следующей формуле – кубу разности.

Куб разности

Возведем многочлен \((a-b)\) в третью степень таким же способом:

\((a-b)^3=(a-b)*(a-b)*(a-b)=(a-b)^2*(a-b)=\)
\(=(a^2-2ab+b^2)*(a-b)=\)
\(=a^2*a-2ab*a+b^2*a-a^2*b+2ab*b-b^2*b=\)
\(a^3-2a^2b+b^2a-a^2b+2ab^2-b^3=a^3-3a^2b+3ab^2-b^3\)

Запишем получившуюся формулу куба разности:

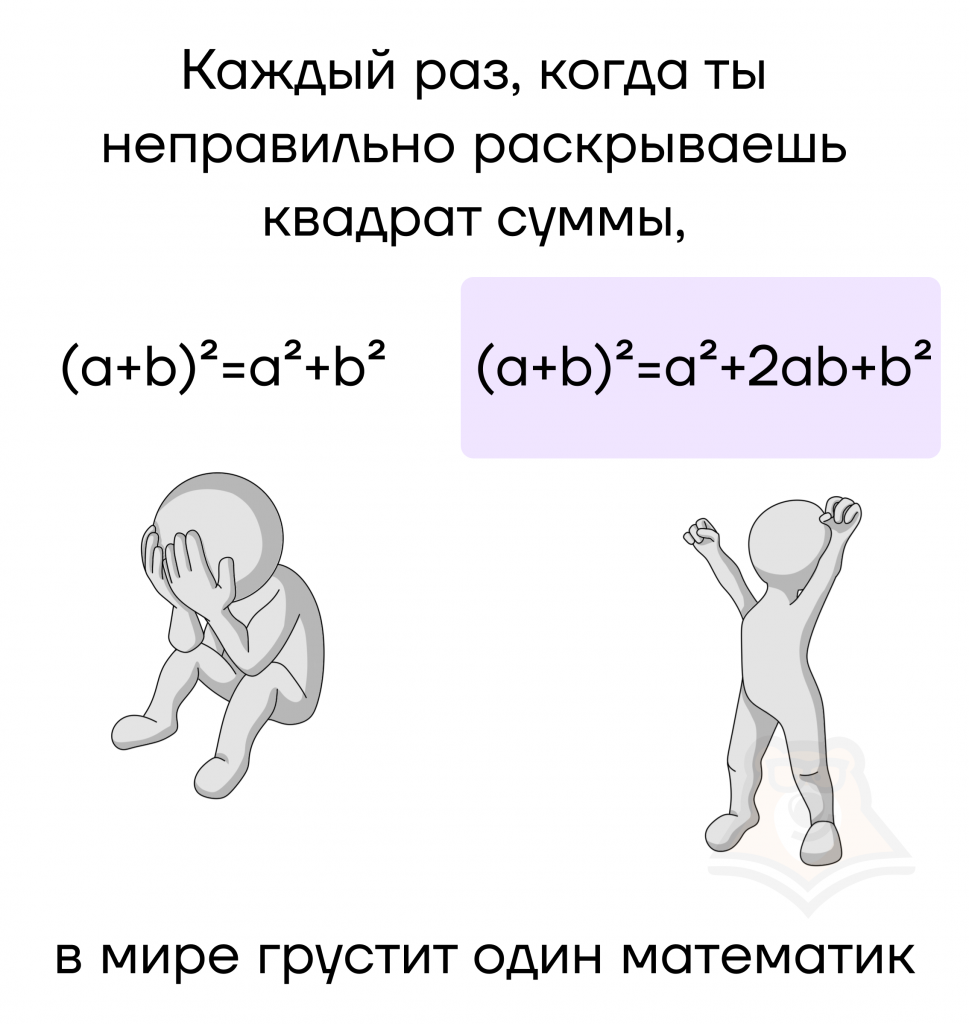
\((a-b)^3=a^3-3a^2b+3ab^2-b^3\)

Эта формула отличается от формулы куба суммы лишь чередованием знаков начиная с первого одночлена со знаком \(«+» (a^3)\). Далее идет чередование:  \(«+-+-»\).

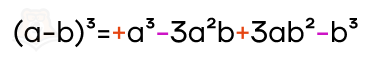
Как обычно, рассмотрим несколько примеров:

\((4-r)^3=4^3-3*4^2*r+3*4*r^2-r^3=64-48r+12r^2-r^3\)

\((ax^2-2n^3)={(ax^2)}^3-3*{(ax^2)}^2*2n^3+3*ax^2*(2n^3)^2-{(n^3)}^3=\)
\(=a^3x^6-6a^2x^4n^3+12ax^2n^6-n^9\)

Двигаемся дальше, следующая формула сокращения на очереди – сумма кубов.

Сумма кубов

Умножим многочлен \(a+b\) на многочлен \(a^2-ab+b^2\):

\((a+b)*(a^2-ab+b^2)=a*a^2+b*a^2-a*ab-b*ab+a*b^2+b*b^2=\)
\(=a^3+a^2b-a^2b-a^2b+a^2b-b^3=a^3+b^3\)

Получили формулу суммы кубов: 

\((a+b)*(a^2-ab+b^2)=a^3+b^3\)

Можно заметить, что выражение \(a^2-ab+b^2\) похоже на полный квадрат разности \((a^2-2ab+b^2)\), отличается лишь отсутствием множителя 2. В таком случае это выражение называют неполным квадратом разности.

Итак, сумма кубов двух одночленов равна произведению суммы этих одночленов на их неполный квадрат разности.

Приведем примеры:

\((y+8)*(y^2-8y+64)=(y+8)*(y^2-8y+8^2)=y^3+8^3=y^3+512\)

\((k^2+2n)*(k^4-2k^2n+4n^2)=(k^2+2n)*((k^2)^2-k^2*2n+(2n)^2)=k^3+(2n)^3=\)
\(=k^3+8n^3\)

Осталось разобрать последнюю формулу сокращенного умножения – разность кубов. Давайте же скорее сделаем это.

Разность кубов

Умножим многочлен \(a-b\) на многочлен \(a^2+ab+b^2\):

\((a-b)*(a^2+ab+b^2)=a*a^2-b*a^2+a*ab-b*ab+a*b^2-b*b^2=\)
\(=a^3-a^2b+a^2b-a^2b+a^2b-b^3=a^3-b^3\)

Получили формулу разности кубов

\((a-b)*(a^2+ab+b^2)=a^3-b^3\)

Выражение \(a^2+ab+b^2\) похоже на полный квадрат суммы \((a^2+2ab+b^2)\), отличается только множителем 2. Аналогично неполному квадрату разности, это выражение называют неполным квадратом суммы.

Разность кубов двух одночленов равна произведению разности этих одночленов на их неполный квадрат суммы.

Разберем несколько примеров:

\((3-2h)*(9+6h+4h^2)=(3-2h)*(3^2+3*2h+(2h)^2)=3^3-(2h)^3=9-8h^3\)

\((x^2z-kz^3)*(x^4z^2+x^2kz^4+k^2z^6)=(x^2z-kz^3)*((x^2z)^2+x^2z*kz^3+(kz^3)^2)=\)
\(=(x^2z)^3-(kz^3)^3=x^6z^3-k^3z^9\)

Как говорилось ранее, формулы сокращенного умножения используют для того чтобы не умножать каждый раз такие выражения «вручную». Как мы видим, эти формулы можно легко запомнить и применять их в дальнейшем для преобразования выражений.

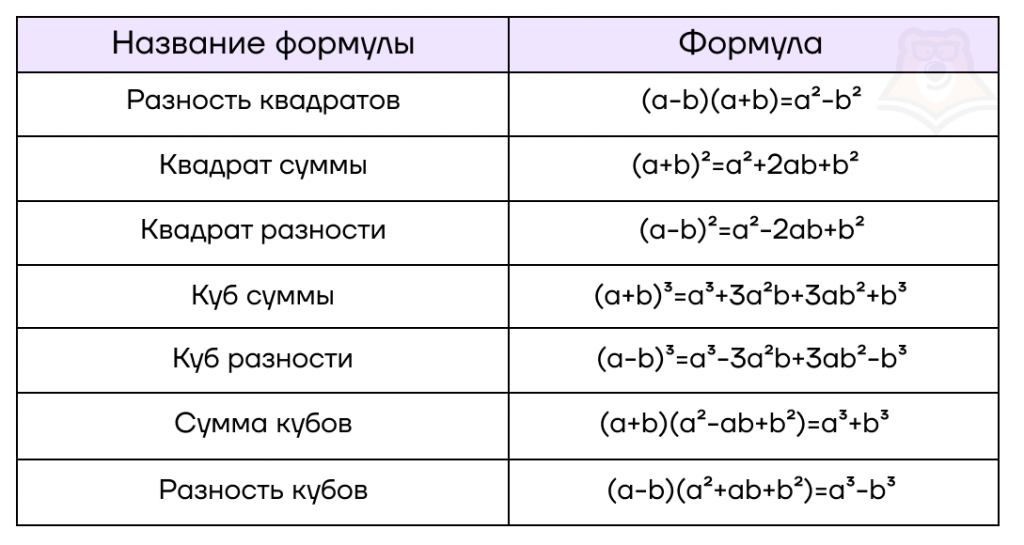
Что в алгебре произошло от геометрии? Сейчас мы самостоятельно вывели семь формул сокращенного умножения, используя правила умножения многочлена на многочлен. На самом же деле, многие из этих формул были введены в использование еще около 4000 лет назад, при этом вывели их через геометрию. Да-да, возможно, в это сложно поверить, но раньше людям казалось куда удобнее выводить формулы, отталкиваясь от геометрических соображений. Ведь геометрию можно легко смоделировать, то есть представить в жизни. Например, выражение \(a^2\) легко можно представить как квадрат со стороной \(a\), а переменную \(b\) – как отрезок длиной \(b\). Так, например, квадрат суммы (a+b)2=a2+2ab+b2 великий ученый Евклид сформулировал следующим образом: «‎Если прямая линия как-либо рассечена, то квадрат на всей прямой равен квадратам на отрезках вместе с дважды  взятым прямоугольником».  «‎Прямая линия как-либо рассечена» – значит отрезок разделен на два отрезка \(a\) и \(b\). «‎Квадрат на всей прямой» – значит квадрат со стороной \((a+b)\), то есть площадью \((a+b)^2\). «‎Квадраты на отрезках» – квадраты со сторонами \(a\) и \(b\), то есть площадью \(a^2\) и \(b^2\) соответственно. «‎Дважды взятый прямоугольник» – два прямоугольника со стороной \(a\) и \(b\) каждый, то есть их суммарная площадь равна \(2ab\). Вот и получается: \((a+b)^2=a^2+2ab+b^2\).

В дальнейшем мы еще столкнемся с формулами сокращенного умножения, а пока поговорим об одном из самых важных видов преобразования выражений – разложением на множители.

Разложение многочлена на множители

Многочлен – это сумма одночленов. При этом для выполнения различных действий с суммой бывает не совсем удобно работать, поэтому для удобства многочлен можно попробовать представить в виде произведения, то есть разложить на множители.

Разложить многочлен на множители – значит представить этот многочлен в виде произведения нескольких множителей.

Далее мы рассмотрим основные способы разложения многочлена на множители, а также разберемся, как это применяется на практике.

Вынесение общего множителя за скобки

И начнем мы с вынесения общего множителя за скобки. В качестве примера возьмем многочлен \(ab+ac\), который представляет собой сумму двух одночленов: \(ab\) и \(ac\). Как видим, и в первом, и во втором одночлене есть множитель a, то есть можно сказать, что этот множитель является общим для этих двух одночленов. Отсюда и название этого множителя – общий множитель.

Общий множитель – это множитель, который включают в себя все слагаемые многочлена.

Теперь вспомним распределительное свойство умножения. Да, это то самое свойство, которым мы пользовались для раскрытия скобок. Теперь же мы посмотрим на него в обратную сторону:

\(ab+ac=a*(b+c)\)

Как видим, в правой части равенства перед скобками стоит как раз наш общий множитель a.

Если при раскрытии скобок \(a*(b+c)\) мы бы умножали \(a\) сначала на \(b\), а затем на \(с\), то здесь ситуация будет обратная: каждое слагаемое (\(ab\) и \(ac\)) нашего многочлена мы можем поделить на их общий множитель: \(\frac{ab}{a}=b\) и \(\frac{ac}{a}=c\). Сам общий множитель при этом выносится за скобки, а в скобках остается выражение с полученными после деления слагаемыми: \(b\) и \(с\). Данная операция называется вынесением общего множителя за скобки.

В рассмотренном примере мы сразу поняли, что общим множителем является именно а, ведь эта переменная является множителем первого и второго слагаемого. 

При этом очень часто в различных выражениях общий может играть в прятки с нами, и прятаться он будет в самих слагаемых выражения. Поэтому наша задача – найти этот общий множитель и правильно вынести его за скобки.

Для того чтобы разобраться в этом, для начала рассмотрим пример многочлена \(6a+12\). У двух слагаемых \(6a\) и 12 напрямую мы общего множителя не видим, но можем заметить, что у коэффициентов этих одночленов (6 и 12)  наибольший общий делитель равен 6, который мы и  можем вынести за скобки:

\(6a+12=6*(\frac{6a}{6}+\frac{12}{6})=6*(a+2)\)

Можем сделать вывод: коэффициент общего множителя выражения равен наибольшему общему делителю коэффициентов всех слагаемых этого выражения.

Бывают случаи, когда единственные общие делители коэффициентов слагаемых выражения равны \(1\) и \(-1\). Единицу выносить за скобки бессмысленно, ведь от деления на \(1\) выражение никак не видоизменится. 

Куда можно вынести минус? \(-1\) мы можем в некоторых случаях вынести за скобки для удобства. Рассмотрим пример: вынесем в выражении \(a-b\) за скобки \(-1\): \(a-b=-1*(\frac{a}{-1}-\frac{b}{-1})=-1*(-a-(-b))=-1*(-a+b)=-1*(b-a)\) Можно заметить, что при вынесении \(-1\) за скобки знаки всех слагаемых выражения меняют свой знак на противоположный. Этим можно воспользоваться в тех случаях, когда нам нужно поменять знаки внутри скобок на противоположные. Саму единицу при таком вынесении не записывают, а ставят просто минус. Например: \(-x-y=-(x+y)\) \(-c+d=-(c-d)\) Такую операцию также называют вынесением минуса за скобки.

С коэффициентами общего множителя мы разобрались, а что же делать с переменными?

Разберем пример выражения \(x^5+x^7\). В обоих слагаемых этого выражения мы видим переменную x c разными показателями степеней. В таком случае мы выносим за скобки наименьшую степень \(x\) из всех степеней, встречающихся в выражении, то есть, в данном случае, пятую степень \((5<7)\). 

\(x^5+x^7=x^5*(\frac{x^5}{x^5}+\frac{x^7}{x^5})=x^5*(1+x^2)\)

Обращаем внимание: в выражении мы можем вынести ту или иную переменную за скобки только в том случае, если она входит в состав всех слагаемых выражения.

Например, в выражении \(3k^2-2xy+7\) даже при большом желании мы не сможем вынести ни одну переменную за скобки, так как переменная k входит в состав только первого слагаемого, переменные \(x\) и \(y\) – только второго слагаемого.

А теперь обобщим то, что мы написали про коэффициент и переменные общего множителя.

Чтобы выделить общий множитель выражения, необходимо:

1) выделить наибольший общий делитель коэффициентов всех слагаемых выражения;

2) выделить все переменные, входящие в состав каждого слагаемого выражения, и взять эти переменные в наименьших показателях степеней из тех, которые встречаются в выражении;

3) произведение выбранного коэффициента на выбранные степени переменных и будет являться общим множителем данного выражения.

Используем полученные знания, выделив общий знаменатель выражения \(2x^2y^{10}+16y^2x^5c-8x^3yd^3\), после чего вынесем этот общий знаменатель за скобки.

1. Выпишем все коэффициенты слагаемых выражения: 2, 16,-8. Их наибольший общий делитель равен 2.
2. Во всех слагаемых выражения встречаются переменные x и y.
   Наименьший показатель степени x из имеющихся, равен 2, значит выносить за скобки будем \(x^2\).
   Наименьший показатель степени y из имеющихся, равен 1, значит выносить за скобки будем y.
3. Запишем в виде произведения выбранный коэффициент и степени переменных: \(2x^2y\), что и будет являться общим множителем рассматриваемого выражения. Вынесем этот общий множитель за скобки:

\(2x^2y^{10}+16y^2x^5c-8x^3yd^3=2x^2y*(\frac{2x^2y^{10}}{2x^2y}+\frac{16y^2x^5c}{2x^2y}-\frac{8x^3yd^3}{2x^2y})=\)
\(=2x^2y*(y^9+8x^3y-4x)\)

Таким образом, с помощью вынесения общего множителя за скобки мы представили многочлен \(2x^2y^{10}+16y^2x^5c-8x^3yd^3\), то есть разложили этот многочлен на множители. 

Способ вынесения общего множителя за скобки получил широкое применение в алгебре, при этом не всегда в выражениях мы имеем возможность им воспользоваться: бывают такие случаи, когда наибольший общий делитель всех коэффициентов равен 1, а среди переменных нет таких, которые встречаются в каждом слагаемом выражения.

В таком случае можно попробовать воспользоваться другим способом разложения многочлена на множители – методом группировки, о котором дальше и пойдет речь.

Метод группировки

Рассмотрим многочлен \(ab+ac+db+dc\). В этом выражении нельзя выделить общий знаменатель, который мы могли бы вынести за скобки. При этом мы можем разбить этот многочлен на две «группы»: \(ab+ac\) и \(db+dc\). Теперь из каждой такой группы вынесем общий знаменатель за скобки. В группе \(ab+ac\) общим знаменателем является множитель \(a\), а в группе \(db+dc\) – множитель \(d\):

\((ab+ac)+(db+dc)=a*(b+c)+d*(b+c)\)

Мы получили выражение, состоящее из двух слагаемых, каждое из которых содержит множитель \((b+c)\). Обозначим этот множитель за переменную \(k\), получим:

\((ab+ac)+(db+dc)=a*k+d*k\)

Видим, что \(k\) является общим множителем данного выражения, значит, мы его за скобки:

\(ak+dk=k(a+b)\)

Теперь произведем обратную замену, то есть вместо \(k\) снова запишем \((b+c)\):

\(k*(a+b)=(b+c)*(a+b)\)

Тогда, вернувшись к самому начальному выражению, получим равенство:

\(ab+ac+db+dc=(b+c)*(a+b)\)

Таким образом, мы разложили данный многочлен на множители. Этот способ разложения на множители называют методом группировки. Суть его заключается в том, что мы разбиваем все выражение на несколько групп, а далее из каждой группы выносим общий знаменатель таким образом, чтобы после всего этого образовалось выражение, в котором также можно будет выделить общий знаменатель и вынести его за скобки. Проще говоря, мы два раза подряд выполняем вынесения общего множителя за скобки.

Приведем еще один пример:

\(x^5+2x^4-6x-12=x^4*(x+2)-6*(x+2)=(x+2)*(x^4-6)\)

Заметим, что вторая группа, которую мы выделили – группа \((-6x-12)\). При вынесении за скобки \(-6\) все знаки внутри скобок поменяют свой знак, отсюда и получается \(-6*(x+2)\).

Так же, как и общий множитель, метод группировки любит прятаться внутри выражений. Давайте же найдем, как этим методом можно воспользоваться в случае выражения \(5x^2-12x+4\). 

На две группы это выражение разбить явно не получится, потому что этот многочлен содержит только 3 члена. Поэтому поступим следующим образом: разложим одночлен \(-12x\) на два других одночлена, а именно \(-12x=-10x-2x\). Тогда получим:

\(5x^2-12x+4=5x^2-10x-2x+4=5x*(x-2)-2*(x-2)=(5x-2)(x-2)\)

Итак, мы разложили многочлен \(5x^2-12x+4\) на множители \((5x-2)(x-2)\). 

Сделаем вывод: если в многочлене нечетное количество членов, то один из его членов можно попробовать разложить на два одночлена так, чтобы сработал метод группировки.

Этим способом часто пользуются для решения уравнений. Например, решим уравнение:

\(5x^2-12x+4=0\)

В правой части уравнений стоит выражение, которое мы выше уже разложили на множители, разложим его и здесь:

\((5x-2)(x-2)=0\)

А теперь можем немного порассуждать. В каком случае произведение двух множителей равно \(0\)?
Конечно, если один из его множителей \(0\). То есть, каждую «скобочку» мы можем приравнять к \(0\).

\((5x-2)(x-2)=0\)
\(5x-2=0\) или \(x-2=0\)

Теперь осталось решить два этих уравнения:

\(5x-2=0\) или \(x-2=0\)
\(5x=2\) или \(x=2\)
\(x=\frac{2}{5}\)

Получили два корня уравнения: \(\frac{2}{5}; 2\).

На этом моменте данная статья подходит к своему завершению. В ней мы прикоснулись к методам преобразования алгебраических выражений, разобрав формулы сокращенного умножения, вынесение общего множителя за скобки и метод группировки. 

При этом даже метод группировки подходит далеко не для всех выражений. Поэтому в статье «Преобразование алгебраических выражений. Часть 2» мы продолжим осваивать искусство разложения на множители и разберем новые способы.

Термины

Квадрат – четырехугольник, все стороны которого равны, а все углы прямые (90°).

Множитель – компонент умножения, участвующий в самой операции умножения.

Произведение – результат умножения.

Прямоугольник – четырехугольник, у которого все углы прямые (90°).

Слагаемое – это число/выражение, которое складывается с другими числами/выражениями.

Сумма – результат сложения.

Фактчек

• В алгебре активно используются формулы сокращенного умножения, которые применяются для преобразования выражений.
• Выделяют семь основных формул сокращенного умножения: разность квадратов, квадрат суммы, квадрат разности, куб суммы, куб разности, сумма кубов, разность кубов.
• Для упрощения многочлена его раскладывают на множители, то есть представляют многочлен в виде произведения нескольких множителей.
• Для разложения многочлена на множители можно использовать такие способы, как вынесение общего множителя за скобки и метод группировки.

Проверь себя

Задание 1.
Какое из перечисленных выражений представляет из себя квадрат суммы?

1. \(a^2+b^2\)
2. \((a-b)^2\)
3. \((a+b)^2\)
4. \(a^2-b^2\)

Задание 2.
Общим множителем в выражении \(6x^2+3x^3\) является:

1. \(3x^2\);
2. \(6x^3\);
3. \(x\);
4. \(3\).

Задание 3.
При разложении выражения \(bc+ba^2\) на множители необходимо воспользоваться:

1. вынесением общего множителя за скобки;
2. методом группировки;
3. данное выражение нельзя разложить на множители;
4. вынесением общего множителя за скобки или методом группировки. 

Задание 4.
Выполнить умножение \((t-5k)(5k+t)\) и указать результат произведения.

1. \(25k^2-t^2\)
2. \(t^2+25k^2\)
3. \(25k^2+t^2\)
4. \(t^2-25k^2\)

Ответы: 1. – 3; 2. – 1; 3. – 1; 4. – 4