Определение и график функции

На этой странице вы узнаете

• Как готовка печенек может описать одно из определений функции?
• С помощью какой функции можно получить цветок, бабочку и сердце на графике? 
• Как с помощью горок и санок запомнить, на каких промежутках возрастает и убывает функция? 

На уроках математики и физики вы нередко сталкиваетесь с функциями. Однако следует понимать, что функция не является сугубо математическим термином, с помощью которого можно описать абстрактные величины х и у. С помощью функции можно описать любое явление в нашем мире. Для более сложных явлений потребуются сложные функции, но этого не стоит бояться. К тому же на экзамене описывать ситуации с помощью функций почти не потребуется (а если и потребуется, то это будет совсем несложно). В этой статье мы узнаем, как с помощью функций можно облегчить решение различных задач.

Определение функции

Так что такое функция? В математике есть несколько определений, но прежде чем перейти к ним, рассмотрим небольшой пример. 

Миша без вреда для здоровья может пить кофе. Причем, чем больше он выпьет кружек кофе, тем выше будет продуктивность и энергия Миши. В нашем случае энергия будет зависеть от количества выпитого кофе. 

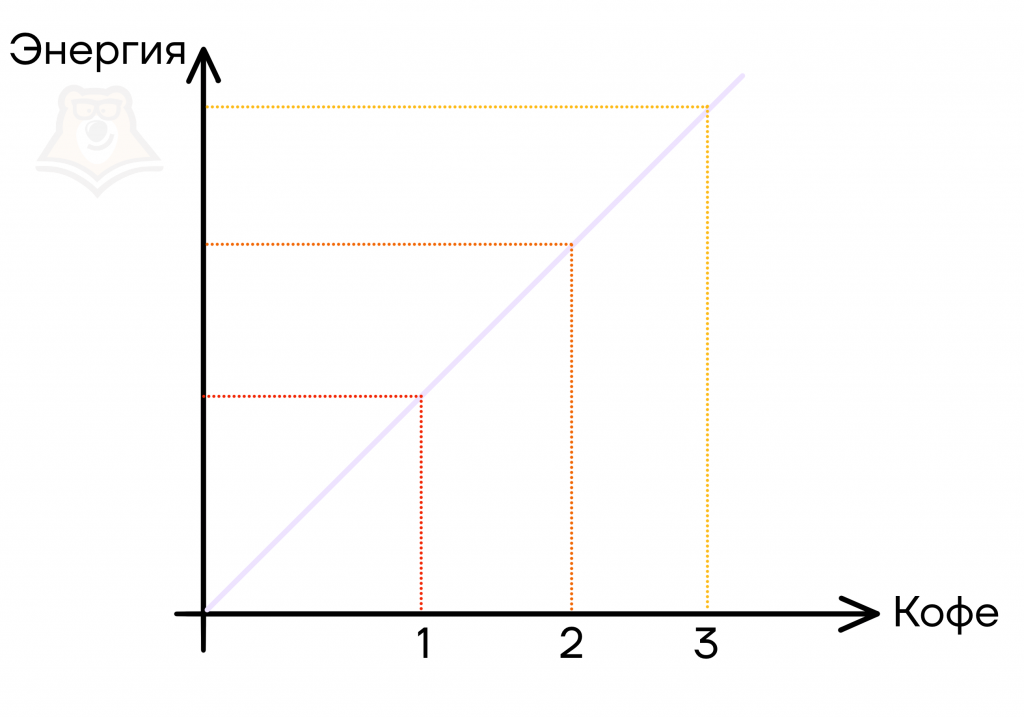
Эту же зависимость мы можем показать с помощью графика: чем больше будет кружек кофе, тем выше будет энергия Миши.

Дадим первое определение функции. 

Функция — это зависимость одной переменной от другой. 

В нашем случае это зависимость энергии Миши от количества выпитого кофе: больше кофе — больше энергия. 

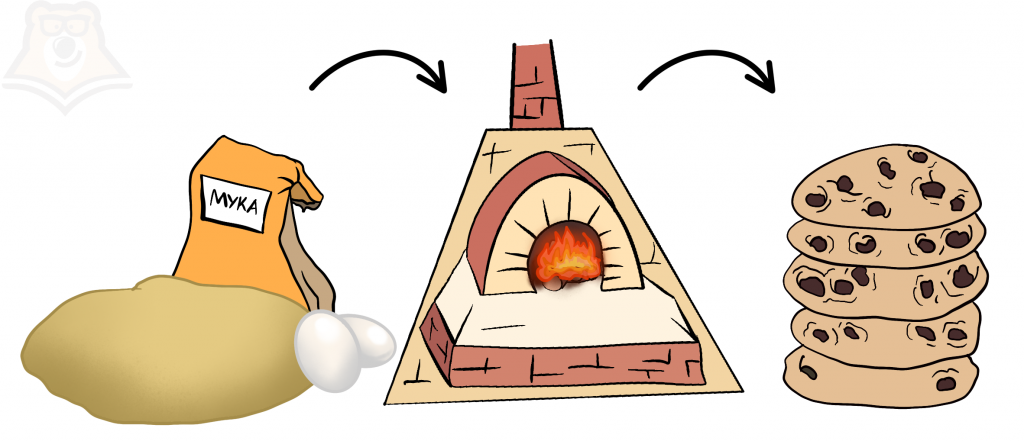
Отвлечемся от Миши и представим завод, где изготавливают печеньки. Упростим процесс их производства. Допустим, на печь отдают тесто и начинку. Заводская печка перерабатывает продукты и выдает вкусные печеньки. 

Как готовка печенек может описать одно из определений функции? Тесто и начинка — это переменные, которые могут меняться. Мы можем взять разные виды теста, выбрать любимые начинки. Даже можем дать печи разное количество продуктов. И от любого изменения этой переменной меняется результат на выходе: количество печенек, их форма или вкус. То есть переменная х (тесто) проходит через функцию (печку) и получается у (печенька).

Таким образом, мы получаем второе определение функции. 

Функция — это действие над переменной. 

Оно означает, что над переменной x проделали определенное действие и получили величину y. Здесь могло быть любое математическое действие: сложение, деление, возведение в степень и так далее.

Однако есть еще одно определение функции. 

Функция — соответствие между двумя множествами, причем элементу из первого множества может соответствовать только один элемент второго множества. 

Рассмотрим на примере доставки еды.

Курьеру нужно срочно доставить пиццу. У него есть два множества — список клиентов и их заказы. При этом каждому клиенту соответствует только один заказ. Ивану из первого множества будет соответствовать «Пицца с ветчиной и грибами» из второго множества, Федору — «Сырная пицца» и так далее.  

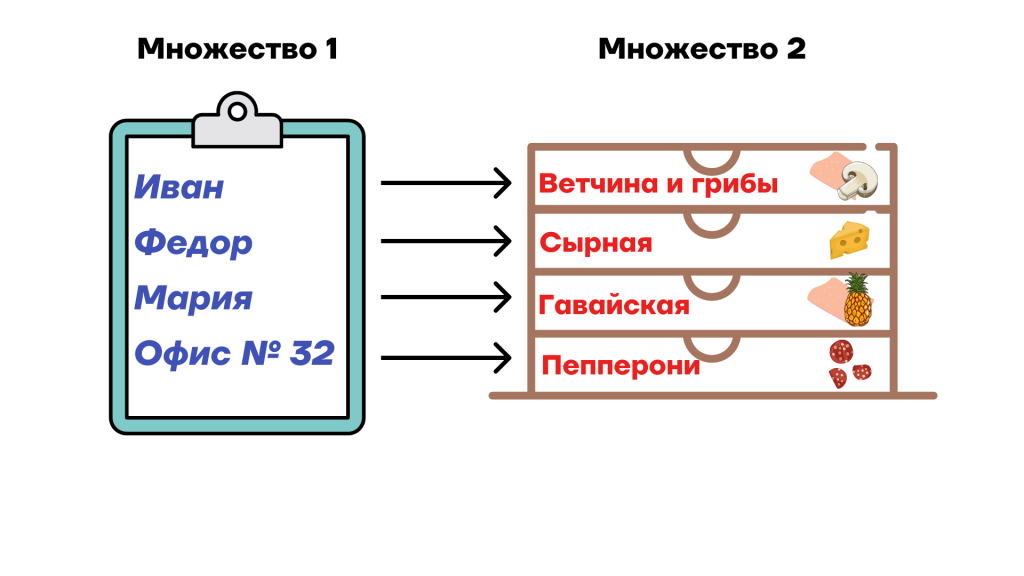
Опишем этот термин на языке математики. 

Допустим, у нас есть функция \(y=\frac{x}{4}\). В этом случае каждому элементу из множества х будет соответствовать только один элемент из множества у, который будет в 4 раза меньше х. 

Например, \(x=16\) и \(y=4\) или \(x=20\) и \(y=5\). Получить одно и то же значение у при разных значениях х невозможно. 

Обычно функция обозначается через переменные у и х. В этом случае у и есть сама функция, иногда ее также обозначают как \(f(x)\). 

У функции также существует и переменная величина, которая может менять свое значение. Эта величина называется аргументом и чаще всего обозначается как х. 

\(х\) — аргумент, который может менять свое значение;
\(f(x)\) или у — зависимая переменная, которая меняет значение в зависимости от аргумента функции. 

С определением функции, а именно с зависимостью одной переменной от другой связано такое явление как пропорциональность.

Пропорциональность – это та же зависимость одного числа от другого, то есть изменение одного из них влечет изменение и другого. 

Можно выделить прямую и обратную пропорциональность. 

• Прямая пропорциональность характерна тем, что при увеличении (уменьшении) одной величины увеличивается (уменьшается) другая величина. То есть как меняется первая переменная, так меняется и вторая.
  
  Например, у нас есть переменные а и b, которые прямо пропорциональны друг другу. Если мы увеличим а в два раза, то и b увеличится во столько же раз. 

• При обратной пропорциональности, напротив, при увеличении (уменьшении) одной величины уменьшается (увеличивается) другая.
  
  Например, если переменные а и b будут обратно пропорциональны, то при увеличении а в два раза переменная b уменьшится во столько же раз.

Способы задать функцию

Что такое задать функцию? Это значит ввести правило, по которому можно найти значение функции в зависимости от аргумента. 

Поиграем в прятки. Мы все знаем правила: пока ведущий считает, остальные игроки прячутся. Без этого правила игра не получится. В нашем случае прятки — функция, а правила игры — то, что ее задает. 

Например, в функции \(y=3x\) такое правило: «значение функции всегда будет в три раза больше аргумента», а в функции \(y=\sqrt{x}\) правилом будет «значение функции равняется квадратному корню из аргумента». 

Существует 4 способа задать функцию. Рассмотрим их по порядку. 

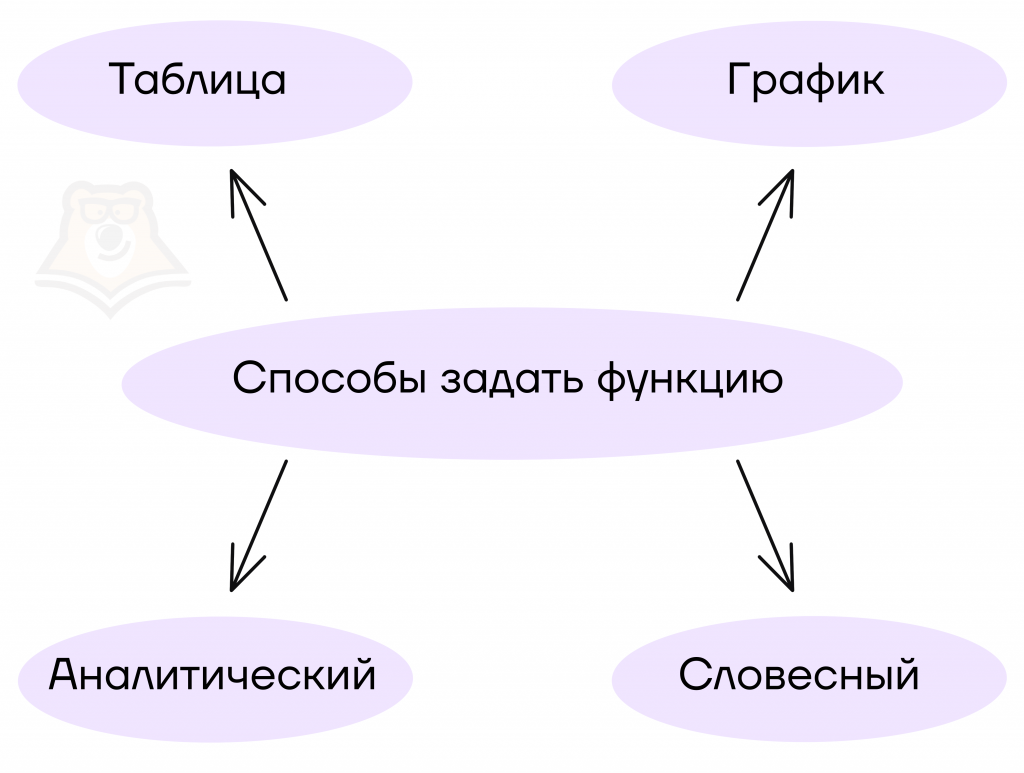
Способ №1. Таблица

Название говорит само за себя: функцию можно задать с помощью таблицы. Построим ее. В первой строке запишем значения аргумента, а во второй строке — значения функции при данном значении аргумента. 

В таблице ниже мы можем сразу отследить зависимость значения функции от значения аргумента. С помощью формулы эту функцию можно записать как \(y=x^2\).  

х	1	2	3	4	5
у	1	4	9	16	25

А вот еще одна таблица. Здесь все значительно проще, в ней представлена функция \(y=-7x\). 

х	– 2	– 1	0	1	2
у	14	7	0	– 7	– 14

С помощью таблицы легко построить график. Достаточно отметить все точки по координатам, которые уже приведены в таблице, а после — соединить их. Однако такой способ получится применить только с относительно простыми графиками. 

Способ №2. График функции

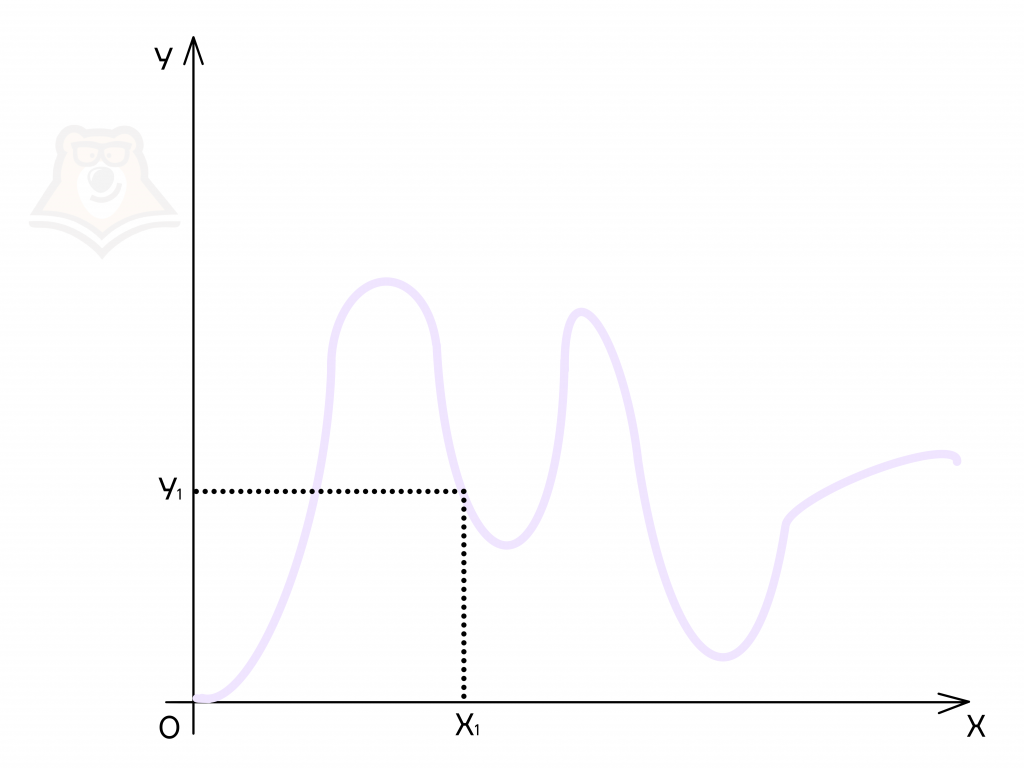
Это самый наглядный способ. С помощью графика мы можем сразу найти значение функции при любом значении аргумента: достаточно найти координаты любой точки.

Примеров графиков функций существует очень много. Рассмотрим один из них. Если мы поднимем до точки пересечения с графиком прямую из любого значения \(х_1\), то сможем найти значение \(у_1\) в этой точке. И такую операцию можно проводить с любой точкой на графике. 

Однако не стоит думать, что графики функций — это всегда скучные параболы, прямые, гиперболы и прочие классические графики. С помощью графиков можно начертить достаточно красивые фигуры. Вот некоторые из них.  

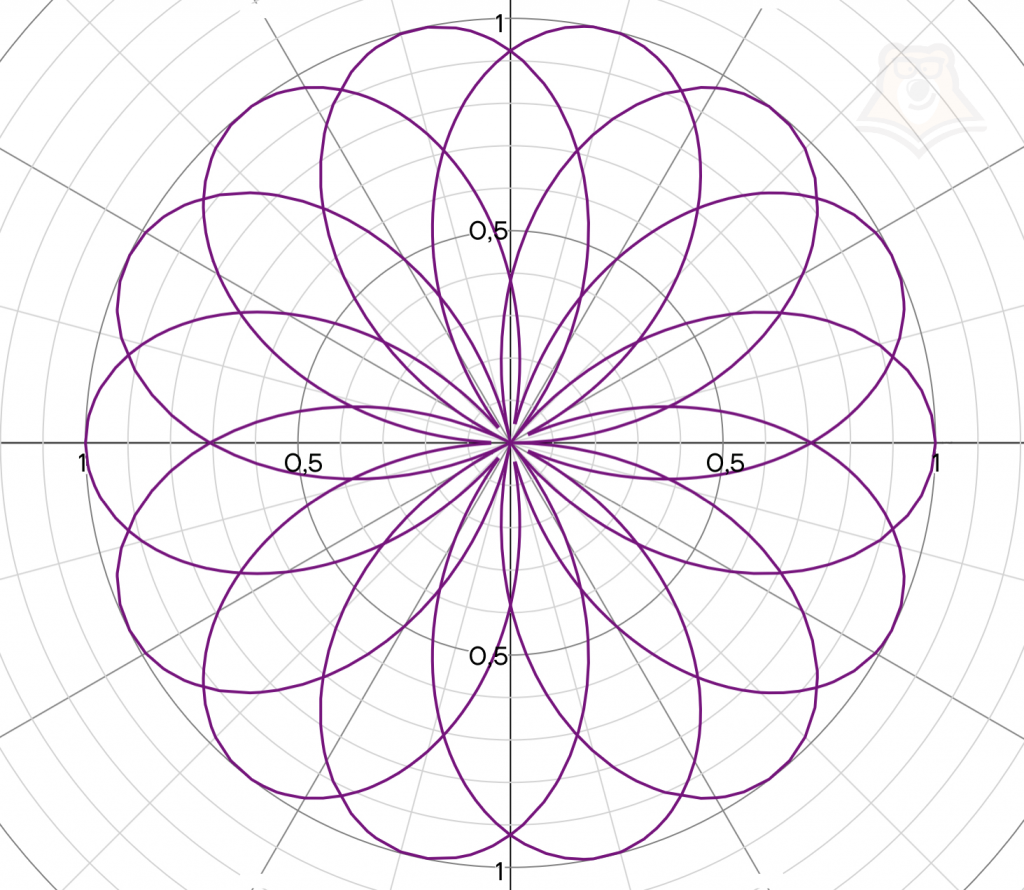
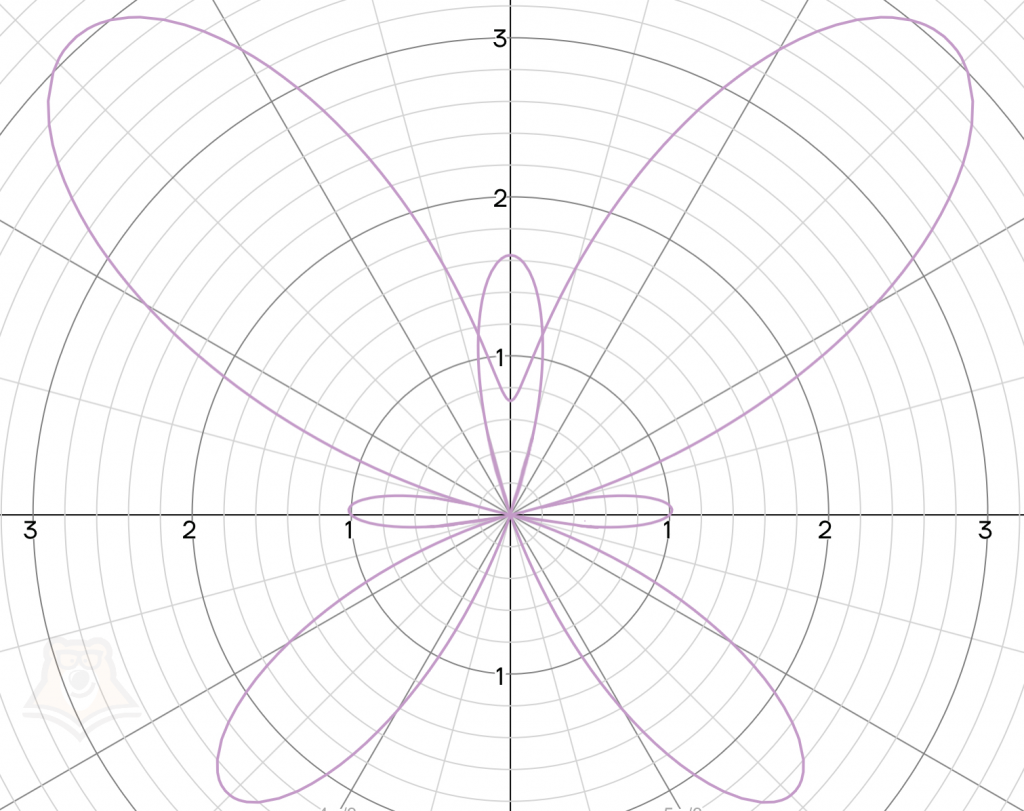
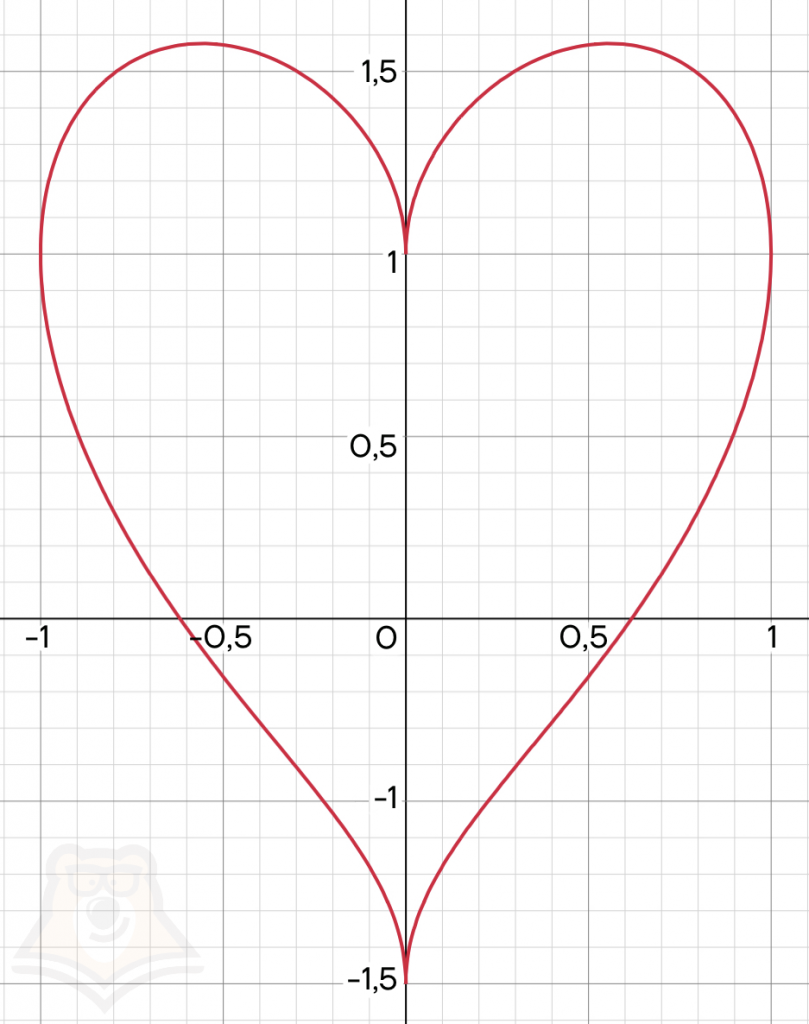
С помощью какой функции можно получить цветок, бабочку и сердце на графике? График цветка на картинке выше задан с помощью функции \(r=\sin\frac{7\theta}{4}\), а график бабочки задан функцией \(r=e^{\sin(\theta)}-2\cos(4\theta)\) в полярной системе координат.  В прямоугольной системе координат можно задать с помощью функции сердце, для этого необходимо использовать функцию \(x^2+(y-\sqrt|x|)^2=1\).

Графики функций встречаются в одном из заданий второй части ОГЭ, а именно в №22. Рассмотрим один из таких примеров. 

Постройте график функции \(y=\frac{(x-1)(x^2-2x-3)}{x+1}\) и определите, при каких значениях а прямая \(y=a\) имеет с графиком ровно одну общую точку. 

Решение.
Попробуем упростить дробь. Для этого разложим многочлен \(x^2-2x-3\) на множители по формуле \(ax^2+bx+c=a(x-x_1)(x-x_2)\). Найдем корни уравнения с помощью дискриминанта:

\(x^2-2x-3=0\)
\(D=b^2-4ac=4-4*1*(-3)=4+12=16\)
\(x_1=\frac{-b+\sqrtD}{2a}=\frac{2+4}{2}=3\)
\(x_2=\frac{-b-\sqrtD}{2a}=\frac{2-4}{2}=-1\)

Раскладывая выражение на множители, получаем:

\(x^2-2x-3=(x-3)(x-(-1))=(x-3)(x+1)\)

Преобразуем дробь: 

\(\frac{(x-1)(x^2-2x-3)}{x+1}=\frac{(x-1)(x-3)(x+1)}{x+1}\)

Заметим, что в числителе и знаменателе стоит один и тот же множитель, а значит, его можно сократить. Однако необходимо учесть важное условие: знаменатель не равен 0. Таким образом мы нашли ОДЗ функции, то есть область допустимых значений, при которых функция существует. 

Тогда получаем:

\(y=(x-1)(x-3), x+1\neq 0\)

Раскроем скобки:

\((x-1)(x-3)=x^2-3x-x+3=x^2-4x+3\)

Получаем функцию:

\(y=x^2-4x+3, x\neq -1\)

Перед нами парабола. Подробнее про параболы и способ их построения можно прочесть в статье «Основные элементарные функции. Часть 2». 

Для построения параболы найдем координаты ее вершины \((x_0; y_0)\).

\(x_0=\frac{-b}{2a}=\frac{4}{2}=2\)

Чтобы найти \(y_0\), нужно просто подставить \(x_0\) в уравнение функции: 

\(y_0=2^2-4*2+3=4-8+3=-1\)

Это лишь одна из точек параболы. Необходимо еще несколько, чтобы можно было ее построить. Составим таблицу:

Построим параболу. Не забываем выколоть точку \(x\neq -1\):

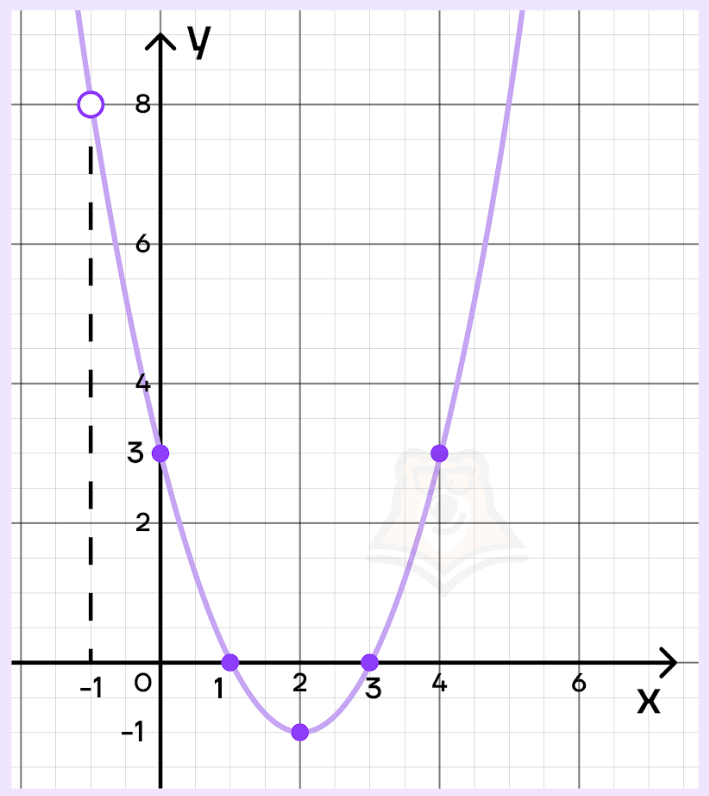
Прямая \(y=a\) — это горизонтальная прямая, которая проходит параллельно оси Ох.

Ровно одну общую точку прямая будет иметь, если будет проходить через вершину параболы А и через выколотую точку В. В остальных случаях прямая либо не будет иметь общих точек с графиком (если будет проходить ниже параболы), либо будет иметь две общие точки с графиком. 

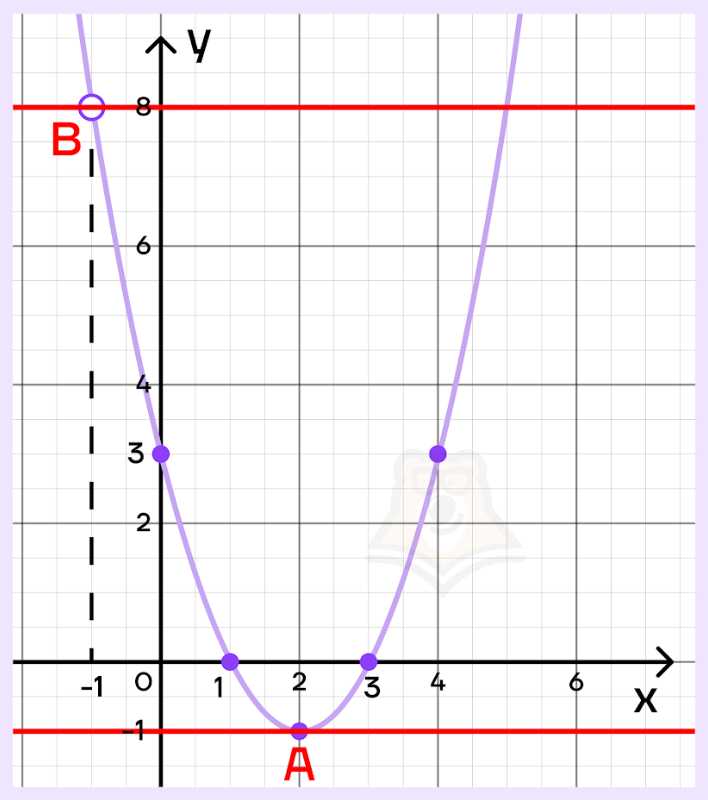
Поскольку точки А и В — точки пересечения двух графиков, то координаты этих точек принадлежат обоим уравнениям.

Мы уже нашли координаты точки А, то есть вершины параболы: \((2;-1)\). Подставим их в уравнение \(y=a\):

\(a=-1\)

Теперь найдем координаты точки В. Мы уже знаем ее абсциссу: \(x=-1\). Подставим это значение в уравнение параболы:

\(y=(-1)^2-4*(-1)+3=1+4+3=8\)

Координаты точки В: \((-1;8)\). Подставим их в уравнение прямой:

\(a=8\). 

Ответ: – 1, 8

Cпособ №3. Аналитический способ

На самом деле, мы рассматривали этот способ с самого начала статьи. Аналитический способ заключается в том, чтобы задать функцию с помощью формулы. 

Чтобы найти значение функции с помощью аналитического способа, достаточно подставить значение аргумента в формулу. 

Например, нам нужно найти значение функции \(y=17x-51+3x^2\) при \(x=2\). Подставим значение \(х\):

\(y=17*2-51+3*4=-5\). 

Способ №4. Словесный способ

Этот способ подразумевает описание поведения функции с помощью слов, то есть про функцию нужно как бы рассказать. 

Допустим, у нас есть функция \(y=5x\). Ее можно описать так: «Значение функции равняется произведению числа 5 и аргумента». 

Этот способ используют для задания сложных функций, которые невозможно описать с помощью формулы. Например, функция «Над натуральным числом провели операцию, в результате которой нашли утроенную сумму всех цифр в его записи». 

Возьмем число \(х=3099\). Тогда, чтобы найти значение функции, необходимо решить уравнение \(у = 3 * (3 + 0 + 9 + 9) = 3 * 21 = 63\). 

Свойства функции

Разумеется, функции, которые встречаются нам на экзамене, обладают достаточно интересными и непростыми свойствами. Но если хорошо в них ориентироваться, то ничего сложного в них не окажется. 

Область определения функции — это все допустимые значения аргумента функции (х), при которых функция будет определена. Область определения обозначается как D(y).  

Речь идет про ограничения на х. Если в уравнении появляются функции с ограничениями, то нужно учесть, какие значения примет х. 

Рассмотрим функцию \(y=14x\). Ограничений в ней нет, поэтому область определения будет \(D(y)=(-\infty;+\infty)\). 

А вот в функции \(y=\sqrt{x}\) уже не все так однозначно. Вспомним, что под корнем может находиться только положительное число. Следовательно, \(x\geq0\), откуда получаем область определения \(D(y)=[0;+\infty)\).

На графике видно, что х принимает только положительные значения, и график функции не лежит левее оси Оу. 

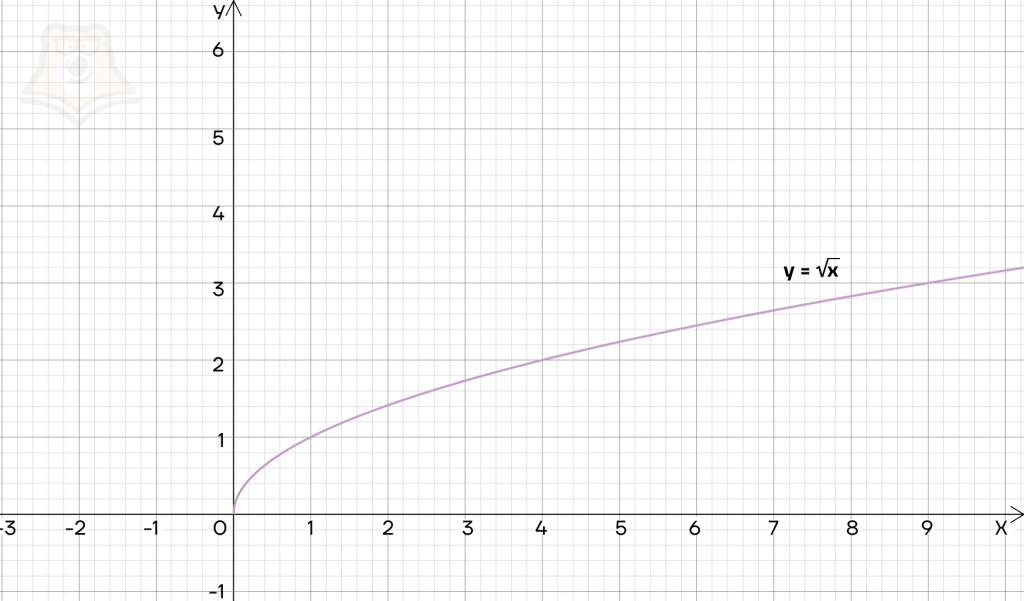
Область значений функции — это все значения, которые может принимать функция. Область значений обозначается как \(Е(у)\). 

Область значений очень похожа на ОДЗ не просто так. ОДЗ как раз задает значения, которые может принимать функция!

Если область определения ограничивает значения аргумента \(х\), то область значений ограничивает уже значения самой функции \(у\). 

Например, мы знаем, что синус и косинус могут принимать значения от -1 до 1 включительно. Следовательно, для функции \(y=\sin(x)\) область значений примет вид \(E(y)=[-1;1]\). Это отлично видно на графике: линия графика не выходит за прямые \(y=-1\) и \(y=1\). 

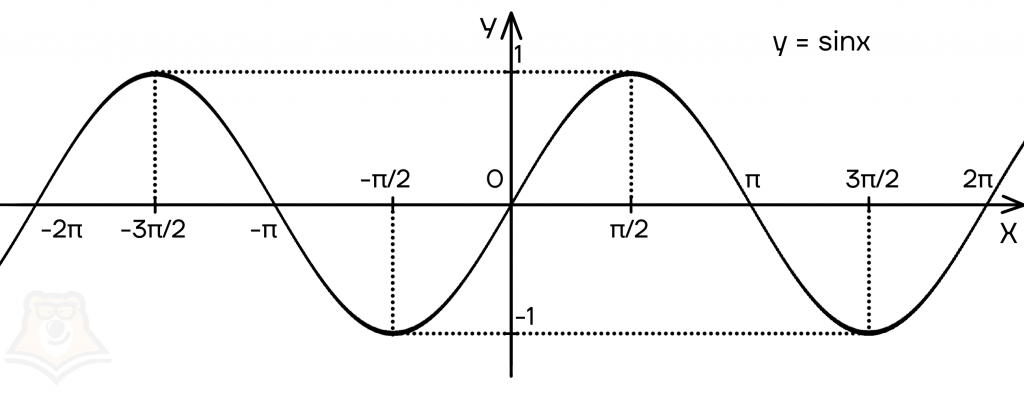
Нули функции — это значение аргумента х, при котором значение функции равно 0. 

Например, нам дана функция \(y=x^2-2x-3\). Чтобы найти нули функции, необходимо решить уравнение \(y=0\):

\(x^2-2x-3=0\)
\(D=4+12=16\)
\(x_1=\frac{2+4}{2}=3\)
\(x_2=\frac{2-4}{2}=-1\). 

Значения аргумента \(x=-1\) и \(x=3\) и будут нулями функции. 

Важно заметить, что на графике любой функции нули функции лежат только на оси Ох. Если функция не пересекает ось Ох и не имеет с ней общих точек, то нулей функции в таком случае нет. 

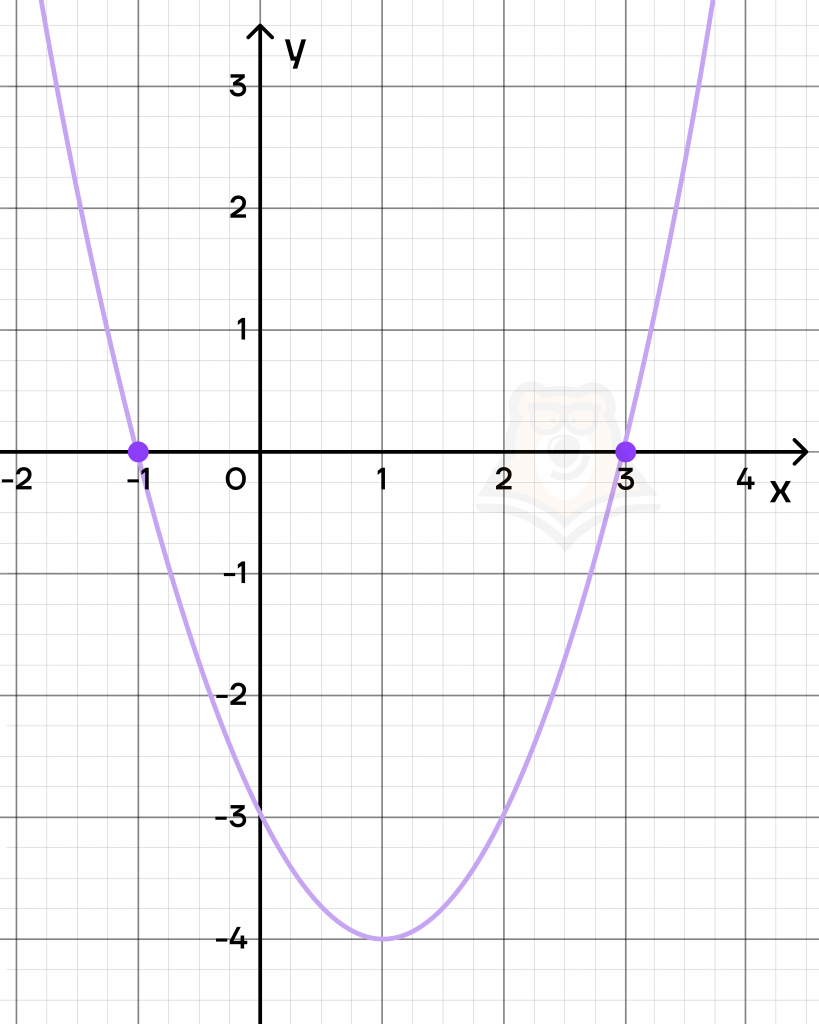
Также нельзя не рассмотреть свойства возрастания и убывания функции. 

Как с помощью горок и санок запомнить, на каких промежутках возрастает и убывает функция? Представим, что наша функция — это снежные горки, по которым катаются дети. Пусть ребенок с санками идёт по горке слева направо (направление в этом случае очень важно). На тех участках функции, где ребенок будет тащить санки в гору, функция будет возрастать. А там, где ребенок будет скатываться на санках с горы, функция будет убывать.

Разберем возрастание и убывание функции на более математическом языке. 

Функция называется возрастающей, если для любой пары аргументов х₁ и х₂ (х₁ < х₂) выполняется неравенство f(x₁) < f(x₂). 

Функция называется убывающей, если для любой пары аргументов х₁ и х₂ (х₁ < х₂) выполняется неравенство f(x₂) < f(x₁). 

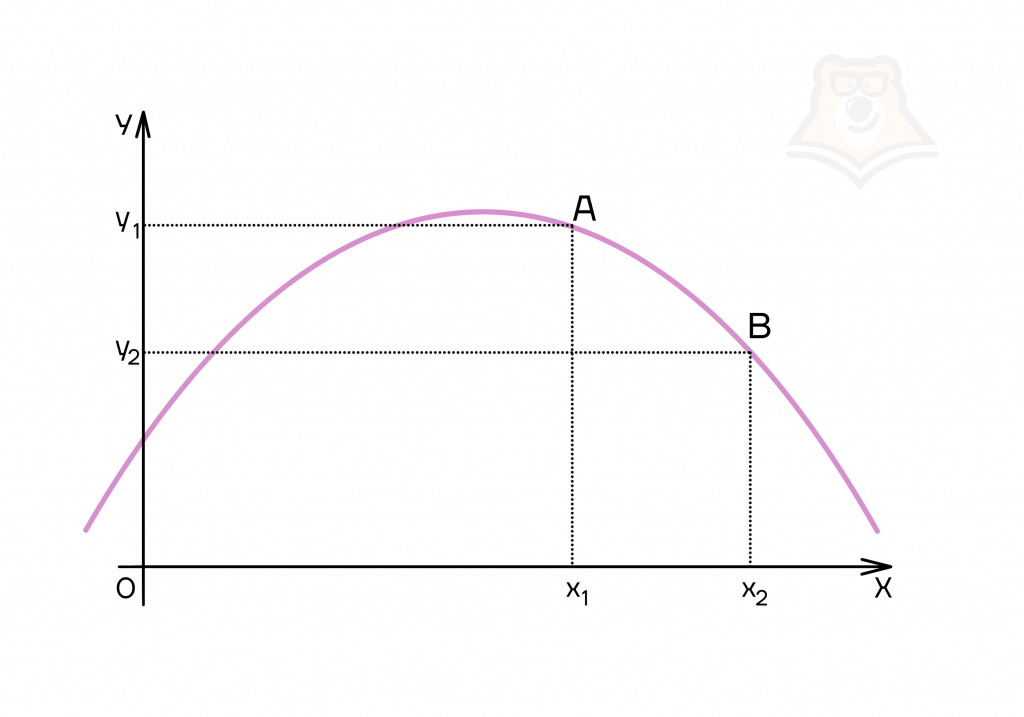
Рассмотрим на графике. Возьмем две точки на участке возрастания функции, которые будут иметь координаты А(х₁;у₁) и В(х₂;у₂). Заметим, что неравенство х₁ < х₂ выполняется. Посмотрим на значения функции у₁ и у₂: у₂ > у₁. Следовательно, выполняется условие f(x₁) < f(x₂), а значит, функция возрастает. 

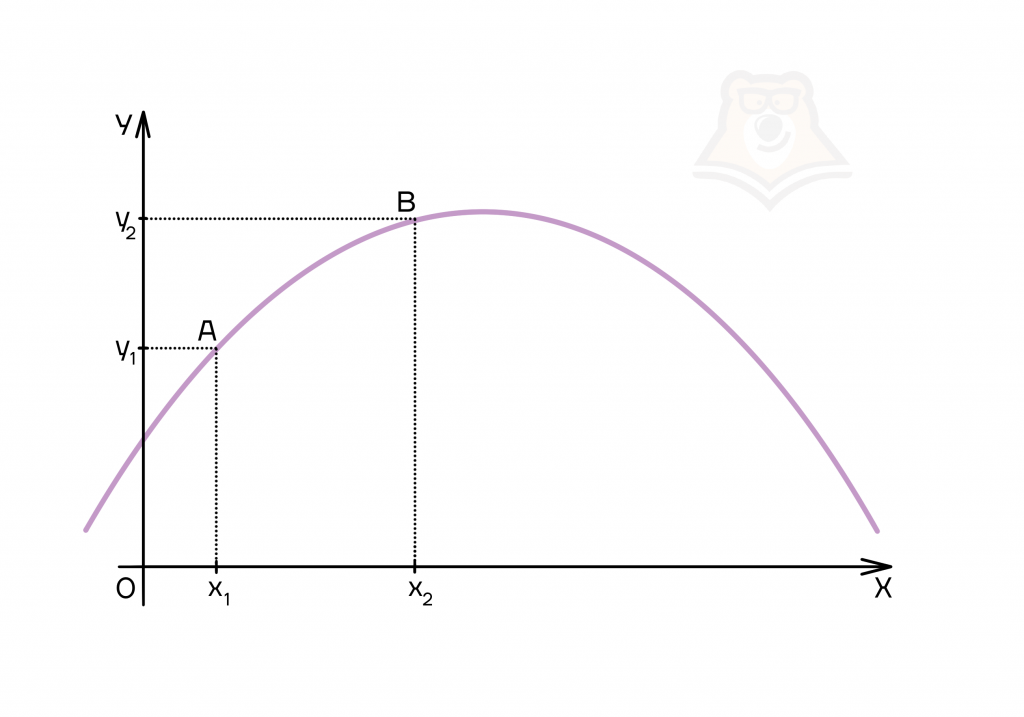
Теперь возьмем две точки на участке убывания функции, которые будут иметь координаты А(х₁;у₁) и В(х₂;у₂). Заметим, что неравенство х₁ < х₂ выполняется. Посмотрим на значения функции у₁ и у₂: у₂ < у₁. Следовательно, выполняется условие f(x₁) > f(x₂), а значит, функция убывает.  

Если функция постоянно возрастает или постоянно убывает, ее называют монотонной. 

Монотонная функция — функция, которая всегда возрастает или убывает. 

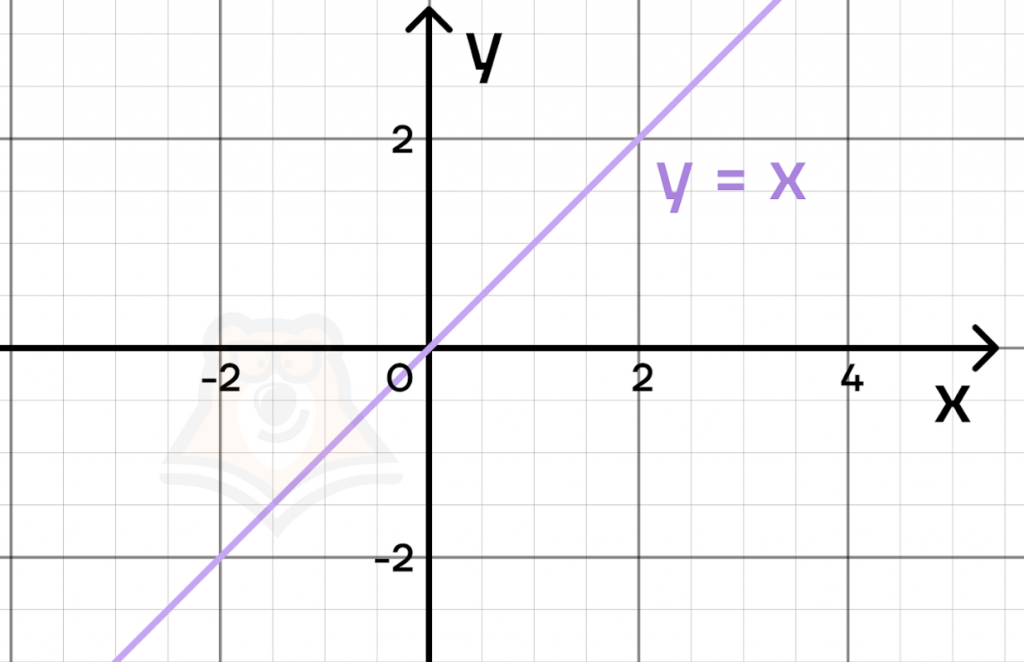
Например, функция \(y=x\) будет монотонно возрастающей. 

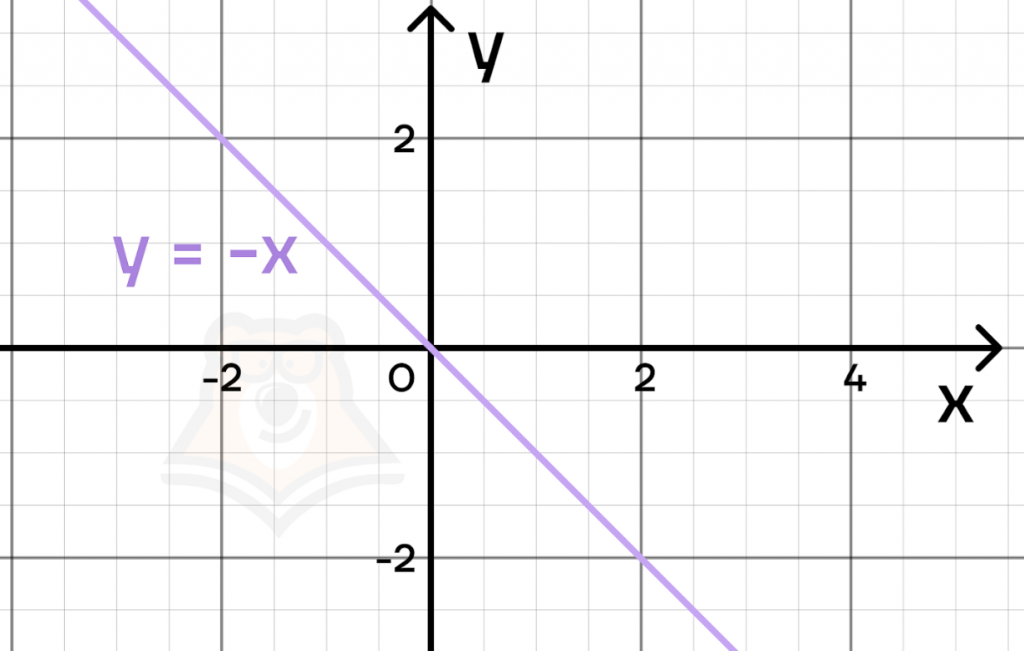
А вот функция \(y=-x\) уже будет монотонно убывающей. 

Функция также может монотонно возрастать или убывать на каком-то из участков графика.

Промежутки знакопостоянства функции — это такие значения аргумента, при которых значение функции имеет постоянный знак (положительный или отрицательный). 

Промежутки знакопостоянства не связаны с возрастанием и убыванием функции: на одном промежутке функция может и возрастать, и убывать. 

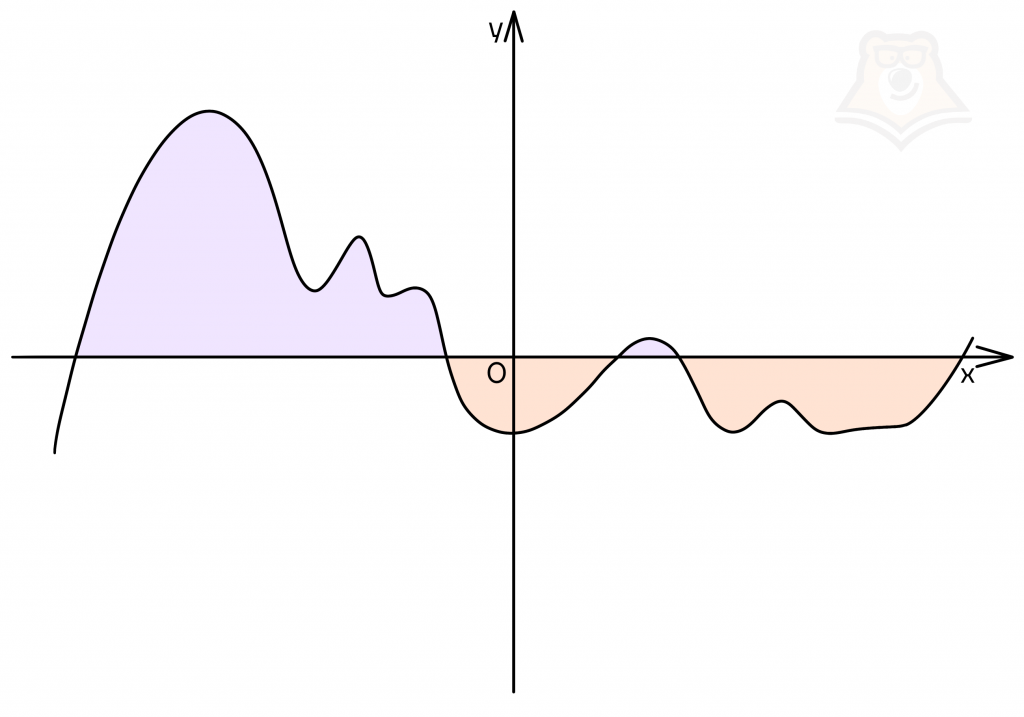
Появляется вопрос, как их найти? Нужно посмотреть, в каких случаях значение функции у будет иметь положительное значение, а в каких отрицательное. Проще всего это сделать на графике: 

• Если функция лежит над осью Ох, то она положительна на этом промежутке.
• Если функция лежит под осью Ох, то она отрицательна на этом промежутке. 

На графике промежутки, на которых функция принимает положительные значения, закрашены фиолетовым, а промежутки с отрицательным значением функции — оранжевым. 

Проговорим про периодичность функции. 

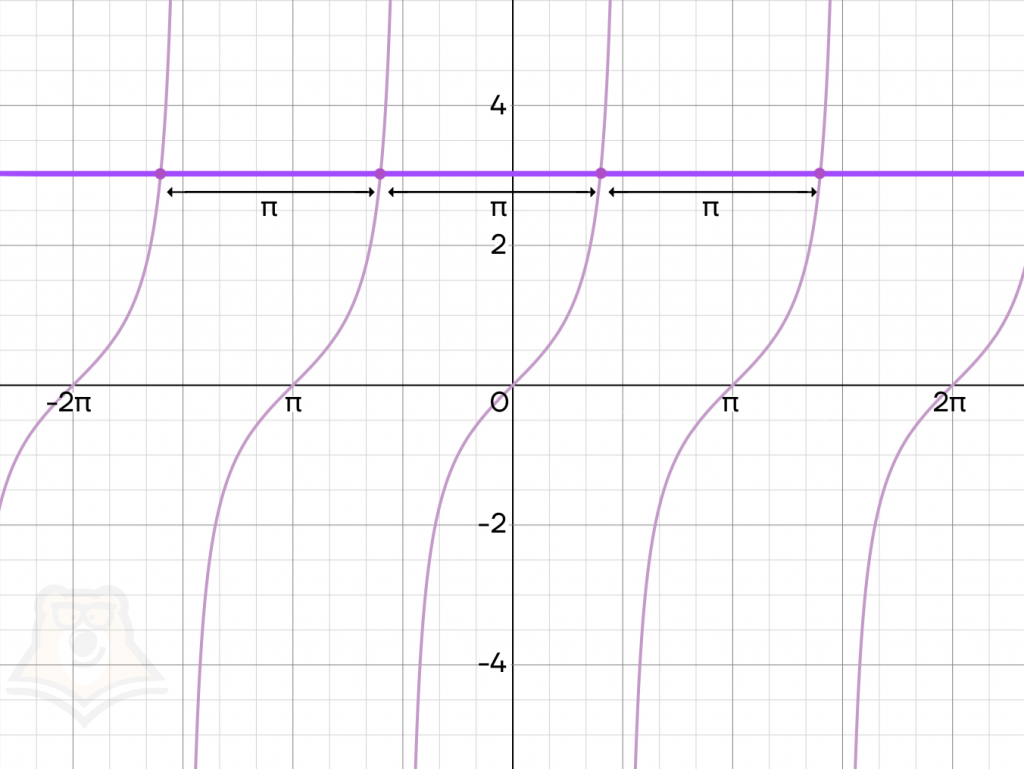
Функция называется периодической, если для любого значения аргумента из области определения функции выполняется условие \(f(x)=f(x+T)\), где \(Т\) — период функции, отличный от 0. 

Определение может показаться запутанным, но ничего сложного в нем нет. Рассмотрим график тангенса и проведем через него горизонтальную линию, параллельную оси Ох. В этом случае мы заметим, что точки пересечения графика и проведенной линии будут лежать через равное расстояние \(\pi\) друг от друга. 

То есть если мы пройдем по оси Ох расстояние вправо или влево, то получим точно такое же значение функции, в котором мы и начинали. 

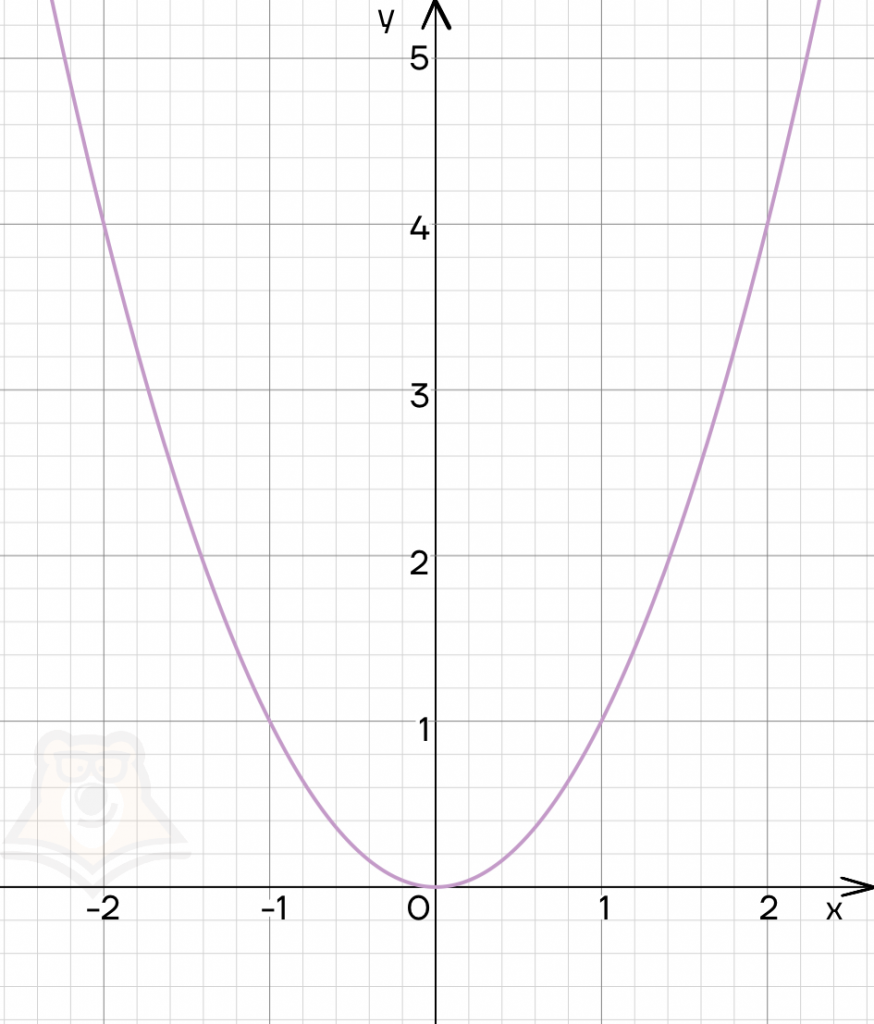
Четной функцией называется такая функция, график которой симметричен относительно оси Оу. 

Для такой функции будет выполняться условие \(f(x) = f(-x)\). 

Примером четной функции может быть парабола, вершина которой лежит на оси Оу. 

Чтобы определить, чётная функция или нет, нужно представить, что к оси Оу приставляется зеркало. Если в этом зеркале правильно отражается функция, то она будет четной. 

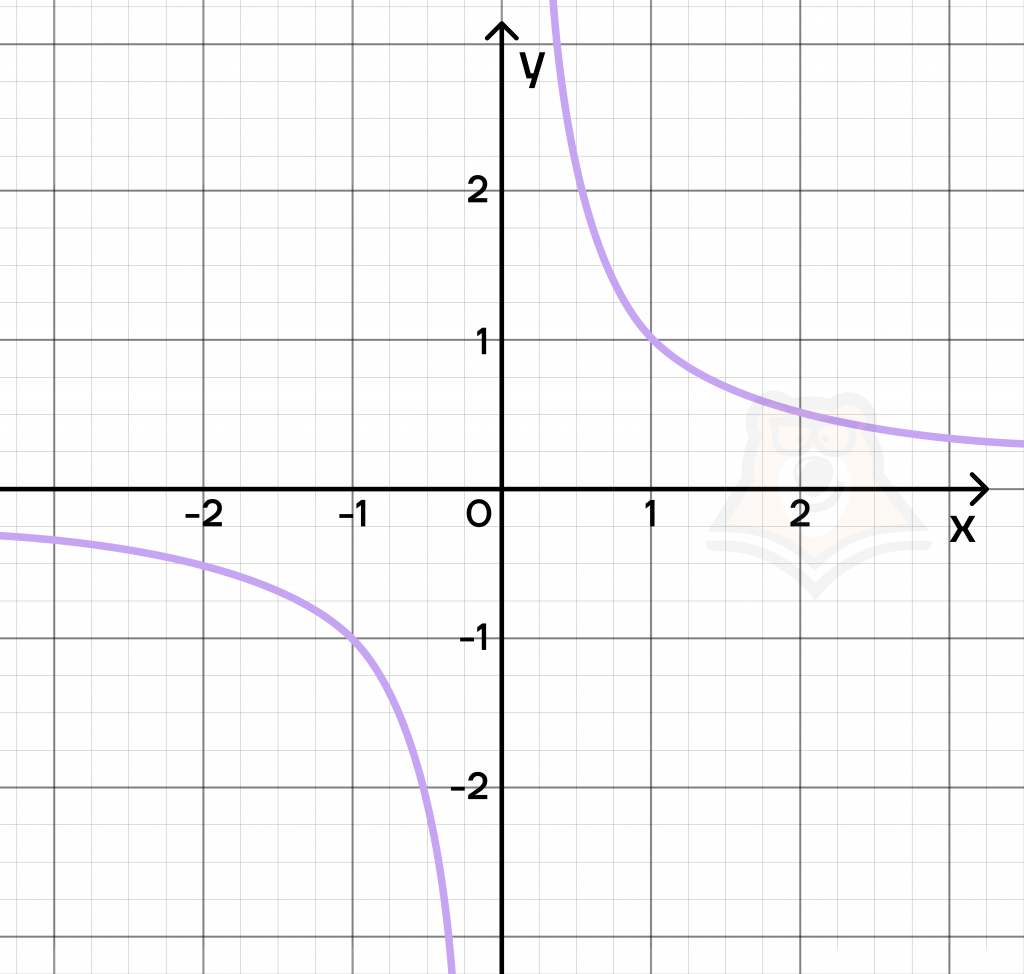
Нечетной функцией называется такая функция, график которой симметричен относительно начала координат. 

Для такой функции будет выполняться условие \(f(-x) = -f(x)\). 

Также примером нечетной функции может служить гипербола. 

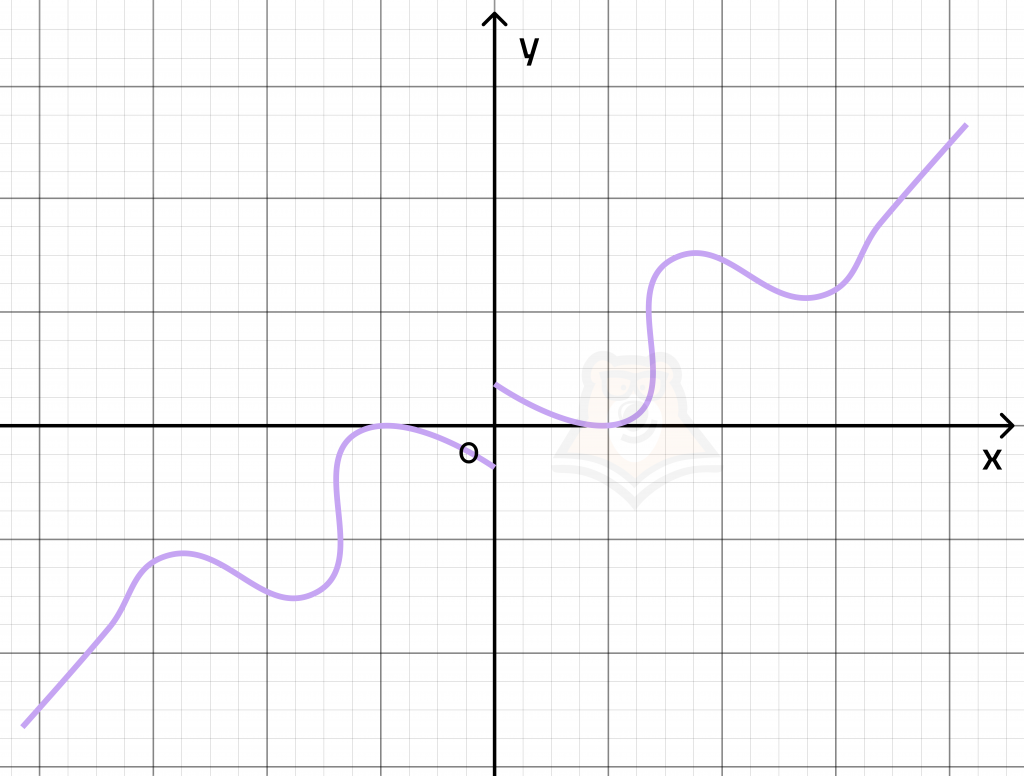
Если для функции не выполняется ни одно из вышеописанных условий, то такая функция является ни четной, ни нечетной функцией. 

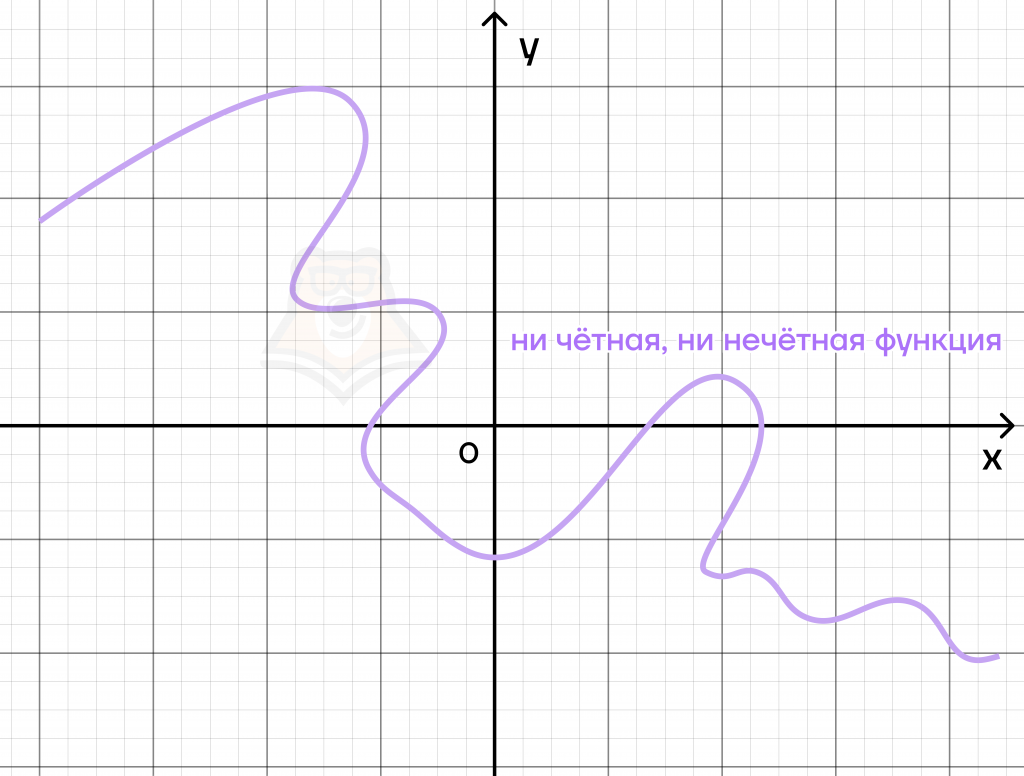
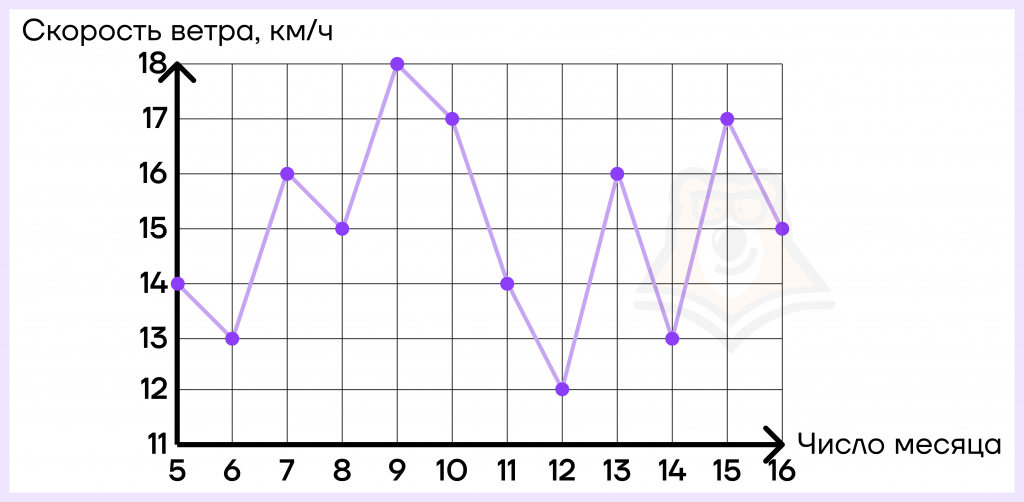
Графики функций могут встретиться и на ЕГЭ по базовой математике в №3.

На графике жирными точками показана скорость ветра в городе N с 5 по 16 мая. По горизонтали указываются числа месяца, по вертикали — скорость ветра в км\ч. Для наглядности точки соединены линией. Определите по графику, какого числа скорость ветра была наибольшей за данный период. 

Решение.
Чтобы найти наибольшую скорость ветра, нам необходимо найти самую «высокую» точку. Эта точка соответствует скорости ветра 18 км\ч. 

Далее опускаем из этой точки прямую до пересечения с осью Ох и попадаем в 9 число. Это и будет ответом. 

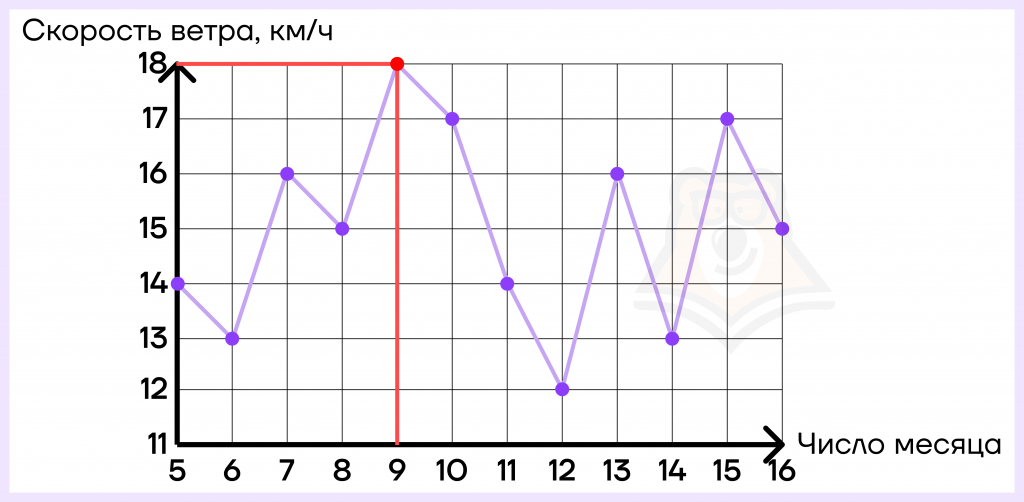
Ответ: 9

Мы познакомились с понятием функции и ее свойствами. Это большой шаг в их изучении, но при этом — самое начало. 

Кроме уже полученных в этой статье навыков, необходимо хорошо знать, как выглядят часто встречающиеся функции, как с ними работать и какие у них есть свойства. А познакомиться с такими функциями вы сможете в статье «Основные элементарные функции».

Термины

Абсцисса — значение координаты х для данной точки. 

Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле \(D=b^2-4*a*c\), где а, b и с берутся из уравнения. Подробнее о нем рассказано в статье «Линейные, квадратные и кубические уравнения». 

Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.

Многочлен — это сумма или разность одночленов, то есть чисел, переменных и их степеней с натуральным показателем. Например, у нас есть одночлены 2, х и у, если мы сложим их, то получим многочлен \(2+x+y\).

Множество — набор из нескольких объектов, которые называются элементами множества. 

Ордината — значение координаты у для данной точки.

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.

Полярная система координат — это система координат, в которой точка описывается с помощью расстояния от начала координат до точки (обозначается как r) и угла между r и положительным направлением оси Ох. Такую систему координат удобно использовать в случаях, когда отношения между точками проще изобразить с помощью радиусов и углов.

Фактчек

• Функция — это зависимость одной переменной от другой. При этом зависимой переменной обычно выступает сама функция (у или f(x)), а переменной величиной является аргумент функции х. 
• Функцию можно задать несколькими способами: табличным способом, графическим способом, аналитическим способом и словесным способом. 
• Функция обладает рядом важных свойств, которые напрямую влияют на ее поведение и график функции. Этими свойствами являются: область определения функции, область значений функции, нули функции, возрастание и убывание функции, монотонность, промежутки знакопостоянства, периодичность и четность. 

Проверь себя

Задание 1.
Какое определение функции неверно?

1. Функция — это зависимость одной переменной от другой. 
2. Функция — это действие над переменной. 
3. Функция — это множество из нескольких переменных. 
4. Функция — соответствие между двумя множествами, причем элементу из первого множества может соответствовать только один элемент второго множества. 

Задание 2.
Какого способа задать функцию не существует?

1. Словесный способ.
2. Табличный способ.
3. Графический способ.
4. Устный способ. 

Задание 3.
Что такое область определения функции?

1. Это все допустимые значения аргумента функции.
2. Это все недопустимые значения аргумента функции.
3. Это все значения, которые может принимать функция.
4. Это все значения, которые не может принимать функция. 

Задание 4.
Что такое область значений функции?

1. Это все допустимые значения аргумента функции.
2. Это все недопустимые значения аргумента функции.
3. Это все значения, которые может принимать функция.
4. Это все значения, которые не может принимать функция. 

Задание 5.
Как называется функция, которая не обладает признаками четной и нечетной функции?

1. Произвольная.
2. Четная.
3. Нечетная.
4. Ни четная и ни нечетная. 

Ответы: 1. — 3; 2. — 4; 3. — 1; 4. — 3; 5. — 4.