Векторы. Часть 1
На этой странице вы узнаете
- Сделать 2700 шагов и не сдвинуться с места – параллельная вселенная или реальность?
- Что вектор украл у точки?
- Почему вектор – тот еще паразит?
Движение – это целая жизнь. То, с чем каждый из нас сталкивается ежедневно в совершенно разных проявлениях: ходьба, бег, перемещение предметов из одной точки в другую, пролетающий в небе самолет и многое другое.
Конечно же, движение не могло обойти стороной и математику. А если быть точнее, то именно направление этого движения. Разберемся же в этом вместе, ведь речь в этой статье пойдет о векторе.

Понятие вектора
| Сделать 2700 шагов и не сдвинуться с места – параллельная вселенная или реальность? Каждый день мы перемещаемся в разные точки: из дома в школу, из школы в парк на прогулку с друзьями, из парка в магазин за хлебом и так далее. В среднем человек проходит в день около 2700 шагов. При этом в конечном итоге каждый из нас в конце дня все равно оказывается дома. Как же так: 2700 шагов прошли, а с места по итогу не сдвинулись? Все дело в том, что наш маршрут состоит из разных направлений. |
Если сделать два шага вперед, а потом развернуться и сделать два шага назад, то мы окажемся в той же точке, где были изначально. При этом мы пройдем два отрезка – каждый длиной в два шага. Если помимо длины этих отрезков мы учтем еще и их направление, то эти направленные отрезки и будут называться векторами.
В данном случае точка, из которой мы начинаем движение, называется началом вектора, а точка, в которую мы приходим в результате движения – концом вектора.
Вектор – это отрезок, для которого указано, какой из его концов считается началом, а какой концом.
Невероятная эффективность: каждый раз, когда мы двигаем стул, мы строим сразу четыре вектора. Началами этих векторов будут являться начальные положения ножек стула, концами векторов – положения ножек после передвижения.

Так как вектор – это в первую очередь отрезок, изображается он практически так же. Только начало вектора отмечается точкой, а конец – стрелочкой. Эта стрелочка и указывает направление вектора.
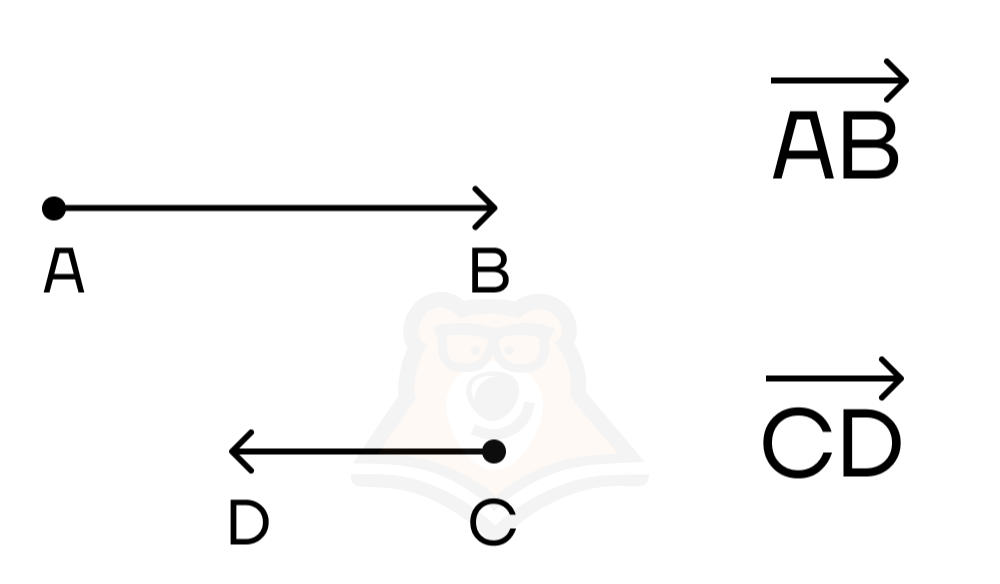
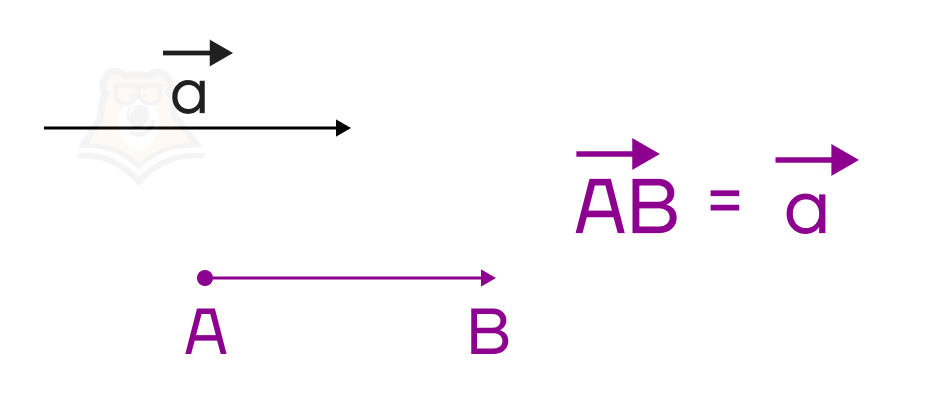
Записывается вектор следующим образом: первая буква – это начало вектора, а вторая буква – конец вектора. Над обозначением вектора также ставится стрелочка.
Например, на рисунке ниже можно увидеть вектор \(\overrightarrow{AB}\) с началом в точке A и концом в точке B, а также вектор \(\overrightarrow{CD}\) с началом в точке C и концом в точке D.
Также вектор можно обозначить одной маленькой буквой над самим вектором. Над этой буквой так же ставится стрелочка.
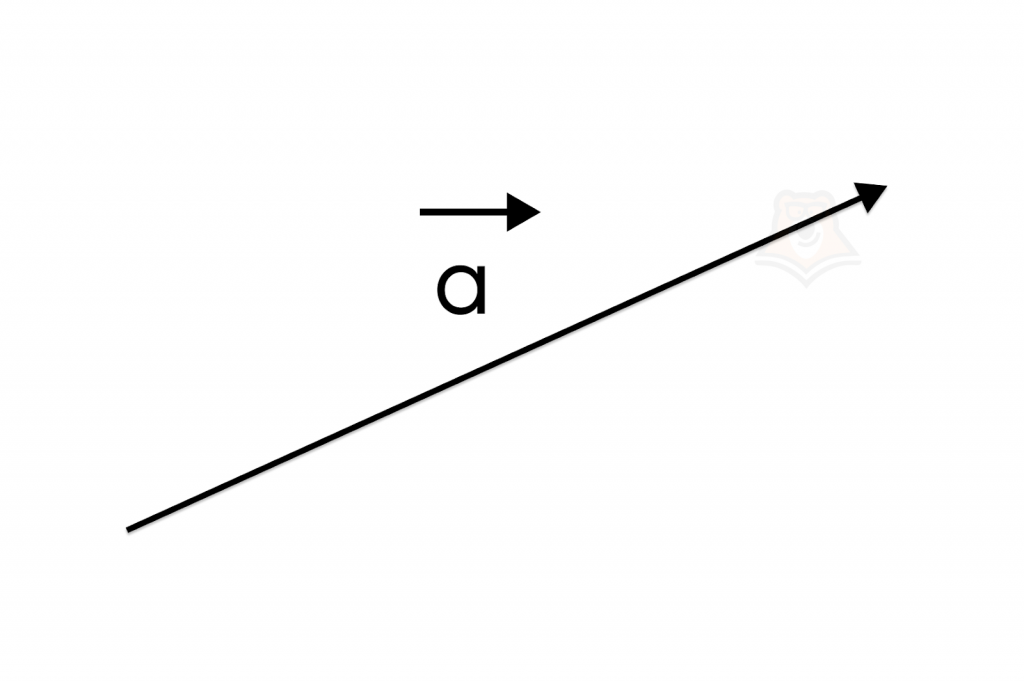
Например, вектор a на рисунке выше.

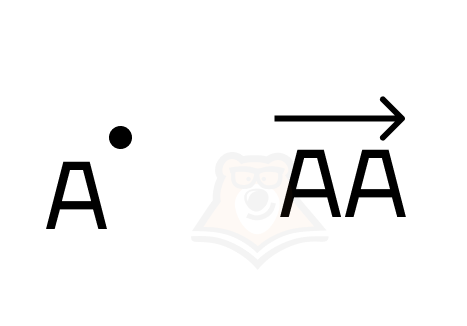
| Что вектор украл у точки? Практически всё! Это вообще законно? Существует такой необычный вектор, который называется нулевым – вектор, у которого начало и конец совпадают. На плоскости он обозначается как точка. |
Так же, как и отрезок, каждый вектор имеет свою длину.
Длина вектора
Длина вектора – это расстояние между началом и концом вектора.
Она не зависит от направления вектора и всегда неотрицательна, поэтому записывается в модульных скобках.

\(|\overrightarrow{AB}|\) и \(|\overrightarrow{DC}|\) – длины векторов \(\overrightarrow{AB}\) и \(\overrightarrow{DC}\).
Длина нулевого вектора, соответственно, равна 0.

Помимо длины и направления, когда речь идет о двух векторах, большую роль играет угол между ними.
Угол между двумя векторами
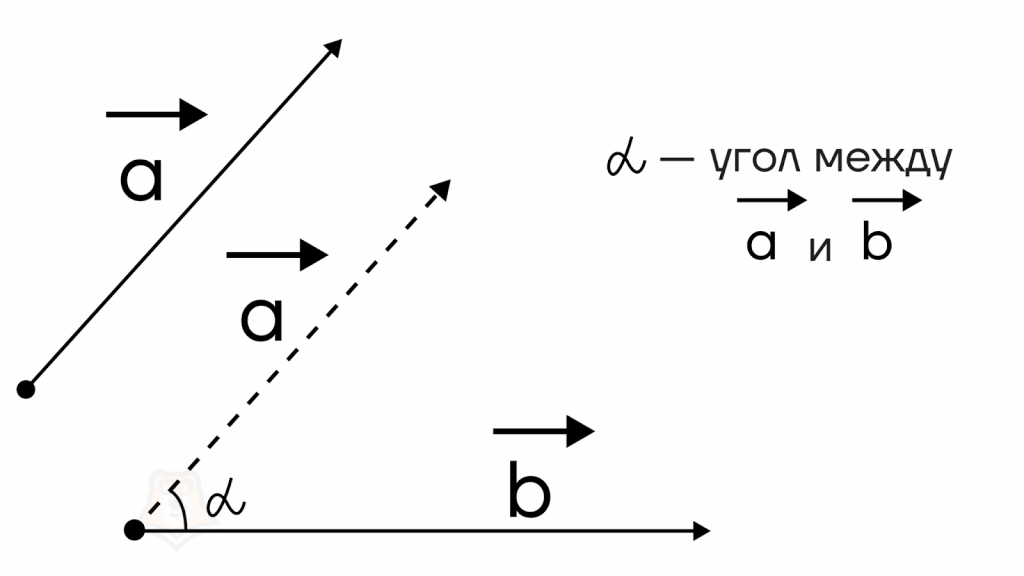
Угол между двумя векторами – это меньший из углов, который образуется между векторами, если расположить векторы таким образом, чтобы их начала совпадали.
Для этого пользуются правилом параллельного переноса: любой вектор можно параллельно перемещать в пространстве, сохраняя его длину и направление.
Например, на рисунке ниже – угол между векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\).
| Почему вектор – тот еще паразит? Мало кто знает, что вектор есть еще и в биологии. Разумеется, в этой науке речь идет не о направленном отрезке. Так называют организм, переносящий инфекцию от одного организма к другому. Например, клещ или тля. При этом можно заметить, что и тут есть связь с математикой, ведь связан этот биологический термин также с перемещением, и тоже имеет свое направление: от первого организма ко второму. |

Итак, мы выяснили, что из себя представляет вектор, как он обозначается, а также рассмотрели такие понятия, как длина вектора и угол между двумя векторами. Самое время разобраться в том, какие бывают векторы.
Коллинеарные векторы
Представим себе канатоходца, идущего по бесконечному канату, то есть по прямой.
Передвигаясь по канату, он откладывает различные векторы при движении вперед или назад. Такие векторы будут называться коллинеарными.
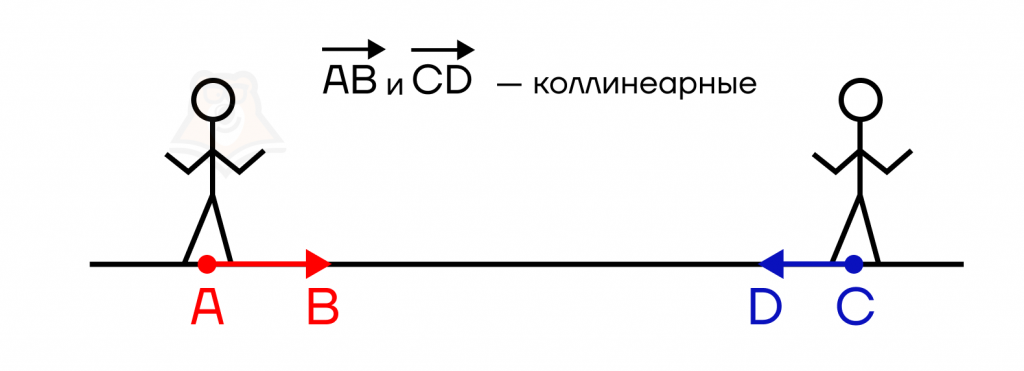
Коллинеарными будут являться векторы, расположенные не только на одной прямой, но и на параллельных прямых. Например, две машины, проезжающие по параллельным дорогам, так же откладывают коллинеарные векторы.
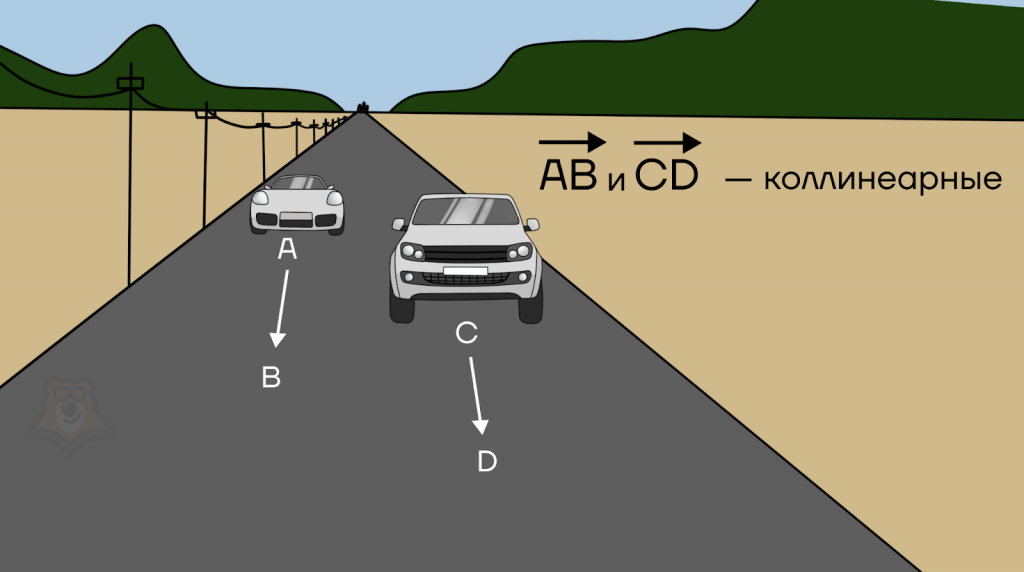
Коллинеарные векторы – это векторы, лежащие на одной прямой или на параллельных прямых.
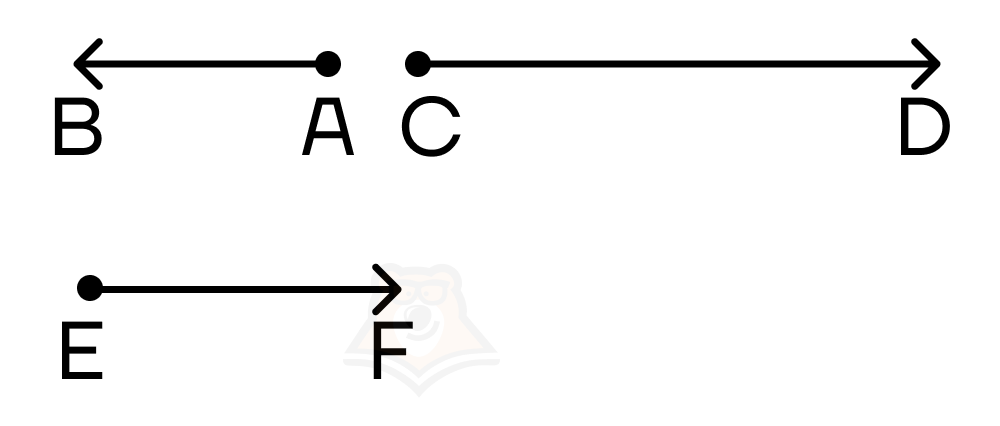
По данной картинке \(\overrightarrow{AB}, \overrightarrow{CD}\) и \(\overrightarrow{EF}\) являются коллинеарными векторами.
Мы уже выяснили, что у вектора особую роль играет направление. Коллинеарные векторы бывают сонаправленными и противоположно направленными.
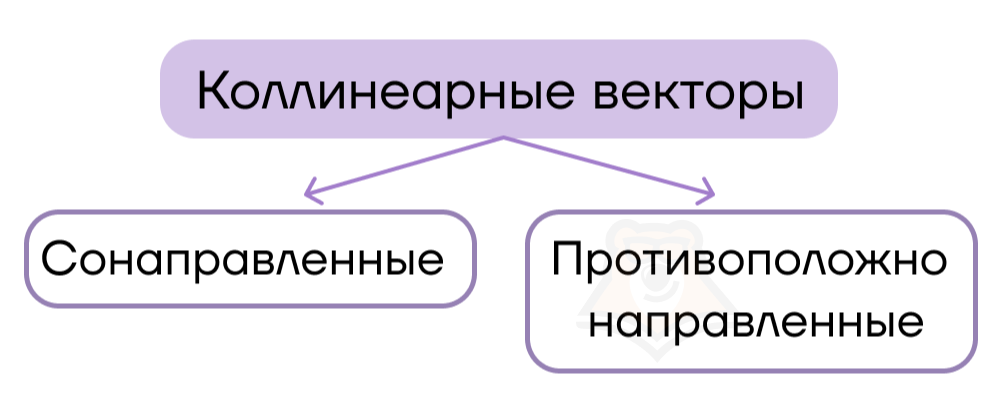
Сонаправленные векторы – это коллинеарные векторы, направленные в одну сторону.
Сонаправленность двух векторов обозначается двумя стрелками, направленными вверх.
Противоположно направленные векторы – это коллинеарные векторы, направленные в противоположные стороны.
Противоположное направление двух векторов обозначается двумя стрелками, направленными в разные стороны.
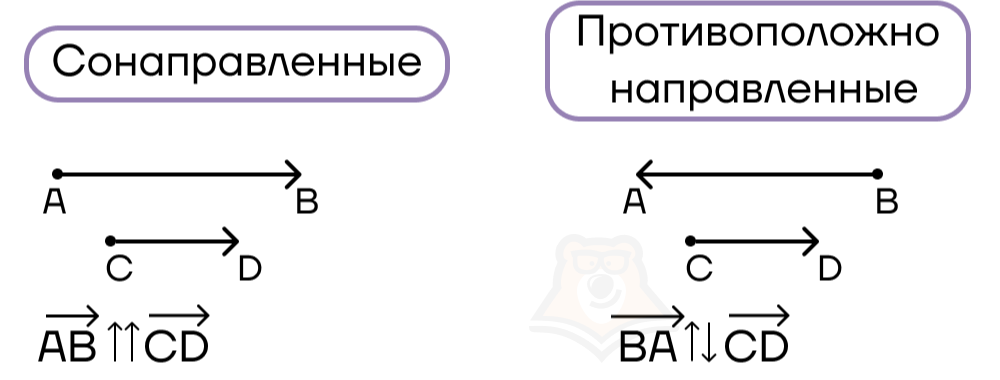
Важно: нулевой вектор сонаправлен с любым вектором.

Из статьи «Точка, прямая, луч, отрезок и угол» мы помним, что два отрезка могут быть перпендикулярны друг другу. Как же называются «перпендикулярные» векторы?
Ортогональные векторы
Ортогональные векторы – это векторы, угол между которыми равен 90°.
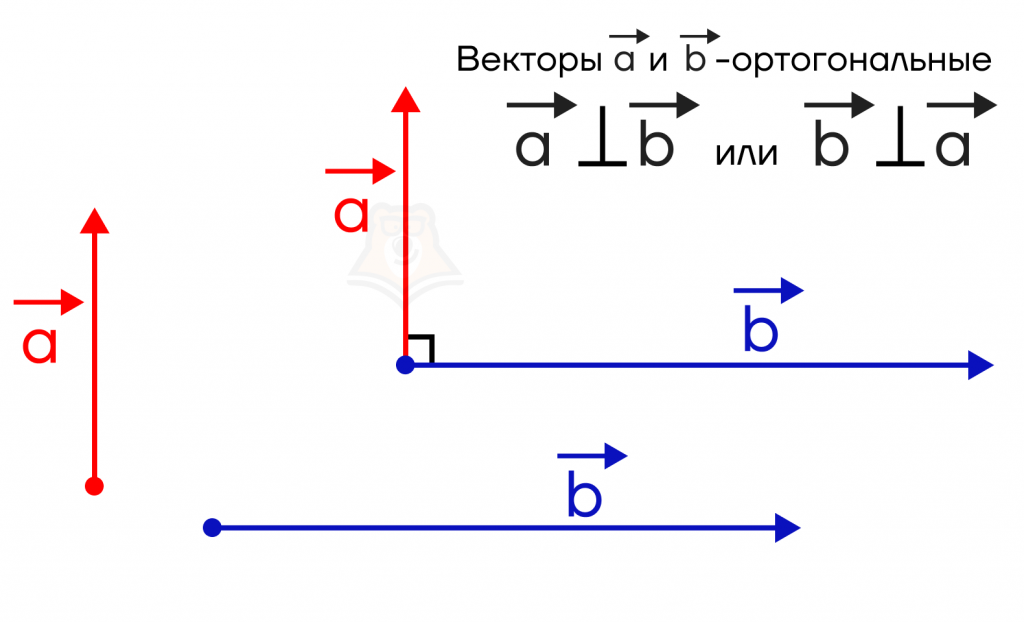
Например, на рисунке выше векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\) – ортогональные. Обозначается это так же, как и перпендикулярность: \(\overrightarrow{a} \perp \overrightarrow{b}\) или \(\overrightarrow{b} \perp \overrightarrow{a}\).
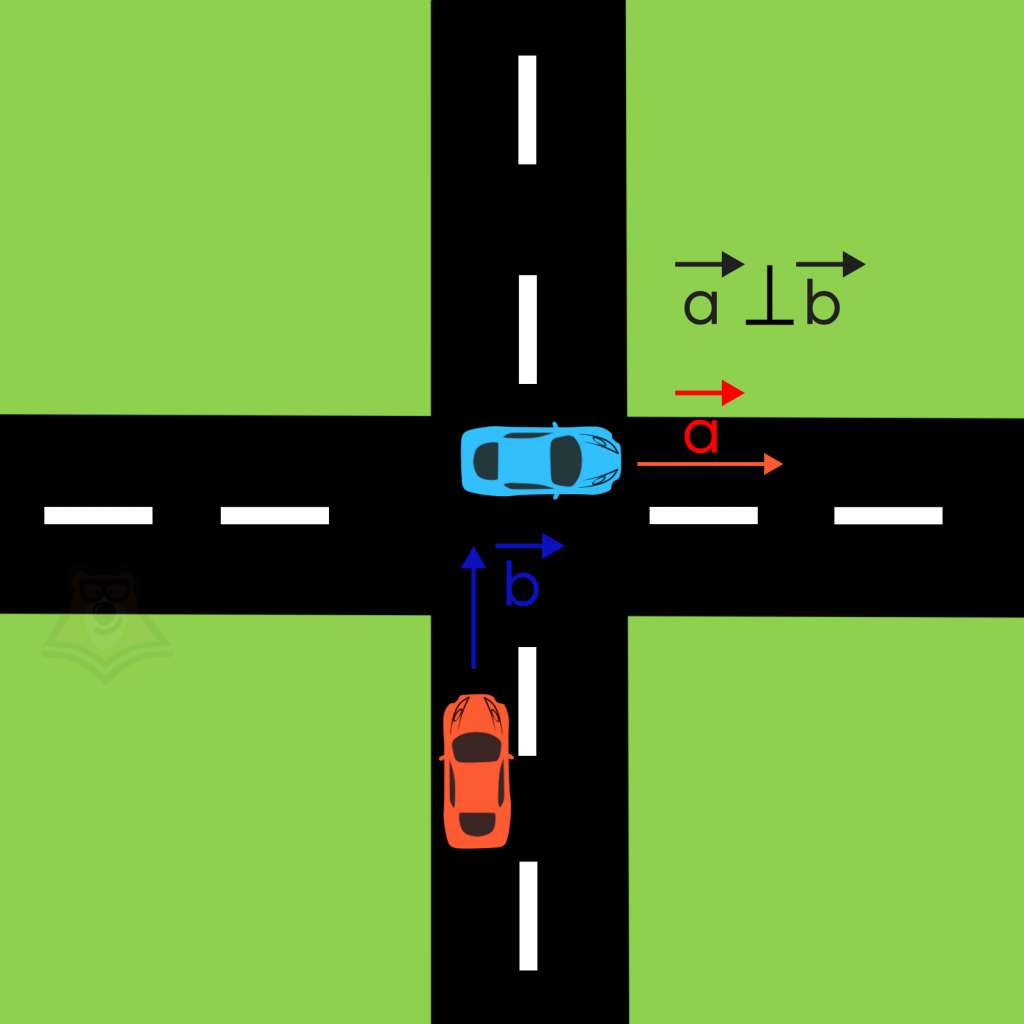
Ортогональные векторы образуются, например, при движении двух машин на перекрестке.
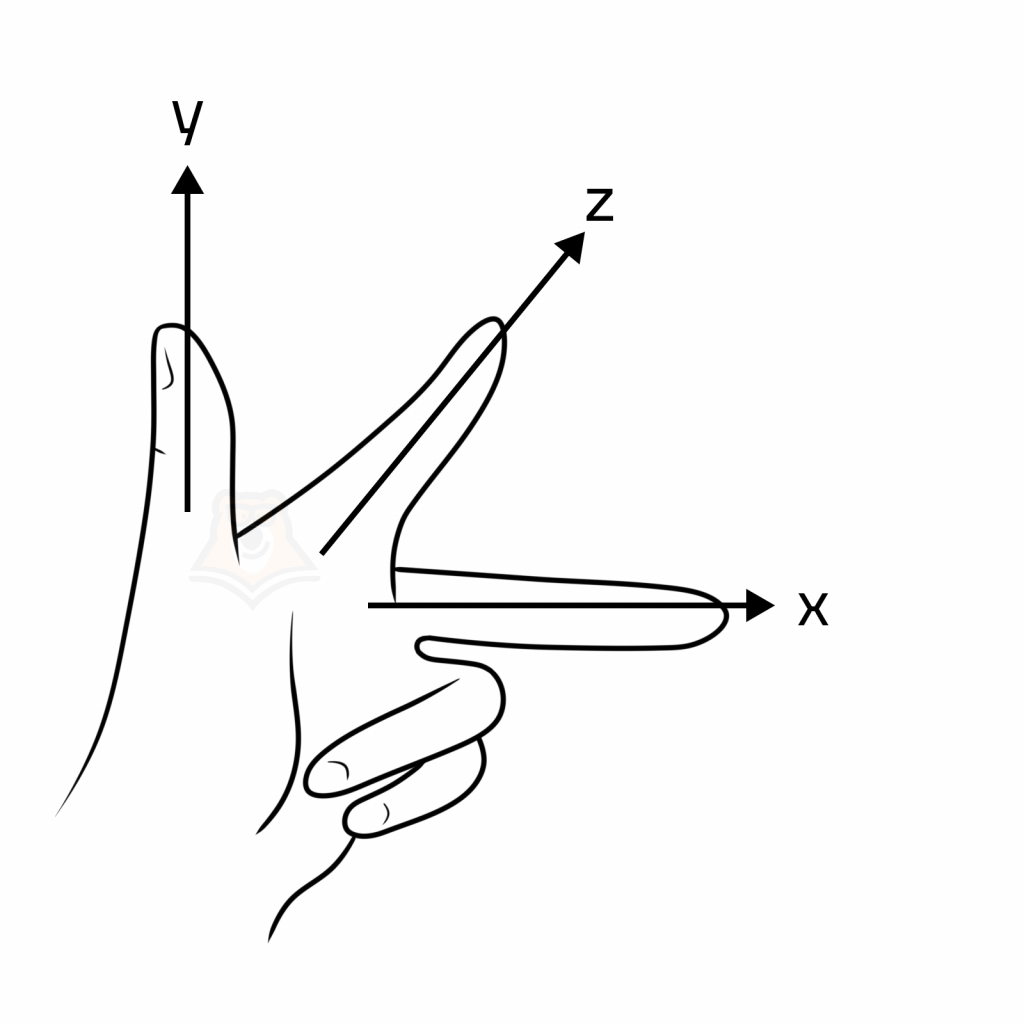
Систему из трех векторов в пространстве, каждый из который ортогонален двум другим, называют системой ортогональных векторов. Например, если мы расположим средний, указательный и большой пальцы руки так, как указано на рисунке ниже, то мы получим систему ортогональных векторов \(\overrightarrow{x}, \overrightarrow{y},\overrightarrow{z}\), направленных вдоль этих пальцев: \(\overrightarrow{z} \perp \overrightarrow{x}, \overrightarrow{z} \perp \overrightarrow{y}, \overrightarrow{x} \perp \overrightarrow{y}\).
При решении задач часто играет большое значение, лежат векторы в одной плоскости или нет. Векторы разделяют еще и по этому принципу.
Компланарные векторы – это векторы, которые лежат в одной плоскости или на параллельных плоскостях.
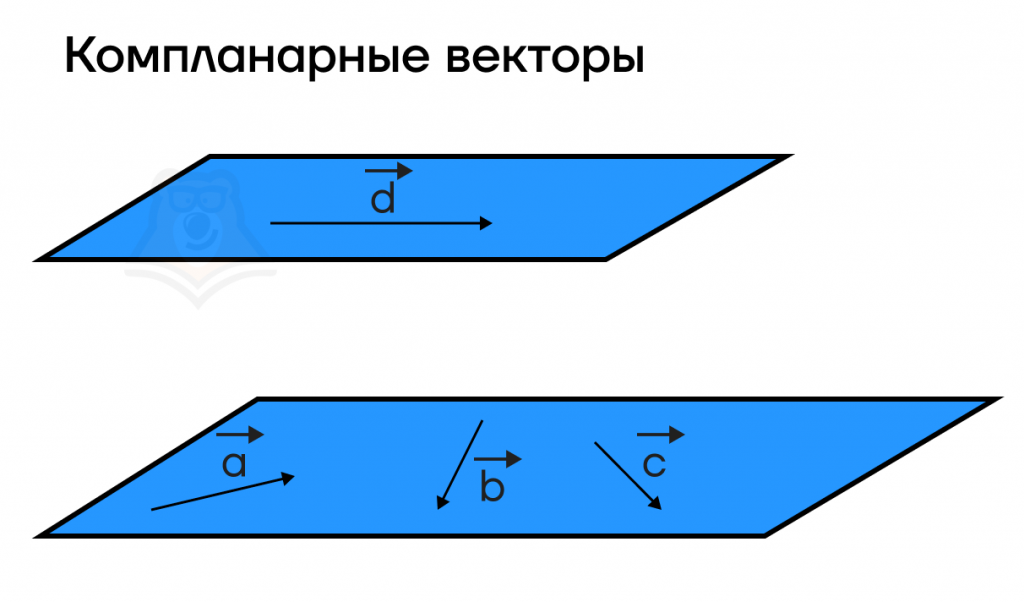
Чтобы определить компланарность векторов, достаточно параллельно переместить их в пространстве так, чтобы все векторы выходили из одной точки. Тогда, если после перемещения все векторы окажутся в одной плоскости, значит, эти векторы компланарные.
Если же после такого перемещения векторы расположились не в одной плоскости, их называют некомпланарными.
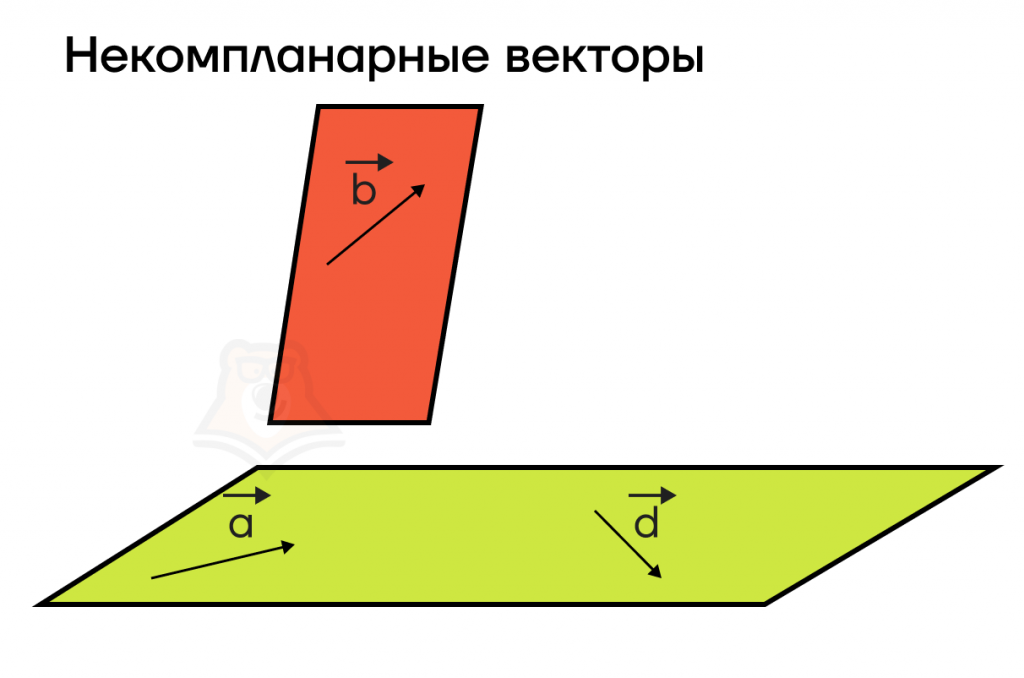
Также стоит отметить, что любые два вектора всегда лежат на одной плоскости, поэтому любые два вектора можно назвать компланарными друг с другом.
Ну а теперь перейдем к самому интересному – какие же векторы называются равными?
Равенство векторов
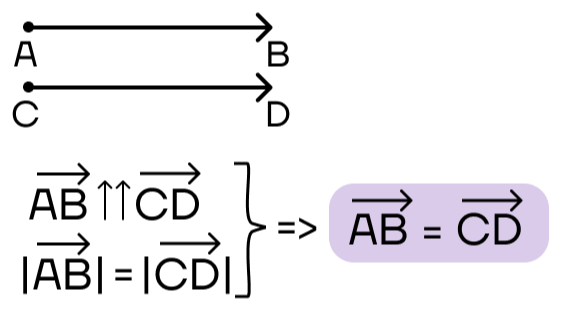
Векторы называются равными, если они сонаправлены и их длины равны.
Да-да, в отличие от отрезков играет роль здесь не только размер (длина), но и направление.

Равенство двух векторов обозначается знаком «=» между двумя векторами, как на рисунке ниже.

Также важно отметить один момент: от одной точки можно отложить единственный (только один) вектор, равный данному.
Если же векторы равны по длине, но при этом являются противоположно направленными, их называют противоположными. При обозначении противоположных векторов перед одним из векторов ставится знак «–», как на рисунке ниже.
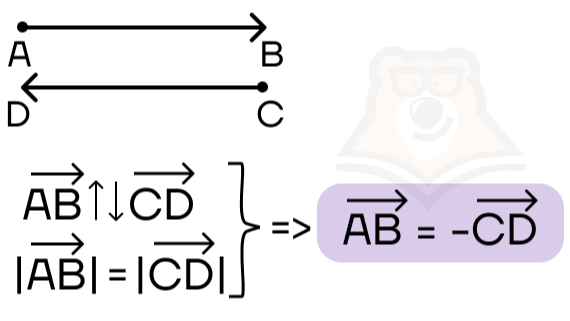
Рассмотрим пример задания №19 из ОГЭ по математике.
Задание. Выберите верные утверждения:
1) Равными векторами называют векторы, длины которых равны;
2) Противоположными называют противоположно направленные векторы, длины которых равны;
3) Коллинеарными называют векторы, лежащие на одной прямой;
4) Любой вектор сонаправлен с нулевым вектором.
Если верных утверждений несколько, в ответе указать их номера в порядке возрастания.
Решение.
1 утверждение. Равными векторами называют векторы, длины которых равны – неверно. Чтобы векторы были равны друг другу, необходимы не только одинаковые длины этих векторов, но и одинаковое направления.
2 утверждение. Противоположными называют противоположно направленные векторы, длины которых равны – верно.
3 утверждение. Коллинеарными называют векторы, лежащие на одной прямой – неверно. Коллинеарными называют векторы, лежащие на одной прямой или на параллельных прямых. В утверждении же сказано только про векторы, лежащие на одной прямой.
4 утверждение. Любой вектор сонаправлен с нулевым вектором – верно.
Утверждения №2 и №4 оказались верными, в ответе укажем их номера в порядке возрастания.
Ответ: 24
Что же, мы двигаемся дальше по вектору нашей статьи. Следующая станция – «Сумма векторов. Правило сложения». Просьба пристегнуть ремни, будет очень интересно.
Сумма векторов. Правила сложения векторов
Играя в футбол или бильярд, мы, не задумываясь, совершаем множество действий с векторами, одно из них – сложение. Давайте разберем его с точки зрения геометрии.
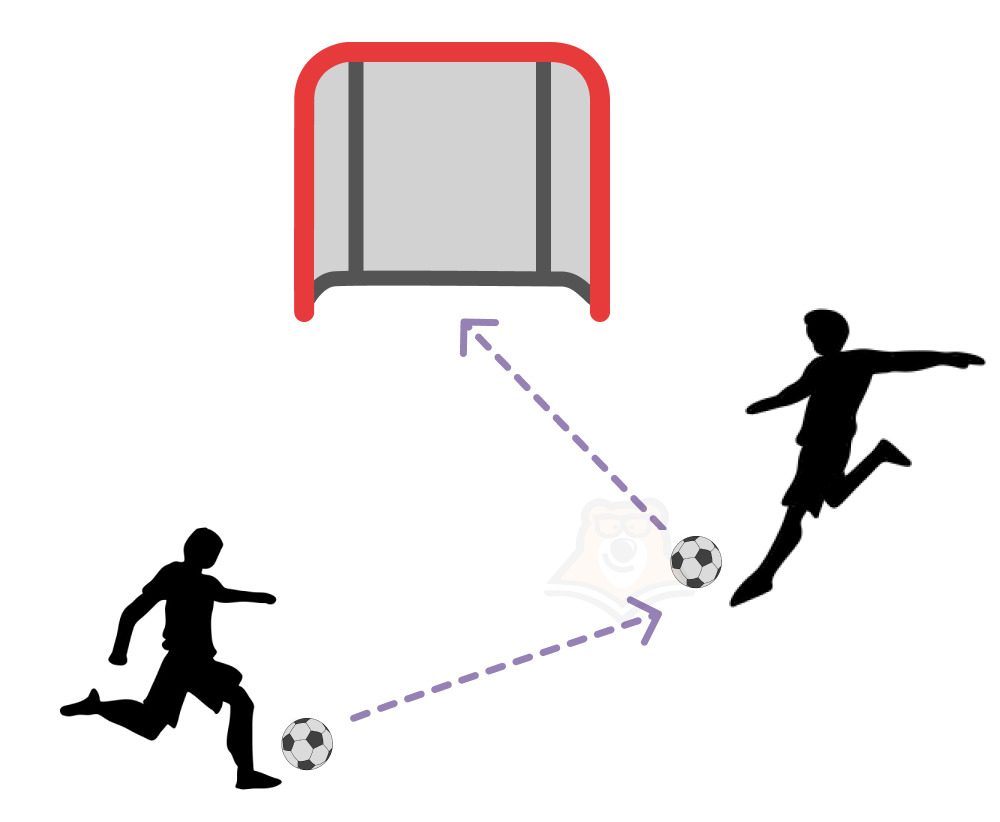
Некий футболист Умналдо совершает удар по мячу, находящемуся в точке A, в результате чего мяч перемещается в точку B. В этой же точке B удар по мячу совершает футболист Умнесси, после чего мяч перемещается в точку C.
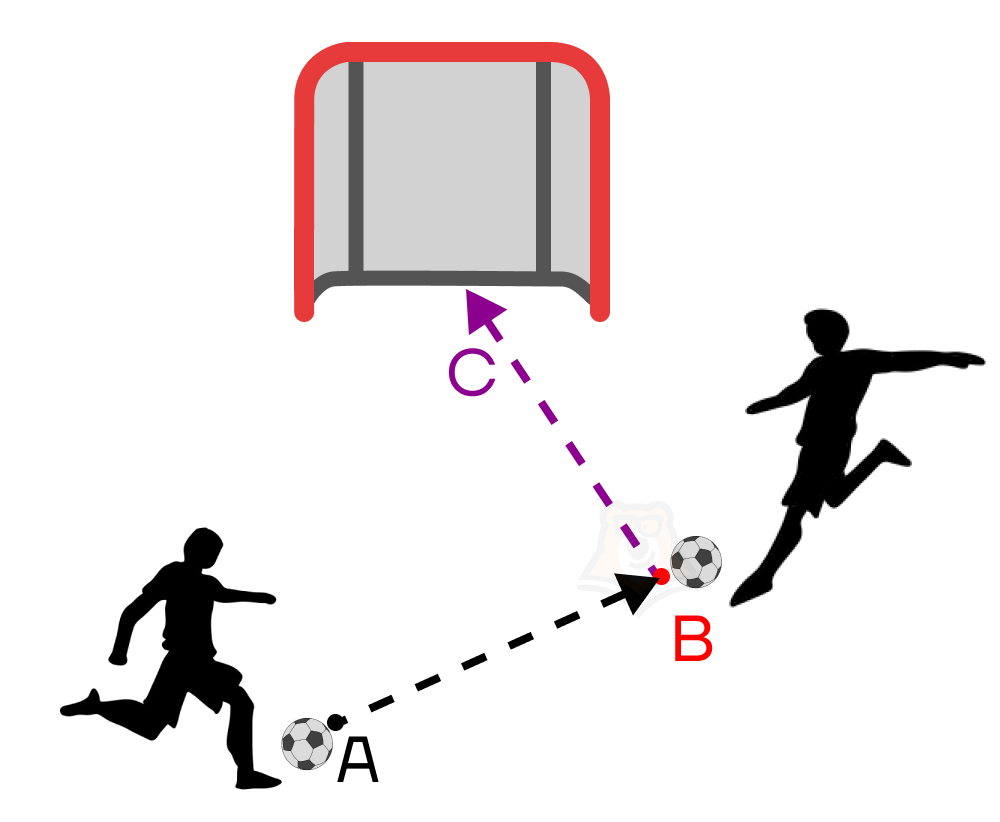
В такой игре при движении мяч образовал два вектора: \(\overrightarrow{AB}\) и \(\overrightarrow{BC}\). При этом по итогу мяч переместился из начальной точки A в конечную точку C. Вектор \(\overrightarrow{AC}\) в этом случае обозначает перемещение мяча. Этот вектор называют суммой векторов \(\overrightarrow{AB}\) и \(\overrightarrow{BC}\). Обозначается это следующим образом: (\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}\).
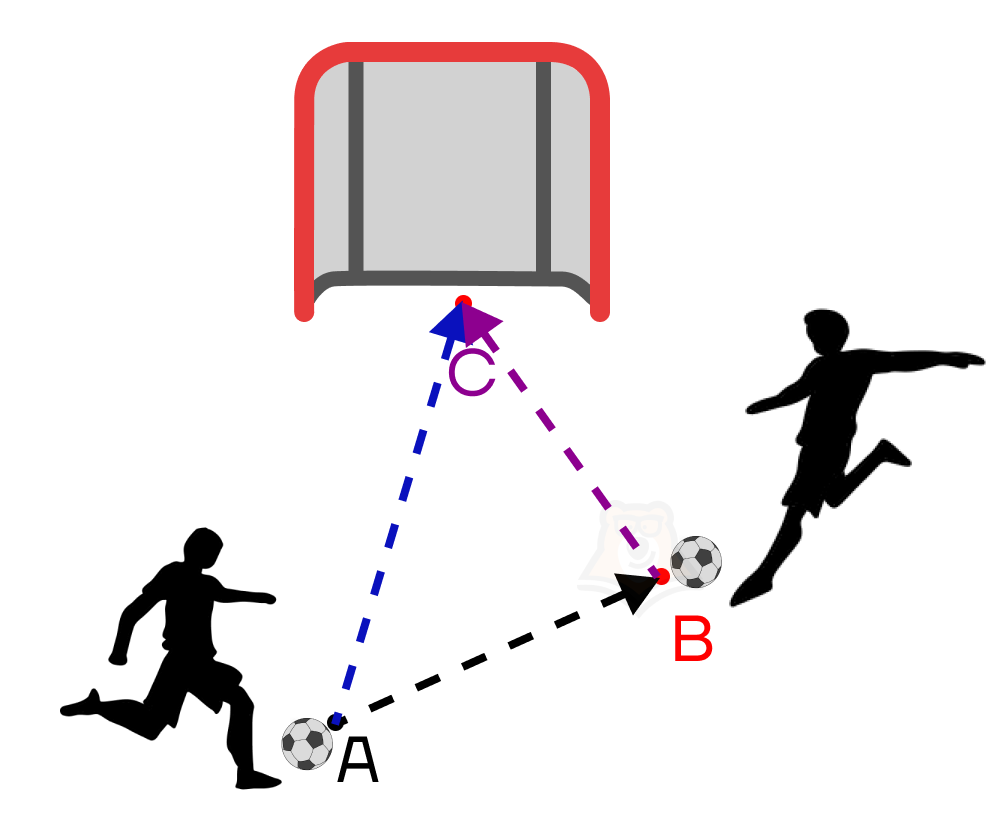
Как видим по рисунку, оба вектора \(\overrightarrow{AB}\) и \(\overrightarrow{BC}\) вместе с вектором (\overrightarrow{AC}\) образуют треугольник. Поэтому такое правило сложения векторов называют правилом треугольника: сумма двух векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\), у которых конец первого вектора \(\overrightarrow{a}\) совпадает с началом второго вектора b, есть вектор \(\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}\), который проведен из начала вектора \(\overrightarrow{a}\) в конец вектора \(\overrightarrow{b}\).
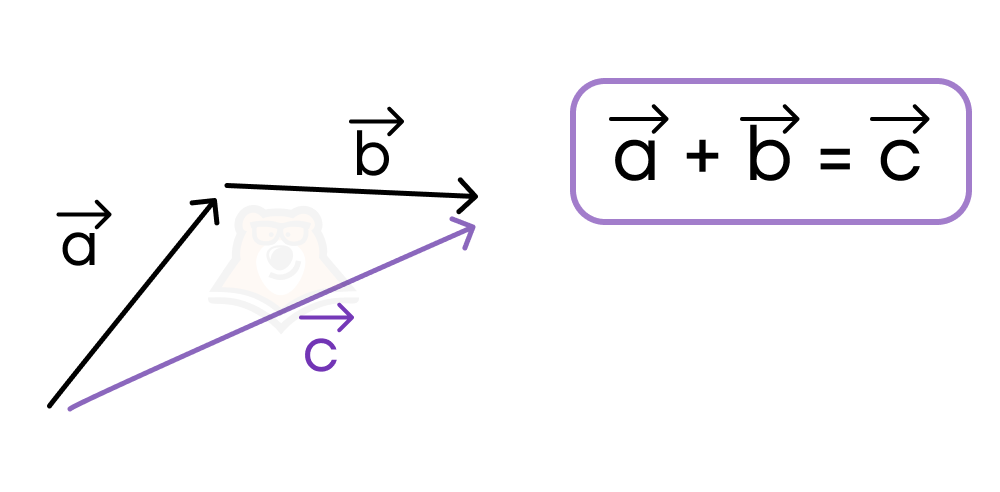
Из правила треугольника следует, что векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а также вектор их суммы \(\overrightarrow{c}\) образуют треугольник со сторонами a, b и c, равными длинам этих векторов. Из неравенства треугольника, которое можно вспомнить из статьи «Треугольник», следует, что \(c<a+b\). То есть,
\(|\overrightarrow{c}|<|\overrightarrow{a}|+|\overrightarrow{b}|\),
где \(\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}\)
Таким образом, длина вектора суммы двух векторов всегда меньше, чем сумма длин этих векторов.
В рассмотренном примере конец первого вектора \(\overrightarrow{AB}\) совпадает с началом второго вектора \(\overrightarrow{BC}\). Как же быть в противном случае? Например, найдем сумму \(\overrightarrow{a}+\overrightarrow{b}\) векторов, представленных на рисунке ниже.
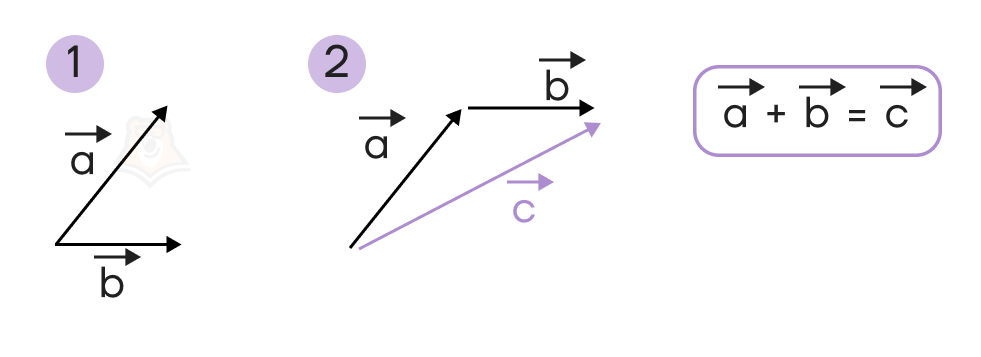
Для этого достаточно, воспользовавшись правилом параллельного переноса, переместить вектор \(\overrightarrow{b}\) так, чтобы его начало совпало с концом вектора \(\overrightarrow{a}\).

Далее вектор \(\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}\) получим, воспользовавшись правилом треугольника, \(\overrightarrow{a}\) именно соединив начало первого вектора a с концом второго вектора \(\overrightarrow{b}\).
Задания на действия с векторами может встретиться в №2 ЕГЭ по профильной математике.
Задание. На рисунке с размером клетки 1×1 представлены векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\). Найти длину вектора a+b. В ответе указать полученное число, возведенное во вторую степень.
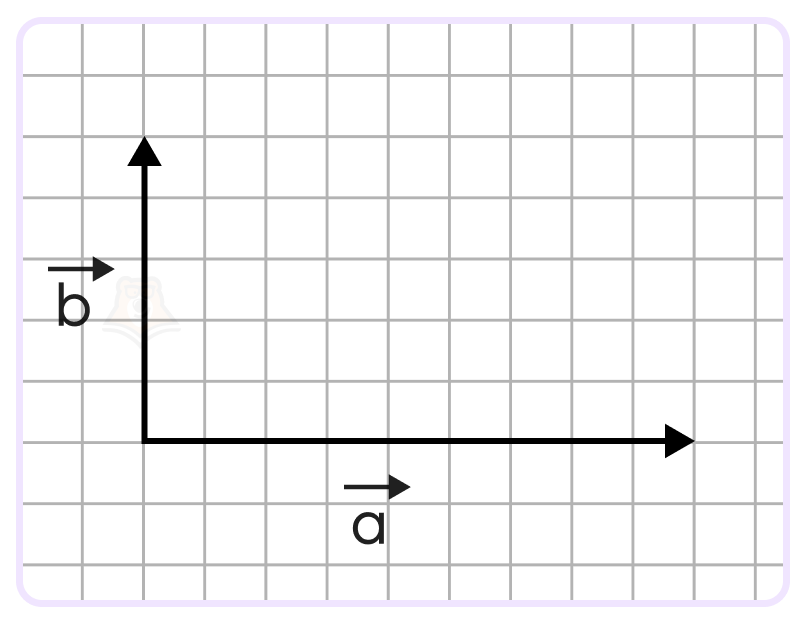
Решение. Для начала построим вектор \(\overrightarrow{a}+\overrightarrow{b}\).Для этого, воспользовавшись параллельным переносом, переместим векторы так, чтобы конец вектора \(\overrightarrow{a}\) совпал с началом вектора \(\overrightarrow{b}\).
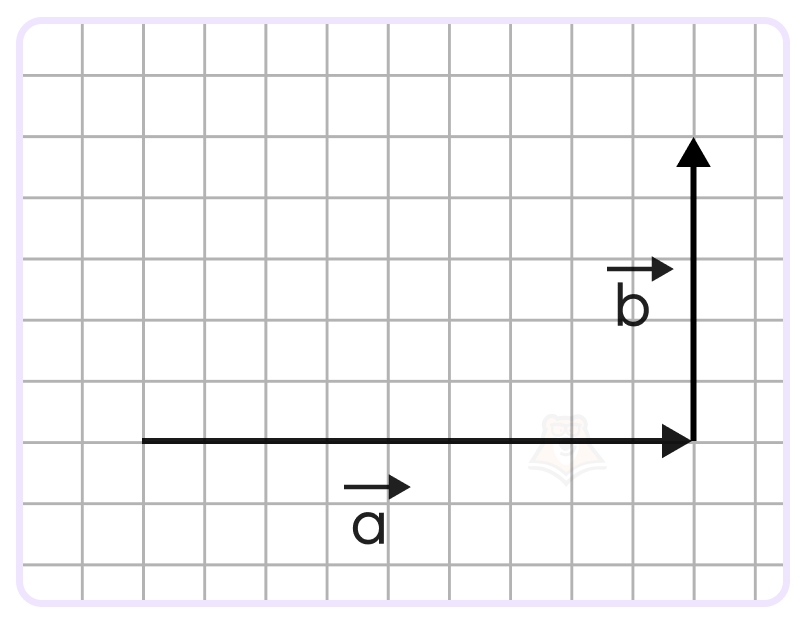
Тогда по правилу треугольника вектор \(\overrightarrow{a}+\overrightarrow{b}\)– вектор, проведенный из начала вектора \(\overrightarrow{a}\)к концу вектора \(\overrightarrow{b}\):
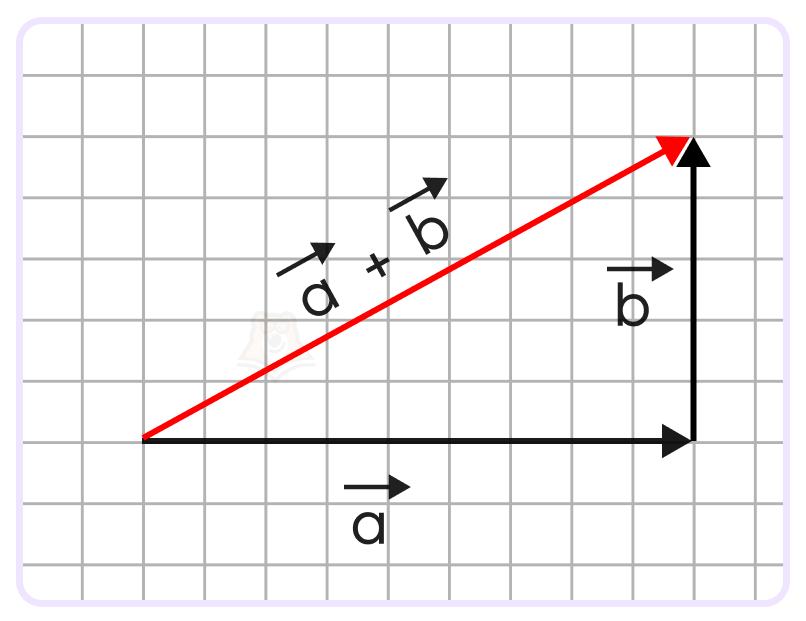
Видим, что этот вектор совпадает с гипотенузой прямоугольного треугольника с катетами, равными 9 и 5. То есть, длина вектора \(\overrightarrow{a}+\overrightarrow{b}\)будет равна длине этой гипотенузы. Воспользуемся теоремой Пифагора для ее нахождения:
\(|\overrightarrow{a}+\overrightarrow{b}|^2=9^2+5^2=81+25=106\)
Тогда:
\(|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{106}\)
В ответе укажем полученное число, возведенное во вторую степень, то есть \((\sqrt{106})^2=106\)
Ответ: 106
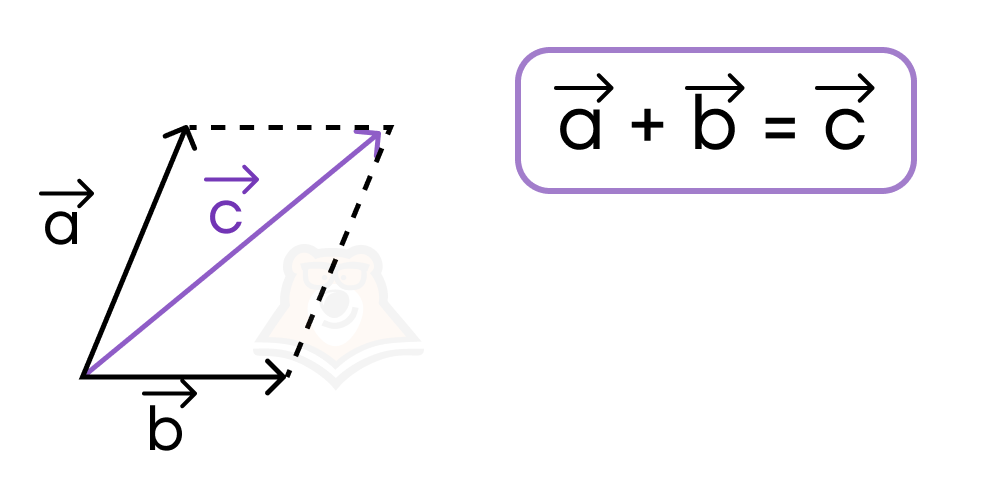
Существует еще одно правило сложения векторов.
Правило параллелограмма. Если оба вектора отложены от одной точки, тогда можно достроить данный рисунок до параллелограмма и провести вектор по диагонали из начальной точки. Полученный вектор будет суммой двух изначальных векторов.
Что такое сумма двух векторов, мы разобрались. А теперь усложним задачу: можно ли сложить три, четыре, пять, тысячу векторов? Оказывается, для этого тоже есть правило.
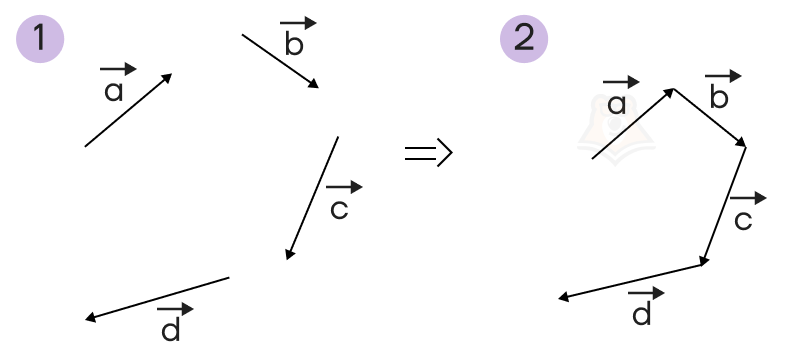
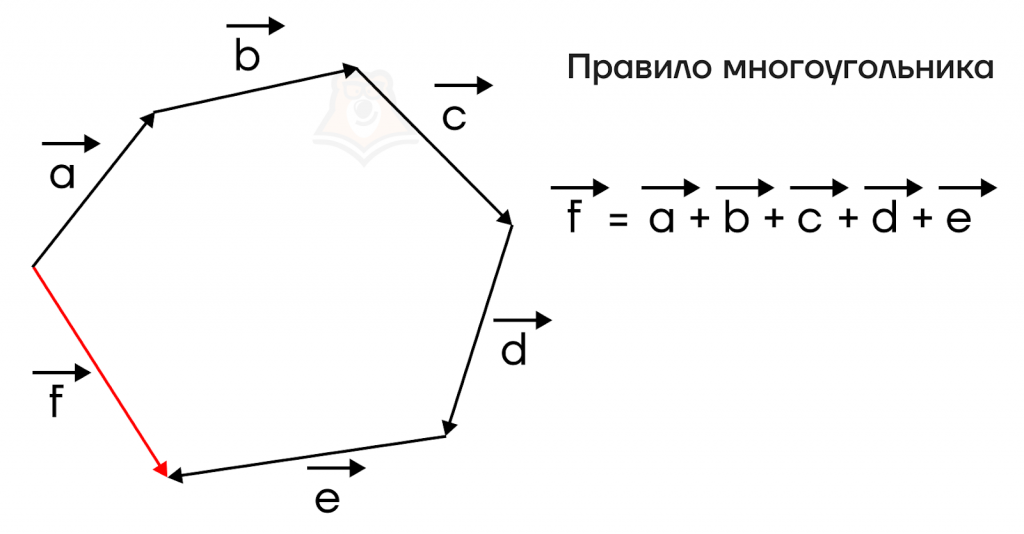
Правило многоугольника. Рассмотрим на примере сумму четырех векторов \(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\). Для начала, воспользовавшись параллельным переносом, разместим векторы таким образом, чтобы конец каждого вектора, кроме последнего, совпадал с началом следующего вектора.
Далее будем складывать векторы по очереди: чтобы построить сумму векторов \(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\), сначала по правилу треугольника построим вектор \(\overrightarrow{a}+\overrightarrow{b}\), затем вектор \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\), и, наконец, вектор \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c})+\overrightarrow{d}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\).
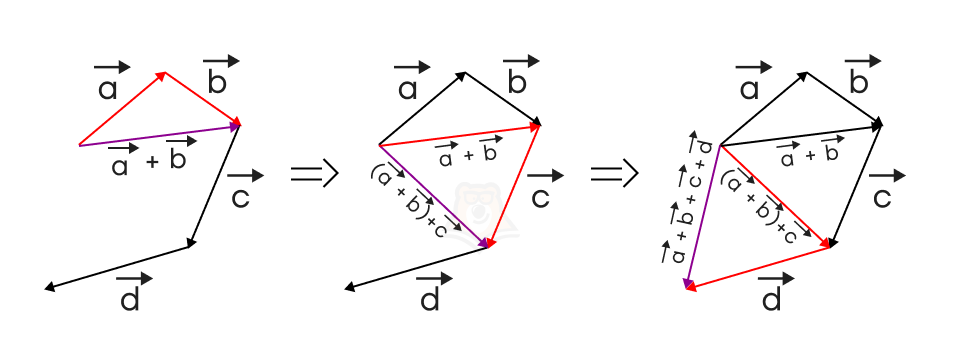
Как видим, полученный вектор \(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}+\overrightarrow{d}\) соединяет начало первого вектора \(\overrightarrow{a}\) с концом последнего вектора \(\overrightarrow{d}\).
В этом и заключается правило многоугольника: сумма некоторого количества векторов, расположенных таким образом, что конец каждого вектора, кроме последнего, совпадает с началом следующего, есть вектор, проведенный из начала первого вектора в конец последнего вектора.

Это правило действует на абсолютно любое количество векторов.
Правила треугольника, параллелограмма, многоугольника действуют для неколлинеарных векторов. Как же быть, если векторы коллинеарны?
На самом деле, для коллинеарных векторов построить вектор суммы еще проще. Для этого достаточно вспомнить, что сумма векторов – это вектор перемещения.
Представим: человек бежит по прямой, пробегает 5 метров, после чего делает остановку, а потом пробегает еще 2 метра. Получается, что в этом же направлении движения он переместился всего на 7 метров. Таким образом, мы сложили два сонаправленных вектора: вектор \(\overrightarrow{a}\) длиной \(|\overrightarrow{a}|=5\) метров и вектор \(\overrightarrow{b}\) длиной \(|\overrightarrow{b}|=5\) метра и получили вектор \(\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}\) длиной \(|\overrightarrow{c}|=|\overrightarrow{a}|+|\overrightarrow{b}|= 7\) метров.
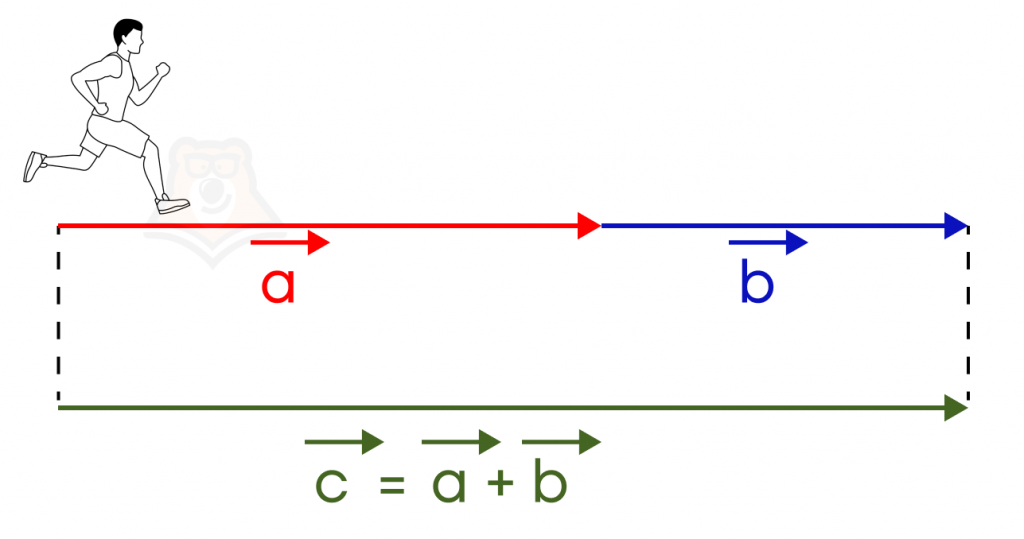
Таким образом, сумма двух сонаправленных векторов есть вектор, сонаправленный этим векторам, а также длина которого равна сумме длин этих векторов.
Отсюда:
- сумма двух равных векторов \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{a}+\overrightarrow{a}=2\overrightarrow{a}\) – это вектор, сонаправленный с вектором a, длина которого в два раза больше длины вектора \overrightarrow{a}, то есть \(|2\overrightarrow{a}|=2|\overrightarrow{a}|\).
- сумма любого вектора \(\overrightarrow{a}\) с нулевым вектором \(\overrightarrow{0}\) есть вектор \(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\)
А что будет, если спортсмен пробежит 5 метров вперед, но после передышки побежит в противоположном направлении и пробежит еще 2 метра. По итогу он переместится с места на 3 метра вперед. Направление здесь определяет вектор с большей длиной. Таким образом, мы сложили два противоположно направленных вектора: вектор \(\overrightarrow{a}\) длиной \(|\overrightarrow{a}|=5\) метров и вектор \(\overrightarrow{b}\) длиной \(|\overrightarrow{b}|=2\) метра и получили вектор \(\overrightarrow{c}=\overrightarrow{a}+\overrightarrow{b}\) длиной \(|\overrightarrow{c}|=|\overrightarrow{a}|-|\overrightarrow{b}|=3\) метра.
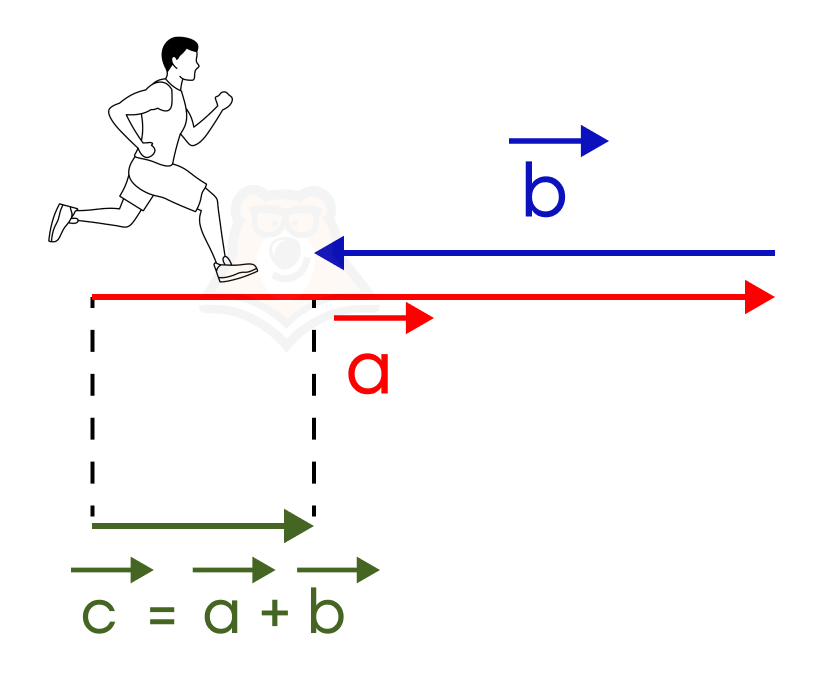
Итак, сумма двух противоположно направленных векторов есть вектор, направление которого совпадает с направлением вектора большей длины, а длина которого равна разности длин этих векторов.
Отсюда: сумма двух противоположных векторов есть нулевой вектор.
Итак, со сложением векторов мы разобрались, идем дальше. Конечно, там, где есть сложение, есть и вычитание.
Разность векторов
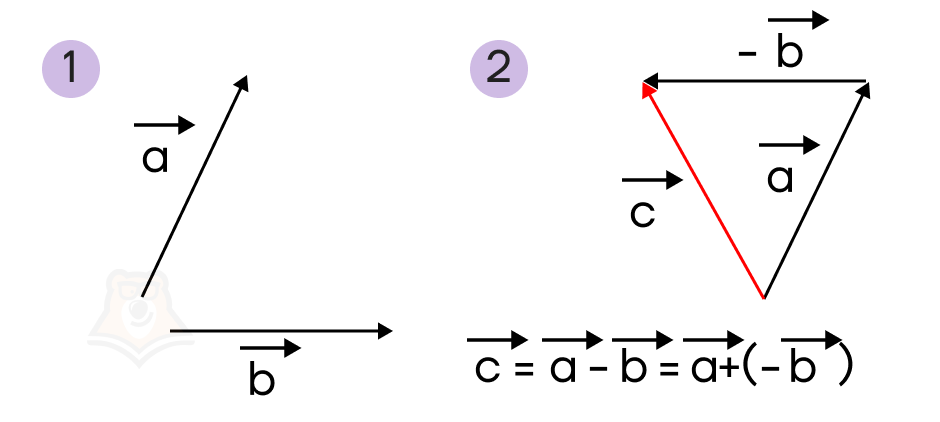
Из статьи «Действия с числами» можно вспомнить, что от вычитания легко можно перейти к сложению: для этого достаточно поменять знак вычитаемого на противоположный.
Так же и с вычитанием векторов: чтобы из вектора \(\overrightarrow{a}\) вычесть вектор \(\overrightarrow{b}\), достаточно к вектору \(\overrightarrow{a}\) прибавить вектор, противоположный вектору \(\overrightarrow{b}\):
\(\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\)
Перейдя от вычитания к сложению, можно воспользоваться правилами для сложения векторов: правило треугольника, параллелограмма или многоугольника, а также правила сложения коллинеарных векторов.

Например, на рисунке ниже показано построение вектора \(\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}\).
Двигаемся дальше по нашему вектору. Следующая станция – «Законы сложения векторов».
Законы сложения векторов
- \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\) – переместительный закон сложения.
Чтобы убедиться в этом, сначала построим вектор \(\overrightarrow{a}+\overrightarrow{b}\), а затем вектор \(\overrightarrow{b}+\overrightarrow{a}\).
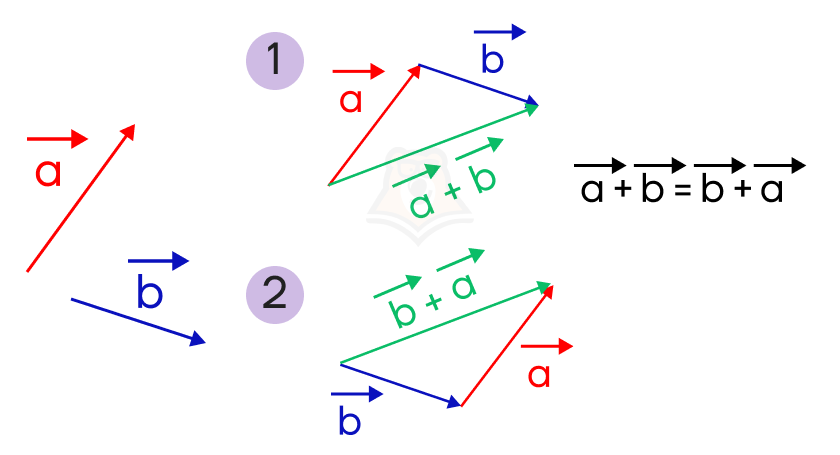
Видим, что получившиеся векторы \(\overrightarrow{a}+\overrightarrow{b}\) и \(\overrightarrow{b}+\overrightarrow{a}\), действительно, равны друг другу, то есть \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}\).
\((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\) – сочетательный закон сложения.
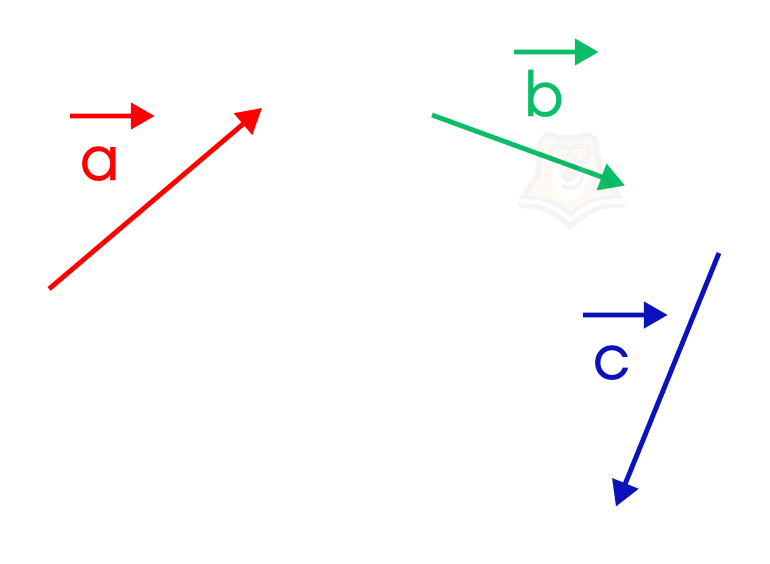
Для доказательства этого закона построим отдельно векторы \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\) и \(\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\). При построении сначала будем выполнять сложение в скобках, пользуясь правилом треугольника, а затем сложение вне скобок. Итак, для начала у нас есть три вектора \(\overrightarrow{a}, \overrightarrow{b}\) и \(\overrightarrow{c}\):
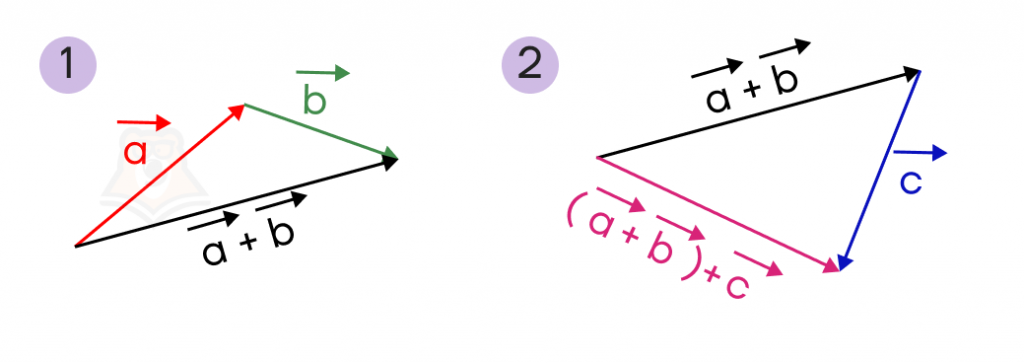
Построим вектор \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\). Для этого сначала выполним сложение векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) , а затем сложим получившийся вектор с вектором \(\overrightarrow{c}\):
Аналогично построим вектор \(\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\). Сначала выполним сложение векторов \(\overrightarrow{b}\) и \(\overrightarrow{c}\), а затем сложим вектор \(\overrightarrow{a}\) с получившимся вектором:
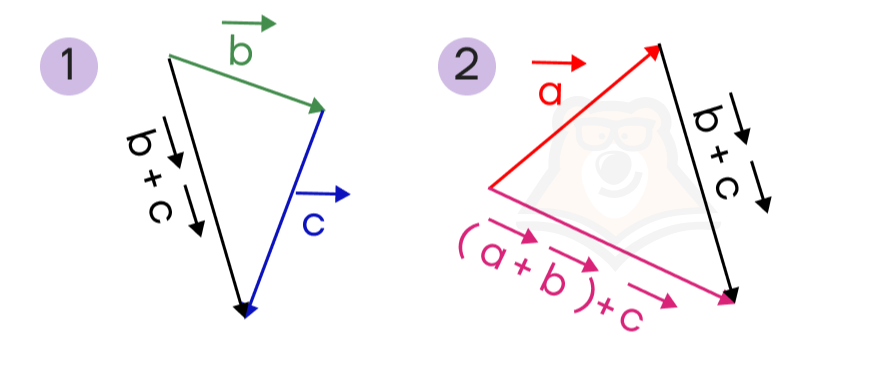
Видим по векторам \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}\)и \(\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\), что они сонаправлены и их длины равны. Значит, эти векторы будут равны друг другу, то есть \((\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})\).
На этом вектор данной статьи подходит к своему завершению. Двумя буквами его обозначить будет сложно, ведь было много важной и полезной информации: начиная от понятия вектора, заканчивая сложением и вычитанием векторов.
Тема векторы очень многогранная и не может ограничиться даже всем тем, что было разобрано в этой статье. Продолжить же изучение векторов можно в статье «Векторы. Часть 2».
Термины
Гипотенуза – сторона, которая лежит напротив прямого угла в прямоугольном треугольнике.
Катеты – стороны, которые образуют прямой угол в прямоугольном треугольнике.
Параллельные прямые – это прямые, не имеющие общей точки.
Фактчек
- Вектор – это отрезок, который имеет заданные начало и конец.
- Коллинеарные векторы – это векторы, лежащие на одной или на параллельных прямых. Они могут быть сонаправленными и противоположно направленными. Выделяют также ортогональные векторы – векторы, угол между которыми равен 90°.
- Векторы могут быть равными, если они сонаправлены и их длины равны, и противоположными, если их длины равны, но они направлены в противоположные стороны.
- Для сложения векторов применяются правила треугольника, параллелограмма или многоугольника.
- Чтобы вычесть из одного вектора другой, можно от вычитания перейти к сложению, заменив второй вектор на противоположный.
Проверь себя
Задание 1.
Какие векторы изображены на картинке?
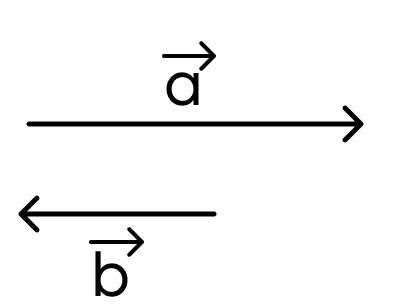
- сонаправленные
- противоположно направленные
- равные
- противоположные
Задание 2.
Какие векторы изображены на картинке?
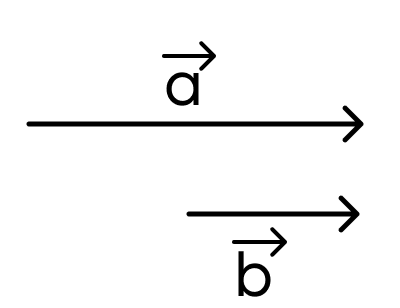
- сонаправленные
- противоположно направленные
- равные
- противоположные
Задание 3.
Выберите верное утверждение для векторов на картинке
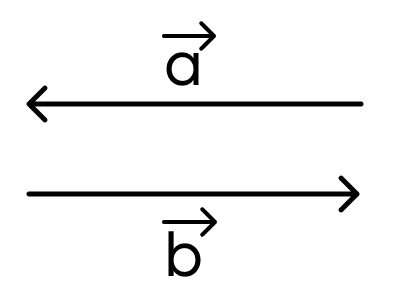
- вектора сонаправленные
- вектора равные
- это нулевые вектора
- длины данных векторов равны
Задание 4.
Какие векторы изображены на картинке?
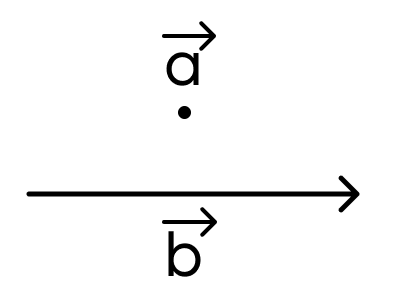
- равные
- противоположно направленные
- сонаправленные
- противоположные
Ответы: 1. – 2; 2. – 1; 3. – 4; 4. – 3


 к списку статей
к списку статей






