Периметр, площадь и объем

На этой странице вы узнаете

• Как с помощью линейки и циркуля построить квадрат, который будет равен окружности по площади? 
• Почему площадь, периметр и объем обозначаются буквами P, S и V?
• А что после трехмерного пространства?

Периметр, площадь и объем встречались нам на протяжении всего обучения в школе. Да и в жизни они нам встречаются, ведь мы живем в пространстве. Настал момент собрать все формулы и знания воедино и узнать, как решать экзаменационные задания на эти темы.

Но прежде чем начнем, вот ссылки на статьи по фигурам и телам, про которые будем сегодня говорить:

• Треугольник
• Параллелограмм
• Трапеция
• Многоугольник
• Окружность
• Призма
• Пирамида
• Цилиндр
• Конус
• Шар

Так, с этим разобрались. Теперь приступим к нашей теме! 

Периметр

Все мы еще в начальной школе проходили, что периметр — сумма длин всех сторон. Это работает для всех фигур, кроме окружности. Теперь вспомним формулы из школьной программы.

Квадрат:

• \(P = 4a\)
• \(P = 2\sqrt{2d}\)

где a — длина стороны квадрата, d — длина диагонали квадрата.

Параллелограмм:

• \(P = 2(a+b)\)

где a и b — длины сторон параллелограмма.

Прямоугольник:

• \(P = 2(a+b)\)

где a и b — длины сторон прямоугольника. 

Прямоугольник — частный случай параллелограмма, поэтому периметры считаются одинаково.

Треугольник:

• \(P = a+b+c\)

где a, b и c — длины сторон треугольника.

Окружность:

• \(P = 2\pi r\)
• \(P =\pi d\)

где r — радиус окружности, d — диаметр окружности, — число пи, равное примерно 3,14.

Трапеция:

• \(P = a+b+c+d\)

где a и b — длины оснований трапеции, c и d — длины боковых сторон трапеции.

Ромб:

• \(P = 4a\)

где a — длина стороны ромба.

Как с помощью линейки и циркуля построить квадрат, который будет равен окружности по площади?  Спойлер: никак. Эта задача называется квадратурой круга, и она является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки.  Над ней бились сотни лет такие ученые, как Архимед, Фибоначчи, да Винчи, Гюйгенс и другие. Никому так и не удалось решить эту задачу. В 1882 году Линдеман, немецкий математик, доказал неразрешимость квадратуры круга.

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №1.

Задание. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 10. Найдите периметр этого квадрата.

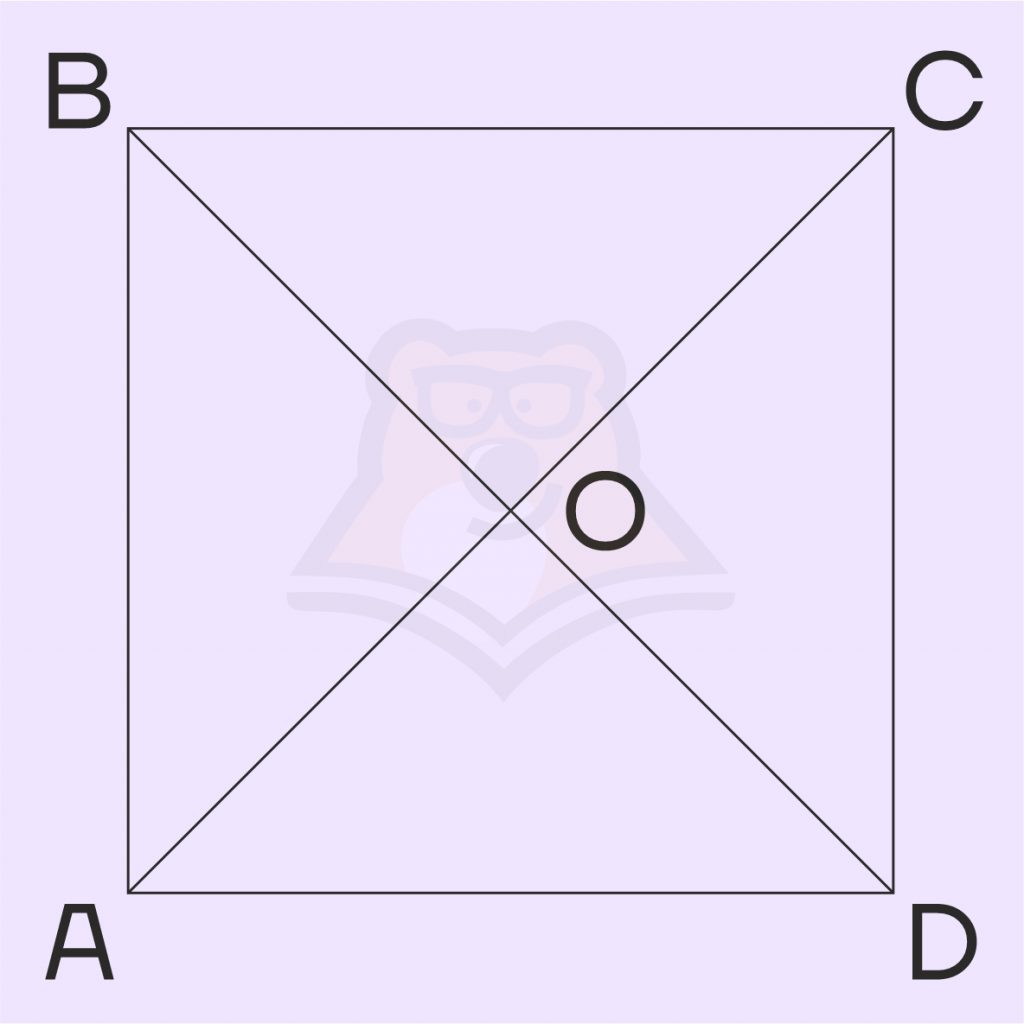
Решение. Под расстоянием обычно понимают перпендикуляр от точки до стороны. Соединим перпендикуляром точку пересечения диагоналей и сторону:

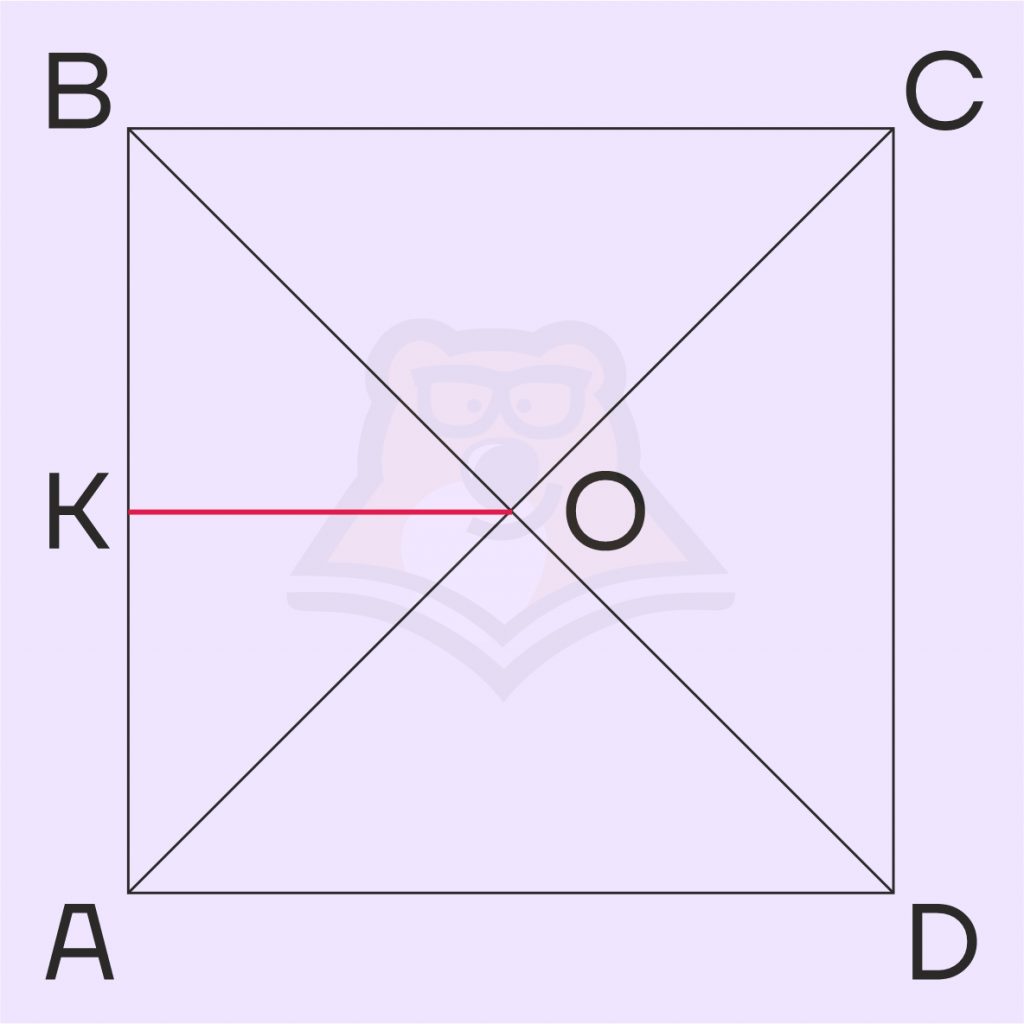
Как мы можем заметить, получившейся отрезок OK равен половине стороны. Значит, сторона квадрата равна 20. Найдем периметр:

\(P = 4a\)
\(P = 4*20 = 80\)

Ответ: 80

С периметрами разобрались, теперь перейдем к площадям.

Метод площадей

Площадь — мера двумерного пространства, которое занимает фигура внутри своих границ. Измеряется в квадратных сантиметрах (см2), квадратных метрах (м2), квадратных километрах (км2) и так далее.

Давайте вспомним основные формулы площадей из школьной программы.

Квадрат:

• \(S = a^2\)
• \(S =\frac{1}{2}d^2\)
• \(S = 4r^2\)
• \(S = 2R^2\)

где a — длина стороны квадрата, d — длина диагонали квадрата, r — радиус вписанной окружности, R — радиус описанной окружности.

Прямоугольник:

• \(S = ab\)

где a и b — длины сторон прямоугольника.

Треугольник:

• \(S =\frac{1}{2}ah\). Здесь важно, что высота h проведена именно к стороне a. 
• Формула Герона: \(S =\sqrt{p(p-a)(p-b)(p-c)}\)
• \(S =\frac{1}{2}ab*sin(γ)\)
• \(S = pr\)
• \(S =\frac{abc}{4R}\)

где a, b и c — длины сторон треугольника, h — высота треугольника, p — полупериметр треугольника, γ — угол между сторонами a и b, r — радиус вписанной окружности, R — радиус описанной окружности.

Окружность:

• \(S =\pi r^2\)
• \(S =\frac{1}{4}d^2\)

где r — радиус окружности, d — диаметр окружности, — число пи, равное примерно 3,14.

Трапеция:

• \(S =\frac{1}{2}(a+b)h\)

где a и b — длины оснований трапеции, h — высота трапеции.

Параллелограмм:

• \(S =ah \)
• \(S = ab*sin(α)\)

где a и b — длины сторон параллелограмма, h — высота параллелограмма, α — угол между сторонами a и b.

Ромб:

• \(S = ah\)
• \(S =\frac{1}{2}d_1d_2\)

где a — длина стороны ромба, h — высота ромба, \(d_1\) и \(d_2\) — диагонали ромба.

Итак, мы вспомнили формулы. Но мы так и не узнали, что же такое метод площадей.

Метод площадей — метод решения геометрических задач с помощью подсчета площадей фигур разными способами. 

Рассмотрим свойства метода площадей.

1. Если вершину треугольника передвигать по прямой, которая параллельна основанию, то площадь не изменится.

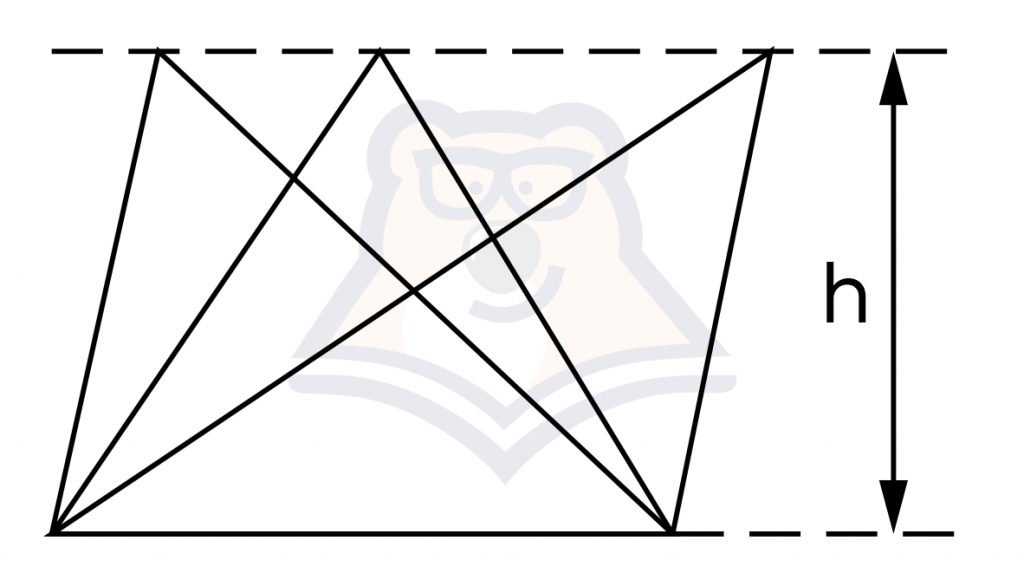
2. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин сторон, на которые опущены эти высоты.

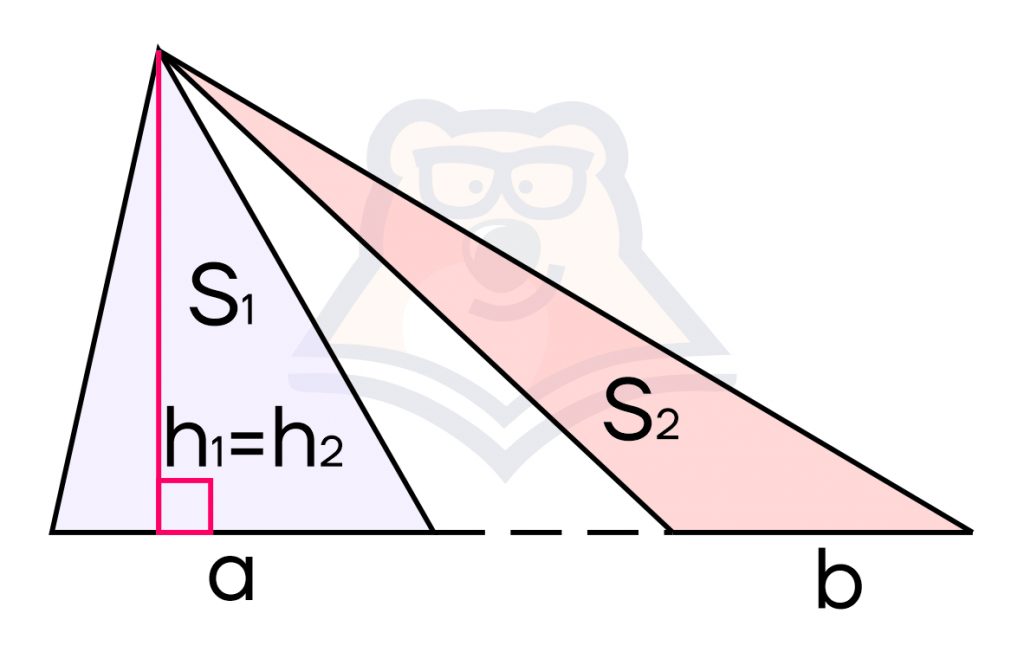
\(\frac{S_1}{S_2}=\frac{a}{b}\)

Доказательство: Пусть \(h_1=h_2\), тогда отношение площадей треугольников:

\(\frac{S_1}{S_2}=\frac{\frac{1}{2}*a*h_1}{\frac{1}{2}*b*h_2}\)

После упрощения получаем:

\(\frac{S_1}{S_2}=\frac{a}{b}\)

Так же доказывается и следующее свойство.

3. Если два треугольника имеют одинаковые стороны, то отношение площадей равно отношению высот, которые к этим сторонам проведены.

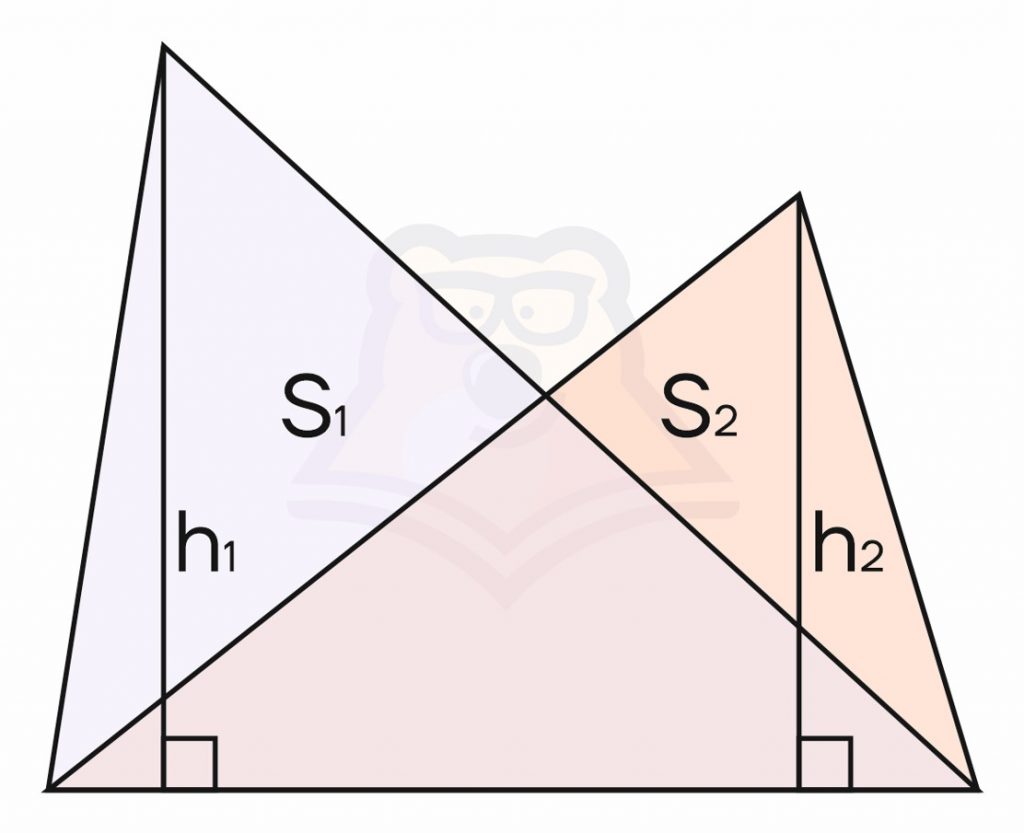
\(\frac{S_1}{S_2}=\frac{h_1}{h_2}\)

4. У подобных треугольников отношение площадей равно квадрату коэффициента подобия. 

Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников. Об этом мы рассказывали в статье про равенство и подобие треугольников.

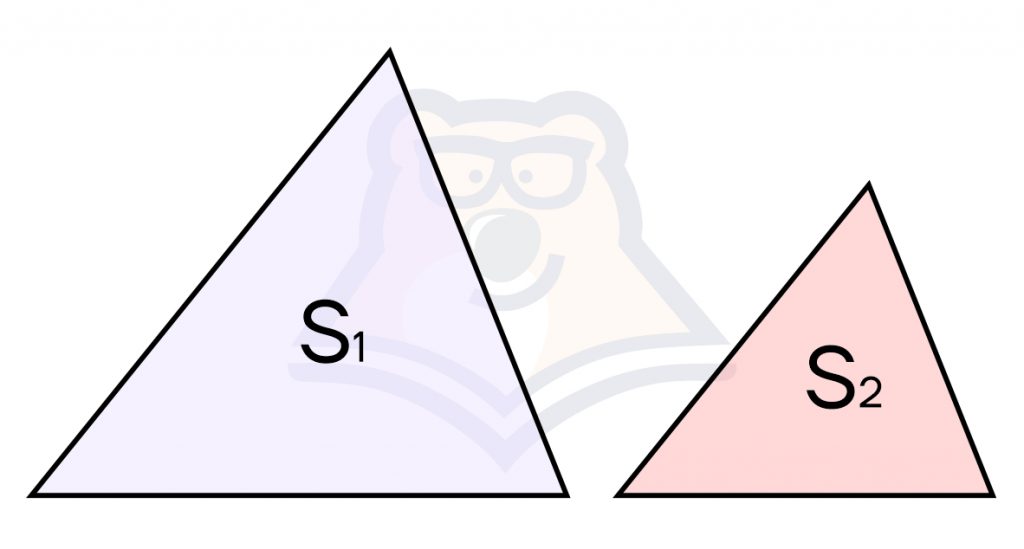
\(\frac{S_1}{S_2}=k^2\)

5. Все средние линии треугольника делят его на четыре маленьких треугольника, у которых равные площади. 

Средняя линия треугольника — отрезок, который соединяет середины двух сторон.

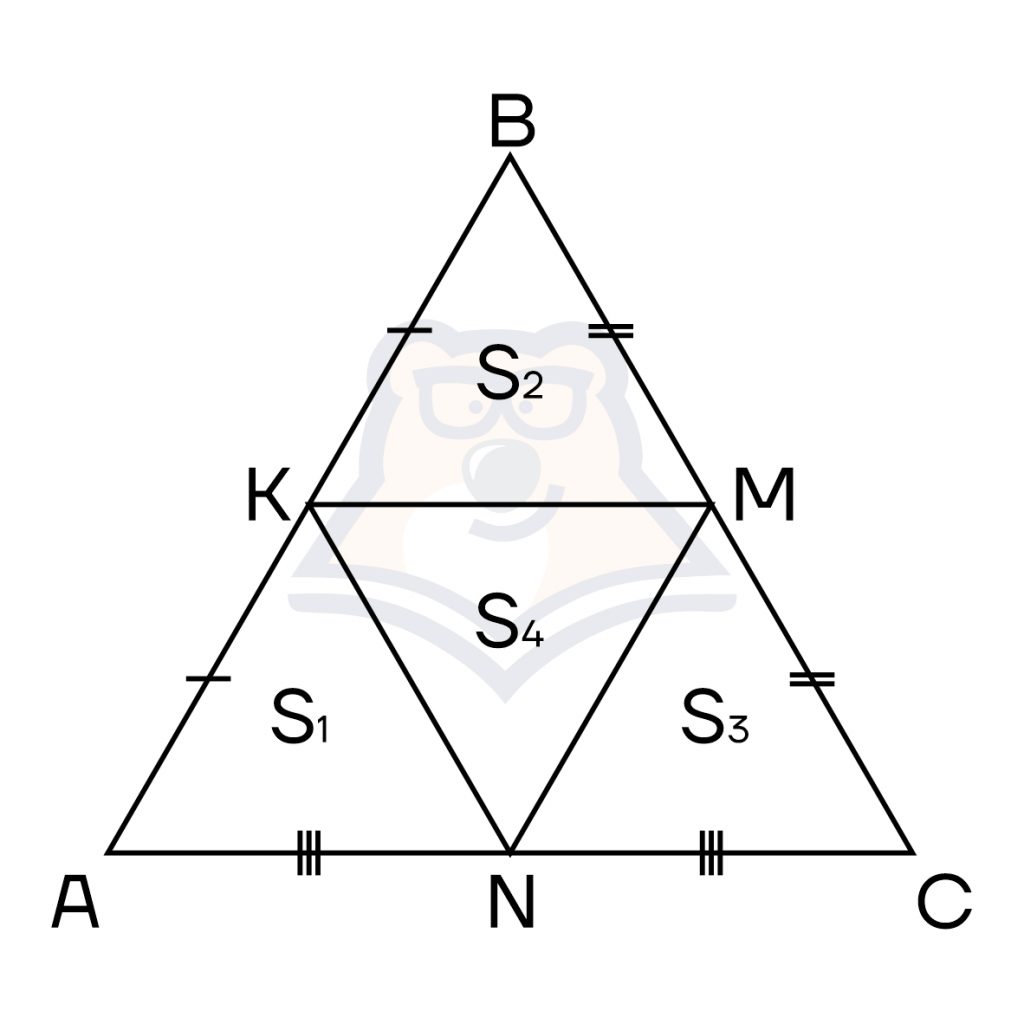
\(S_1=S_2=S_3=S_4=\frac{1}{4}S\)

6. Если два треугольника имеют по равному углу, то их площади относятся как произведения сторон, которые заключают эти углы.

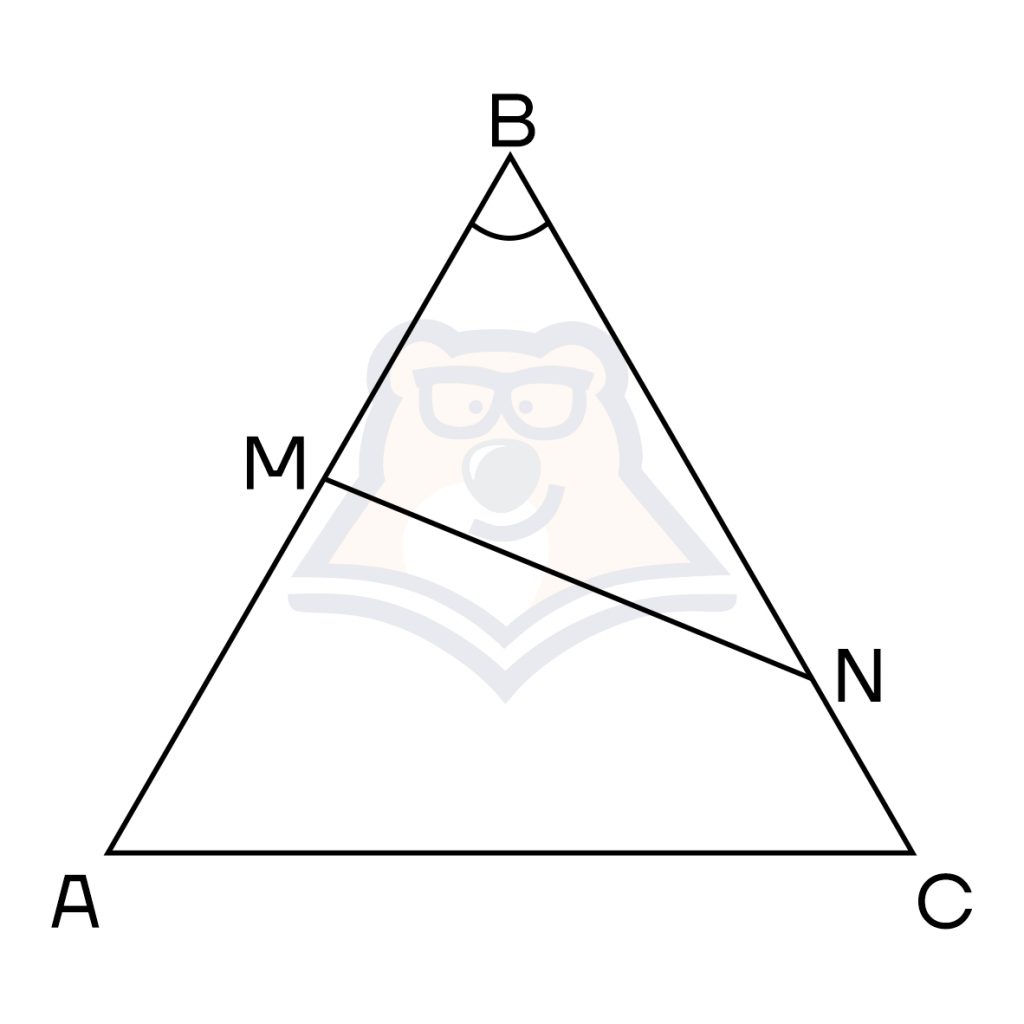
\(\frac{S_{ABC}}{S_{MBN}}=\frac{AB*BC}{MB*BN}\)

Теперь решим задачу, чтобы отработать метод площадей.

Такое задание может попасться на ЕГЭ по профильной математике в №17. Решим только пункт а.

Задание. Диагонали AC и BD трапеции ABCD пересекаются в точке O, BC и AD  — основания трапеции.

а) Докажите, что \(\frac{S_{DOC}}{S_{AOD}}=\frac{BC}{AD}\)
б) Найдите площадь трапеции, если \(AD  =  4BC, S_{OCD} = 2\)

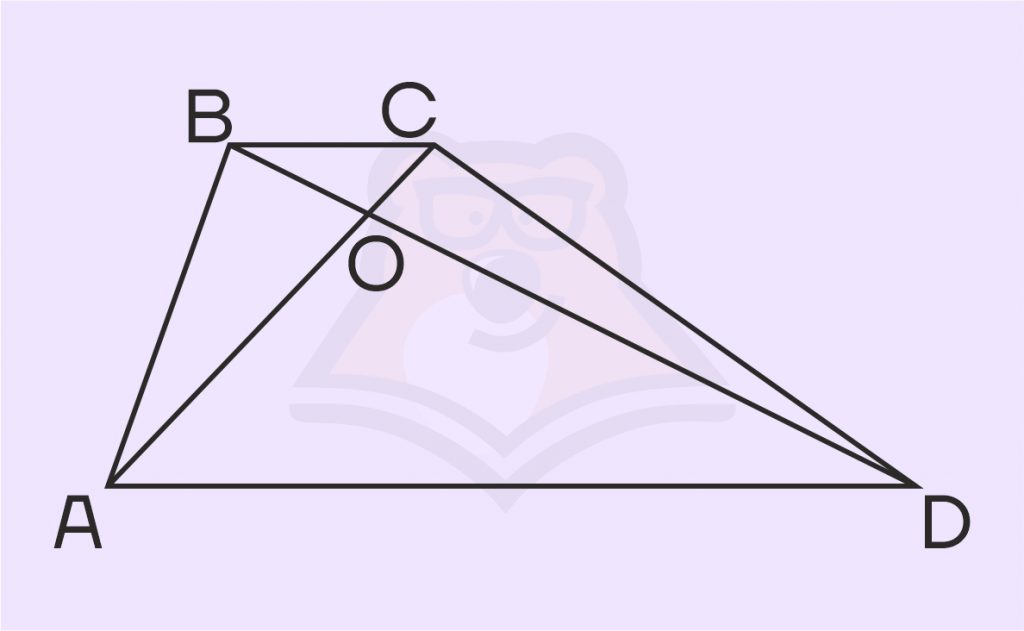
Решение. а) У треугольников AOD и DOC есть общая высота, проведенная из вершины D. Значит, что их площади относятся так же, как основания, к которым проведена высота, как это было в нашем втором свойстве метода площадей:

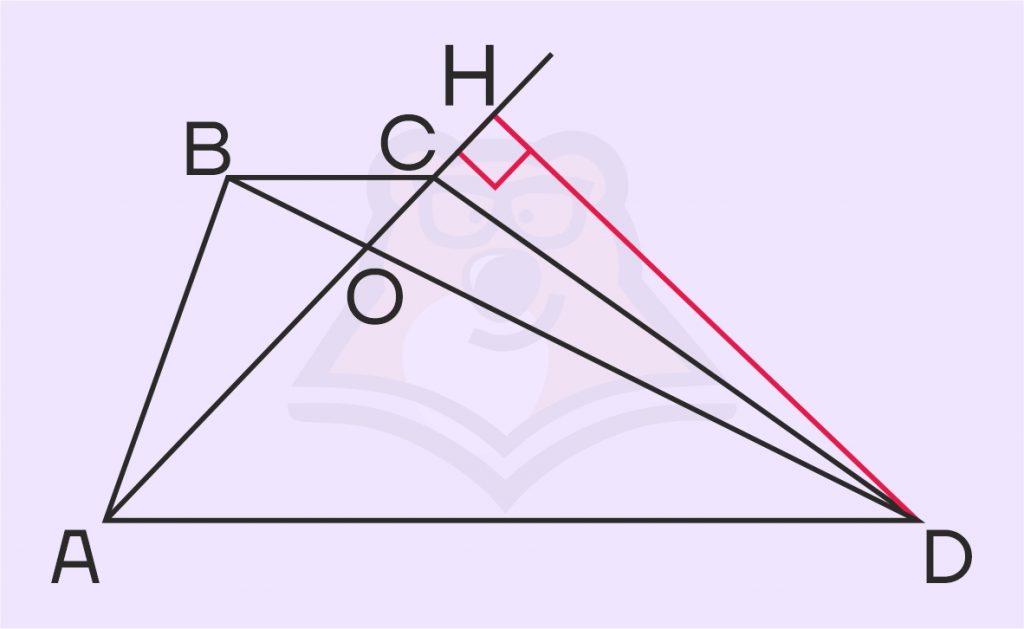
Значит, получаем:

\(\frac{S_{DOC}}{S_{AOD}}=\frac{CO}{AO}\)

Теперь рассмотрим треугольники AOD и BOC. Угол CAD равен углу BCA, а угол ADB равен углу CBD, так как они накрест лежащие: BC и AD параллельны, так как это основания трапеции, а отрезки AC и BD — секущие. Повторить тему параллельных прямых можете в статье про основы планиметрии. 

Следовательно, треугольники AOD и BOC подобны. Значит, 

\(\frac{BC}{AD}=\frac{CO}{OA}=\frac{BO}{OD}\)

Так как \(\frac{S_{DOC}}{S_{AOD}}=\frac{CO}{AO}\) и \(\frac{BC}{AD}=\frac{CO}{OA}\), то \(\frac{S_{DOC}}{S_{AOD}}=\frac{BC}{AD}\).
Что и требовалось доказать.

С методом площадей разобрались, осталось самое на первый взгляд сложное — метод объемов.

Метод объёмов

Объем — мера трехмерного пространства, которое занимает тело внутри своих границ. Измеряется в кубических сантиметрах (\(см^3\)), кубических метрах (\(м^3\)) и так далее.

Почему площадь, периметр и объем обозначаются буквами P, S и V? Периметр обозначается заглавной латинской буквой P, так как происходит от английского слова Perimeter. Площадь — латинской буквой S, так как происходит от слова Square. А объем — латинской буквой V, так как происходит от Volume.

Давайте вспомним основные формулы объема и площади поверхности из школьной программы.

Куб:

• \(V = a^3\)
• \(S = 6a^2\)

где a — длина ребра куба.

Параллелепипед:

• \(V = S_{осн}*h\)
• \(S =2S_{осн}+S_{бок}\)

где \(S_{осн}\) — площадь основания, \(h\) — высота, \(S_{бок}\) — площадь боковой поверхности. 

Прямоугольный параллелепипед:

• \(V = abc\)
• \(S = 2ab+2ac+2bc\)

где a, b и c — длины ребер прямоугольного параллелепипеда.

Призма:

• \(V = S_{осн}*h\)
• \(S =2S_{осн}+S_{бок}\)

где \(S_{осн}\) — площадь основания, \(h\) — высота, \(S_{бок}\) — площадь боковой поверхности.

Пирамида:

• \(V =\frac{1}{3}S_{осн}*h\)
• \(S =S_{осн}+S_{бок}\)

где \(S_{осн}\) — площадь основания, \(h\) — высота, \(S_{бок}\) — площадь боковой поверхности.

Цилиндр:

• \(V =\pi R^2h \)
• \(S =2S_{осн}+S_{бок}=2\pi R^2+2\pi Rh\)

где R — радиус оснований, h — высота, \(S_{осн}\) — площадь оснований, \(S_{бок}\) — площадь боковой поверхности, \(\pi\) — число пи, равное примерно 3,14.

Конус:

• \(V =\frac{1}{3}S_{осн}*h\)
• \(S =2S_{осн}+S_{бок}=\pi R^2+\pi RL\)

где \(S_{осн} — площадь основания, h — высота, R — радиус основания, L — образующая, \(\pi\) — число пи, равное примерно 3,14.

Шар:

• \(V =\frac{4}{3}\pi R^3\)
• \(S =4\pi R^2\)

где R — радиус, \(\pi\) — число пи, равное примерно 3,14.

Супер, с формулами разобрались, переходим к методу объемов.

Метод объемов применяется, когда мы записываем объем какой-нибудь фигуры двумя разными способами и с помощью этого находим определенную величину. 

Чтобы лучше понять принцип метода объемов, решим задачу. 

Решим задание, которое может попасться на ЕГЭ по профильной математике в задании №14. Мы решим только пункт б.

Задание. В правильной треугольной пирамиде SABC с основанием ABC боковое ребро равно 20, а сторона основания равна 24.
а) Докажите, что высоты пирамиды, проведенные из вершин A и S, пересекаются в одной точке.
б) Найдите расстояние от вершины A до плоскости SBC.

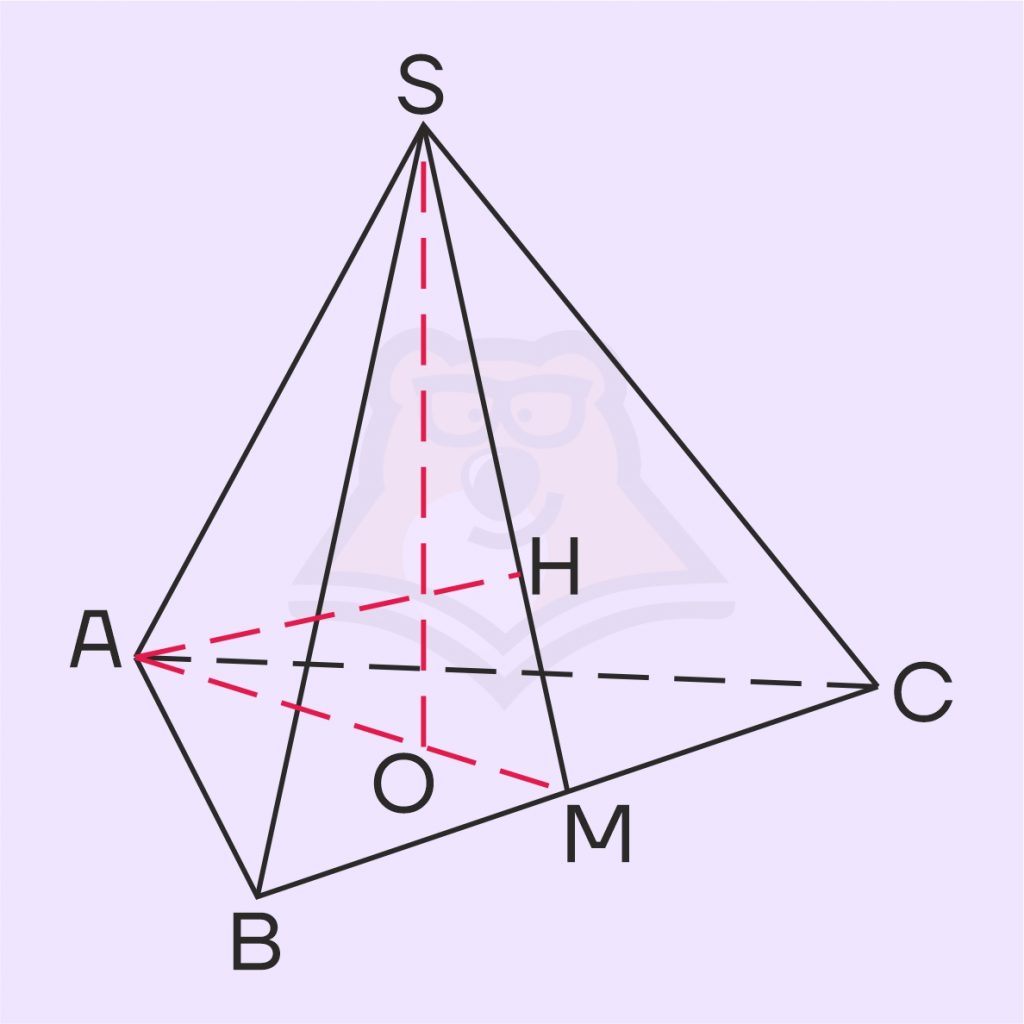
Решение. б)SO  — высота пирамиды. Чтобы найти эту высоту, нам нужны AS и OA. AS знаем по условию задачи, этот отрезок равен 20. Найдем OA, используя формулу нахождения расстояния от вершины до точки пересечения высот треугольника через сторону и угол в треугольнике ABC.

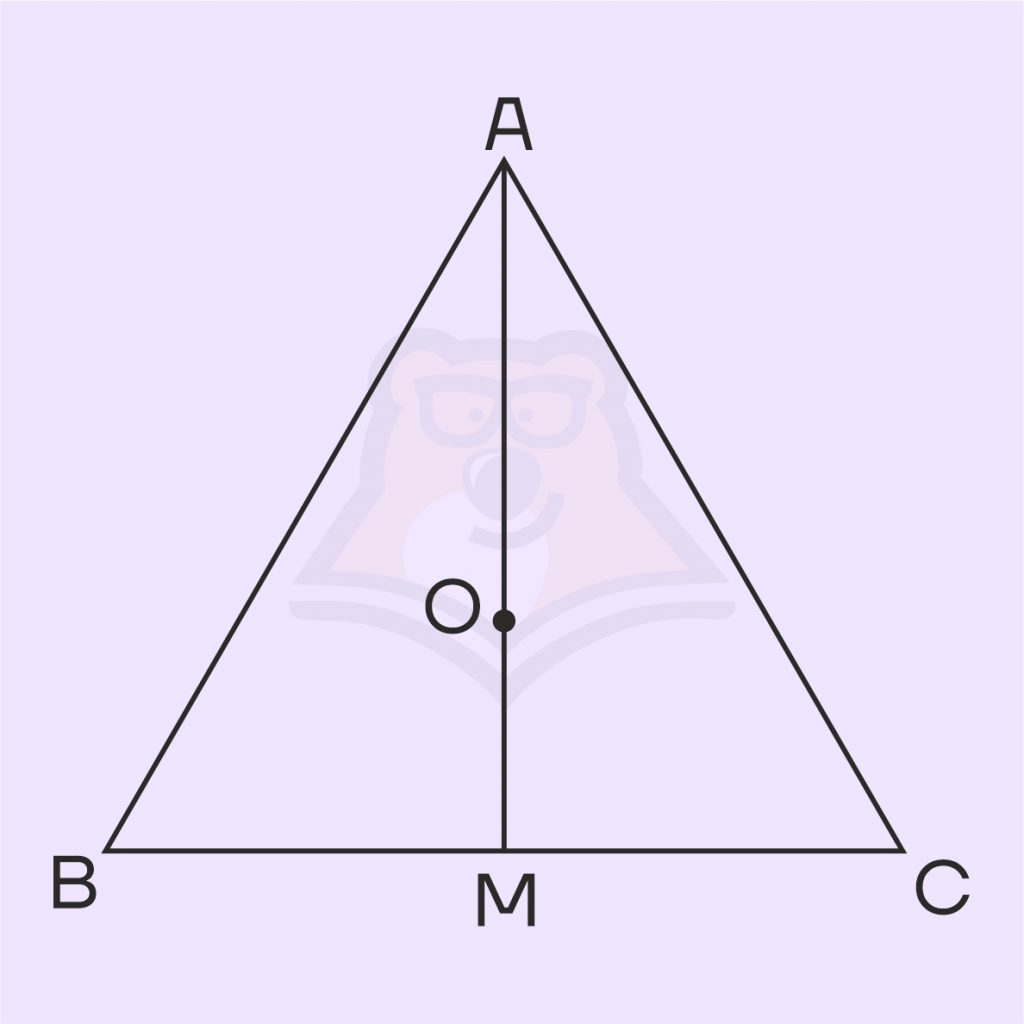
\(AO =BC*|ctg(A)|\)

BC – сторона основания, равная 12, а угол A равен 60°, так как в основании правильный треугольник. 

\(AO =24*\frac{\sqrt{3}}{3}=8\sqrt{3}\)

Найдем SO по теореме Пифагора:

\(SO =\sqrt{AS^2-AO^2}=\sqrt{400-192}=\sqrt{208}=4\sqrt{13}\)

Формула объема пирамиды: 

\(V =\frac{1}{3}S_{осн}*h\)

Найдем площадь основания, по совместительству площадь правильного треугольника:

\(S_{осн}=\frac{a^2\sqrt{3}}{4}\)
\(S_{осн}=\frac{24^2\sqrt{3}}{4}=144\sqrt{3}\)

Теперь найдем объем:

\(V =\frac{1}{3}*144\sqrt{3}*4\sqrt{13}=192\sqrt{39}\)

Теперь воспользуемся методом объемов. Мы знаем, что объем пирамиды SABC можно найти и другим способом:

\(V =\frac{1}{3}S_{BSC}*AH\)

AH — расстояние от точки A до плоскости BSC, которое нам нужно найти. Соответственно, нам нужно найти площадь треугольника \(S_{BSC}\). Найдем высоту SM по теореме Пифагора:

\(SM =\sqrt{SB^2-BM^2}=\sqrt{400-144}=\sqrt{256}=16\)

Площадь треугольника SBC равна:

\(S_{SBC}=\frac{1}{2}SM*BC=\frac{1}{2}*16*24=192\)

Наконец, можем найти AH:

\(V =\frac{1}{3}S_{BSC}*AH\)
\(AH =\frac{3V}{S_{BSC}}=\frac{3*192\sqrt{39}}{192}=3\sqrt{39}\)

Ответ: \(3\sqrt{39}\)

В предыдущем примере мы использовали формулу объема треугольной пирамиды, только для разных высот и оснований, с помощью чего у нас и получилось найти расстояние от вершины до плоскости. По такой же логике можно найти и угол между прямой и плоскостью, угол между плоскостями и расстояние между скрещивающимися прямыми.

А что после трехмерного пространства? Четырехмерное, конечно. Физики выделяют время как четвертое измерение, и такая физическая модель называется пространство-время. Ну а как представить себе четырехмерное пространство, в котором четвертое измерение — геометрическое, а не время? Никак. Как Марио и Пакман, которые находятся в двумерном пространстве, не смогли бы себе представить третье измерение и увидеть игрока, так и мы не можем представить четвертое.

В этой статье мы разобрали, что такое периметр, метод площадей и объемов. В следующей статье мы узнаем, как решать линейные и квадратные уравнения и неравенства с параметрами.

Фактчек

• Периметр — длина границы фигуры.
• Площадь — мера двумерного пространства, которое занимает фигура.
• Объем — мера трехмерного пространства, которое занимает тело.
• Методы площадей и объемов помогают решать задачи с помощью подсчета площади или объема разными способами. 
• С помощью метода объемов можно находить угол между прямой и плоскостью, угол между плоскостями, расстояние между скрещивающимися прямыми и расстояние между точкой и плоскостью.

Проверь себя

Задание 1.
Как называется мера трехмерного пространства, которое занимает тело?

1. Периметр
2. Площадь
3. Метод площадей
4. Объем

Задание 2.
В каком варианте ответа дана формула площади НЕ треугольника?

1. \(S =\frac{1}{2}ah\)
2. \(S =\sqrt{p(p-a)(p-b)(p-c)}\)
3. \(S =\frac{1}{2}d_1d_2\)
4. \(S = pr\)

Задание 3.
В чем измеряют объем?

1. В сантиметрах
2. В квадратных сантиметрах
3. В кубических сантиметрах
4. В Ньютонах

Задание 4.
Объем какого тела находится по формуле \(V =\frac{1}{3}S_{осн}*h\)?

1. Пирамиды
2. Призмы
3. Шара
4. Куба

Ответы: 1. — 4; 2. — 3; 3. — 3; 4. — 1.