Действия с числами

На этой странице вы узнаете:

• Решать последовательно нельзя менять местами — что это значит?  
• Как выполнять действия с числами разных знаков? 
• В каких случаях правильно будет пойти против правил? 

Что будет, если сначала надеть куртку, а затем свитер? Или поставить выпекаться тесто, а потом его перемешать? Нарушение порядка действий влечет за собой плачевный результат. Так и в математике: решать примеры необходимо в строго определенном порядке, иначе получить верный ответ будет невозможно. Тому, как правильно это делать, посвящена наша статья.

Порядок выполнения действий с числами

В математике, как и в жизни, почти не встречаются вычисления в одно действие. Как уже было сказано, ошибка в последовательности счета приводит к неверному ответу.

1. Если в примере только сложение или вычитание, то действия выполняются в порядке слева направо. 

Например, 

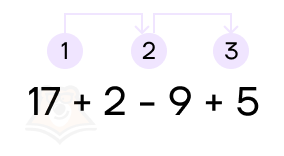
1. Сначала складываем 17 и 2, получаем 19 – 9 + 5.
2. Теперь вычитаем 9 из 19 и получаем 10 + 5.
3. Складываем полученные числа: 10 + 5 = 15.

Если в примере только умножение или деление, то действия выполняются в порядке слева направо.

Например,

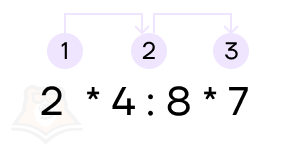
1. Сначала умножаем 2 на 4, получаем 8 : 8 * 7.
2. Делим 8 на 8, получаем 1 * 7. 
3. Умножаем 1 на 7: 1 * 7 = 7. 

Получаем: 2 * 4 : 8 * 7 = 8 : 8 * 7 = 1 * 7 = 7

Но что делать, если в примере и сложение, и вычитание, и деление, и умножение? Для дальнейших рассуждений необходимо ввести новые понятия:

Действия первой ступени — это сложение и вычитание, которые выполняются слева направо. 

Действия второй ступени — это умножение и деление, которые выполняются слева направо.

2. Если в примере встречаются действия и первой, и второй ступени, то для вычислений необходимо пользоваться следующим порядком: 

• Сначала выполняются действия второй ступени по порядку слева направо.
• После выполняются действия первой ступени по порядку слева направо.

Например,   

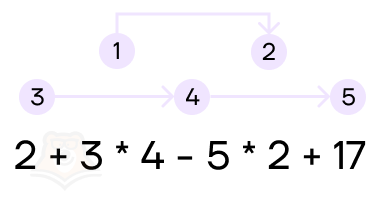
 Получаем: 2 + 3 * 4 — 5 * 2 + 17 = 2 + 12 — 10 + 17 = 14 — 10 + 17 = 4 + 17 = 21. 

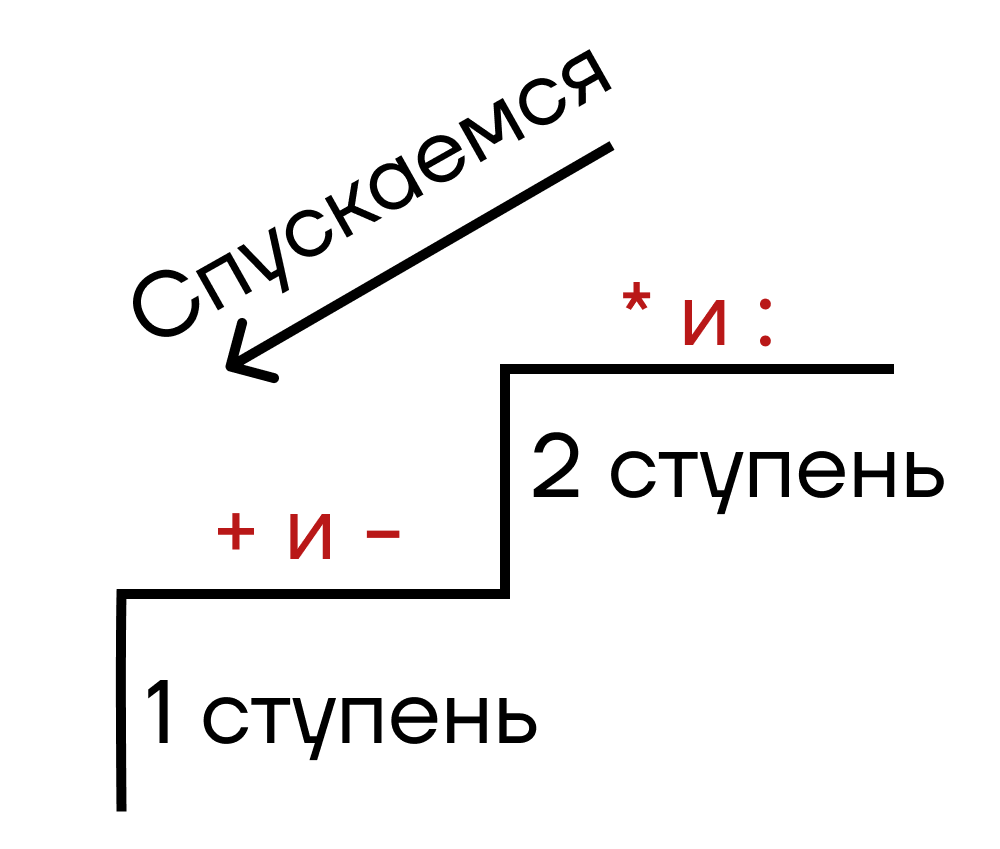
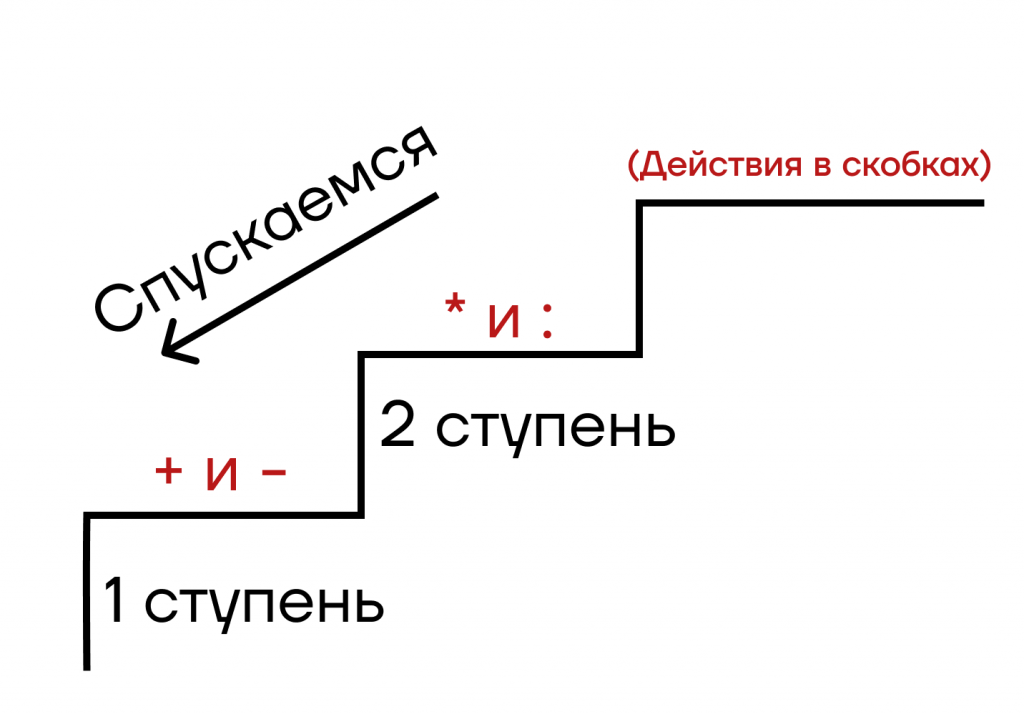
Это можно сравнить со спуском по лестнице. На второй снизу ступеньке у нас стоят умножение и деление, а на первой — сложение и вычитание. И если мы спускаемся по такой лестнице, то мы не можем перескочить сразу через ступень (если, конечно, не хотим упасть).

Рассмотрим порядок выполнения арифметических действий в выражениях со скобками. 

3. Если в примере появляются скобки.

• Сначала считаются действия в скобках. При этом соблюдается такой же порядок, как и в выражениях без скобок, то есть сначала действия второй ступени, а после — первой. 
• После выполняются действия вне скобок, сохраняя правильный порядок счета. 

Например,
20 — 3 + (4 * 8 — 2 * 3) + 3 * 6 = 
= 20 — 3 + (32 — 6) + 3 * 6 = 
= 20 — 3 + 26 + 3 * 6 = 
= 20 — 3 + 26 + 18 = 
= 17 + 26 + 18 = 
= 43 + 18 = 61. 

Так к нашей лесенке добавляется еще одна ступень со скобками. И теперь мы начинаем спускаться с третьей ступеньки.

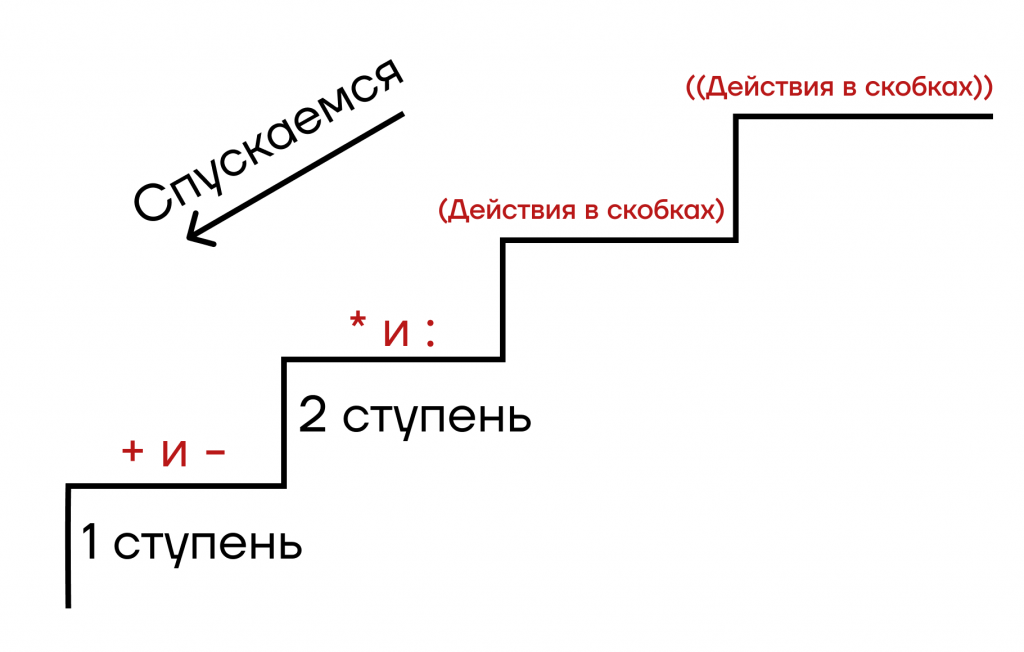
Если в выражении появляется скобка в скобке, то сначала выполняются действия во внутренней скобке, а после – во внешней: 

1 + (12 — 3 * 2 + (24 — 3 * 6)) = 
= 1 + (12 — 3 * 2 + (24 — 18)) = 
= 1 + (12 — 3 * 2 + 6) = 
= 1 + (12 — 6 + 6) = 
= 1 + 12 = 13. 

И это уже четвертая ступенька!

4. Если в выражении появляются степени, корни или другие функции. 

• Сначала считаются значения функций. 
• Дальше вычисляются значения в скобках, сохраняя правильный порядок счета.
• Потом выполняются действия вне скобок, сохраняя правильный порядок счета. 

Например,
2³  + 12 — √4 — 2 * 3 = 
= 8 + 12 — 2 — 2 * 3 = 
= 8 + 12 — 2 — 6 = 
= 20 — 2 — 6 = 
= 18 — 6 = 12. 

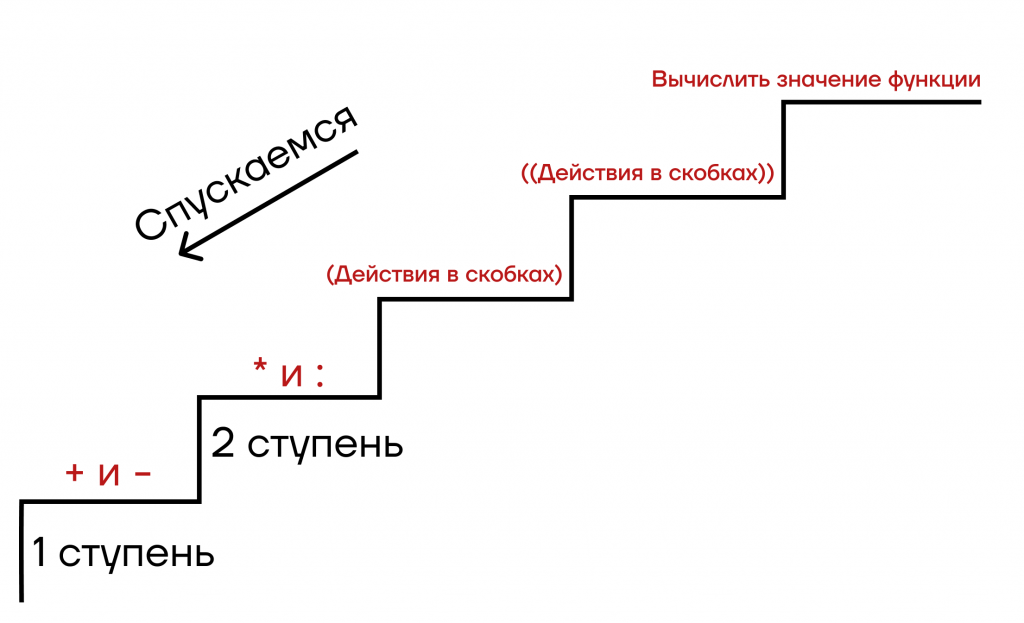
И, таким образом, мы завершаем нашу лесенку. Пятая и последняя ступень — это значения функций. Решая любой пример, нам нужно спуститься по этой лесенке, а если какой-то ступени нет — просто пропустить ее.

Решать последовательно нельзя менять местами — что это значит? Если решать пример в неправильном порядке действий, то верный ответ не получится. Именно поэтому всегда работает правило: «Решать последовательно, нельзя менять местами». Действия в выражениях выполняются в следующем порядке: 1.Вычисление значений функций; 2. Вычисление значений в скобках; 3.Вычисление значений вне скобок. При этом, если в примере: — и умножение с делением (действия второй ступени), — и сложение с вычитанием (действия первой ступени),  то сначала выполняются действия второй ступени, а после действия первой ступени.

Действия с числами разных знаков

Для подробного разбора этой темы необходимо ввести понятие абсолютной величины или модуля числа. 

Рассмотрим числовую прямую и числа на ней: 

• положительные числа будут расставляться в порядке возрастания слева направо, 
• отрицательные числа, напротив, будут уменьшаться справа налево. 

Можно представить, что мы подставляем к 0 зеркало, тогда в нем в обратном порядке отображаются положительные числа, но с отрицательным знаком, то есть они зеркально повторяют положительную часть прямой. 

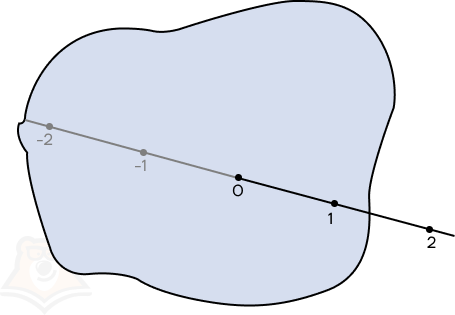
Рассмотрим числа -4 и 4. Относительно ноля они лежат на одинаковом расстоянии: четыре условных единицы, отложенные влево и вправо. 

Отсюда мы можем вывести определение модуля — это расстояние от начала координат (ноля) до точки. Модуль обозначается двумя вертикальными палочками. 

Тогда |4| = 4, и |-4| = 4. 

Подробнее про модуль и его свойства можно узнать в другой нашей статье.

Теперь мы можем рассмотреть действия с числами разных знаков. 

Сложение

Если мы складываем числа с одинаковым знаком, то складываются их абсолютные величины, а перед суммой ставится общий знак. 

Например, \(3+2=5, -3+(-2)=-5\).

Если мы складываем числа с разными знаками, то из абсолютной величины большего из них вычитается абсолютная величина меньшего, а перед разностью ставится знак числа с большей абсолютной величиной. 

Например, \(-5+3=-(5-3)=-2; -4+10=6\).

Вычитание 

Для удобства счета вычитание можно заменить сложением, при этом уменьшаемое сохраняет знак, а вычитаемое его меняет. 

Например, \(10-(+12)=10+(-12)=-2 или 6-(-3)=6+3=9\).

Умножение и деление 

При умножении умножаются абсолютные величины чисел. 

При делении абсолютная величина одного числа делится на абсолютную величину другого числа. 

При этом для определения знака необходимо воспользоваться следующими правилами:

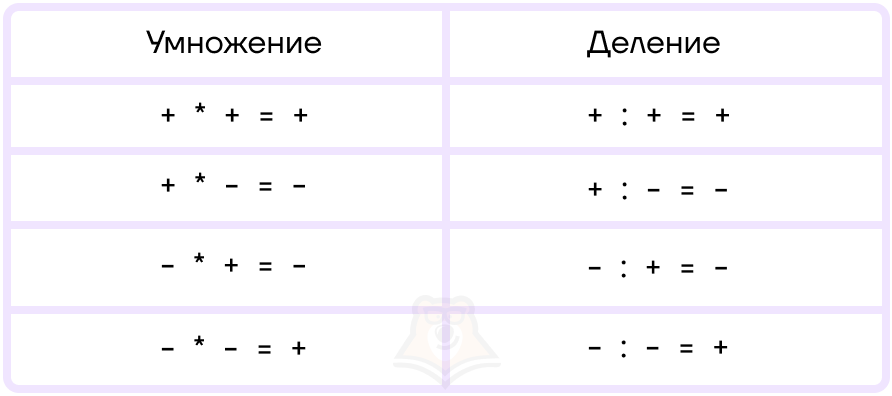
1. Произведение и частное одинаковых знаков будет положительным (плюс на плюс дают плюс; минус на минус дают плюс).

2. Произведение и частное чисел с разными знаками будут отрицательными (плюс на минус дают минус; минус на плюс дают минус).

Для удобства запоминания можно воспользоваться следующей таблицей:

Например,
3 * (-2) = -6
8 : 4 = 2
(-10) : 5 = -2
 (-4) * (-7) = 28.

Как выполнять действия с числами разных знаков? Для сложения: 1. Из абсолютной величины большего числа вычитается абсолютная величина меньшего числа. 2. В ответе ставим знак числа с большей абсолютной величиной. Для вычитания: 1. Вычитание можно заменить сложением, при этом вычитаемое меняет знак. 2. Решаем пример со сложением чисел разных знаков.  Для умножения и деления:  1. Умножаются абсолютные величины чисел, либо абсолютная величина одного числа делится на абсолютную величину другого числа. 2. Определяем знак по правилам.

Сравнение чисел

Помните, мы рассматривали числовую прямую? 

Когда мы сравниваем числа, мы определяем, какое больше, а какое меньше, то есть какое находится правее на числовой прямой, а какое — левее. 

Давайте для примера сравним числа -3 и -5. Вернемся к числовой прямой. На ней мы можем увидеть, что -3 находится правее, чем -5, а значит -3 > -5.

Перед тем, как закончить с этой темой, разберемся с основными свойствами действий с рациональными числами.

Свойства действий с рациональными числами

1. Сочетательный закон сложения: a+(b+c)=(a+b)+c
2. Коммуникативное свойство сложения: a+b=b+a
3. Сложение с нулем не изменяет число: a+0=a
4. Для любого числа a есть такое число -a, что a+(-a)=0
5. Коммуникативное свойство умножения: a*b=b*a
6. Сочетательный закон умножения: a*(b*c)=(a*b)*c
7. Умножение на единицу не изменяет число: a*1=a
8. Распределительное свойство умножения относительно сложения: a*(b+c)=a*b+a*c

Это были основные свойства действий с рациональными числами. Теперь разберем подобные слагаемые.

Подобные слагаемые

Подобные слагаемые — слагаемые, у которых одинаковая буквенная часть. 

Для того, чтобы привести подобные слагаемые, нужно сложить или вычесть коэффициенты при одинаковой буквенной части. Например:

\(10a+3a-9a\)

Как мы можем заметить, буквенная часть одинаковая, значит, можем сложить и вычесть коэффициенты:

\((10+3-9)a = 4a\)

Получили ответ 4a. Теперь рассмотрим что-нибудь посложнее:

\(21x+3y-1x-3y\)

В этом примере уже две разные буквенные части. Складываем коэффициенты для подобных слагаемых:

\((21-1)x+(3-3)y=20x\)

С подобными слагаемыми все понятно, это не очень тяжелая тема. Теперь будем разбираться с округлением чисел.

Округление чисел

В реальной жизни нам нередко встречаются неточные значения, и для удобства мы заменяем их приблизительными, то есть значениями, наиболее близкими к нужным. Например, часто можно услышать фразы «почти 7 килограмм», «чуть больше часа», «около 100 градусов». Данные выражения подразумевают, что в этих числах существует некоторая погрешность, которая не учитывается. 

Чтобы понять, как округлять числа, необходимо немного подробнее разобрать их состав. Большие числа можно разбить на единицы, десятки, сотни, тысячи и т.д. Так, в числе 2309 две тысячи, три сотни, ноль десятков и девять единиц. 

Положение (позиция) каждой цифры в записи числа называется разрядом. 

В целых числах разряды увеличиваются справа налево (единицы, десятки, сотни и т.д.).
В дробной записи числа разряды уменьшаются слева направо (десятые, сотые, тысячные и т.д.) 

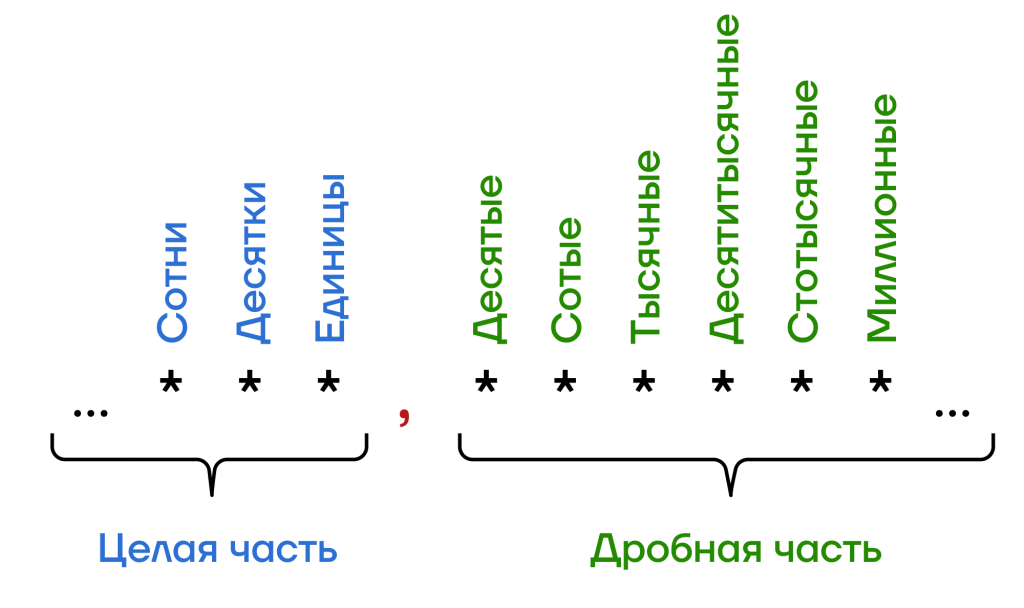
Например, в числе 249,0836:

• 2 относится к разряду сотен;
• 4 — к десяткам;
• 9 — к единицам;
• 0 — к десятым;
• 8 — к сотым;
• 3 — к тысячным;
• 6 — к десятитысячным. 

При делении чисел мы не всегда получаем точные значения, например, 2 не делится на 3. Но мы можем воспользоваться округлением, если невозможно достичь полной точности или она не нужна. 

Приближенное значение числа — это число, полученное при округлении. 

Округление – это операция, когда мы меняем число на его приближенное значение. При этом округлить можно до любого разряда. 

Чтобы округлить число до какого-либо разряда, необходимо записать число на один разряд правее, после чего округлить его по правилам. 

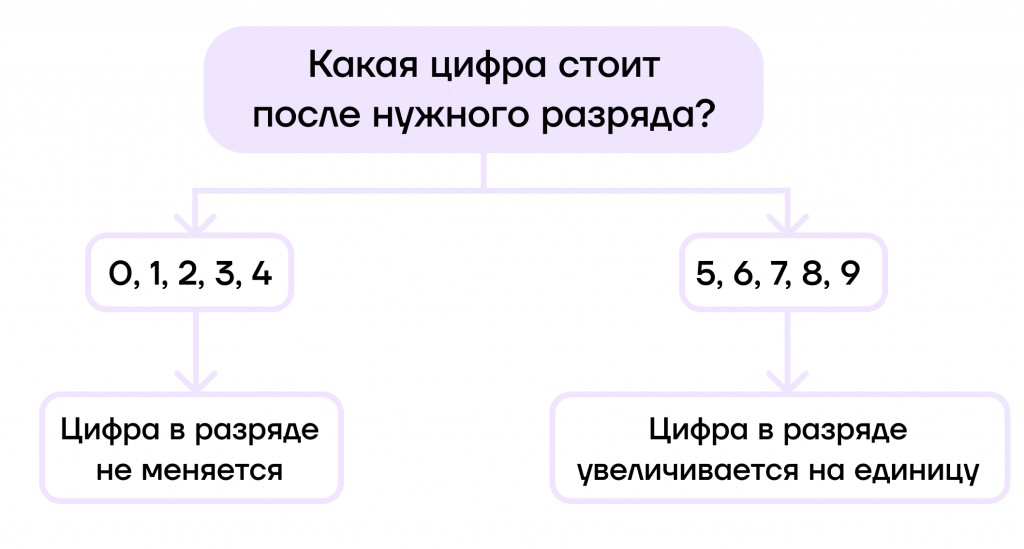
• Если после нужного для округления разряда стоят цифры 0, 1, 2, 3 или 4, то цифра в разряде не меняется и остается прежней. 

• Если после нужного для округления разряда стоят числа 5, 6, 7, 8 или 9, то цифра в разряде увеличивается на единицу. 

Округление до целых 

Чтобы округлить число до целых значений, необходимо узнать значение только одной цифры после запятой (то есть цифру, стоящую в разряде десятых), а после воспользоваться правилами округления. 

Например, при округлении числа 3,4 до целых получится 3, а при округлении 3,7 получится 4. 

Округление до десятых

Чтобы округлить число до десятых, необходимо узнать две цифры после запятой, а после округлить число до одной цифры после запятой по правилам. 

Например, 67,22 при округлении даст 67,2, а 67,29 ≈ 67,3. 

Округление до сотых

Чтобы округлить число до сотых, необходимо узнать значение трех цифр после запятой, а после округлить число до двух цифр после запятой по правилам. 

Например, при округлении числа 140,225 получится 140,23, а 140,221 ≈ 140,22. 

Пользуясь этим алгоритмом, можно округлить число до любого нужного разряда.

Округление с недостатком — это округление числа в меньшую сторону. 

Например, округлением с недостатком будет 4,072 ≈ 4,07

Округление с избытком — это округление числа в большую сторону. 

Например, округлением с избытком будет 79,28 ≈ 79,3. 

Округление с недостатком и избытком может использоваться для решения текстовых задач, при этом не всегда получается пользоваться правилами для округления с числами. Рассмотрим несколько примеров. Для этого решим несколько задач №1 из ЕГЭ по базовой математике.

Пример 1. Апельсины стоят 95 рублей за килограмм. Сколько килограмм апельсинов можно купить на 361 рубль?

Решение. Разделим 361 на 95, получаем:
361:95=3,8.

То есть на всю сумму можно будет купить 3 килограмма и 800 грамм апельсинов. Однако в задаче спрашивается только про килограммы, поэтому на 361 рубль можно будет купить только 3 килограмма апельсинов.

Ответ: 3. 

В решении получилось число 3,8, и по правилам мы должны были округлить его до 4. Однако на 4 килограмма у нас уже не хватило бы денег, поэтому тут применяется округление с недостатком. 

Пример 2. В жилом доме пять подъездов. В каждом подъезде по 20 квартир. Саша живет в 68 квартире. В каком подъезде живет Саша?

Решение. Разделим 68 на 20:
68:20=3,4.

Тогда 68-ая квартира будет располагаться в четвертом подъезде, поскольку в трех подъездах будет всего 60 квартир, значит еще восемь располагаются в следующем подъезде.

Ответ: 4. 

Несмотря на то, что в решении получилось число 3,4, мы воспользовались округлением с избытком из-за ситуации в самой задаче. 

В каких случаях правильно будет пойти против правил?   При действиях с обычными числами обязательно пользоваться правилами.  Но иногда при решении задач на округление необходимо пользоваться не правилами, а логикой: если в описанной в задаче ситуации невозможно округлить в большую или меньшую сторону, то округлять нужно так, чтобы ситуация была выполнимой.

Числа — незаменимый инструмент в математике. Как и слова в предложениях, из чисел (а также из переменных, обозначаемых буквами) складываются выражения, которые имеют свой неповторимый смысл. Следовательно, если мы хотим научиться решать любые задачи, то должны уметь работать с числами, правильно считать примеры, округлять. С этими знаниями примеры любой сложности будут нам очень легко даваться.

Термины

Произведение чисел — это результат их умножения.

Частноечисел — это результат деления одного числа на другое.

Фактчек

• Если в задании встречается выражение в несколько действий, то сначала считаются значения функций, после значения в скобках и в конце значения вне скобок (при этом сначала вычисляются действия второй ступени, а потом действия первой ступени). 
• Чтобы посчитать значение действия с числами разных знаков, необходимо воспользоваться абсолютной величиной числа и правильно определить знак в ответе. 
• Иногда невозможно (или не нужно) получить точное значение числа, в этом случае можно воспользоваться округлением. 
• Округление в большую сторону называется округлением с избытком, а в меньшую — с недостатком. 

Проверь себя

Задание 1. 
В каком порядке выполняются действия в выражениях с числами? Какое действие выполняется первым в примере \(7+36-5*(29+8:4)-3*4^3+27*9:6\)?

1. \(8:4\)
2. \(7+36\)
3. \(4^3\)
4. \(29+8\) 

Задание 2.
Выберите верно решенный пример:

1. \(6*7=42\)
2. \(81:9=-9\)
3. \((-3)*4=12\) 
4. \((-7):(-1)=-7\)

Задание 3.
Выберите верно решенный пример:

1. \(-3-2=5\)
2. \(21-5=-16\)
3. \(-2-(+34)=36\)
4. \(42-50=-8\)

Задание 4.
Какое число будет округляться в большую сторону при округлении до сотых?

1. 6,7842
2. 27,89076
3. 1,2654
4. 5,461 

Задание 5.
Какое число будет округляться в меньшую сторону при округлении до целых? 

1. 28,52 
2. 101,034 
3. 36,98
4. 486,607 

Ответы: 1. — 3; 2. — 1; 3. — 4; 4 — 3; 5. — 2.