Аксиомы стереометрии. Прямые и плоскости в пространстве

На этой странице вы узнаете

• Три В: как получаются объемные фигуры?
• Как сделать из бумаги елочку и с ее помощью проверить одну из аксиом стереометрии?
• Скрестить шпаги! Как запомнить отличие скрещивающихся и пересекающихся прямых? 

Мы живем в трехмерном пространстве. Почти все предметы, которые нас окружают, обладают высотой, шириной и длиной. Стол, стул, ноутбук, телефон, — все эти предметы состоят из геометрических тел. В стереометрии мы изучаем то, что нас окружает. Давайте же углубимся в нее.

Аксиомы стереометрии

Чем отличается параллелепипед от телефона? Шар от апельсинки? А конус от кухонной воронки? Ответ прост: ничем. Изучая стереометрию, мы узнаем много нового об окружающем нас мире. 

Стереометрия — это раздел геометрии, в котором изучаются трехмерные фигуры. 

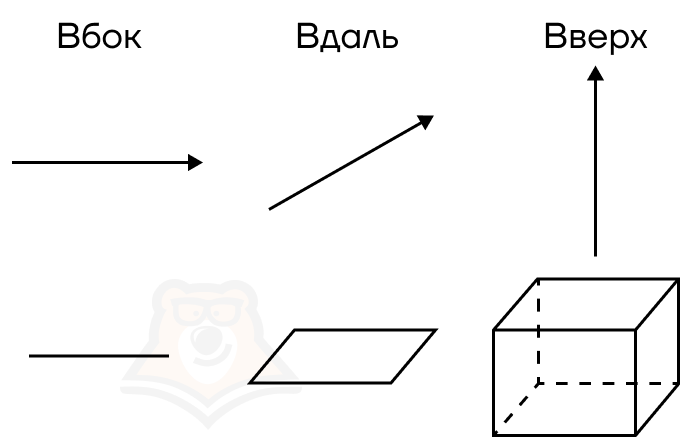
Три В: как получаются объемные фигуры? Объемные фигуры являются частью трехмерного пространства и обладают не только длиной и шириной, но и высотой. Три измерения — три направления развития фигуры. Проще запомнить с помощью “Трех В”: Вбок, Вдаль, Вверх.

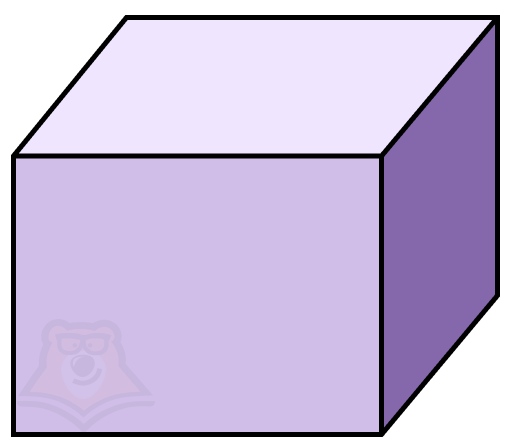
На рисунке мы получили кубик. Не удивляйтесь, что не все его грани показаны сплошной линией: в черчении невидимые линии обозначаются пунктиром. Так мы точно можем определить, с какого ракурса смотрим на кубик: при взгляде на настоящий кубик ребра, начерченные пунктиром, мы не увидим. 

Но начнем изучать стереометрию с самых основ. Невозможно прочесть книгу, не зная букв, и невозможно полностью изучить стереометрию, не зная ее аксиом. 

Аксиомы — это факты, не нуждающиеся в доказательстве. Нам не нужно доказывать, что яблоко — это яблоко, также не нужно и доказывать эти аксиомы. 

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит единственная плоскость. 

Что такое плоскость? В математике плоскость объясняется следующим термином. 

Плоскость — поверхность, которая полностью содержит каждую прямую, соединяющую любые две ее точки. 

Представим лист бумаги. Нарисуем на нем несколько точек и соединим их в произвольном порядке. Все начерченные нами линии будут принадлежать только этому листу. Следовательно, лист — это плоскость. 

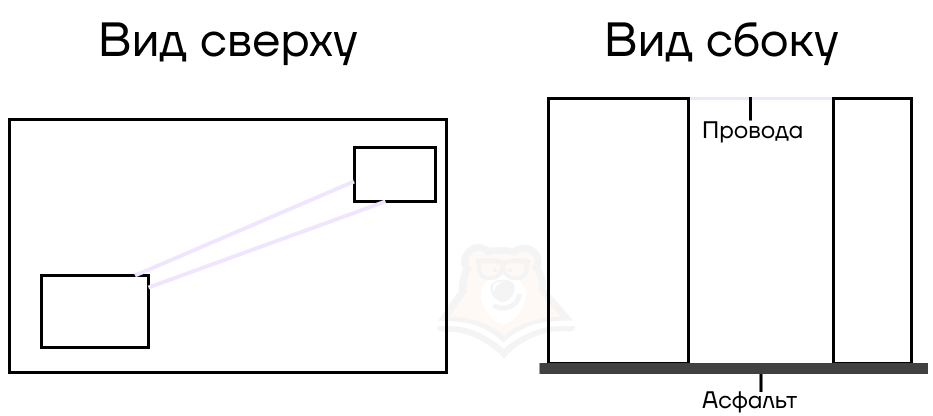
Могут ли линии не принадлежать листу, если доподлинно неизвестно, где они проведены? На самом деле, да. Представим, что мы летим на самолете и смотрим на землю. Нам будет казаться, что провода лежат на асфальте, хотя плоскость асфальта лежит значительно ниже уровня, на котором висят провода. Однако это мы можем заметить только рассматривая улицу сбоку. 

Вернемся к нашей аксиоме. Почему плоскость строится через три точки? Все достаточно просто: единственную плоскость невозможно построить через одну только прямую. Например, через одну и ту же прямую может пройти горизонтальная плоскость, вертикальная плоскость, наклонная плоскость и многие другие.

Следовательно, чтобы построить единственную плоскость, нам нужны две точки, которые образуют прямую, и еще одна, которая задаст направление плоскости. Таким образом, мы получаем следствие из аксиомы. 

Следствие из аксиомы 1. Через прямую и не лежащую на ней точку проходит единственная плоскость. 

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки этой прямой лежат в плоскости. 

Как это понять? Если начертить на листе бумаги прямую, то она вся будет принадлежать этому листу. Следовательно, какие бы две точки мы ни взяли, они будут принадлежать одной и той же прямой, которая принадлежит листу бумаги. 

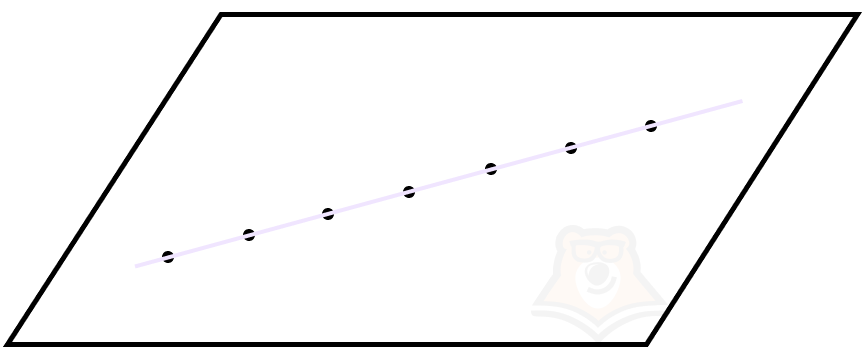
Следствие из аксиомы 2. Прямая, не лежащая в плоскости, может иметь с ней только одну общую точку. 

Возьмем тот же лист бумаги и проколем его иголкой. Иголка и лист будут иметь только одну общую точку — место прокола. 

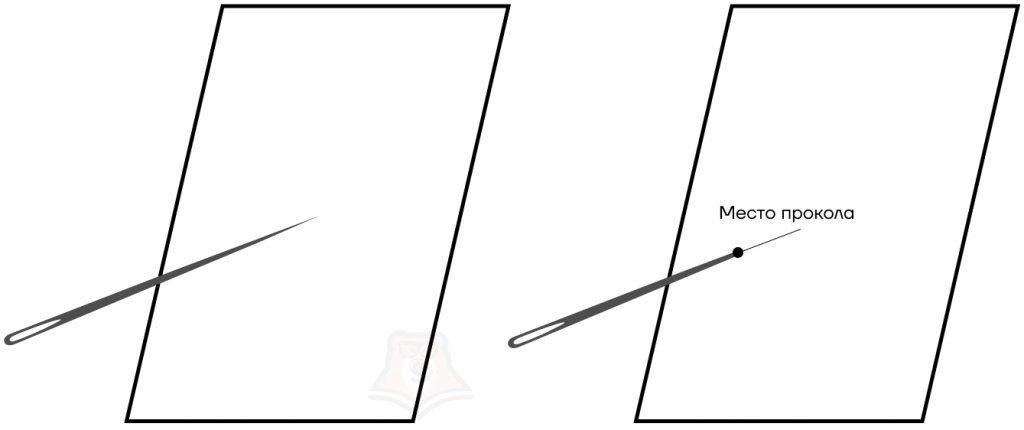
В случае когда прямая имеет с плоскостью только одну общую точку, она будет пересекать плоскость. 

Аксиома 3. Если две плоскости имеют общую точку, то они будут пересекаться по прямой. 

Немного вспомним макетирование. 

Как сделать из бумаги елочку и с ее помощью проверить одну из аксиом стереометрии? Если вырезать две одинаковые елочки из бумаги, а потом сделать разрезы на каждой из них, то мы сможем соединить их в объемную фигуру.   В этом случае каждая елочка будет отдельной плоскостью. А если мы внимательнее посмотрим на место их соединения, то заметим, что они действительно пересекаются по прямой. Эта прямая обозначена на рисунке красным цветом.

Так как линия соединения деталей будет строго прямой , мы можем сделать вывод о соответствии третьей аксиоме стереометрии: если две плоскости имеют общую точку, то они будут пересекаться по прямой. 

Мы рассмотрели аксиомы стереометрии. Осталось только чуть внимательнее посмотреть на еще несколько следствий из них. 

Теорема 1. Через две пересекающиеся прямые проходит плоскость и притом только одна. 

Пересекающиеся прямые — это прямые, у которых только одна общая точка.

Это как взять два карандаша и сложить их крест-накрест. Карандаши — прямые, место их соприкосновения — общая точка. 

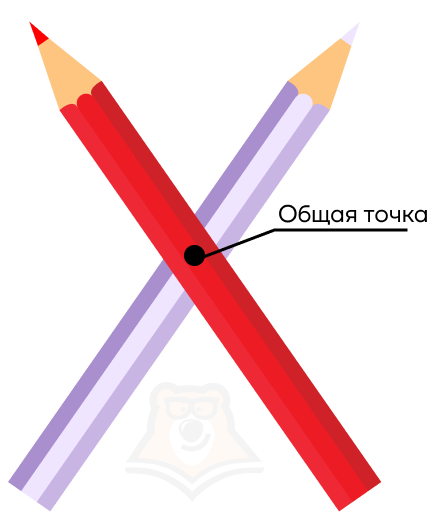
Как уже было сказано в аксиоме 1, чтобы провести плоскость нужно три точки или прямую и еще одну точку. Следовательно, вместо двух пересекающихся прямых мы можем взять одну из них и точку на второй. Важно, чтобы это была не точка их пересечения. Таким образом, прямая и точка зададут плоскость. 

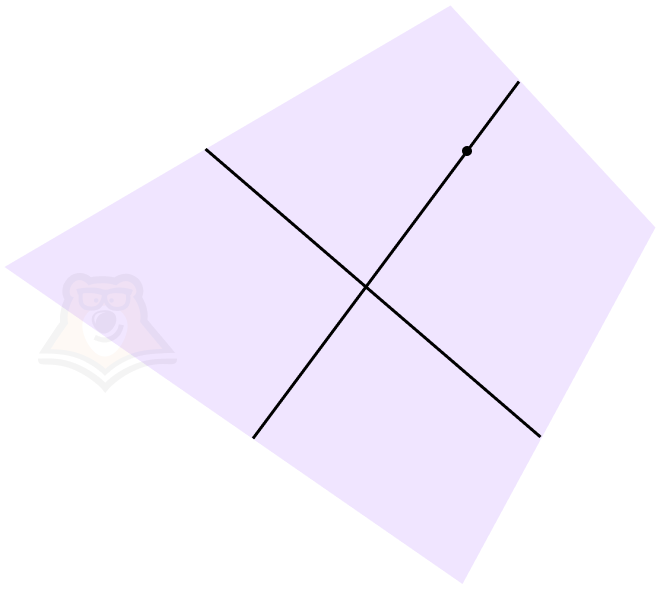
Теорема 2. Через две параллельные прямые проходит плоскость и притом только одна.

Можно привести те же рассуждения. Чтобы провести через две прямые плоскость, достаточно взять одну прямую и любую точку на другой. А поскольку параллельные прямые никогда не пересекутся, то и точки их пересечения не будет, значит, можно брать любую точку. 

Уравнение плоскости в пространстве

Мы разобрались с тем, какие различные элементы задают плоскость в пространстве. Давайте теперь изучим более формальный, но очень полезный способ задать плоскость  — с помощью уравнения.

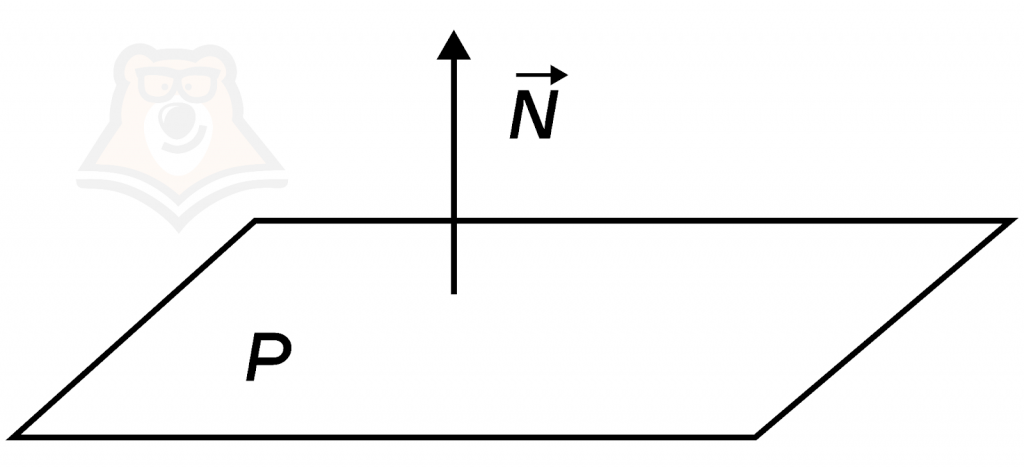
Уравнение плоскости в пространстве выглядит следующим образом:

\(A*x+B*y+C*z+D=0\)

Здесь, A, B, C — координаты вектора N, перпендикулярного к нашей плоскости P. Такой вектор называется нормалью.

Прямые и плоскости в пространстве

Возьмем иголку и лист. Пусть иголка будет прямой, а лист бумаги — плоскостью. Как мы можем их расположить относительно друг друга?

Мы можем положить иголку на лист. В этом случае наша прямая будет принадлежать плоскости. 

Мы можем поднять иголку, при этом не меняя угла ее наклона. Тогда прямая будет параллельна плоскости. 

А еще мы можем проткнуть иголкой лист бумаги. Здесь прямая и плоскость будут пересекаться. 

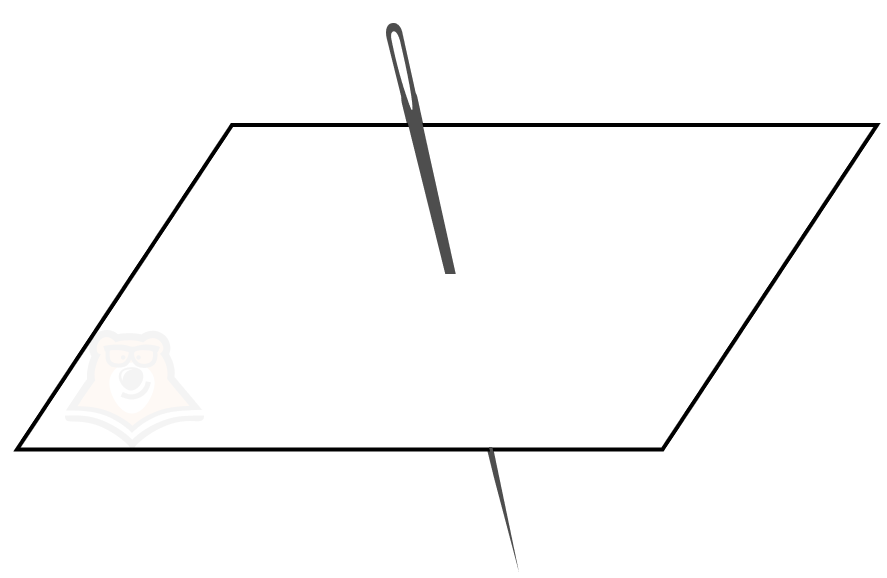
Таким образом, мы нашли все случаи взаимного расположения прямой и плоскости в пространстве. 

• Прямая принадлежит плоскости. 

Все точки прямой также принадлежат этой плоскости. 

• Прямая параллельна  плоскости. 

Плоскость и прямая не имеют общих точек. 

• Прямая пересекает плоскость. 

Прямая и плоскость имеют единственную общую точку. 

Рассмотрим чуть подробнее параллельность прямой и плоскости. В этом случае, как уже было сказано, прямая и плоскость не будут иметь общих точек. Но это необходимо доказать.

Существует признак параллельности прямой и плоскости в пространстве. 

• Если прямая, не лежащая в данной плоскости, параллельна прямой, лежащей в этой плоскости, то она будет параллельна данной плоскости. 

Построим плоскость а, в которой лежит прямая b, и параллельную ей прямую а. Вспомним, что через две параллельные прямые можно провести только одну плоскость. Проведем плоскость r. 

Следовательно, в плоскости r лежат две параллельные прямые а и b, не имеющие общих точек.  

А поскольку b принадлежит плоскости а, то прямая а не имеет и с ней общих точек. 

В плоскости а можно по-разному провести прямые b, и каждый раз ситуация будет повторяться. 

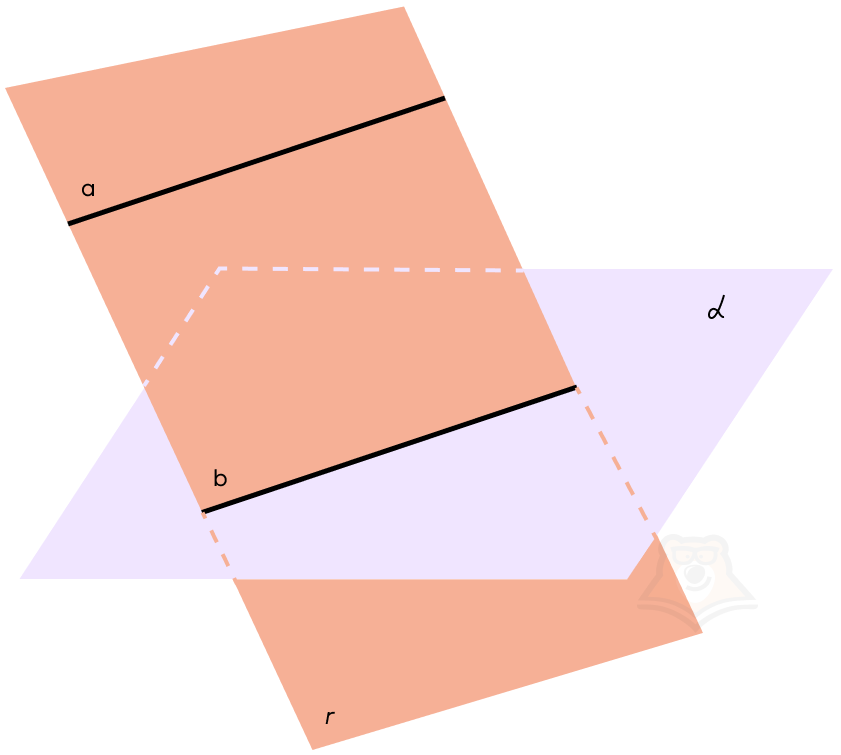
Предположим, мы доказали, что прямая и плоскость параллельны. Теперь проведем через прямую вторую плоскость. 

Существует два варианта, как получившиеся плоскости могут располагаться относительно друг друга: 

• Плоскости будут параллельны, следовательно, не будут иметь общих точек;
• Плоскости будут пересекаться. 

Параллельность двух плоскостей рассмотрим чуть позже, а сейчас остановимся на их пересечении. Здесь появляется еще одна теорема.

Теорема. Если через прямую, параллельную плоскости, провести другую плоскость, пересекающую данную плоскость, то линия пересечения плоскостей будет параллельна данной прямой. 

Это мы уже рассмотрели в предыдущем пункте, проводя через параллельные линии еще одну плоскость. Рисунок будет повторяться. 

Взаимное расположение двух прямых в пространстве

Снова возьмем два карандаша и посмотрим, как их можно расположить относительно друг друга в пространстве. 

Во-первых, мы можем расположить два карандаша параллельно друг другу, и у них не будет общих точек. 

Во-вторых, мы можем крест-накрест наложить один карандаш на другой. Тогда у них будет одна общая точка, а значит, они будут пересекающимися прямыми. 

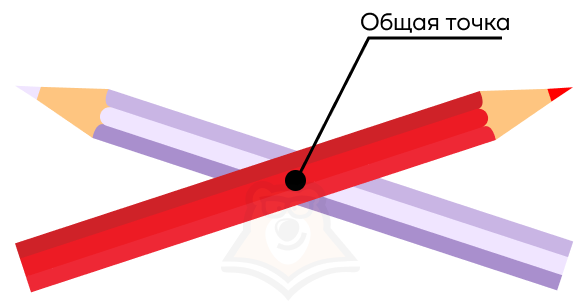
Теперь из этого же положения отодвинем карандаши друг от друга. Например, поднимем верхний карандаш строго по вертикальной прямой. В этом случае у них не будет общих точек. Более того, поскольку карандаши находятся под углом друг к другу, через них невозможно провести одну и ту же плоскость. 

Так мы вывели три основных расположения прямых в пространстве. 

• Прямые параллельны друг другу и не имеют общих точек. 

• Прямые пересекаются и имеют одну общую точку. 

• Прямые скрещиваются. Общих точек в этом случае также не будет. 

Чуть подробнее рассмотрим параллельные прямые в пространстве, поскольку с ними связаны интересные теоремы. 

Теорема 1. Допустим, нам дана одна произвольная прямая. Тогда через любую точку пространства, которая не принадлежит данной прямой, может пройти только одна прямая, параллельная данной. 

Это легко отследить. Зафиксируем строго вертикально одну зубочистку. Теперь мы сможем разместить другую зубочистку, параллельную ей (то есть тоже вертикальную) в любом положении относительно первой зубочистки. 

Теорема 2. Если одна из параллельных прямых пересекает данную плоскость, то и другая параллельная прямая будет пересекать эту плоскость. 

Возьмем вилку, в которой 4 параллельных зубчика и проткнем лист бумаги. Невозможно проткнуть его так, чтобы все четыре зубчика не пересекли эту плоскость. 

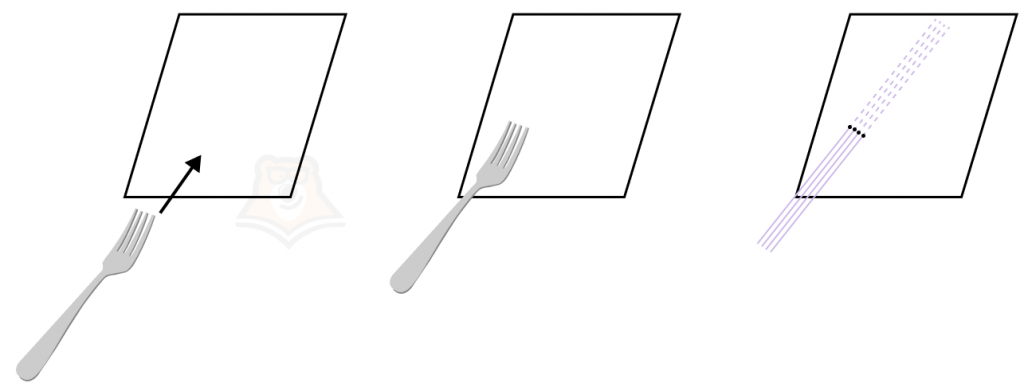
Разумеется, лист можно проткнуть с краю, но нужно вспомнить, что любая плоскость в пространстве бесконечна. Лист бумаги будет лишь ее частью, а сама плоскость будет продолжаться и за его пределами. 

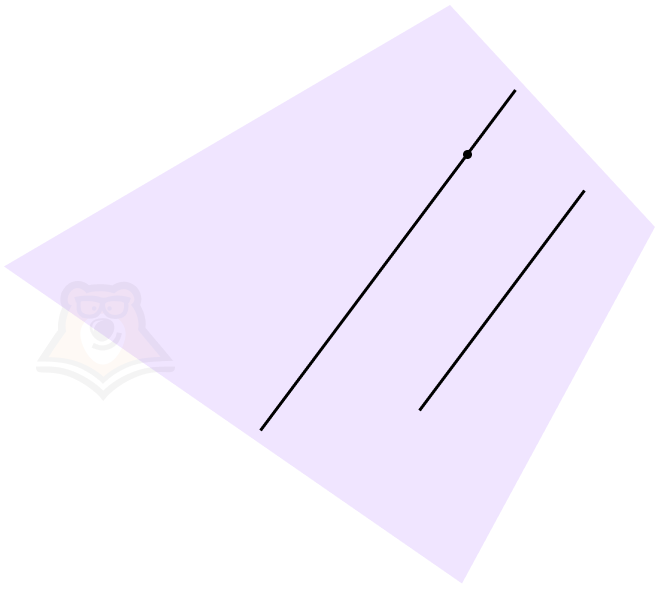
Выше мы уже упомянули про скрещивающиеся прямые. Что это такое и чем они отличаются от пересекающихся?

Прямые будут называться скрещивающимися, если не существует плоскости, содержащей обе эти прямые. 

На ум приходит фраза “Скрестить шпаги”. На самом деле, она недалека от этого термина. До тех пор, пока шпаги не будут касаться друг друга и будут иметь разный наклон в пространстве, невозможно будет провести плоскость сразу через две из них. 

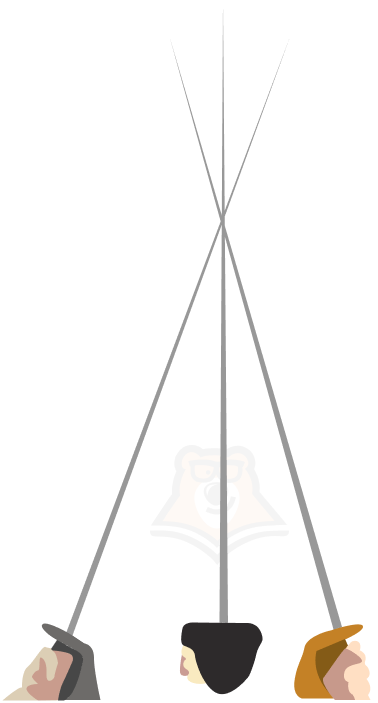
Скрестить шпаги! Как запомнить отличие скрещивающихся и пересекающихся прямых?  Пересекающиеся прямые имеют одну общую точку, следовательно, через них можно провести плоскость.  Скрещивающиеся же прямые не имеют общих точек и невозможно провести через них общую плоскость. Если представить шпаги во время фехтования: пока они не касаются и имеют разный угол наклона в пространстве, они будут оставаться скрещивающимися.

Разумеется, в задаче мы не сможем просто так объяснить, что прямые являются скрещивающимися. Более того, на рисунке не всегда видно, что прямые именно скрещиваются, а не пересекаются, поскольку рисунок — двухмерное изображение трехмерного пространства и не имеет глубины. Следовательно, для доказательства, что прямые скрещиваются, нужно воспользоваться признаком. 

Признак скрещивающихся прямых. Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на данной прямой, то такие прямые являются скрещивающимися. 

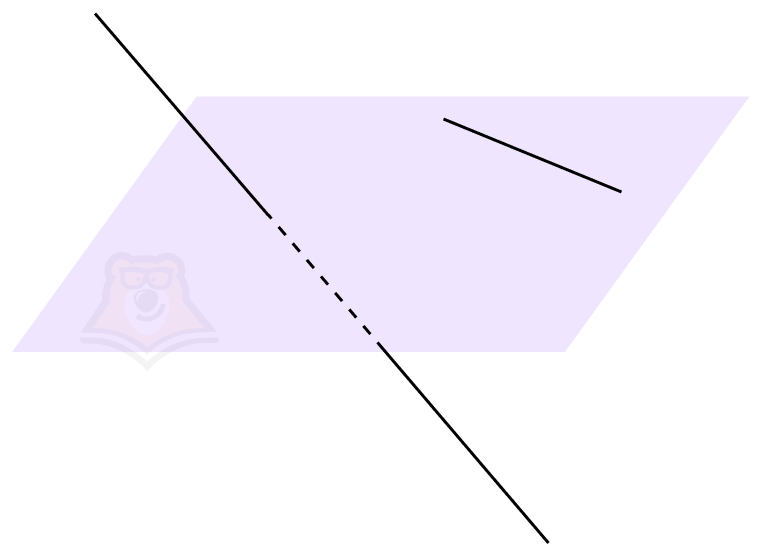
Этот признак можно понять, если нарисовать на листе бумаги линию и взять иголочку. Предположим, что иголка также будет прямой. А теперь нужно проткнуть лист в любой точке, кроме уже нарисованной линии, главное, чтобы иголка располагалась под углом к листу бумаги. Таким образом, мы получим скрещивающиеся прямые. 

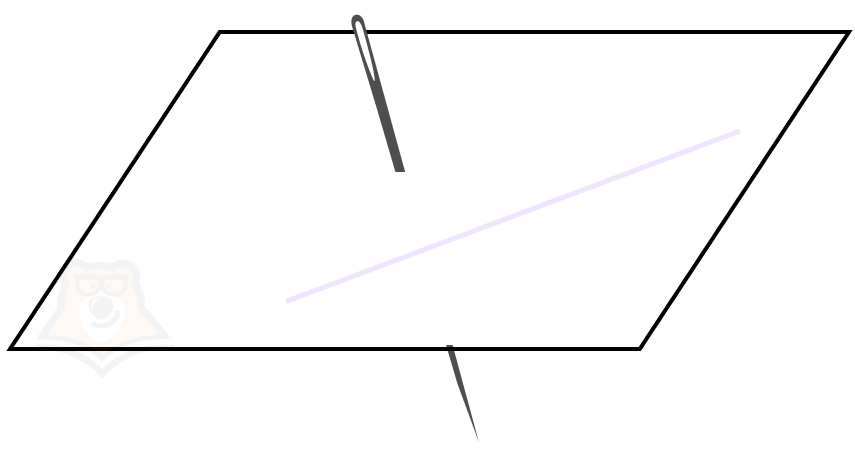
Важно разобраться в понятии угла между скрещивающимися прямыми. 

Возьмем еще одну такую же иголку, которой до этого прокалывали лист. Параллельно первой иголке проткнем лист уже в точке на имеющейся прямой. Здесь угол между второй иголкой и прямой на листе и будет углом между скрещивающимися прямыми!

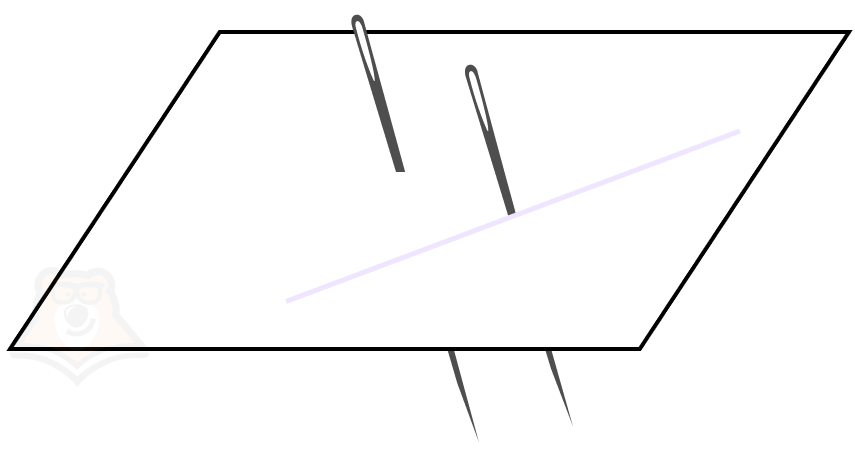
Угол между скрещивающимися прямыми — это угол между пересекающимися прямыми, параллельными скрещивающимся прямым. 

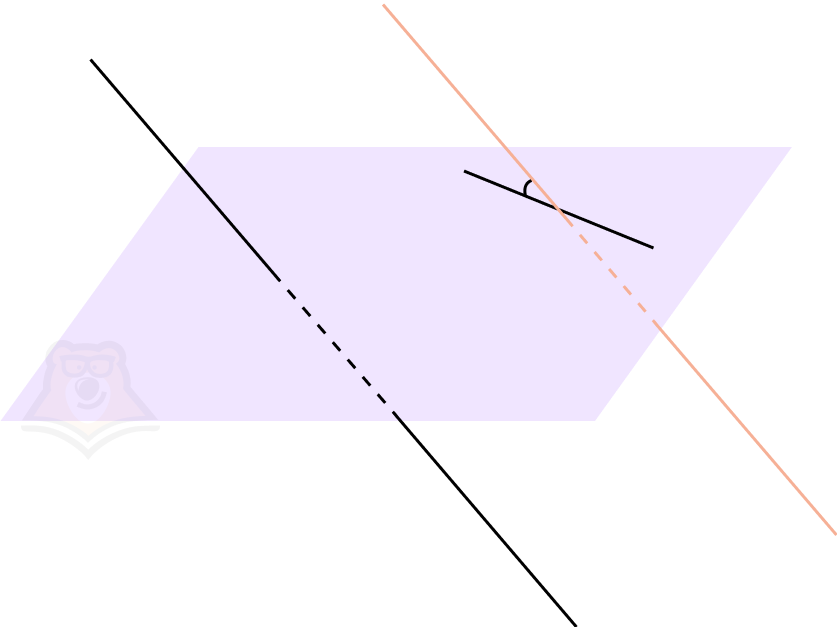
Как найти угол между скрещивающимися прямыми? Достаточно параллельно перенести одну из них так, чтобы прямые из скрещивающихся превратились в пересекающиеся. Это мы и сделали с иголкой. 

При этом если угол между скрещивающимися или пересекающимися прямыми равняется 90°, то такие прямые называются перпендикулярными. 

Взаимное расположение двух плоскостей в пространстве 

Рассмотрим, как могут относительно друг друга располагаться плоскости в пространстве. 

Возьмем два листочка бумаги. Мы можем либо расположить их под наклоном друг к другу, либо параллельно относительно друг друга. 

В первом случае мы получаем пересекающиеся плоскости. 

Пересекающиеся плоскости — это плоскости, которые не совпадают и имеют общие точки. 

Все точки пересечения двух плоскостей лежат на одной прямой, что мы уже доказывали выше. 

В задачах ЕГЭ по профильной математике часто встречаются вопросы об угле между пересекающимися плоскостями. В некоторых случаях задачу легко решить, сведя ее к планиметрии. Но бывает и такое, что совсем непонятно, как и что надо достроить, чтобы получить плоскую фигуру. В таких ситуациях на помощь приходят уравнения плоскостей.

Пусть у нас есть две плоскости α и β, которые заданы уравнениями \(A_{\alpha}x+B_{\alpha}y+C_{\alpha}z+D_{\alpha}= 0\) и \(A_{\beta}x+B_{\beta}y+C_{\beta}z+D_{\beta}= 0\) соответственно, а φ – это угол между ними, который нам надо найти.

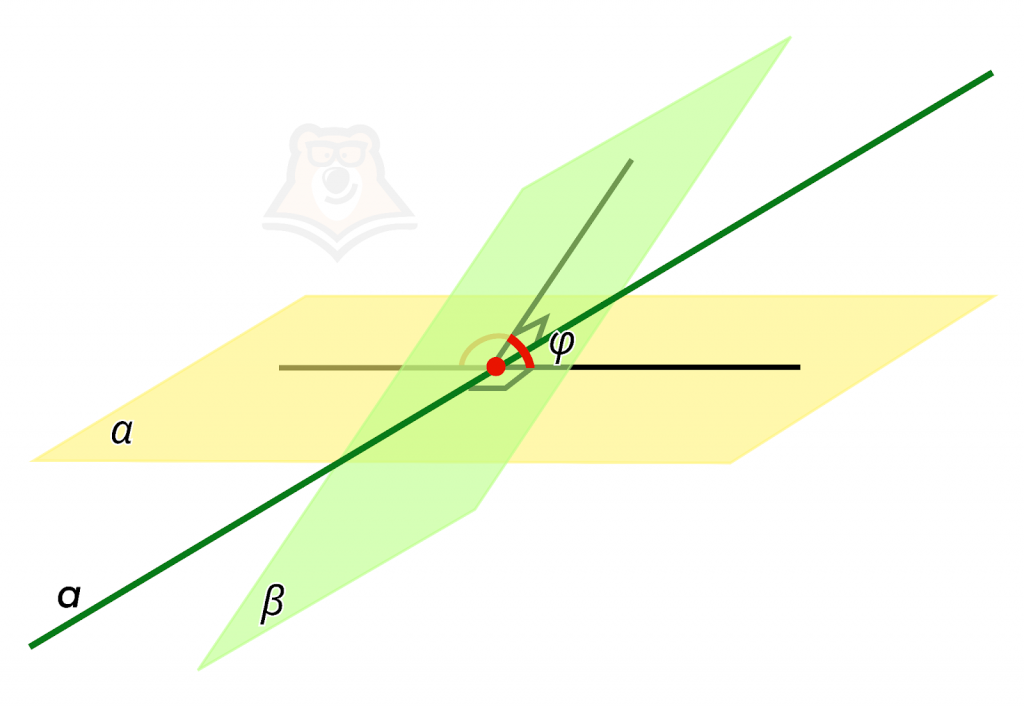
В таком случае нам надо использовать следующую формулу:

\(cos\varphi=\frac{A_{\alpha}A_{\beta}+B_{\alpha}B_{\beta}+C_{\alpha}C_{\beta}}{\sqrt{A^2_{\alpha}+B^2_{\alpha}+C^2_{\alpha}}*\sqrt{A^2_{\beta}+B^2_{\beta}+C^2_{\beta}}}\)

Величину угла мы узнаем с помощью обратной тригонометрической функции – арккосинуса.

Во втором случае мы получаем параллельные плоскости. 

Параллельные плоскости — это плоскости, которые не имеют общих точек. 

Как доказать, что две плоскости параллельные? Ведь любой, даже самый небольшой угол, уже влияет на то, что рано или поздно плоскости пересекутся. Для этого существуют признаки параллельности плоскостей. 

Признак 1. Если две пересекающиеся прямые одной плоскости соответственно параллельны пересекающимся прямым в другой плоскости, то такие плоскости параллельны. 

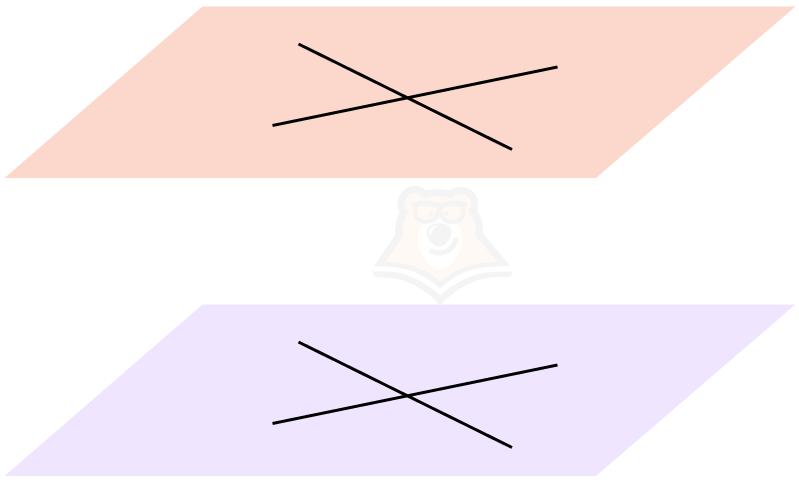
В этом случае важно, чтобы было именно две пересекающиеся прямые в каждой плоскости. Если в каждой плоскости будет по одной прямой, то такие плоскости могут пересекаться. 

Признак 2. Если две пересекающиеся прямые одной плоскости параллельны другой плоскости, то такие плоскости параллельны.

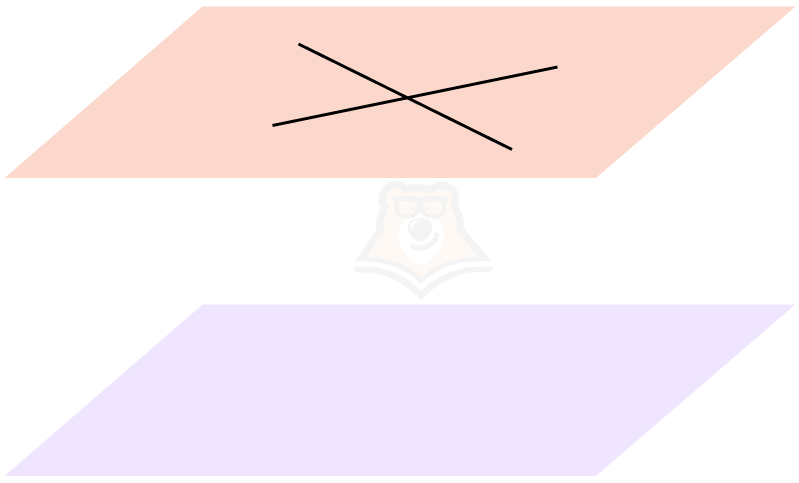
В параллельной плоскости можно дочертить точно такие же прямые, и получится признак 1. 

Однако параллельные плоскости обладают некоторыми интересными свойствами. 

Теорема 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны между собой. 

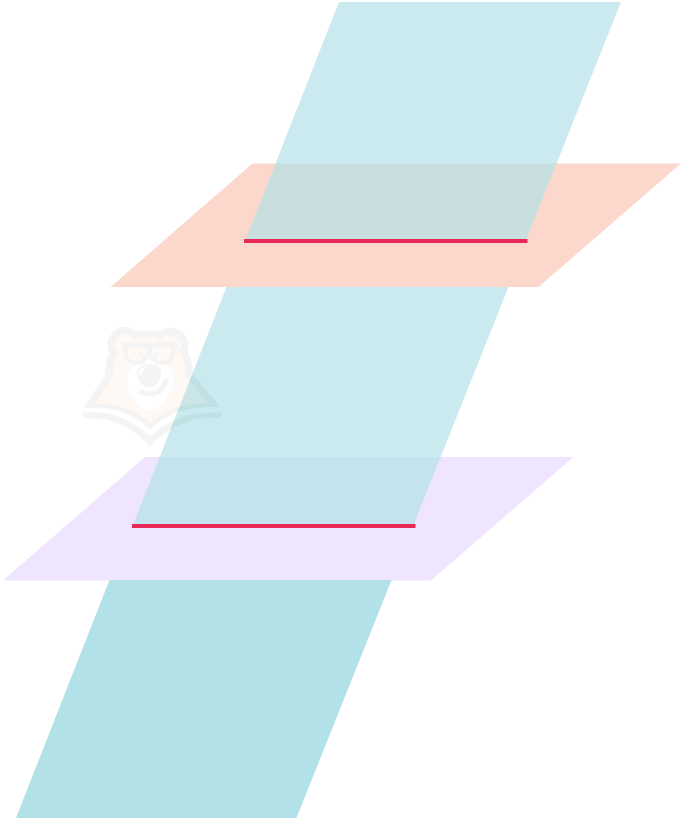
Теорема 2. Через точку, не лежащую на данной плоскости, проходит единственная плоскость, параллельная данной. 

Мы рассмотрели основы стереометрии. Любую теорему или признак, свойство можно легко объяснить с помощью окружающих нас вещей. 

Когда мы сталкиваемся со стереометрией, важно в уме представлять именно объемную картинку, которую можно прокрутить во все стороны. Это может потребовать некоторых усилий и фантазии, но именно такой способ помогает легче решать задачи и понимать основные свойства стереометрии. 

Фактчек 

• Стереометрия изучает трехмерные фигуры, то есть фигуры, которые имеют длину, ширину и высоту. В стереометрии существует три аксиомы, которые не нуждаются в доказательстве и являются основными при изучении этого раздела геометрии. 
• Прямая и плоскость в пространстве могут располагаться относительно друг друга в трех вариантах: прямая будет принадлежать плоскости, прямая будет параллельна плоскости, прямая будет пересекать плоскость. Во втором случае прямая и плоскость не будут иметь общих точек. В третьем случае прямая и плоскость будут иметь только одну общую точку. 
• Две прямые в пространстве могут располагаться по-разному относительно друг друга. В первом случае прямые будут параллельны друг другу и не иметь общих точек, во втором случае прямые будут пересекаться и иметь одну общую точку и в третьем случае прямые будут скрещивающимися и не иметь общих точек. 
• Скрещивающиеся прямые — это прямые, которые не имеют общих точек и через которые невозможно провести одну плоскость, содержащую обе эти прямые. Чтобы найти угол между скрещивающимися прямыми, необходимо параллельно перенести одну из них так, чтобы они стали пересекающимися. Тогда угол между пересекающимися прямыми и будет углом между скрещивающимися прямыми. 
• Две плоскости в пространстве могут быть либо параллельны друг другу и не иметь общих точек, либо пересекаться. Чтобы доказать параллельность двух плоскостей необходимо воспользоваться одним из признаков параллельности. 

Проверь себя

Задание 1.
Известно, что две плоскости пересекаются. Какой будет линия  их пересечения? 

1. Прямой
2. Кривой
3. Ломаной
4. Пересекающиеся плоскости не имеют линии пересечения 

Задание 2. 
Известно, что прямая пересекает плоскость. Сколько у них общих точек?

1. 0
2. 1
3. 2
4. Бесконечное множество 

Задание 3.
Какое утверждение верно для скрещивающихся прямых?

1. Прямые имеют одну общую точку, но через них невозможно провести единственную плоскость.
2. Прямые не имеют общих точек, но через них возможно провести единственную точку.
3. Прямые имеют общую точку и через них возможно провести единственную плоскость.
4. Прямые не имеют общих точек и через них невозможно провести единственную плоскость. 

Задание 4. 
Сколько общих точек у параллельных плоскостей?

1. 0
2. 1
3. Бесконечное множество
4. Зависит от ситуации 

Ответы: 1. — 1 2. — 2 3. — 4 4. — 1