Обратные тригонометрические функции

На этой странице вы узнаете

• Насколько нужны тригонометрические функции в реальной жизни?
• Как легко запомнить значения аркфункций?
• Как легко построить графики обратных тригонометрических функций?

Тригонометрия достаточно сложный, но очень интересный раздел математики. В том числе она изучает тригонометрические функции. Однако математика была бы не математикой, если бы к этим функциям не существовали обратные! 

Зная угол, мы легко можем найти его синус. А что если нам поставят обратную задачу? А если еще и значение не табличное? Неужели эта задача неразрешима?

Определение обратной тригонометрической функции

Прежде чем приступать к изучению дальнейшего материала, рекомендуем вам освежить в памяти теорию по тригонометрии. В этом вам помогут наши статьи: 

• Тригонометрическая окружность. Часть 1
• Тригонометрическая окружность. Часть 2
• Графики тригонометрических функций
• Формулы тригонометрии и простейшие уравнения
• Формулы приведения

Обратные тригонометрические функции – название длинное и сложное, кажется, что может и не стоит с этим разбираться? На самом деле, все не так страшно, как может показаться на первый взгляд. 

Давайте начнем с обратных функций. Мы хорошо знаем, что, например, обратным действием к возведению в квадрат будет извлечение квадратного корня. Соответственно функцией обратной к \(y=x^2\) при \(x\geq 0\) будет функция \(y=\sqrt{x}\) (почему только при \(x\geq 0\) поговорим дальше).

Обратимыми будут называться функции, которые принимают каждое свое значение только в одной точке области определения (то есть одному y соответствует только одинx). 

Именно поэтому мы говорили только о \(x\geq 0\) для функции \(y=x^2\). Ведь если мы будем рассматривать данную функцию на всей ее области определения, то каждому y будут соответствовать два разных x. Например, \(y(-1)=(-1)^2=1, y(1)=1^2=1\).

Получается, что не каждая функция будет обратимой, то есть не каждая функция будет иметь обратную функцию. Так что за обратная функция?

Функции \(f(x)\) и \(g(x)\) будут называться обратными друг другу, если \(f(g(x))=x\).

То есть функции будут обратными, если при применении действия одной из них на другую, мы получим наше первоначальное значение \(x\). Например, \((\sqrt{x})^2=x\).

А что насчет тригонометрический функций? Есть ли функции обратные к ним? Да, есть. О них и пойдет речь в этой статье. 

Обратные тригонометрические функции ― это функции, обратные к тригонометрическим функциям: \(sin(x), cos(x), tg(x), ctg(x)\).

Обратные тригонометрические функции будут отвечать нам на вопрос: «синус, косинус, тангенс или котангенс какого угла будет равняться определенному значению?»

Чтобы назвать обратную тригонометрическую функцию нужно приставить арк- в начало. Так, функцией обратной к синусу, будет арксинус, к косинусу ― арккосинус, к тангенсу ― арктангенс, к котангенсу ― арккотангенс. Аналогично обозначать будем и на письме: \(arcsin, arccos, arctg, arcctg\).

Арксинусом числа \(a\) такого, что \(-1\leq a\leq 1\), будет называться такое число \(\alpha \in [-\frac{\pi}{2}; \frac{\pi}{2}]\), что \(sin(\alpha)=a\).

То есть \(arcsin(a)=\alpha\), если \(sin(\alpha)=a\).

Арккосинусом числа \(a\) такого, что \(-1\leq a\leq 1\), будет называться такое число \(\alpha \in [0;\pi]\), что \(cos(\alpha)=a\).

Арктангенсом числа \(a\) будет называться такое число \(\alpha \in (-\frac{\pi}{2}; \frac{\pi}{2})\), что \(tg(\alpha)=a\).

Арккотангенсом числа \(a\) будет называться такое число \(\alpha \in (0;\pi)\), что \(ctg(\alpha)=a\).

И здесь возникает вполне справедливый вопрос, для чего в наших определениях мы указываем в каком числовом промежутке лежит наш угол. Для этого давайте обратимся к тригонометрической окружности.

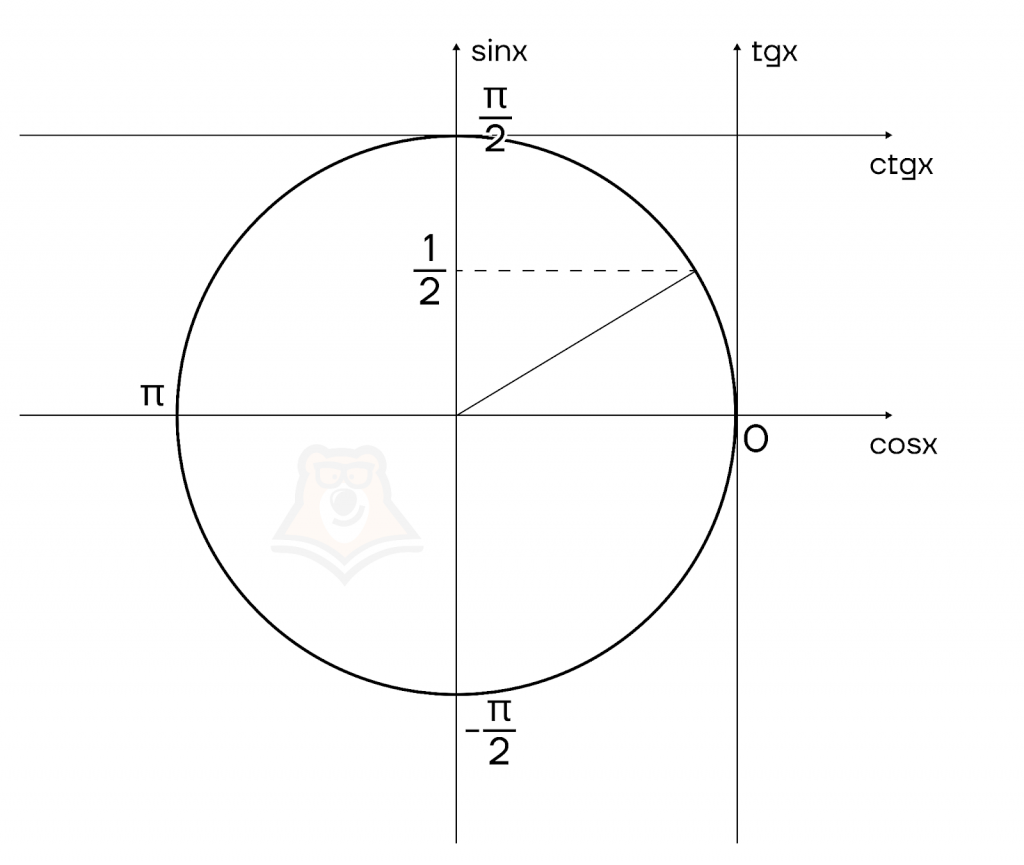
На самом деле углов, синус которых будет равен, например \(\frac{1}{2}\) бесконечное множество, но на отрезке \([-\frac{\pi}{2}; \frac{\pi}{2}]\) такой угол всего один. Более того, на данном отрезке синус принимает все свои возможные значения \([-1; 1]\), при этом каждому углу соответствует только одно значение синуса, а каждому синусу ― единственный угол. То есть на данном промежутке функция будет обратимой. Аналогичная ситуация будет и с другими функциями.

Насколько нужны тригонометрические функции в реальной жизни? Вопрос хороший, и ответов на него довольно много. Начнем с самого очевидного. Например, в геометрии обратные тригонометрические функции нужны нам для решения треугольника, когда мы знаем стороны, а нам нужно найти углы. Такие задачи встречаются в обеих частях ОГЭ и ЕГЭ по математике. Помимо геометрии нам нужно уметь работать с обратными тригонометрическими функциями для решения тригонометрических уравнений, которые встречаются как в тестовой части ЕГЭ по профильной математике, так и в части с развернутыми ответами. Ну а если немного отойти от школьной математики, то обратные тригонометрические функции активно используются в физике для анализа движения объектов или гармонических колебаний, в волновой оптике и многих других областях. Обратные тригонометрические функции используются для многих инженерных расчетов. Не обходится без них и в компьютерной графике, где обратные тригонометрические функции используются для определения углов наклона объектов и вычисления их координат. Арксинусы и арккосинусы используют даже в статистике, чтобы преобразовывать данные.

Про связь тригонометрических функций с обратными им важно помнить при решении тригонометрических уравнений, которые могут встретиться, например, в 6 задании ЕГЭ по профильной математике.

Задание. Решите уравнение \(cos(\frac{\pi (4x+4)}{6})=\frac{\sqrt{3}}{2}\). В ответе укажите наибольший отрицательный корень.

Решение. Если вы еще не знакомы с решением тригонометрических уравнений, рекомендуем вам обратиться к статье «Формулы тригонометрии и простейшие уравнения».

\(cos(\frac{\pi (4x+4)}{6})=\frac{\sqrt{3}}{2}\)
\(\frac{\pi (4x+4)}{6}=\pm arccos(\frac{\sqrt{3}}{{2}})+2\pi n, n\in Z\)
\(\frac{\pi (4x+4)}{6}=\pm \frac{\pi}{6}+2\pi n |*\frac{\pi}{6}, n\in Z\)
\(4x+4=\pm 1+12n, n\in Z\)
\(4x+4=1+12n\) или \(4x+4=-1+12n, n\in Z\)
\(4x=1-4+12n\) или \(4x=-1-4+12n,  n\in Z\)
\(4x=-3+12n\) или \(4x=-5+12n,  n\in Z\)
\(x=-\frac{3}{4}+3n\) или \(4x=-\frac{5}{4}+3n,  n\in Z\)

Наибольшим отрицательным корнем будет \(x=-\frac{3}{4}=-0,75\) при \(n=0\).

Ответ: \(-0,75\)

Мы помним, что функции \(sin(x), cos(x), tg(x), ctg(x)\) являются периодическими, а как насчет обратных им функций?

Периодичность обратных тригонометрических функций

Для начала вспомним, какая функция может считаться периодической. 

Функция называется периодической, если для любого значения аргумента из области определения функции выполняется условие \(f(x)=f(x+T)\), где \(T\) — период функции, отличный от \(0\). 

Согласно этому определению, синус, косинус, тангенс и котангенс являются периодическими функциями. Например: \(sin(\frac{\pi}{6})=\frac{1}{2}\) и \(sin(\frac{\pi}{6}+2\pi)=sin(\frac{13\pi}{6})=\frac{1}{2}\).

• У синуса и косинуса период равен \(2\pi\).
• У тангенса и котангенса период равен \(\pi\). 

Несмотря на то что все тригонометрические функции периодичны, обратные тригонометрические функции периодическими являться не будут.

Никакие из участков обратных тригонометрических функций не повторяются, то есть каждому значению y соответствует только одно значение x.

Кроме периодичности, функции обладают еще рядом свойств. Поговорим теперь про четность и нечетность аркфункций. 

Четность и нечетность обратных тригонометрических функций

Перед тем как рассуждать какими будут обратные тригонометрические функции, давайте вспомним, какие функции являются четными, какие нечетными и бывают ли функции, которые не являются ни теми, ни другими.

Функция называется четной, если для любого x из ее области определения соблюдается: \(f(x)=f(-x)\).

Графики четных функций симметричны относительно оси \(Oy\). Такими функциями являются, например \(y=x^2, y=|x|, y=cos(x)\).

Функция называется нечетной, если для любого \(x\) из ее области определения соблюдается: \(-f(x)=f(-x)\).

Графики нечетных функций симметричны относительно начала координат \(O(0;0)\). Нечетными являются функции \(y=x^3, y=\frac{1}{x}, y=sin(x)\). 

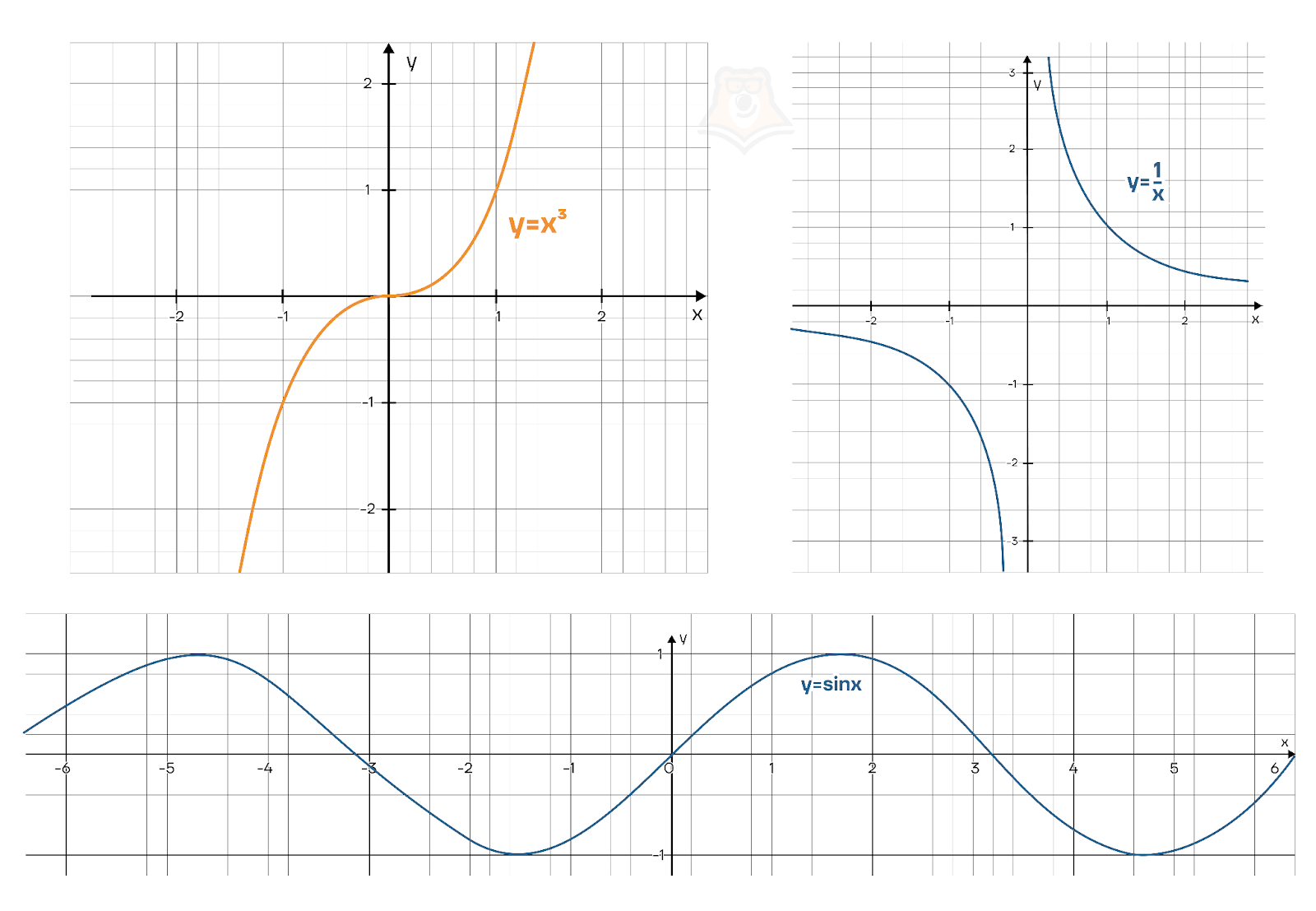
Функции, для которых не соблюдается ни одно из данных неравенств, то есть \(f(x)\neq f(-x), -f(x)\neq f(-x)\), называются функциями общего вида.

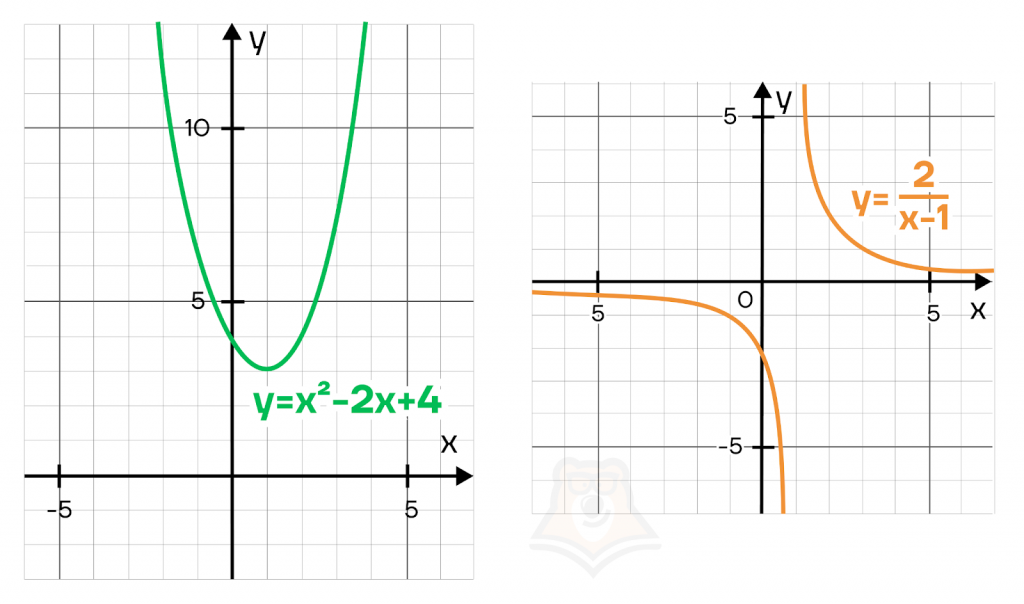
Иногда такие функции называют «ни четная, ни нечетная функция». Такими функциями являются, например, \(y=x^2-2x+4, y=\frac{2}{x-1}\).

Давайте проверим, какими являются обратные тригонометрические функции.

Начнем с арксинуса. Для того чтобы нам было проще ориентироваться, обратимся к тригонометрической окружности.

Рассмотрим некоторый угол \(\alpha \in [-\frac{\pi}{2}; \frac{\pi}{2}]\), синус которого равен \(a\). Тогда по определению арксинуса получим, что \(arcsin(a)=\alpha\).

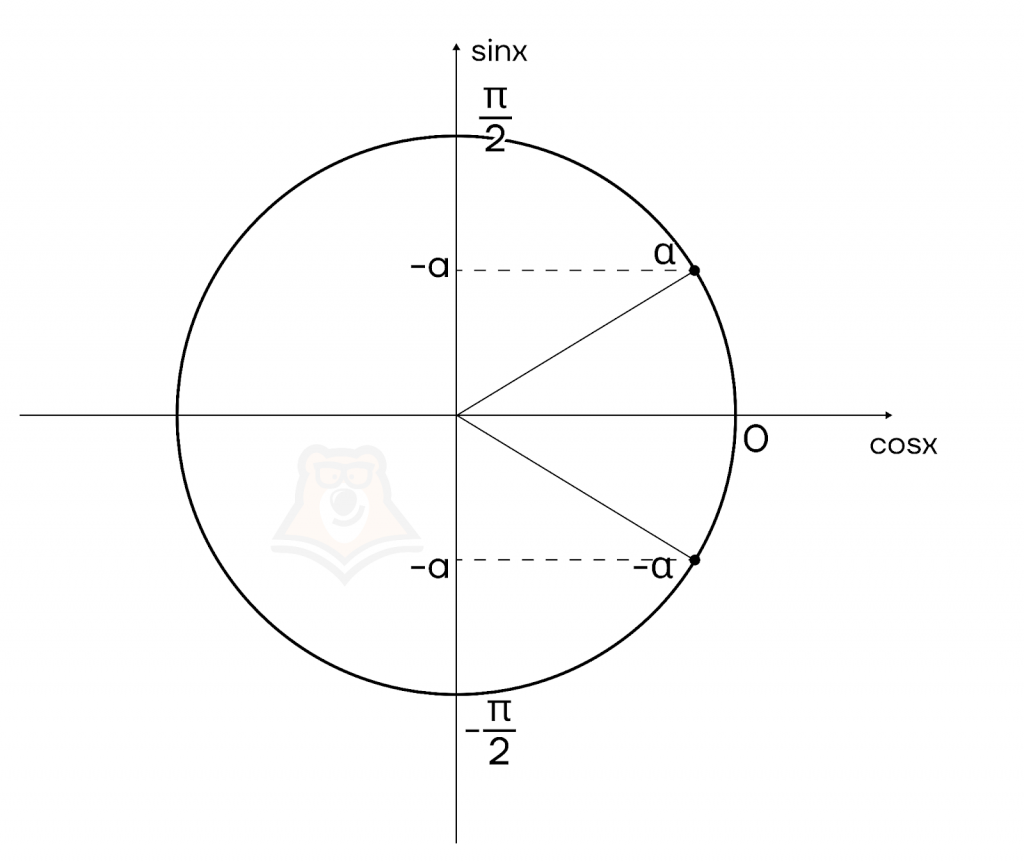
По тригонометрической окружности мы видим: чтобы синус был равен \((-a)\), мы должны повернуть на угол \((-\alpha)\). Значит, \(arcsin(-a)=-\alpha\).

Таким образом, получаем, что \(arcsin(-a)=-arcsin(a)\). То есть \(f(-x)=-f(x)\).

Функция \(y=arcsin(x)\) является нечетной

Проведем аналогичный анализ для арккосинуса. 

Рассмотрим угол \(\alpha \in [0;\pi]\), косинус которого равен a, получается, что \(arccos(a)=\alpha\).

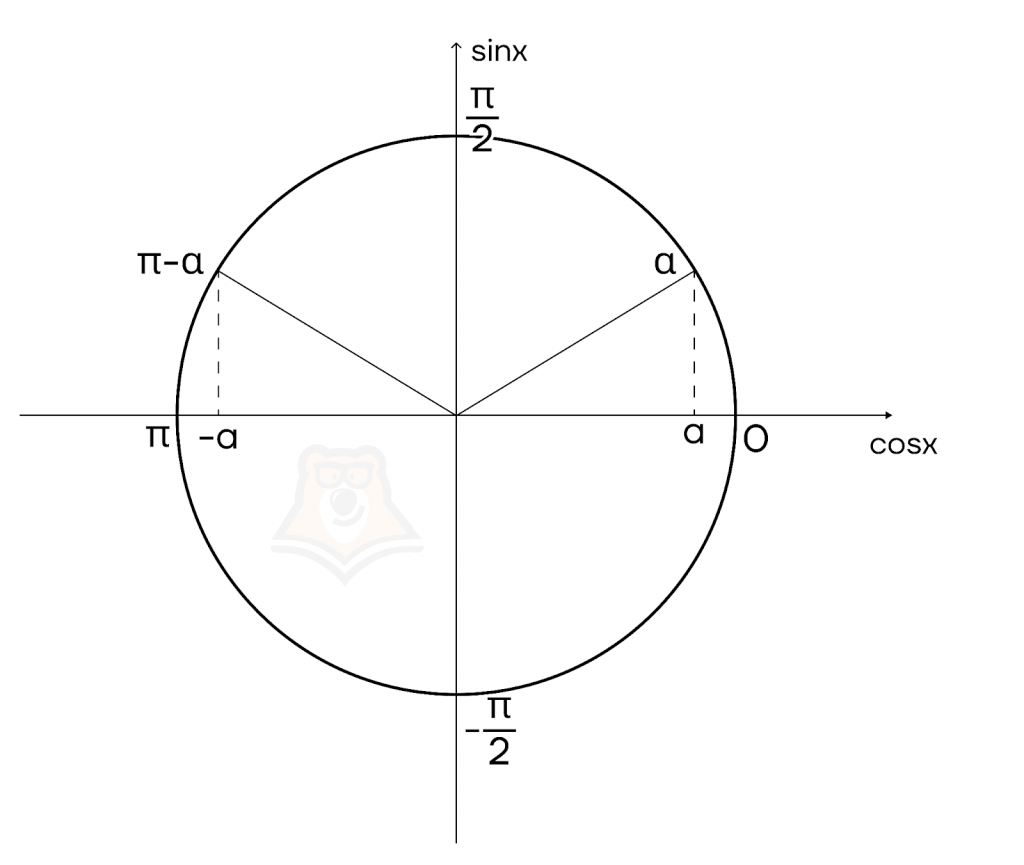
Чтобы косинус угла был равен \((-a)\), нужно повернуть на угол \((\pi -\alpha)\), то есть \(arccos(-a)=\pi -\alpha\). То есть \(arccos(-a)\neq arccos(a)\) и \(arccos(-a)\neq -arccos(a)\). Значит, \(f(-x)\neq f(x)\) и \(f(-x)\neq -f(x)\). 

Функция \(y=arccos(x)\) является функцией общего вида

Теперь давайте рассмотрим арктангенс.

Возьмем такой  угол \(\alpha \in (-\frac{\pi}{2}; \frac{\pi}{2})\), что его тангенс равен \(a\). По определению арктангенса получаем, что \(arctg(a)=\alpha\).

На тригонометрической окружности легко увидеть, что тангенс будет равняться \((-a)\), если мы повернем на тот же угол, но в противоположном направлении. То есть \(arctg(-a)=-\alpha\). Выходит, что \(arctg(-a)=-arctg(a)\Rightarrow f(-x)=-f(x)\).

Функция \(y=arctg(x)\) является нечетной  

И, наконец, проанализируем арктангенс. 

Снова рассмотрим угол \(\alpha \in (0;\pi)\), такой, что его котангенс равен \(a\), а значит \(arcctg(a)=\alpha\).

Обратимся к тригонометрической окружности и увидим, чтобы котангенс угла равнялся \((-a)\), это должен быть угол \((\pi -\alpha)\). Получаем, что \(arcctg(-a)=\pi -\alpha\), то есть \(f(-x)\neq f(x)\) и \(f(-x)\neq -f(x)\).

Функция \(y=arcctg(x)\) является функцией общего вида

До этого мы изучали свойства тригонометрических функций, но пока что не очень понятно, как их применять в решении задач. Зачастую для использования обратных тригонометрических функций нужно знать их значения. 

Значения обратных тригонометрических функций

Значения синусов, косинусов тангенсов и котангенсов основных углов можно запомнить с помощью тригонометрической окружности или просто таблицы, о которых мы говорили в этой статье. 

Давайте попробуем составить такую таблицу основных значений и для обратных тригонометрических функций.

В этом нам снова поможет наша любимая тригонометрическая окружность.

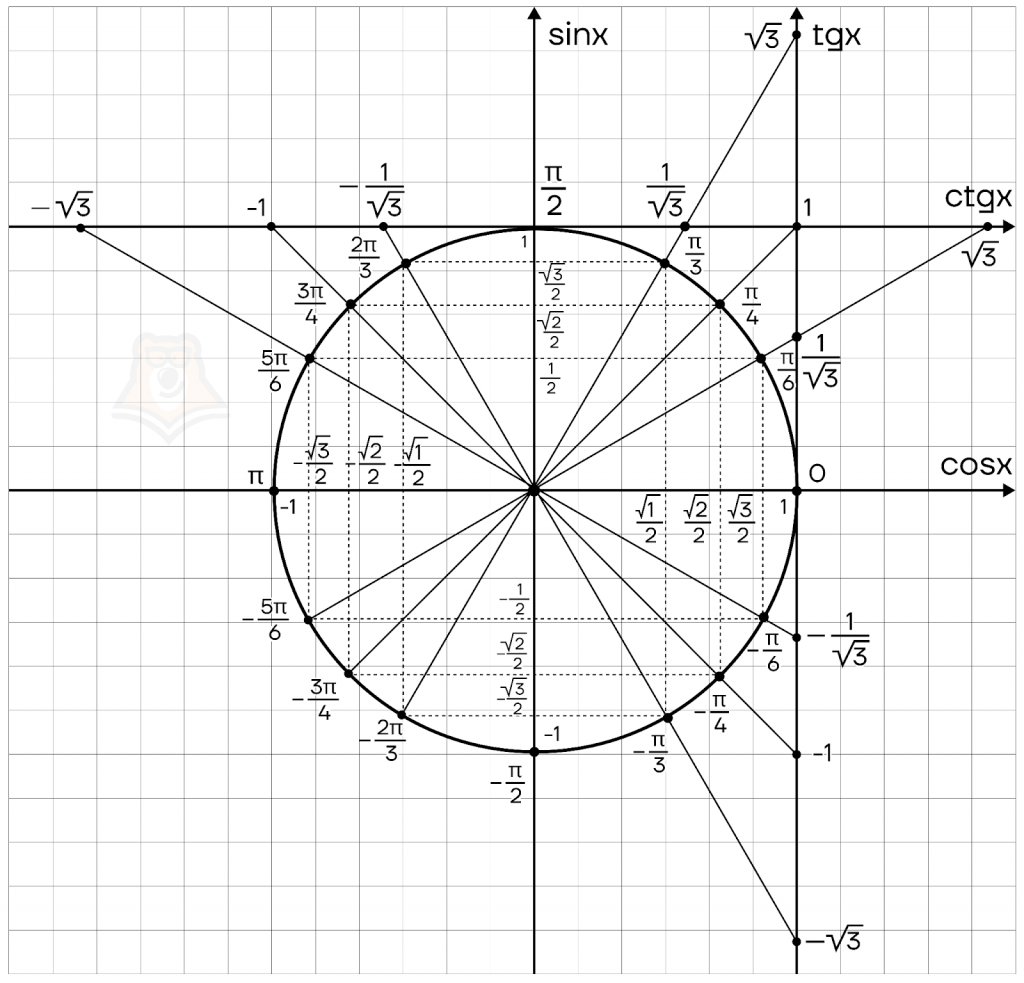
При определении значений важно помнить, что нас интересуют углы \(\alpha \in [-\frac{\pi}{2}; \frac{\pi}{2}]\) для арксинуса, \(\alpha \in [0;\pi]\); ― для арккосинуса, \(\alpha \in (-\frac{\pi}{2}; \frac{\pi}{2})\) ― для арктангенса, \(\alpha \in (0;\pi)\); ― для арккотангенса.

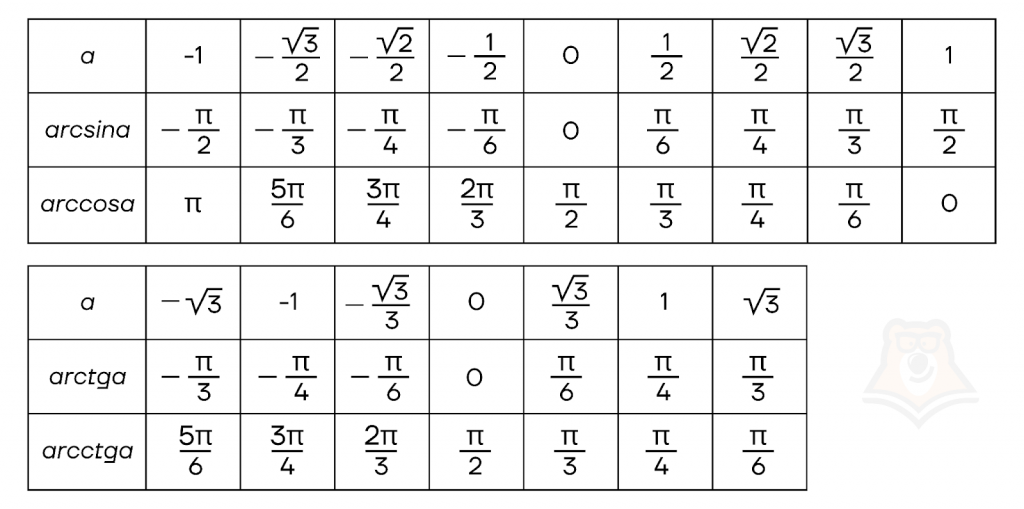
Если внимательно сравнить таблицы для значений тригонометрических функций и таблицы, что мы составили выше, можно прийти к выводу, что они почти одинаковые! Все не просто так, на самом деле при поиске значения аркфункций мы совершаем обратную операцию поиску значений обычных функций, то есть делаем то же самое действие наоборот. Отсюда и схожесть таблиц: никаких новых значений не могло быть просто из определения аркфункций. 

Как легко запомнить значения аркфункций? Весь секрет в том, что вам не нужно запоминать ничего нового! Если вы знаете значения синусов, косинусов и тангенсов основных углов, то вы знаете значения и обратных тригонометрических функций. И конечно не забываем про тригонометрическую окружность, она наш друг, а не враг.

Знание значений обратных тригонометрических функций может пригодиться нам для решений задач по геометрии, например, задачи №1 из ЕГЭ по профильной математике.

Задание. В остроугольном треугольнике \(ABC AB=6, BC=7\), площадь равняется \(10,5\sqrt{2}\). Найдите угол, противолежащий стороне \(AC\).

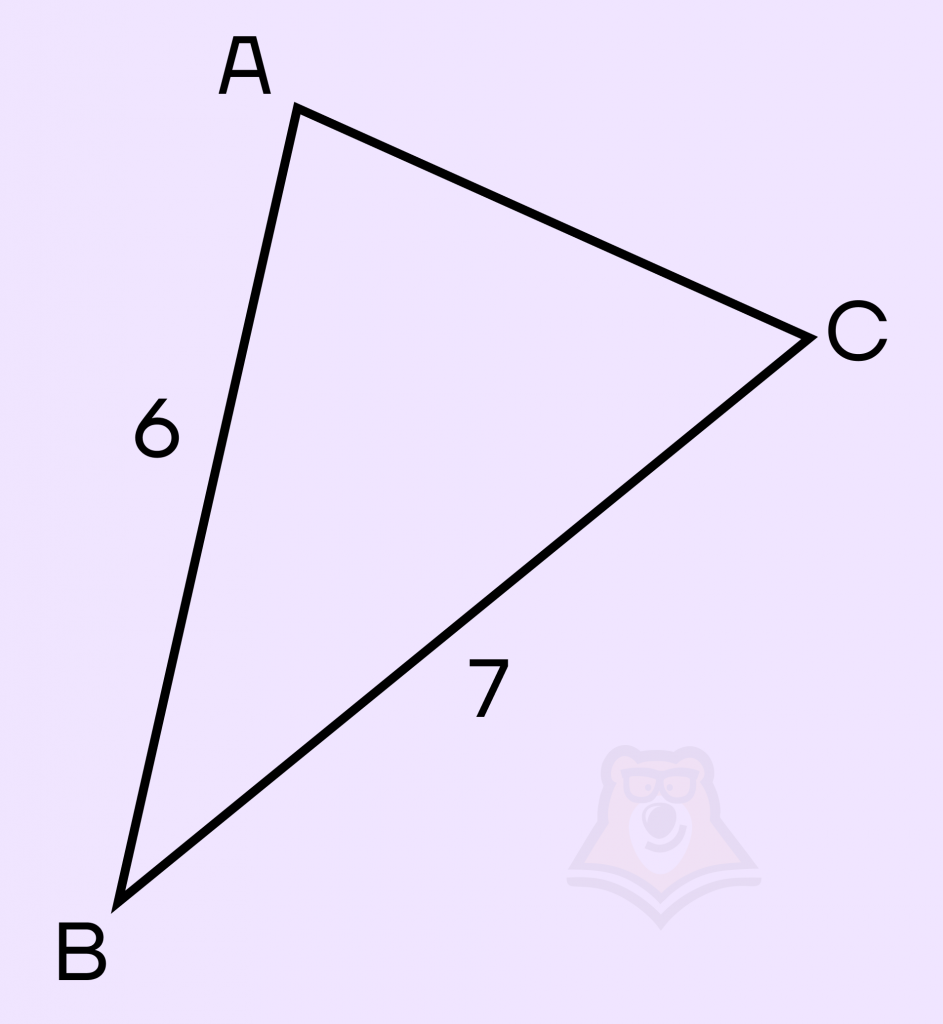
Решение. Напротив стороны \(AC\) лежит \(∠B\), значит нам нужно найти именно этот угол.

Воспользуемся формулой площади треугольника:

\(S=\frac{1}{2}*AB*BC*sin(∠B)\)

Подставим известные нам значения:

\(10,5\sqrt{2}=\frac{1}{2}*6*7*sin(∠B)\)
\(10,5\sqrt{2}=21*sin(∠B)\)
\(sin(∠B)=\frac{10,5\sqrt{2}}{21}\)
\(sin(∠B)=\frac{\sqrt{2}}{2}\)

Значит, \(∠B=arcsin(\frac{\sqrt{2}}{2})=\frac{\pi}{4}=45⁰\)

Ответ: \(45\)

Мы обсудили уже очень много вещей, касающихся обратных тригонометрических функций, но так до сих пор и не рассмотрели как выглядят их графики. Давайте это исправлять!

Графики обратных тригонометрических функций

Чтобы изучать графики аркфункций, важно помнить, как выглядят графики обычных тригонометрических функций. При необходимости вы можете заглянуть в эту статью. 

Как мы уже сказали выше, арксинус, арккосинус, арктангенс и арккотангенс  ― функции, обратные к тригонометрическим, а взаимно обратные функции будут симметричны относительно прямой y=x.

Этим можно воспользоваться при их построении, но мы выполним построение по точкам, а данный факт используем для проверки верности нашего графика.

Как легко построить графики обратных тригонометрических функций? На самом деле, если вы хотите быстро понять как выглядит график обратной тригонометрической функции (на самом деле, любой функции обратной данной) и при этом не хотите заморачиваться с точками или симметрией, есть один очень классный способ. Вы можете воспользоваться им на бумаге или на ноутбуке/планшете. Для начала, давайте рассмотрим как действовать по старинке. Чертим график любой тригонометрической функции. Давайте, например возьмем \(y=sin(x)\). Далее выделяем пожирнее нужный нам участок, в случае с синусом это отрезок \([-\frac{\pi}{2}; \frac{\pi}{2}]\). Лучше выделить этот участок и оси фломастером, сейчас поймете зачем Далее мы переворачиваем лист на обратную сторону. На обратной стороне вероятнее всего видно очертания нашего рисунка, но если нет, то можно посмотреть на просвет, или для удобства приложить к экрану ноутбука или компьютера, тогда все точно станет видно. Теперь поворачиваем наш лист на 90⁰ по часовой стрелке, и обводим все, что выделено ярко. Все! Мы получили график \(y=arcsin(x)\). А с новыми технологиями все еще проще. Чертим нужный нам график и точно так же выделяем нужную область. Затем отражаем изображение и поворачиваем на 90⁰ по часовой стрелке. Готово!

Важно помнить, что из определения арксинуса следует, что для функции \(y=arcsin(x)\) должно соблюдаться условие \(x\in [-1; 1], y\in [-\frac{\pi}{2}; \frac{\pi}{2}]\). Составим таблицу для точек:

\(x\)	\(-1\)	\(-\frac{1}{2}\)	\(0\)	\(\frac{1}{2}\)	\(1\)
\(y\)	\(-\frac{\pi}{2}\)	\(-\frac{\pi}{6}\)	\(0\)	\(\frac{\pi}{6}\)	\(\frac{\pi}{2}\)

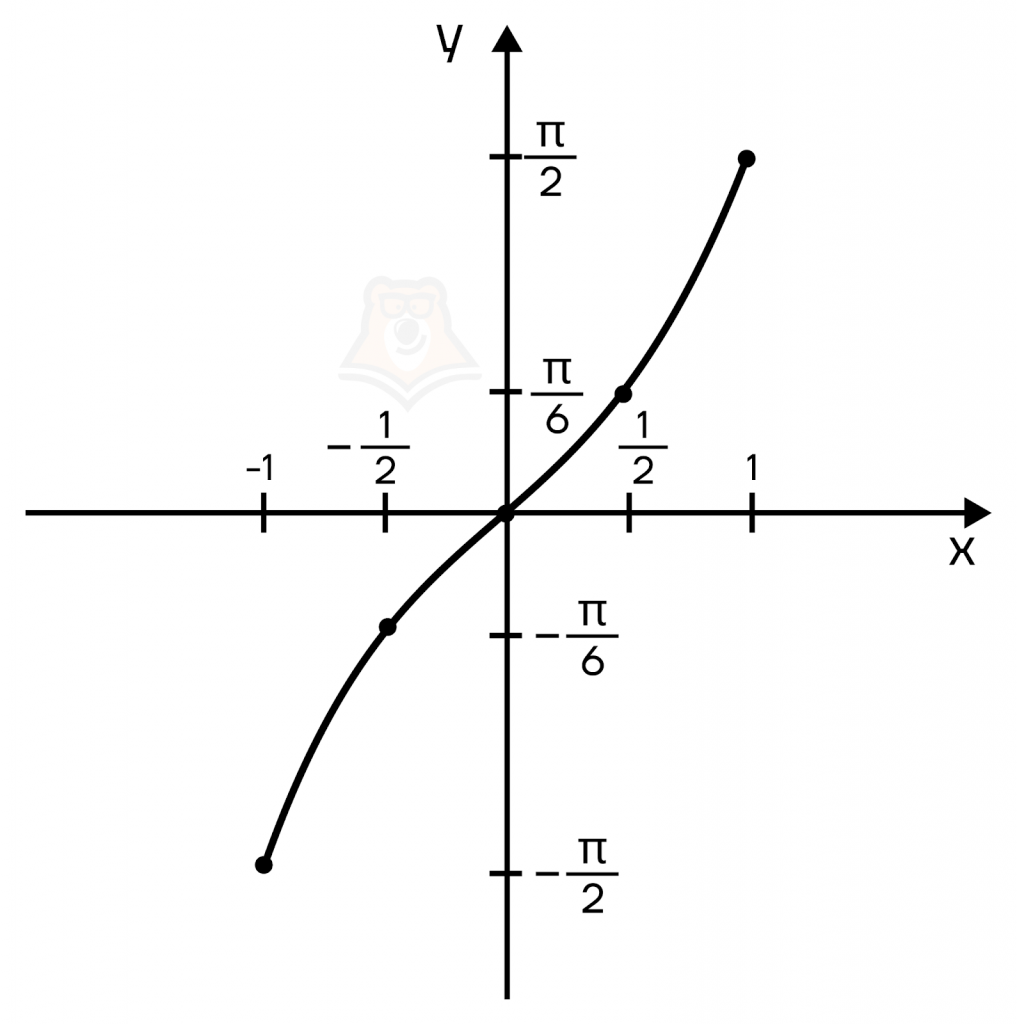
Проверим, будет ли соблюдаться, что функции \(y=arcsin(x)\) и \(y=sin(x)\) (на отрезке \([-\frac{\pi}{2}; \frac{\pi}{2}]\)) будут симметричны относительно прямой \(y=x\).

Барабанная дробь…

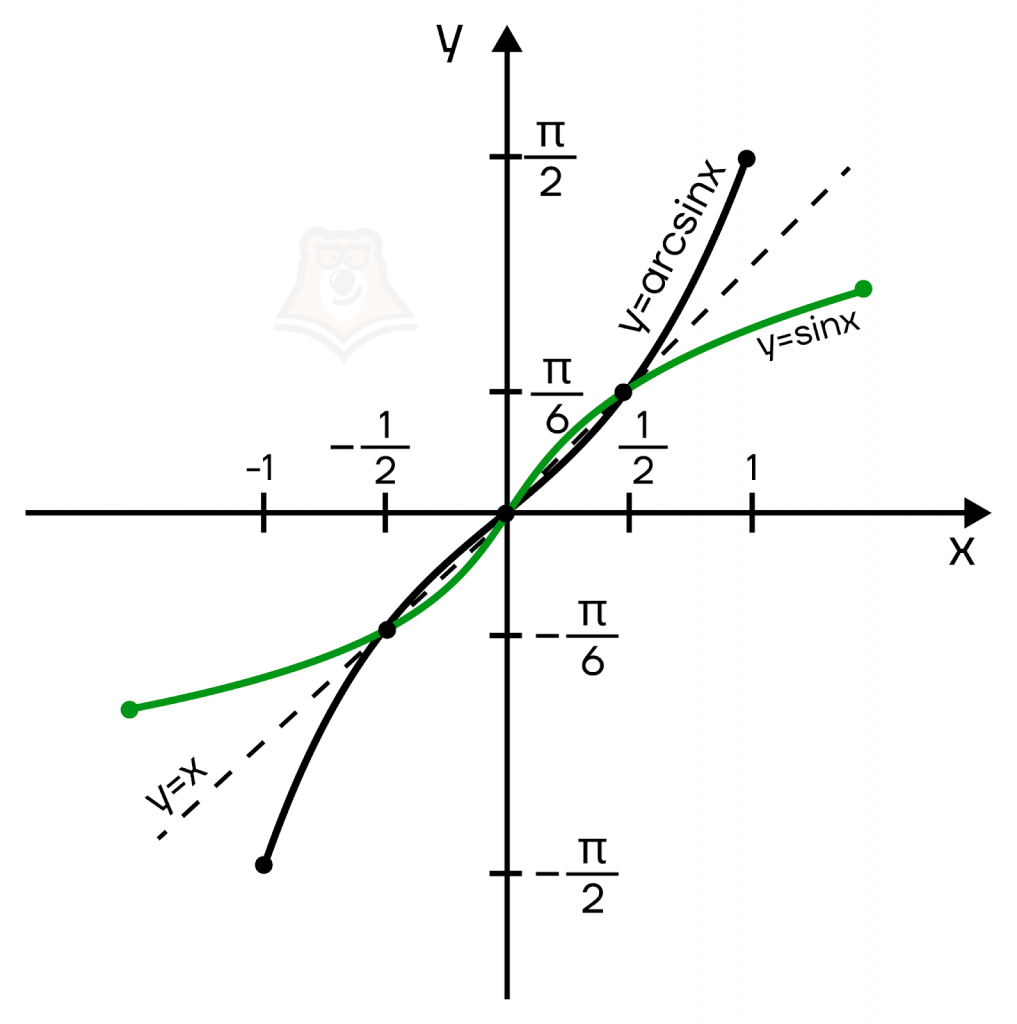
Да, все так! А теперь подведем небольшой итог для арксинусов и рассмотрим основные свойства функции. 

Свойства \(y=arcsin(x)\)

1. Область определения функции \(D(y): x\in [-1; 1]\).
2. Область значений \(E(y):y\in [-\frac{\pi}{2}; \frac{\pi}{2}]\).
3. \(y=arcsin(x)\) ― непрерывна на всей области определения.
4. Функция монотонно возрастает на всей области определения.
5. Имеет наибольшее ― \(\frac{\pi}{2}\) при \(x=1\) и наименьшее  ― \(-\frac{\pi}{2}\) при \(x=-1\) значения.
6. Является нечетной (доказательство мы рассмотрели ранее), а значит график этой функции симметричен относительно начала координат.
7. Принимает положительные значения при \(x\in (0; 1]\), отрицательные ― при \(x\in [-1; 0)\).
8. Не является периодической.

Теперь рассмотрим арккосинус. Для него уже другие ограничения: \(x\in [-1; 1]\), а вот \(y\in [0;\pi ]\).  Составим таблицу точек для \(y=arccos(x)\):

\(x\)	\(-1\)	\(-\frac{1}{2}\)	\(0\)	\(\frac{1}{2}\)	\(1\)
\(y\)	\(\pi\)	\(\frac{2\pi}{3}\)	\(\frac{\pi}{2}\)	\(\frac{\pi}{3}\)	\(0\)

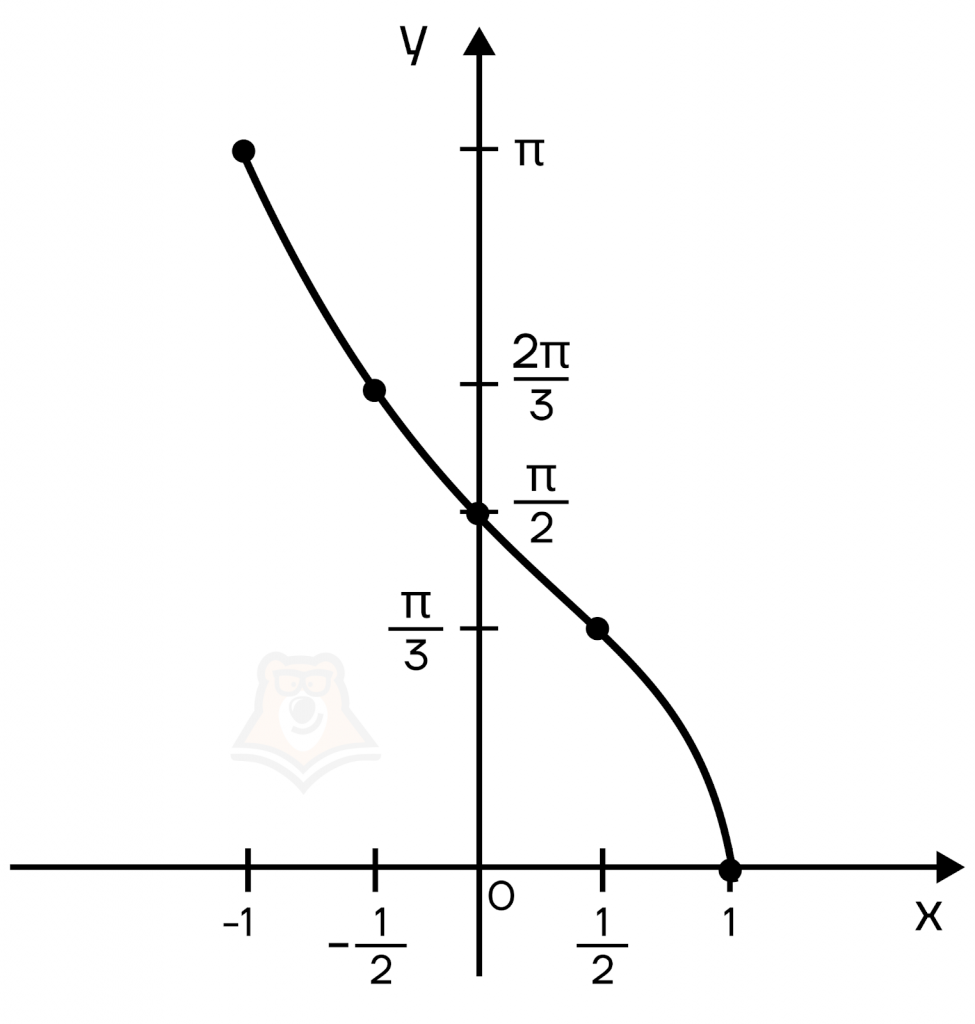
Проверим, будут ли симметричны \(y=arccos(x)\) и \(y=cos(x)\) (на отрезке \([0;\pi ]\)) относительно прямой \(y=x\).

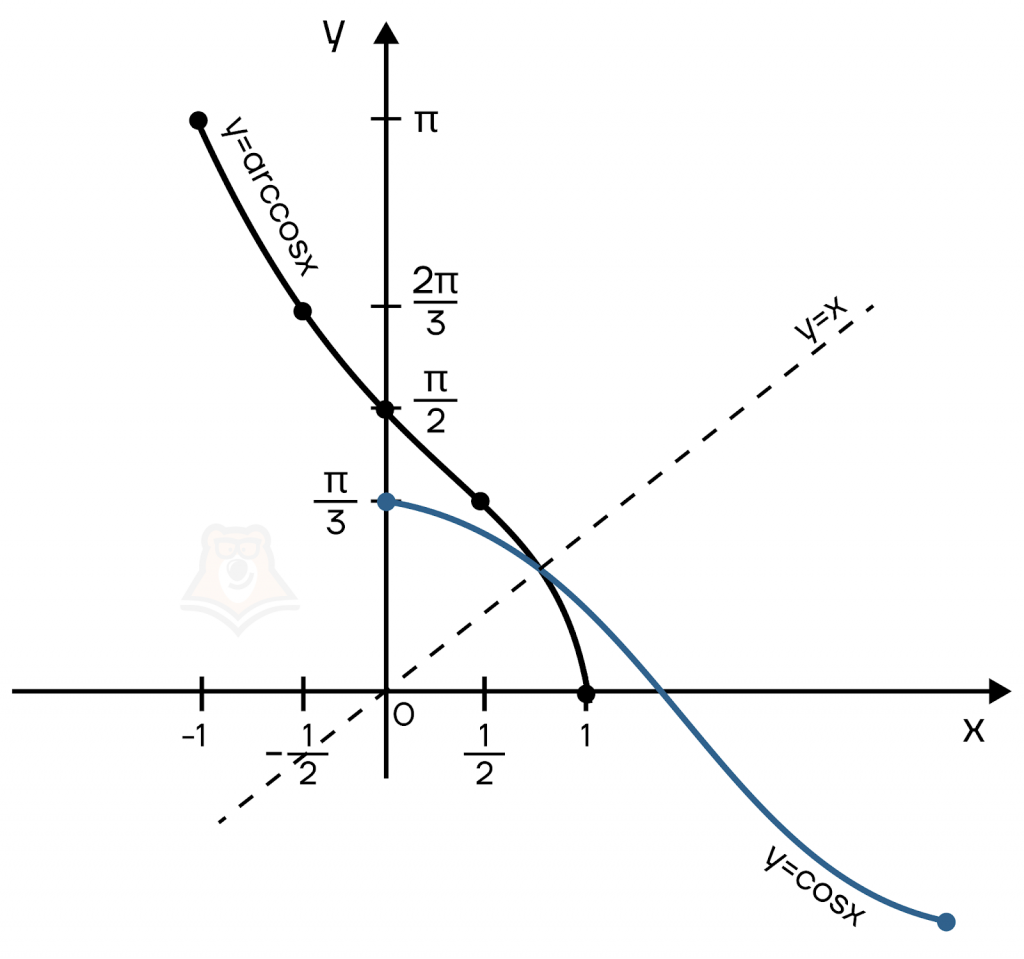
И… снова успех!

Свойства \(y=arccos(x)\)

1. Область определения функции \(D(y): x\in [-1; 1]\).
2. Область значений \(E(y):y \in[ 0;\pi ]\).
3. \(y=arccos(x)\) ― непрерывна на всей области определения.
4. Функция монотонно убывает на всей области определения.
5. Имеет наибольшее ― \(\pi\) при \(x=1\) и наименьшее  ― \(0\) при \(x=-1\) значения.
6. Является функцией общего вида, то есть ее график не является симметричным ни относительно оси \(Oy\), ни относительно начала координат.
7. Принимает положительные значения при любых \(x\) из области определения.
8. Не является периодической.

Проделаем ту же работу для арктангенса, помня, что из определения на \(y=arctg(x)\) накладываются следующие ограничения: \(y\in (-\frac{\pi}{2}; \frac{\pi}{2})\) (получается, что \(y=-\frac{\pi}{2}\) и \(y=\frac{\pi}{2}\) ― асимптоты).

Старая добрая таблица для точек: 

x	\(-\sqrt{3}\)	\(-1\)	\(0\)	\(1\)	\(\sqrt{3}\)
y	\(-\frac{\pi}{3}\)	\(-\frac{\pi}{4}\)	\(0\)	\(\frac{\pi}{4}\)	\(\frac{\pi}{3}\)

И ни для кого уже не сюрприз \(y=arctg(x)\) и \(y=tg(x)\) тоже симметричны относительно \(y=x\).

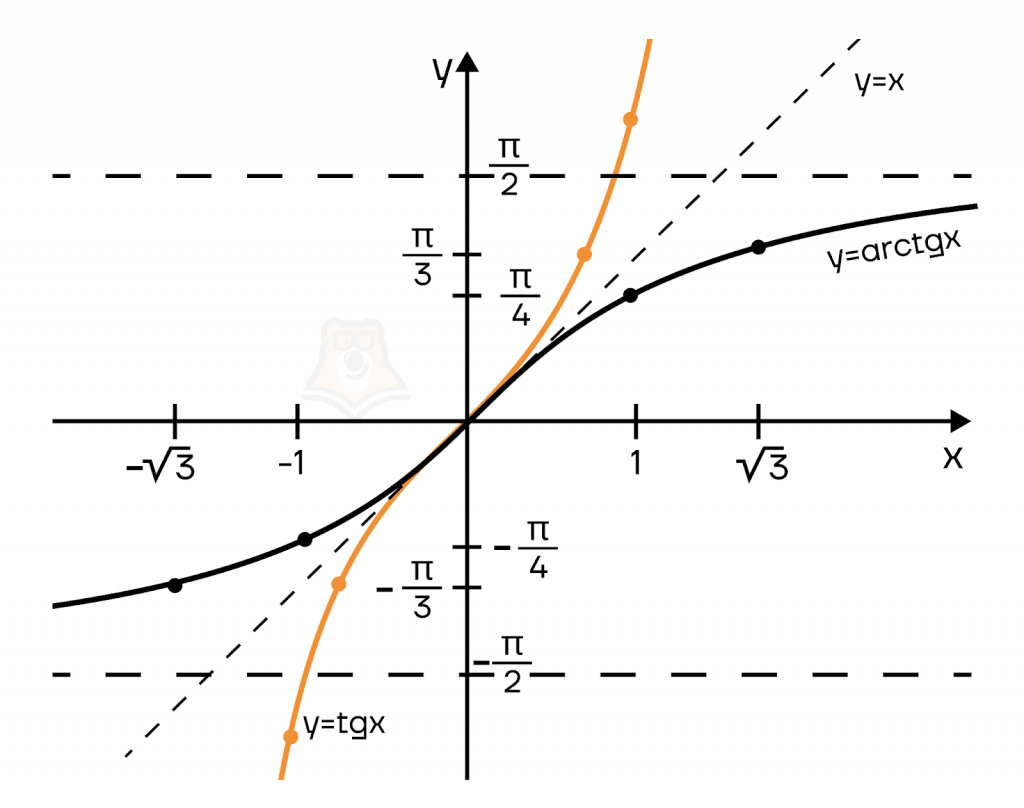
Свойства \(y=arctg(x)\)

1. Область определения функции \(D(y): x-;+\).
2. Область значений \(E(y):y\in (-\frac{\pi}{2}; \frac{\pi}{2})\).
3. \(y=arctg(x)\) ― непрерывна на всей области определения.
4. Функция монотонно возрастает на всей области определения.
5. Не имеет наибольшего и наименьшего значения.
6. Прямые \(y=-\frac{\pi}{2}\) и \(y=\frac{\pi}{2}\) являются горизонтальными асимптотами.
7. Нечетная функция, значит, ее график симметричен относительно начала координат.
8. Принимает положительные значения при \(x\in ( 0;+\infty)\) , отрицательные ― при \(x\in ( -\infty; 0 )\).
9. Не является периодической.

Наконец, арккотангенс, из определения которого следуют вот такие ограничения: \(y\in (0;\pi)\) (получается, что \(y=0\) и \(y=\pi \) ― асимптоты).

Составим таблицу с точками для построения графика:

x	\(-\sqrt{3}\)	\(-1\)	\(0\)	\(1\)	\(\sqrt{3}\)
y	\(\frac{5\pi}{6}\)	\(\frac{3\pi}{4}\)	\(\frac{\pi}{2}\)	\(\frac{\pi}{4}\)	\(\frac{\pi}{6}\)

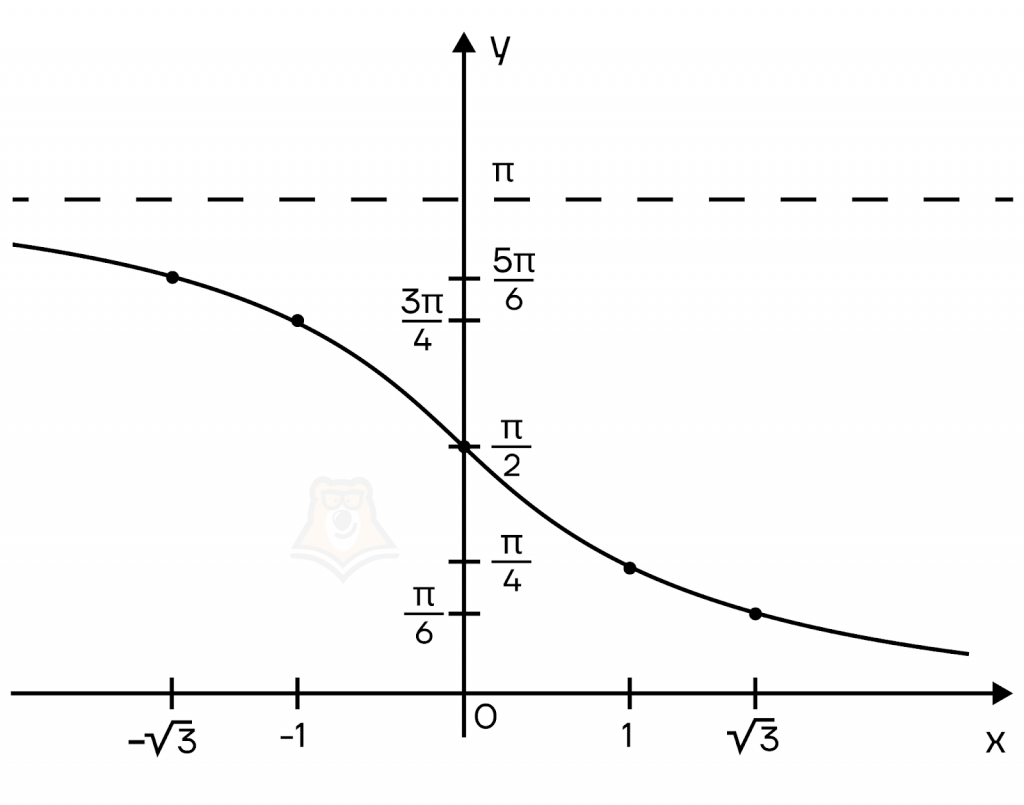
И, конечно, функции \(y=arcctg(x)\) и \(y=ctg(x)\) симметричны относительно прямой \(y=x\).

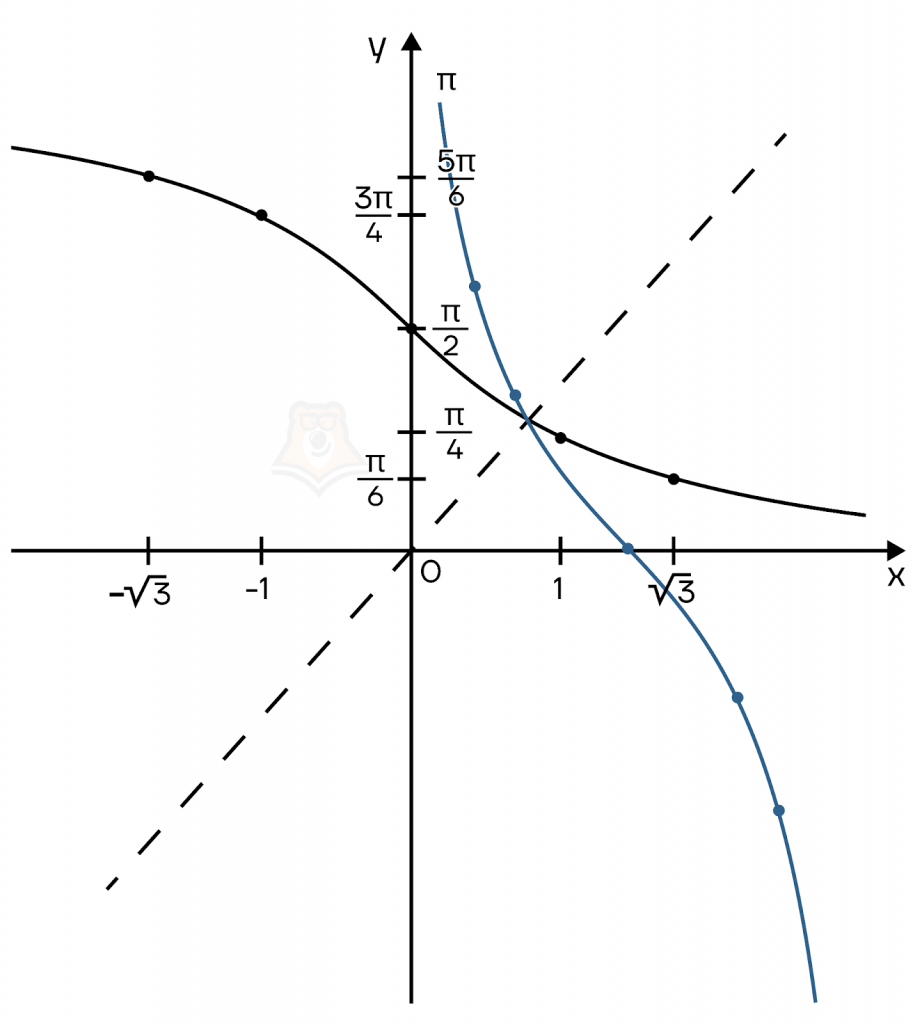
Свойства \(y=arcctg(x)\)

1. Область определения функции \(D(y): x\in (-\infty;+\infty)\).
2. Область значений \(E(y):y\in (0;\pi )\).
3. \(y=arcctg(x)\) ― непрерывна на всей области определения.
4. Функция монотонно убывает на всей области определения.
5. Не имеет наибольшего и наименьшего значения.
6. Прямые \(y=0\) и \(y=\pi\) являются горизонтальными асимптотами.
7. Функция общего вида.
8. Принимает положительные значения при любых \(x\) из области определения.
9. Не является периодической.

Вот мы и закончили обсуждение аркфункций. Это было хоть и непросто, но очень интересно! 

Однако тригонометрия не заканчивается и на этой теме… Вы знали, что можно упростить решение тригонометрических уравнений? А как это сделать, вы узнаете в статье «Тригонометрические подстановки».

Термины

Асимптота ― это прямая, к которой график функции бесконечно стремится, но никогда ее не пересекает.

Фактчек

• Обратные тригонометрические функции ― функции обратные к основным тригонометрическим функциям. Их названия образуются с помощью приставки арк-: арксинус, арккосинус, арктангенс, арккотангенс.
• Обратные тригонометрические функции не являются периодическими. Одному y соответствует только один x.
• Чтобы найти значение обратной тригонометрической функции в данной точке, достаточно взглянуть на тригонометрическую окружность или запомнить таблицу.

Проверь себя

Задание 1.
Какие утверждения верны для функции \(y=arcsin(x)\)?

1. Область значений \(y\in [-\frac{\pi}{2}; \frac{\pi}{2}]\)
2. Является периодической
3. Не имеет наибольшего и наименьшего значения
4. Монотонно возрастает

Задание 2.
Какой является функция \(y=arcctg(x)\)?

1. Четная
2. Нечетная
3. Функция общего вида
4. Невозможно определить

Задание 3.
Относительно чего симметричны взаимно обратные функции? 

1. Прямой \(y=x\)
2. Оси \(Oy\)
3. Начала координат
4. Нет точного ответа

Задание 4.
Чему равен \(arccos(-\frac{\sqrt{3}}{2})\)?

1. \(-\frac{\pi}{6}\)
2. \(\frac{5\pi}{6}\)
3. \(\frac{2\pi}{3}\)
4. \(-\frac{\pi}{3}\)

Задание 5.
Какова область определения функции \(y=arctg(x)\)?

1. \(x\in [-1; 1]\)
2. \(x\in (-1; 1)\)
3. \(x\in (-\frac{\pi}{2}; \frac{\pi}{2})\)
4. \(x\in (-\infty;+\infty)\)

Ответы: 1. ―1, 4;  2. ― 3; 3. ― 1; 4. ― 2; 5. ― 4.