Основы планиметрии. Точка, прямая, луч, отрезок и угол

На этой странице вы узнаете

• Что использовали раньше для измерения длины?
• Почему в окружности 360 градусов?
• Почему может существовать сразу несколько миров?

В жизни мы часто встречаемся с такими выражениями  как «точка на карте», «идти по прямой» или «угол комнаты». Но знали ли вы, что в этих фразах упоминаются термины из геометрии?

Точка, прямая, луч

Для начала давайте разберемся именно с геометрическими терминами.
Что такое точка, прямая, луч, отрезок и угол?

Точка – это математический абстрактный объект, не имеющий измеримых характеристик, кроме координат. 

Другими словами, точка не имеет ни длины, ни ширины, ни высоты, ни каких-либо других характеристик. Она настолько мала, что ее невозможно измерить. Но при этом точка выполняет очень важную роль – задает положение объекта в пространстве. 

Любую фигуру можно разбить на бесконечное количество точек, которые будут иметь свои координаты. 

Но если мы будем описывать каждую фигуру как множество точек, мы как минимум устанем. В любой, даже самой маленькой фигуре, их бесконечное количество. Поэтому в математике существует еще несколько понятий, которые упрощают описание объекта. 

Например, если мы выстроим бесконечное количество точек на одной прямой линии, то получим прямую. 

А вот если рассмотреть множество последовательно идущих в произвольном направлении друг за другом точек, то мы получим произвольную линию. 

Линия – длинный и тонкий объект, способный принимать произвольную форму. 

Линии мы встречаем каждый день, например, когда пишем. Ручка выводит линию, которая складывается в буквы, а буквы в слова. 

Линию можно задать с помощью уравнения линии на плоскости. С помощью уравнения задается множество точек, координаты которых удовлетворяют уравнению. 

При этом с помощью уравнений можно задать любую произвольную линию, будь то прямая, окружность или изогнутая кривая. Примерами уравнений линий могут служить элементарные функции. 

Прямая – это бесконечная линия, не имеющая углов, скруглений, «изломов».

Но не все прямые бесконечны. Иначе мы бы не смогли описать ими фигуры, существующие в мире. Представьте, если бы у стола были бесконечные грани. Таким предметом мебели было бы невозможно пользоваться. 

Поэтому прямую можно ограничить. Если мы ограничим ее с одной стороны, то получим луч. 

Луч – это прямая, ограниченная точкой с одной стороны. У луча есть начало, но нет конца.

Но что будет, если мы ограничим луч и со второй стороны? Мы получим отрезок. 

Отрезок

В основном все геометрические фигуры и тела строятся именно из отрезков. 

Отрезок – это прямая, ограниченная точками с обеих сторон. Отрезок состоит из бесконечного множества точек, лежащих на линии между концами отрезка.

Поскольку у отрезка есть начало и конец, он обладает одним очень важным свойством: длиной. 

Длина отрезка – это расстояние между его концами. 

При этом любой отрезок можно разбить на единичные отрезки. К единичным отрезкам относят единицу измерения, в которой задается отрезок. 

Длина может измеряться с помощью любой единицы: сантиметров, метров, дюймов или произвольного предмета. 

Под измерением отрезков подразумевается подсчет количества единиц, которые лежат в отрезке. 

Длина отрезка либо задана изначально, либо ее можно вычислить геометрическими действиями, либо ее можно измерить. В настоящее время для измерения длин отрезков используют линейки, сантиметры и любые другие измерительные приборы. 

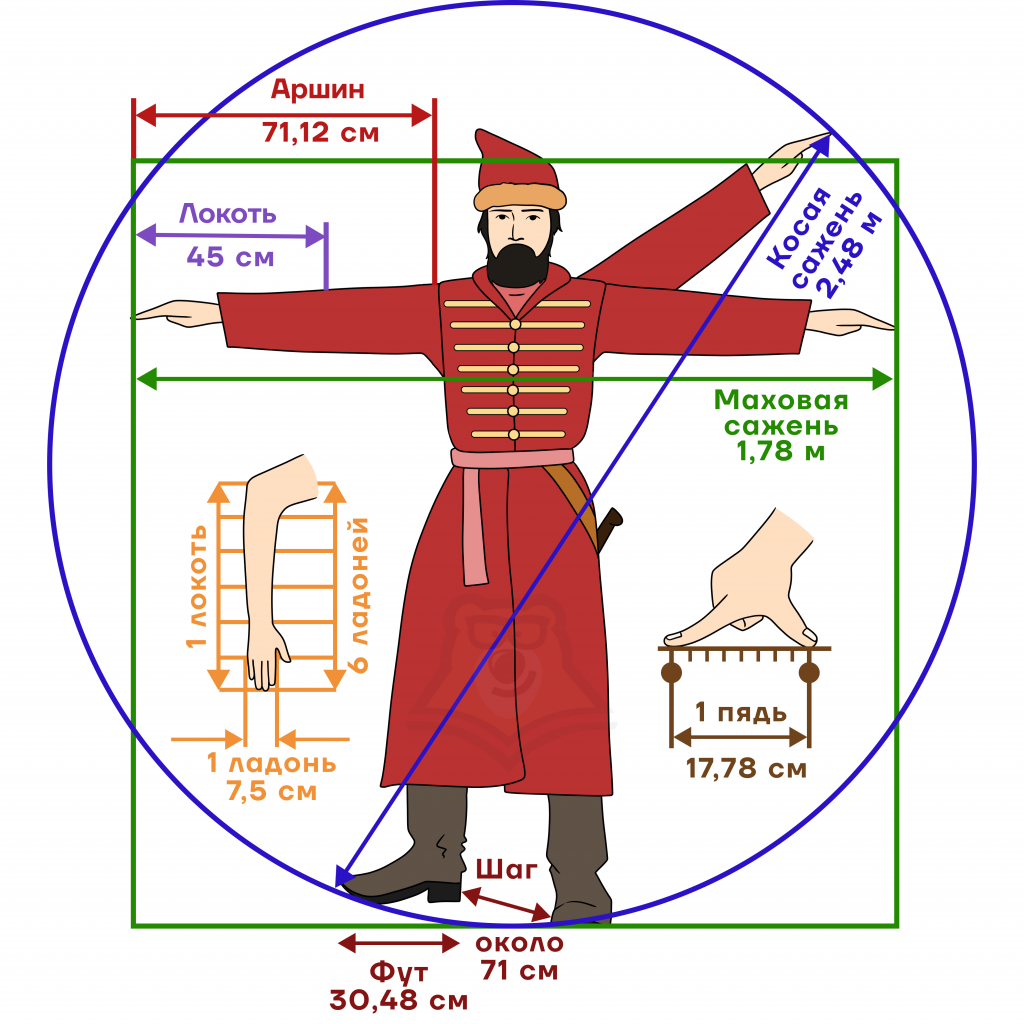
Что использовали раньше для измерения длины? Единицы измерения, которые мы используем в настоящее время, относятся к СИ – международной системе единиц. Длина по СИ измеряется в метрах. Однако раньше существовали другие единицы измерения. В их основе лежало человеческое тело. Так, например, были такие единицы измерения как локоть (примерно 45 см), шаг (примерно 71 см) или ладонь (примерно 7,5 см). Позже эта система измерений заменилась на знакомую нам метрическую.

Длину отрезков можно изменять. Например, если мы увеличим отрезок АВ длиной 10 см в 3 раза, то получим отрезок CD длиной 30 см. 

При этом отношение длин отрезков друг к другу будут равны:

\(\frac{AB}{CD}=\frac{1}{3}\) или \(\frac{CD}{AB}=3\)

Возьмем еще два отрезка произвольной длины, например, EF=6 см, GH = 18 см. Заметим, что их отношение будет равно:

\(\frac{EF}{GH}=\frac{1}{3}\) или \(\frac{GH}{EF}=3\)

Следовательно, отношение отрезков AB и CD и отношение отрезков EF и GH равны между собой. Такие отрезки называются пропорциональными. 

Пропорциональные отрезки – пары отрезков, отношения которых равны. 

Пропорциональные отрезки активно используют для составления пропорций, которые могут пригодиться, например, в решении задач с процентами. 

Вернемся к лучам и отрезкам. Чем отличается луч от отрезка?

Представим, что у нас есть прядильный станок, который может работать бесконечно. Допустим, мы решили создать ниточку, включили станок и начали прясть. Начало нитки будет ограничено ее концом. 

Пока мы прядем ниточку, и она не имеет конца, ее можно сравнить с лучом. У луча есть начало и нет конца. Но как только мы отрежем ниточку от станка, то получим отрезок. У отрезка есть и начало, и конец. 

А теперь попробуем из точки «выпустить» два луча. Тогда мы получим еще одну геометрическую фигуру – угол. 

Угол

Сформулируем понятие угла. 

Угол – это фигура, образованная двумя лучами, исходящими из одной точки.

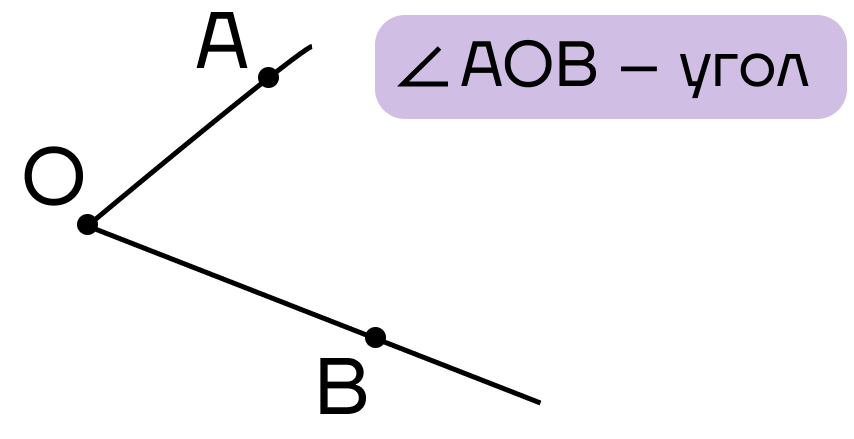
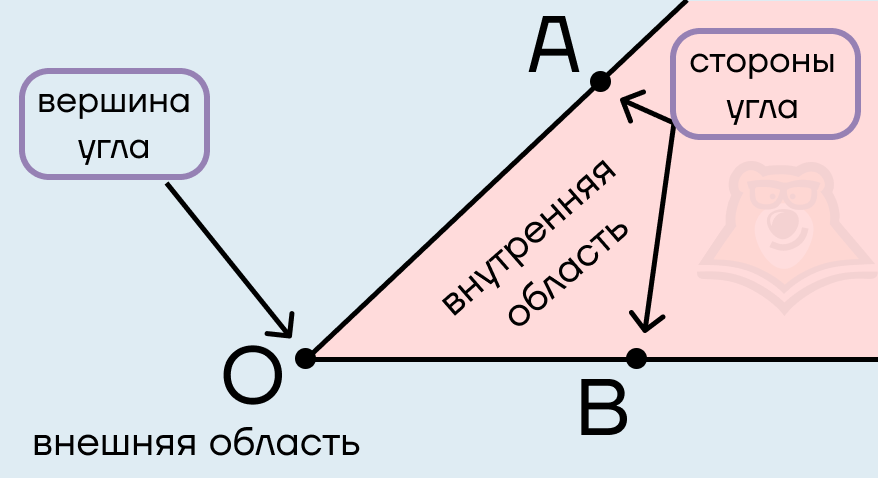
При этом лучи, выходящие из точки, будут называться сторонами угла. Точка – вершиной. 

Угол делит плоскость на две части: 

• внутренняя область угла;
• внешняя область угла. 

В основном углы измеряются с помощью градусов. Градус равен \(\frac{1}{360}\) окружности. То есть из точки мы можем выпустить 360 лучей с равным шагом, и мы получим 360 градусов. 

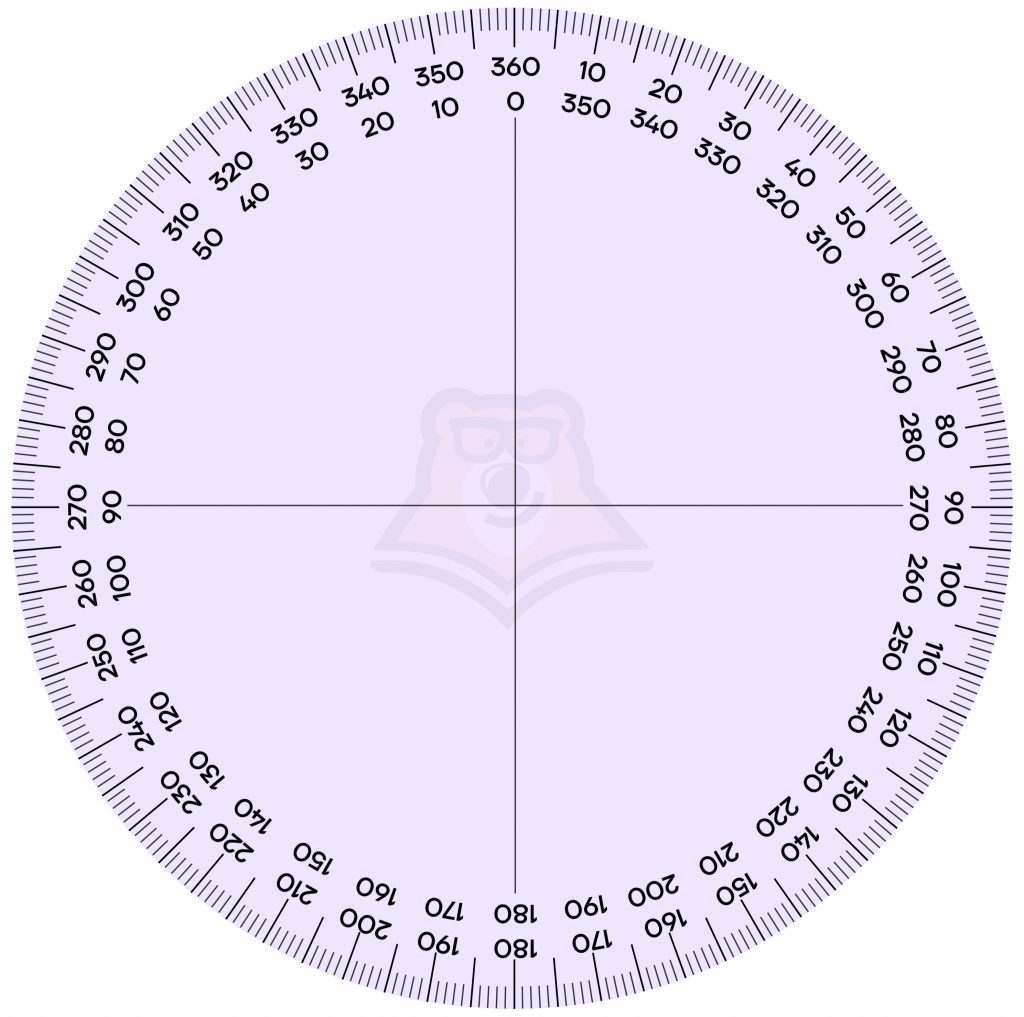
Почему в окружности 360 градусов? Существует большое множество систем счисления. Однако сейчас нас интересует шестидесятеричная система, которая зародилась в Древнем Вавилоне. Число 60 было ритуальным для вавилонцев и стало основой для их календаря. Люди наблюдали за движением Солнца и пришли к выводу, что в году примерно 360 дней. Именно поэтому они разделили окружность на 360 равных частей. Каждый день Солнце делало «шаг». Это отразилось и в названии единицы измерения: слово градус с латыни означает «шаг, ступень».

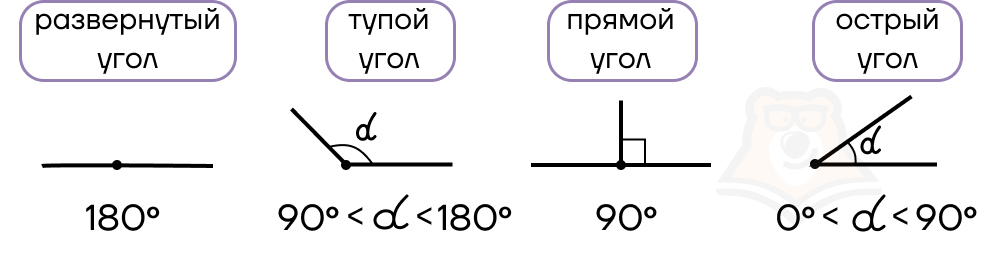
По величине углы можно разделить на 4 вида:

• Острые – углы до 90°.
• Прямые – углы, равные 90°.
• Тупые – углы больше 90°.
• Развернутый – угол, равный 180°.

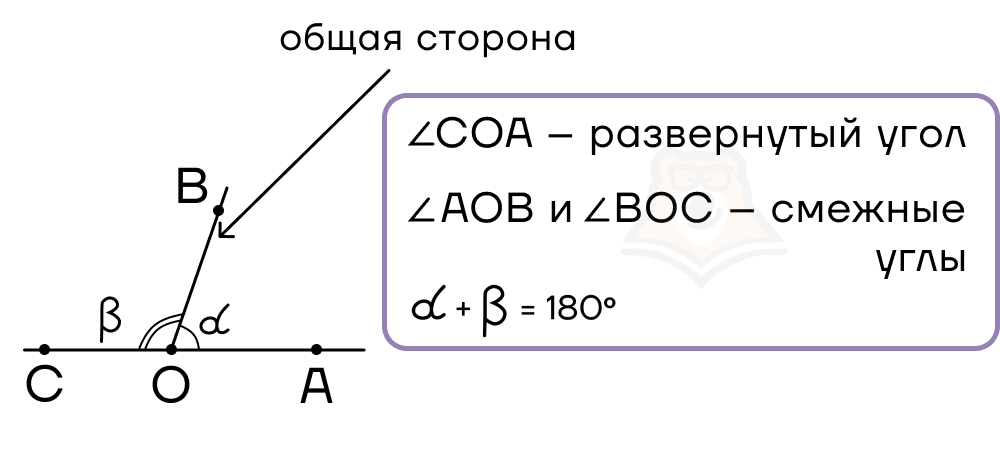
В зависимости от расположения углов друг от друга можно выделить два вида. 

Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 180°.

В жизни смежные углы можно встретить в любой комнате: стены это общая сторона углов, а две другие образуются полом. В комнате смежные углы равны по 90°. 

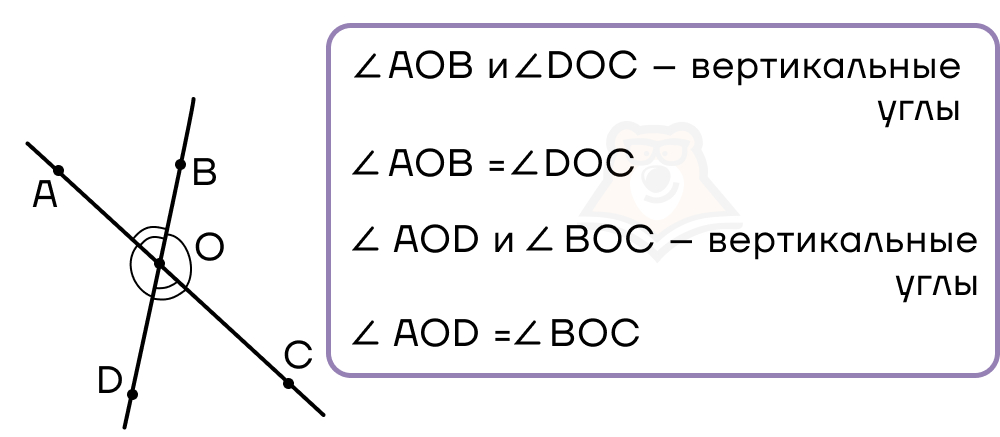
А вот если продолжить лучи угла за точку с «другой стороны», то получим вертикальные углы. 

Вертикальные углы – это углы, вершиной которых является одна и та же точка, стороны одного такого угла являются продолжениями сторон другого такого угла. Вертикальные углы всегда равны.

Вертикальные углы образуют палочки, когда мы кушаем японскую кухню. 

Смежные и вертикальные углы могут встретиться в №15 ОГЭ по математике. 

Углы, отмеченные на рисунке одной дугой, равны. Найдите угол х. Ответ дайте в градусах.

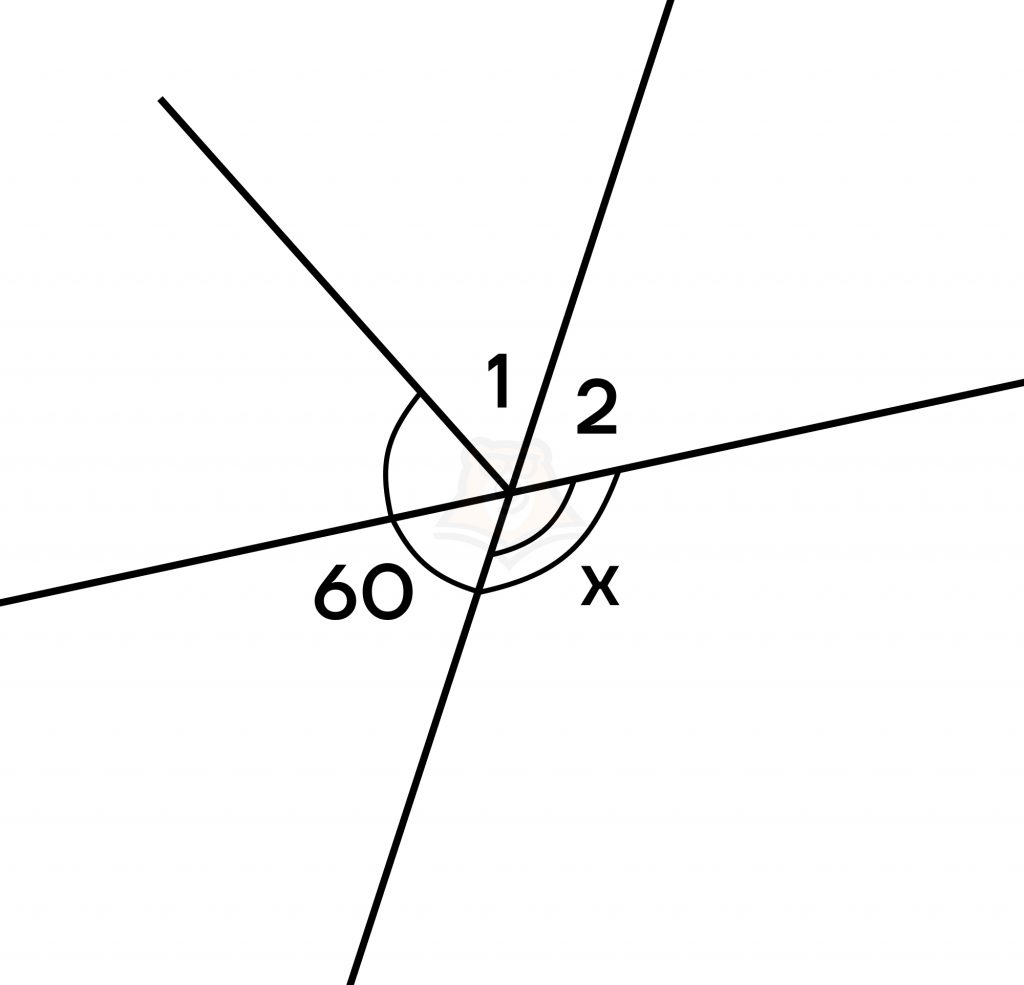
Решение.
Заметим, что угол 2 и угол в 60° вертикальные, значит, угол 2 равен 60 градусам. 

Углы 2 и х смежные, значит, их сумма равна 180°. Откуда получаем:

∠x+60°=180°
∠x=180°-60°
∠x=120°

Ответ: 120

При работе с углами мы нередко будем встречаться с понятием биссектрисы. 

Биссектриса угла — это луч, который делит угол пополам. 

На рисунке ниже АЕ – биссектриса угла ВАС, которая делит его на два равных угла ВАЕ и ЕАС. 

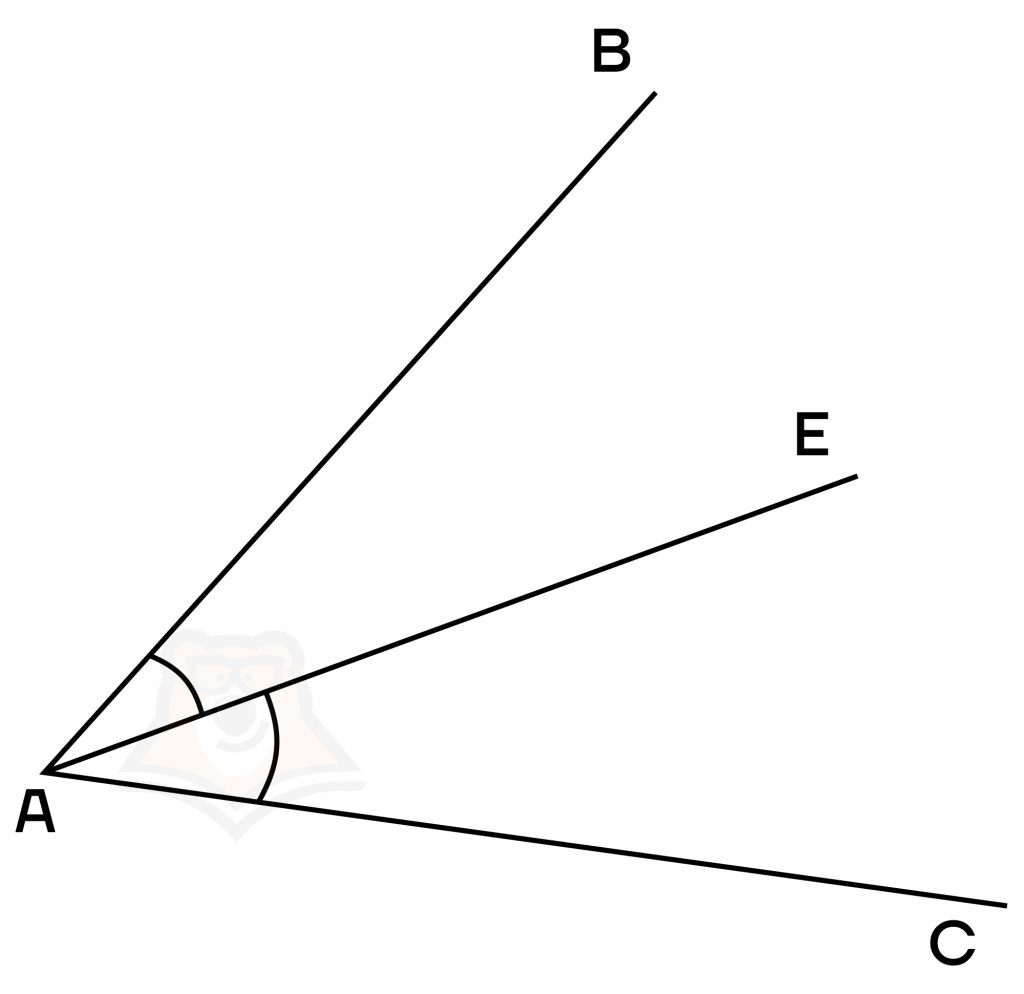
А теперь перейдем к прямым. 

Взаимное расположение прямых

Прямые, как и углы, имеют несколько вариантов взаимного расположения. Представим, что мы рисуем несколько линий на листочке в произвольном положении. Одним из вариантов их расположения будет, когда линии пересекают друг друга. А второй вариант: линии никогда не пересекутся.

В геометрии каждый из вариантов имеют свое название. Рассмотрим первый. 

Пересекающиеся прямые – это прямые, у которых есть одна общая точка.

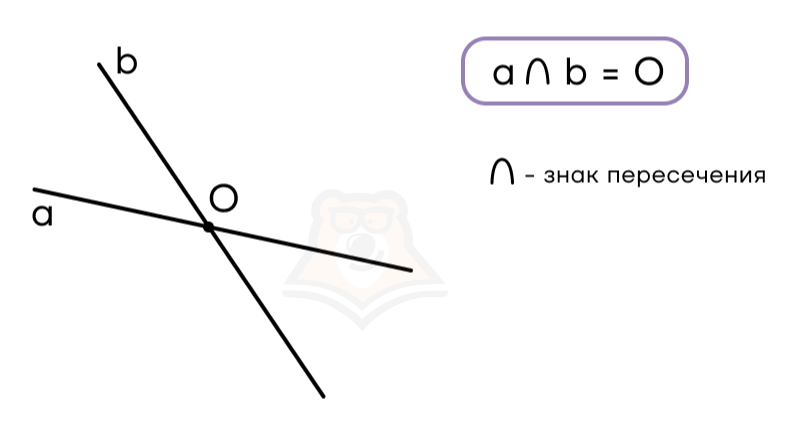
Рисунок не просто так похож на вертикальные углы. На самом деле, любые вертикальные углы образованы двумя пересекающимися прямыми! 

Среди пересекающихся прямых можно выделить один особенный случай. 

Перпендикулярные прямые – это прямые, пересекающиеся под прямым углом. Такие прямые образуют четыре прямых угла при пересечении.

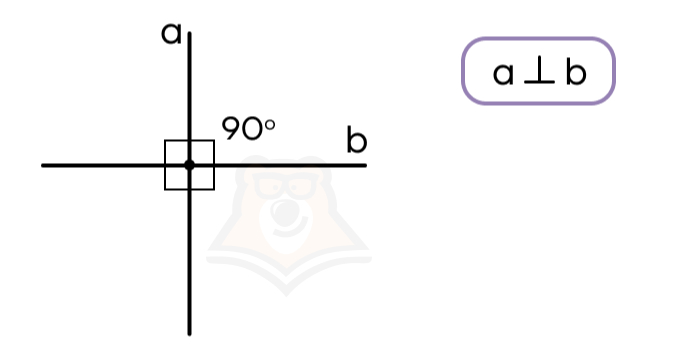
Для углов в этом случае также существует свое название: это углы с взаимно перпендикулярными сторонами. 

Итак, мы уже сказали, что существует еще одна ситуация, когда прямые никогда не пересекаются. Такие прямые называются параллельными. 

Параллельные прямые – это прямые, не имеющие ни одной общей точки.

Почему может существовать сразу несколько миров? В квантовой физике существует множество теорий о строении нашего мира, и одна из них – теория множественных миров. По этой теории существует бесконечное количество параллельных Вселенных (как и прямые, эти Вселенные не пересекаются друг с другом). Каждый раз, как в нашем мире происходит какое-то действие, выбор или ситуация, появляется несколько новых Вселенных, которые отличаются друг от друга только результатом. Например, мы случайно уронили кружку с соком, пока читали книжку. По теории множественных миров при этом образовалось две Вселенной: в одной мы действительно уронили кружку, а в другой не уронили. Таким образом, любое событие лишь один из путей развилки, которая образовывается во Вселенной, а мы лишь странники по череде ветвящихся миров.

Параллельные и перпендикулярные прямые можно встретить не только в планиметрии, но и в повседневной жизни, например, рельсы и шпалы. Относительно друг друга они  будут параллельными прямыми, а вот если рассмотреть один рельс и одну шпалу, то это уже перпендикулярные прямые. 

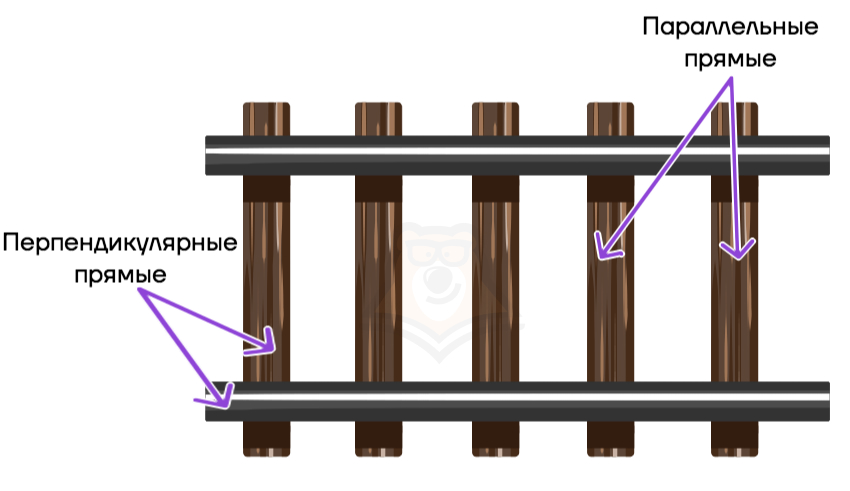
Заметим, что параллельные прямые имеют одинаковый угол наклона относительно любого элемента в пространстве: только в этом случае они никогда не пересекутся. Если угол наклона одной из прямых изменится хотя бы на долю градуса, то они станут пересекающимися и рано или поздно у них появится общая точка. 

Итак, подведем итог: прямые по их взаимному расположению можно разделить на параллельные и пересекающиеся. При этом пересекаться прямые могут либо под произвольным, либо под прямым углом. Прямые для последнего случая называются перпендикулярными. 

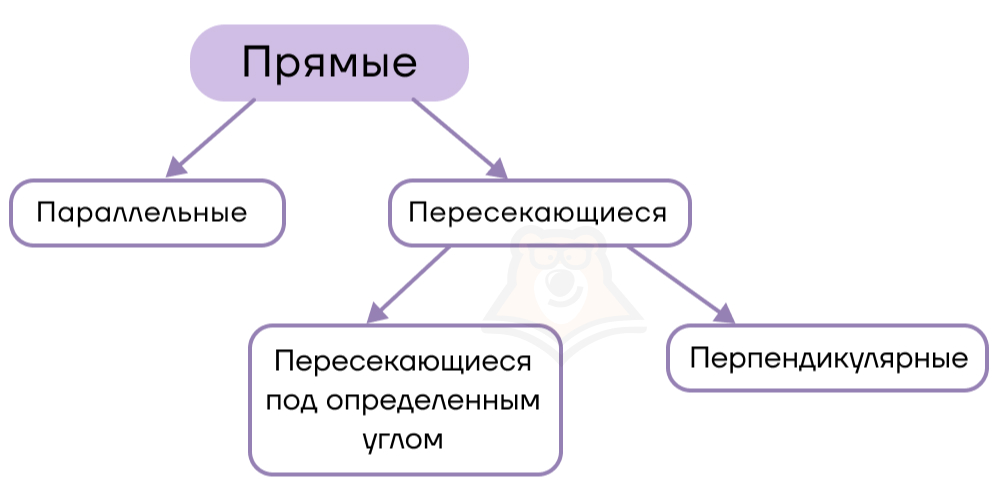
Параллельные прямые являются важной частью геометрии, на которой строится множество свойств, доказательств, фигур и тел. Поскольку параллельные прямые лежат «в основе» многих вещей, они имеют свою аксиому. 

Под аксиомой подразумеваются свойства, которые нет необходимости доказывать. 

Аксиома параллельных прямых

Эту аксиому также называют аксиомой Евклида.

Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

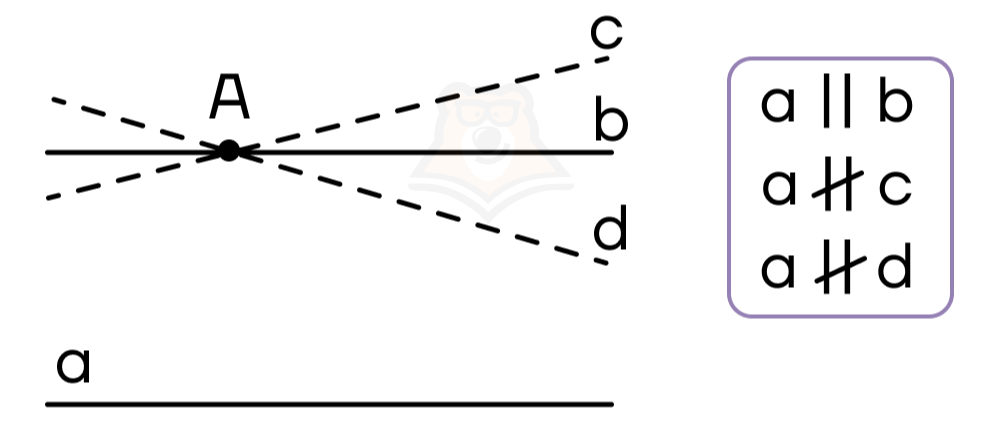
Это легко проследить: поскольку параллельные прямые должны иметь одинаковый угол наклона, то существует только один вариант, как можно ее провести через точку. 

Следствия из аксиомы параллельных прямых:

1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую параллельную прямую.

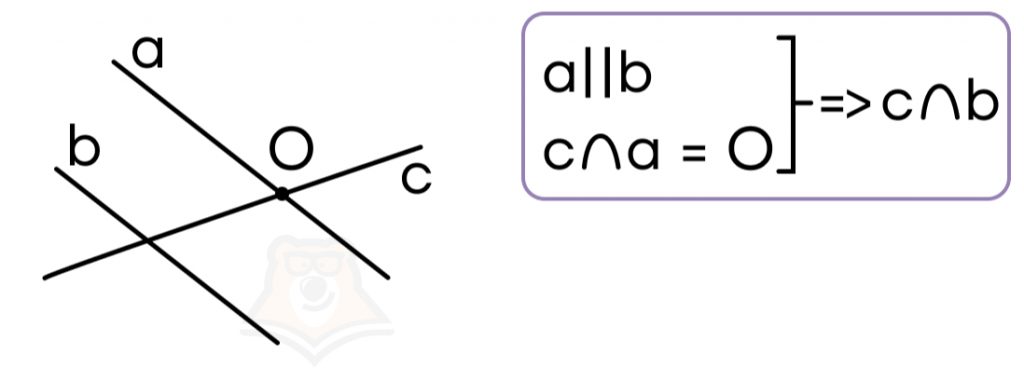
2. Если одна из двух параллельных прямых параллельна третьей прямой, то все эти прямые параллельны друг другу.

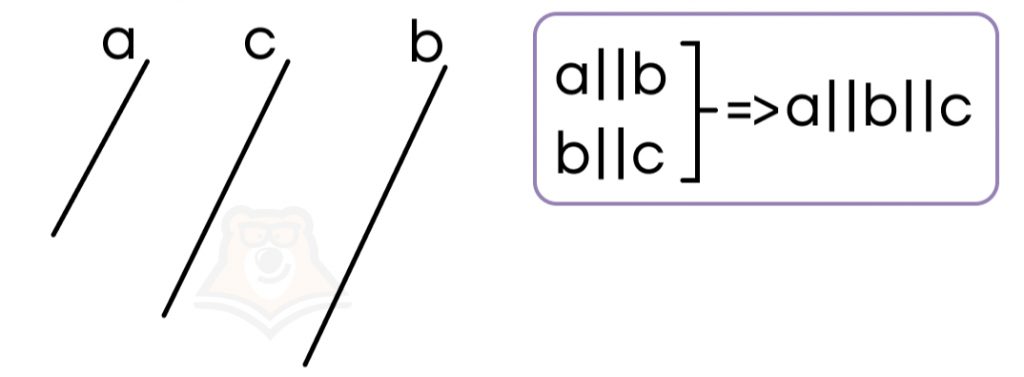
Но в геометрии не все так просто! Нельзя просто сказать, что прямые параллельны, это обязательно нужно доказать. Чтобы доказать, что прямые являются параллельными, используются признаки параллельности прямых.

Признаки параллельности прямых

Прежде чем перейти к признакам параллельности прямых, рассмотрим углы при пересечении двух прямых секущей. 

Секущая – это прямая, пересекающая несколько других прямых.

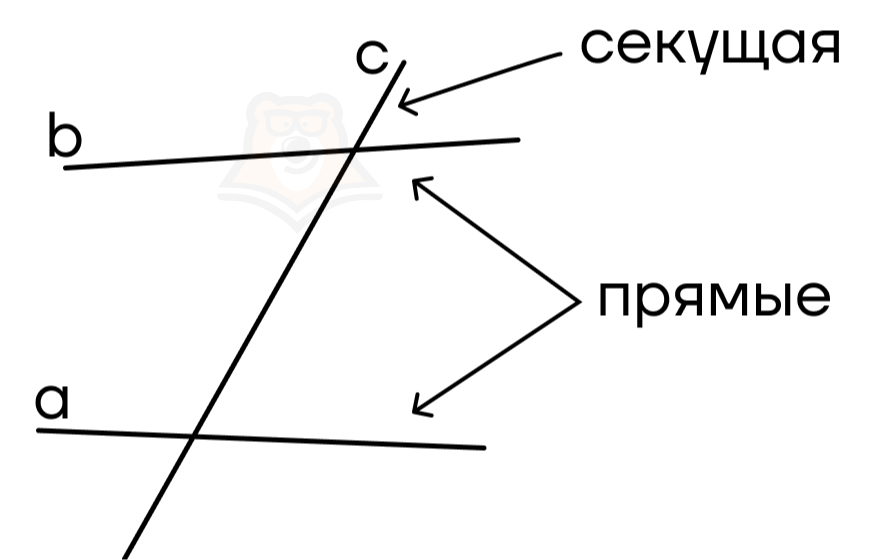
При таком расположении прямых можно выделить три вида углов:

• накрест лежащие углы,
• односторонние углы,
• соответственные углы.

Рассмотрим данные углы на примере.

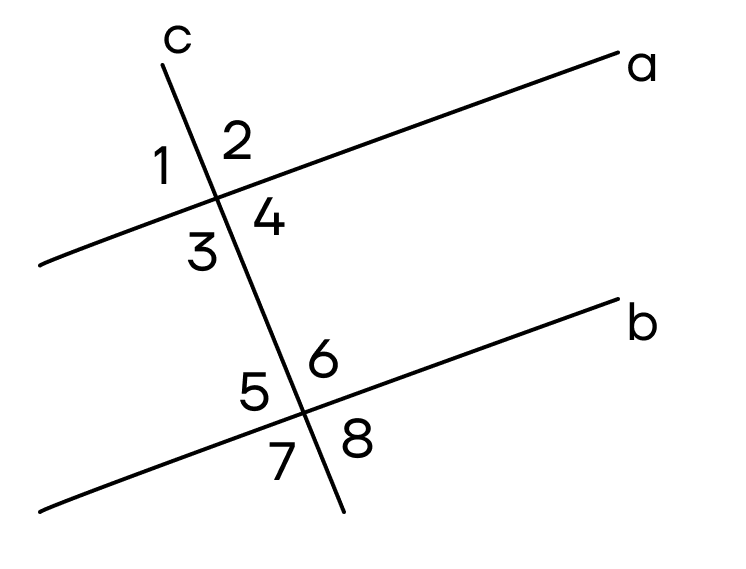
Если мы «поставим крест» на секущей, то попадем в пары углов. Такие углы называются накрест лежащими. Важно заметить, что накрест лежащие углы находятся «внутри» прямых. 

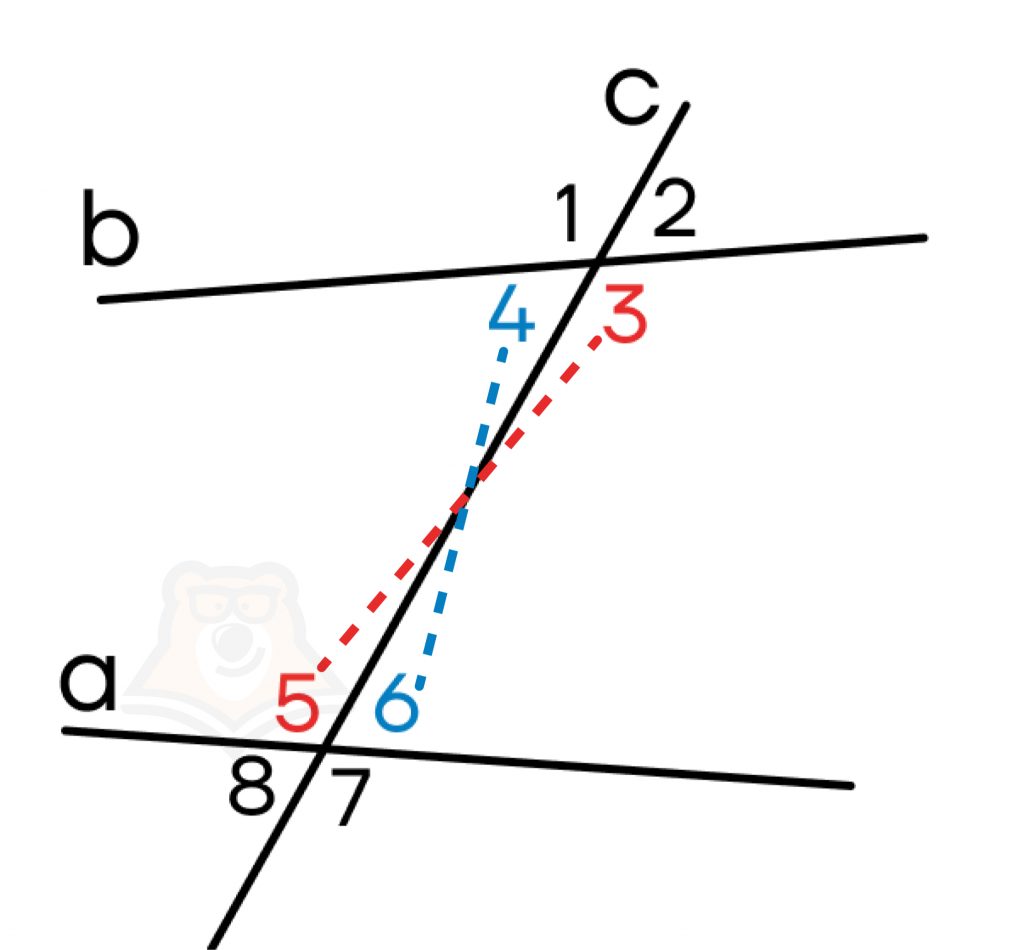
Углы «внутри» прямых создают еще две пары: 4 и 5, 3 и 6. Эти углы лежат с одной стороны от секущей, потому и называются односторонними. 

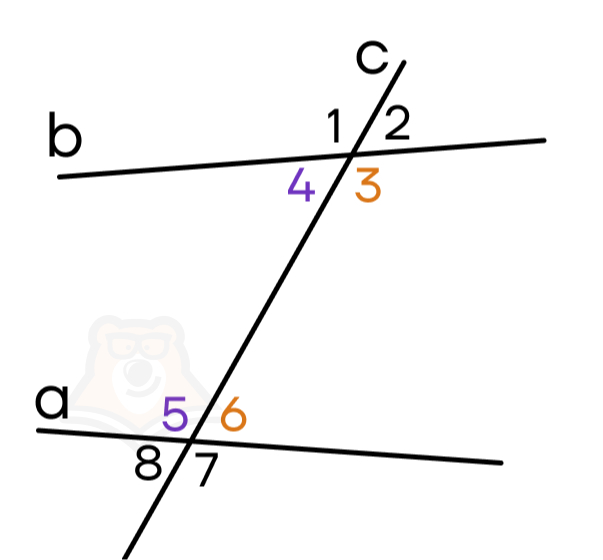
А вот если мы рассмотрим пары 1 и 5, 4 и 8, то заметим, что расположение одного угла относительно секущей и одной из прямых соответствует расположению второго угла при секущей и другой прямой. Такие углы называют соответственными. К соответственным углам также можно отнести 2 и 6, 3 и 7.

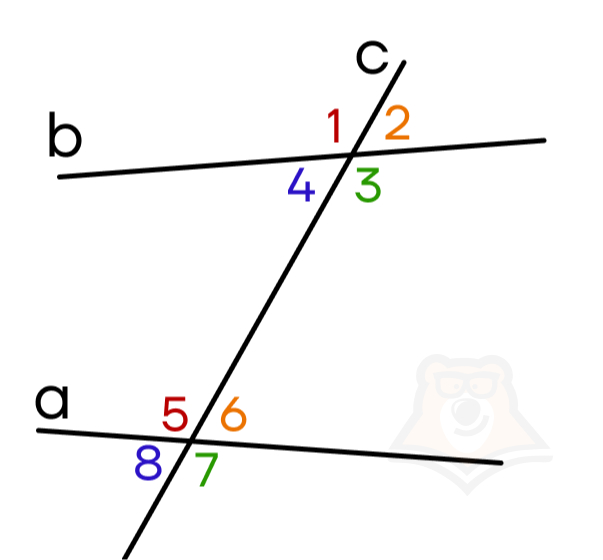
Итак, на иллюстрациях выше: 

• накрест лежащие углы: 4 и 6, 3 и 5;
• односторонние углы: 4 и 5, 3 и 6;
• соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Теперь, зная названия углов при прямых и секущей, мы можем перейти к изучению признаков параллельности прямых. 

Признаки параллельности прямых:

Теорема 1: если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

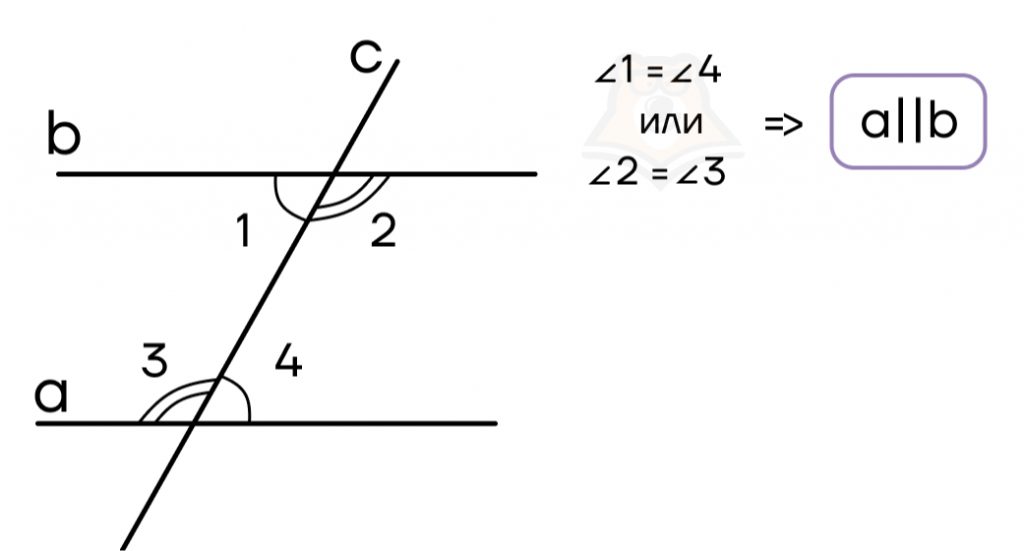
Теорема 2: если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

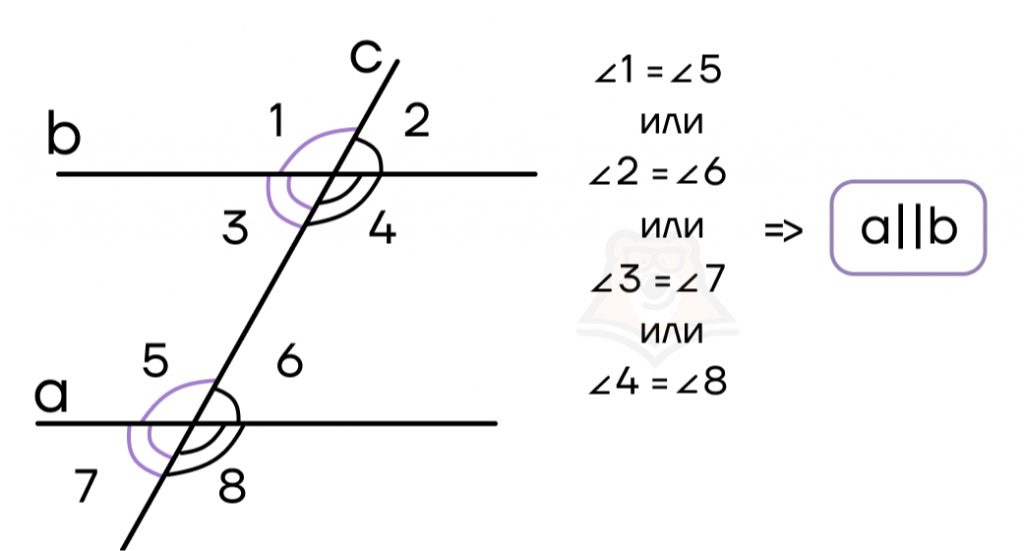
Теорема 3: если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.

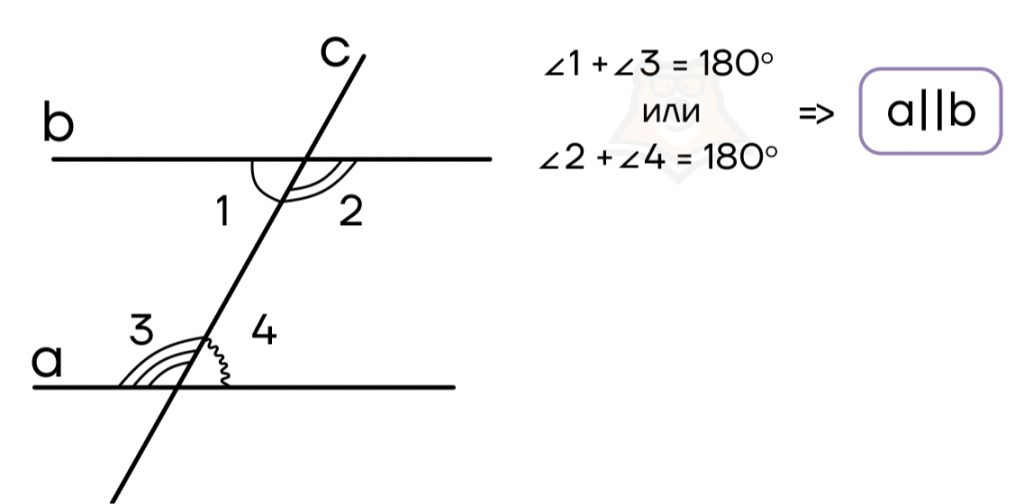
Но что, если мы уже знаем, что прямые параллельны? Мы все еще можем использовать признаки, однако теперь они будут называться свойствами параллельных прямых. 

1. Если прямые параллельны, то при пересечении этих прямых секущей накрест лежащие углы равны.
2. Если прямые параллельны, то при пересечении этих прямых секущей соответственные углы равны.
3. Если прямые параллельны, то при пересечении этих прямых секущей сумма односторонних углов равна 180°.

Свойства параллельных прямых могут пригодиться при решении задач по геометрии. Пример такой задачи можно встретить в №15 ОГЭ по математике. 

Задание. Прямые a и b параллельны. ∠1=105°, ∠2=58°, ∠3=75°. Найдите ∠4. Ответ дайте в градусах.

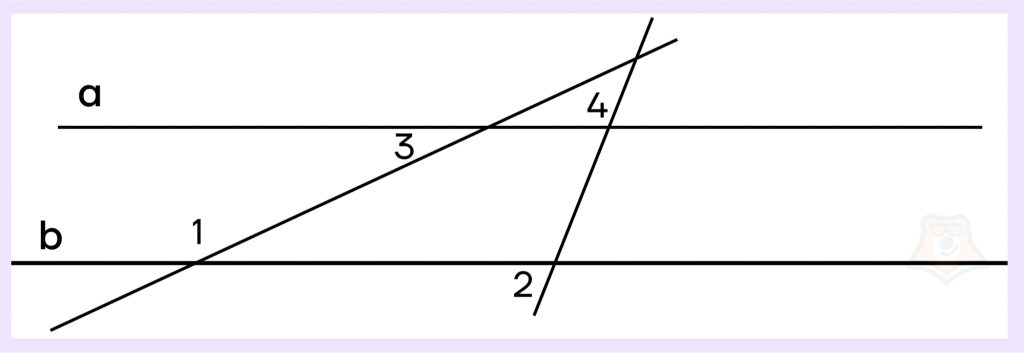
Решение.
Заметим, что ∠1+∠3=105°+75°=180°. Эти углы односторонние. Следовательно, по признаку параллельности прямых прямые a и b параллельны.

Введем новое обозначение и назначим угол ∠5:

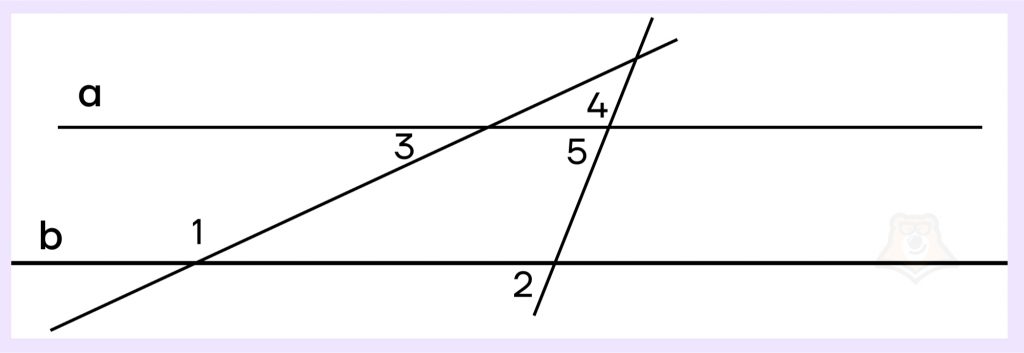
Углы ∠2 и ∠5 соответственные, тогда по свойству параллельных прямых они равны между собой, откуда ∠5=58°. 

Углы ∠4 и ∠5 смежные, а значит, их сумма равна 180°. Получаем:

∠4+58°=180°
∠4=180°-58°
∠4=122°

Ответ: 122

Равенство геометрических фигур

В нашей жизни всегда присутствует сравнение: мы сравниваем фасоны одежды, модели гаджетов, вкус напитков. Что-то нам нравится больше, а что-то меньше. 

Сравнение есть и в геометрии: нам необходимо уметь видеть разницу между геометрическими фигурами. С помощью сравнения определяется и равенство геометрических фигур. 

Геометрические фигуры – это часть плоскости, ограниченная конечным числом линий. 

К геометрическим фигурам относятся знакомые нам треугольники, круги, квадраты и т.д. Практически любая геометрическая фигура ограничена ломаной замкнутой (начало и конец которой совпадают) линией. 

Равными называются фигуры, если стороны и углы одной фигуры соответственно равны сторонам и углам другой фигуры. 

Если у фигур нет углов или сторон (например, окружность), то у них должны быть равны все присущие фигуре элементы (для окружности это радиус). 

Важно заметить, что равные фигуры можно наложить друг на друга и они полностью совпадут.

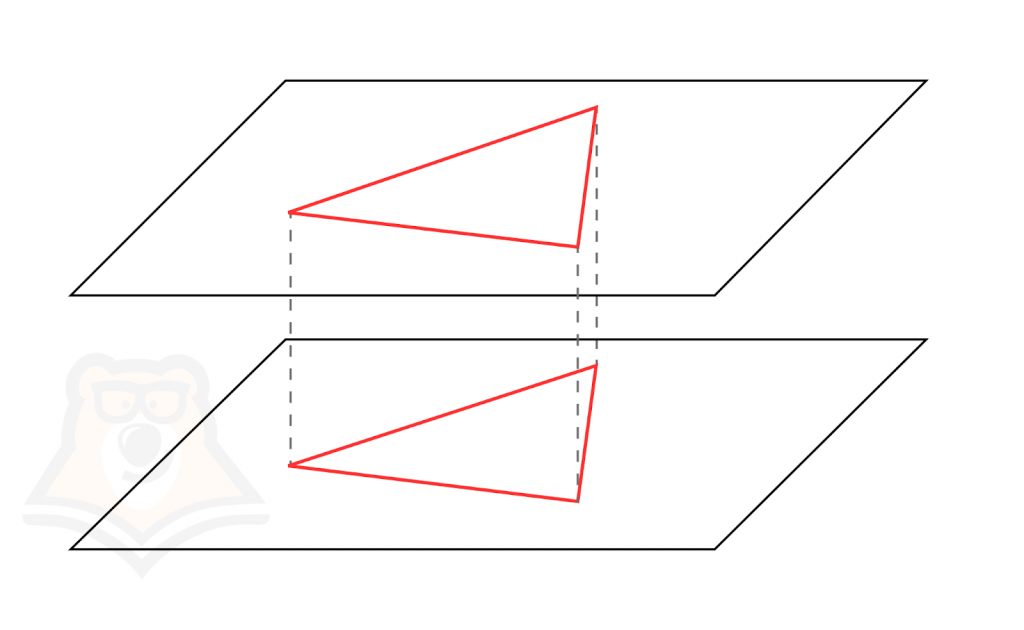
Наложение похоже на стопку бумаги: если мы совместим прямоугольник одного листа с прямоугольников второго, третьего, сотого, то они совпадут, и в итоге образуется ровная стопочка. 

Наложение – это мысленный эксперимент. Разумеется, никто не будет вычерчивать, вырезать и накладывать фигуры друг на друга. 

Другими словами, равные фигуры – это одинаковые фигуры. 

Чтобы определить равенство отрезков, необходимо сравнить их длины. Если длины отрезков нам неизвестны, то нужно совместить начало обоих отрезков и проверить, совпадают ли конец. 

Если начало и конец одного отрезка совпадает с началом и концом другого отрезка, то такие отрезки равны. 

Аналогично и с углами: мы либо можем сравнить их градусные меры, либо наложить друг на друга. Для этого необходимо совместить вершины углов. Если при этом стороны углов совпадут, то такие углы равны. 

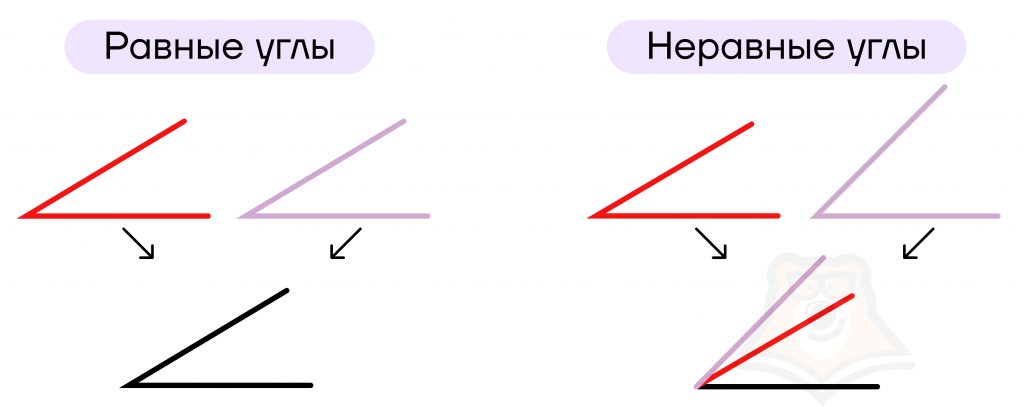
Равные фигуры часто используют при решении задач или доказательствах. 

Аксиомы геометрии

Мы уже узнали, что аксиомы не требуют доказательств. В геометрии существует несколько важных аксиом, которые необходимо знать.

• Через любые две точки проходит единственная прямая. 
• Любая точка прямой делит ее на две части так, что точки из разных частей лежат по разные стороны от данной точки. 
• На любом луче от его начала можно отложить только один отрезок, равный данному.
• От любого луча в заданную сторону на плоскости можно отложить только один равный данному угол.
• Отрезки (углы) полученные сложением или вычитанием соответственно равных отрезков (углов) равны между собой. 
• Любая фигура равна самой себе. 

Мы познакомились с основными понятиями геометрии, узнали про точку, прямую, луч, отрезок и углы. Даже разобрали несколько аксиом. Однако это лишь фундамент в изучении геометрии и впереди множество интересных тем! Например, в статье «Векторы» можно узнать о том, как задать фигуре направление. 

Фактчек

• Основными геометрическими элементами являются точка, прямая, луч, отрезок, угол.
• Углы бывают смежные и вертикальные. Сумма смежных углов равна 180°. Вертикальные углы равны между собой. 
• Прямые бывают пересекающиеся и параллельные. К пересекающимся прямым относятся и перпендикулярные прямые, то есть прямые, которые пересекаются под углом 90°. Параллельные прямые никогда не пересекаются. 
• Углы при пересечении двух параллельных прямых секущей: накрест лежащие, односторонние и соответственные. 
• Для определения параллельных прямых существует три признака. Также существуют и свойства параллельных прямых, которыми являются обратные признакам утверждения.
• Равными называются фигуры, если все элементы одной фигуры соответственно равны всем элементам другой фигуры. Равные фигуры можно определить наложением. 

Термины

Аксиома – это утверждение, не требующее доказательства.

Координаты – величины, определяющие положение точки в системе координат. Для прямоугольной системы координат положение точки задается координатами (x;y).

Проверь себя

Задание 1.
Какие характеристики имеет точка? 

1. Координаты, длину, ширину.
2. Только длину.
3. Только ширину.
4. Только координаты.

Задание 2.
Что такое луч?

1. Бесконечная прямая, не имеющая начала и конца.
2. Прямая, имеющая начало, но не имеющая конца.
3. Прямая, имеющая начало и конец.
4. Ни один из вышеперечисленных вариантов.

Задание 3.
Что такое вертикальные углы?

1. Два угла, у которых общая сторона, а две другие лежат на одной прямой.
2. Углы, вершинами которых является одна точка, а стороны одного являются продолжением сторон другого.
3. Углы, равные 90 градусов.
4. Углы, лежащие с одной стороны от секущей «внутри» прямых.

Задание 4.
Угол 4 равен 60°. Чему равен угол 7? 

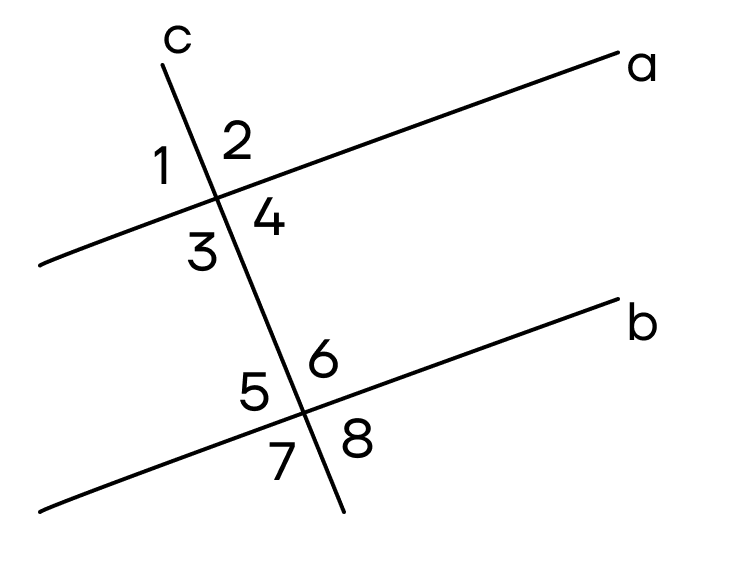
1. 120°
2. 60°
3. 30°
4. 20°

Задание 5.
Угол 5 равен 50°. Чему равен угол 8? 

1. 150°
2. 65°
3. 130°
4. 50°

Ответы:1. – 4; 2. – 2; 3. – 2; 4. – 1; 5. – 4