Равнобедренный, равносторонний и прямоугольный треугольник

На этой странице вы узнаете

• Из чего состоит «звезда Пифагора»? 
• Какой треугольник использовали для строительства пирамид?
• Как с помощью квадрата доказать теорему Пифагора?

Мы прекрасно знаем, что все стороны квадрата равны. А могут ли быть равны все стороны треугольника? Или, может, только две стороны из трех? Как тогда будут называться такие треугольники? О разновидностях треугольниках мы и поговорим в статье.

Равнобедренный и равносторонний треугольник 

Треугольники могут различаться не только по величине углов, но и по соотношению сторон. Чуть подробнее рассмотрим несколько случаев. 

Допустим, у нас дан треугольник, две стороны которого равны. Такой треугольник будет называться равнобедренным. 

Равнобедренный треугольник — это треугольник, у которого две стороны равны. 

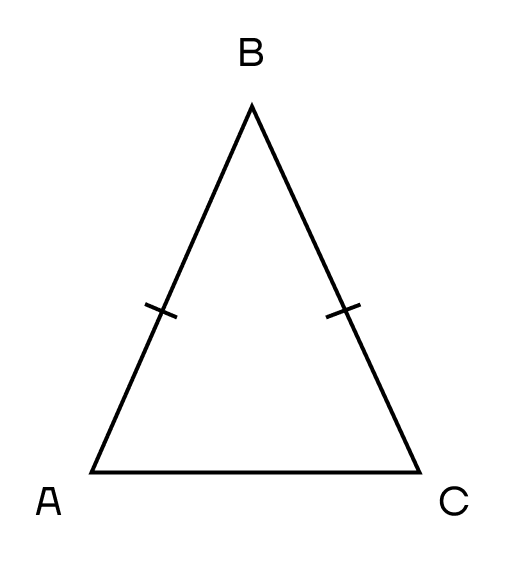
При этом две равные стороны будут называться боковыми, а третья сторона — основанием. 

На рисунке АВ и ВС — боковые стороны, АС — основание. 

Из чего состоит «звезда Пифагора»? Одним из прародителей математики является древнегреческий ученый Пифагор. Им была основана школа, символ которой — пятиконечная звезда. Пифагор и его сторонники считали, что основой мира являются числа и математические правила. Если мы внимательно рассмотрим звезду, то увидим, что она состоит из равнобедренных треугольников.

Равнобедренный треугольник обладает важными свойствами, которые значительно упрощают решение задач. 

Свойство 1. Углы при основании равнобедренного треугольника равны между собой. 

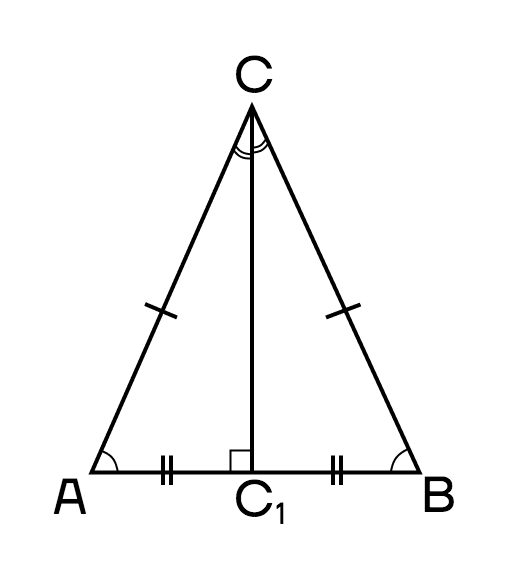
Свойство 2. Медиана, высота и биссектриса, проведенные к основанию, совпадают. 

Пусть СС₁ — высота, тогда этот же отрезок будет и медианой, и биссектрисой. 

Чтобы определить, что перед нами равнобедренный треугольник, существуют признаки равнобедренного треугольника. Они очень похожи на его свойства. 

Признак 1. Если в треугольнике два угла равны, то он является равнобедренным. 

Признак 2. Если в треугольнике проведена высота, и она совпадает с медианой и биссектрисой, то такой треугольник равнобедренный. 

Этот признак можно записать в трех видах, они будут меняться только тем, какой отрезок проведен изначально. 

Поэтому второго признака также будут справедливы следующие формулировки:

• Если в треугольнике проведена биссектриса, и она совпадает с высотой и медианой, то такой треугольник равнобедренный. 

• Если в треугольнике проведена медиана, и она совпадает с высотой и биссектрисой, то такой треугольник равнобедренный. 

Может ли быть такое, что основание также будет равняться боковым сторонам? В этом случае мы получаем равносторонний треугольник. 

Равносторонний треугольник — это треугольник, все стороны которого равны. Такой треугольник еще могут называть «правильным». 

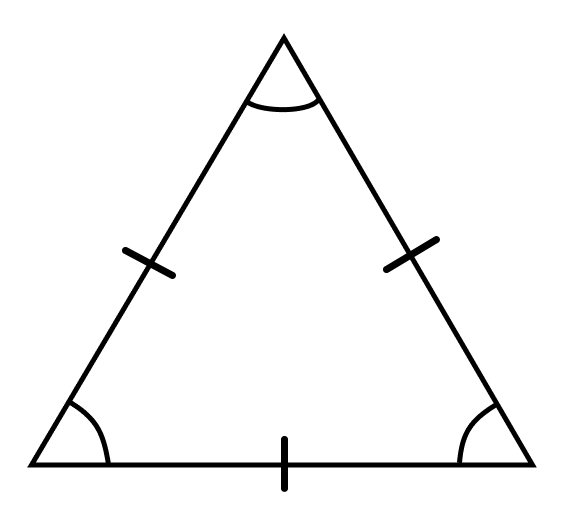
Рассмотрим свойства равностороннего треугольника.

Свойство 1. Все углы в равностороннем треугольнике равны 60°. 

Это легко доказать. Поскольку стороны треугольника равны, то и углы в нем также равны. Пусть угол такого треугольника равен х, тогда сумма его углов равна x + x + x = 3x. 

Сумма углов любого треугольника равна 180°, следовательно, мы получаем уравнение 

3x = 180, откуда можем найти значение одного угла: x = 60. 

Свойство 2. Как и в равнобедренном треугольнике, в равностороннем треугольнике будут совпадать медиана, высота и биссектриса, проведенные к одной стороне. 

При этом в равностороннем треугольнике они будут совпадать независимо от того, к какой стороне они будут проведены. 

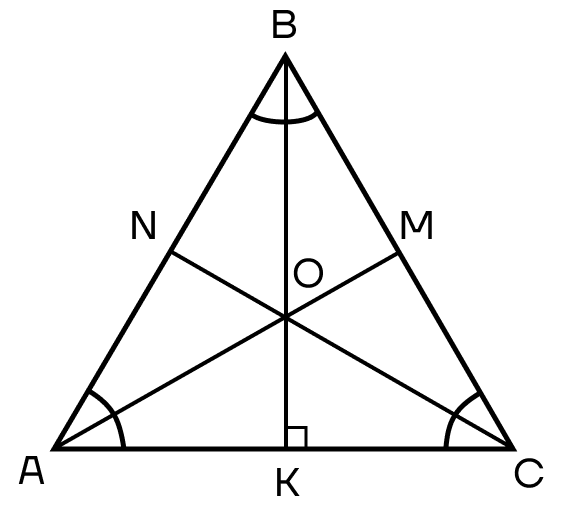
Свойство 3. Поскольку медианы, высоты и биссектрисы совпадают, то и точки их пересечения также будут совпадать. Тогда точка О будет точкой пересечения и медиан, и высот, и биссектрис (см. рисунок к свойству 2).

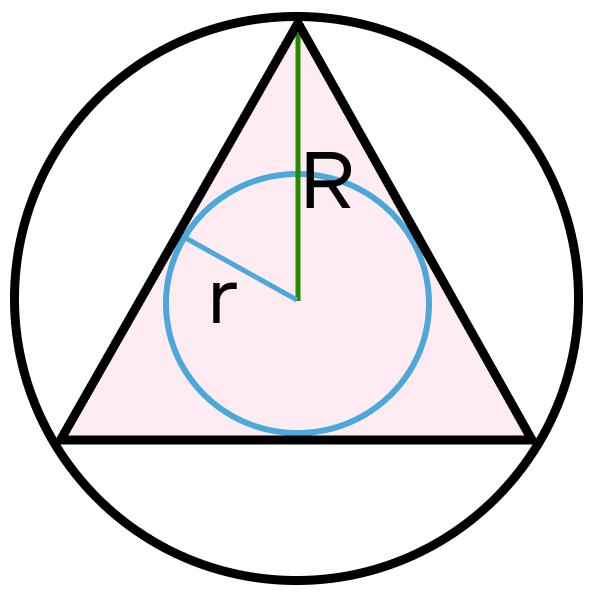
Свойство 4. Центры вписанной и описанной окружности будут совпадать. 

Прямоугольный треугольник

Остановимся на прямоугольном треугольнике чуть подробнее. 

Прямоугольный треугольник — это треугольник, один из углов которого прямой. 

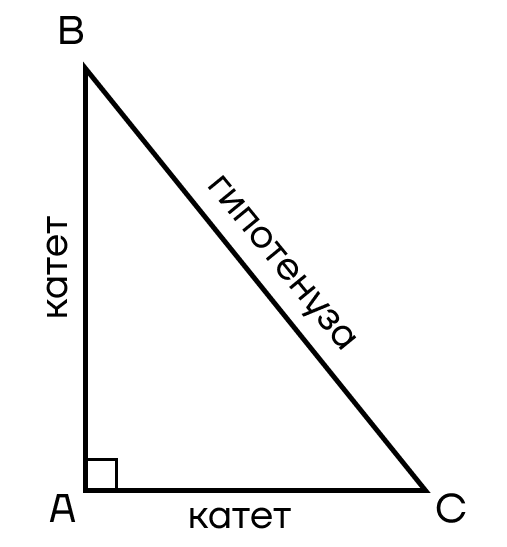
У прямоугольного треугольника также есть свои названия длин сторон: 

• Катеты — стороны, которые образуют прямой угол в треугольнике. 
• Гипотенуза — сторона, которая лежит напротив прямого угла в треугольнике. 

Стоит заметить, что в прямоугольном треугольнике самой длинной стороной всегда будет гипотенуза. Достаточно вспомнить, что напротив большего угла лежит большая сторона, а в прямоугольном треугольнике самый большой угол — это прямой угол. 

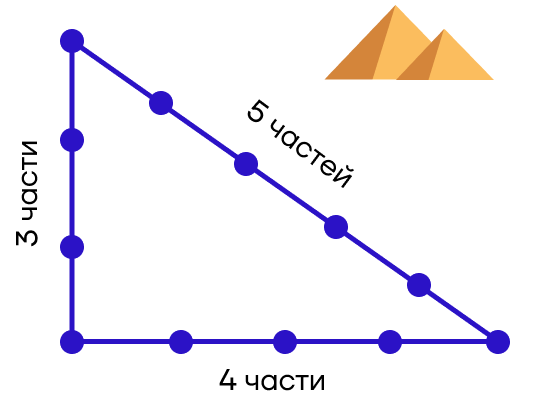
Какой треугольник использовали для строительства пирамид? Существует понятие «египетского» треугольника. Его стороны относятся друг к другу в пропорции 3 : 4 : 5 и это прямоугольный треугольник.  «Египетский» треугольник служил основой в строительстве для разметки и построения правильных углов. С его помощью были возведены те самые, знаменитые пирамиды Древнего Египта.

Для прямоугольного треугольника также существуют свои признаки равенства и подобия, которые можно применить только к такому типу треугольников. 

Признаки равенства прямоугольных треугольников 

Для прямоугольного треугольника справедливы те же признаки равенства, что и для обычного треугольника. Однако можно вывести еще несколько признаков, которые будут сводиться к общим признакам равенства. 

Признак 1. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого прямоугольного треугольника, то такие треугольники равны. 

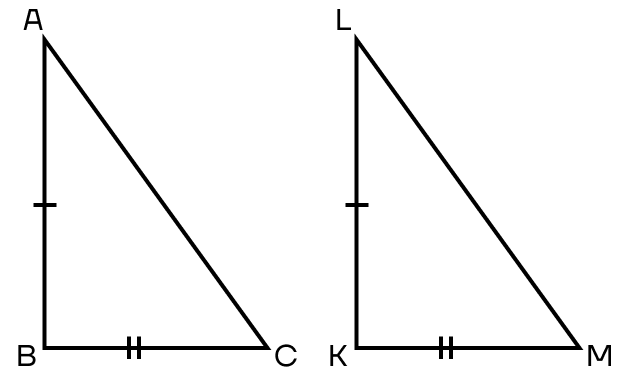
Признак 2. Если катет и прилежащий к нему острый угол одного треугольника соответственно равны катету и прилежащему к нему острому углу другого треугольника, то такие треугольники равны. 

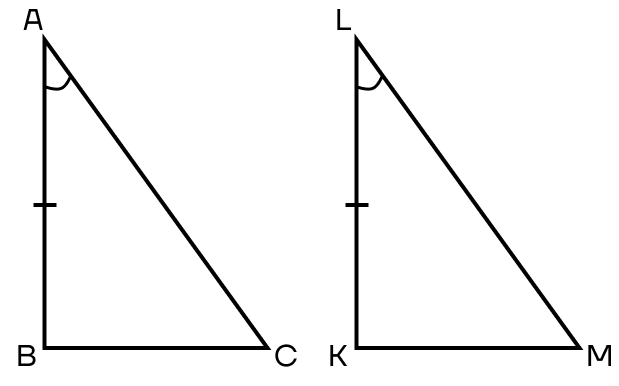
Признак 3. Если катет и противолежащий ему острый угол одного треугольника соответственно равны катету и противолежащему ему углу другого треугольника, то такие треугольники равны. 

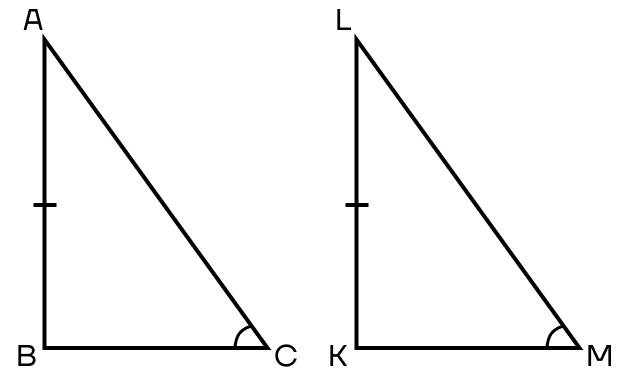
Признак 4. Если катет и гипотенуза одного треугольника соответственно равны катету и гипотенузе другого треугольника, то такие треугольники равны. 

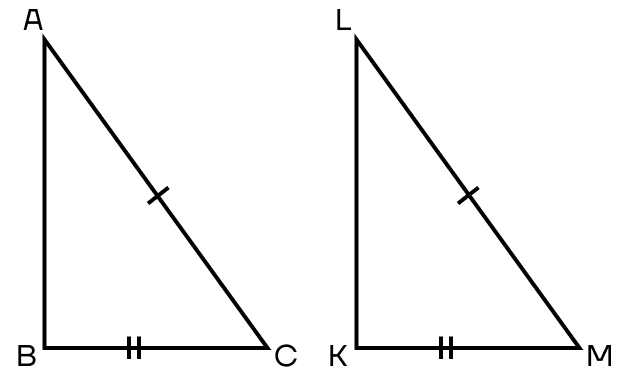
Признак 5. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие треугольники равны. 

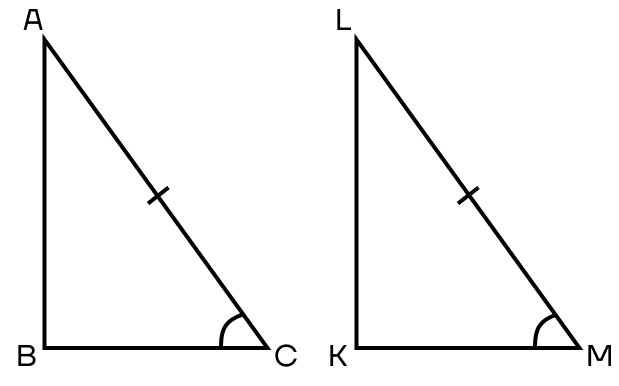
Признаки подобия прямоугольных треугольников

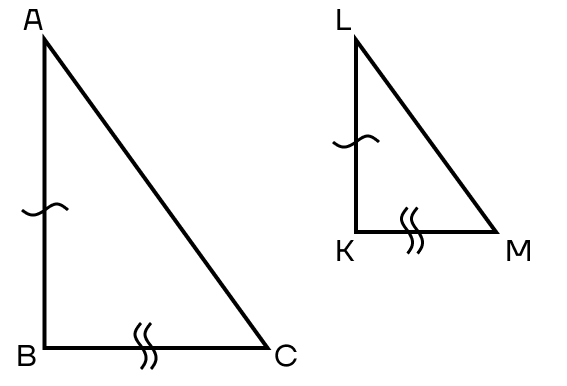
1 признак. Если два катета одного треугольника пропорциональны двум катетам другого треугольника, то такие треугольники подобны. 

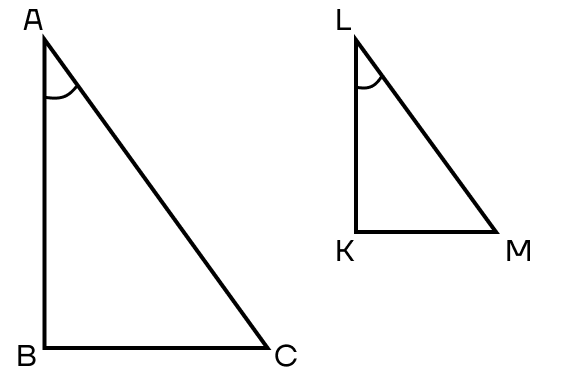
2 признак. Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то такие треугольники подобны. 

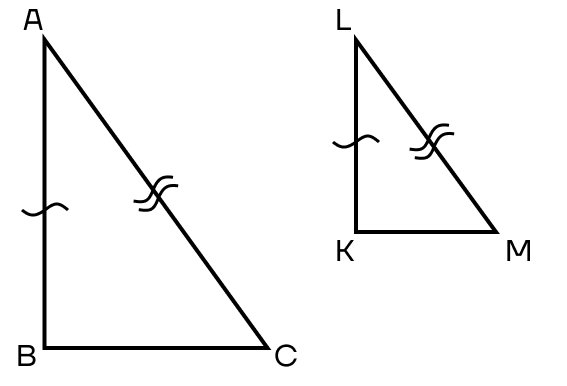
3 признак. Если гипотенуза и катет одного треугольника соответственно пропорциональны гипотенузе и катету другого треугольника, то такие треугольники подобны. 

Рассматривая прямоугольные треугольники, нельзя не вспомнить и про теорему Пифагора. Ее формулировка звучит так.

Теорема Пифагора
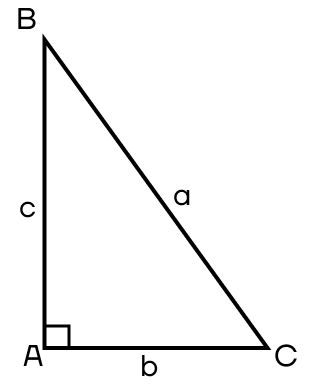
Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. a² = b² + c²

Как с помощью квадрата доказать теорему Пифагора? Пусть а и b — катеты нашего прямоугольника. Построим квадрат со стороной a + b, и разобьем его на два квадрата и два прямоугольника так, как это показано на рисунке. 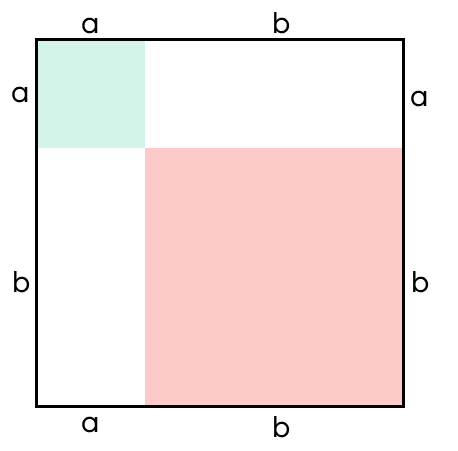 Заметим, что площадь этого квадрата равна (a + b)2. По формуле сокращенного умножения получаем, что S = a2 + 2ab + b2, что также можно заметить на рисунке, если посмотреть на площади квадратов и прямоугольников. Достроим четыре прямоугольных треугольника с катетами a и b, а их гипотенузу назовем с. Сторона квадрата также останется равной a + b, а вот площадь теперь можно найти как сумму площадей четырех треугольников и квадрата посередине. Получаем \(S = 4 * \frac{1}{2} * a * b + c^2 = 2ab + c^2\). 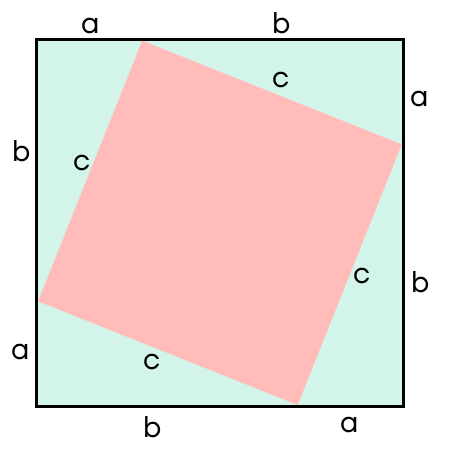 Поскольку мы нашли площади одного и того же квадрата, мы их можем приравнять и преобразовать полученное уравнение. a2 + 2ab + b2 = 2ab + c2 a2 + b2 = c2 Значит, теорема Пифагора доказана.

Также нельзя не рассмотреть отношение сторон и углов в прямоугольном треугольнике. Поэтому сейчас нам предстоит вспомнить синусы, косинусы, тангенсы и котангенсы. Будем рассматривать их на примере угла АСВ.

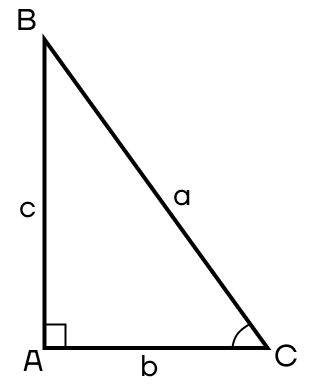
Синус — это отношение противолежащего катета к гипотенузе. Запишем это определение с помощью сторон.

\(\sin C = \frac{c}{a}\)

Косинус — это отношение прилежащего катета к гипотенузе. 

\(\cos C = \frac{b}{a}\)

Тангенс — это отношение противолежащего катета к прилежащему катету. 

\(tg \, C = \frac{c}{b}\)

Котангенс — это отношение прилежащего катета к противолежащему катету. 

\(ctg \, C = \frac{b}{c}\)

Руководствуясь теми же правилами, можно вывести значения тригонометрических функций и для угла В. 

Важно запомнить, что такие отношения будут работать только в прямоугольном треугольнике. Если дан произвольный треугольник, то применять эти правила уже нельзя. 

И в завершение разговора про прямоугольный треугольник рассмотрим его основные свойства. 

1 свойство. Если два катета прямоугольного треугольника равны, то это равнобедренный прямоугольный треугольник. Острые углы такого треугольника будут равняться 45°. 

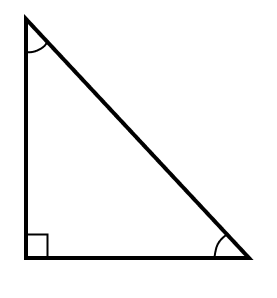
2 свойство. Катет, лежащий против угла в 30°, равен половине гипотенузы. 

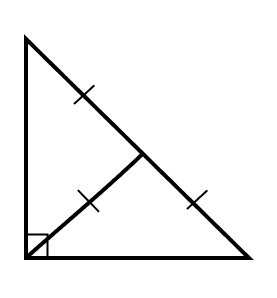
3 свойство. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы. 

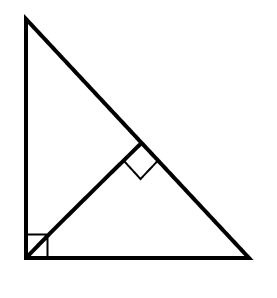
4 свойство. Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. 

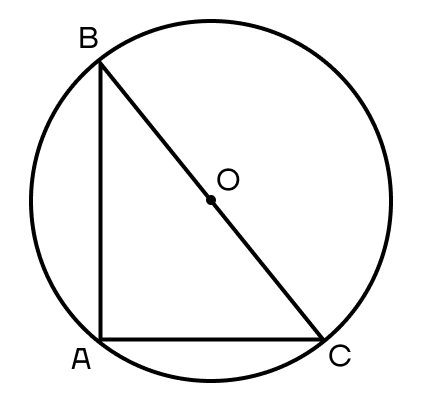
5 свойство. Центр описанной окружности лежит на середине гипотенузы. Отсюда же следует, что радиус описанной окружности равен половине гипотенузы. 

6 свойство. Высота, опущенная на гипотенузу, равна среднему пропорциональное между проекциями катетов на гипотенузу.

Среднее пропорциональное двух чисел – это корень из их произведения. 

Например, если есть числа а и b, то их среднее пропорциональное будет равно \(\sqrt{a*b}\). 

Начертим треугольник с высотой, опущенной на гипотенузу. 

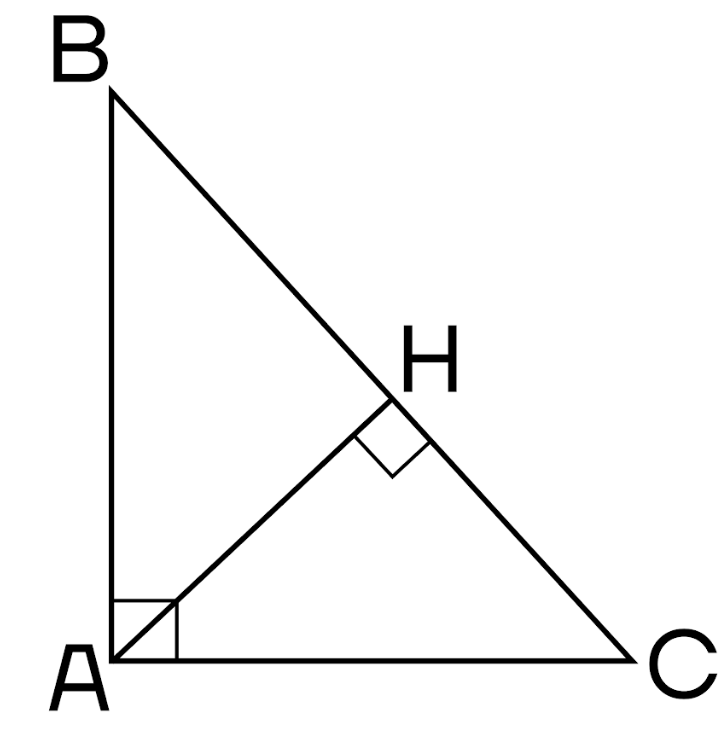
Что такое проекция? В нашем случае, это отрезки, образованные перпендикуляром, проведенным к гипотенузе, то есть высотой. Если быть точнее, ВН – проекция катета АВ на гипотенузу, а НС – проекция катета АС на гипотенузу. 

Таким образом, получаем следующую формулу. 

\(AH=\sqrt{BH*HC}\)

7 свойство. Катет равен среднему пропорциональному между гипотенузой и проекцией этого катета на гипотенузу. 

Это свойство очень похоже на предыдущее, поэтому использовать мы будем тот же чертеж. Разберем свойство на примере катета АС. 

Его проекцией на гипотенузу будет отрезок НС. Следовательно, мы получаем формулу:

\(AС=\sqrt{ВС*НC}\)

Аналогично для второго катета. Проекцией катета АВ на гипотенузу будет отрезок ВН. Следовательно, получаем формулу:

\(AB=\sqrt{BC*BH}\)

Фактчек

• По соотношению сторон можно выделить равнобедренные и равносторонние треугольники. 
• В равнобедренном треугольнике боковые стороны равны. При этом углы при основании равнобедренного треугольника равны между собой. В равностороннем треугольнике все стороны равны, а все углы имеют величину 60 градусов. 
• В прямоугольном треугольнике один из углов равен 90 градусов. При этом сторона, лежащая напротив прямого угла, называется гипотенузой, а оставшиеся две стороны катетами. У прямоугольного треугольника есть свои признаки равенства и подобия, которые могут упростить решение задач. Также для острых углов прямоугольного треугольника можно составить тригонометрические отношения. 
• Для прямоугольного треугольника всегда будет справедлива теорема Пифагора: сумма квадратов катетов равняется квадрату гипотенузы. 

Проверь себя

Задание 1. 
В равнобедренном треугольнике угол при основании 50 градусов. Чему равен угол, лежащий против основания?

1. 100°
2. 80°
3. 50°
4. 60°

Задание 2. 
Как называется сторона прямоугольного треугольника, которая лежит напротив прямого угла?

1. катет
2. гипотенуза
3. боковая сторона
4. основание 

Задание 3. 
Катеты равнобедренного треугольника равны 3 и 4. Чему равна гипотенуза этого треугольника?

1. 5
2. 25
3. 7
4. 6

Задание 4. 
Катет, лежащий напротив угла в 30 градусов, равен 12. Чему равна гипотенуза этого треугольника?

1. 6
2. 12
3. 24
4. 36

Задание 5.
Медиана, проведенная из прямого угла, равняется 5. Чему равна гипотенуза этого треугольника?

1. 5
2. 10
3. 15
4. 20 

Ответы: 1. — 2; 2. — 2; 3. — 1; 4. — 3; 5. — 2.