Векторы. Часть 2

На этой странице вы узнаете

• В чем заключается сила?
• Как вектор устроил революцию?
• Что из себя представляют две знаменитые тройки векторов?

В статье «Векторы. Часть 1» мы уже познакомились с понятием вектора, а также с разными способами сложения и вычитания векторов. Предлагаем продолжить путешествие в эту тему и разобрать не менее важные моменты. 

Сложение и вычитание мы разобрали, а как насчет умножения? Можно ли умножать векторы?

Умножение вектора на число

Конечно, умножение не могло обойти стороной и векторы, в данном случае – умножение вектора на число.

Умножить вектор \(\overrightarrow{a}\) на число \(k>0\) – значит взять этот вектор \(k\) раз:

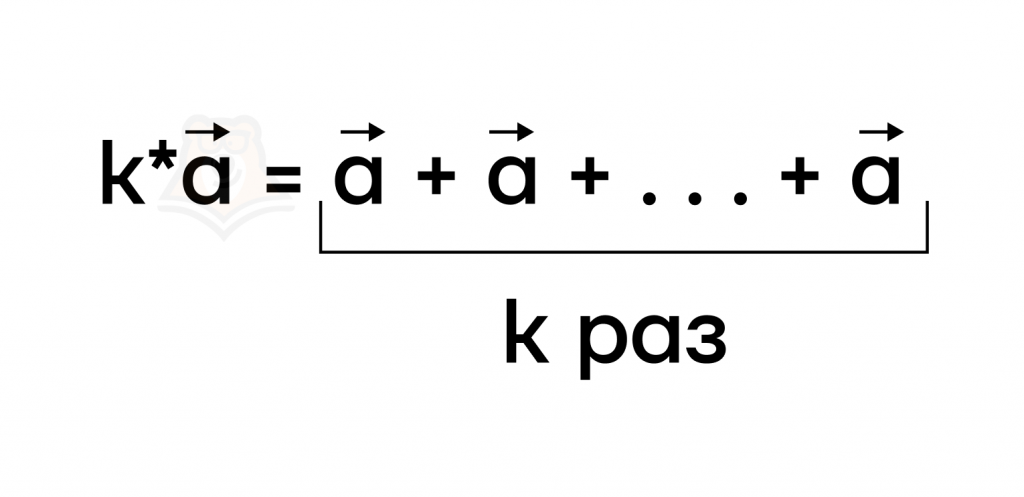
Вспомним, что при сложении сонаправленных векторов мы получаем вектор, сонаправленный этим векторам,  длина которого равна сумме длин этих векторов. Так как при умножении вектора на число мы складываем равные векторы, то \(|\overrightarrow{a}|+|\overrightarrow{a}|+…+|\overrightarrow{a}|=k*|\overrightarrow{a}|\)

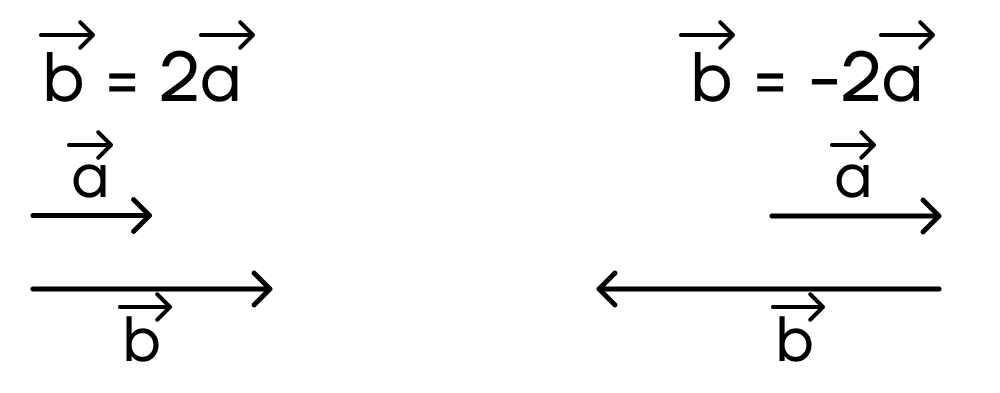
• Таким образом,  произведением ненулевого вектора \(\overrightarrow{a}\) на число \(k>0\) называется такой вектор \(\overrightarrow{b}\), что:

1. \(\overrightarrow{b}\uparrow\uparrow\overrightarrow{a}\)
2. \(|\overrightarrow{b}|=k*|\overrightarrow{a}|\)

• Произведением ненулевого вектора \(\overrightarrow{a}\) на число \(k<0\) называется такой вектор \(\overrightarrow{b}\), что:

1. \(\overrightarrow{b}\uparrow\downarrow\overrightarrow{a}\)
2. \(|\overrightarrow{b}|=k*|\overrightarrow{a}|\)

• Произведение ненулевого вектора \(\overrightarrow{a}\) на число \(k=0\) есть нулевой вектор \(\overrightarrow{0}\)

Приведем несколько примеров умножения вектора на число:

В чем заключается сила? Пожалуй, наибольшее применение векторы нашли именно в физике, ведь многие физические величины имеют свое направление. В частности – сила.  Любая сила в физике рассматривается как вектор. В зависимости от рода этой силы, она может иметь различные направления. Например, человек, сидящий на стуле, оказывает на этот стул силу, направленную «вниз». В свою очередь, стул оказывает сопротивление человеку силой реакции опоры, направленной «вверх», благодаря чему человек все-таки способен сидеть на этом стуле, а не продавливает его. Чем большую силу прикладывает тот или иной объект, тем больше будет длина вектора, обозначающего эту силу. Именно на векторах основывается один из самых важных законов в физике – первый закон Ньютона. Он гласит: тело находится в состоянии покоя или движется по прямой с постоянной скоростью, если сумма всех сил, оказываемых на это тело, равна нулю. Речь здесь именно о сумме векторов сил. То есть, если при сложении векторов всех сил, действующих на тело, мы получаем нулевой вектор, значит тело покоится или движется по прямой с постоянной скоростью.

Таким образом, с помощью умножения вектора на число мы получаем векторы, сонаправленные данному, но отличающиеся по длине. При этом ни в коем случае нельзя сравнивать сами векторы, сравнивать можно только их длины. То есть, сказать, что какой-то вектор больше, а какой-то меньше, мы не можем. 

Также мы помним, что деление – это действие, обратное умножению. В таком случае вектор мы можем не только умножить, но и разделить на число. 

Например, вектор \(\frac{\overrightarrow{a}}{5}=\frac{1}{5}\overrightarrow{a}\) – вектор, сонаправленный вектору \(\overrightarrow{a}\), длина которого в 5 раз меньше вектора \(\overrightarrow{a}\). 

При этом разделить вектор на вектор нельзя.

Помимо самих действий с векторами, так же, как и с обычными числами, большую роль играют законы умножения, которые часто помогают нам упростить решение той или иной задачи. Рассмотрим основные из них.

Законы умножения вектора на число

1. \((\overrightarrow{a}+\overrightarrow{b})*k=\overrightarrow{a}*k+\overrightarrow{b}*k\)  – распределительный закон умножения суммы векторов на число.

Чтобы доказать это свойство, по правилу треугольника построим вектора \(\overrightarrow{a}+\overrightarrow{b}\) и \(\overrightarrow{a}*k+\overrightarrow{b}*k\), где \(\overrightarrow{a}*k\) – вектор, сонаправленный вектору \(\overrightarrow{a}\), длина которого равна \(k*|\overrightarrow{a}|,\overrightarrow{b}*k\) – вектор, сонаправленный вектору \(\overrightarrow{b}\), длина которого равна \(k*|\overrightarrow{b}|\).

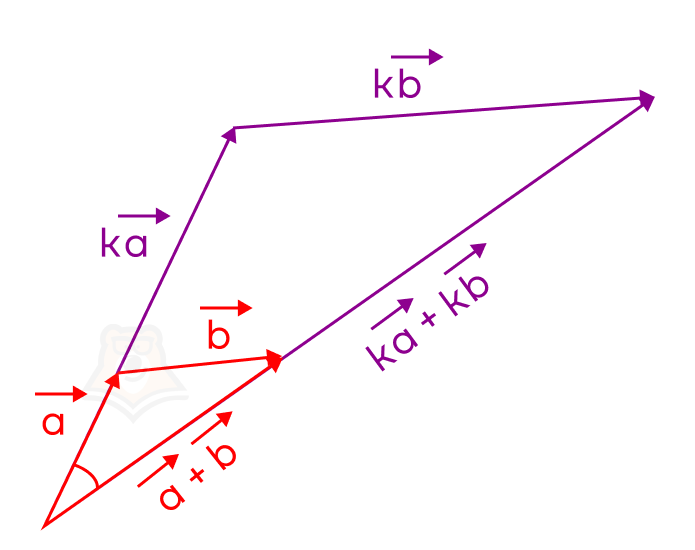
Из рисунка видим, что образовалось два подобных треугольника (второй признак подобия) с коэффициентом подобия \(k\). Значит, \(\overrightarrow{a}*k+\overrightarrow{b}*k=(\overrightarrow{a}+\overrightarrow{b})*k\).

2. \((с+b)*\overrightarrow{a}=\overrightarrow{a}*с+\overrightarrow{a}*b\) – распределительный закон умножения суммы двух чисел на вектор.

Вектор \(\overrightarrow{a}*с\) сонаправлен вектору \(\overrightarrow{a}\) и имеет длину \(c*|\overrightarrow{a}|\).
Вектор \(\overrightarrow{a}*b\) сонаправлен вектору \(\overrightarrow{a}\) и имеет длину \(b*|\overrightarrow{a}|\).
Значит, векторы \(\overrightarrow{a}*c\) и \(\overrightarrow{a}*b\) оба сонаправлены вектору \(\overrightarrow{a}\), то есть они сонаправлены друг другу. Тогда сумма сонаправленных векторов \(\overrightarrow{a}*c+\overrightarrow{a}*b\) есть вектор, сонаправленный этим векторам (а значит, сонаправленный и вектору \(\overrightarrow{a}\)), а также имеющий длину \(|\overrightarrow{a}*c+\overrightarrow{a}*b|=|\overrightarrow{a}*c|+|\overrightarrow{a}*b|=c*|\overrightarrow{a}|+b*|\overrightarrow{a}|=(c+b)*|\overrightarrow{a}|\)
Вектор, сонаправленный вектору \(\overrightarrow{a}\) и имеющий длину \((c+b)*|\overrightarrow{a}|\), и есть вектор \((c+b)*\overrightarrow{a}\). Итого мы получили, что \(\overrightarrow{a}*c+\overrightarrow{a}*b=(c+b)*\overrightarrow{a}\)

Ранее было разобрано произведение вектора на число. А можно ли умножить вектор на вектор? 

Скалярное произведение векторов

Скалярное произведение двух векторов – число, равное произведению длин этих векторов на косинус угла между ними.

\(\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|*cos{\alpha}\)

где \(\alpha\) – угол между векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\). 

Что же будет, если косинус угла между векторами равен 0? Из статьи «Тригонометрическая окружность. Часть 1» мы помним, что такое произойдет, если угол между векторами будет равен 90°, то есть когда векторы ортогональны. Тогда

\(\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|*0=0\)

Таким образом, можно сделать вывод: скалярное произведение ортогональных векторов равно 0.

Это же можно использовать и как признак ортогональности векторов: если скалярное произведение двух ненулевых векторов равно 0, то эти векторы ортогональны.

Если два вектора являются коллинеарными, то угол между ними равен 0°. В таком случае скалярное произведение этих векторов будет равно:

\(\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|*cos0°=|\overrightarrow{a}|*|\overrightarrow{b}|\)

Вывод: скалярное произведение двух коллинеарных векторов равно произведению длин этих векторов.

Отсюда следует, что скалярное произведение вектора a на самого себя равно:

\(\overrightarrow{a}*\overrightarrow{a}=\overrightarrow{a}^2=|\overrightarrow{a}|^2\geq 0\)

А теперь рассмотрим свойства скалярного произведения. Из основных свойств можно выделить следующие:

1. \(\overrightarrow{a}*\overrightarrow{b}=\overrightarrow{b}*\overrightarrow{a}\) – переместительное свойство скалярного произведения
2. \((k\overrightarrow{a})*\overrightarrow{b}=k(\overrightarrow{a}*\overrightarrow{b})\) – сочетательное свойство скалярного произведения
3. \(\overrightarrow{a}*(\overrightarrow{b}+\overrightarrow{c})=\overrightarrow{a}*\overrightarrow{b}+\overrightarrow{a}*\overrightarrow{c}\) – распределительное свойство скалярного произведения

Часто при решении задач по планиметрии приходится рассматривать вектор на координатной плоскости, ведь так же, как и отрезок, у вектора есть свои координаты.

Векторы на плоскости

Перед тем как начать говорить о координатах вектора на плоскости, нужно для начала разобраться с одной немаловажной теоремой – теоремой о разложении вектора на плоскости по двум неколлинеарным векторам.

В произвольной плоскости проведем два неколлинеарных вектора \(\overrightarrow{b}\) и \(\overrightarrow{c}\), а также вектор \(\overrightarrow{a}\). Данная теорема гласит: для вектора a в таком случае найдутся некоторые числовые коэффициенты \(k_1\) и \(k_2\) такие, что \(\overrightarrow{a}=k_1\overrightarrow{b}+k_2\overrightarrow{c}\). 

Равенство \(\overrightarrow{a}=_1\overrightarrow{b}+k_2\overrightarrow{c}\) называется разложением вектора \(\overrightarrow{a}\) по двум неколлинеарным векторам \(\overrightarrow{b}\) и \(\overrightarrow{c}\), а коэффициенты \(k_1\) и \(k_2\) – коэффициентами  разложения вектора \(\overrightarrow{a}\) по двум неколлинеарным векторам \(\overrightarrow{b}\) и \(\overrightarrow{c}\). Для каждого вектора, взятого на этой же плоскости, также найдется свое разложение по этим векторам, причем только одно.

Любой вектор на плоскости можно разложить единственным образом по двум произвольным неколлинеарным векторам, лежащим в этой же плоскости.

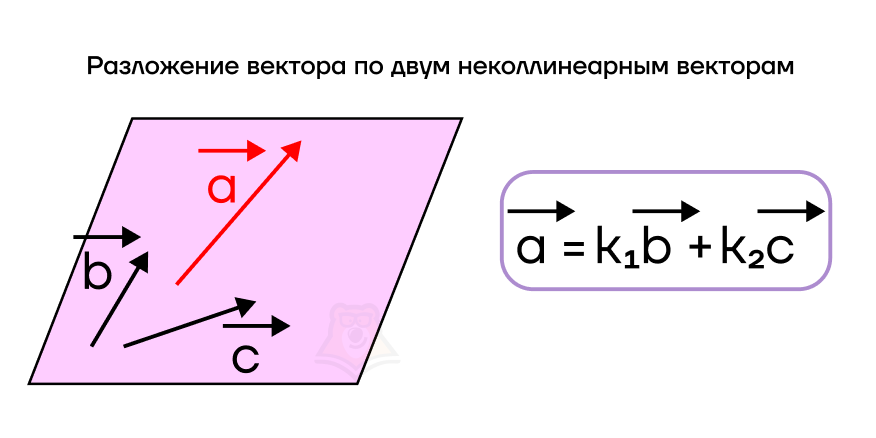
Ознакомившись с данной теоремой, можем идти дальше. Ранее мы знакомились с таким понятием, как проекция точки на ось, и, безусловно, с проекциями мы часто встречаемся в математике, когда речь заходит о координатах.

На самом деле, вектор так же, как и точку, можно спроецировать на ось. Осталось только понять, как это сделать.

Проекция вектора на ось

Рассмотрим вектор \(\overrightarrow{AB}\) и и прямую b, изображенные на рисунке ниже . Если построить проекции точек A и B на прямую b (\(A_1\) и \(B_1\) соответственно), то мы получим вектор \(\overrightarrow{A_1B_1}\), который также называют проекцией вектора \(\overrightarrow{AB}\) на ось b.

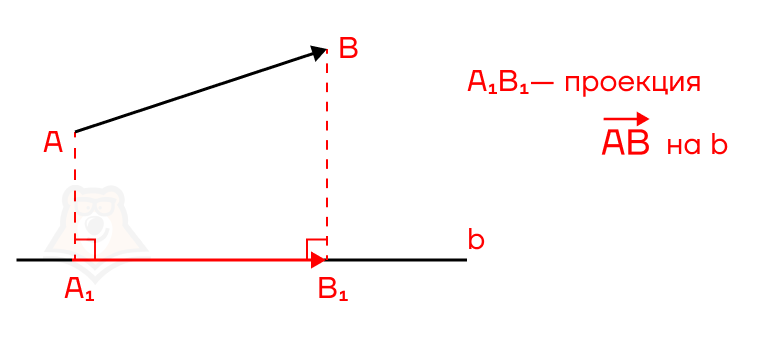
Проекция вектора \(\overrightarrow{a}\) на ось \(\overrightarrow{b}\) – это вектор, началом которого является проекция начала вектора \(\overrightarrow{a}\) на ось b, а концом – проекция конца вектора \(\overrightarrow{a}\) на ось b.

Можно ли найти длину проекции вектора \(\overrightarrow{AB}\) на ось b, зная длину самого вектора \(\overrightarrow{AB}\)? Конечно, можно: для этого сначала переместим вектор AB таким образом, чтобы его начало лежало на оси b. 

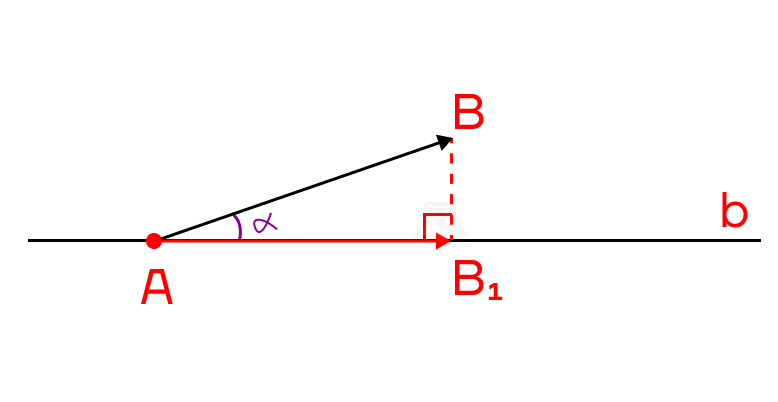
Тогда проекцией вектора \(\overrightarrow{AB}\) на ось b будет вектор \(\overrightarrow{AB_1}\). Длину этого вектора можно найти из прямоугольного треугольника \(\vartriangle ABB_1\), зная косинус угла \(\alpha\) между вектором \(\overrightarrow{AB}\) и осью b. По определению косинуса:

\(cos(\alpha)=\frac{AB_1}{AB}=\frac{|\overrightarrow{AB_1}|}{|\overrightarrow{AB}|}\)

Откуда:

\(|\overrightarrow{AB_1}|=|\overrightarrow{AB}|*cos(\alpha)\)

Можем сделать вывод: длина проекции вектора \(\overrightarrow{a}\) на ось b равна произведению длины этого вектора и косинуса угла между этим вектором и осью b.

\(|\overrightarrow{a_b}|=|\overrightarrow{a}|*cos(\alpha)\),
где \(\overrightarrow{a_b}\) – проекция вектора \(\overrightarrow{a}\) на ось b;
\(\alpha\) – угол между вектором \(\overrightarrow{a}\) и осью b

Из статьи «Формулы тригонометрии и простейшие тригонометрические уравнения» мы помним, что косинус и синус одного угла связаны между собой основным тригонометрическим тождеством:

\(sin^2(\alpha)+cos^2(\alpha)=1\)

Отсюда:

\(cos(alpha)=\sqrt{1-sin^2(\alpha)}\)

Так как угол между вектором и осью всегда острый (\(\alpha<90°\)), то косинус этого угла будет положительным, то есть \(cos(alpha)=\sqrt{1-sin^2(alpha)}\). Подставим это выражение в нашу формулу:

\(|\overrightarrow{a_b}|=|\overrightarrow{a}|*\sqrt{1-sin^2(\alpha)},\)
где \(\overrightarrow{a_b}\) – проекция вектора \(\overrightarrow{a}\) на ось b;
\(\alpha\) – угол между вектором \(\overrightarrow{a}\) и осью b

Таким образом, длину проекции вектора на ось можно найти не только с помощью косинуса, но и с помощью синуса угла между вектором и осью.

Ознакомившись с теоремой о разложении вектора на плоскости и с понятием проекции вектора на ось, можем, наконец, с уверенностью переходить к координатам вектора на плоскости.

Координаты вектора на плоскости

Итак, у нас есть прямоугольная система координат OXY. Вспомнить, что эта система координат из себя представляет, а также как по ней определять координаты точек, можно в статье «Основные элементарные функции. Часть 1». 

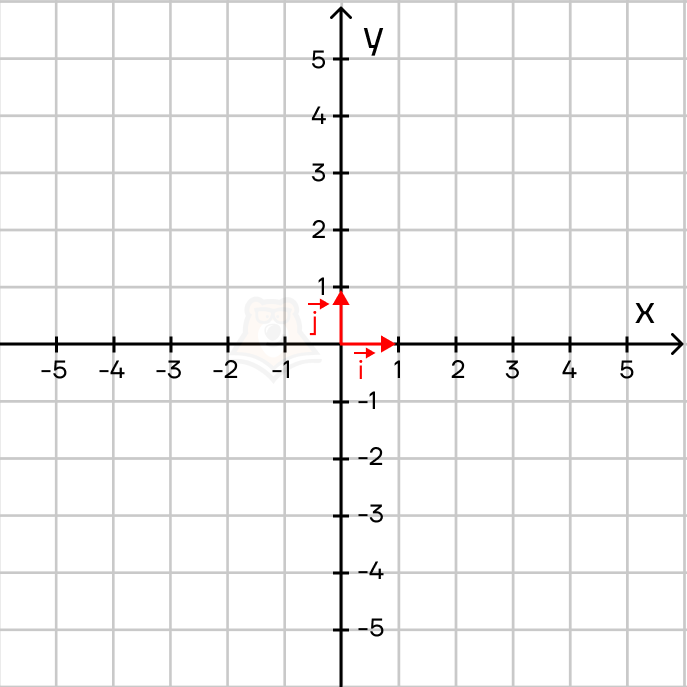
Отметим на прямоугольной системе координат два вектора i и j такие, что:

1. \(|\overrightarrow{i}|=|\overrightarrow{j}|=1\);
2. начала векторов \(\overrightarrow{i}\) и \(\overrightarrow{j}\) совпадают с началом координат
3. вектор \(\overrightarrow{i}\) лежит на оси OX и сонаправлен с ней,
   вектор \(\overrightarrow{j}\) лежит на оси OY и сонаправлен с ней.

Данные векторы \(\overrightarrow{i}\) и \(\overrightarrow{j}\) также называют координатными единичными векторами. С их помощью мы и будем задавать координаты векторов на плоскости.

Отметим на плоскости точку B(3;4) и проведем вектор \(\overrightarrow{OB}\), начало которого совпадает с центром координат. 

Этот вектор можно представить в виде суммы двух ортогональных векторов \(\overrightarrow{OB_1}\) и \(\overrightarrow{B_1B}\).

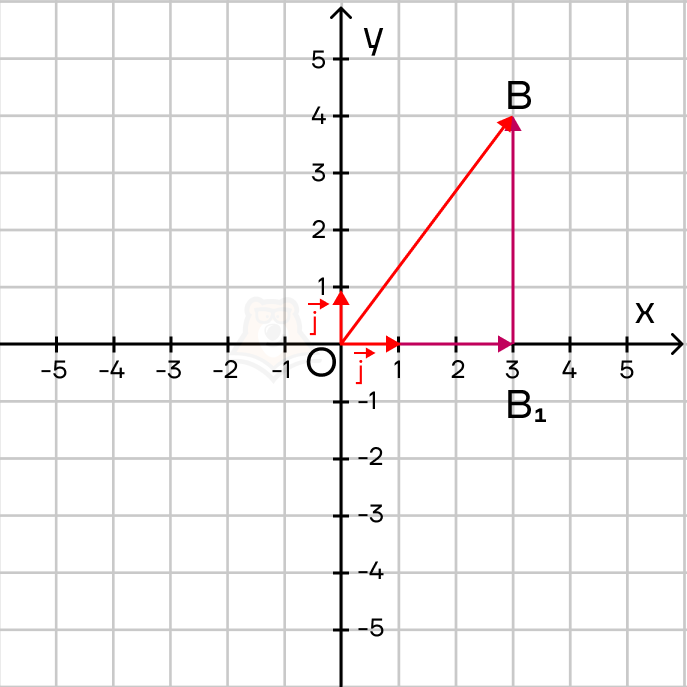
Так как вектор \(\overrightarrow{OB_1}\) лежит на оси OX, то есть сонаправлен с вектором \(\overrightarrow{i}\), и из рисунка видно, что \(|OB_1|=3=3|\overrightarrow{i},|\) то можем сделать вывод, что \(\overrightarrow{OB_1}=3\overrightarrow{i}\).

Аналогично с вектором \(\overrightarrow{B_1B}\): он параллелен оси OY, то есть сонаправлен с вектором \(\overrightarrow{j}\) и \(|B_1В|=4=4 \overrightarrow{j}\), откуда \(\overrightarrow{B_1B}=4\overrightarrow{j}\).

Тогда получаем: \(\overrightarrow{OB}=\overrightarrow{OB_1}+\overrightarrow{B_1B}=3\overrightarrow{i}+4\overrightarrow{j}\).

Согласно теореме о разложении вектора на плоскости по двум неколлинеарным векторам, любой вектор на координатной плоскости можно единственным способом представить в виде суммы векторов \(\overrightarrow{i}\) и \(\overrightarrow{j}\), взятых с определенными коэффициентами. 

Эти коэффициенты и называют координатами вектора на плоскости: коэффициент перед вектором \(\overrightarrow{i}\) равен координате вектора по оси OX, коэффициент \(\overrightarrow{j}\) – его координате по оси OY. Координаты вектора ставятся в фигурные скобки после обозначения вектора. В данном случае, \(\overrightarrow{OB}\){3;4}.

Что же мы замечаем в таком случае? Конечно, координаты вектора \(\overrightarrow{OB}\){3;4} совпали с координатами точки B(3;4). Таким образом, можем сделать вывод: координаты вектора, выходящего из начала координат, равны координатам конца этого вектора.

Косинусы углов \(\alpha\) и \(\beta\), которые данный вектор образует с положительными направлениями осей OX и OY соответственно, называют направляющими косинусами вектора.

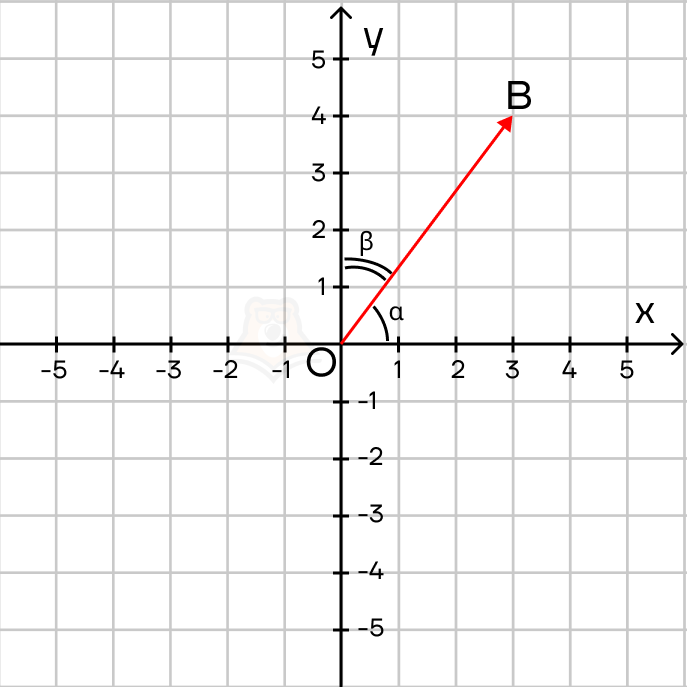
Произведения направляющих косинусов вектора на длину вектора равны координатам данного вектора по соответствующим осям.

Для вектора \(\overrightarrow{a}\){\(x_0;y_0\)} с направляющими косинусами \(cos(\alpha)\) по оси OX и \(cos(\beta)\) по оси OY:

\(x_0=|\overrightarrow{a}|cos(\alpha)\)
\(x_0=|\overrightarrow{a}|cos(\beta)\)

Убедимся в этом, рассмотрев прямоугольные треугольники \(\vartriangle OBB_1\) и \(\vartriangle OBB_2\), представленные на рисунке ниже.

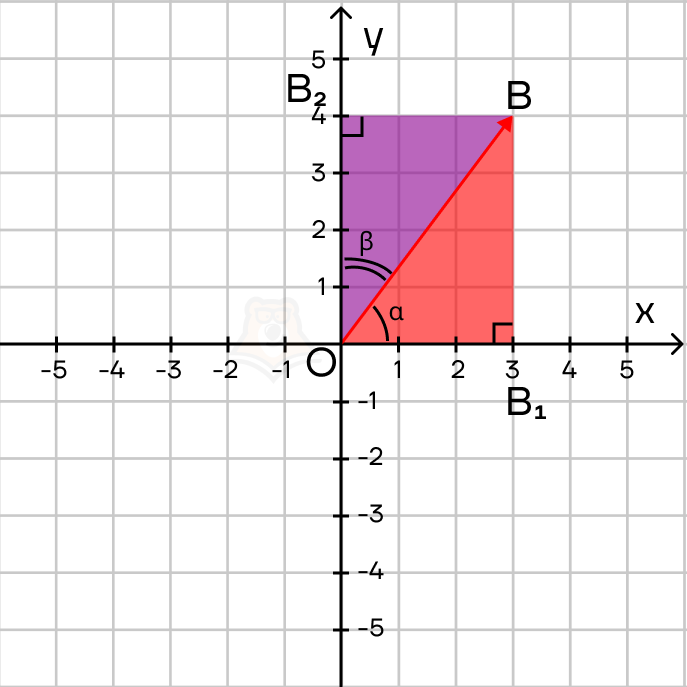
В этих треугольниках, по определению косинуса: 

\(cos(\alpha)=\frac{OB_1}{OB}=\frac{OB_1}{|\overrightarrow{OB}|}\)
\(cos(\beta)=\frac{OB_2}{OB}=\frac{OB_2}{|\overrightarrow{OB}|}\)

Откуда:

\(OB_1=|\overrightarrow{OB}|cos(\alpha)\)
\(OB_2=|\overrightarrow{OB}|cos(\beta)\)

В свою очередь, длины отрезков \(OB_1\) и \(OB_2\) как раз равны координатам точки B по осям OX и OY соответственно, то есть, равны координатам вектора \(\overrightarrow{OB}\).

Если длина вектора равна 1 (такие векторы называют единичными), тогда получается, что координаты таких векторов будут равны их направляющим косинусам.

Для единичного вектора \(\overrightarrow{a}\){\(x_0;y_0\)} с направляющими косинусами \(cos(\alpha)\) по оси OX и \(cos(\beta)\) по оси OY:

\(x_0=cos(\alpha)\)
\(y_0=cos(\beta)\)

Таким образом, координаты вектора можно найти либо по координатам его конца (если вектор выходит из начала координат), либо через длину вектора и его направляющие косинусы. При этом об одном способе нахождения координат вектора мы еще не сказали.

 Рассмотрим вектор \(\overrightarrow{AC}\), где A(1;1), С(5;3).

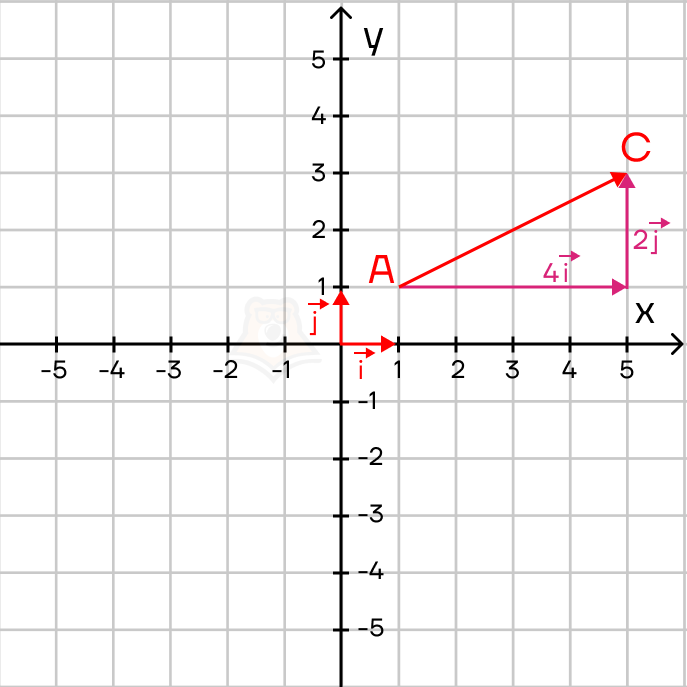
Видим, что этот вектор можно опять же представить в виде суммы двух ортогональных векторов \(4\overrightarrow{i}\) и \(2\overrightarrow{j}\), то есть \(\overrightarrow{AC}=4\overrightarrow{i}+2\overrightarrow{j}\), а значит, \(\overrightarrow{AC}\){4;2}.

Можно заметить, что координаты вектора AC получились путем вычитания координат конца вектора из координат начала вектора. Так можно посчитать координаты для абсолютно любого вектора на плоскости:

\(\overrightarrow{a}\){\(x_к-x_н ; y_к-y_н\)},

где (\(x_к ; y_к\)) – координаты конца вектора, (\(x_н;y_н\)) – координаты начала вектора.

Например, если T(1;2), K(5;3), то \(\overrightarrow{TK}\){\(5-2;3-2\)}. Получаем: \(\overrightarrow{TK}\){\(3;1\)}

Итак, мы выяснили, что из себя представляют координаты вектора на плоскости, и разобрали несколько способов для их определения.

Радиус-вектор точки на плоскости

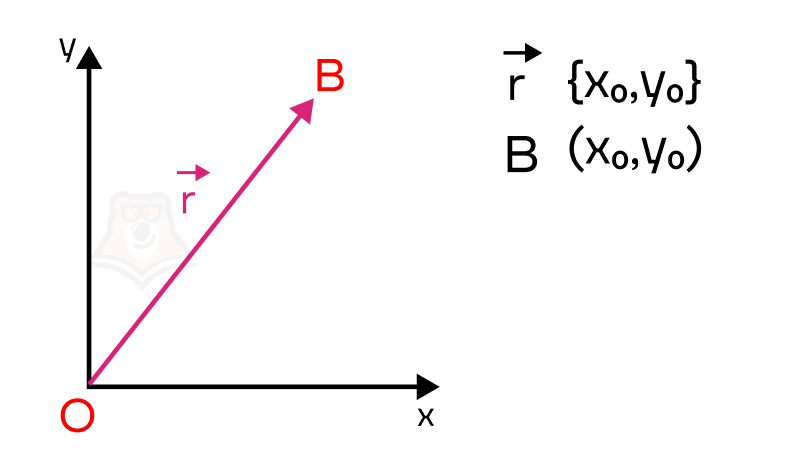
Вернемся к ранее рассмотренному вектору \(\overrightarrow{OB}\). Этот вектор проведен из начала координат в точку B. В таком случае его называют радиус-вектором точки B на плоскости.

Радиус-вектор точки – это вектор, проведенный из начала координат к этой точке. 

Координаты вектора \(\overrightarrow{OB}\){\(3;4\)} равны координатам точки \(B(3;4)\). То есть,  координаты точки равны координатам радиус-вектора этой точки на плоскости. Зная координаты радиус-вектора точки на плоскости, можно определить координаты этой точки, и наоборот.

\(\overrightarrow{r}\){\(x_0;y_0\)}\(\Leftrightarrow B(x_0;y_0),\)
где \(\overrightarrow{r}\){\(x_0;y_0\)} – радиус-вектор точки Bб 

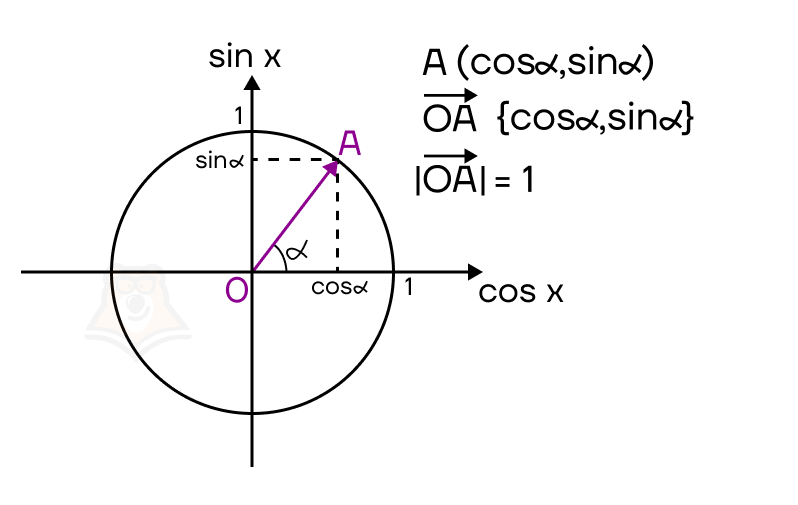
Понятие радиус-вектора и его координат используется для определения координат точки. Чтобы разобраться в этом, обратимся к тригонометрической окружности. Вспомнить, что из себя эта окружность представляет, можно в статье «Тригонометрическая окружность. Часть 1». 

Итак, на тригонометрической окружности выберем точку A и проведем ее радиус-вектор \(\overrightarrow{OA}\). Так как радиус тригонометрической окружности равен 1, \(|\overrightarrow{OA}|=1\).Напомним, что на координатной плоскости горизонтальная ось – это ось косинусов(cos x), вертикальная ось – ось синусов  (sin x). В таком случае запишем координаты точки A следующим образом: \(A(cos\alpha ; sin\alpha )\), где – угол между осью косинусов и отрезком OA, отложенный от оси косинусов против часовой стрелки. Тогда координаты радиус-вектора этой точки будут такими же:
\(\overrightarrow{OA}\){\(cos \alpha; sin \alpha\)}.

Далее выберем точку B на этой координатной плоскости так, чтобы точки O,A и B лежали на одной прямой, и проведем вектор \(\overrightarrow{OB}\). 

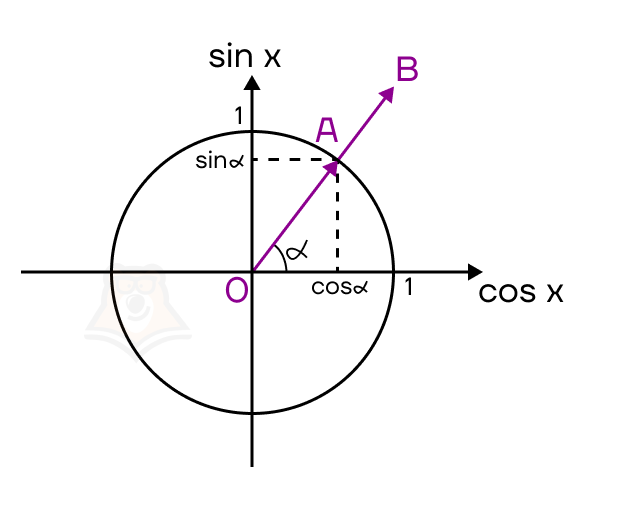
Так как \(\overrightarrow{OA}\uparrow\uparrow \overrightarrow{OB}\) и \(\frac{|\overrightarrow{OB}|}{|\overrightarrow{OA}|}=\frac{OB}{1}=OB\), то \(\overrightarrow{OB}=OB*\overrightarrow{OA}\).

Воспользовавшись свойством координат произведения вектора на число, получим: \(\overrightarrow{OB}= OB*\overrightarrow{OA} \Rightarrow \overrightarrow{OB}\){\(OB*cos\alpha ; OB*sin\alpha\)}

В таком случае координаты точки B будут равны координатам радиус-вектора OB. Получаем формулу координат точки на плоскости:

\(B(OB*cos\alpha ; OB*sin\alpha)\),

где OB – длина отрезка, соединяющего точку B с началом координат,
\(\alpha\)– угол между горизонтальной осью и отрезком OB, отложенный от горизонтальной оси против часовой стрелки

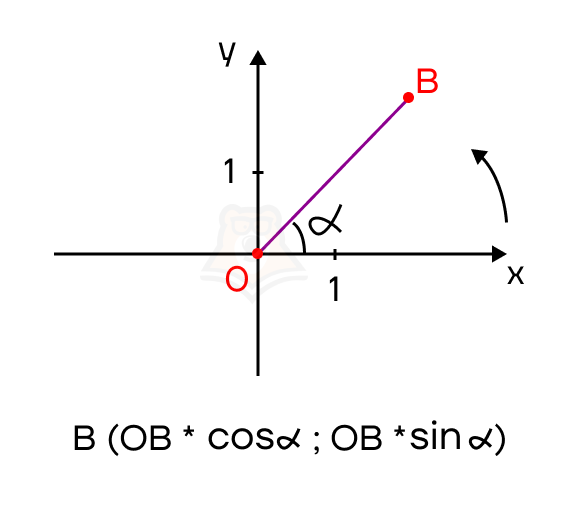
Таким образом, с помощью понятия вектора мы вывели формулу, которая позволяет определить координату любой точки на плоскости.

Ранее мы разобрали, как различными способами можно найти координаты вектора. Отсюда может возникнуть несколько вопросов. Можно ли определить координату суммы или разности векторов? Или, может быть, координаты произведения вектора на число? Давайте разберемся в этом в следующем разделе. 

Координаты произведения вектора на число. Координаты суммы и разности векторов на плоскости

С помощью координат произвольного вектора \(\overrightarrow{b}\) на плоскости можно найти координаты вектора \(k*\overrightarrow{b}\), где k – числовой коэффициент:

\(\overrightarrow{b}\){\(x_0;y_0\)}\(\Rightarrow k*\overrightarrow{b}\){\(k*x_0;k*y_0\)}

Например, если \(\overrightarrow{a}\){1;2}, то \(5\overrightarrow{b}\){5*1;5*2}. Получаем: \(5\overrightarrow{b}\){5;10}

Помимо этого, зная координаты двух произвольных векторов a и b, можно найти координаты вектора их суммы или разности, воспользовавшись формулой:

\(\overrightarrow{a}\){\(x_1;y_1\)},\(\overrightarrow{b}\){\(x_2;y_2\)}\(\Rightarrow a\overrightarrow{\pm}\){\(x_1 \pm x_2; y_1 \pm y_2\)}

Например, если \(\overrightarrow{a}\){-3;2}, \(\overrightarrow{b}\){7;0}, то: 

1. \(a\overrightarrow{+}b\){-3+7;2+0}, то есть \(a\overrightarrow{+}b\){4;2}
2. \(a\overrightarrow{-}b\){-3-7;2-0}, то есть \(a\overrightarrow{-}b\){-10;2}

С помощью координат вектора можно не только задать его положение на плоскости, но и найти его длину.

Длина вектора через его координаты на плоскости

Вернемся к вектору \(\overrightarrow{AC}=4\overrightarrow{i}+2\overrightarrow{j}\). 

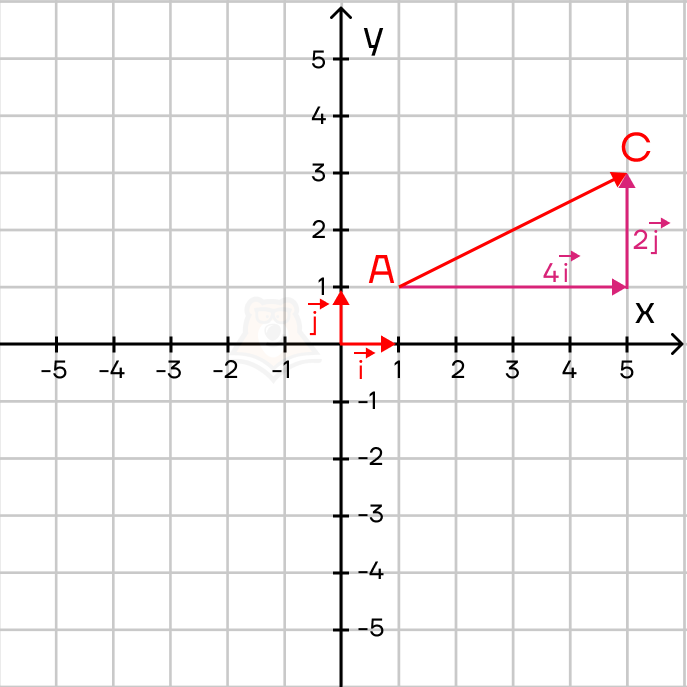
Из рисунка видно, что при сложении векторов методом треугольника образуется прямоугольный треугольник, где сам вектор \(\overrightarrow{AC}\) является гипотенузой. Вспомнить составляющие прямоугольного треугольника, а также теорему Пифагора для прямоугольного треугольника, можно в статье «Равнобедренный, равносторонний и прямоугольный треугольник». Воспользовавшись теоремой Пифагора, найдем эту гипотенузу:

\(|\overrightarrow{AC}|=\sqrt{|4\overrightarrow{i}|^2+|2\overrightarrow{j}|^2}=\sqrt{4^2+2^2}=\sqrt{16+4}=\sqrt{20}=2\sqrt{5}\)

Заметим, что длина вектора равна квадратному корню из суммы квадратов его координат:

\(|\overrightarrow{a}|=\sqrt{x^2+y^2}\),

где x и y – координаты вектора \(\overrightarrow{a}\) на плоскости.

Ну и, пожалуй, самое важное: координаты векторов позволяют даже находить скалярное произведение.

Скалярное произведение двух векторов через координаты векторов на плоскости

С помощью координат двух векторов на плоскости можно найти их скалярное произведение:

\(\overrightarrow{a}*\overrightarrow{b}=x_1*x_2+y_1*y_2,\)

где \(\overrightarrow{a}\){\(x_1;y_1\)}, \(\overrightarrow{b}\){\(x_2;y_2\)}

Например, найдем скалярное произведение векторов \(\overrightarrow{f}\){3;2}, \(\overrightarrow{h}\){8;-1}

\(\overrightarrow{f}*\overrightarrow{h}=38+2*(-1)=24-2=22\)

Теперь вспомним классическое определение скалярного произведения:

\(\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|*cos(\alpha)\),

где \(\alpha\) – угол между векторами \(\overrightarrow{a}\) и \(\overrightarrow{b}\)

Получается что:

\(\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|*cos(\alpha)\),
\(\overrightarrow{a}*\overrightarrow{b}=x_1*x_2+y_1*y_2\)

То есть:

\(|\overrightarrow{a}|*|\overrightarrow{b}|*cos(\alpha)=x_1*x_2+y_1*y_2\)

Выразим отсюда косинус угла между векторами:

\(cos(\alpha)=\frac{x_1*x_2+y_1*y_2}{|\overrightarrow{a}|*|\overrightarrow{b}|}\)

А теперь сделаем последний шаг: подставим в эту формулу длины векторов: \(|a|=\sqrt{x_1^2+y_1^2}\) и \(|b|=\sqrt{x_2^2+y_2^2}\). Получим формулу угла между двумя векторами на плоскости:

\(cos(\alpha)=\frac{x_1*x_2+y_1*y_2}{\sqrt{x_1^2+y_1^2}*\sqrt{x_2^2+y_2^2}}\),

где \(\overrightarrow{a}\){\(x_1;y_1\)}, \(\overrightarrow{b}\){\(x_2;y_2\)}, – угол между \(\overrightarrow{a}\) и \(\overrightarrow{b}\)

Эта формула позволяет вычислить угол между двумя векторами на плоскости, зная только их координаты.

Как вектор совершил революцию? На данный момент векторы широко используются в векторной графике, суть которой заключается в том, что изображение строится не из пикселей (маленьких точек), а из векторов. Объекты такой графики задаются с помощью координат. Благодаря векторной графике, человеку стало доступно получать изображения, которые не меняют своего качества при изменении размера. Наверняка каждый сталкивался с проблемой появления пикселей при сильном увеличении картинки. Порой это действительно доставляет неудобства. Векторная графика смогла решить эту проблему, тем самым совершим целую революцию в графическом мире. Сейчас векторная графика широко применяется в веб-дизайне.

Координатная плоскость, безусловно, часто используется для решения задач по планиметрии. Если же говорить о стереометрии, то будет задействовано уже целое пространство.

Векторы в пространстве

По аналогии с плоскостью, вектор в пространстве также можно разложить. Только уже не на два, а на три вектора. Для этого существует теорема о разложении вектора в пространстве по трем некомпланарным векторам.

Проведем три некомпланарных вектора \(\overrightarrow{b}\), \(\overrightarrow{c}\) и \(\overrightarrow{d}\), а также вектор \(\overrightarrow{a}\). В таком случае для вектора a найдутся некоторые числовые коэффициенты \(k_1, k_2\) и \(k_3\) такие, что \(\overrightarrow{a}=k_1\overrightarrow{b}+k_2\overrightarrow{c}+k_3\overrightarrow{d}\). Равенство \(\overrightarrow{a}=k_1\overrightarrow{b}+k_2\overrightarrow{c}+k_3\overrightarrow{d}\) называется разложением вектора \(\overrightarrow{a}\) по трем некомпланарным векторам \(\overrightarrow{b}\), \(\overrightarrow{c}\) и \(\overrightarrow{d}\), а коэффициенты \(k_1, k_2\) и \(k_3\) – коэффициентами  разложения вектора a по трем неколлинеарным векторам \(\overrightarrow{b}\), \(\overrightarrow{c}\) и \(\overrightarrow{d}\). Для любого вектора найдется свое разложение по этим векторам, причем только одно.

Итак, любой вектор можно разложить единственным образом по трем некомпланарным векторам.

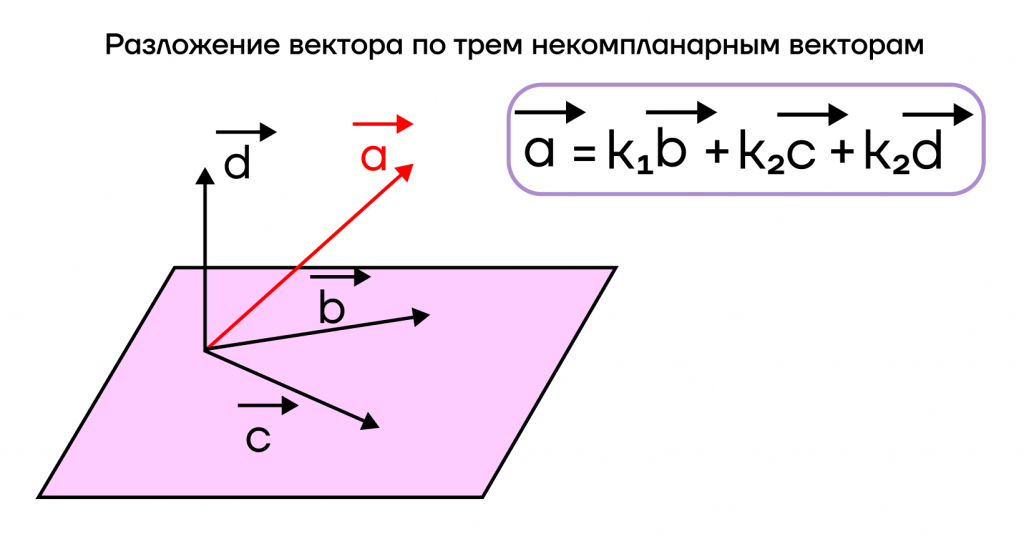
Помимо проекции вектора на ось, мы также можем спроецировать вектор на плоскость. 

Проекция вектора на плоскость

Рассмотрим вектор \(\overrightarrow{AB}\) и плоскость \(\alpha\), изображенные на рисунке ниже. Спроецируем точки A и B на плоскость \(\alpha\) и назовем их \(A_1\) и \(B_1\) соответственно. В таком случае вектор \(\overrightarrow{A_1B_1}\) называют проекцией вектора \(\overrightarrow{AB}\) на плоскость \(\alpha\).

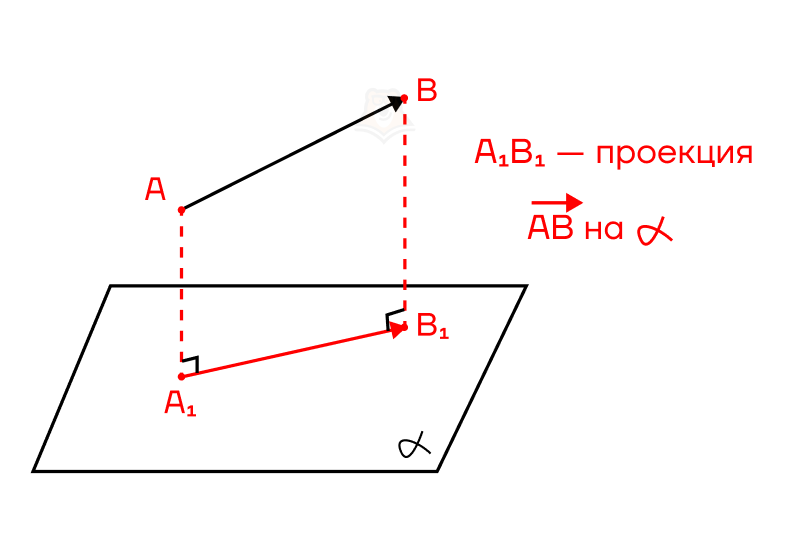
Проекция вектора \(\overrightarrow{b}\) на плоскость \(\alpha\) – это вектор, началом которого является проекция начала вектора \(\overrightarrow{b}\) на плоскость \(\alpha\), а концом – проекция конца вектора \(\overrightarrow{b}\) на плоскость \(\alpha\).

Разобравшись с понятием проекции вектора на плоскость, мы, наконец, можем переходить к самому главному – координатам вектора в пространстве.

Координаты вектора в пространстве

Рассмотрим классическую систему координат, используемую в пространстве – XYZ. На осях OX, OY и OZ из начала координат отложим единичные координатные векторы: вектор \(\overrightarrow{i}\) вдоль оси OX, вектор \(\overrightarrow{j}\) вдоль оси OY, вектор \(\overrightarrow{k}\) вдоль оси OZ. 

Эта ортогональная система единичных векторов \(\overrightarrow{i}\),\(\overrightarrow{j}\),\(\overrightarrow{k}\) используется для описания положения вектора в пространстве.

Что из себя представляют две знаменитые тройки векторов? Любую тройку некомпланарных векторов векторов можно отнести к одному из двух видов – правая тройка векторов или левая тройка векторов. Возьмем упорядоченную систему векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\) и \(\overrightarrow{c}\), то есть в этой системе каждый вектор имеет свой порядковый номер: \(\overrightarrow{a}\) – первый, \(\overrightarrow{b}\) – второй и \(\overrightarrow{c}\) – третий. Посмотрим с конца третьего вектора \(\overrightarrow{c}\) на векторы \(\overrightarrow{a}\) и \(\overrightarrow{b}\). В таком случае если поворот от первого вектора (\(\overrightarrow{a}\)) ко второму вектору (\(\overrightarrow{b}\)) осуществляется против часовой стрелки, то тройку векторов \(\overrightarrow{a}\), \(\overrightarrow{b}\) и \(\overrightarrow{c}\) называют правой, если по часовой – левой.  Правую тройку ортогональных единичных векторов \(\overrightarrow{i}\), \(\overrightarrow{j}\) и \(\overrightarrow{k}\) активно используют для решения стереометрических задач координатным способом.  Также с помощью правой и левой троек векторов в физике часто определяют направление той или иной векторной величины, образующей с двумя другими величинами, направления которых известны, правую или левую тройку векторов.

Рассмотрим вектор \(\overrightarrow{OA}\), начало которого лежит в начале координат, а A(3;2;5). 

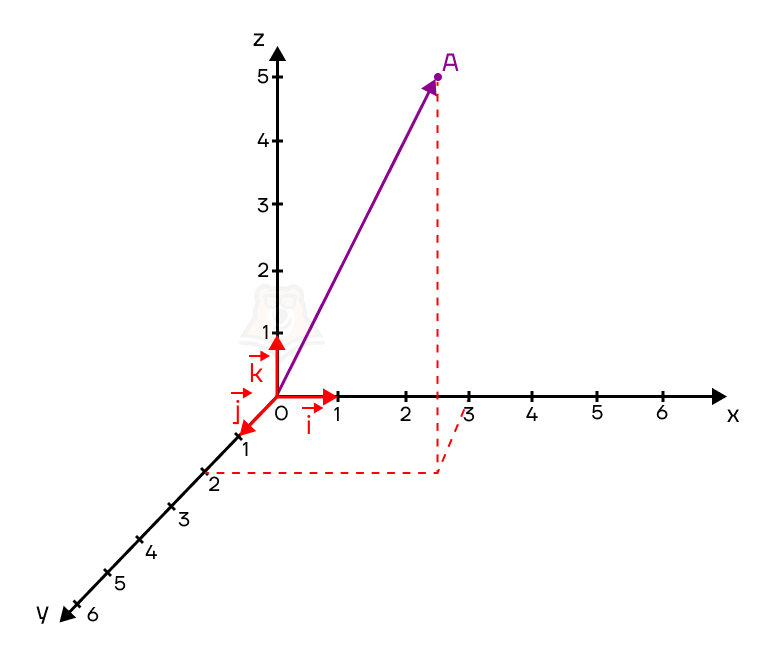
Согласно теореме о разложении вектора по трем некомпланарным векторам, разложим этот вектор на векторы \(\overrightarrow{i}\), \(\overrightarrow{j}\) и \(\overrightarrow{k}\). 

Вектор \(\overrightarrow{OA}\) можно представить в виде суммы трех ортогональных векторов: \(\overrightarrow{OB}\), \(\overrightarrow{BC}\) и \(\overrightarrow{CA}\) таких, что:

1.  \(\overrightarrow{OB}\upuparrows \bar{i}\) и \(OB=3=3|\overrightarrow{i}|\), то есть \(\overrightarrow{OB}=3\overrightarrow{i}\)
2.  \(\overrightarrow{BС}\upuparrows \bar{j}\) и \(BC=2=2|\overrightarrow{j}|\), то есть \(\overrightarrow{BC}=2\overrightarrow{j}\)
3.  \(\overrightarrow{CA}\upuparrows \bar{k}\) и \(CA=5=5|\overrightarrow{k}|\), то есть \(\overrightarrow{CA}=5\overrightarrow{k}\)

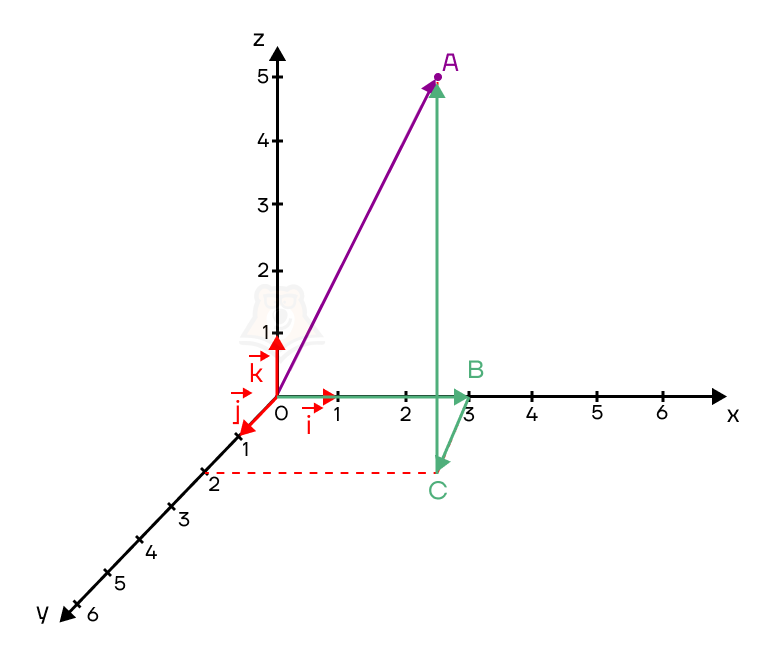
Таким образом, получаем, что \(\overrightarrow{OA} = 3\overrightarrow{i}+2\overrightarrow{j}+5\overrightarrow{k}\). Коэффициенты перед координатными векторами  \(\overrightarrow{i}\), \(\overrightarrow{j}\), \(\overrightarrow{k}\) называют координатами вектора  в пространстве: коэффициент перед вектором \(\overrightarrow{i}\) равен координате вектора по оси OX, коэффициент \(\overrightarrow{j}\) – его координате по оси OY, а коэффициент перед \(\overrightarrow{k}\) отвечает за координату по оси OZ. Так же, как и на плоскости, координаты вектора в пространстве заключаются в фигурные скобки. В данном случае, обозначим это так: \(\overrightarrow{OA}\) {3;2;5}.

Можем заметить, что координаты вектора \(\overrightarrow{OA}\) {3;2;5} совпали с координатами точки A(3;2;5). Действительно, координаты вектора, выходящего из начала координат, равны координатам конца этого вектора.

Косинусы углов \(\alpha\),\(\beta\) и \(\gamma\), которые данный вектор образует с положительными направлениями осей OX, OY и OZ соответственно, в случае с плоскостью называют направляющими косинусами вектора.

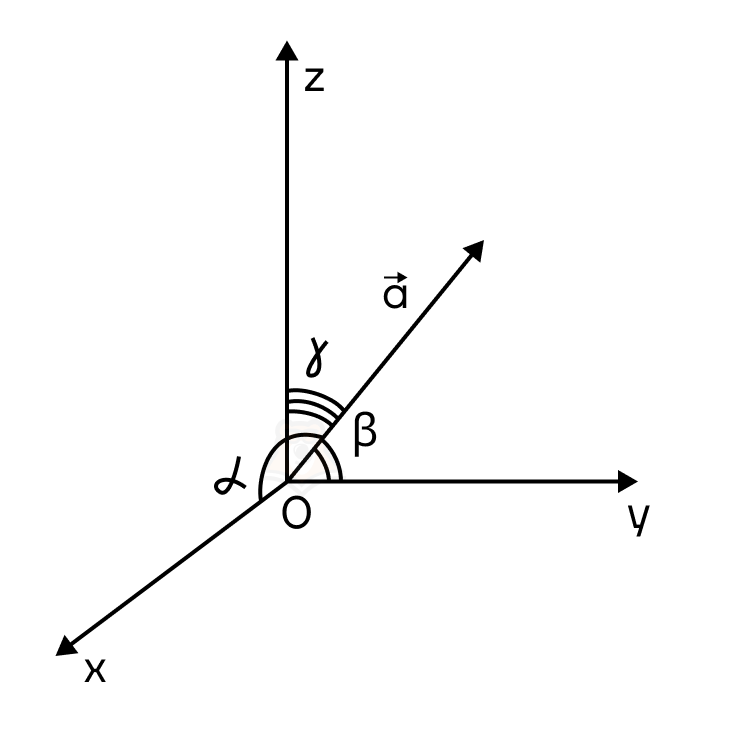
Напомним, что произведения направляющих косинусов вектора на длину вектора равны координатам данного вектора по соответствующим осям. Это же правило распространяется и на пространство.

Для вектора \(\overrightarrow{a}\){\(x_0;y_0;z_0\)} с направляющими косинусами \(cos(\alpha)\) по оси OX, \(cos(\beta)\) по оси OY и \(cos(\gamma)\) по оси OZ:

\(x_0=|\overrightarrow{a}|cos(\alpha)\)
\(y_0=|\overrightarrow{a}|cos(\beta)\)
\(z_0=|\overrightarrow{a}|cos(\gamma)\)

Разберем еще один способ нахождения координат вектора в пространстве. Если координаты вектора, выходящего из начала координат, равны координатам конца этого вектора, то, чтобы определить координаты вектора, выходящего не из начала координат, можно вычесть из координат конца вектора координаты начала вектора: 

\(\overrightarrow{a}\){\(x_к-x_н ; y_к-y_н; z_к-z_н\)},

где (\(x_к ; y_к; z_к\)) – координаты конца вектора, (\(x_н; y_н; z_н\)) – координаты начала вектора.

Например, вектор с началом в точке A\((1;6;-5)\) и концом в точке B\((4;-3;7)\) будет иметь координаты \(\overrightarrow{AB}\){\(4-1 ;-3-6; 7-(-5)\)}\(=\){\(3;-9;12\)}. 

Радиус-вектор точки в пространстве

Начало рассмотренного вектора \(\overrightarrow{OA}\) совпадает с началом координат. В таком случае вектор \(\overrightarrow{OA}\) называют радиус-вектором точки A в пространстве.

Ранее мы уже заметили, что координаты радиус-вектора \(\overrightarrow{OA}\){\(3;2;5\)} совпадают с координатой точки A\((3;2;5)\). Отсюда делаем вывод: координаты точки равны координатам радиус-вектора этой точки в пространстве. То есть, зная координаты радиус-вектора точки в пространстве, можно определить координаты этой точки, и наоборот.

\(\overrightarrow{r}\){\(x_0;y_0;z_0\)}\(\Leftrightarrow A(x_0;y_0;z_0)\),

где \(\overrightarrow{r}\){\(x_0;y_0;z_0\)} – радиус-вектор точки A 

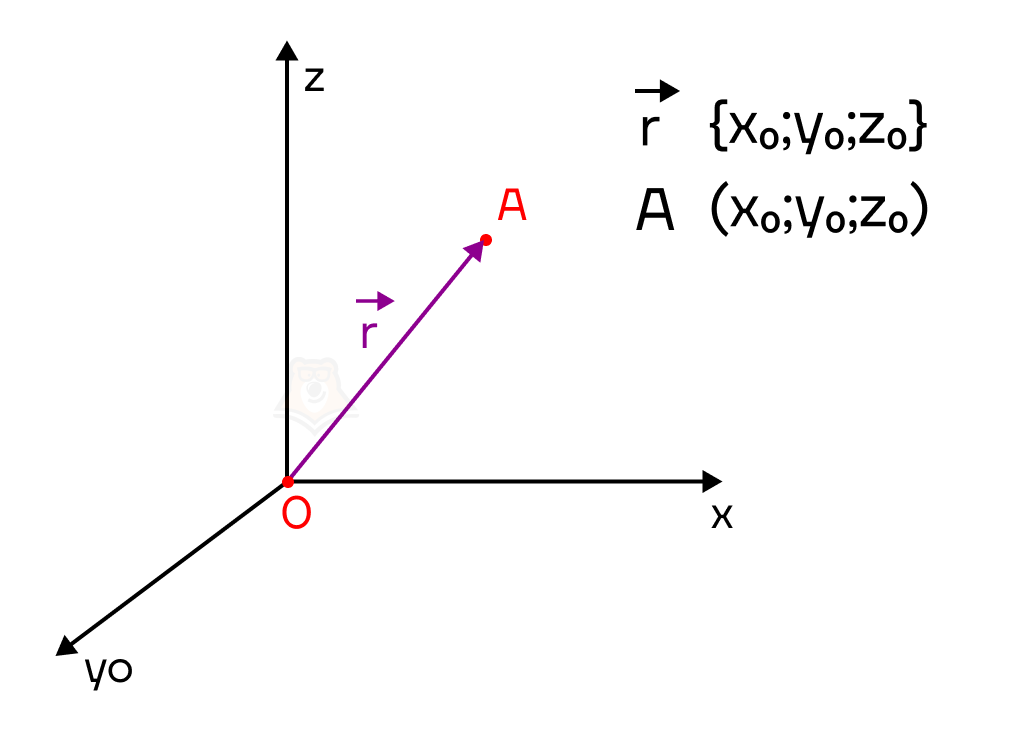
Координаты векторов в пространстве так же, как и на плоскости, позволяют найти длину вектора, координаты произведения вектора на число, координаты суммы и разности векторов, а также скалярное произведение двух векторов. По сути, во все формулы просто будет добавляться третья координата. Остановимся подробнее на каждой из них.

Координаты произведения вектора на число. Координаты суммы и разности векторов в пространстве

С помощью координат произвольного вектора \(\overrightarrow{b}\) в пространстве можно найти координаты вектора \(k*\overrightarrow{b}\), где k – числовой коэффициент:

\(\overrightarrow{b}\) {\(x_0;y_0;z_0\)} \(k*\overrightarrow{b}\){\(k*x_0;k*y_0;k*z_0\)}

Например, если \(\overrightarrow{b}\){\(2;5;-1\)}, то \(3\overrightarrow{b}\){\(32;35;3(-1)\)}. Получаем: \(3\overrightarrow{b}\){\(6;15;-3\)}

Помимо этого, зная координаты двух произвольных векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\), можно найти координаты вектора их суммы или разности, воспользовавшись формулой:

\(\overrightarrow{a}\) {\(x_1;y_1;z_1\)}, \(\overrightarrow{b}\) {\(x_2;y_2;z_2\)} \(\Rightarrow a\overrightarrow{\pm}b\) {\(x_1\pm x_2;y_1\pm y_2;z_1\pm z_2\)}

Например, если \(\overrightarrow{a}\){\(-2;1;3\)}, \(\overrightarrow{b}\) {\(0;4;-1\)}, то: 

1. \(a\overrightarrow{+}b\){\(-2+0;1+4;3+(-1)\)}, то есть \(a\overrightarrow{+}b\){\(-2;5;2\)}
2. \(a\overrightarrow{-}b\){\(-2-0;1-4;3-(-1)\)}, то есть \(a\overrightarrow{-}b\){\(-2;-3;4\)}

Длина вектора через его координаты в пространстве

Зная координаты вектора в пространстве, так же, как и на плоскости, мы можем найти длину этого вектора. Она будет равна квадратному корню из суммы квадратов его координат: 

\(|\overrightarrow{a}|=\sqrt{x_2+y_2+z_2}\),

где x,y и z – координаты вектора в пространстве.

Векторы и их координаты часто используют для решения различных задач по стереометрии. Особенно удобно это делать, если в задаче речь идет о фигуре, в которой можно ввести прямоугольную систему координат. Рассмотрим пример одной из таких задач.

Разберем пример задания №2 из ЕГЭ по профильной математике.

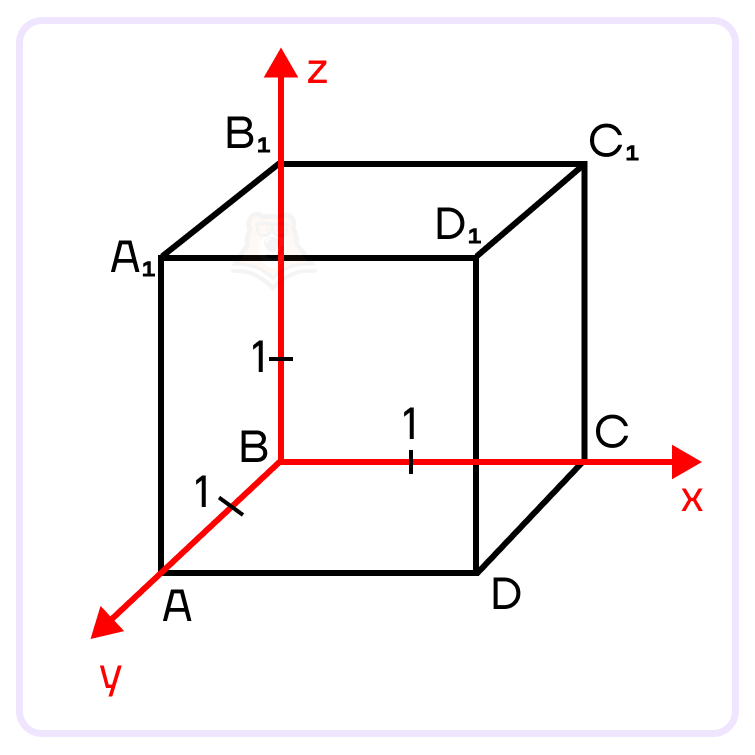
Задание. Найти диагональ куба, если его ребра равны \(\sqrt{3}\).

Решение. Вспомнить, что такое куб, можно в статье «Призма». Нарисуем куб \(ABCDA_1B_1C_1D_1\) и введем в этом кубе прямоугольную систему координат XYZ так, что начало координат будет лежать в точке В(0;0;0), ось OX направлена вдоль BС, ось OY направлена вдоль BA, ось OY – вдоль \(ВВ_1\), как показано на на рисунке ниже:

Так как каждое ребро куба по условию равно \(\sqrt3\), то точка \(D_1\) будет иметь координаты \(D_1(\sqrt3;\sqrt3;\sqrt3)\) Начало вектора \(\overrightarrow{BD_1}\) лежит в начале координат, а значит, координаты этого вектора будут равны координатам точки \(D_1(\sqrt3;\sqrt3;\sqrt3)\), то есть \(\overrightarrow{BD_1}\){\(\sqrt3;\sqrt3;\sqrt3)\)}

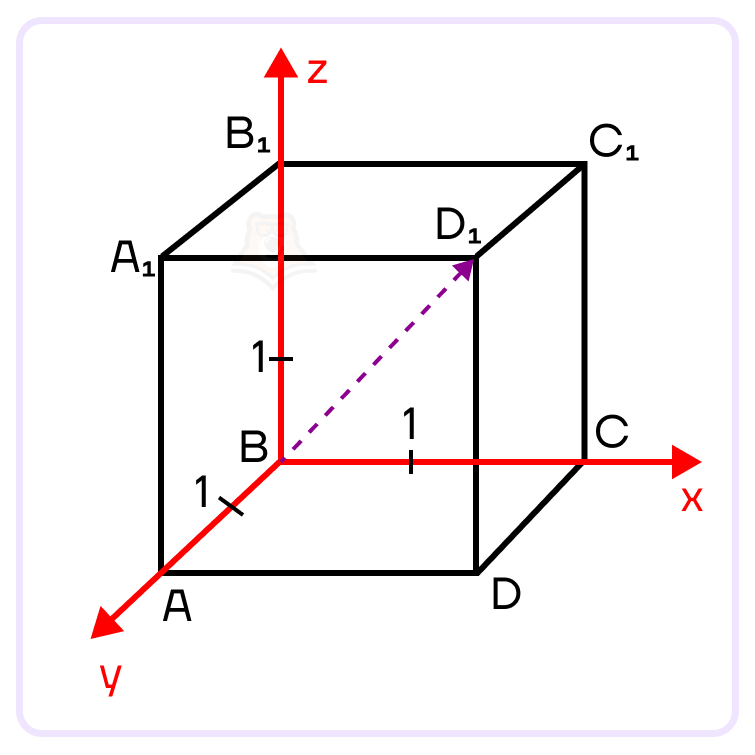
По формуле длины вектора найдем длину вектора \(\overrightarrow{BD_1}\):

\(|\overrightarrow{BD_1}|=\sqrt{x_2+y_2+z_2}=\sqrt{(\sqrt3)^2+(\sqrt3)^2+(\sqrt3)^2}=\sqrt{3+3+3}=\sqrt9=3\)

Таким образом, мы нашли длину вектора \(\overrightarrow{BD_1}\), которая, в свою очередь, и будет равна длине отрезка \(BD_1\), то есть искомой диагонали куба. 

Ответ: 3

Еще одна не менее важная возможность, которую предоставляют нам координаты – найти скалярное произведение двух векторов в пространстве. 

Скалярное произведение двух векторов через координаты векторов в пространстве

Формула также очень похожа на формулу для плоскости, отличается лишь добавлением третьей координаты:

\(\overrightarrow{a}*\overrightarrow{b}=x_1*x_2+y_1*y_2+z_1*z+2\),

где \(\overrightarrow{a}\){\(x_1;y_1;z_1\)}, \(\overrightarrow{b}\){\(x_2;y_2;z_2\)}

Скалярное произведение двух векторов часто используется для того чтобы доказать перпендикулярность прямых/отрезков. Рассмотрим пример пункта (а) задания №13 из ЕГЭ по профильной математике.

Задание. Дан куб \(ABCDA_1B_1C_1D_1\), ребра которого равны 5. Доказать, что \(BD_1\perp AC\).

Доказательство. Введем в кубе прямоугольную систему координат XYZ так, что начало координат будет лежать в точке \(B(0;0;0)\), ось OX направлена вдоль BС, ось OY направлена вдоль BA, ось OZ – вдоль \(ВВ_1\), как показано на на рисунке ниже:

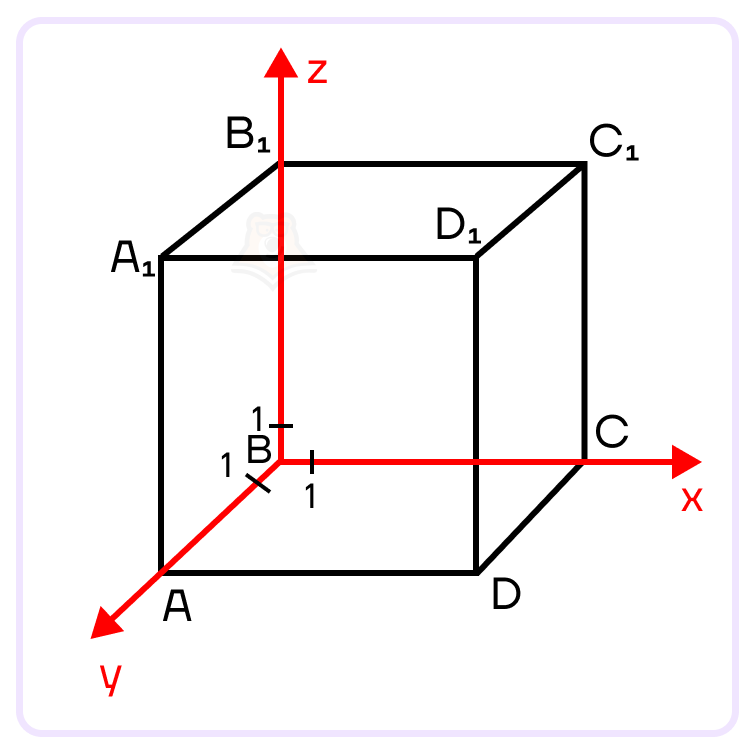
Для того чтобы доказать перпендикулярность \(BD_1\) и \(AC\), проведем векторы \(\overrightarrow{BD_1}\) и \(\overrightarrow{AC}\) и найдем координаты начал и концов этих векторов.

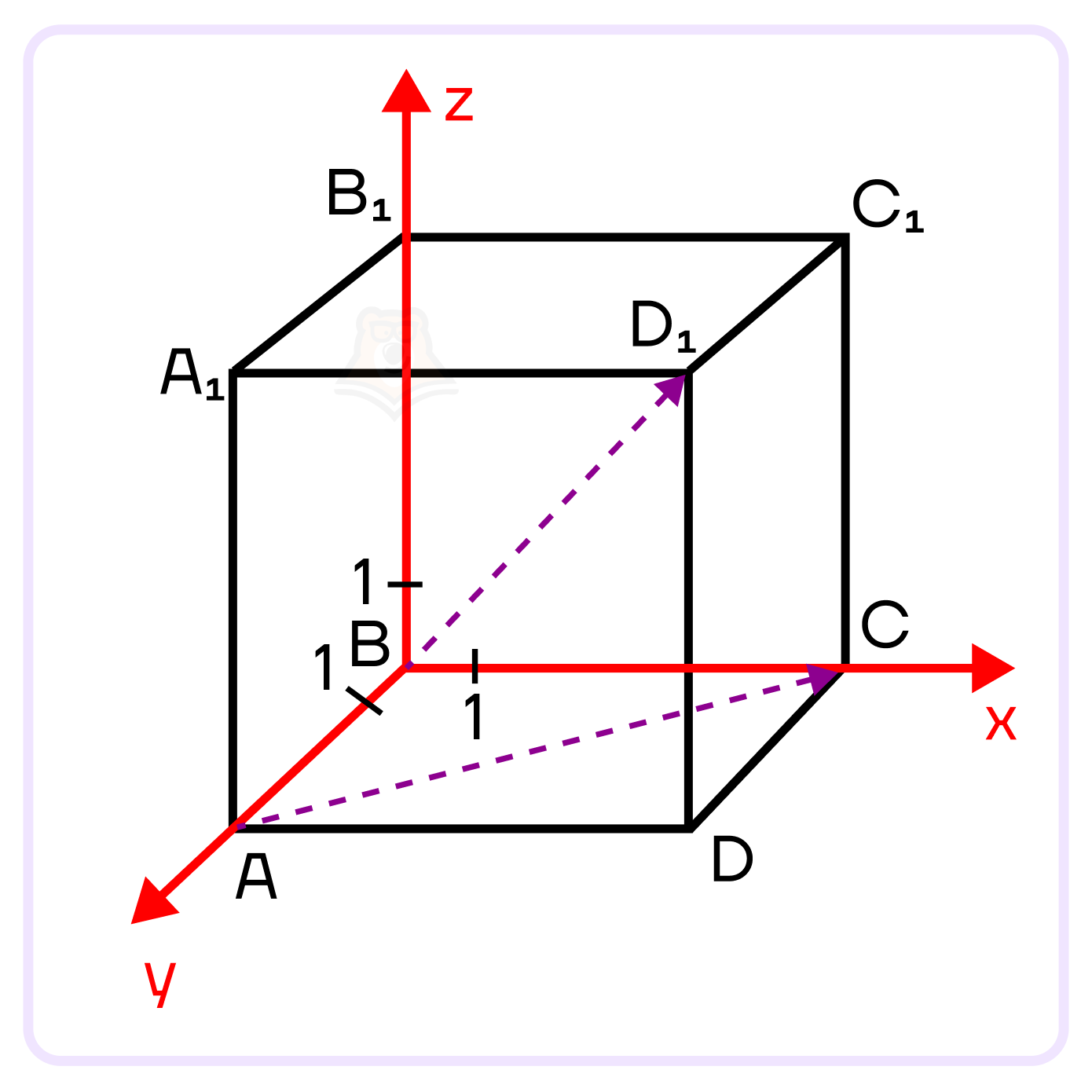
Мы уже знаем координаты точки  \(B(0;0;0)\). Так как каждое ребро куба по условию равно 5, то \(D_1(5;5;5), C(5;0;0), A(0;5;0)\).

Теперь найдем координаты векторов \(\overrightarrow{BD_1}\)и \(\overrightarrow{AC}\).

Вектор \(\overrightarrow{BD_1}\) исходит из начала координат, а значит, его координаты будут равны координатам конца этого вектора, точки \(D_1(5;5;5)\), то есть \(\overrightarrow{BD_1}\){\(5;5;5\)}.

Чтобы найти координаты вектора \(\overrightarrow{AC}\), вычтем из координат конца вектора \(C(5;0;0)\) координаты начала \(A(0;5;0)\): 

\(\overrightarrow{AC}\){\(5-0 ;0 -5; 0-0\)}\(=\){\(5;-5;0\)}

Теперь, зная координаты векторов \(\overrightarrow{BD_1}\) и \(\overrightarrow{AC}\), вычислим по формуле их скалярное произведение:

\(\overrightarrow{BD_1}*\overrightarrow{AC}=x_{BD_1}*x_{AC}+y_{BD_1}*y_{AC}+z_{BD_1}*z_{AC}= 5*5+5*(-5)+5*0= 0\)

Таким образом, скалярное произведение векторов \(\overrightarrow{BD_1}\) и \(\overrightarrow{AC}\) равно 0, из чего по признаку ортогональности векторов следует, что эти векторы ортогональны друг другу, то есть угол между ними равен 90°. Значит, и угол между отрезками \(\overrightarrow{BD_1}\) и \(\overrightarrow{AC}\) равен \(90° \Rightarrow BD_1\perp AC\)

Что и требовалось доказать.

С помощью классического определения скалярного произведения \((\overrightarrow{a}*\overrightarrow{b}=|\overrightarrow{a}|*|\overrightarrow{b}|cos(\alpha))\) и формулы для скалярного произведения через координаты \((\overrightarrow{a}*\overrightarrow{b}=x_1*x_2+y_1*y_2+z_1*z_2)\), можно вывести формулу угла между двумя векторами в пространстве:

\(cos(\alpha)=\frac{x_1*x_2+y_1*y_2+z_1*z_2}{\sqrt{x_1^2+y_1^2+z_1^2}*\sqrt{x_2^2+y_2^2+z_2^2}}\),

где \(\overrightarrow{a}\){\(x_1;y_1;z_1\)},\(\overrightarrow{b}\){\(x_2;y_2;z_2\)},\(\alpha\) – угол между \(\overrightarrow{a}\) и \(\overrightarrow{b}\)

Эта формула часто используется для решения стереометрических задач. Ее основное преимущество – возможность найти угол между двумя векторами в пространстве при помощи одних лишь координат этих векторов. 

Вот и все: наше знакомство с векторами на этом подошло к концу. В этой статье мы разобрали, как умножить вектор на число, что такое скалярное произведение векторов,  как задать положение вектора на плоскости и в пространстве. 

Рекомендуем не останавливать движение и сразу перейти к следующей статье «Треугольник», в которой речь пойдет об основах этой прекрасной фигуры

Термины

Гипотенуза – сторона в прямоугольном треугольнике, лежащая напротив прямого угла.

Катеты – стороны в прямоугольном треугольнике, образующие прямой угол.

Координаты – величины, определяющие положение точки в системе координат. Для прямоугольной системы координат положение точки задается координатами (x;y), для системы координат в пространстве – координатами (x;y;z).

Косинус – это отношение прилежащего катета к гипотенузе.

Плоскость – поверхность, которая полностью содержит каждую прямую, соединяющую любые две ее точки. 

Проекция точки на ось – это основание перпендикуляра, опущенного от этой точки к данной оси.

Произведение – результат умножения.

Прямоугольный треугольник – треугольник, у которого один угол равен 90°.

Синус – это отношение противолежащего катета к гипотенузе.

Фактчек

• Любой вектор можно умножить на число и получить другой вектор, направленный в ту же или в противоположную сторону.
• Существуют законы сложения и умножения для векторов, которые позволяют упростить выполнение действий над векторами. 
• Для любых двух векторов, зная их длины и угол между ними, можно найти их скалярное произведение. Если оно равно 0, то векторы ортогональны.
• С помощью координат вектора можно задавать его положение на плоскости, найти длину вектора, а также посчитать скалярное произведение двух векторов 

Проверь себя

Задание 1.
Длина вектора \(\overrightarrow{a}\) равна 3. Чему равна длина вектора \(4\overrightarrow{a}\)?

1. 1
2. 9
3. 12
4. 7

Задание 2.
Вектор \(\overrightarrow{a}\) имеет координаты: 

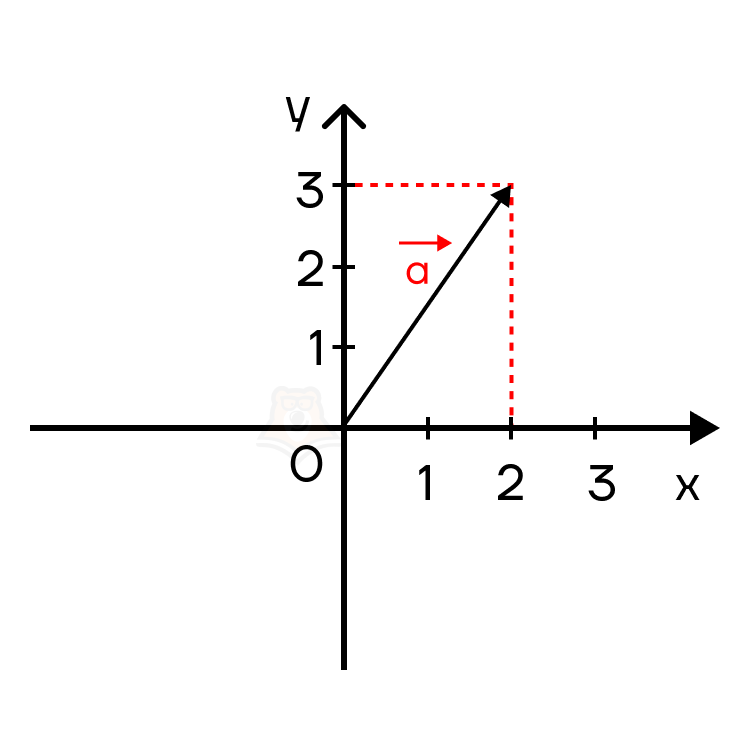
1. (2;3)
2. (3;3)
3. (3;2)
4. (2;2)

Задание 3.
Даны два вектора: \(\overrightarrow{a}(3;-1;5)\) и \(\overrightarrow{b}(-2;6;2)\). Чему равно их скалярное произведение? 

1. -1
2. 2
3. -3
4. Нет верного варианта

Задание 4.
Чему равна длина вектора \(a(3;2;-1)\)?

1. \(\sqrt{13}\)
2. \(\sqrt{14}\)
3. \(-\sqrt{13}\)
4. \(-\sqrt{14}\)

Ответы: 1. – 3; 2. – 1; 3. – 4; 4. – 2