Треугольник

На этой странице вы узнаете

• Что общего у эчпочмака, паруса и дорожного знака?
• Какая буква в алфавите треугольная?
• Что такое «невозможный треугольник»?

Бермудский треугольник — один из самых загадочных участков на нашей планете. В нем бесследно исчезают корабли и самолеты, а изучить природу этого места человеку до сих пор не удалось. Треугольники повсюду встречаются в природе: гора и ель, крылышко бабочки и лист папоротника. Давайте же разгадаем магию этой простой геометрической фигуры.

Треугольник

Что общего у эчпочмака, паруса и дорожного знака? … а еще у музыкального инструмента и онигири? Все правильно, они имеют форму треугольника.  Треугольник не случайно так часто встречается в нашей жизни. Это одна из самых интересных фигур. С точки зрения психологии эту фигуру связывают с движением, энергией (не просто так мы показываем направление стрелочкой, на конце которой треугольник). Следовательно, нет ничего удивительного в том, что его используют в условных обозначениях, дизайне, инфографике, архитектуре и других областях нашей жизни.

Для решения любых задач по планиметрии и стереометрии необходимо хорошо ориентироваться в свойствах основных геометрических фигур. Зная свойства и умея их применять, можно решить даже самую сложную задачу из второй части ЕГЭ. Сегодня мы рассмотрим одну из наиболее часто встречающихся фигур: треугольник.

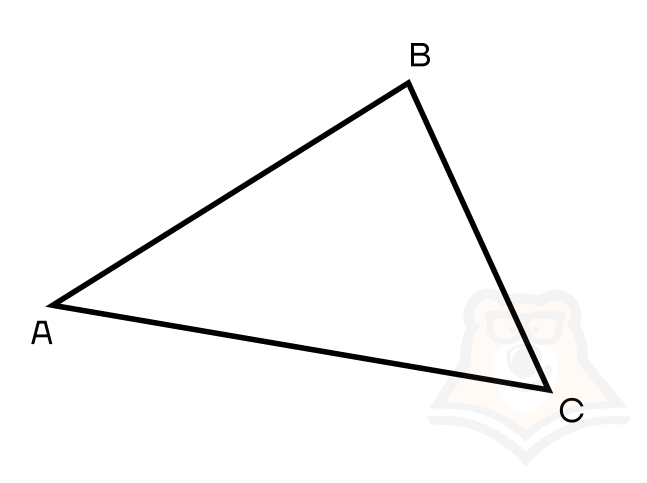
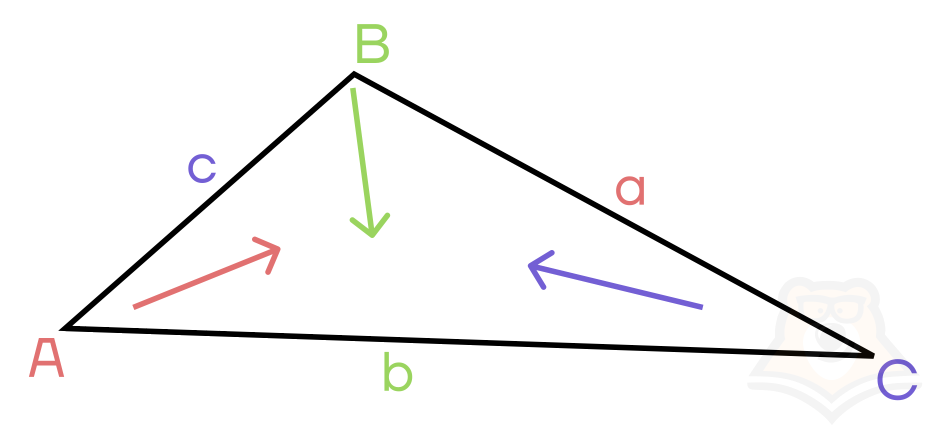
Треугольник — это геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, а также отрезками, которые соединяют эти точки. 

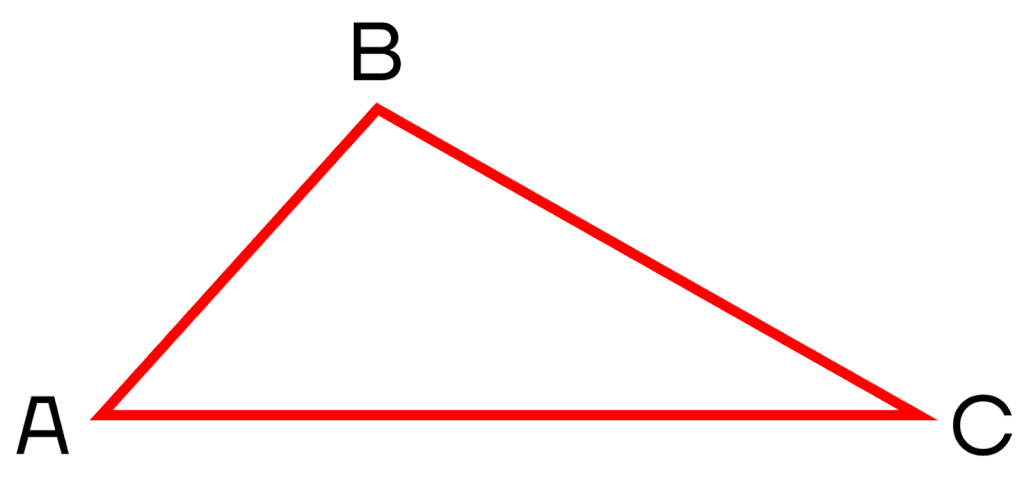
Рассмотрим рисунок. 
АВС – треугольник.
АВ, ВС, АС – стороны треугольника.
А, В, С – вершины треугольника – это точки, в которых сходятся по две стороны.

Какая буква в алфавите треугольная? А — первая буква в большинстве алфавитов. Она произошла от финикийской буквы «алеф», которая — что удивительно — обозначала согласный звук.  В изображении основных алфавитов мира заглавная А имеет треугольную форму с перекладиной посередине. В таком ее начертании усматривается отсылка к пирамидальной форме, к горам и, разумеется, к самому треугольнику, который является одной из древнейших фигур.

Когда мы уже узнали, что такое треугольник, может возникнуть вопрос: а как построить его на плоскости?

Построение треугольника

Геометрия невозможна без чертежей, поэтому нам необходимо знать, как можно построить треугольник. Несмотря на простоту фигуры, есть несколько способов ее построения. А для самого построения нам потребуются обычные чертежные инструменты: линейка, транспортир и циркуль.

Стоит заметить, что в треугольнике не просто так преобладает число 3: три стороны, три угла. Для его построения нам тоже необходимо 3 элемента.

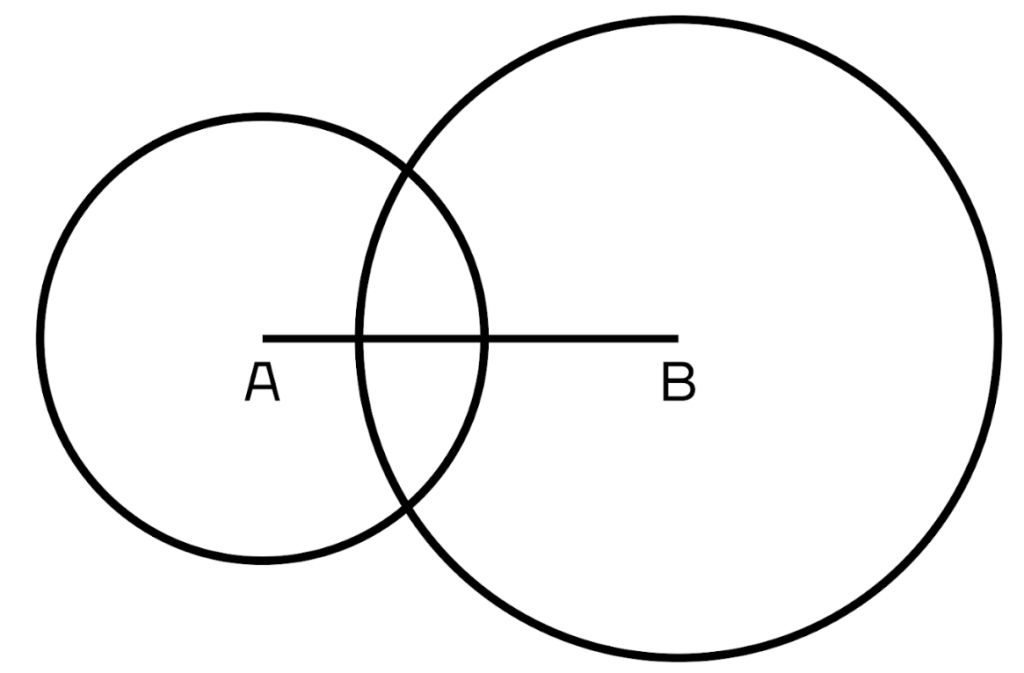
1. Построение треугольника по трем сторонам.

Предположим, нам даны три отрезка различной длины. Как построить из них треугольник?

Первым делом возьмем любой из них и начертим. Мы получили точки А и В – начало и конец отрезка.

Из этих точек будут выходить еще две стороны. Но как найти, где именно они между собой пересекутся? 

Здесь нам на помощь придет окружность. Если мы возьмем за центры точки А и В, то в какую бы сторону мы ни провели радиус, он не поменяет своего значения. 

Поэтому построим окружности с центром в точке А и в точке В. Их радиусы будут равны длине оставшихся двух сторон.

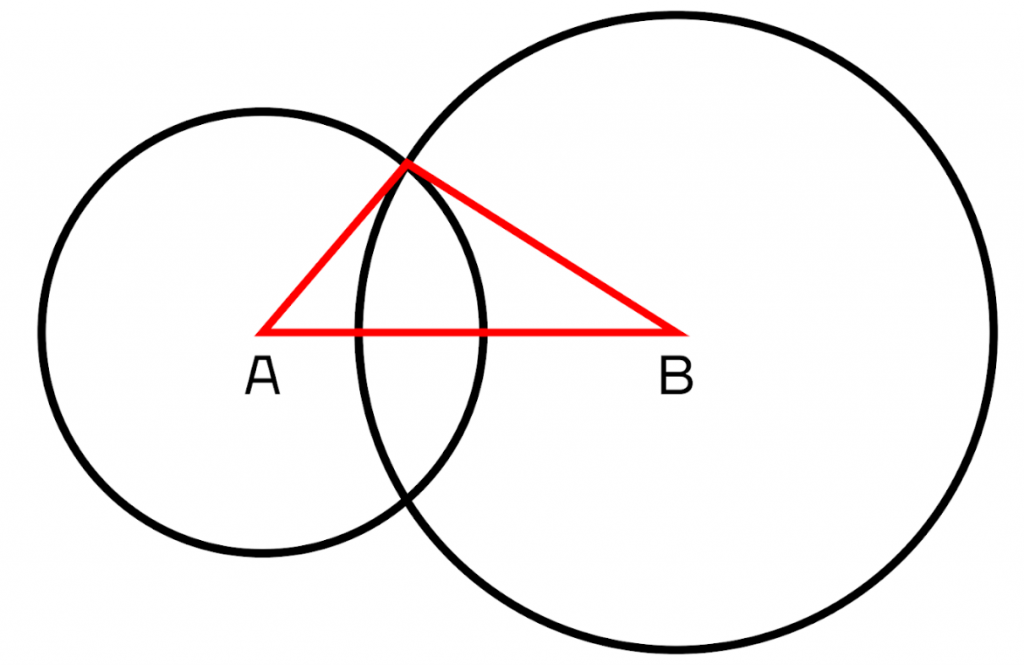
Получив точку пересечения, мы нашли третий угол – С. Осталось только соединить все точки отрезками и наш треугольник АВС готов.

2. Построение треугольника по двум сторонам и углу между ними. 

Предположим, мы знаем величину угла и длины двух сторон. Как построить треугольник в этом случае?

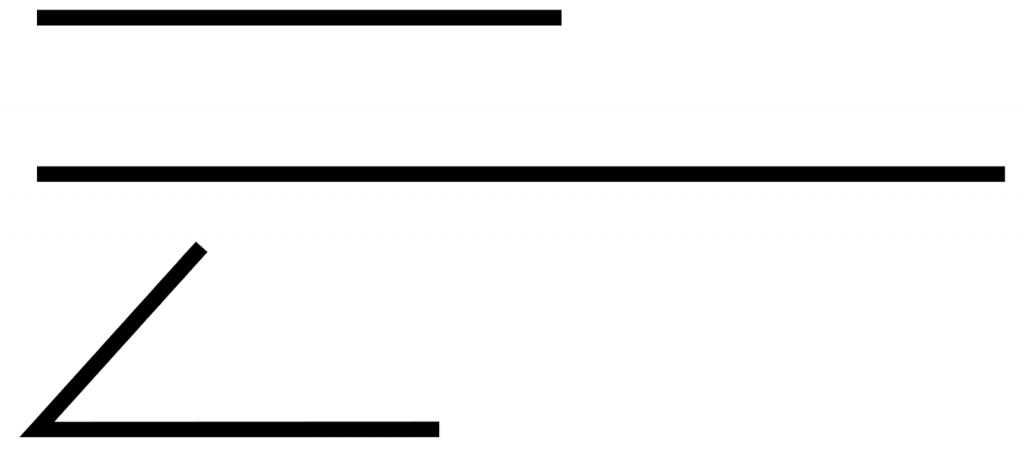
Первым делом начертим угол, из которого выходят два луча. Назовем его угол А. 

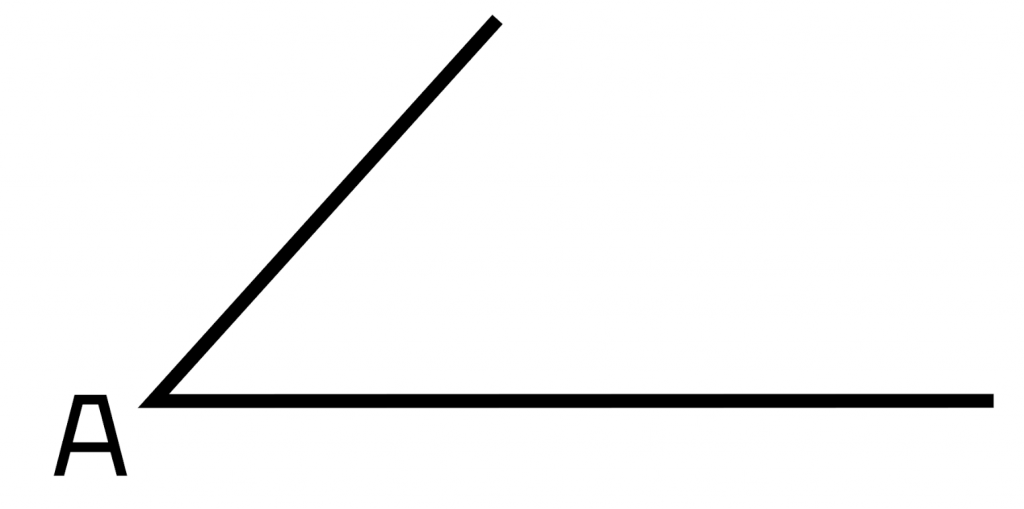
После этого на лучах отмеряем длины сторон, которые нам даны. Мы получили точки В и С.

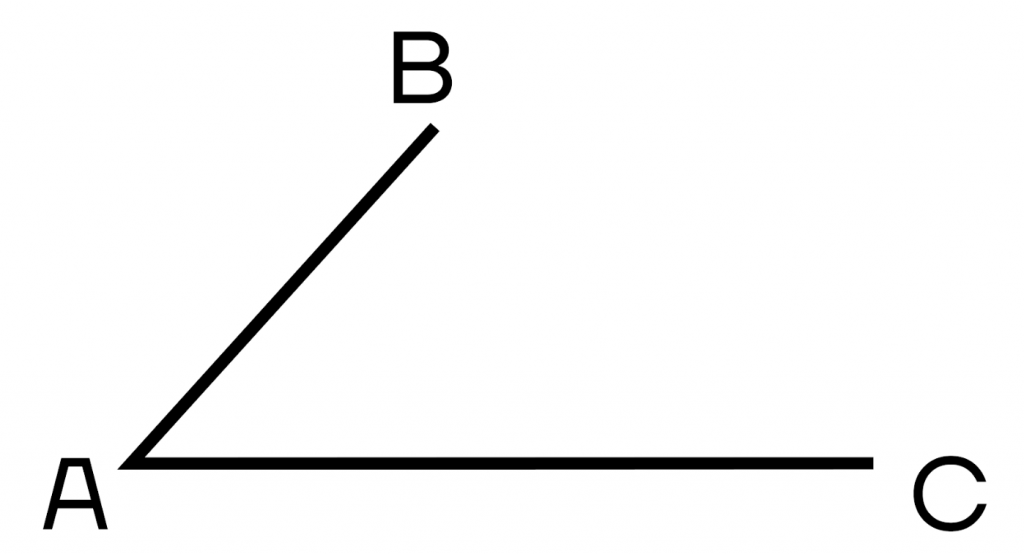
Осталось просто соединить их между собой. Треугольник готов!

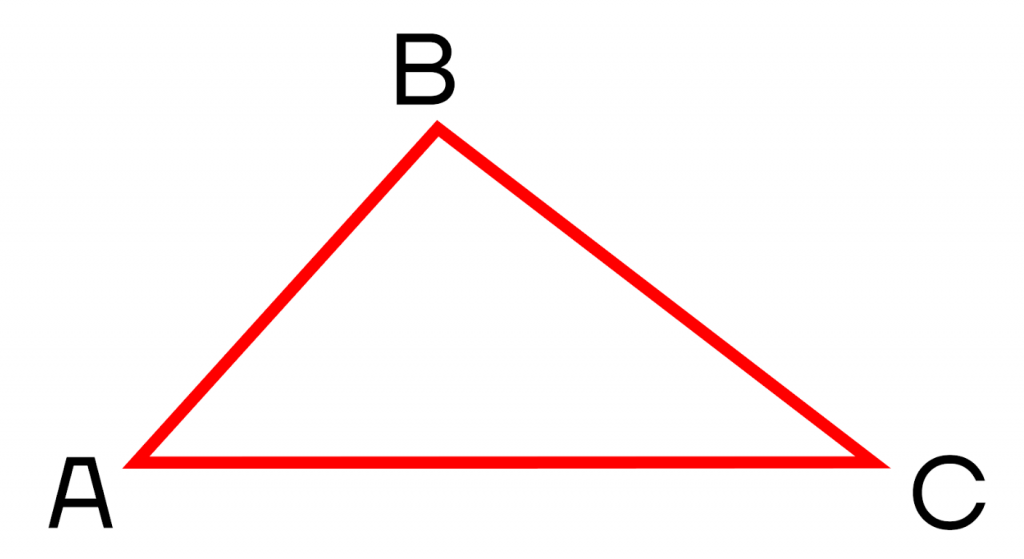
3. Построение треугольника по стороне и двум прилежащим к ней углам. 

В этом случае нам уже даны два угла и одна сторона. 

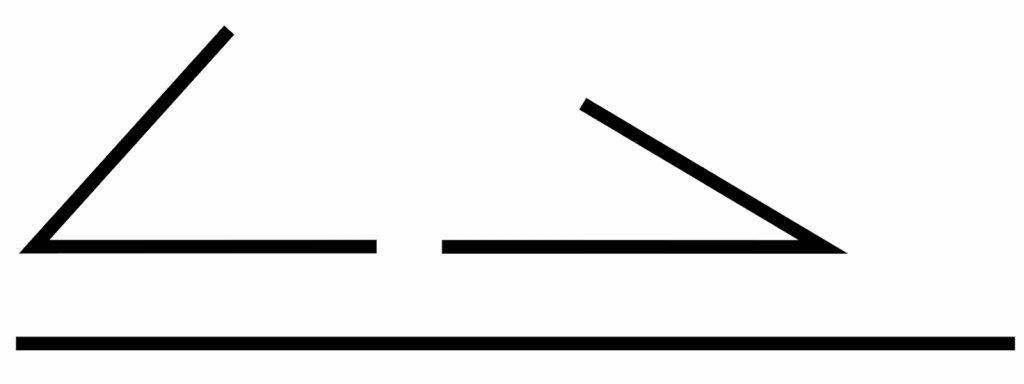
Для начала построим один из углов с двумя лучами. Назовем его угол А.

После этого на одном из лучей откладываем длину данной стороны. Так мы получили точку В.

Теперь из этой точки достраиваем второй данный нам угол. Причем один из его лучей нам уже дан – это построенная сторона. 

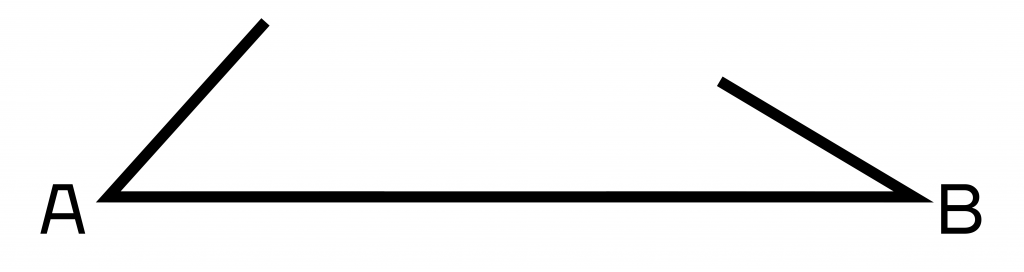
В конце нужно провести оставшиеся лучи до их пересечения, и мы получим точку С, а следовательно, и весь треугольник.

Построить треугольник по трем углам нельзя, несмотря на то, что нам даны три элемента. Дело в том, что углы могут не менять свое значение при разной длине сторон, а значит, угадать точный размер треугольника невозможно. Такие треугольники называются подобными, о них мы рассказали в статье «Равенство и подобие треугольников». 

Мы уже столкнулись с углами треугольника, но при построении рассматривали только внутренние углы. А какие еще бывают углы у треугольника?

Внутренние и внешние углы треугольника

Для треугольника существуют понятия внешних и внутренних углов. 

Внутренние углы треугольника — это три угла, образованные отрезками, выходящими из вершин треугольника. 

∠BAC, ∠ABC, ∠ACB — внутренние углы треугольника. На рисунке ниже они изображены красным. 

Но что такое внешние углы?
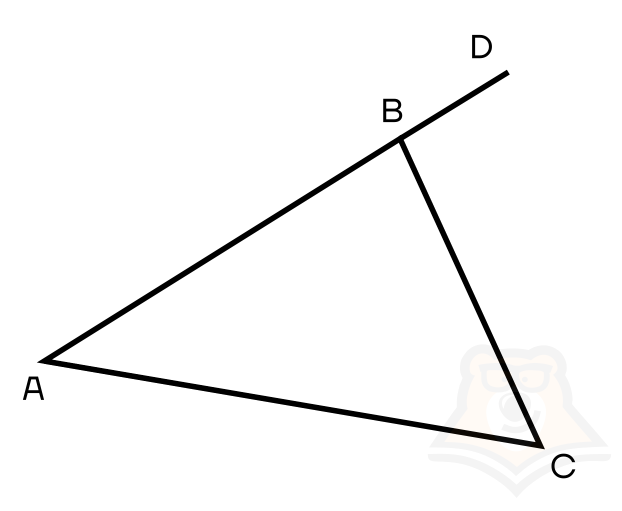
Продолжим любую из сторон треугольника за его вершину, например, построим прямую AD. Тогда угол, образованный стороной ВС и прямой AD — внешний угол треугольника.

Внешний угол треугольника — это смежный угол внутреннего угла треугольника. 

На рисунке внешний угол изображен зеленым. 

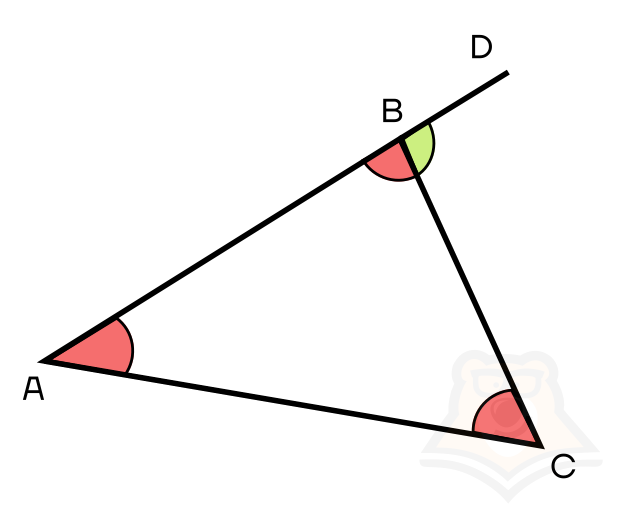
Заметим, что углы мы можем называть либо тремя буквами, либо одной. Если мы называем угол с помощью трех букв, то посередине обязательно должно быть обозначение вершины угла.

Обозначение с помощью трех букв используется в случае, когда задействовано несколько смежных углов. Например, если мы просто скажем ∠B для рисунка выше, то понять это можно и как красный, и как зеленый угол, что вызывает некоторую путаницу. 

Также называть углы можно с помощью строчных букв. 

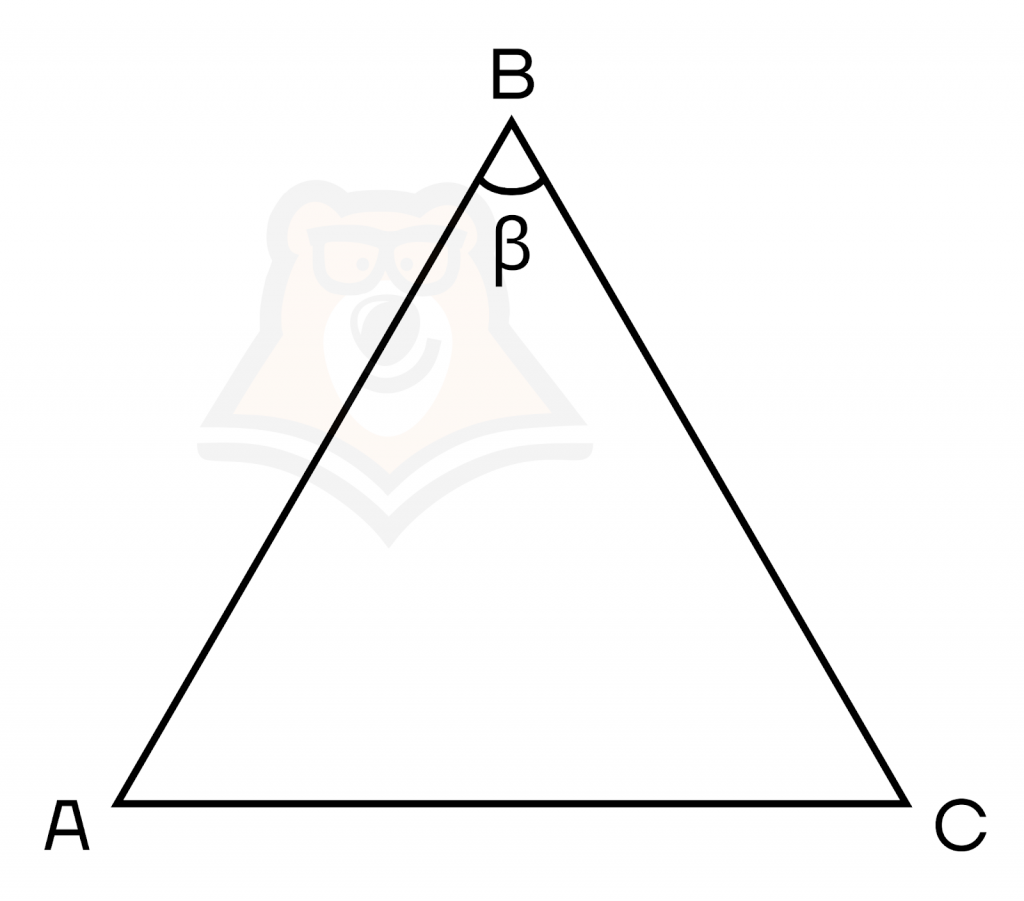
Таким образом, на рисунке ниже мы можем назвать один и тот же угол несколькими способами: ∠B, ∠АBС и ∠β. 

Никакая геометрическая фигура не обходится без своих свойств, с помощью которых можно решать задачи или доказывать теоремы. У треугольника их тоже немало. Но начнем мы с основных! 

Основные свойства треугольника

Рассмотрим основные свойства, которые применимы для любого треугольника.
1 свойство. Сумма углов треугольника равна 180°. 

2 свойство. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Разберем, почему выполняется это свойство. В качестве примера рассмотрим треугольник АВС с иллюстрации ниже. 

Вспомним первое свойство: сумма углов треугольника равна 180°. Тогда ∠А + ∠B + ∠С = 180°. Выразим угол В: ∠В = 180° — ∠А — ∠C

Рассмотрим смежные углы АВС и CBD: сумма смежных углов равна 180°, следовательно, ∠B + ∠CBD = 180° \(\Rightarrow\) ∠B = 180°-∠CBD. 

Поскольку угол В в обоих уравнениях один и тот же, мы можем приравнять правые части: ∠СBD = ∠A + ∠C. 

Свойство будет выполняться для любого внешнего угла треугольника. 

Это свойство может пригодиться на экзамене, например, встретиться в №15 ОГЭ.

Задание. В треугольнике АВС ∠A=12°, ∠C=154°. Найдите внешний угол при вершине В. Ответ дайте в градусах. 

Решение. По рассмотренному выше свойству: внешний угол при вершине В будет равен сумме двух внутренних углов, не смежных с ним. Тогда он будет равен:

∠A+∠C=12°+154°=166°

Ответ: 166

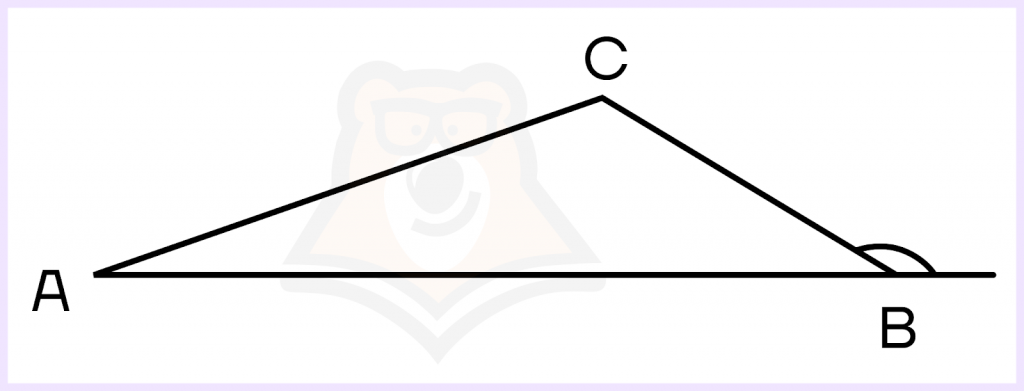
3 свойство. В треугольнике против большей стороны лежит больший угол, против меньшей стороны лежит меньший угол. 

Чтобы понять, что значит выражение «лежит против», нужно посмотреть на треугольник: напротив угла А лежит сторона а, напротив угла В лежит сторона b, напротив угла С лежит сторона с. Следовательно, в данном случае можем применить выражение «против угла А лежит сторона а». 

Рассмотрим рисунок чуть подробнее и расставим углы в порядке возрастания: ∠С < ∠A < ∠B. Тогда также можно расставить и стороны в порядке возрастания: c < a < b. 

4 свойство. В треугольнике против равных сторон лежат равные углы и против равных углов лежат равные стороны. 

Это свойство является следствием предыдущего.

Рассмотрим еще одно задание, которое может встретиться на экзамене. В этот раз в качестве примера возьмем №12 из ЕГЭ по базовой математике.

Задание. В треугольнике АВС AB=BC. Внешний угол при вершине А равен 108°. Найдите угол В. Ответ дайте в градусах.

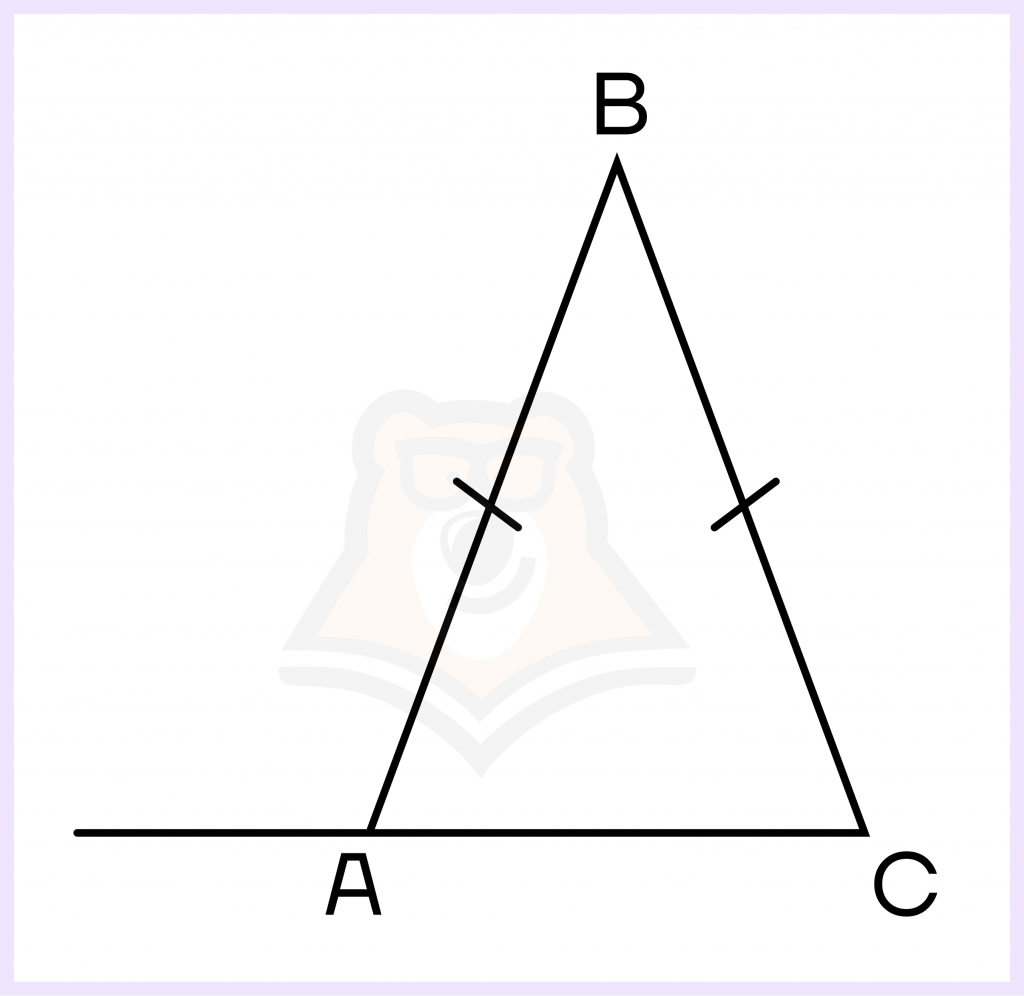
Решение. Поскольку стороны АВ и ВС равны, то и углы, лежащие против них, будут равны. Треугольник с двумя равными сторонами называется равнобедренным, а подробнее узнать про такие треугольники можно в этой статье. Обозначим равные углы за х. 

Внешний и внутренний углы при вершине А смежные, тогда:
\(x=180°-108°=72°\). 

Сумма углов в треугольнике равна 180°. Следовательно, угол В будет равен:

\(180°-2x=180°-2*72°=36°\)

Ответ: 36

Мы рассмотрели самые основные свойства, хотя у треугольника их намного больше. Однако остальные свойства присущи для разных видов треугольника. Тогда может возникнуть вопрос: а какие виды треугольников существуют?

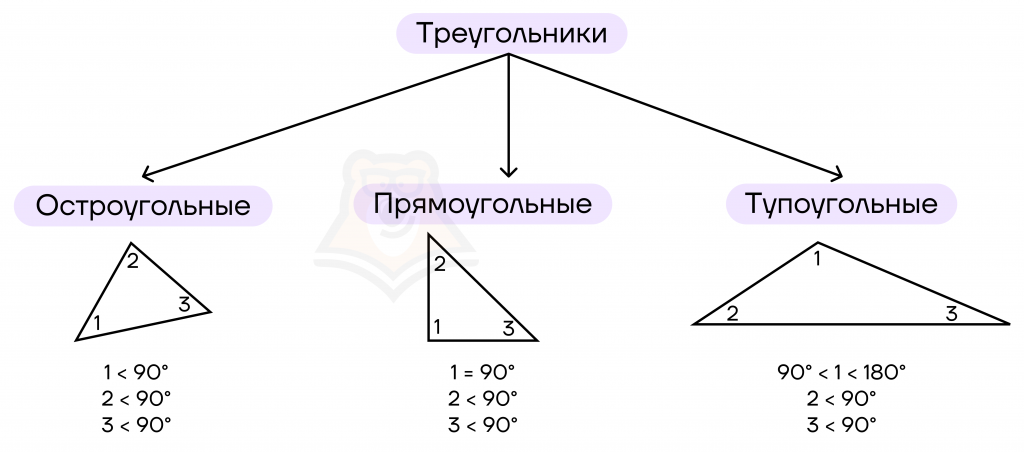
Виды треугольников по величине углов

Одной из самых удобных классификаций является распределение треугольников по величине углов. В зависимости от внутренних углов треугольника существует три вида треугольников: 

1. Остроугольный. Все углы в треугольнике острые, то есть меньше 90°.

2. Прямоугольный. Один из углов треугольника равен 90°, а два других угла будут острыми. Угол, равный 90°, также называют прямым. 

Важно заметить, что прямой угол в треугольнике может быть только один. Это напрямую связано с тем, что сумма углов в треугольнике равна 180°, тогда, если один угол равен 90°, то на сумму двух других остается 180° – 90° = 90°. Следовательно, два оставшихся угла будут острыми. 

3. Тупоугольный. Один из углов будет больше 90°, а два других угла будут острыми. 

В тупоугольном треугольнике также может быть только один тупой угол. Чтобы доказать это, можно привести такие же рассуждения, как и для прямоугольного треугольника. 

Что такое «невозможный треугольник»? Существует такое любопытное понятие, как невозможная фигура. Треугольник Пенроуза или невозможный треугольник — одна из них. 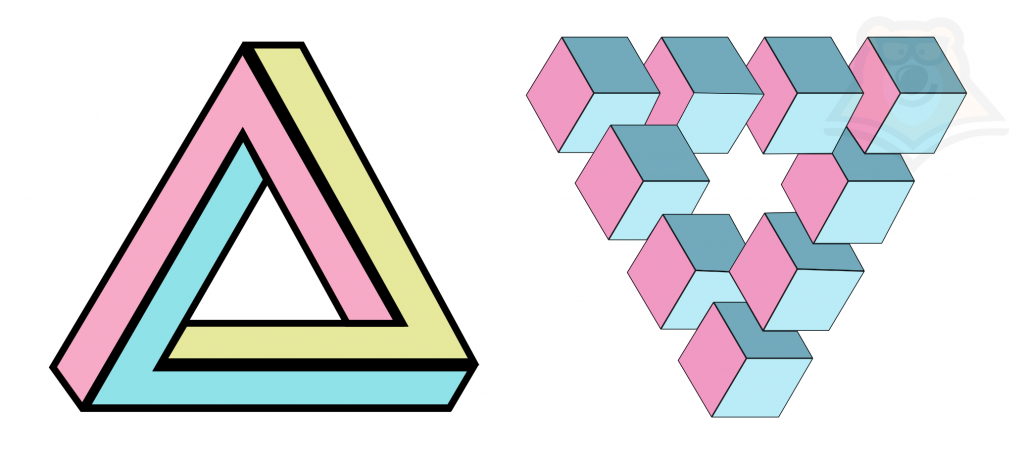Это оптическая иллюзия, которая производит впечатление обычного рисунка. Но если внимательно вглядеться, можно заметить странности в соединениях элементов фигуры. Подобные фигуры используются в компьютерной графике и им посвящено целое направление в искусстве под названием «имп-арт».

Следовательно, мы можем начертить любой треугольник, определить его вид по величине углов и будем знать его основные свойства. Но любой ли треугольник мы можем начертить?

Неравенство треугольника

Для любой фигуры существуют ограничения, за рамки которой она не может выходить. Сумма углов многоугольника не может быть больше определенной величины, а стороны квадрата не могут быть разной длины (потому что в этом случае квадрат уже не будет квадратом). Так и с треугольником: существует ограничение на длину его сторон, которое называется неравенство треугольника. 

Сумма длин двух сторон треугольника всегда будет больше длины его третьей стороны. 

Для треугольника на рисунке будут справедливы следующие неравенства:

a < b + c
b < a + c
c < a + b

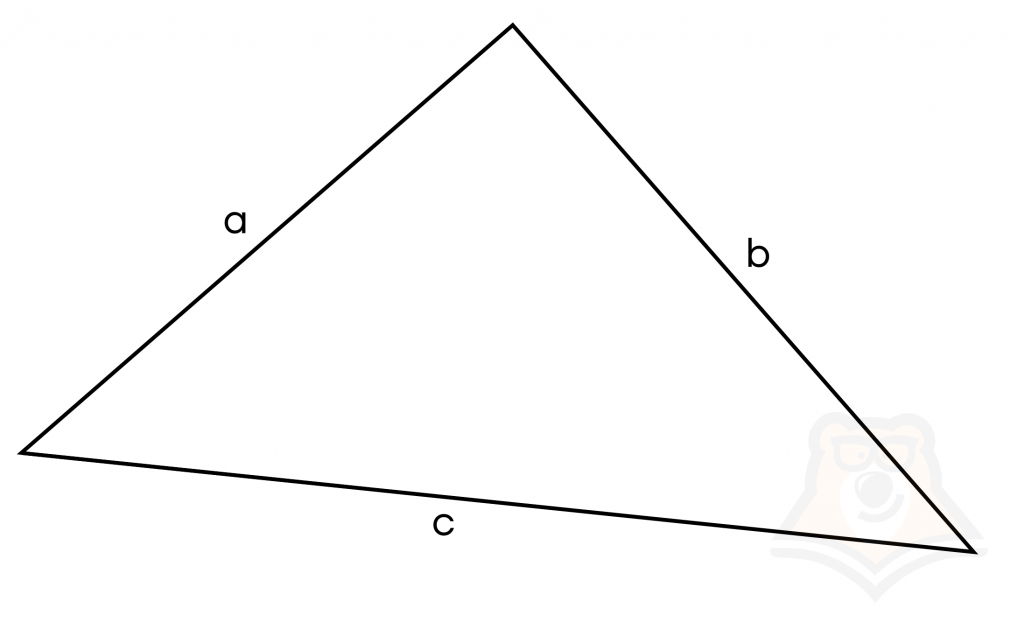
Знание неравенства треугольников в первую очередь помогает определить, может ли существовать треугольник с определенной длиной сторон. 

Например, возьмем треугольник со сторонами 2, 3 и 6.
Такой треугольник не будет существовать, поскольку 2 + 3 = 5, а 5 < 6. 

А если мы возьмем треугольник со сторонами 3, 3 и 5, то с уверенностью можем сказать, что он существует, поскольку выполняются все три неравенства:

3 < 8
5 < 6
3 < 8

Мы рассмотрели все основные понятия, связанные с треугольниками, узнали про его углы и основные свойства. Однако треугольник – очень обширная тема, знакомство с которой можно продолжить в статье «Равенство и подобие треугольников». 

Термины

Квадрат – четырехугольник, у которого все стороны и углы равны. 

Радиус – отрезок, построенный от центра окружности до любой точки на окружности.
Смежные углы – это два угла, у которых одна общая сторона, а две другие лежат на одной прямой. Такие углы в сумме дают 180°.

Фактчек

• Треугольник — это геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, а также отрезками, которые соединяют эти точки. 
• В треугольнике можно выделить внутренние и внешние углы. Внутренние углы — это углы, образованные отрезками, выходящими из вершин треугольника, а внешние углы — углы, смежные внутренним. 
• Сумма углов любого треугольника равна 180°. Также в треугольнике против большей стороны лежит больший угол и наоборот.
• Чтобы треугольник существовал, должно выполняться неравенство треугольника.
• Треугольники бывают остроугольными, прямоугольными и тупоугольными. В остроугольном треугольнике все углы меньше 90°, в прямоугольном треугольнике один из углов равен 90°, в тупоугольном треугольнике один из углов больше 90°. 

Проверь себя

Задание 1. 
Какие углы образуют внутренний и внешний углы треугольника?

1. смежные
2. вертикальные
3. накрест-лежащие
4. соответственные 

Задание 2. 
Чему равняется сумма углов треугольника?

1. 90°
2. 180°
3. 360°
4. 150°

Задание 3. 
Даны длины всех сторон треугольников. Какой из треугольников не может существовать? 

1. 3, 5 и 7
2. 2, 6 и 7
3. 11, 12, 30
4. 3, 4, 5

Задание 4.
Два угла треугольника равны 18 и 59 градусов. Чему равен внешний угол треугольника, смежный с третьим углом? 

1. 77°
2. 103°
3. 121°
4. 162°

Задание 5. 
В треугольнике углы равны 89, 31 и 60 градусов. Какой это треугольник?

1. остроугольный
2. тупоугольный
3. прямоугольный
4. равнобедренный 

Ответы: 1. — 1; 2. — 2; 3. — 3; 4. — 1; 5. — 1.