Вписанная и описанная окружность

На этой странице вы узнаете

• Чудо-фигура: возле какой фигуры всегда можно описать окружность и в какую фигуру всегда можно вписать окружность?
• Почему нужно любить правильные многоугольники? 

«Не вписался в коллектив», – знакомая фраза, верно? Обычно она обозначает, что кто-то не подошел по виду или характеру окружающим. А если мы говорим «Не вписался в окружность» – о чем это? Вопрос странный, давайте разбирать. 

Описанная окружность

Оказывается, в математике существует вписанная и описанная окружность. Что же это такое? 

Описанная окружность – это окружность, на которой лежат все вершины многоугольника. 

При этом многоугольник, около которого описана окружность, называется вписанным. 

Описанные окружности можно встретить в окружающем мире. Например, ювелирные камни, которые имеют форму многогранника, вставляются в круглую оправу. Поскольку драгоценные камни имеют очень много граней, они приближены к окружности, но все равно остаются вписанным многоугольником.

Свойства описанной возле многоугольников окружности

1 свойство. Центр описанной возле треугольника окружности будет лежать в точке пересечения серединных перпендикуляров. 

Серединный перпендикуляр – это перпендикуляр, проведенный к середине стороны треугольника. 

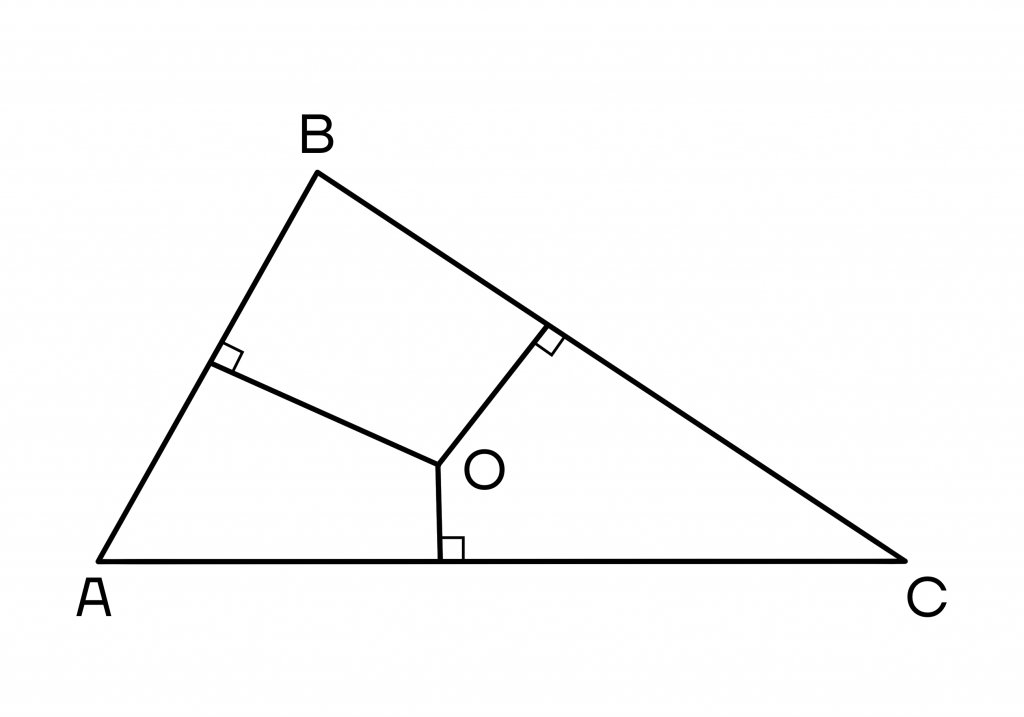
2 свойство. Окружность можно описать около любого треугольника, и притом только одну. 

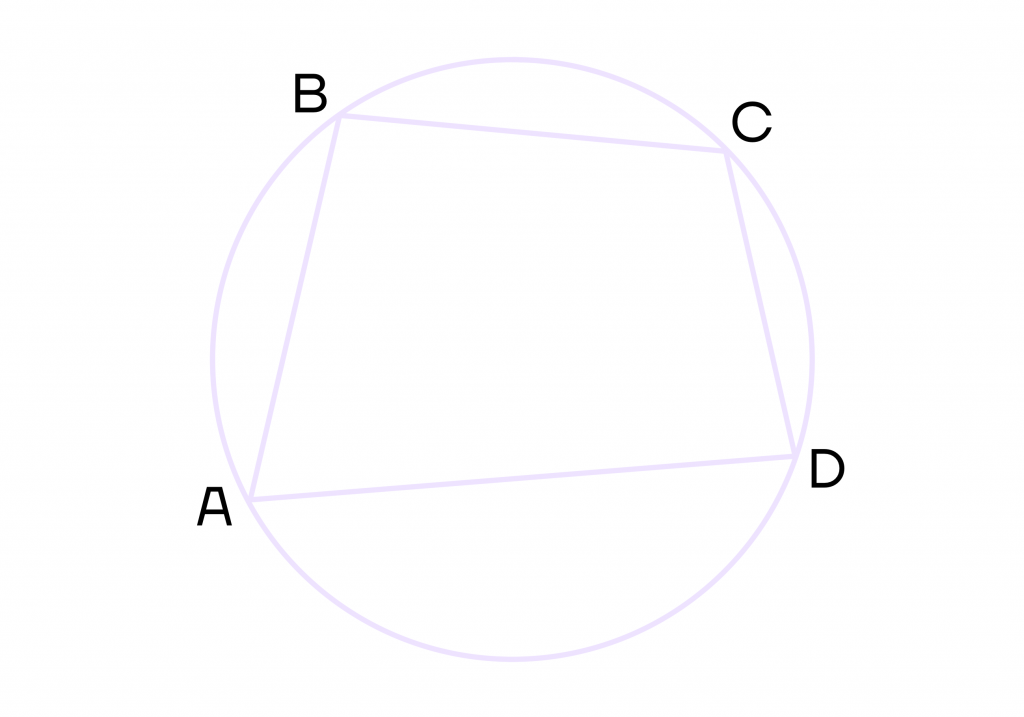
3 свойство. Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равна 180. 

Рассмотрим четырехугольник ABCD, который вписали в окружность. Поскольку этот четырехугольник вписанный, то выполняется равенство ∠A+∠C=∠B+∠D=180°. 

4 свойство. Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная, то есть ее боковые стороны равны. 

Рассмотрим трапецию ABCD, которую вписали в окружность. Поскольку эта трапеция вписанная, то ее боковые стороны равны, следовательно, АВ = CD. 

5 свойство. Если четырехугольник вписан в окружность, то можно воспользоваться теоремой Птолемея. 

Теорема Птолемея Если четырехугольник вписан в окружность, то произведение диагоналей равняется сумме произведений его противоположных сторон.

Рассмотрим четырехугольник ABCD, который вписан в окружность. Поскольку это вписанный четырехугольник, то можно применить теорему Птолемея. Тогда выполняется равенство AC*BD=AB*CD+BC*AD. 

Рассмотрим формулы для вычисления радиуса описанной окружности. 

Фигура	Формула	Обозначения
Треугольник	\(R=\frac{abc}{4S}\)	R – радиус окружностиa, b, c – стороны треугольника S – площадь треугольника
Прямоугольный треугольник	\(R=\frac{a}{2}\)	R – радиус окружности a – гипотенуза
Правильный треугольник	\(R=\frac{a\sqrt{3}}{3}\)	R – радиус окружности a –  сторона треугольника
Квадрат	\(R=\frac{d}{2}\)	R – радиус окружности d – диагональ квадрата
Прямоугольник	\(R=\frac{d}{2}\)	R – радиус окружности d – диагональ прямоугольника
Правильный шестиугольник	\(R=a\)	R – радиус окружности a –  сторона шестиугольника

Вписанная окружность

Вписанная окружность – это окружность, которая касается всех сторон многоугольника. 

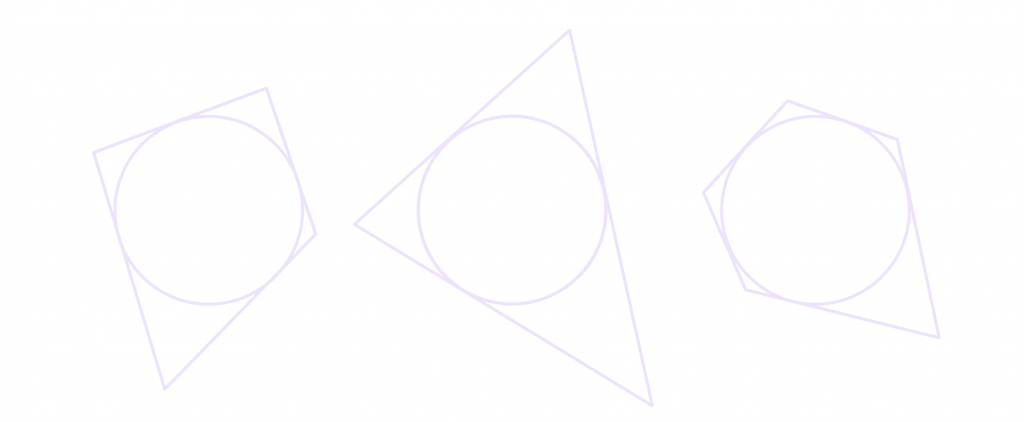
При этом многоугольник, в который вписана окружность, называется описанным. 

Чтобы увидеть вписанную окружность, достаточно посмотреть на любую гайку. Ее резьба будет круглой, а форма – шестиугольником. 

Свойства вписанной окружности

1 свойство. Центр вписанной окружности лежит на пересечении биссектрис углов многоугольника. 

2 свойство. В любой треугольник можно вписать окружность, притом только одну. 

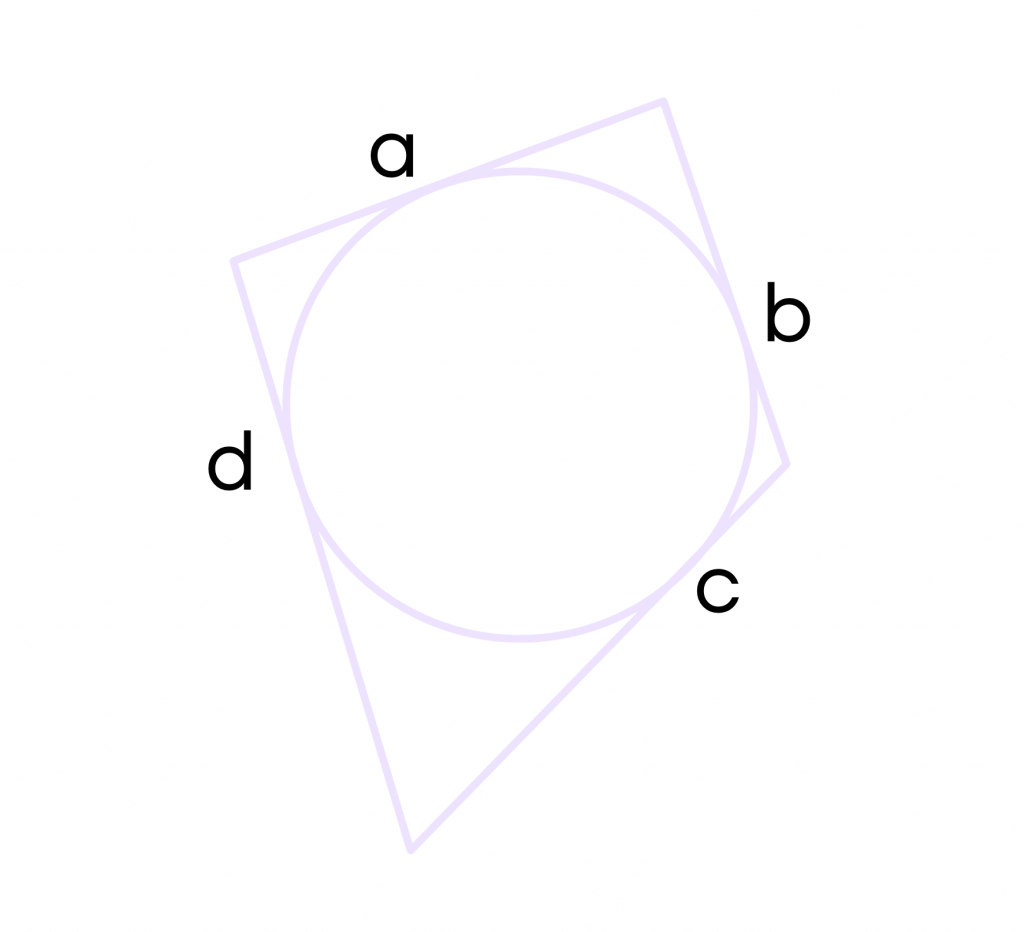
3 свойство. В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. 

Рассмотрим четырехугольник со сторонами a, b, c, d, в который вписана окружность. Поскольку это описанный четырехугольник, то выполняется равенство a+c=b+d. 

Рассмотрим формулы для вычисления радиуса вписанной окружности. 

Фигура	Формула	Обозначения
Треугольник	\(r=\frac{S}{p}\)	r – радиус окружности p – полупериметр S – площадь треугольника
Прямоугольный треугольник	\(r=\frac{a+b-c}{2}\)	r – радиус окружности a – гипотенуза a, b – катеты
Правильный треугольник	\(r=\frac{a\sqrt{3}}{6}\)	r – радиус окружности a –  сторона треугольника
Квадрат	\(r=\frac{a}{2}\)	r – радиус окружности а – сторона квадрата
Ромб	\(r=\frac{h}{2}\)	r – радиус окружности h – высота ромба
Трапеция	\(r=\frac{h}{2}\)	r – радиус окружности h – высота трапеции
Правильный шестиугольник	\(r=\frac{a\sqrt{3}}{2}\)	r – радиус окружности a –  сторона шестиугольника

Чудо-фигура: возле какой фигуры всегда можно описать окружность и в какую фигуру всегда можно вписать окружность? Этой фигурой является треугольник. Независимо от того, является он правильным или нет, какие у него стороны и углы, треугольник всегда можно вписать в окружность или описать вокруг нее.

Окружности и правильные многоугольники

Существуют специальные формулы, которые применяются для правильных многоугольников. Благодаря этим формулам можно найти и радиусы вписанной и описанной окружностей, и площадь фигур, и отношение между радиусами вписанной и радиусами описанной окружности. 

Именно благодаря этим формулам очень удобно решать большинство задач, в которых встречаются правильные фигуры. Применение этих формул значительно сокращает решение и упрощает счет, а значит и вероятность решить задачу значительно повышается. 

Почему нужно любить правильные многоугольники?  В правильные многоугольники всегда можно вписать окружность или описать ее около фигуры. Также в правильных многоугольниках очень легко найти периметры, величину углов, радиусы вписанной и описанной окружности и площади.

Ниже приведена таблица с формулами для правильных фигур. 

Количество сторон	Величина углов	r	R	S	Связь между r и R
3	\(60\)	\(\frac{a\sqrt{3}}{6}\)	\(\frac{a\sqrt{3}}{3}\)	\(\frac{a^2\sqrt{3}}{4}\)	\(R=2r\)
4	\(90\)	\(\frac{a}{2}\)	\(\frac{a\sqrt{2}}{2}\)	\(a^2\)	\(R=r\sqrt{2}\)
6	\(120\)	\(\frac{a\sqrt{3}}{2}\)	\(a\)	\(\frac{3a^2\sqrt{3}}{2}\)	\(R=\frac{2\sqrt{3}r}{3}\)
8	\(135\)	\(\frac{a(1+\sqrt{2})}{2}\)	\(\frac{a\sqrt{4+2\sqrt{2}}}{2}\)	\(2a^2(1+\sqrt{2})\)	\(\frac{r}{R}=cos\frac{\pi}{8}=\frac{\sqrt{2+\sqrt{2}}}{2}\)
12	\(150\)	\(\frac{a(2+\sqrt{3})}{2}\)	\(a\sqrt{2+\sqrt{3}}\)	\(3a^2(2+\sqrt{3})\)	\(\frac{r}{R}=cos\frac{\pi}{12}=\frac{\sqrt{2+\sqrt{3}}}{2}\)

Фактчек

• Описанная окружность – это окружность, на которой лежат все вершины вписанного многоугольника. При этом четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противоположных углов равняется 180. 
• Вписанная окружность – это окружность, которая касается всех сторон многоугольника. В четырехугольник можно вписать окружность тогда и только тогда, когда сумма противоположных сторон четырехугольника равна.
• В треугольник всегда можно вписать окружность, притом только одну. Также около треугольника всегда можно описать окружность, притом только одну. 
• Если в задаче попадается правильный многоугольник, то можно смело пользоваться формулами, которые приведены в таблице для правильных многоугольников. 

Проверь себя

Задание 1.
В какой точке будет лежать центр описанной около треугольника окружности?

1. В точке пересечения биссектрис;
2. В точке пересечения серединных перпендикуляров;
3. В точке пересечения медиан;
4. В точке пересечения высот. 

Задание 2.
Даны боковые стороны трапеции. Возле какой трапеции можно описать окружность?

1. 2 и 5;
2. 7 и 11;
3. 19 и 15;
4. 12 и 12. 

Задание 3.
В какой точке будет лежать центр вписанной в треугольник окружности? 

1. Точка пересечения биссектрис;
2. Точка пересечения серединных перпендикуляров;
3. Точка пересечения медиан;
4. Точка пересечения высот. 

Задание 4.
Площадь треугольника равна 20, радиус вписанной окружности равен 5. Чему равен периметр треугольника?

1. 4;
2. 8;
3. 2;
4. 10.

Задание 5.
Сторона квадрата равна 3√2. Найдите радиус описанной окружности. 

1. 6;
2. 3;
3. 12;
4. 15. 

Ответы: 1. – 2 2. – 4 3. – 1 4. – 2 5. – 2