Конус

На этой странице вы узнаете

• Как сделать праздничный колпак?
• Может ли у конуса быть два основания?
• Как конус спасает жизни?

Добро пожаловать на вечеринку! Не забываем надевать праздничные колпачки, они очень нравятся нашему имениннику. Ведь в центре событий у нас сегодня конус.

Строение конуса

Как иногда случается на праздновании дня рождения, гостям интересно узнать подробности жизни виновника торжества. Похоже, кому-то придется раскрыть все секреты… Например, почему наши праздничные колпачки так похожи на ведьминские шляпки? Что ты скрываешь, друг?

Действительно, что будет, если вокруг своей оси повернуть прямоугольный треугольник? У нас получится конус.

Все помнят, что у прямоугольного треугольника есть гипотенуза и два катета? Это важный момент для понимания темы. Если что, за подробностями всегда можно заглянуть в статью «Равнобедренный, равносторонний и прямоугольный треугольник».

Конус — фигура, полученная при вращении прямоугольного треугольника вокруг одного из его катетов. 

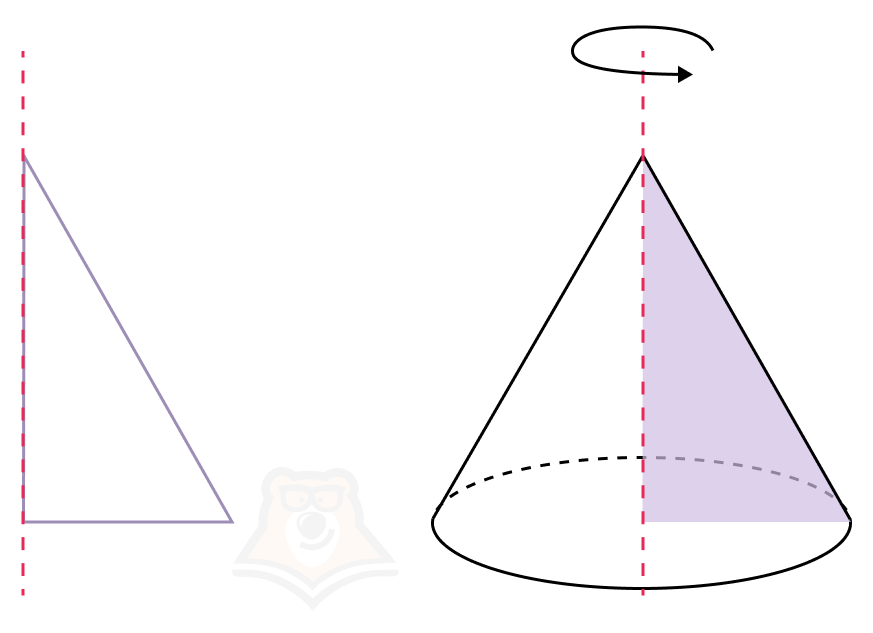
В этом случае и в дальнейшем тексте имеется в виду прямой конус. Существует и наклонный конус, но его вершина будет лежать в другой точке пространства. 

Вспомним дорожные конусы, рожок от мороженого, воронку. Все это примеры прямого конуса.

Наклонный конус — конус, ось которого не перпендикулярна основанию. 

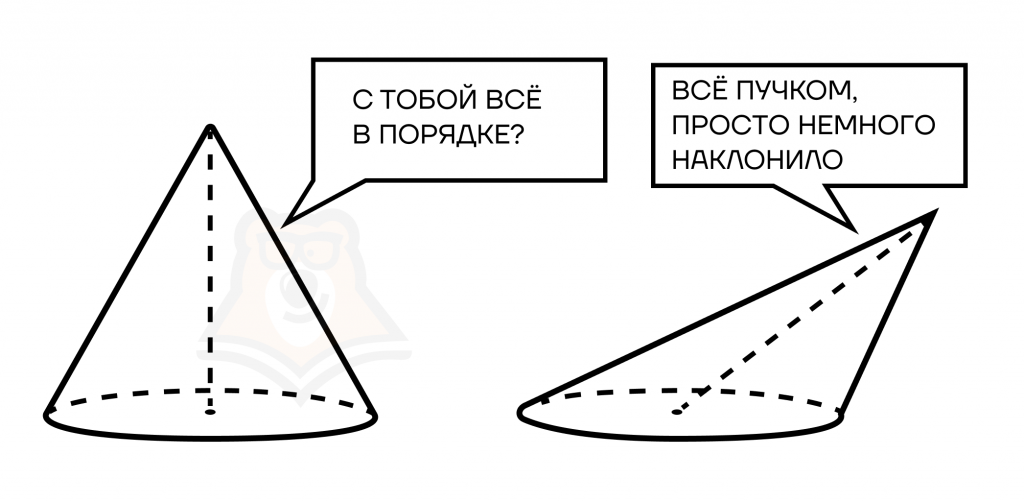
Из чего состоит конус? Немного понаблюдаем за вращением прямоугольного треугольника вокруг одного из его катетов. Все точки, лежащие на этом катете, соответственно, будут оставаться на своих местах. В том числе, и верхняя точка. Эту точку называют вершиной конуса. 

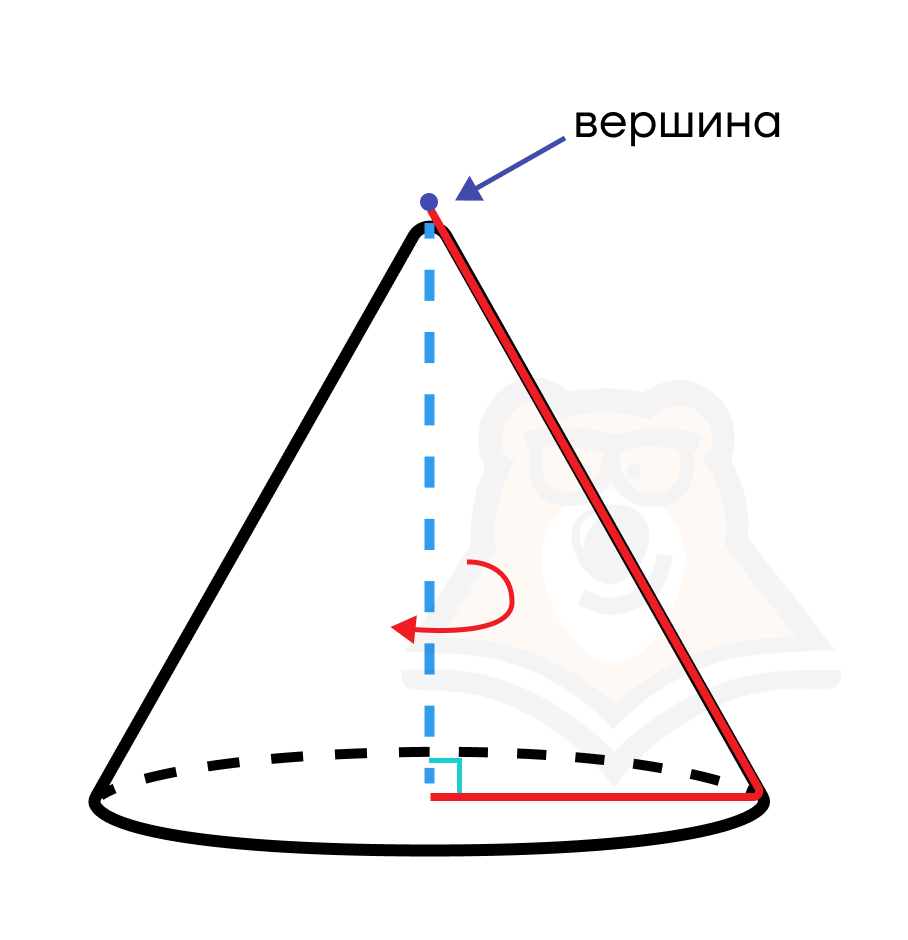
Как говорилось ранее, конус образуется при вращении прямоугольного треугольника вокруг одного из его катетов. Второй катет при вращении образует круг, и он будет называться основанием конуса. При этом радиус основания будет равен катету треугольника.

В конусе, так же как и в «Цилиндре», существует образующая. Но она немного отличается.

Образующая конуса — отрезок, соединяющий вершину конуса и любую точку на окружности его основания. 

Образующую можно очень легко найти с помощью теоремы Пифагора: мы вращали прямоугольный треугольник, в котором гипотенуза — образующая. Подробнее о теореме Пифагора можно также прочесть в статье «Равнобедренный, равносторонний и прямоугольный треугольник». 

Мы отметили, что в первоначальном прямоугольном треугольнике гипотенуза — образующая, катет в основании — радиус. Чем тогда будет являться третья сторона, вокруг которой мы вращали треугольник?

Это будет высота конуса.

Высота конуса — перпендикуляр, опущенный из вершины конуса на его основание. Следовательно, высота и ось прямого конуса совпадают. 

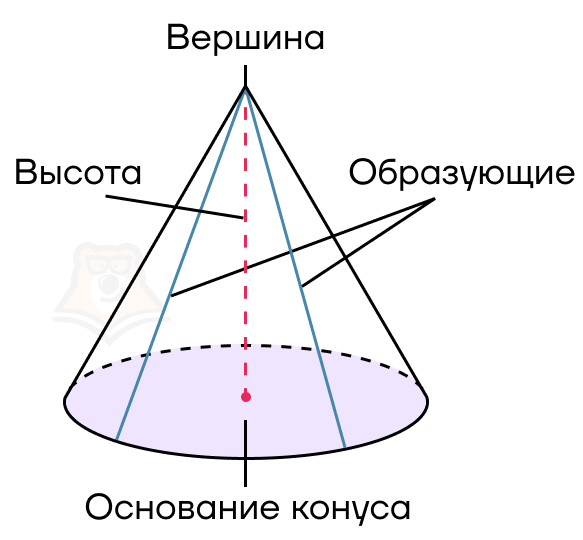
Вспомним наш праздничный колпачок. Он состоит только из стенок конуса, а основания у него нет. Эти стенки и будут боковой поверхностью конуса. 

Итак, мы разобрались с понятиями конуса и его составляющими, а теперь поговорим о свойствах этого геометрического тела.

Свойства конуса

Свойство 1. Все образующие конуса равны между собой. 

Это легко доказать, если заметить, что образующие — гипотенузы одного и того же треугольника. 

Свойство 2. Осевое сечение конуса — равнобедренный треугольник.

Осевое сечение – сечение, которое проходит через ось тела вращения.

В основании такого треугольника будет лежать диаметр окружности основания, а боковые стороны будут образующими. 

Свойство 3. Сечение, перпендикулярное оси конуса, будет кругом. 

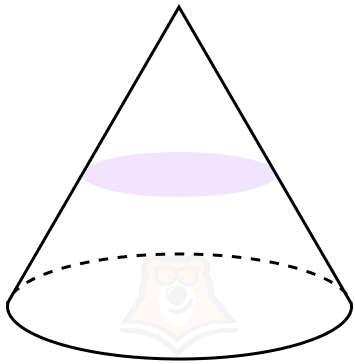
Ну и, наконец, перейдем к самому интересному – формулам, которые смогут помочь нам при решении задач.

Формулы для конуса

Рассмотрим, как найти площадь боковой поверхности конуса. Опять вернемся к праздничным колпакам. Если мы разберем их, то получим сектор круга. 

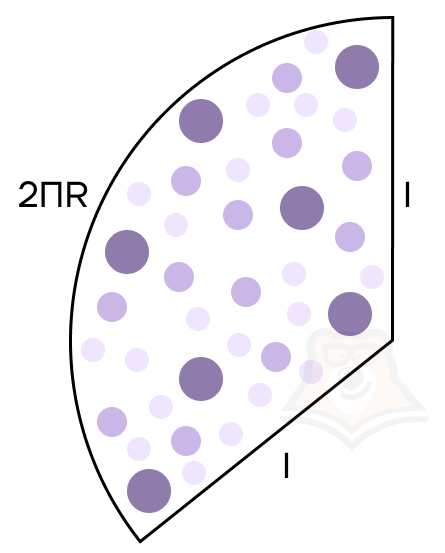
Как сделать праздничный колпак? Для этого нужно на бумаге вычертить сектор круга. Радиусы этого сектора будут равны длинам образующих, а длина дуги будет равняться дуге окружности основания. Если провести небольшие математические вычисления, то можно создать праздничный колпак нужного размера, который будет идеально подходить конкретному гостю.

Формулу площади для сектора круга мы знаем из статьи «Окружность». 

Из нее можно вывести формулу боковой поверхности конуса. 

1. Площадь сектора круга равна \(S_n=\frac{\pi R^2}{360}*a\), где R — радиус, a — угол дуги в градусах. Так как боковая поверхность конуса представляет собой сектор круга с радиусом, равным длине образующей l, получаем формулу \(\frac{\pi l^2}{360}*a\).

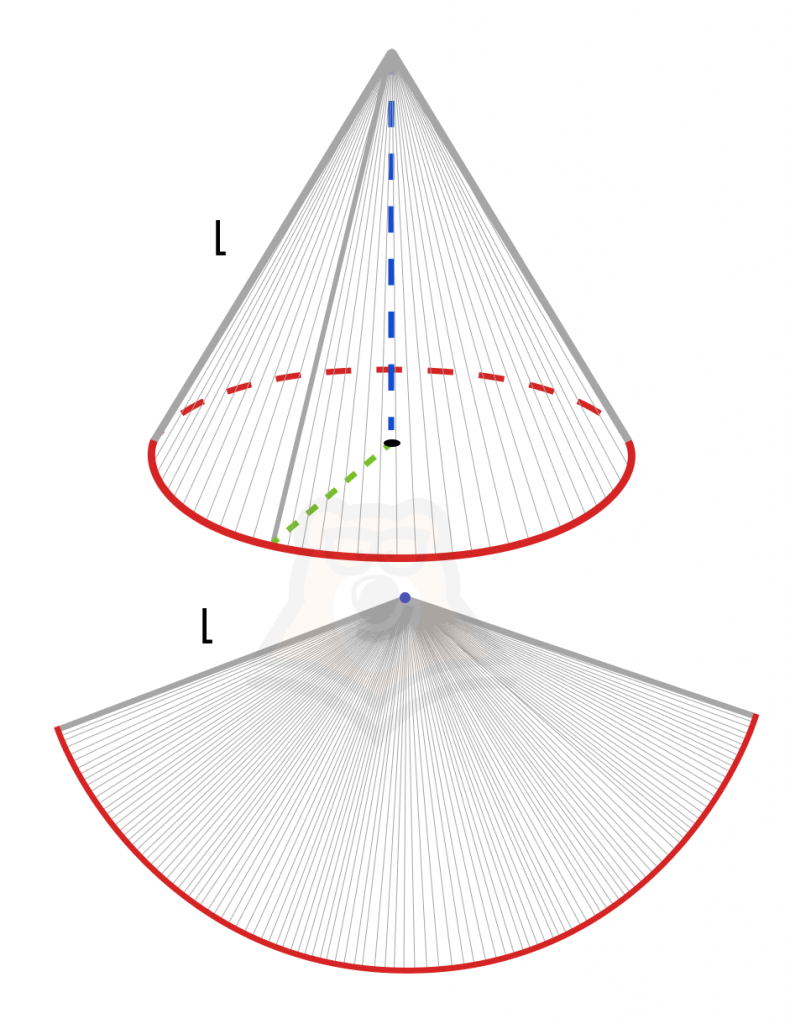
2. Поскольку у нас развертка конуса, а в основании конуса лежит круг, то длина дуги будет равна длине окружности, то есть \(2\pi R\). В этом случае R — радиус основания. 

3. Выразим эту длину через формулу длины дуги, получаем \(\frac{\pi R_д}{180}*a=\frac{\pi l}{180}*a\).

Заметим, что через последние две формулы мы выразили одну и ту же величину, а значит, их можно приравнять. Получаем:
\(2\pi R=\frac{\pi l}{180}*a\)

Преобразуем формулу площади сектора:
\(\frac{\pi l^2}{360}*a=\frac{\pi*l*l}{2*180}*a=\frac{\pi*l}{180}*a*\frac{l}{2}=2\pi R*\frac{l}{2}=\pi Rl\).

В этой формуле R — радиус основания, l — длина образующей. Получаем следующую формулу. 

\(S_{бок.}=\pi Rl\)

Разберем пример задачи из №2 ЕГЭ по профильной математике.

Задание. Образующая конуса равна 4, а длина окружности основания равна 2. Найти площадь боковой поверхности конуса.

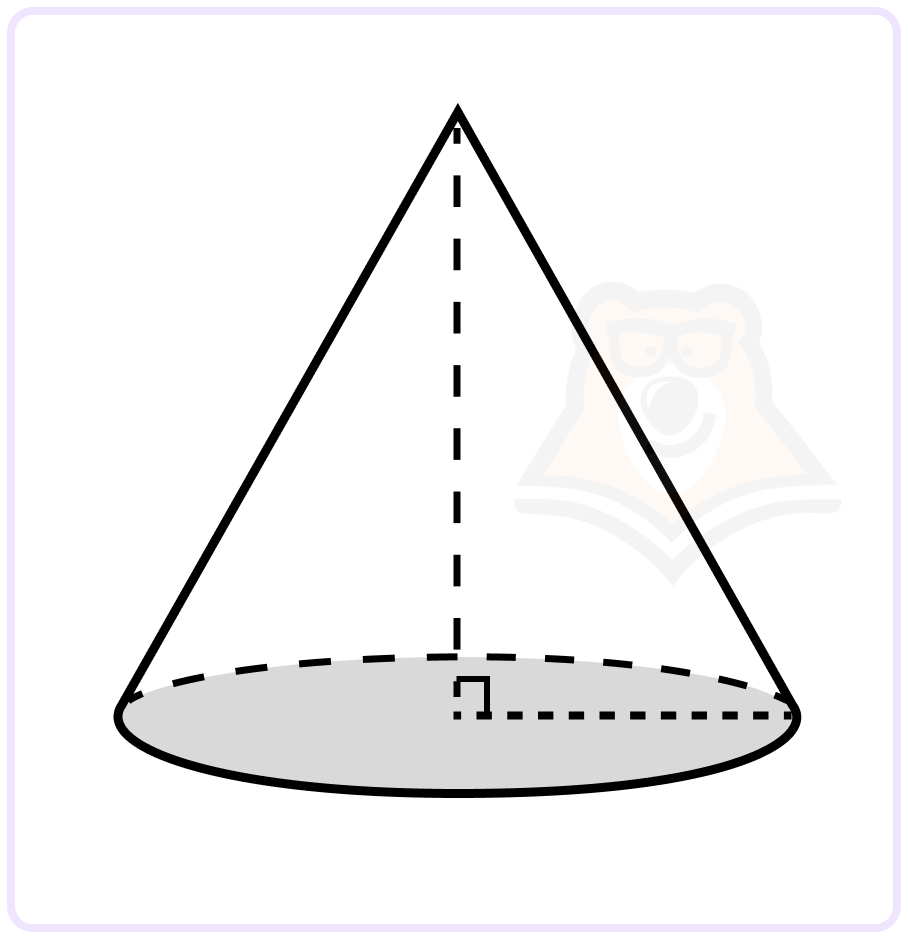
Решение. Формулу длины окружности основания L мы также знаем из статьи «Окружность и круг». Выразим из нее радиус окружности основания R:
\(L = 2\pi R\)

Откуда: \(R=\frac{L}{\pi 2}\)

Подставим выраженный радиус R и длину образующей \(l=2\) в формулу боковой поверхности конуса:
\(S_{бок}=\pi Rl=\pi*\frac{L}{2\pi}*l=\frac{L}{2}*l=\frac{2}{2}*4=4\)

Ответ: 4

Чтобы найти площадь полной поверхности конуса, к площади боковой поверхности нужно добавить площадь основания. 

\(S=S_{бок}+S_{осн}=\pi Rl+\pi R^2=\pi R(l+R)\)

А вот чтобы найти объем конуса, нужно воспользоваться следующей формулой. 

\(V=\frac{1}{3}S_{осн}H=\frac{1}{3}\pi R^2H\)

В этой формуле R — радиус основания, Н — высота конуса. 

Решим задачу, аналогичную №2 ЕГЭ по профильной математике.

Задание. Образующая конуса наклонена под углом 30° к плоскости основания и равна 6. Найти объем конуса. В ответе указать полученное значение, деленное на \(\pi\).

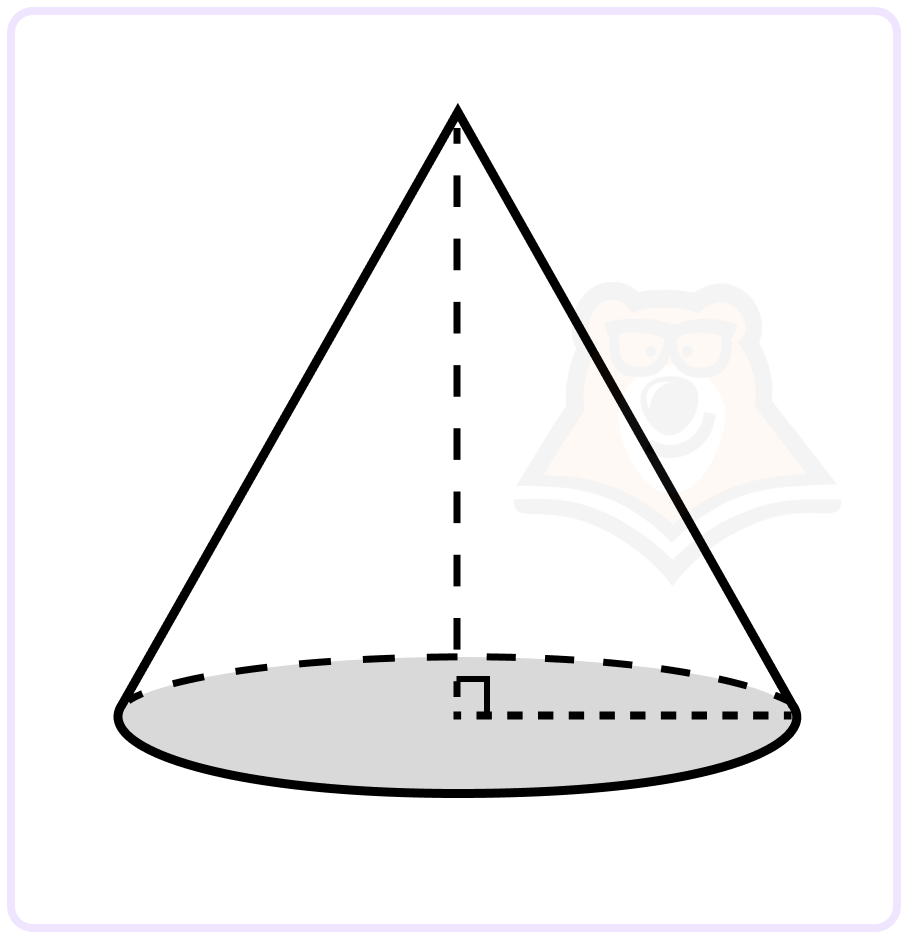
Решение. Рассмотрим прямоугольный треугольник, катетами которого являются высота конуса H и радиус основания R, а гипотенуза – образующая конуса l.

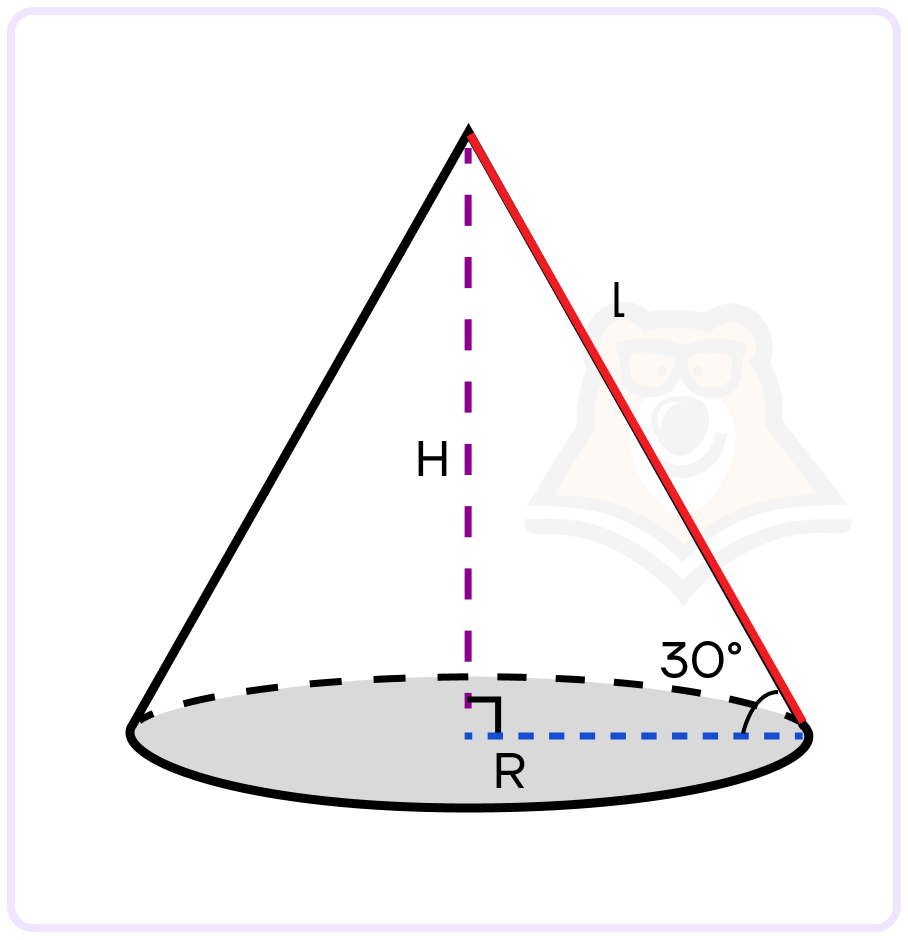
Катет, который лежит напротив угла 30°, равен половине гипотенузы. Значит, 
\(H=\frac{1}{2}*l=\frac{1}{2}*6=3\)

Из этого же прямоугольного треугольника, воспользовавшись теоремой Пифагора, найдем радиус R:
\(R=\sqrt{l^2-H^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{27}\)

Подставим найденные значения радиуса основания R и высоты конуса H в формулу объема конуса:
\(V=\frac{1}{3}\pi R^2H=\frac{1}{3}*\pi*(\sqrt{27})^2*3=\frac{1}{3}*27*3=27\pi\)

В ответе укажем найденное значение, деленное на \(\pi\), то есть 27.

Ответ: 27

Что же будет, если отрезать верхушку конуса? Разберемся с этим в следующем разделе.

Усеченный конус

Тем временем наш праздник продолжается, пора задувать свечи на торте. Постойте, какой необычный по форме торт…

Такой торт и представляет из себя конус без верхушки, то есть усеченный конус. 

По третьему свойству основанием такого конуса все также будет круг в месте среза.

Усеченный конус — тело вращения, получающееся при вращении прямоугольной трапеции вокруг меньшей боковой стороны. 

Это определение также дано для прямого конуса. 

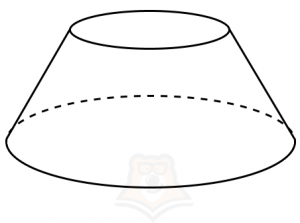
Может ли у конуса быть два основания? Да, но это уже будет усеченный конус. То есть второе основание мы получим, если срежем верхушку обычного конуса.

Так как усеченный конус образован вращением трапеции, для начала предлагаем вспомнить основные понятия этой фигуры в статье «Трапеция».

Теперь давайте разберем, какими элементами обладает усеченный конус.

У усеченного конуса есть два основания: большее и меньшее. Эти основания образованы основаниями трапеции и имеют форму круга. 

Высота усеченного конуса — расстояние между основаниями или перпендикуляр, опущенный из одного основания на второе. 

Высота совпадает с осью усеченного конуса. 

В нашей трапеции осталась еще одна сторона, а именно большая боковая сторона.

Образующая усеченного конуса — отрезок, соединяющий точки на окружностях оснований конуса. 

Важно следить, чтобы этот отрезок совпадал с боковой стороной трапеции, иначе он уже не будет образующей. Образующие создают боковую поверхность усеченного конуса. 

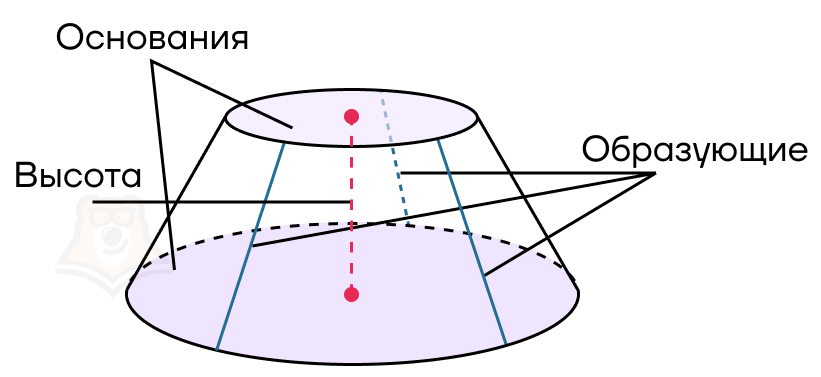
Рассмотрим сечения такого конуса.

Осевое сечение будет равнобедренной трапецией. Ее боковые стороны — большие боковые стороны трапеции, которую мы вращали, а основания равны удвоенным основаниям первоначальной трапеции. 

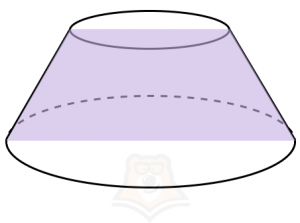
А вот сечение, которое проходит параллельно основаниям, будет кругом. 

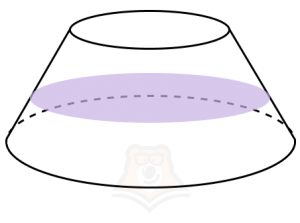
Чтобы найти площадь боковой поверхности в усеченном конусе, необходимо воспользоваться следующей формулой. Пусть \(R_1\) — радиус большего основания, \(R_2\) — радиус меньшего основания, l — образующая. 

\(S_{бок}=\pi l(R_1+R_2)

А вот чтобы найти площадь полной поверхности, необходимо прибавить площади оснований.

\(S=\pi l(R_1+R_2)+\pi R_1^2+\pi R_2^2\)

Пусть Н — высота усеченного конуса. Тогда его объем мы сможем найти по следующей формуле.

\(V=\frac{1}{3}\pi H(R_1^2+R_1R_2+R_2^2)\)

Как конус спасает жизни? По некоторым оценкам, в мире от удара молнии погибает 6000 человек в год. Этого бы не случилось, если бы везде были громоотводы, образующие конус безопасности.

Итак, в этой статье мы узнали о том, что такое конус, какие у него есть составляющие, какими свойствами он обладает, а также какими формулами можно воспользоваться для решении задач. При этом помимо конуса есть и другие тела вращения, которые могут встретиться на ЕГЭ. В следующей статье «Шар» мы подробно познакомимся с еще одним из них.

Термины

Гипотенуза — сторона, которая лежит напротив прямого угла в треугольнике. 

Диаметр окружности – это отрезок, соединяющий две точки на окружности и проходящий через центр окружности. 

Длина дуги – это длина части кривой, которая образует окружность. 

Катеты — стороны, которые образуют прямой угол в треугольнике.

Равнобедренная трапеция – это трапеция, боковые стороны которой равны. 

Равнобедренный треугольник – это треугольник, у которого две стороны равны.

Радиус – это отрезок, построенный от центра окружности до любой точки на окружности.

Сектор круга – это часть круга, которую ограничивают радиусы и дуга. 

Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 

Фактчек

• Конус — фигура, полученная при вращении прямоугольного треугольника вокруг одного из его катетов. В основании конуса лежит круг. 
• Образующая конуса — отрезок, соединяющий вершину конуса и любую точку на окружности его основания. В конусе все образующие равны между собой. Высота конуса — перпендикуляр, опущенный из вершины конуса на его основание. Следовательно, высота и ось конуса совпадают. 
• Осевое сечение конуса будет иметь форму равнобедренного треугольника, основание которого равно диаметру окружности основания конуса, а боковые стороны — его образующие. Сечение, перпендикулярное оси конуса, будет кругом. 
• Усеченный конус — тело вращения, получающееся при вращении прямоугольной трапеции вокруг меньшей боковой стороны. В усеченном конусе два основания, каждое из которых имеет форму круга. 
• Высота усеченного конуса — расстояние между основаниями или перпендикуляр, опущенный из одного основания на второе. Образующая усеченного конуса — отрезок, соединяющий точки на окружностях оснований конуса. 
• Осевое сечение в усеченном конусе будет равнобедренной трапецией, боковые стороны которой — образующие. Перпендикулярное сечение будет иметь форму круга. 

Проверь себя

Задание 1.
Что такое образующая конуса?

1. Ось вращения конуса.
2. Перпендикуляр, опущенный из вершины конуса на его основание.
3. Диаметр основания конуса.
4. Отрезок, соединяющий вершину конуса и любую точку на окружности его основания. 

Задание 2.
Какую форму имеет осевое сечение конуса?

1. прямоугольный треугольник
2. равнобедренный треугольник
3. равносторонний треугольник
4. круг

Задание 3.
Что такое образующая усеченного конуса?

1. Расстояние между основаниями усеченного конуса.
2. Перпендикуляр, опущенный из одного основания конуса на другое.
3. Отрезок, соединяющий точки на окружностях оснований конуса.
4. Любая окружность, получаемая при сечении конуса плоскостью, перпендикулярной оси вращения. 

Задание 4.
Какую форму имеет осевое сечение усеченного конуса?

1. равнобедренная трапеция
2. прямоугольная трапеция
3. равнобедренный треугольник
4. круг

Ответы: 1. — 4; 2. — 2; 3. — 3; 4. — 1.