Равенство и подобие треугольников

На этой странице вы узнаете

• Почему в доказательстве нельзя использовать аргумент: «Так видно же!»?
• В чем разница между равными и подобными треугольниками и как в них не запутаться?

С ранних лет мы учимся делиться поровну и играть наравне. Мы пониманием значение этих слов интуитивно. Но в математике, как иногда и в жизни, равенство сначала нужно доказать.

Равенство треугольников

Предположим, нам в задаче будут даны два треугольника, но мы не будем знать некоторые их данные. Например, не будут известны углы или не будут известны некоторые стороны. Сможем ли мы тогда доказать равенство этих треугольников?

Для этого существуют признаки равенства треугольников, которые можно применять. Но, прежде чем рассматривать эти признаки, давай разберемся, какие же треугольники называются равными. 

Равные треугольники — это треугольники, у которых соответствующие стороны и углы равны. 

Представим, что мы на листе бумаги начертили два равных треугольника и вырезали их. Если после этого мы наложим один треугольник на другой, то они полностью совпадут друг с другом. 

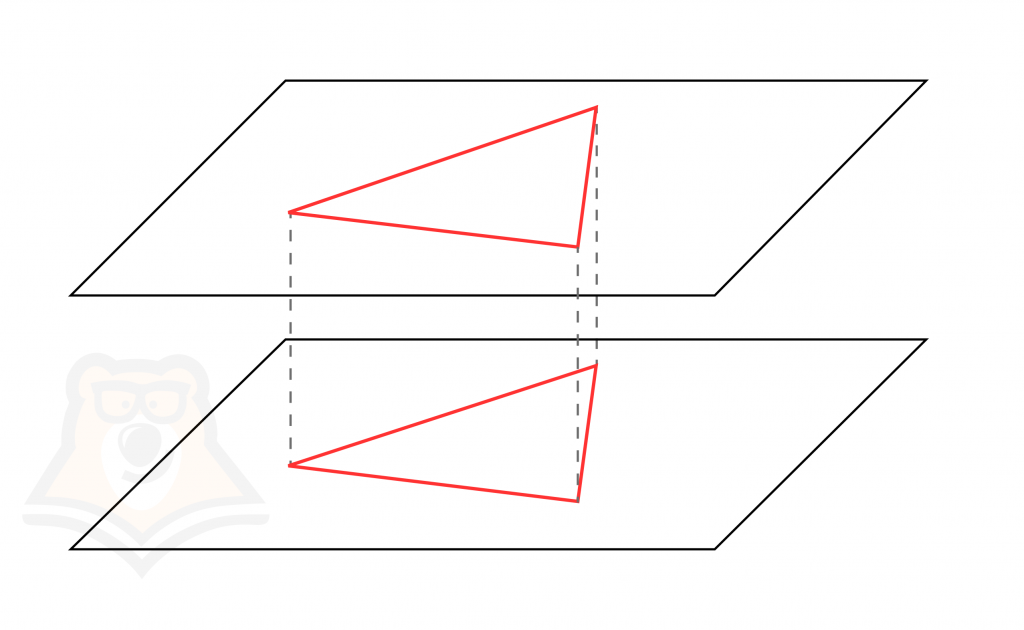
Почему в доказательстве нельзя использовать аргумент: «Так видно же!»? При решении задач доказывать равенство треугольников наложением их друг на друга нельзя. Математика — точная наука, и любое доказательство должно быть неоспоримым.  При выполнении чертежа даже в самых точных программах может появиться погрешность, а значит, треугольники уже не будут равны. Следовательно, чтобы доказать их равенство, необходимо пользоваться известными величинами углов и длинами сторон.

Чтобы доказывать геометрические факты, мы должны отталкиваться от известных фактов и величин, используя свойства, признаки и теоремы. Поэтому для доказательства равенства треугольников существуют 3 признака их равенства.

1 признак равенства треугольников

Если две стороны и угол, заключенный между ними, одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны. 

Фраза «соответственно равны» означает, что мы сравниваем две одинаковые стороны, например, стороны АС и КМ. Сравнение стороны АС в одном треугольнике и стороны KL в другом уже будет некорректно. 

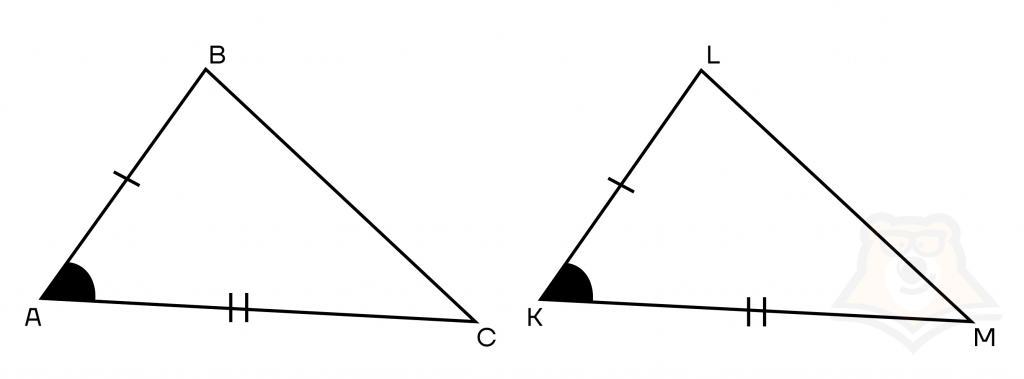
При решении задач обязательно подписывать, по какому признаку доказано равенство треугольников. В этом случае можно не писать громоздкое определение признака, а ограничиться только фразой: «Треугольники равны по двум сторонам и углу между ними». 

2 признак равенства треугольников

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны. 

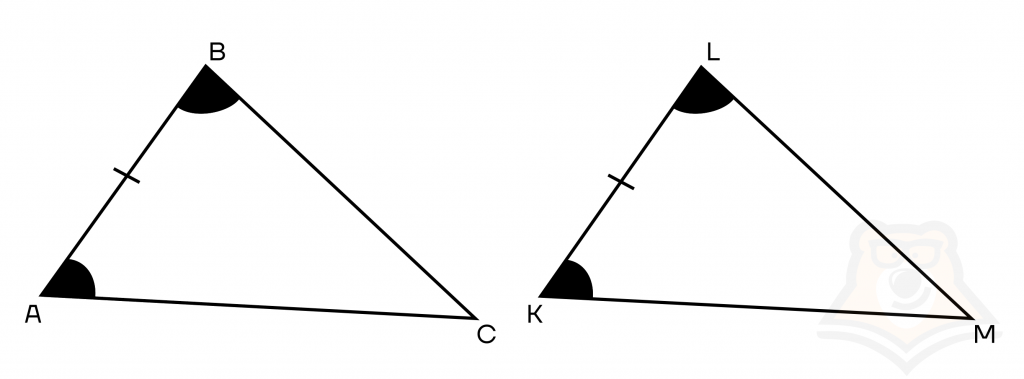
Иначе этот признак можно сформулировать так: «Треугольники равны по стороне и двум прилежащим к ней углам». 

3 признак равенства треугольников

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны между собой. 

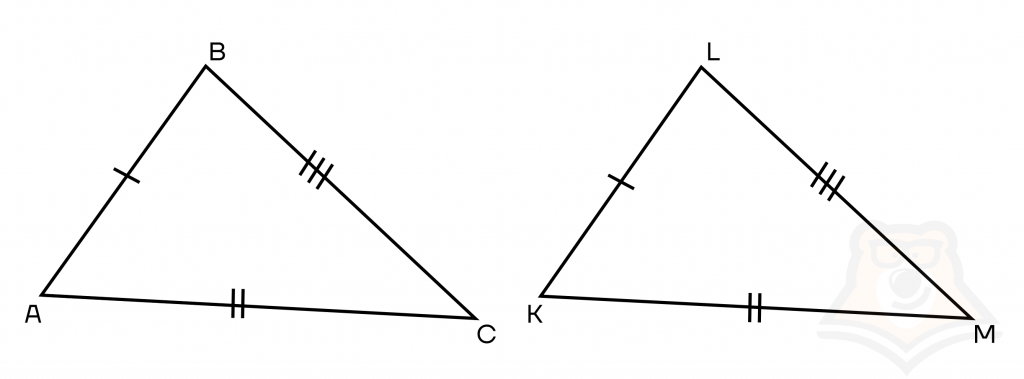
Иначе этот признак можно сформулировать так: «Треугольники равны по трем сторонам». 

Если хотя бы один из этих признаков будет выполняться, то смело можно утверждать, что треугольники равны. При этом, чтобы доказать равенство треугольников, не обязательно доказывать сразу все признаки: достаточно выбрать один, наиболее подходящий к задаче. 

Подведем итог.

Равенство треугольников можно доказать по одному из трех признаков:

• По равенству двух сторон и угла между ними.
• По равенству стороны и двум прилежащим к ней углам.
• По равенству трех сторон. 

Подобие треугольников

Предположим, мы возьмем треугольник и уменьшим его в два раза. Сможем ли мы назвать такие треугольники равными? Нет, поскольку не будет выполняться ни один из признаков равенства треугольников из-за неравенства их сторон. Тогда возникает вопрос: как называются такие фигуры? 

Для дальнейших рассуждений введем термин подобных треугольников. 

Подобные треугольники — это треугольники, все углы которых соответственно равны, а стороны соответственно пропорциональны. 

Подобные треугольники обозначаются с помощью знака ~, например, ABC ~ KLM. 

В чем разница между равными и подобными треугольниками и как в них не запутаться? Равные треугольники абсолютно равны между собой: по длинам сторон, по величине углов и так далее.  В подобных же треугольниках меняются пропорции одного из них. Иначе можно представить, что мы открыли картинку треугольника на телефоне и приблизили ее. Расположение сторон и углов не поменяется, но величина самого треугольника увеличится. Следовательно, в подобных треугольниках равны углы, но стороны соответственно пропорциональны — то есть отличаются в одно и то же количество раз.

Разберемся, что означает формулировка «соответственно пропорциональны». Возьмем две соответственные стороны в треугольниках АВС и KLM. Для удобства обозначим стороны первого треугольника как a, b, c, стороны второго треугольника как k, l, m. 

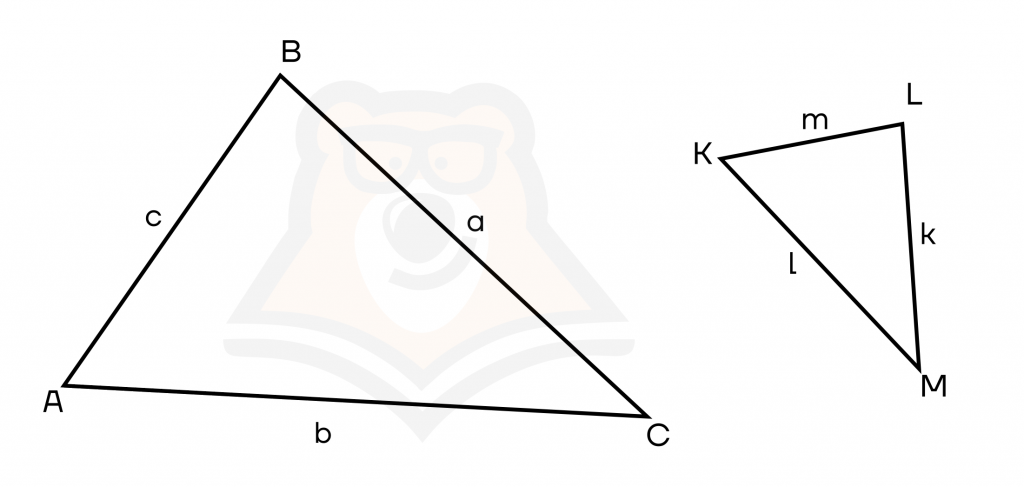
Найдем отношение сторон \(\frac{a}{k}\), \(\frac{b}{l}\), \(\frac{c}{m}\). Если эти отношения будут равны между собой, то у нас получится пропорция, то есть равенство нескольких отношений. 

Пусть отношение сторон будет равно k: \(\frac{BC}{LM} = \frac{AC}{KM} = \frac{AB}{KL} = k\). В этом случае k будет коэффициентом подобия. Заметим, что коэффициент подобия и обозначение стороны треугольника — это разные величины. 

Коэффициент подобия — это коэффициент, который показывает, во сколько раз отличаются длины сторон подобных треугольников. 

Например, k = 2, тогда длины сторон одного треугольника в два раза больше длин сторон другого треугольника.
Если k = 20, то длины сторон одного треугольника будут в двадцать раз больше длин сторон другого треугольника. 
Коэффициентом подобия может быть любое число. 

Рассмотрим, как доказать, что треугольники подобны. Для этого также существуют признаки подобия треугольника. 

1 признак подобия треугольников

Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключенные между ними, равны, то такие треугольники подобны.

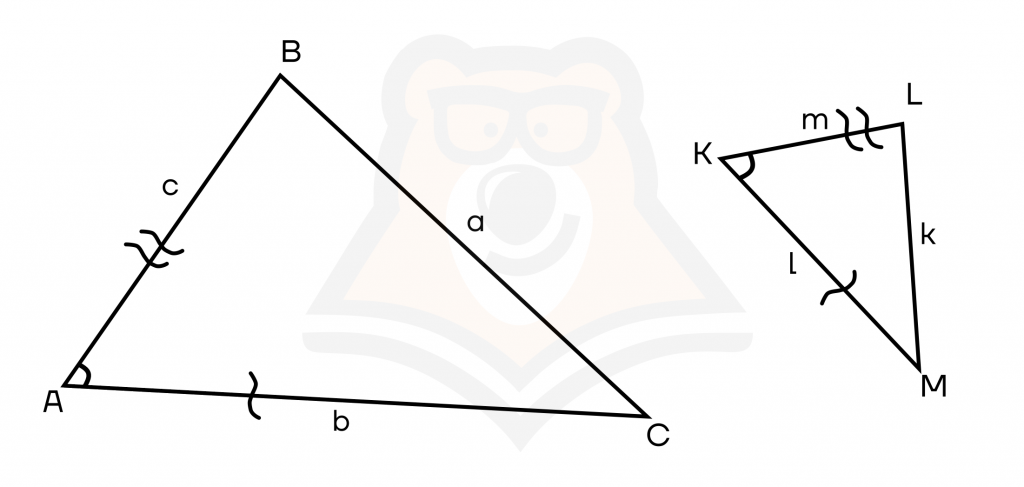
Если углы А и К треугольников АВС и KLM равны, а также выполняется равенство АСКМ=АВKL, то ABC ~ KLM. 

2 признак подобия треугольников

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. 

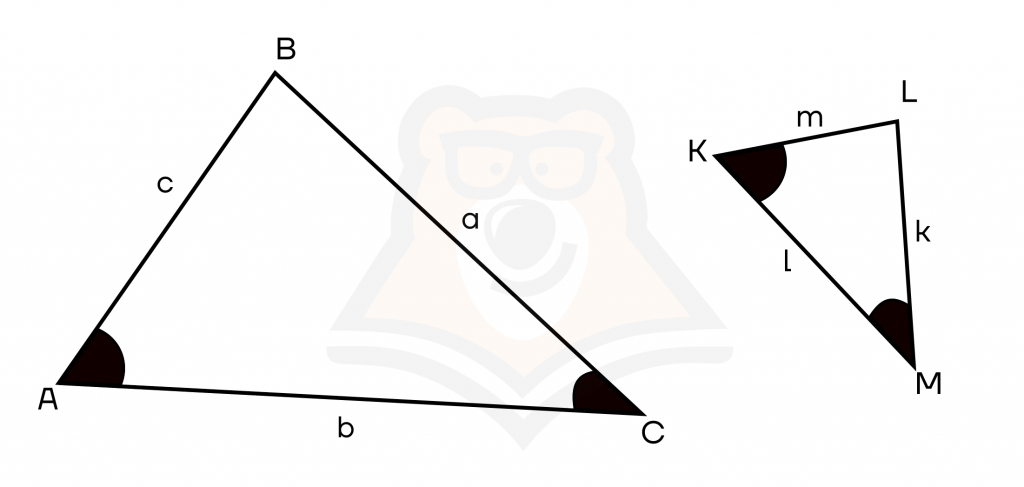
Например, если ∠А=∠К и ∠С=∠М, то АВС ~ KLM.

3 признак подобия треугольников

Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны. 

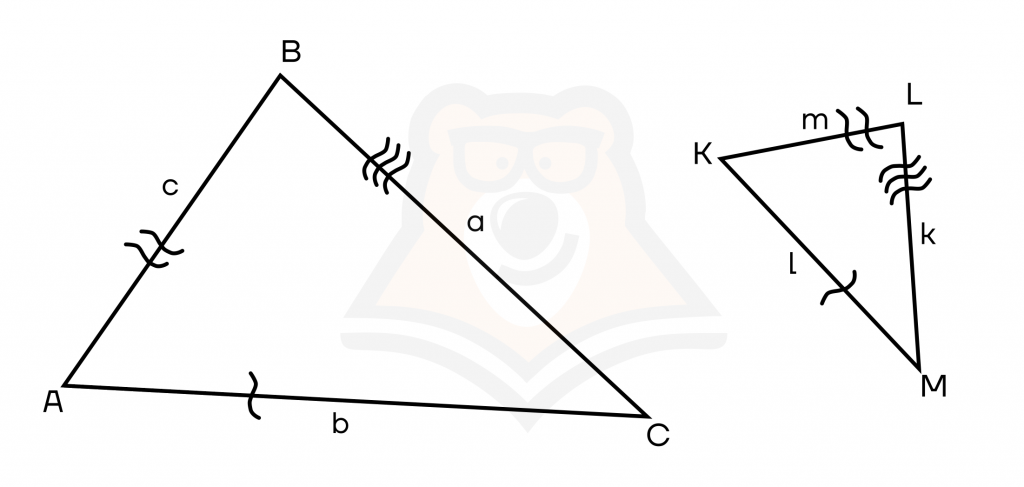
Если для треугольников будет выполняться равенство \(\frac{AC}{KM} = \frac{AB}{KL} = \frac{BC}{LM} = k\), то ABC ~ KLM. 

Для чего нужно подобие треугольников? Оно незаменимо при решении задач: если треугольники подобны, то можно получить очень много необходимых для решения данных. 

Рассмотрим еще несколько важных фактов, которые могут пригодиться для решения задач с подобными треугольниками. 

1. Отношение всех элементов подобных треугольников равняется коэффициенту подобия. То есть не только стороны, но и высоты, биссектрисы, медианы, радиусы вписанных и описанных окружностей — отношения всех этих элементов можно приравнять к коэффициенту подобия. 

2. Отношение периметров подобных треугольников равняется коэффициенту подобия. 

\(\frac{P_1}{P_2} = k\)

3. Отношение площадей подобных треугольников равняется квадрату коэффициента подобия. 

\(\frac{S_1}{S_2} = k^2\)

Также следует разобрать еще одну очень важную особенность подобных треугольников.

Составлять отношение сторон можно только с соответственными сторонами, причем в числителе должны быть только стороны одного треугольника, а в знаменателе только стороны другого.

Рассмотрим чуть подробнее этот момент. Как определить, с какими сторонами в треугольнике нужно составить отношение? Тем более что не всегда треугольники имеют одинаковое расположение: один из них может быть повернут или отзеркален. 

К соответственным сторонам будут примыкать равные углы. Рассмотрим рисунок. Нам даны два подобных треугольника, следовательно, их углы между собой равны. 

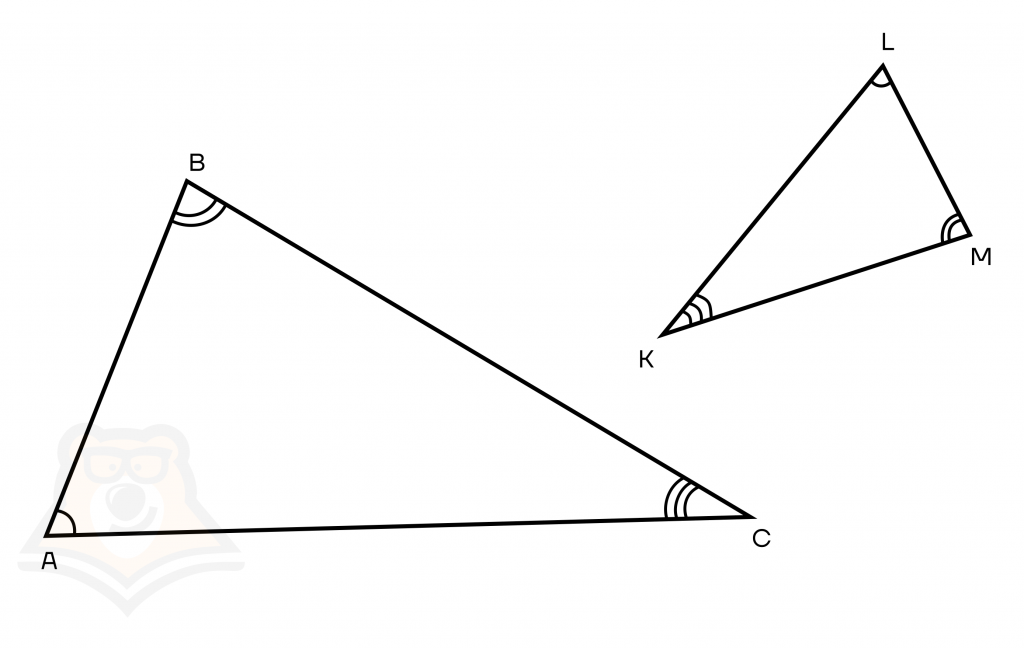
Выделим в каждом треугольнике разными цветами стороны, к которым прилегают разные углы:

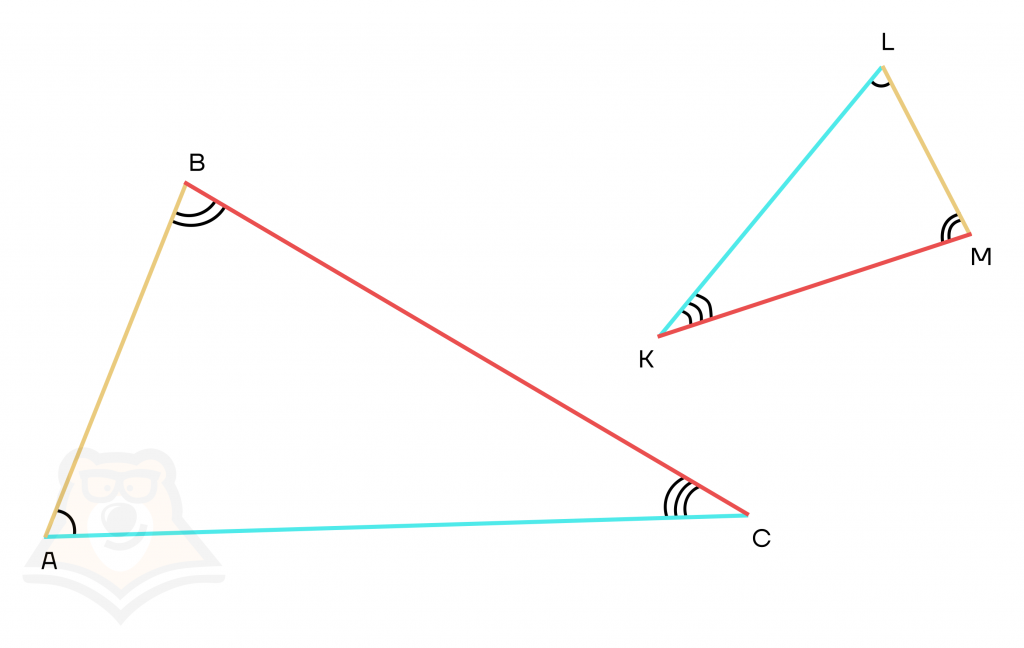
Теперь мы можем составить пропорцию: \(\frac{AB}{ML} = \frac{BC}{KM} = \frac{AC}{KL}\). 

Стоит обратить внимание, что в подобии в числителе мы взяли стороны большего треугольника, а в знаменателе стороны меньшего. Менять их местами в одном и том же равенстве нельзя. 

Правильные варианты: \(\frac{AB}{ML} = \frac{BC}{KM} = \frac{AC}{KL}\) или \(\frac{ML}{AB} = \frac{KM}{BC} = \frac{KL}{AC}\).

Неправильные варианты: \(\frac{AB}{ML} = \frac{KM}{BC} = \frac{KL}{AC}\) или \(\frac{ML}{AB} = \frac{KM}{BC} = \frac{AC}{KL}\). 

Фактчек

• Равные треугольники — это треугольники, у которых все стороны и углы равны. Чтобы доказать равенство треугольников, необходимо воспользоваться одним из признаков равенства. 
• Подобные треугольники отличаются от равных тем, что один из них имеет другие пропорции: он может быть больше или меньше.
• В подобных треугольниках все углы равны, а стороны соответственно пропорциональны. Чтобы доказать подобие треугольников, необходимо воспользоваться одним из признаков подобия. 
• В равных треугольниках все элементы также будут равны. В подобных треугольниках все элементы будут пропорциональны с одинаковым коэффициентом подобия. При этом отношение периметров подобных треугольников равняется коэффициенту подобия, а отношение площадей подобных треугольников равняется квадрату коэффициента подобия. 

Проверь себя

Задание 1. 
По какому признаку можно определить равенство треугольников? 

1. Два угла одного треугольника соответственно равны двум углам другого треугольника.
2. Две стороны одного треугольника соответственно равны двум сторонам другого треугольника.
3. Сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.
4. Три угла одного треугольника равны трем углам другого треугольника. 

Задание 2. 
По какому признаку можно определить подобие треугольников? 

1. Две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника.
2. Угол одного треугольника соответственно равен углу другого треугольника. 
3. Две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, а углы, заключенные между ними, равны. 
4. Ни по одному из вышеперечисленных признаков. 

Задание 3. 
Коэффициент подобия двух треугольников равен 2. Во сколько раз будут отличаться их периметры?

1. в 2 раза
2. в 4 раза
3. в 8 раз
4. периметры отличаться не будут 

Задание 4. 
Коэффициент подобия двух треугольников равен 3. Во сколько раз будут отличаться их площади? 

1. в 3 раза
2. в 9 раз
3. в 27 раз
4. площади отличаться не будут 

Задание 5. 
Коэффициент подобия двух треугольников равен 4. Радиус описанной окружности меньшего из них равен 8. Чему равен радиус описанной окружности второго треугольника? 

1. 2
2. 4
3. 16
4. 32

Ответы: 1. — 3; 2. — 3; 3. — 1; 4. — 2; 5. — 4.