Шар

На этой странице вы узнаете

• Какая сфера является самой большой в мире?
• Может ли шар быть опасным? 
• Почему шар считается идеальной фигурой?

Если и существует идеальная фигура, то это шар. Так считали еще древние греки. Наша планета, Солнце, звезды и другие космические тела стремятся к форме шара. В чем же особенность этой фигуры, если сама Вселенная взяла ее за основу? 

Сфера и шар

Во многих спортивных играх задействован мяч. В волейболе, футболе, баскетболе и большинстве других игр он имеет круглую форму, которую также мы привыкли называть шаром. 

Но прежде чем начать рассматривать шар, вспомним тела вращения. Чуть подробнее про них можно прочесть в одноименной статье. 

Попробуем повернуть круг вокруг его диаметра.
У нас получится обычный шар. Как будет называться поверхность его вращения?

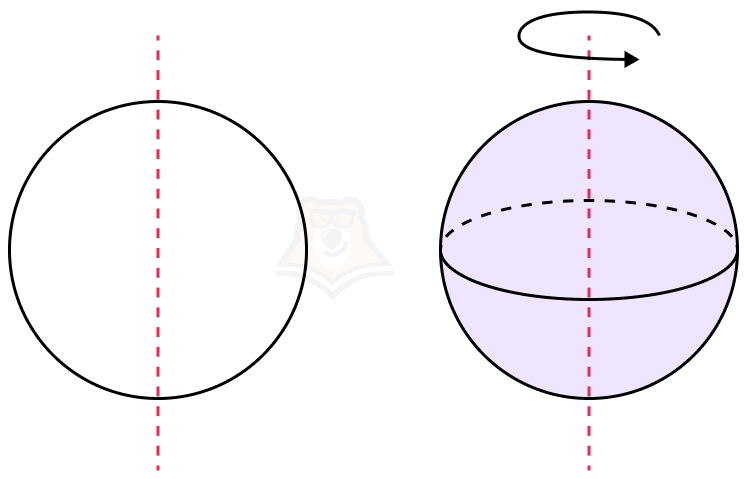
Сфера — поверхность, состоящая из множества точек пространства, равноудаленных от ее центра. 

Вспомним воздушный шарик, который улетает в небо: он пустой внутри и состоит только из оболочки. То есть он будет являться сферой.

Сфера очень похожа на круг, все точки которого также равноудалены от центра. А вот все, что лежит внутри сферы (и сама сфера), будет называться шаром.

Какая сфера является самой большой в мире? Это сама Вселенная. Если не углубляться сильно в астрофизику, то мы знаем, что Вселенная постоянно расширяется, а все космические тела удаляются от нас со скоростью, пропорциональной расстоянию до них. Чем дальше тело, тем больше скорость его удаления. Получается, что существуют тела настолько далекие, что их скорость достигает скорости света. На этом расстоянии и дальше свет уже не будет достигать нас, а значит, Вселенная за пределами этой границы для нас невидима и непостижима. То есть в какую бы сторону мы ни посмотрели, мы получим равное расстояние до любой из «крайних» точек пространства, что соответствует определению сферы.

Шар — тело, ограниченное сферой. 

Воздушный шарик и газ, который его наполняет, вместе уже будут шаром. 

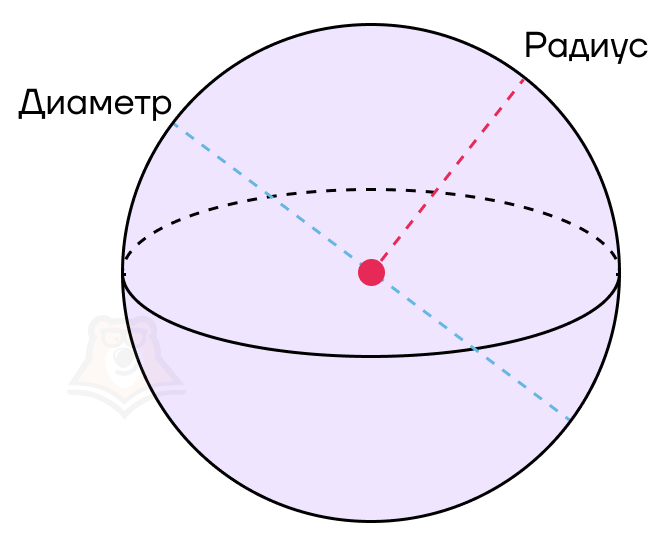
Шар, так же как и круг, обладает радиусом и диаметром.

Радиус шара — отрезок, соединяющий центр шара и любую точку на его поверхности.

Диаметр шара — отрезок, соединяющий две точки на поверхности шара и проходящий через его центр. 

Какими же свойствами обладает это уникальное геометрическое тело? Разберем это в следующем разделе.

Свойства сферы и шара

Свойство 1. Все точки сферы равноудалены от ее центра.
Следовательно, все радиусы равны между собой.

Свойство 2. Любое сечение шара плоскостью является кругом. 

Неважно, как будет проведено сечение, будет ли оно осевым или нет — всегда будет получаться круг. 

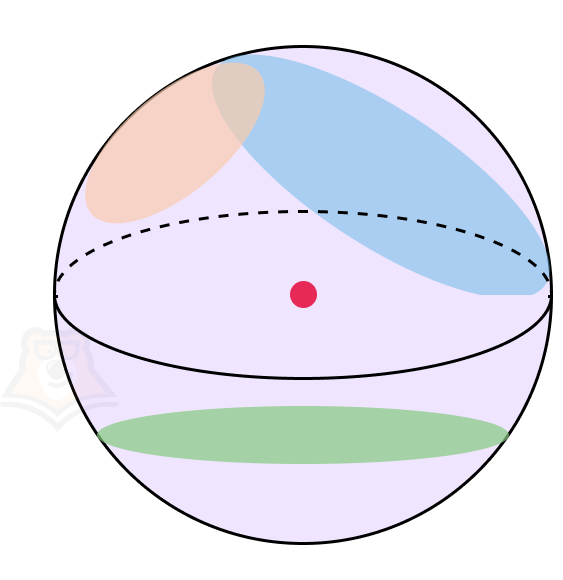
Свойство 3. Любое сечение сферы является окружностью.
Чуть подробнее про различия круга и окружности можно прочесть в статье «Окружность и круг». 

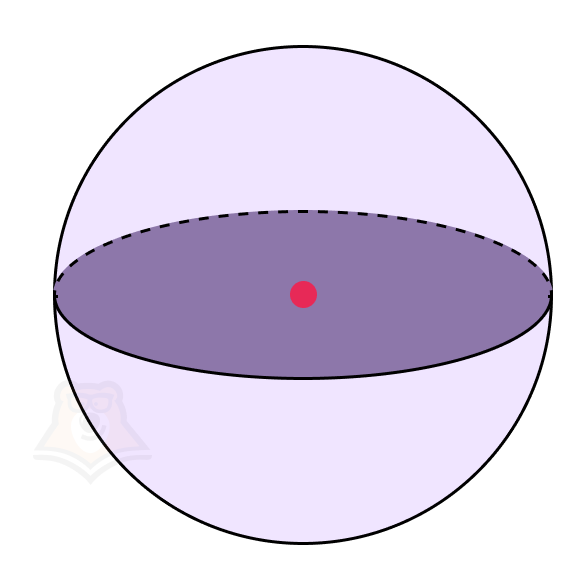
Свойство 4. Сечение, проходящее через центр шара, называется диаметральным или большим кругом шара.
Этот круг не просто так назван большим: действительно из всех кругов сечения шара наибольшим диаметром будет обладать именно круг, проходящий через его центр. 

Представим, что шар наполняют водой. Тогда ее поверхность будет сначала постепенно увеличиваться, а потом уменьшаться. Самый большой круг на поверхности получится именно в диаметральном сечении шара. 

В круге есть сегмент и сектор. Логично будет предположить, что подобное есть и в шаре. 

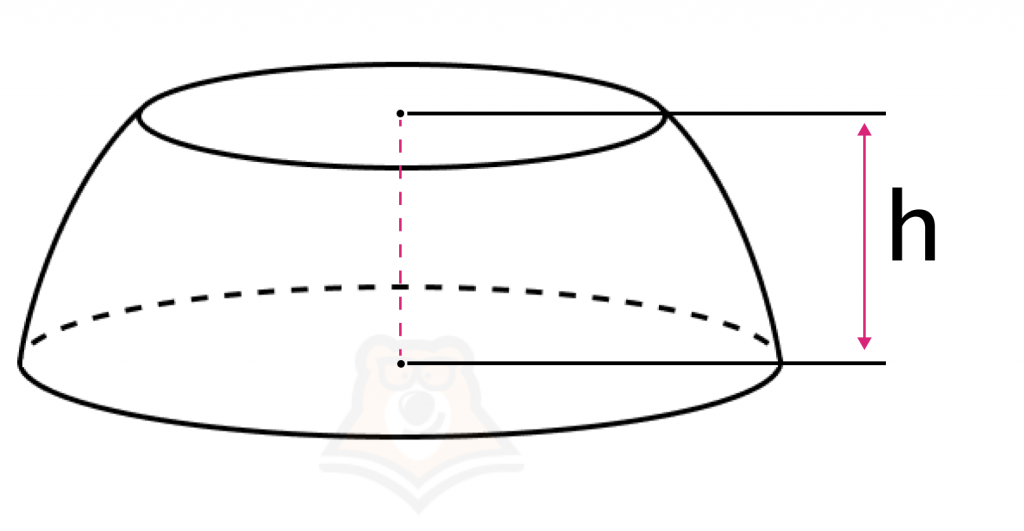
Сегмент шара (шаровой сегмент) — часть шара, отсеченная плоскостью. 

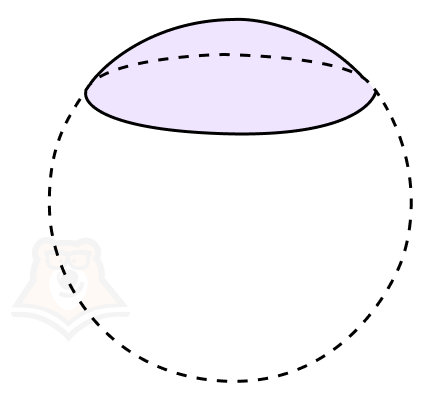
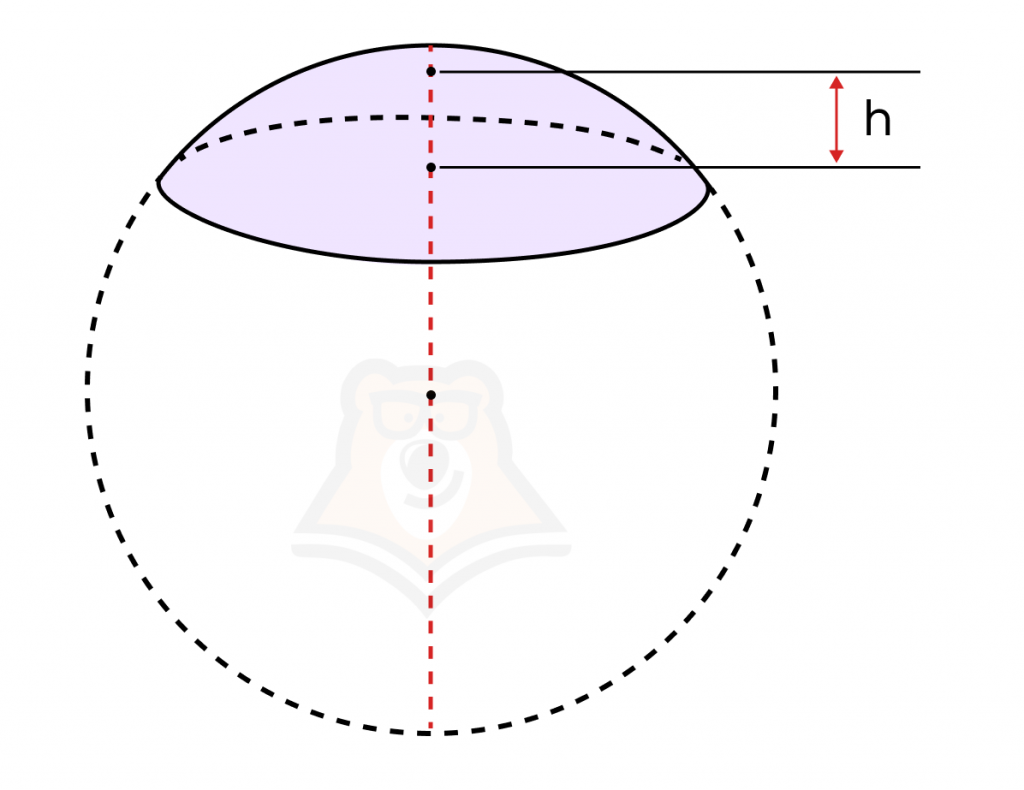
При сечении шара плоскостью образуется круг, который называют основанием шарового сегмента.

Проведем через центр основания шарового сегмента диаметр шара. Та часть этого диаметра, которая лежит внутри шарового сегмента, называется высотой шарового сегмента (на рисунке обозначена как h).

Высота шарового сегмента перпендикулярна основанию.

Срез шара (шаровой слой) — часть шара, заключенная между двумя параллельными секущими плоскостями. 

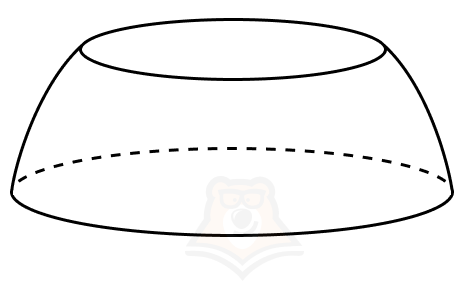
Представьте, что мы нарезали помидор кружочками. Каждый этот кружочек будет срезом шара. 

Круги, образующиеся при сечении шара двумя параллельными плоскостями, называются основаниями шарового слоя. 

Расстояние между двумя параллельными плоскостями называют высотой шарового слоя (на рисунке обозначена как h). Высота шарового слоя перпендикулярна обоим основаниям.

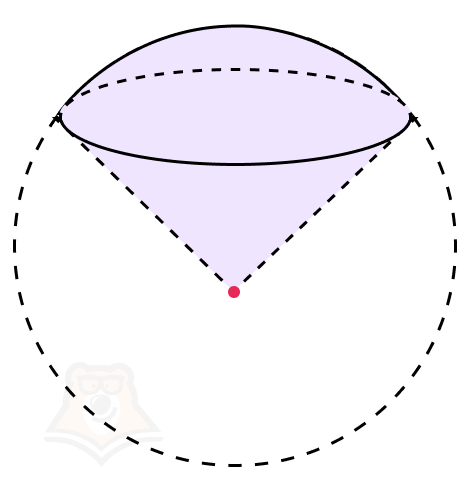
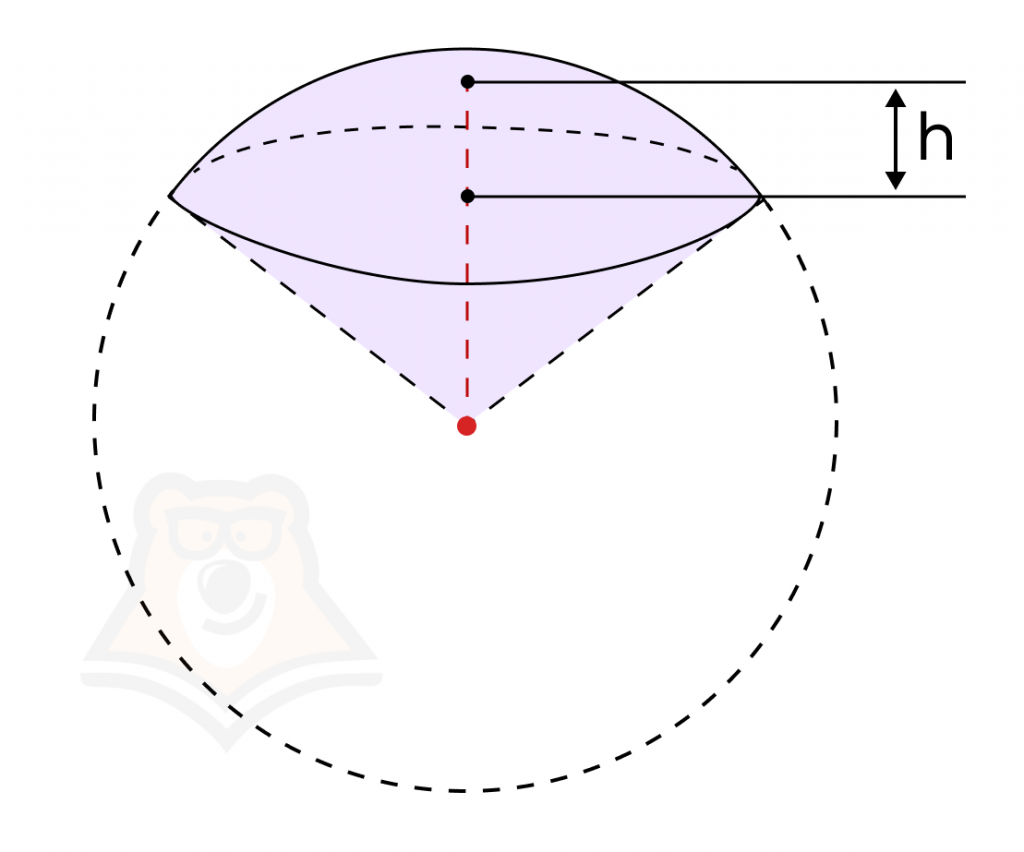
Сектор шара — часть шара, ограниченная совокупностью лучей, выходящих из центра шара и ограничивающих на его поверхности круг. 

Иными словами, сектор шара состоит из сегмента и конуса, который соединяет этот сегмент с центром шара. 

Может ли шар быть опасен?  В природе существует немало опасных явлений, и среди них шаровые молнии. То есть электричество тоже может принять форму шара. По данным Википедии, вплоть до 2010 года вопрос существования шаровых молний был под сомнением. Некоторые ученые считали это природное явление галлюцинацией. В настоящее время шаровые молнии слабо изучены, на очень многие вопросы про них до сих пор нет ответа. Если переполненный электричеством шар дотронется до живого существа, дело вполне может закончиться трагедией. По свидетельствам очевидцев, при встрече с шаровой молнией нельзя делать резких движений: она чрезвычайно чувствительна к любым завихрениям воздуха и может последовать за человеком.

Формулы для шара

Мы рассмотрели основные свойства и определения для шара и сферы. 

Теперь разберемся: как решать задачи с шаром. Для этого нужно воспользоваться формулами для шара.

Заметим, что в шаре нет оснований, поэтому формула площади поверхности у него будет только одна.

\(S=4\pi R^2\)

В этой формуле R — радиус шара. 

Пример 1. Дан шар, площадь большого круга которого равна 5. Чему равна площадь поверхности этого шара?

Решение. Большой круг — это диаметральное сечение шара, а значит, если найти радиус этого круга, то найдем и радиус шара.

Площадь круга вычисляется по формуле \(S=\pi R^2\), откуда мы можем выразить радиус в квадрате:
\(R^2=\frac{S}{\pi}=\frac{5}{\pi}\). 

Подставим найденный радиус в формулу площади поверхности шара:
\(S_{поверхности}=\pi 4*\frac{\pi}{5}=4*5=20\). 

Ответ: 20

Рассмотрим пример задания из №2 ЕГЭ по профильной математике

Задание. Диаметр первого шара в 3 раза больше диаметра второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго шара?

Решение. Пусть диаметр первого шара \(D_1\), диаметр второго шара – \(D_2\), тогда по условию \(D_1=3D_2\). Воспользуемся формулой площади поверхности шара, а также вспомним, что радиус равен половине диаметра:
\(S_{пов.2}=4\pi R_2^2=4\pi*(\frac{D_2}{2})^2=4\pi*\frac{D_2^2}{4}=\pi D_2^2\) – площадь поверхности второго шара.

\(S_{пов.1}=4\pi R_1^2=4\pi*(\frac{D_1}{2})^2=4\pi*\frac{D_1^2}{4}=\pi D_1^2=\pi*(3D_2)^2=9\pi D_2^2\) – площадь поверхности первого шара.

Чтобы понять, во сколько раз площадь поверхности первого шара больше, чем площадь поверхности второго, нужно площадь поверхности первого шара разделить на площадь поверхности второго шара:
\(\frac{S_{пов.1}}{S_{пов.2}}=\frac{9\pi D_1^2}{\pi D_1^2}=9\)

Ответ: 9

Объем шара также можно найти, пользуясь одной единственной формулой.

Пусть R — радиус шара, тогда получаем следующую формулу. 

\(V=\frac{4}{3}\pi R^3\)

Пример 2. Во сколько раз уменьшится объем шара, если уменьшить его радиус в 4 раза? 

Решение. Пусть \(R_1\) — радиус до уменьшения, \(R_2\) — радиус после уменьшения. Тогда из условия \(R_1=4R_2\). 

Найдем отношение объемов: 

\(\frac{V_1}{V_2}=\frac{\frac{4}{3}\pi R_1^3}{\frac{4}{3}\pi R_2^3}=\frac{R_1^3}{R_2^3}=\frac{(4R)2)^3}{R_2^3}=\frac{64R_2^3}{R_2^3}=64\)

Объем шара уменьшится в 64 раза. 

Ответ: 64

Разберем еще один пример задачи из №2 ЕГЭ по профильной математике

Задание. Объем шара равен \(972\pi\). Чему равна площадь поверхности этого шара? В ответе указать полученное значение, деленное на \(\pi\).

Решение. Формула для объема шара:
\(V=\frac{4}{3}\pi R^3\)

Откуда:
\(R=\sqrt[3]{\frac{3*V}{4*\pi}}=\sqrt[3]{\frac{3*972*\pi}{\pi 4}}=\sqrt[3]{729}=9\)

Подставим полученное значение R в формулу площади поверхности шара:
\(S=4\pi R^2 = 4\pi*9^2=4\pi*81=324\pi\)

В ответе укажем полученное значение, деленное на \(\pi\), то есть 324.

Ответ: 324

Так же, как и для шара, существуют формулы для шарового сегмента. Его объем можно найти так:

\(V_{шар. сегм.}=\pi h^2(R-\frac{1}{3}h)\)

Где h – высота шарового сегмента, R – радиус основания.

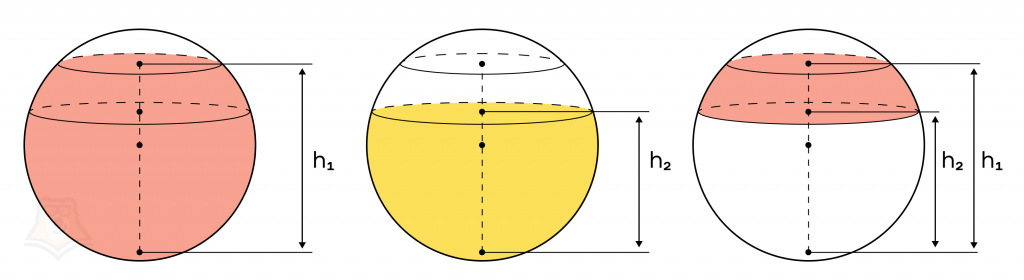
При сечении шара двумя параллельными плоскостями над этими плоскостями образуются два шаровых сегмента, показанных на рисунке ниже. 

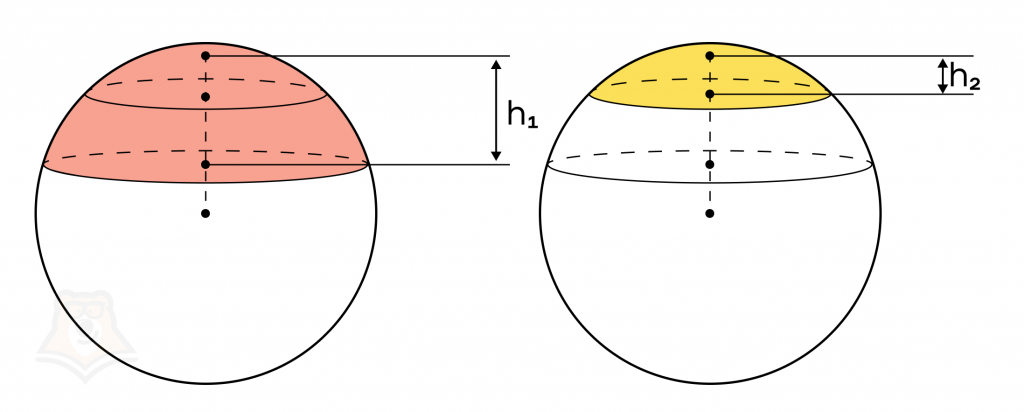
Для того чтобы вычислить объем шарового слоя, заключенного между секущими плоскостями, достаточно из объема большего шарового сегмента вычесть объем меньшего шарового сегмента: 

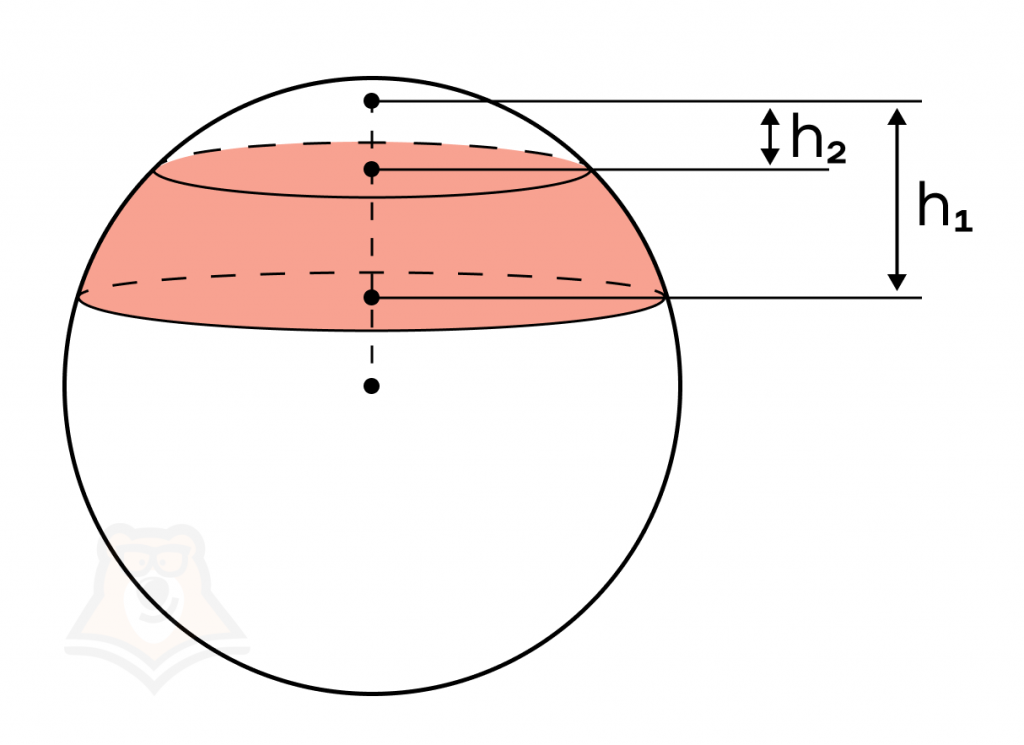
\(V_{шар. слоя}=V_{шар.сегм.1}-V_{шар.сегм.2}=\pi(h_1^2(R-\frac{1}{3}h_1)-h_2^2(R-\frac{1}{3}h_2))\),

Где \(h_1\) – высота первого шарового сегмента, \(h_2\)– высота второго шарового сегмента (показаны на рисунке), \(R\) – радиус шара.

Аналогично при вычислении объема шарового слоя можно было бы рассмотреть два шаровых сегмента, лежащих под секущими плоскостями. Суть все та же – из объема большего шарового сегмента вычитаем объем меньшего шарового сегмента.

Объем шарового сектора вычисляется по формуле:

\(V_{шар.сект.}=\frac{2}{3}\pi R^2h\),

где \(h\) – высота шарового сегмента, \(R\) – радиус шара.

Почему шар считается идеальной фигурой? Присмотритесь вокруг: многие предметы стремятся к форме шара, даже планеты.  Шар считается идеальной фигурой потому, что среди различных тел с равным объемом, шар будет иметь наименьшую площадь поверхности. А при равных площадях поверхности различных тел шар будет обладать наибольшим объемом.

В этой статье мы познакомились с еще одной удивительной геометрической фигурой – шаром. 

Предлагаем не останавливаться на достигнутом и сразу перейти к следующей статье, где мы вместе погрузимся в мир числовых последовательностей.

Термины

Круг – это геометрическая фигура, которая ограничена окружностью. 

Окружность – это замкнутая кривая, все точки которой равноудалены от центра. 

Поверхность вращения – граница тела вращения.

Сечение – это изображение фигуры, получающееся при мысленном рассечении предмета секущей плоскостью. 

Тело вращения — тело в пространстве, которое возникает при вращении какой-то фигуры вокруг определенной оси. 

Фактчек

• Сфера — поверхность, состоящая из множества точек пространства, равноудаленных от ее центра. 
• Шар — тело, ограниченное сферой. Это тело вращения, получающееся при вращении круга вокруг одного из его диаметра.
• Радиус шара — расстояние от его центра до любой точки на его поверхности. Диаметр шара соединяет две точки на его поверхности и проходит через центр шара. 
• Любое сечение шара плоскостью будет являться кругом. Самым большим из них будет сечение, которое проходит через центр шара. 
• Сегмент шара — часть шара, отсеченная плоскостью. Срез шара — часть шара, заключенная между двумя параллельными секущими плоскостями. Сектор шара — часть шара, ограниченная совокупностью лучей, выходящих из центра шара и ограничивающих на его поверхности круг. 

Проверь себя

Задание 1.
Что такое диаметр шара?

1. Отрезок, соединяющий две любые точки шара.
2. Отрезок, соединяющий центр шара и любую точку на его поверхности.
3. Отрезок, соединяющий две точки на поверхности шара и проходящий через его центр.
4. Только вертикальный отрезок, проходящий через центр шара. 

Задание 2.
Что такое срез шара?

1. Часть, отсекаемая секущей плоскостью от шара.
2. Часть шара, заключенная между двумя параллельными секущими плоскостями.
3. Часть шара, ограниченная совокупностью лучей, выходящих из центра шара и ограничивающих на его поверхности круг. 
4. Сама секущая плоскость шара.

Задание 3.
Диаметр шара равен 6. Чему равна площадь поверхности шара?

1. 144
2. 36
3. 864
4. 108

Задание 4.
Радиус шара равен 33. Чему равен его объем?

1. 4
2. 16
3. 36
4. 108

Ответы: 1. — 3; 2. — 2; 3. — 2; 4. — 1.