Трапеция

На этой странице вы узнаете

• В чем секрет одной оптической иллюзии? 
• Можно ли найти трапецию на небе?
• Какие трапеции можно вписать в окружность или описать вокруг окружности? 

Уважаемые знатоки, внимание, вопрос! Каким греческим словом, обозначающим обеденный стол, названа форма юбки и мышца в теле человека? 

Элементы трапеции

Многие уже догадались, что речь пойдет о трапеции. Рассмотрим этот частный случай многоугольников, а конкретнее — вид четырехугольников.

Поскольку это четырехугольник, мы уже можем сделать вывод, что у трапеции четыре угла и четыре стороны. Но чем тогда трапеция отличается от прямоугольника, квадрата или параллелограмма?

Трапеция — это четырехугольник, две стороны которого параллельны, а две другие не параллельны друг другу. 

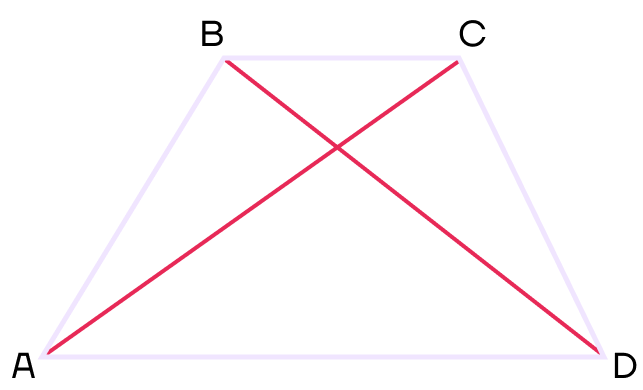
Начертим трапецию ABCD. Пусть АD || BC.
В нашей трапеции AD, BC — основания трапеции (основания всегда параллельные стороны).
AB, CD — боковые стороны трапеции (то есть непараллельные стороны).
АС и BD — диагонали трапеции. 

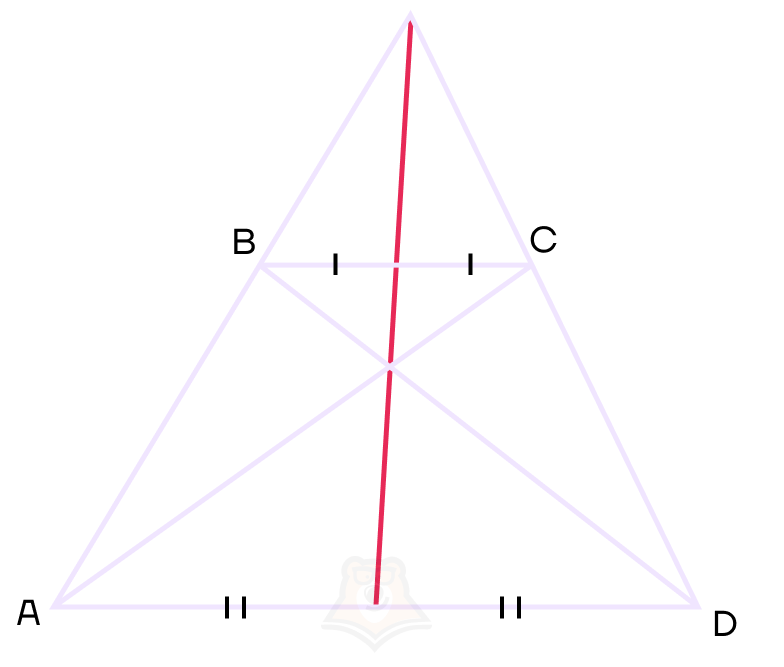
Рассмотрим одно очень интересное свойство диагоналей трапеции. 

Точка пересечения диагоналей трапеции лежит на одной прямой с точкой пересечения боковых сторон трапеции и серединами оснований. 

У трапеции также есть высота, у которой есть своя особенность. 

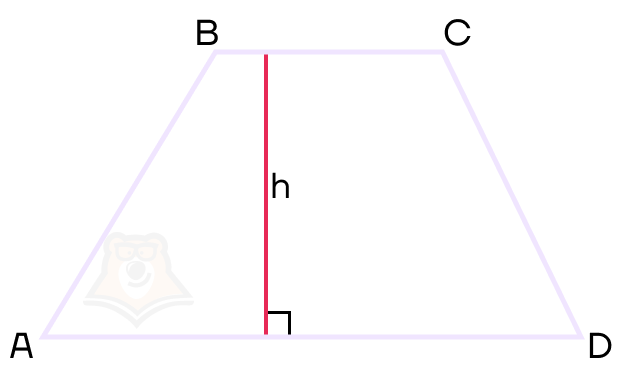
Высота трапеции — это отрезок, соединяющий основания трапеции и перпендикулярный им. 

При этом высота может быть опущена из любой точки одного основания на другое. Из какой бы точки мы не опустили высоту, она всегда будет одной и той же длины для каждой трапеции. 

На рисунке h — высота. 

Вспомним треугольник: одним из его элементов является средняя линия. Оказывается, средняя линия бывает и у трапеции. 

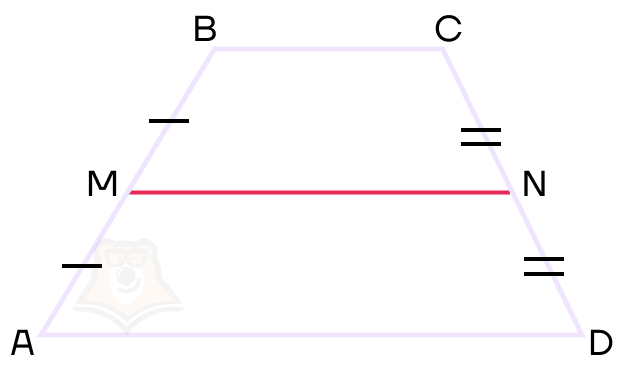
Средняя линия трапеции — это линия, соединяющая середины боковых сторон трапеции. 

На рисунке MN — средняя линия трапеции АВСD. Следовательно, АМ = МВ, СN = ND. 

Средняя линия также обладает своими свойствами. 

1 свойство. Средняя линия трапеции параллельна ее основаниям.
Если MN средняя линия, то выполняется условие AD || MN || BC. 

2 свойство. Средняя линия трапеции равна полусумме ее оснований.
Пусть MN — средняя линия, тогда чтобы ее найти, необходимо решить следующее уравнение: \(MN = \frac{AD + BC}{2}\). 

Выведем общую формулу. Пусть m — средняя линия, a, b — основания трапеции. Тогда найти среднюю линию можно по следующей формуле. 

\(m = \frac{a + b}{2}\)

В чем секрет одной оптической иллюзии? Комната Эймса — помещение неправильной формы, в котором трапеция используется для создания оптической иллюзии. Если в комнату зайдут два наших друга примерно одинакового роста, а мы будем наблюдать за ними в замочную скважину, произойдут невероятные превращения. Наш друг, стоящий в одном углу, окажется гигантом. В то время друг, стоящий в другом углу, превратится в карлика. Иллюзия настолько убедительна, что, когда друзья решат поменяться местами, они начнут «расти» или «уменьшаться» на глазах. Секрет комнаты в том, что привычная нам прямоугольная форма помещения заменена на трапециевидную, но наш мозг этого не замечает. 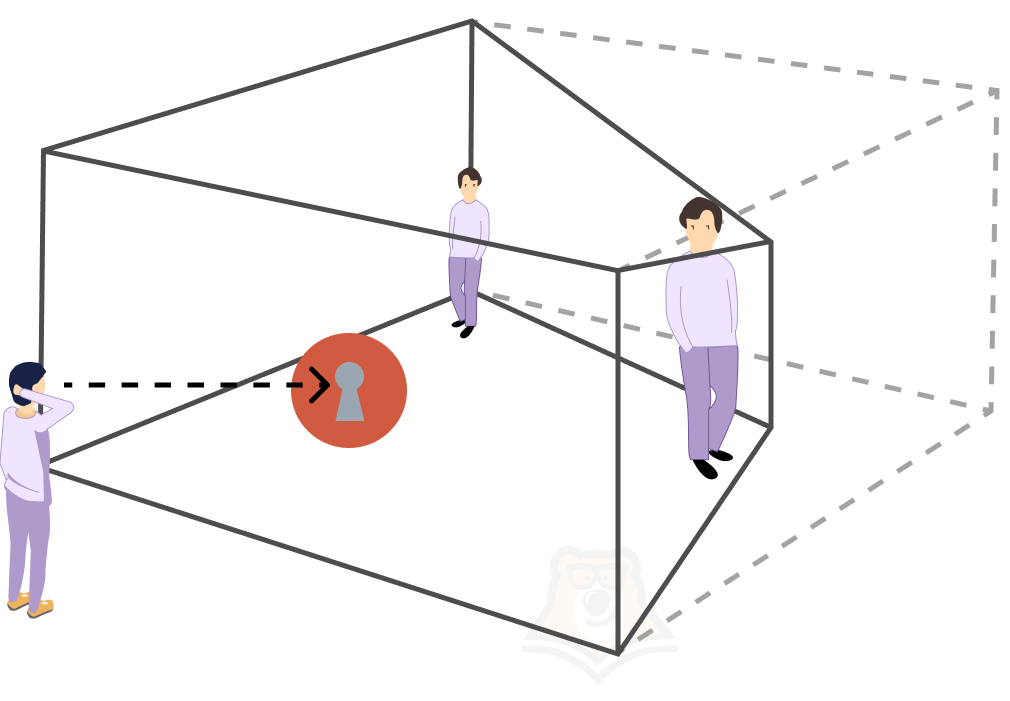Этот простой эффект иногда используется при съемке фильмов и телешоу. Например, многие эпизоды фильма «Властелин Колец» снимали, создав декорации, отвечающие принципам комнаты Эймса.

Мы познакомились с основными элементами трапеции, но пока еще ни слова не сказали о том, какими они бывают. Есть ли какое-то разнообразие трапеций? Или все они как одна похожи?

Виды трапеций

Трапеций существует великое множество, но среди всего их разнообразия можно выделить три вида, которые имеют схожие признаки. Рассмотрим их. 

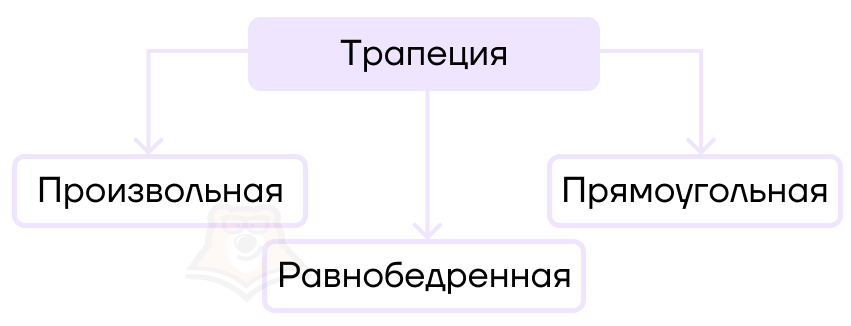
Равнобедренная трапеция — это трапеция, боковые стороны которой равны. 

Нам дана трапеция ABCD. Поскольку она равнобедренная, то АВ = CD. 

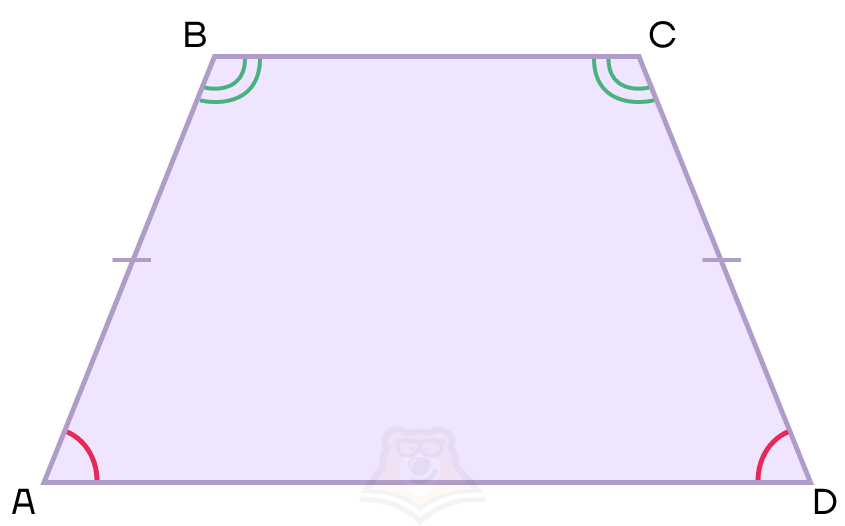
Рассмотрим свойства равнобедренной трапеции. 

1 свойство. Углы при основании равнобедренной трапеции равны. 

То есть ∠BAD = ∠BCD, ∠ABC = ∠BCD. 

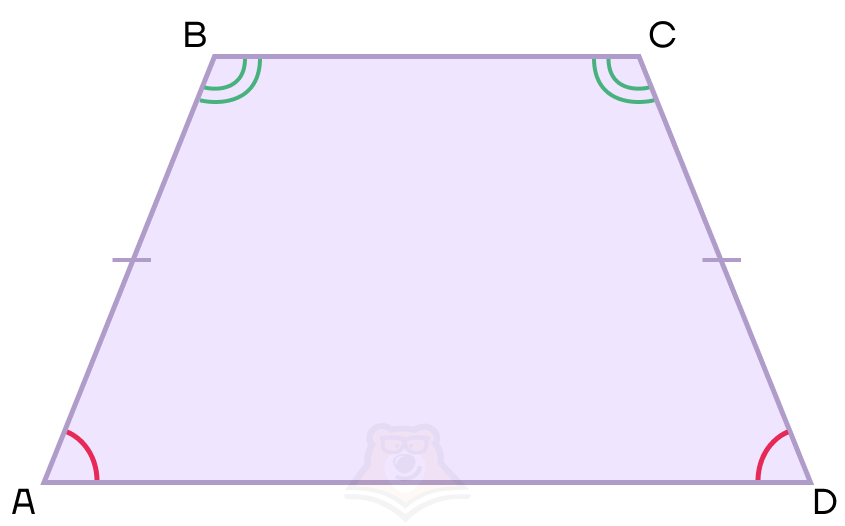
2 свойство. В равнобедренной трапеции диагонали равны. 

3 свойство. В равнобедренной трапеции диагонали образуют равные углы с каждым основанием. 

Рассмотрим трапецию ABCD. В ней будет выполняться равенство ∠ACB = ∠CAD = ∠BDA = ∠DBC

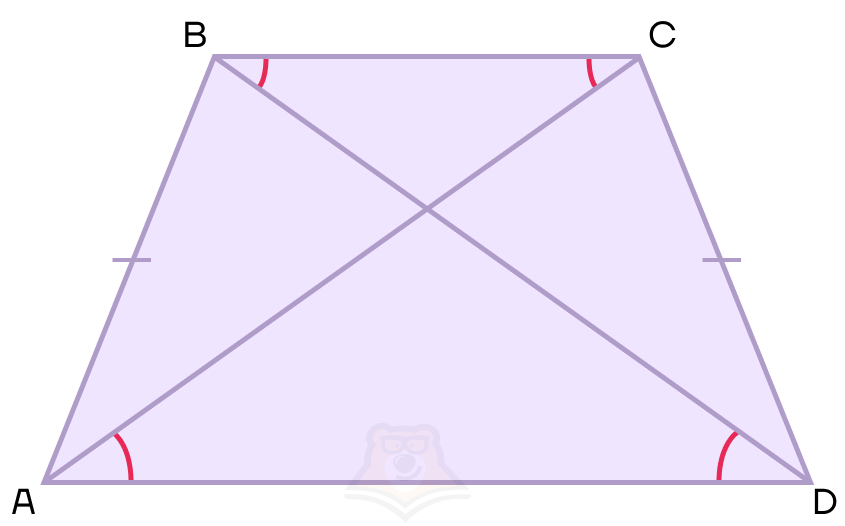
Как связаны средняя линия, высота и перпендикулярные диагонали? У трапеции есть одно довольно интересное свойство. 

Если диагонали равнобедренной трапеции взаимно перпендикулярны, то ее средняя линия будет равняться высоте.  

Почему так получается? Давайте попробуем доказать.

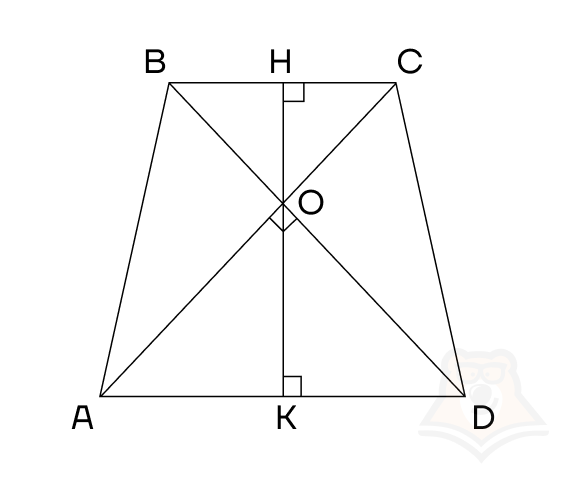
У нас есть трапеция ABCD с основаниями AD и BC, при этом AC\(\bot\)BD, проведем высоту HK так, чтобы она проходила через точку пересечения диагоналей O.

Как было сказано ранее, в равнобедренной трапеции диагонали образуют равные углы с основаниями, то есть ∠OBC=∠BCO=∠OAD=∠ODA, а это значит, что треугольники AOD и BOC являются не только прямоугольными, но и равнобедренными
\(\Rightarrow\)
∠OBC=∠BCO=∠OAD=∠ODA=45॰.
А значит и ∠HOB=∠HOC=∠AOK=∠DOK=45॰ \(\Rightarrow\) треугольники AOK, DOK, BOH, COH тоже являются прямоугольными и равнобедренными

\(AK=KD=KO=\frac{1}{2}AD\)
\(BH=HC=HO=\frac{1}{2}BC\)

Тогда

\(HK=HO+OK=\frac{1}{2}BC+\frac{1}{2}AD\frac{1}{2}(BC+AD)\)

Cредняя линия трапеции равна:

\(m=\frac{1}{2}(AD+BC)\)

Вуаля! Вот и получилось, что высота такой трапеции равна ее средней линии.

Прямоугольная трапеция — это трапеция, в которой одна из боковых сторон перпендикулярна основаниям. 

Например, в прямоугольной трапеции ABCD AB \(\perp\) BC и AB \(\perp\)AD. 

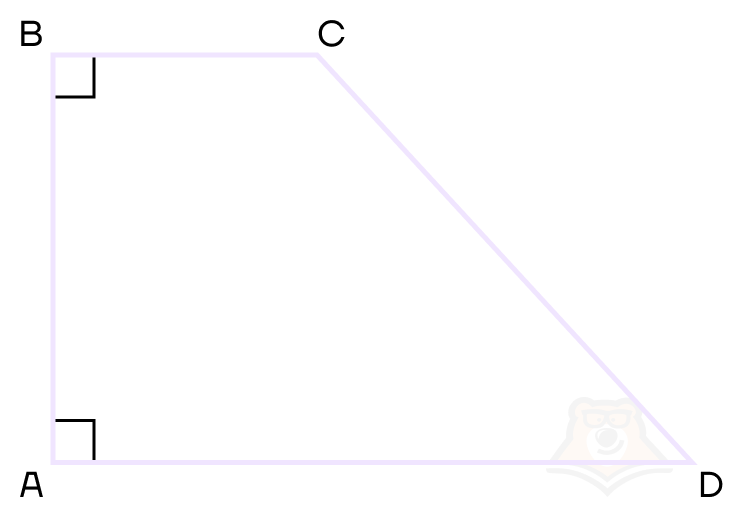
Рассмотрим свойства прямоугольной трапеции. 

1 свойство. Два угла в прямоугольной трапеции равны 90^॰. 

2 свойство. Высота трапеции совпадает с боковой стороной, которая перпендикулярна основаниям. 

В трапеции ABCD за высоту можно принять сторону АВ. 

Можно ли найти трапецию на небе?  Иногда так приятно просто смотреть на звездное небо и ни о чем не думать, наслаждаясь красотой и величием природы. Но… что, и здесь геометрия? Да! Созвездие Ориона является одним из самых известных и ярких созвездий, а благодаря своему расположению, его можно увидеть буквально из любой точки земного шара.  Довольно большую часть данного созвездия составляет Туманность Ориона, в самом сердце которой находится группа звезд. На первый взгляд они выглядят как одна большая звезда, но если посмотреть на них через телескоп или даже бинокль, можно увидеть самые яркие 4 звезды данной группы, которые образуют фигуру, названную Трапецией Ориона.

Мы разобрались с тем какие бывают трапеции, как называются элементы этой фигуры и рассмотрели некоторые свойства «особенных трапеций». А что насчет самых обычных, ничем не примечательных представителях этой фигуры? Есть ли у них какие-то свойства?

Свойства трапеции

Для решения задач могут пригодиться свойства трапеции. Они могут упростить доказательство или сократить вычисления. 

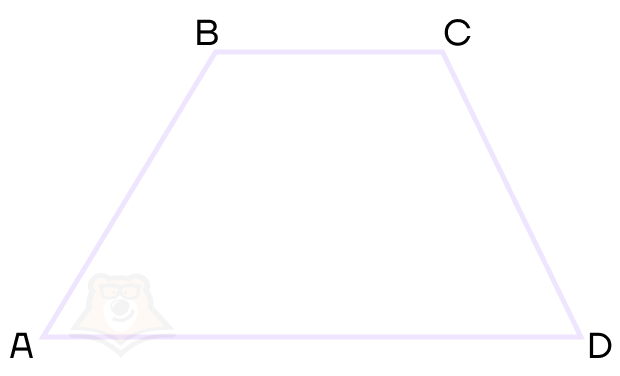
1 свойство. Сумма углов, которые прилежат к одной боковой стороне, равняется 180॰. 

Попробуем разобраться, почему это так. Вспомним углы при параллельных прямых и секущей, в нашем случае параллельные прямые — основания, а секущие — боковые стороны. Подробнее про углы при параллельных прямых можно прочесть в этой статье.

Углы ABC и BAD, а также углы BCD и ADC — односторонние углы при параллельных прямых, а следовательно, их сумма равняется 180°. 

Получаем, что ∠ABC + ∠BAD = ∠BCD + ∠ADC = 180॰.

2 свойство. Биссектриса угла трапеции отсекает равнобедренный треугольник.
Докажем это. Проведем в трапеции ABCD биссектрису DE.

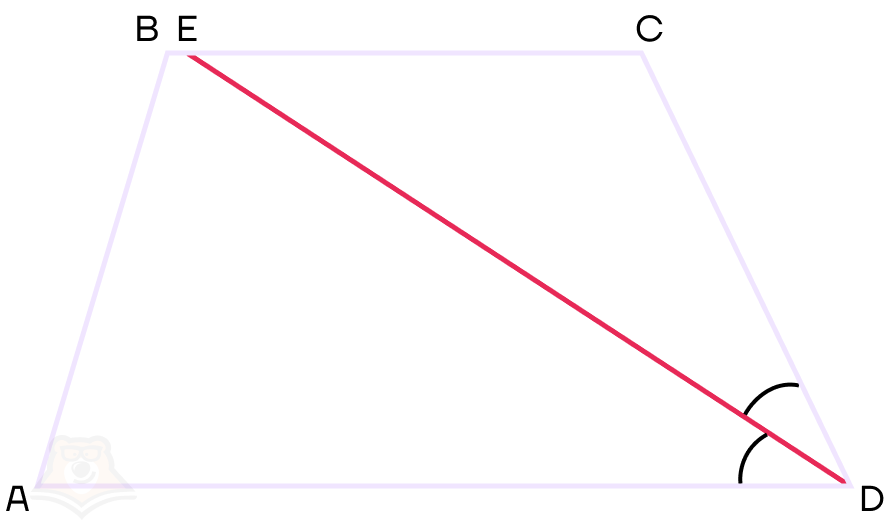
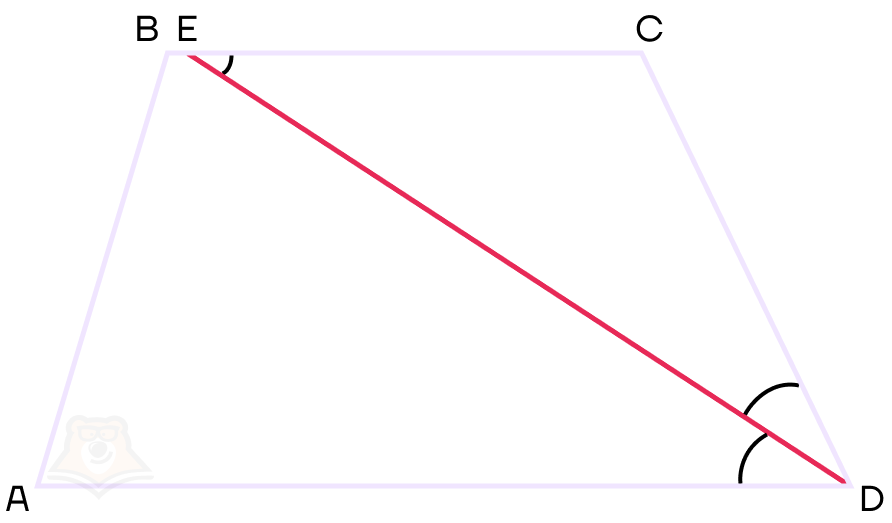
Пусть угол ADC равняется 2a. Поскольку DE — биссектриса, то ∠EDA = ∠EDC = a. 

Рассмотрим углы ADE и DEC. Это накрест-лежащие углы при параллельных прямых, а значит выполняется равенство ∠DEC = ∠ADE = a = ∠EDC. В равнобедренном треугольнике углы при основании  равны, следовательно, ЕС = CD. 

3 свойство. Треугольники, которые образованы диагоналями трапеции и основаниями, подобны. 

Докажем это. Углы AOD и BOC — вертикальные, а следовательно, они равны между собой. Углы CAD и ACB — накрест-лежащие при параллельных прямых, а следовательно, они равны между собой. Таким образом, мы получаем, что треугольник ВОС подобен треугольнику AOD по двум углам. 

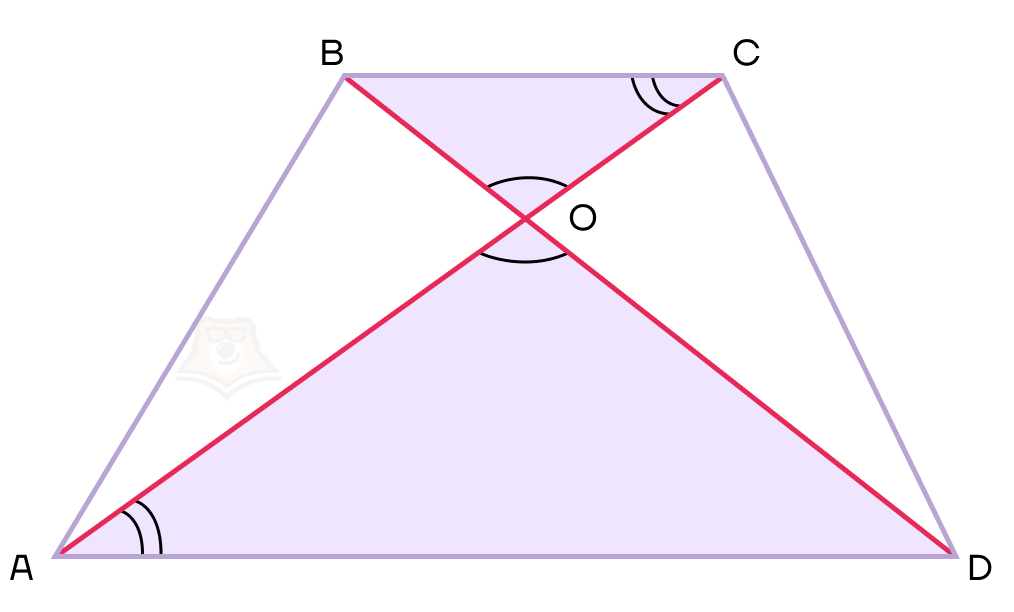
Данное свойство будет полезно для решения задач первой и второй части ОГЭ и ЕГЭ по математике. В качестве примера рассмотрим задачу №15 из ОГЭ по математике.

Задание. Диагонали AC и BD трапеции ABCD  с основаниями AD и BC пересекаются в точке O, BC = 5, AD = 9, BD = 21. Найдите OD.

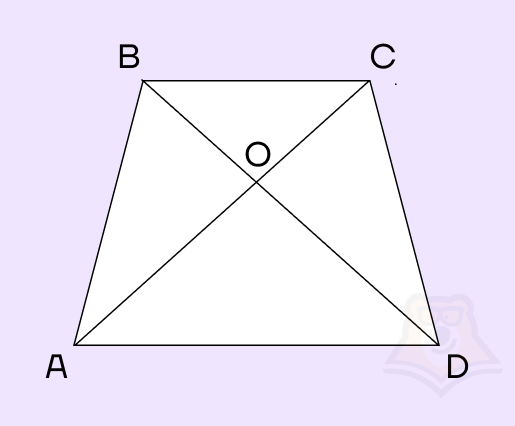
Решение. Рассмотрим \(AOD\) и \(COB\):

\(∠AOD=∠COB\) (так как эти углы являются вертикальными)
\(∠OAD=∠OCB\) (накрест лежащие углы при \(AD॥ BC\) и секущей \(AC)\)

Получается, что \(\Delta AOD\) подобен \(\Delta COB\) по двум углам.

Из подобия треугольников следует, что все их сходственные стороны пропорциональны друг другу:

\(\frac{AO}{OC}=\frac{OD}{OB}=\frac{AD}{BC}\)

Нас интересует отношение сторон \(BO\) и \(OD, BC\) и \(AD\):

\(\frac{OD}{OB}=\frac{AD}{BC}\)

Подставив известные нам значения, получаем: 

\(\frac{OD}{OB}=\frac{9}{5}\)


При этом мы знаем, что \(BD=21\), и что отрезок \(BD\) разбит точкой \(O\) на отрезки \(BO\) и \(OD\).


Значит, 

\(BD=BO+OD\)

Поскольку \(\frac{OD}{OB}=\frac{9}{5}\), давайте примем \(OD\) равным \(9x\), тогда \(BO\) будет равен \(5x\).Подставим эти значения в равенство выше и получим:

\(21=5x+9x\)
\(21=14x\)
\(x=\frac{21}{14}\)
\(x=\frac{3}{2}\)
\(x=1,5\)

Следовательно, 

\(OD=9x=9*1,5=13,5\)

Ответ: 13,5

4 свойство. Треугольники, образованные диагоналями трапеции и боковыми сторонами, имеют равную площадь. 

Докажем это. В этот раз доказательство будет чуть объемнее. 

В доказательстве к третьему свойству трапеции мы установили, что треугольники \(BOC\) и \(AOD\) — подобные. Следовательно, выполняются отношения \(\frac{CO}{OA} = \frac{BO}{OD}\). Немного преобразуем равенство: \(CO * OD = OA * BO\). 

Теперь рассмотрим углы \(АОВ\) и \(COD\) — вертикальные, следовательно, они равны между собой. Синусы равных углов также равны, следовательно, \(sinAOB = sinCOD\). 

Найдем площади треугольников \(АОВ\) и \(COD\), для этого воспользуемся формулой \(S = \frac{1}{2} * a * b * \sin a\). 

\(S_{AOB} = \frac{1}{2} * OB * AO * \sin \angle AOB\)
\(S_{COD} = \frac{1}{2} * CO * OD * \sin \angle COD\)

Таким образом, мы можем сделать вывод, что S_AOB = S_COD. 

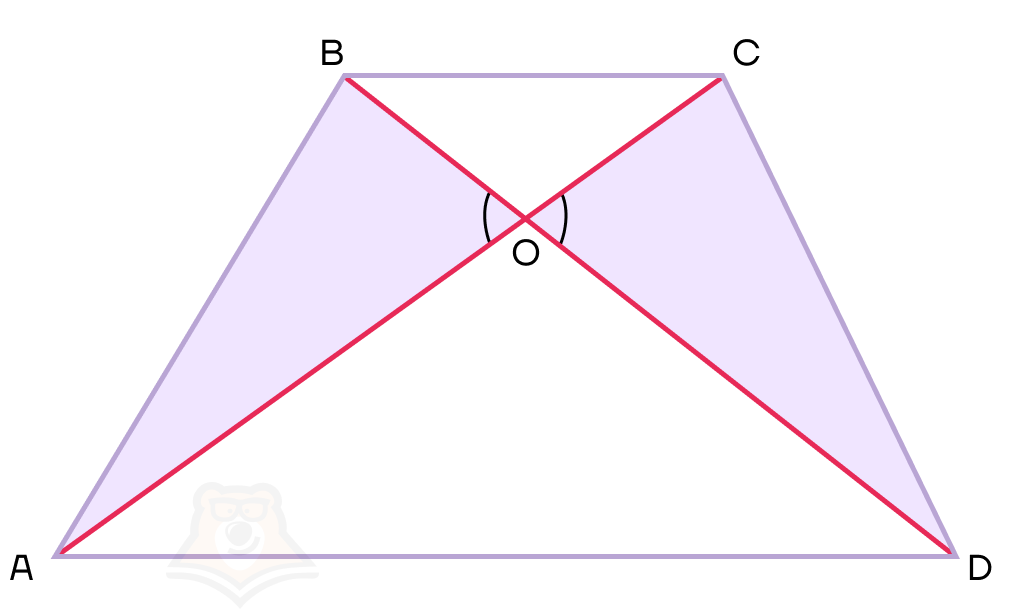
5 свойство. Отрезок, соединяющий середины диагоналей трапеции равен полуразности оснований.

Попробуем доказать.

Рассмотрим трапецию ABCD. Пусть M — середина диагонали AC, N — середина диагонали BD, K — середина боковой стороны CD.

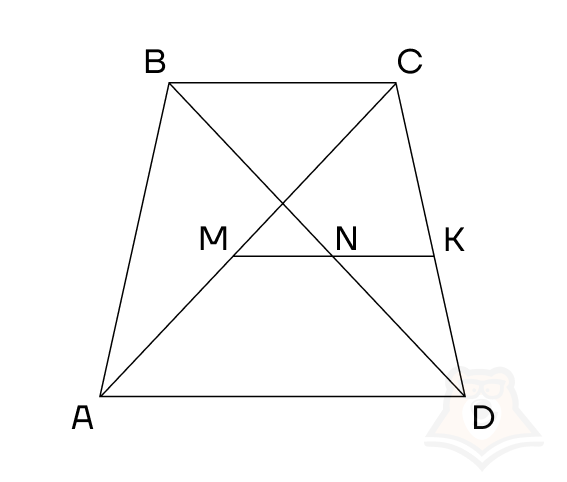
Тогда получается, что MK — средняя линия треугольника ACD, так как M — середина AC, K — середина CD. Значит, MK параллелельна AD и равна ее половине:

\(MK ‖ AD\)
\(MK=\frac{AD}{2}\)

Аналогично, KN — средняя линия треугольника BCD\(\Rightarrow\)

\(KN ‖ BC\)
\(KN=\frac{BC}{2}\)

Важно заметить, что \(MK ‖ AD\), при этом \(BC ‖ AD \Rightarrow MK ‖ BC\) (две прямые, параллельные третьей прямой, параллельны), \(KN ‖ BC\). Получается что точки M, N, K лежат на одной прямой, поскольку через точку K можно провести одну и только одну прямую, параллельную BC.

Раз эти точки лежат на одной прямой, выходит, что

\(MN=MK-NK=\frac{AD}{2}-\frac{BC}{2}=\frac{AD-BC}{2}\)

Мы поговорили о свойствах трапеции, которые помогут вам при решении разных задач. Но все ли это, что мы можем сказать про эту фигуру? Или у нее есть еще какие-то секреты?

Вписанная и описанная трапеция

Вписанная в окружность трапеция — это трапеция, все вершины которой лежат на окружности. 

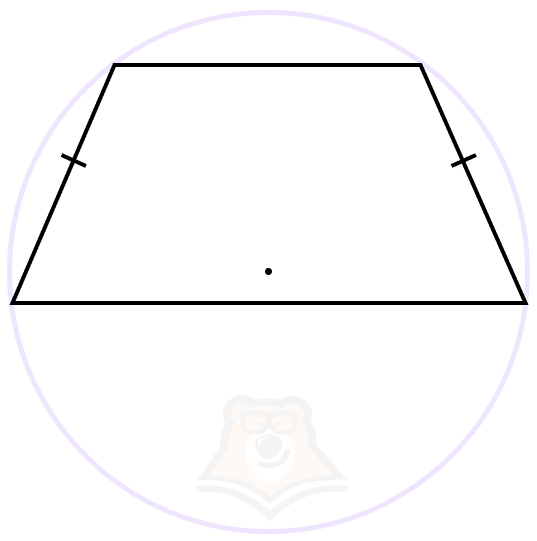
Какие трапеции можно вписать в окружность или описать вокруг окружности? Вспомним, что в трапецию можно вписать только тот четырехугольник, в котором сумма противоположных углов равняется 180°. Для трапеций это условие выполняется только в том случае, если трапеция равнобедренная.  Описать окружность можно только вокруг трапеции, сумма оснований которой равна сумме боковых сторон.

Следовательно, в окружность можно вписать только равнобедренную трапецию.

Однако это свойство работает и в обратную сторону: если в окружность вписана трапеция, то она обязательно будет равнобедренной.

Есть три варианта, где будет лежать центр окружности. Рассмотрим их.

1. Центр окружности будет лежать «внутри трапеции», если диагональ образует с боковой стороной острый угол.

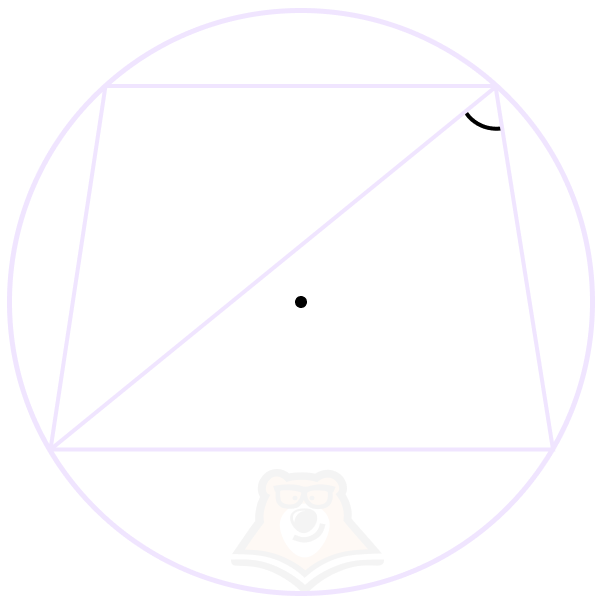
2. Центр окружности будет лежать на большем основании, если диагональ образует с боковой стороной прямой угол. 

3. Центр окружности будет лежать “вне” трапеции, если диагональ образует с боковой стороной тупой угол. 

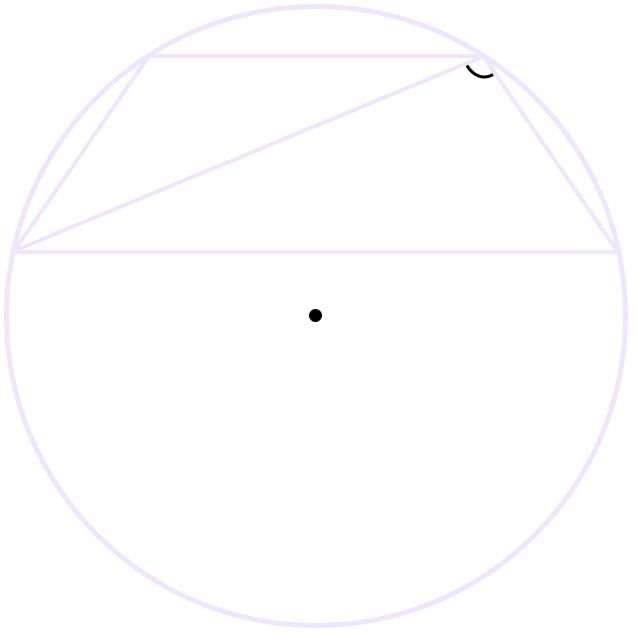
Задачи на вписанные в окружность трапеции могут встретиться как в тестовых заданиях ОГЭ и ЕГЭ, так и в более сложных примерах с развернутым ответом. Поэтому очень важно уметь пользоваться всеми свойствами вписанных трапеций. Рассмотрим, например, задание №1 ЕГЭ по профильной математике.

Задание. В равнобедренной трапеции ABCD основание AD равно 16, а основание BC равно 12. Радиус окружности, описанной около этой трапеции равен 10. Центр окружности, лежит внутри трапеции. Найдите высоту этой трапеции.

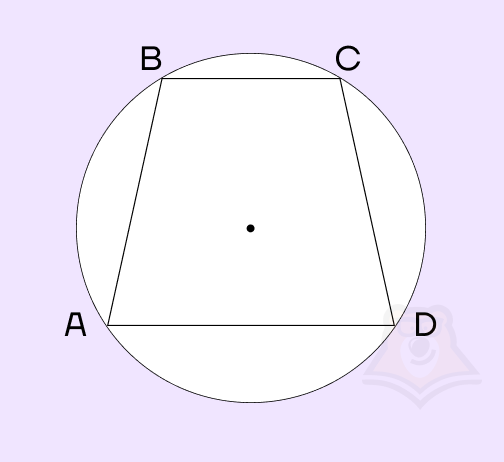
Решение. Для решения данной задачи проведем дополнительные построения. Пусть \(O\) — центр окружности. Проведем радиусы окружности \(OA, OB, OC, OD\) и высоту трапеции KH, проходящую через центр окружности.

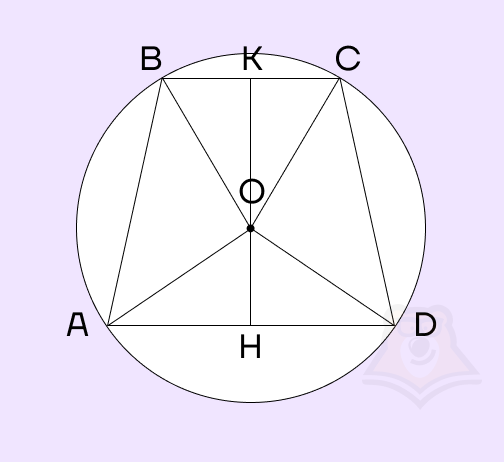
Рассмотрим \(\Delta AOD, AO=OD\), так как это радиусы окружности, значит \(\Delta AOD\) — равнобедренный, \(AD\) — основание этого треугольника. 

\(OH \bot AD\), значит, \(OH\) — высота \(\Delta AOD\), проведенная к основанию. В равнобедренном треугольнике высота, проведенная к основанию, является также медианой и биссектрисой \(⇒ OH\) — медиана, \(H\) — середина \(AD\), то есть

\(AH=HD=\frac{1}{2}AD\)
\(AH=\frac{1}{2}*16=8\)

Далее рассмотрим \(\Delta AOH\):

\(OH \bot AH ⇒ ∠H=90°\), значит, \(AOH\) — прямоугольный.

\(AO=10\) (радиус окружности)
\(AH= 8\)

Воспользуемся теоремой Пифагора, в которой говорится, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов:

\(AO^2=OH^2+AH^2\)
\(OH^2=AO^2-AH^2\)
\(OH^2=10^2-8^2=100-64=36\)
\(OH=6\)

Аналогично рассмотрев \(\Delta BOC\), получаем:

\(BK=KC=\frac{1}{2}BC\)
\(BK=\frac{1}{2}*12=6\)

Далее запишем теорему Пифагора для BOK:

\(OK^2=OB^2-BK^2\)
\(OK^2=10^2-6^2=100-36=64\)
\(OK=8\)

Высота \(KH\) разбита точкой \(O\) на отрезки \(KO\) и \(OH\), значит

\(KH=KO+OH\)
\(KH=8+6=14\)

Ответ: 14

Описанная вокруг окружности трапеция — это трапеция, все стороны которой являются касательными к окружности. 

Вспомним, что окружность можно вписать в четырехугольник только в том случае, если суммы его противоположных сторон равны. Следовательно, в трапецию можно вписать окружность только в том случае, если сумма оснований равна сумме боковых сторон. 

Также важно заметить, что в описанной трапеции высота будет равна диаметру окружности.

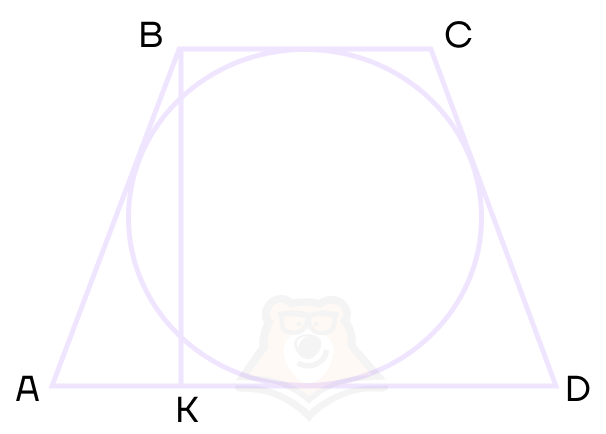
Рассмотрим важное свойство, которое может облегчить вам решение сложных задач.
Радиус окружности, вписанной в трапецию, равен среднему геометрическому отрезков, на которые делит боковую сторону окружность:

\(r=\sqrt{ab}\)

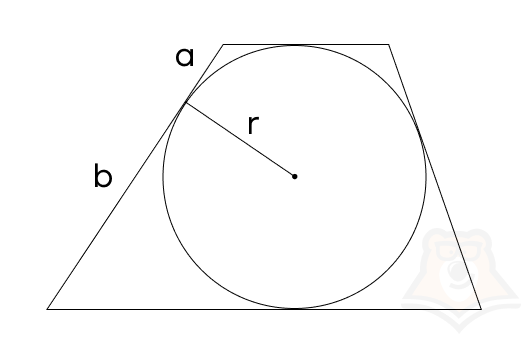
Давайте докажем эту теорему.

Рассмотрим трапецию ABCD и вписанную в нее окружность с центром O. Пусть K — точка касания стороны AB к окружности. Проведем отрезки OA и OB. 

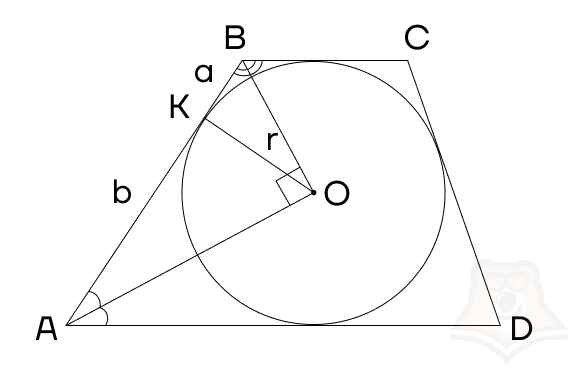
Центр, вписанной в трапецию окружности, лежит в точке пересечения биссектрис углов. Значит, OB и OA — биссектрисы. Поскольку сумма углов ∠BAD и ∠ABC равна 180°, то сумма их половинок ∠BAO и ∠ABO равна 90°. Значит, из суммы углов треугольника, которая равна 180°, находим, что
\(∠AOB=180°-(∠BAO+∠ABO)=180°-90°=90°\).

То есть треугольник ABO — прямоугольный. OK — радиус, проведенный в точку касания ⇒ OK⊥AB (если вы еще не сталкивались с этим свойством касательной, рекомендуем вам познакомиться со статьей «Касание к окружности»), то есть OK — высота треугольника ABO, проведенная из вершины прямого угла. Значит, мы можем воспользоваться свойством пропорциональных отрезков в прямоугольном треугольнике:

\(OK=\sqrt{BK*AK}\)
\(r=\sqrt{ab}\)

Подведем итог

В окружность можно вписать только равнобедренную трапецию. 

Описать окружность можно только вокруг трапеции, сумма оснований которой равна сумме боковых сторон. 

В предыдущих пунктах мы рассмотрели довольно большое количество разных фактов о трапеции и формул для решения задач, пожалуй, было бы неплохо структурировать эту информацию в небольшую памятку, которой будет удобно пользоваться.

Основные формулы для трапеции

Ниже приведена таблица с основными формулами для решения задач с трапециями. Эти формулы обязательно знать, поскольку с их помощью можно решить большинство задач, в которых встречается трапеция. 

Сегодня мы познакомились с одним из представителей четырехугольников — трапецией. Узнали какие свойства и формулы помогут вам при решении задач, а также рассмотрели как трапеция взаимодействует с окружностью. А что из себя представляет окружность? Какие элементы есть у нее? И причем здесь градусы? Об этом и многом другом вы можете узнать в статье «Окружность».

Фактчек

• Трапеция — это четырехугольник, две стороны которого параллельны, а две другие нет. Параллельные стороны называются основаниями, а непараллельные — боковыми сторонами. 
• Средняя линия трапеции проходит через середины боковых сторон, параллельна основаниям и равна их полусумме. 
• Трапеции бывают произвольными, равнобедренными и прямоугольными. У равнобедренных трапеций боковые стороны равны. У прямоугольных трапеций одна из боковых сторон перпендикулярна основаниям. 
• В окружность можно вписать только равнобедренную трапецию. Вписать окружность в трапецию можно только в том случае, если сумма боковых сторон равна сумме оснований. 

Проверь себя

Задание 1. 
Какие бывают виды трапеций?

1. Трапеции не делятся на виды.
2. Только прямоугольные.
3. Прямоугольные и равнобедренные.
4. Произвольные, прямоугольные и равнобедренные. 

Задание 2. 
Основания трапеции равны 13 и 3. Чему равна средняя линия трапеции? 

1. 16
2. 7,5
3. 1,5
4. 8

Задание 3. 
В трапецию вписана окружность. Сумма боковых сторон равна 20. Чему равна средняя линия трапеции? 

1. 10
2. 20
3. 5
4. 40

Задание 4.
В трапецию вписана окружность. Сумма оснований равна 15. Чему равен периметр трапеции? 

1. 15
2. 7,5
3. 45
4. 30 

Задание 5. 
Средняя линия трапеции равна 4, высота равна 7. Найдите площадь трапеции. 

1. 14
2. 28
3. 32
4. 7

Ответы: 1. — 4 2. — 4 3. — 1 4. — 4 5. — 2