Пирамида
На этой странице вы узнаете
- Какая высота у пирамиды Хеопса и как ее можно измерить?
- Почему у треугольной пирамиды есть собственное название?
- Как рассчитать ингредиенты для тортика в виде пирамиды?
С самого раннего детства мы слышим о пирамидах. Нас манят тайны и загадки древних египетских пирамид. Дети и взрослые строят их в песочнице или на пляже. Секретам этой геометрической фигуры посвящена наша статья.
Пирамида
Зная, как выглядит пирамида, можем ли мы описать, что это такое? Это точно объемная фигура, у которой есть основание и боковые грани. При этом мы не можем назвать ее призмой. Ведь по определению призмы в основаниях лежат равные параллельные многоугольники, а у пирамиды только одно основание, на котором она стоит.
Так что такое пирамида? Посмотрим внимательно: внизу лежит многоугольник. А из всех вершин этого многоугольника выходят отрезки, которые пересекаются в какой-то одной точке пространства. Это и есть краткое описание пирамиды. Теперь дадим точное определение.
Пирамида — это многогранник, в основании которого лежит многоугольник, а остальные грани — треугольники с общей вершиной.
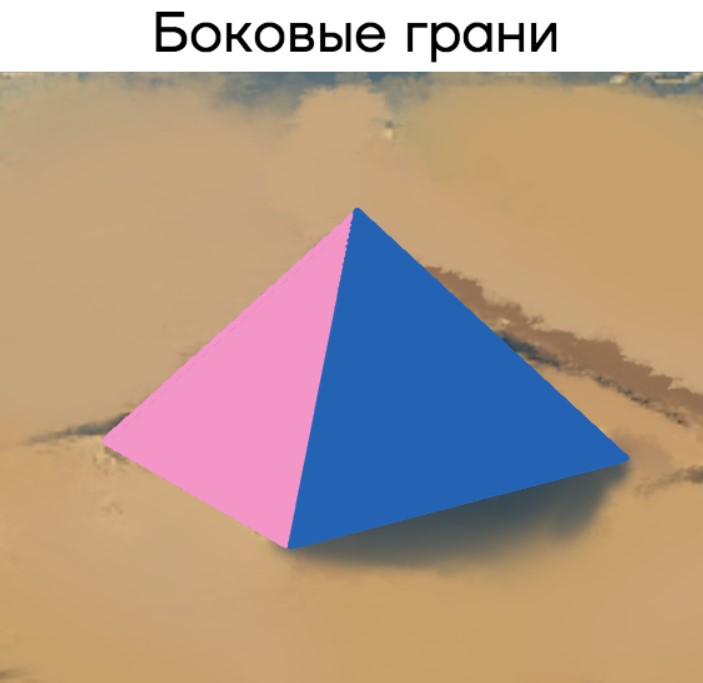
Вспомним египетские пирамиды. Обычно в основании, на котором и стоят пирамиды, лежит четырехугольник, а вот все «стены» являются треугольниками, что полностью подходит под определение. В математике стены пирамиды будут называться боковыми гранями.
Еще раз посмотрим на египетские пирамиды. Нам хорошо видна самая высокая точка — вершина.
Вершина пирамиды — общая точка боковых граней, которая не принадлежит плоскости основания.
Отрезки, которые соединяют вершины многоугольника, лежащего в основании, и вершину пирамиды — это боковые ребра. Она как бы ограничивают «бока» пирамиды.
Стороны многоугольника в основании будут называться ребрами основания.
| Какая высота у пирамиды Хеопса и как ее можно измерить? Все просто: нужно найти расстояние от вершины пирамиды до ее основания. А это — расстояние от точки до плоскости. Чтобы измерить высоту пирамиды, необходимо опустить из ее вершины перпендикуляр к плоскости основания. Например, высота пирамиды Хеопса на сегодняшний день составляет 138,75 метра (изначально была 146,6 метра). |

Высота пирамиды — перпендикуляр, проведенный из вершины пирамиды к плоскости основания.
Чуть подробнее про расстояние от точки до плоскости можно прочесть в статье «Расстояния между фигурами».
Точка, в которой высота пирамиды пересечет ее основание, называется основанием высоты.
Стоит заметить, что высота может опуститься в совершенно разные точки на основании. Основание высоты может располагаться:
- На основании пирамиды.
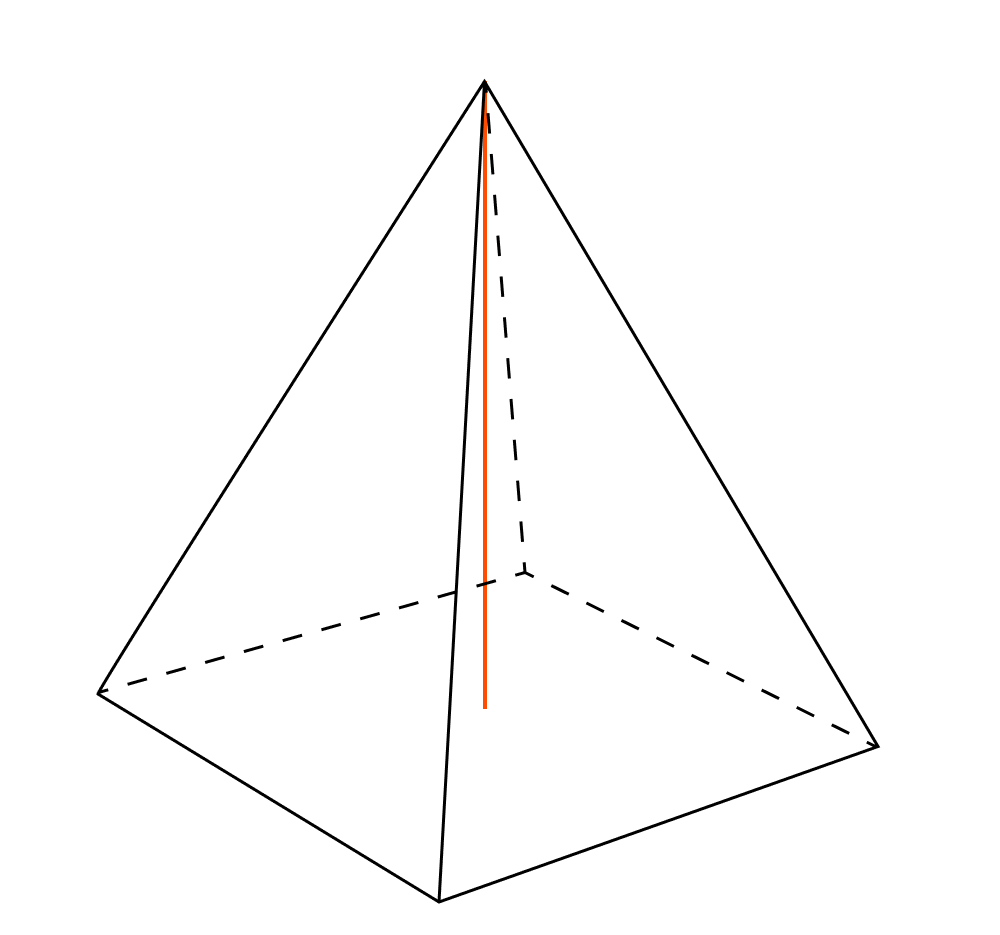
- На стороне основании пирамиды.
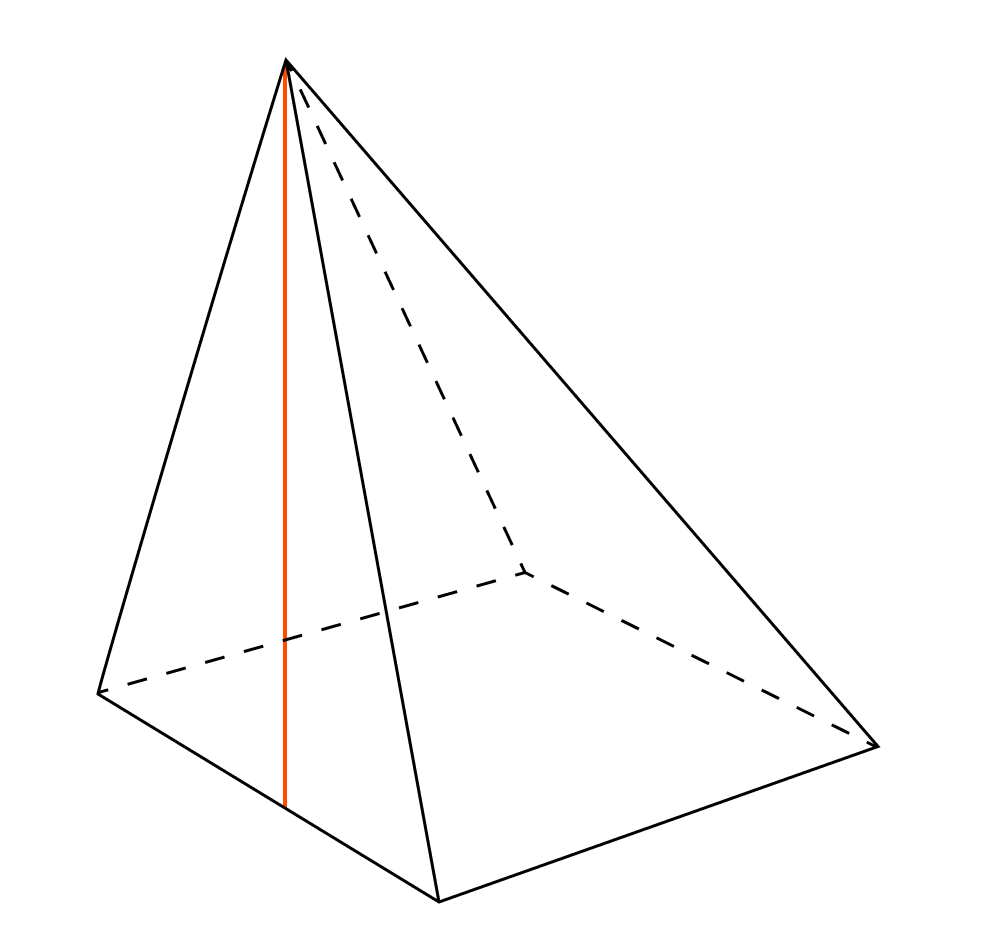
- За пределами основания пирамиды.
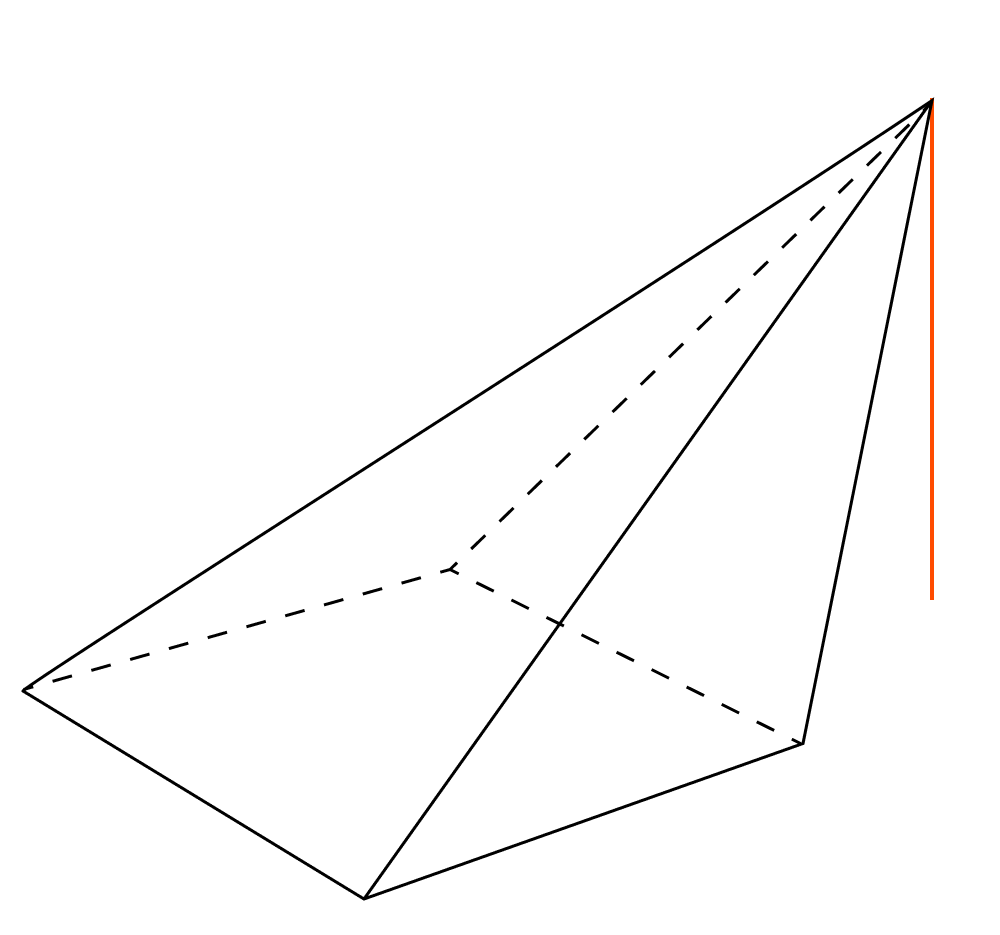
Какие бывают пирамиды? Мы знаем, в египетских пирамидах в основании лежит четырехугольник. А если в основании будет лежать треугольник, шестиугольник, пятнадцатиугольник и так далее?
Пирамиды называются по многоугольнику, который лежит в основании.
- В основании треугольной пирамиды лежит треугольник.
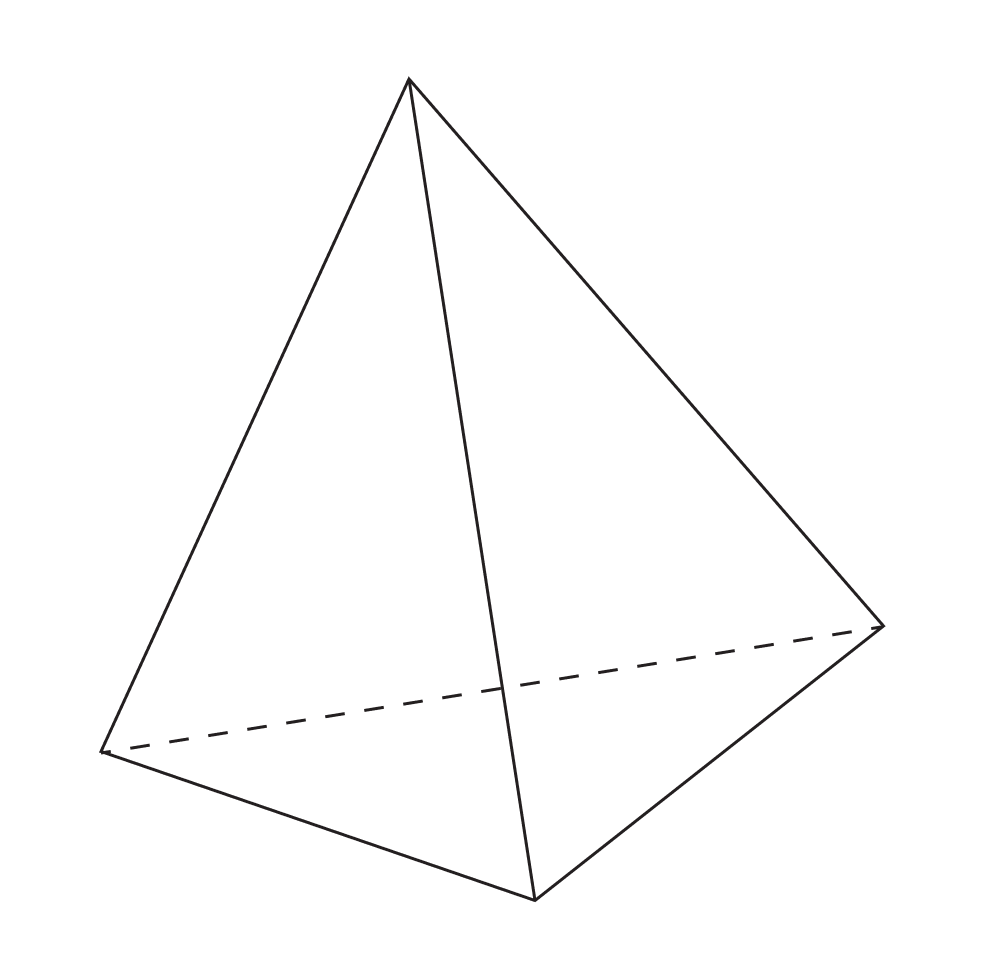
| Почему у треугольной пирамиды есть собственное название? Такие пирамиды называются тетраэдром, а все грани такой пирамиды будут треугольниками. Этой пирамиде дали свое имя, поскольку основанием в ней может быть любая грань. |
- В основании четырехугольной пирамиды лежит четырехугольник.
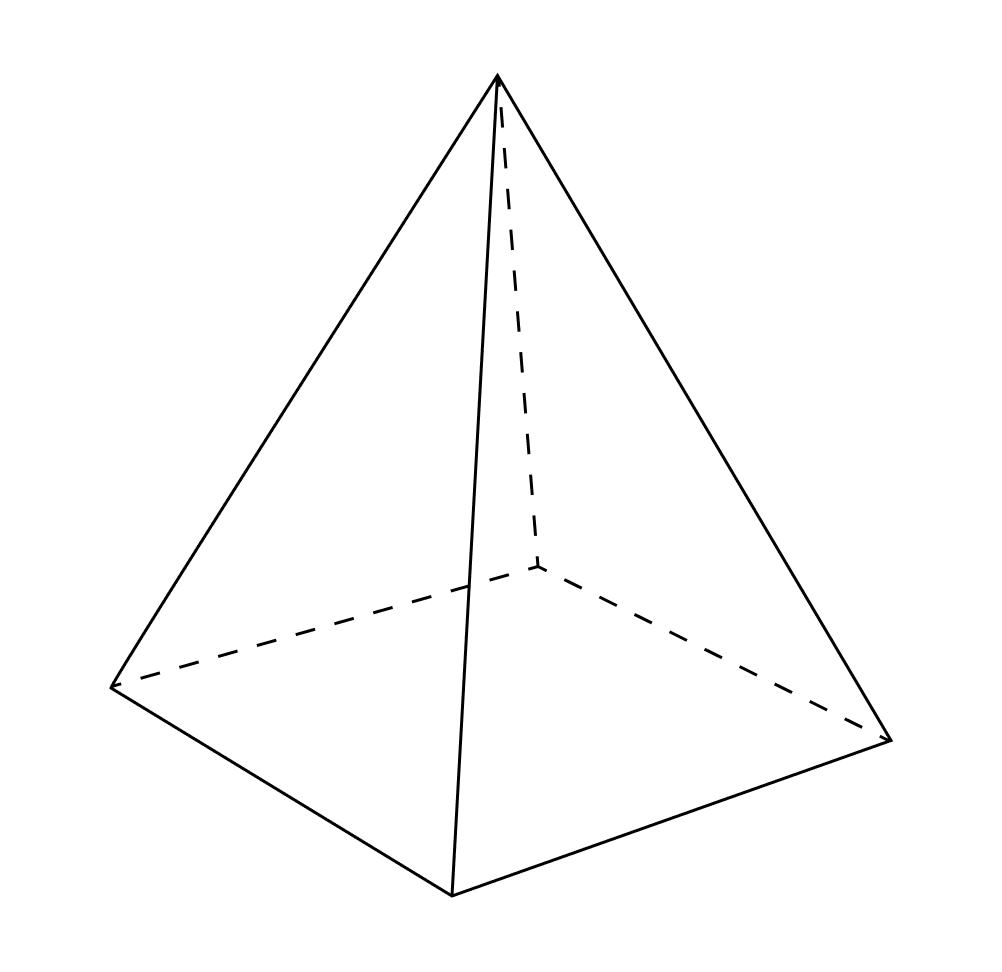
- В основании шестиугольной пирамиды лежит шестиугольник.
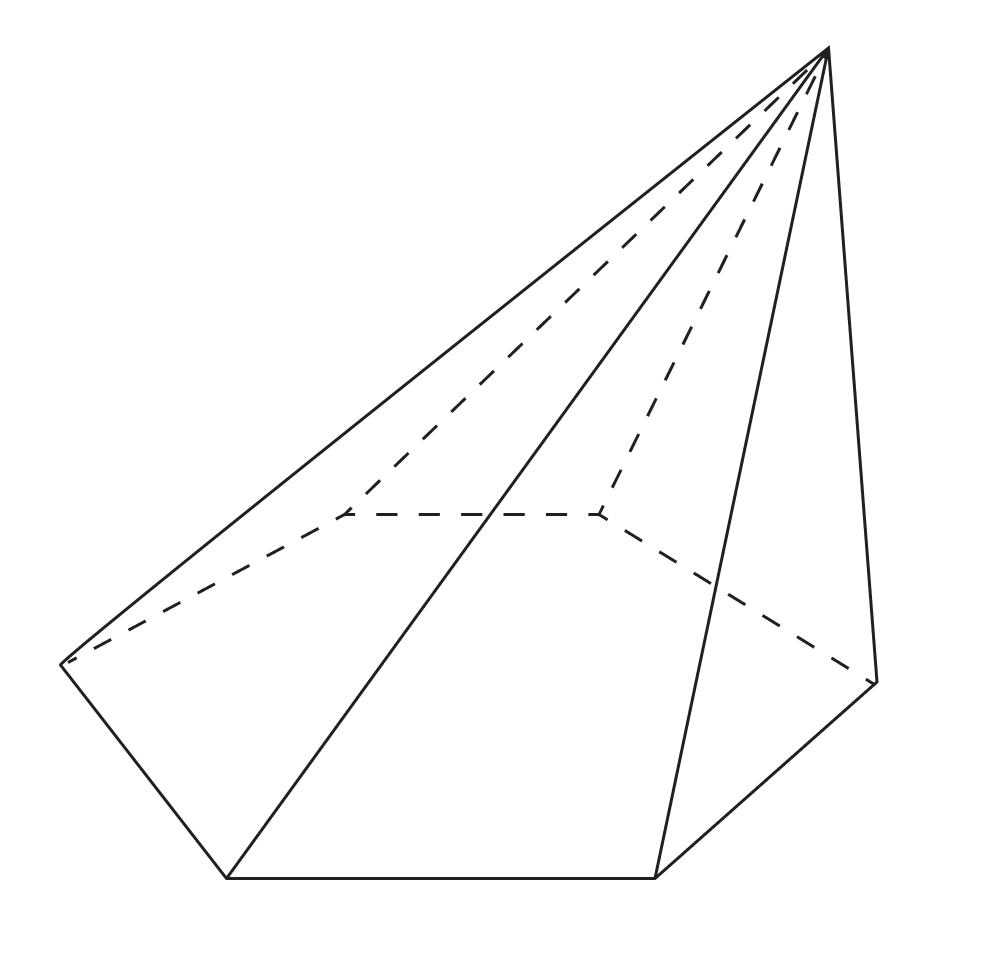
Правильная пирамида
Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а вершина проецируется в центр этого многоугольника.
Разберем фразу «вершина проецируется в центр этого многоугольника». Если мы проведем высоту пирамиды, то основание высоты будет лежать в центре основания пирамиды.
Например, центр правильного треугольника будет лежать в точке пересечения биссектрис, медиан, высот и серединных перпендикуляров. Центры квадрата и шестиугольника — точки пересечения их диагоналей.
В правильном многоугольнике центр будет равноудален от всех его вершин. Следовательно, и основание высоты будет равноудалено от всех вершин основания пирамиды.
Рассмотрим свойства правильной пирамиды.
Свойство 1. Все боковые ребра правильной пирамиды равны.
Давай разбираться, почему это работает.
В правильной четырехугольной пирамиде проведем высоту, а основание высоты соединим с вершинами квадрата в основании. Таким образом, у нас получится несколько прямоугольных треугольников. Отметим два из них голубым и зеленым цветом.
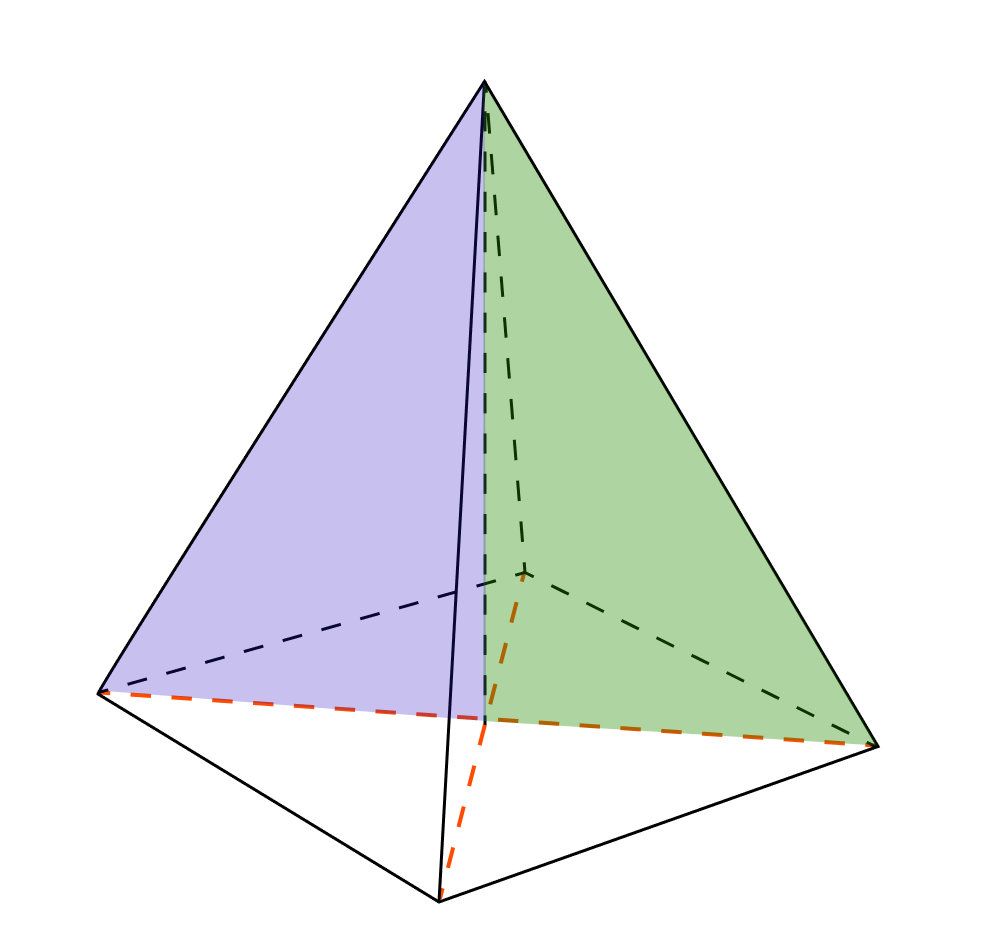
Заметим, что эти треугольники равны, поскольку у них равны катеты. Катеты, лежащие в основании пирамиды, являются половинами диагонали квадрата (диагонали квадрата точкой пересечения делятся пополам), а катеты, образованные высотой, совпадают. Следовательно, в равных треугольниках равны и гипотенузы.
Таким же образом можно проверить равенство всех боковых ребер в пирамиде.
Свойство 2. Все боковые грани являются равнобедренными треугольниками, которые равны между собой.
Основания боковых граней будут равны между собой, поскольку в основании пирамиды лежит правильный многоугольник. А в предыдущем свойстве мы доказали, что боковые ребра также равны между собой.
Следовательно, в боковых гранях лежат равнобедренные треугольники, которые равны между собой по трем сторонам.
Свойство 3. Все высоты, проведенные в боковых гранях правильной пирамиды, равны.
Мы уже доказали, что все боковые грани правильной пирамиды — равные треугольники, а значит, и все их элементы равны между собой, в том числе высоты.
В боковых гранях правильной пирамиды можно провести высоты.
Апофема — высота, проведенная в боковой грани правильной пирамиды из вершины.
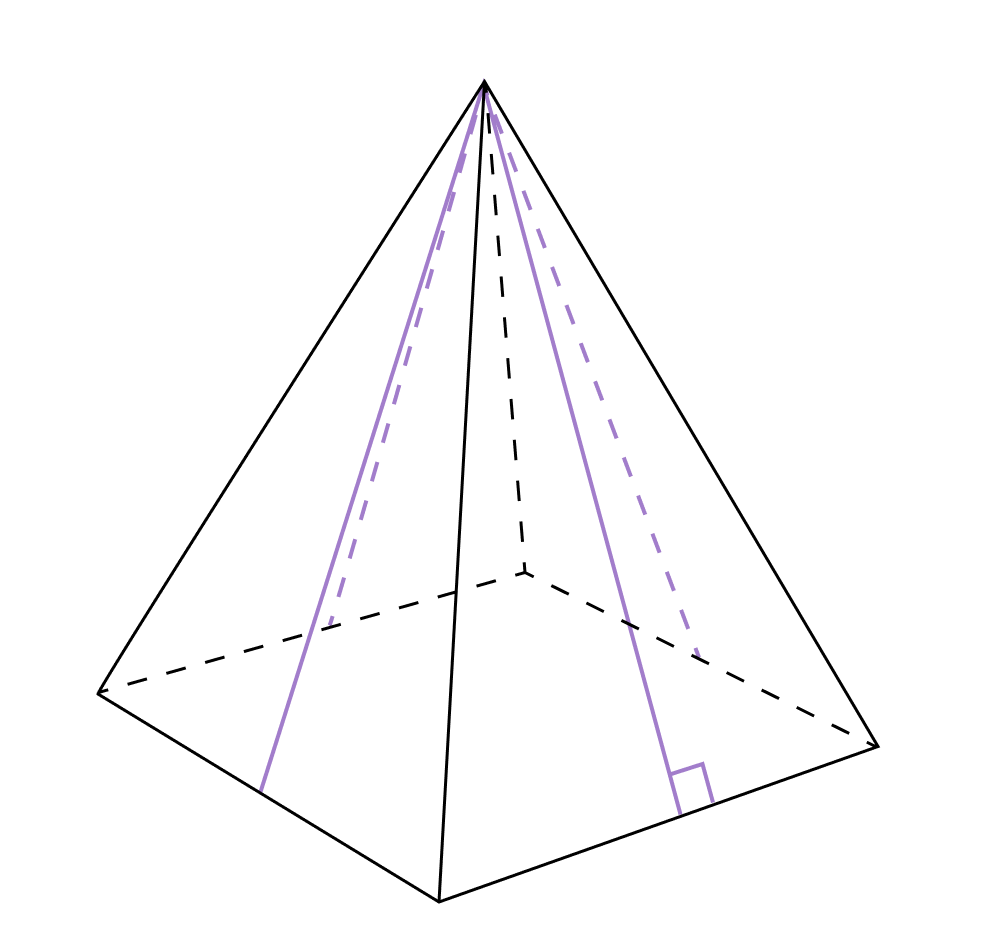
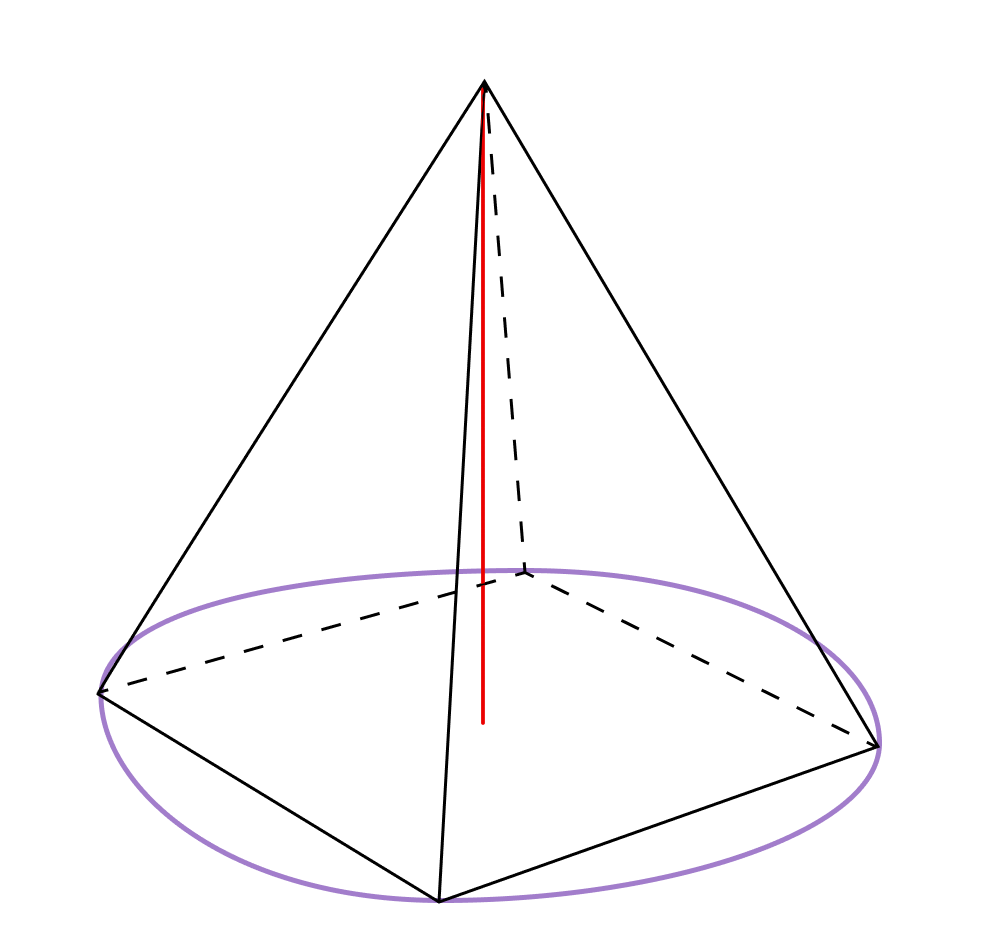
Свойство 4. Вершина пирамиды проектируется в центр описанной возле основания окружности.
Как уже было сказано выше, вершина пирамиды проектируется в центр правильного многоугольника, который равноудален от всех вершин этого многоугольника. Если описать окружность вокруг этого многоугольника, где будет лежать ее центр? В точке, которая равноудалена от всех точек окружности. А значит, и в точке, которая равноудалена от всех вершин вписанного многоугольника.
Свойство 5. Все боковые ребра правильной пирамиды имеют равные углы с плоскостью основания.
Это тоже достаточно легко доказать. Возьмем такой же рисунок, как и в свойстве 1. Обратим внимание, что все прямоугольные треугольники будут равны, тогда равны и их углы. Следовательно, и углы, образованные боковыми ребрами пирамиды и диагоналями квадрата будут равны.
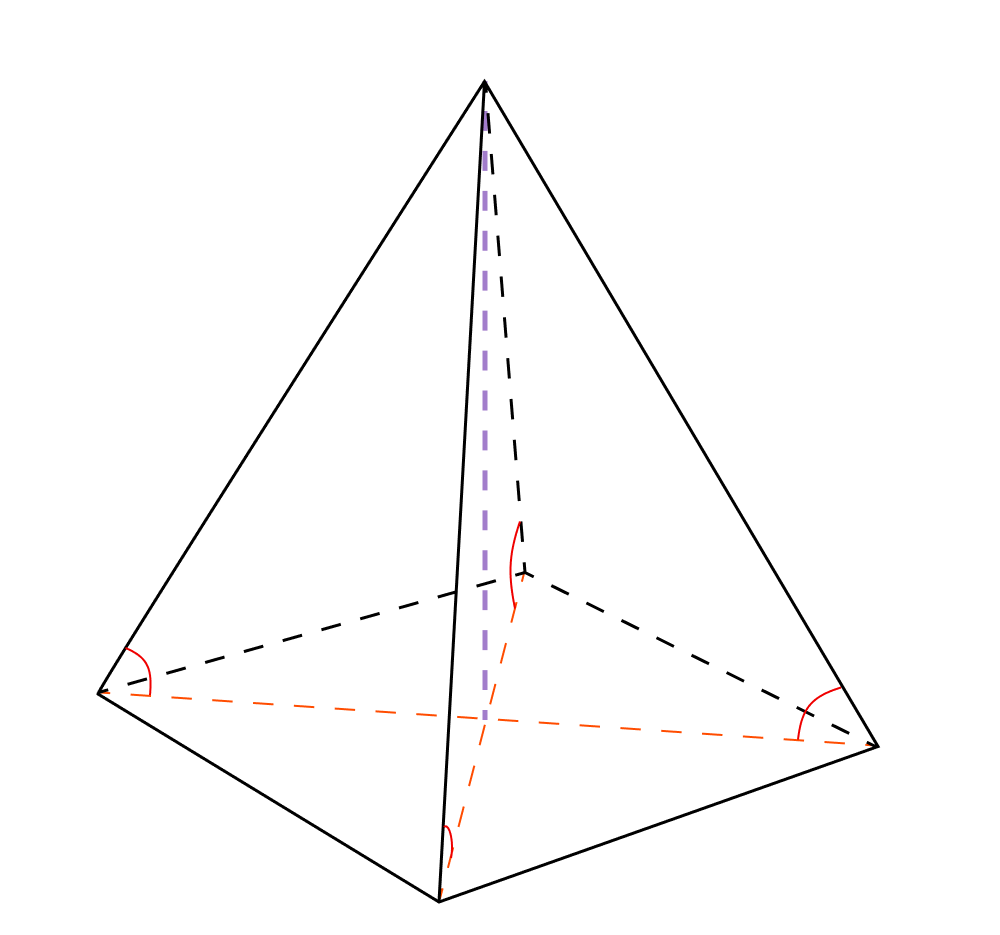
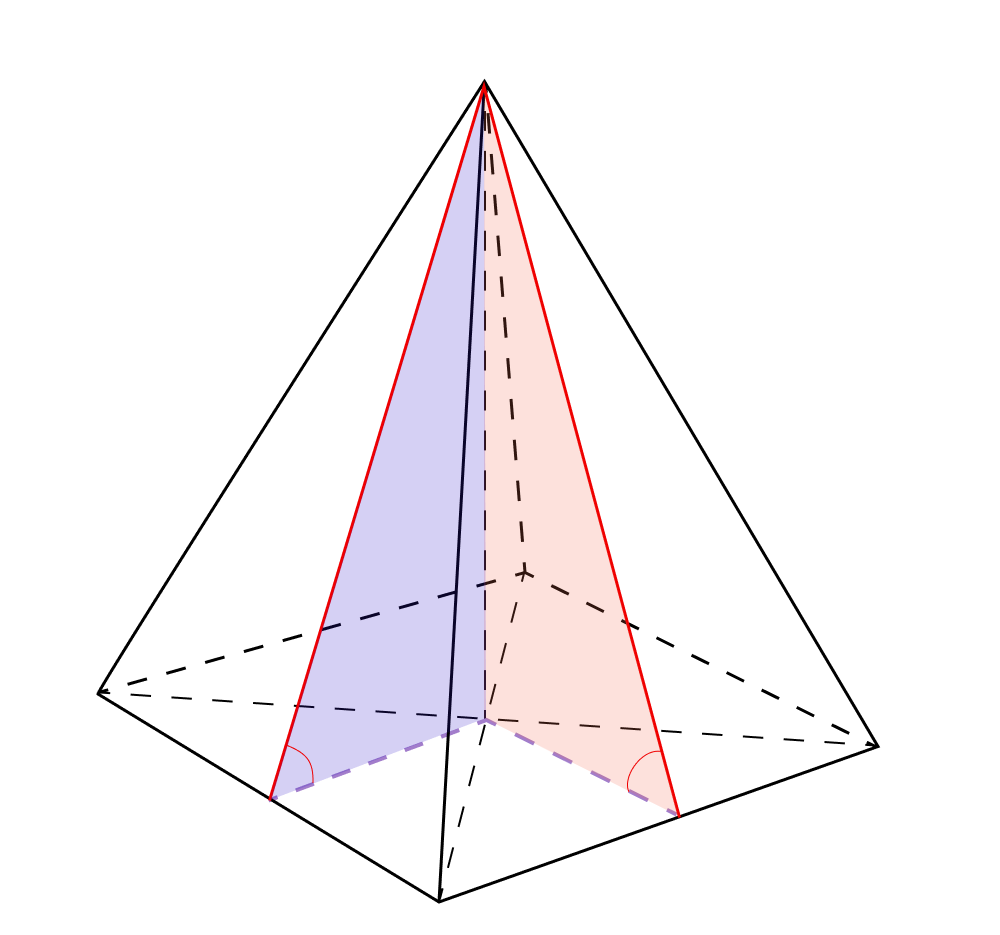
Свойство 6. Все боковые грани правильной пирамиды имеют равные двугранные углы с плоскостью основания.
Боковые грани и плоскость основания — пересекающиеся плоскости. Угол между такими плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Подробнее про углы между плоскостями можно прочитать в статье «Углы в пространстве».
В правильной четырехугольной пирамиде опустим апофемы — они будут перпендикулярами к линии пересечения плоскостей в боковых гранях.
Поскольку в правильной призме боковые грани — равнобедренные треугольники, то апофема также будет делить ребро основания пополам.
В основании проведем перпендикуляры к точкам пересечения апофем и ребер основания. Поскольку эти точки — середины ребер основания, то перпендикуляры пройдут через центр квадрата.
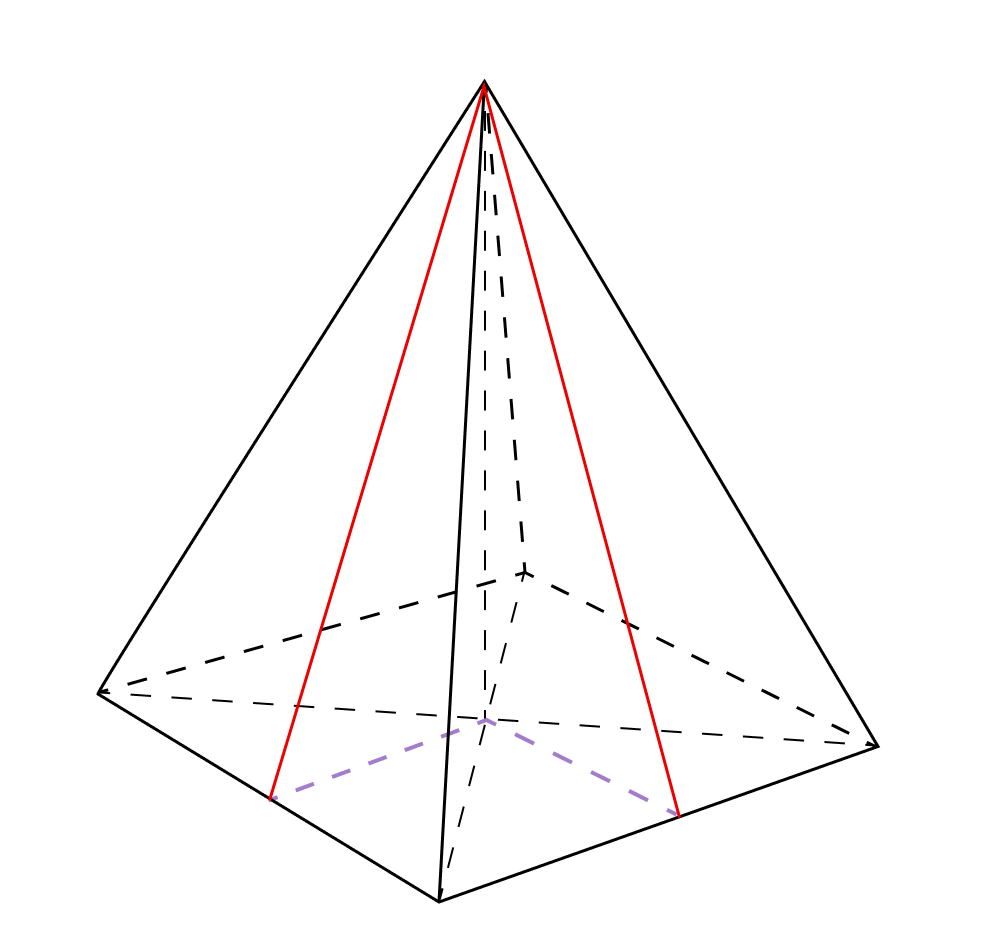
Заметим, что у нас снова получилось два равных по двум катетам прямоугольных треугольника. Прямые, соединяющие центр основания и точку пересечения апофем и ребер основания равны между собой и равняются половине стороны квадрата.
А в равных треугольниках равны и углы. Следовательно, углы между боковыми гранями и основанием равны. Аналогично можно проверить все оставшиеся углы.
Формулы для пирамиды
Предположим, мы захотели приготовить очень вкусный и необычный тортик в форме пирамиды. Для этого нам нужны крем, коржи и начинка. Как рассчитать ингредиенты для тортика?

Начнем с коржиков и начинки. Допустим, что мы будем замешивать определенный объем теста, в которое уже будет включена начинка. После выпекания объем теста не изменится. Как найти, сколько теста нам нужно замешать?
Для этого нужно найти объем самой пирамиды.
Для всех пирамид существует одна общая формула, по которой можно найти объем. Разумеется, формулу можно преобразовывать под каждую конкретную пирамиду, а вот общая формула выглядит следующим образом.
V=\frac{1}{3}S_{осн}*H | Где Sосн. — площадь основания; Н — высота. |
Допустим, мы хотим тортик, в основании которого будет лежать квадрат со стороной 15 см. А высоту возьмем 56 см. Тогда объем теста, который нужно замешать, будет равен:
V=\frac{1}{3}*15*15*56=4200см3 -или- 4,2 л.(1 литр равен 1000 кубических сантиметров).
Если внимательно посмотреть на формулу, можно заметить, что объем пирамиды равен трети объема призмы с таким же основанием и высотой.
Мы сделали коржи и начинку и выпекли их. Теперь нам нужно покрыть тортик кремом. Пусть основание тортика и его стенки будут покрыты кремом разных цветов. Все равно нам придется замешать изначально одну основу, в которую уже позже добавим разные красители.
Для расчета объема крема нам нужно будет узнать площадь поверхности, которую он должен покрыть. А значит, узнать площадь поверхности пирамиды.
Для этого нужно сложить площади основания и боковых граней. Сумма площадей боковых граней будет называться площадью боковой поверхности пирамиды. Тогда получаем следующую формулу.
| Sпов. = Sосн. + Sбок. |
Для начала найдем площадь основания. Поскольку в нем лежит квадрат со стороной 15 см, то площадь основания равна 225 см2.
Далее вычислим площадь боковой поверхности. В произвольных пирамидах площадь боковой поверхности пришлось бы считать как сумму площадей всех граней и формула бы выглядела так:
| Sбок. = S1 + S2 +…+ Sn |
Однако в правильной пирамиде площадь боковой поверхности можно посчитать чуть проще, а именно воспользоваться формулой:
S_{бок}=\frac{1}{2}Pl| Где Р — периметр основания; l — апофема. |
Поскольку в правильной пирамиде все боковые грани — равные треугольники, то ее площадь можно найти следующим образом:
S_{бок}=\frac{1}{2}a_1l+\frac{1}{2}a_2l+...+\frac{1}{2}a_nl=\frac{1}{2}l(a_1+a_2+...+a_n)Где а1, а2, аn — стороны основания, сумма которых равна его периметру. Так и получается формула
S_{бок}=\frac{1}{2}PlПериметр основания в нашем тортике равен 4 * 15 = 60 см.
Найдем апофему. Для этого нужно выполнить дополнительные построения: провести высоту и из основания высоты провести перпендикуляр к любой из сторон. У нас получится прямоугольный треугольник. Отметим, что катеты в нем равны 56 и
\frac{15}{2}=7,5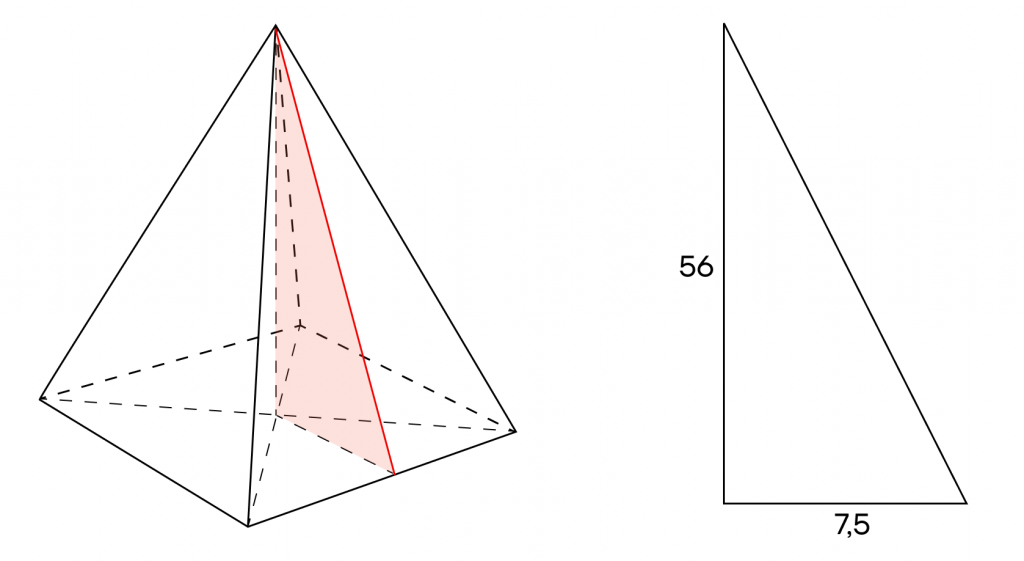
По теореме Пифагора найдем гипотенузу в треугольнике, она и будет апофемой. Получаем:
\sqrt{56^2+7,5^2}=\sqrt{3136+56,25}=\sqrt{3192,25}=56,5Осталось рассчитать площадь боковой поверхности.
S=\frac{1}{2}*60*56,5=1695см^2Следовательно, нам понадобится столько крема, чтобы покрыть площадь S = 1695 + 225 = 1920 см2, и из них 1695 квадратных сантиметров уйдет на стенки тортика, а 225 на основание.
| Как рассчитать ингредиенты для тортика в виде пирамиды? Для этого нам нужно найти: — Объем самого тортика. Так мы рассчитаем объем теста и начинки для него. — Площади боковой и полной поверхности пирамиды. Они нужны нам, чтобы рассчитать количество крема. Все эти формулы приведены выше. |
Усеченная пирамида
Мы испекли наш тортик и решили дать его попробовать друзьям. Чтобы не возиться с правильным разрезанием тортика и не сильно портить его внешний вид, мы просто срезали верхушку и отдали ее друзьям. Какой формы тортик у нас остался?
Такая форма называется усеченной пирамидой.
Усеченная пирамида — часть пирамиды, заключенная между основанием и параллельной ему плоскостью, которая как бы отрезает верхушку пирамиды.
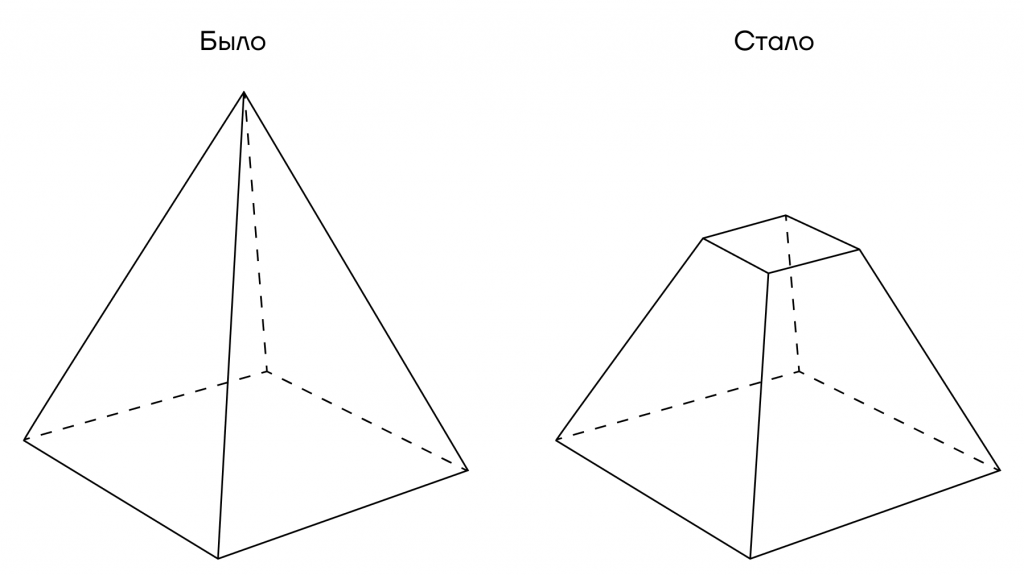
При этом названия элементов сохраняются, но добавляется еще одной основание — верхнее основание пирамиды.
Боковые грани в усеченной пирамиде из треугольников превращаются в трапеции.
Также немного меняется высота. В усеченной пирамиде она будет расстоянием между плоскостями верхнего и нижнего основания.
Высота усеченной пирамиды — перпендикуляр, опущенный из одного основания на другое.
Если срезать верхушку в правильной пирамиде, получится правильная усеченная пирамида.
Правильная усеченная пирамида — усеченная пирамида, полученная из правильной пирамиды сечением, которое проходит параллельно ее основанию.
Сохранится ли в правильной усеченной пирамиде апофема? Да. Но она будет не высотой равнобедренного треугольника, а высотой равнобедренной трапеции.
Рассмотрим свойства правильной усеченной пирамиды.
Свойство 1. Все боковые ребра правильной усеченной пирамиды равны и образуют с плоскостями нижнего и верхнего оснований равные углы.
Свойство 2. Все боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями, а также образуют с плоскостями верхнего и нижнего оснований равные двугранные углы.
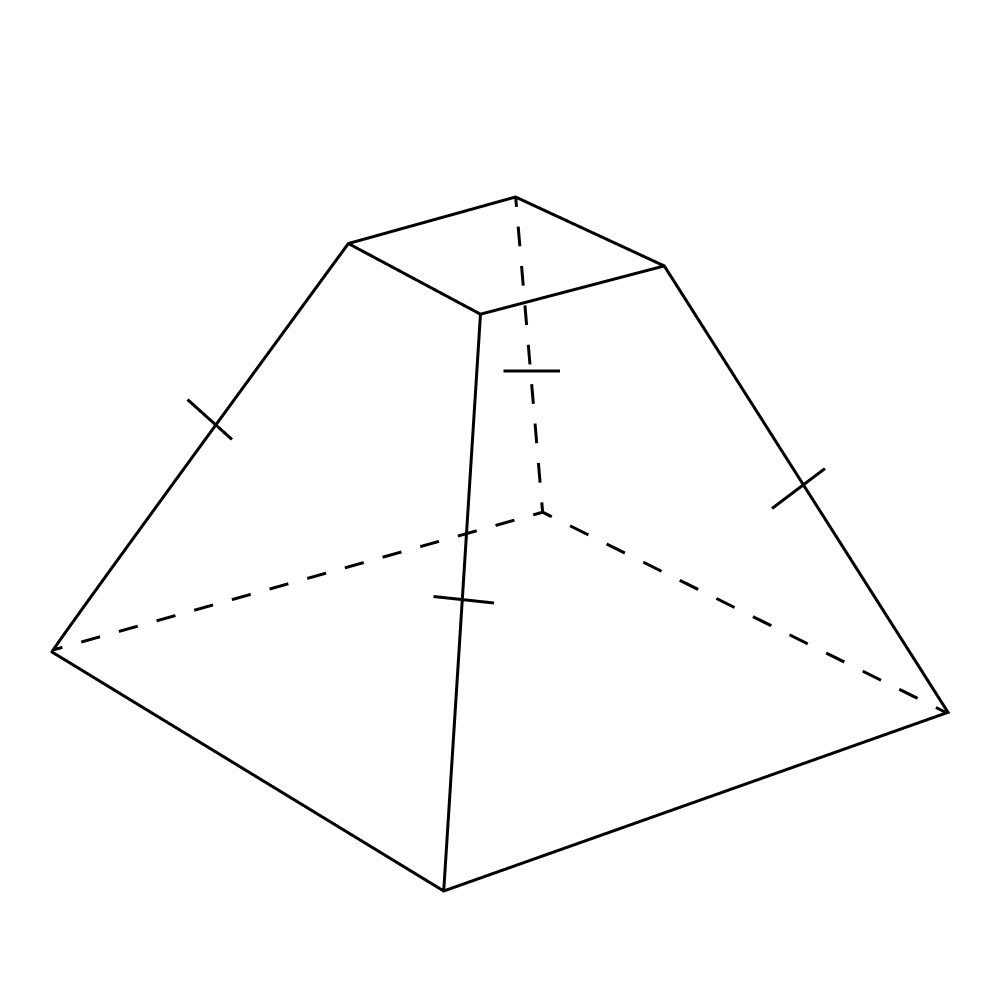
Свойство 3. Все апофемы в правильной усеченной пирамиде равны.
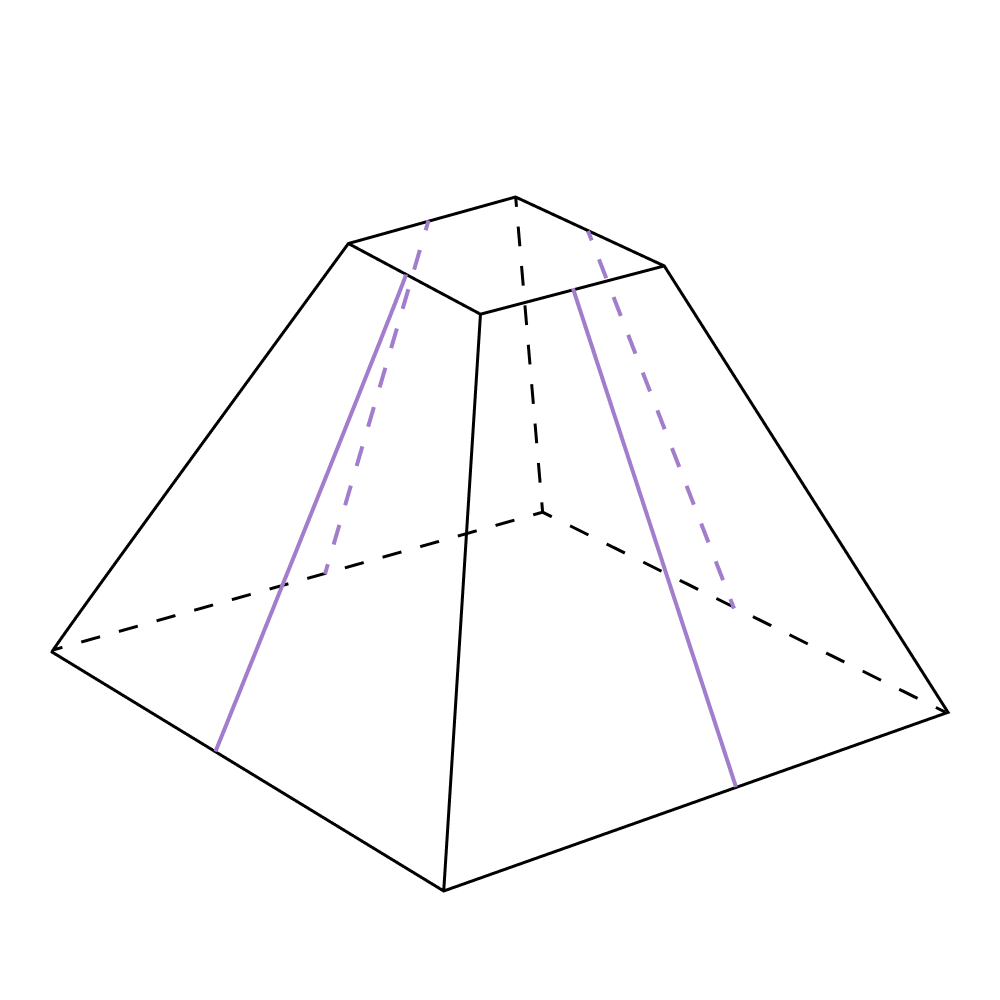
Все эти свойства можно доказать так же, как и доказывались свойства для обычной пирамиды, однако в этом случае будут использоваться не треугольники, а трапеции.
Теперь найдем объем, площадь полной и боковой поверхности усеченной пирамиды.
Начнем с объема. У нас был тортик объемом 4200, мы отдали его часть. Значит, объем оставшейся части можно найти как разность объема целой и отсеченной пирамиды.
| V = V1 — V2 |
Однако объем можно найти и по другой формуле:
V=\frac{1}{3}H(S_1+S_2+\sqrt{S_1S_2})| Где S1, S2 — площади оснований усеченной пирамиды; Н — ее высота. |
Чтобы найти площадь боковой поверхности, нужно сложить площади всех боковых граней.
Для правильной усеченной пирамиды можно вывести общую формулу.
S_{бок}=\frac{1}{2}l(P_1+P_2)| Где P1, P2 — периметры оснований; l — апофема. |
Чтобы найти площадь полной поверхности, необходимо сложить площадь боковой поверхности и площадь оснований.
| S = Sб.осн. + Sм.осн. + Sбок. |
Фактчек
- Пирамида — это многогранник, в основании которого лежит многоугольник, а остальные грани — треугольники с общей вершиной. Вершина пирамиды — общая точка боковых граней, которая не принадлежит плоскости основания. Прямые, соединяющие вершины многоугольника в основании и вершину пирамиды, называются боковыми ребрами. А вот треугольники, образованные боковыми ребрами и ребром основания называются боковыми гранями.
- Правильная пирамида — пирамида, в основании которой лежит правильный многоугольник, а вершина проецируется в центр этого многоугольника. В правильной пирамиде все боковые ребра равны, боковые грани — равные равнобедренные треугольники.
- Апофема — высота, проведенная в боковой грани правильной пирамиды из вершины. В правильной пирамиде все апофемы равны.
- С помощью формул можно найти объем пирамиды, площади ее боковой и полной поверхности. При этом объем пирамиды равен трети объема призмы с равными основаниями и высотой.
- Усеченная пирамида — часть пирамиды, заключенная между основанием и параллельной ему плоскостью, которая как бы отрезает верхушку пирамиды. В усеченной пирамиде появляется второе основание. Боковые грани превращаются из треугольников в трапеции. Если отсечь верхушку в правильной пирамиде, то получится правильная усеченная пирамида.
Проверь себя
Задание 1.
Что такое вершина пирамиды?
- Любая вершина многоугольника, лежащего в основании пирамиды.
- Углы, образованные основанием и боковыми ребрами.
- Общая точка боковых граней, которая не принадлежит основанию.
- Точка на основании, в которую падает высота пирамиды.
Задание 2.
Что такое высота пирамиды?
- Это перпендикуляр, опущенный из вершины на плоскость основания пирамиды.
- Это перпендикуляр, опущенный из любой точки боковой грани на основание пирамиды.
- Это произвольная прямая, проведенная к основанию пирамиды.
- Это перпендикуляр, опущенный из вершины на ребро основания в боковой грани.
Задание 3.
Что такое апофема пирамиды?
- Это перпендикуляр, опущенный из вершины на плоскость основания пирамиды.
- Это перпендикуляр, проведенный из вершины многоугольника в основании к его стороне.
- Это высота, проведенная в боковой грани правильной пирамиды из вершины.
- Это высота, проведенная в боковой грани любой пирамиды из вершины.
Задание 4.
Какой фигурой являются боковые грани в правильной пирамиде?
- Произвольный многоугольник.
- Произвольный треугольник.
- Всегда равносторонний треугольник.
- Равнобедренный треугольник.
Задание 5.
Что такое усеченная пирамида?
- Это любая пирамида.
- Часть пирамиды, заключенная между основанием и параллельной ему плоскостью, которая как бы отрезает верхушку пирамиды.
- Часть пирамиды, заключенная между основанием и пересекающей его плоскостью, которая как бы отрезает верхушку пирамиды.
- Часть пирамиды, заключенная между основанием и перпендикулярной ему плоскостью, которая как бы отрезает боковую часть пирамиды.
Ответы: 1. — 3; 2. — 1; 3. — 3; 4. — 4; 5. — 2.


 к списку статей
к списку статей