Первообразная

На этой странице вы узнаете:

• Родственные связи первообразной. Как первообразная связана с производной?
• Одна функция, но много ее первообразных. Как такое происходит?

Понятие первообрвообразной

Легко догадаться, что термин “первоОбразная” происходит от двух слов: первый и образ. Первым образом у автомобиля была повозка, а у пюре — картофель.

Вернемся к математике.

Ранее мы уже рассматривали, что такое Производная и как найти её.  Давайте быстро вспомним, что нахождение производной или дифференцирование — это совершение математической операции над функцией. То есть, следуя определенным правилам, любая функция может быть преобразована в новую функцию, которая и будет производной.  

В обычной жизни, совершая несколько действий, мы можем преобразовать муку в тесто, а затем и в пирожки. Но разобрать готовый пирожок на муку у нас уже не получится. Зато в математике всегда можно вернуться на шаг назад: сложили два числа — вычтем обратно, возвели в степень — извлечем корень. 

Похожим образом мы можем поступить с функцией. 

Возьмем любую функцию, например, f(x) = x² и найдем для нее производную f'(x) = 2x — получилась новая функция. Теперь для того, чтобы вернуться на шаг назад, нам нужно найти первообразную от новой функции (f'(x) = 2x).

Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x). 

То есть, если взять производную от первообразной какой-либо функции, получится сама эта функция. Процесс нахождения множества первообразных называется интегрированием.

F'(x) = f(x)

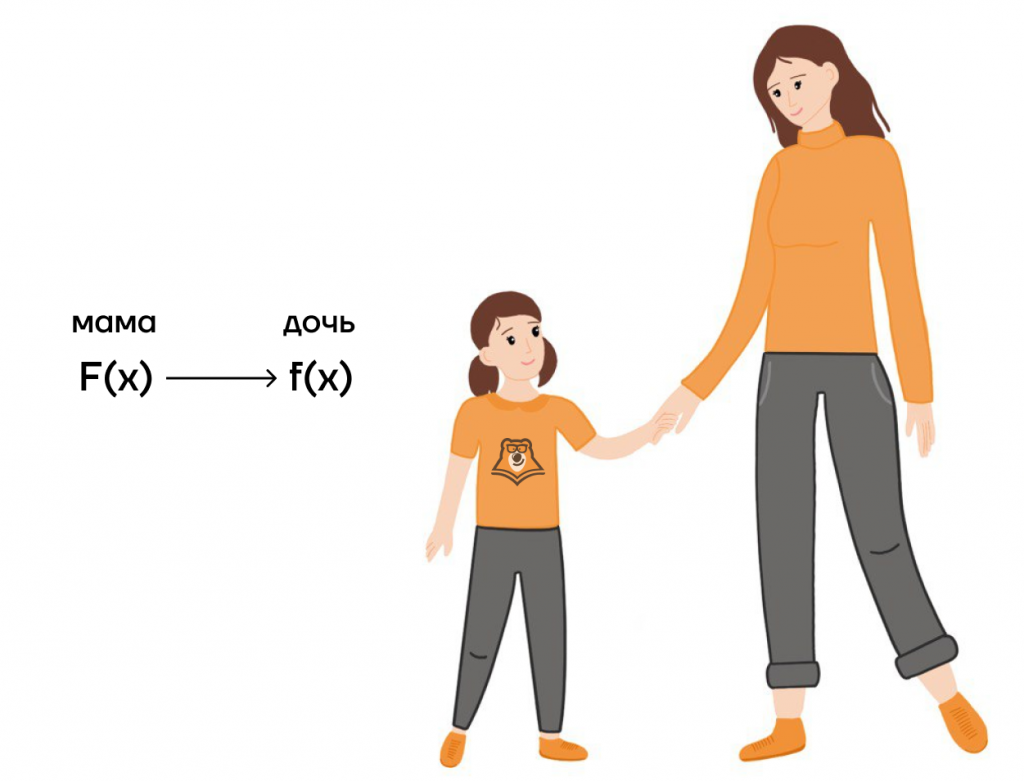
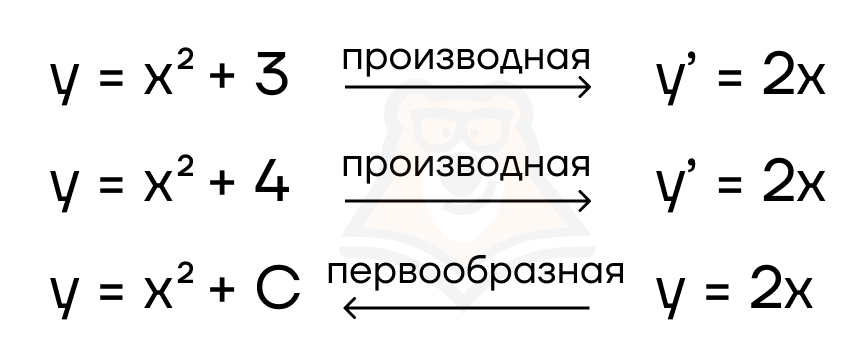
Для нахождения первообразных существует специальная таблица. В ней приведены первообразные для каждой функции. А чтобы убедиться в этом, можно найти производную от первообразной и сравнить с функцией. Они будут одинаковые.

Таблица первообразных

 Где С — произвольное число

Важно:  F(x) первообразная f(x) только на том промежутке, где F(x) и f(x) существуют. То есть, \(F(x) = \frac{1}{2} * ln (2x) + C\) первообразная \(f(x) = \frac{1}{2}x\) на промежутке 2х > 0 \(\rightarrow\) x > 0

Рассмотрим нахождение первообразной от следующей функции
y = 2x³

Применим правило интегрирования для степенной функции из таблицы первообразных

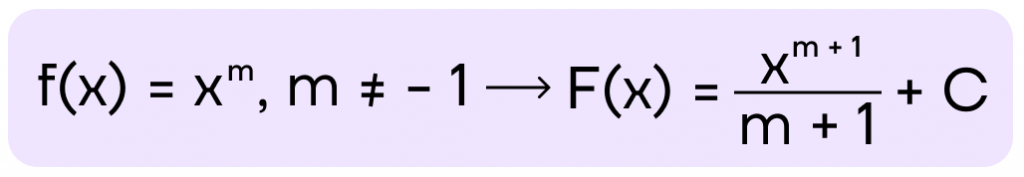
\(F(x) = \frac{2x^4}{4} + C\)
\(F(x) = \frac{1}{2} x^4 + C\)

Правила нахождения первообразных:

1. Если нужно найти первообразную от произведения числа на функцию, то первообразной выражения будет произведение этого числа на первообразную функции.

a*f(x) \(\rightarrow\) a*F(x)

Пример:
f(x) = 4x \(\rightarrow F(x) = 4 * \frac{x^2}{2} = 2x^2\)

2. Если нужно найти первообразную от суммы/разности двух функций, то первообразной выражения будет сумма/разность первообразных этих двух функций. 

g(x) \(\pm\) f(x) \(\rightarrow\) G(x) \(\pm\) F(x)

Пример:
f(x) = x² + 2 \(\rightarrow F(x) = \frac{x^3}{3} + 2x\)

Фактчек

• Первообразной для функции f(x) называется такая функция F(x), для которой выполняется равенство: F'(x) = f(x)
• Для нахождения первообразных существует специальная таблица первообразных
• Правила нахождения первообразных:
  a*f(x) \(\rightarrow\) a*F(x)
  g(x) \(\pm\) f(x) \(\rightarrow\) G(x) \(\pm\) F(x)

Проверь себя

Задание 1.
Найдите первообразную функции y = 4x⁵

1. F(x) = 20x⁴
2. \(F(x) = \frac{1}{3}x^6\)
3. \(F(x) = \frac{1}{3}x^5\)
4. \(F(x) = \frac{2}{3}x^6\)

Задание 2.
Найдите первообразную функции y = 4

1. F(x) = 4x
2. F(x) = x
3. \(F(x) = \frac{1}{2}x^2\)
4. \(F(x) = \frac{1}{2}x\)

Задание 3.
Найдите первообразную функции \(y = 2\sin x\)

1. F(x)= x
2. \(F(x) = -2\cos x\)
3. \(F(x) = \frac{1}{2}\cos x\)
4. \(F(x) = -2\sin x\)

Задание 4.
Найдите первообразную функции y = 2^x

1. \(F(x) = \frac{2^x}{ln2}\)
2. F(x) = ln2
3. F(x) = 2
4. F(x) = x²

Ответы: 1. — 4; 2. — 1; 3. — 2; 4. -1