Многоугольники
На этой странице вы узнаете
- Из 2D в 3D. А что там по пространству?
- Каким может быть максимальное количество углов у правильного многоугольника?
- Где в природе можно встретить описанный многоугольник?
Треугольники, квадраты, прямоугольники, параллелограммы, трапеции, шестиугольники — это лишь малая часть примеров многоугольников. Что же такое многоугольник и причем тут часы?
Определение многоугольников
В жизни мы сталкиваемся с многоугольниками достаточно часто. Для упрощения изучения частных случаев важно знание и понимание общей теории.
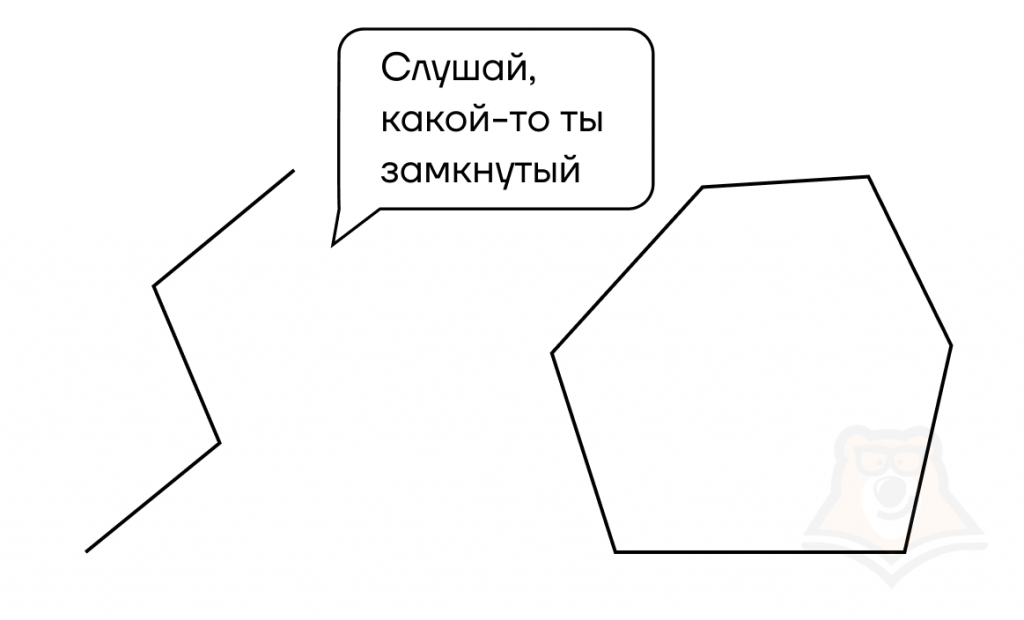
Многоугольник — это замкнутая ломаная линия, которая ограничивает часть плоскости.
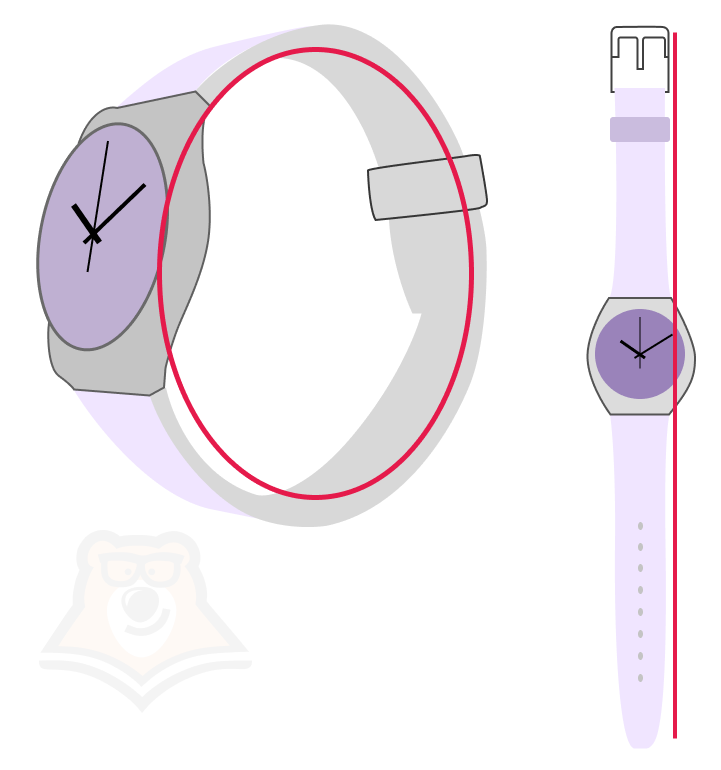
Разберемся в термине чуть подробнее. Что значит «замкнутая»? Вспомним, например, часы. Пока ремешок не застегнут, они не замкнуты. Но как только мы надеваем их на запястье и застегиваем, ремешок замыкается, то есть не прерывается ни на одном участке.
Но можно дать и другое определение для многоугольника: это замкнутая линия, соединяющая несколько точек на плоскости, не лежащих на одной прямой.
Возьмем на плоскости пять точек А, В, С, D, Е:
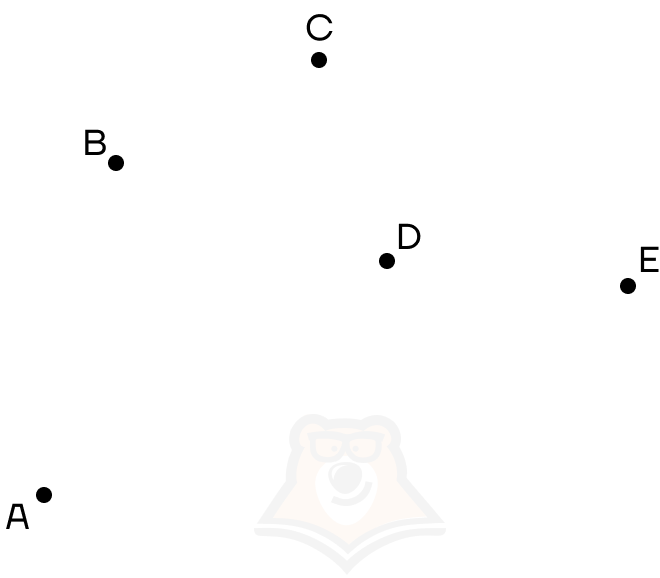
Если мы теперь соединим все эти точки между собой отрезками, то получим многоугольник. Но есть важные правила:
- Точки должны соединяться последовательно.
Ненадолго вернемся в детство и вспомним рисование по номерам. Нам давали лист с точками, которые нужно было последовательно соединить. И если точки соединить в неправильном порядке, рисунок не получится. Точно также работает и с многоугольником.
- Стороны, имеющие общую вершину (например, АВ и ВС), не должны лежать на одной прямой.
- Несмежные стороны, то есть стороны с разными вершинами, не должны пересекаться.
Например, нельзя делать так, поскольку стороны АС и BD пересекаются между собой. Такая фигура уже не будет многоугольником.
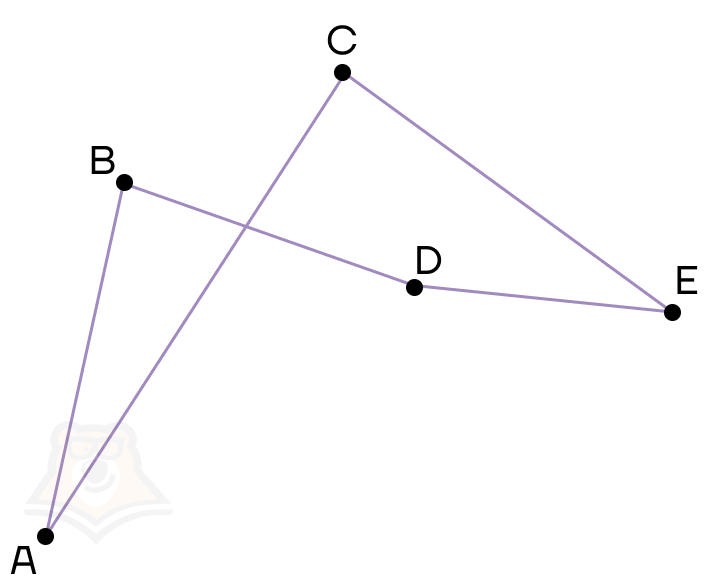
Чтобы было легче запомнить данные правила, вспоминайте про игру, где нужно соединять точки одного цвета и заполнять линиями все поле. Как в этой игре нельзя, чтобы линии разных цветов пересекали друг друга, так и в многоугольнике недопустимо, чтобы несмежные стороны пересекались.
Рассмотрим построенный ниже многоугольник. ABCDE — многоугольник.
A, B, C, D, E — вершины многоугольника.
AB, BC, CD, DE, AE — стороны многоугольника.
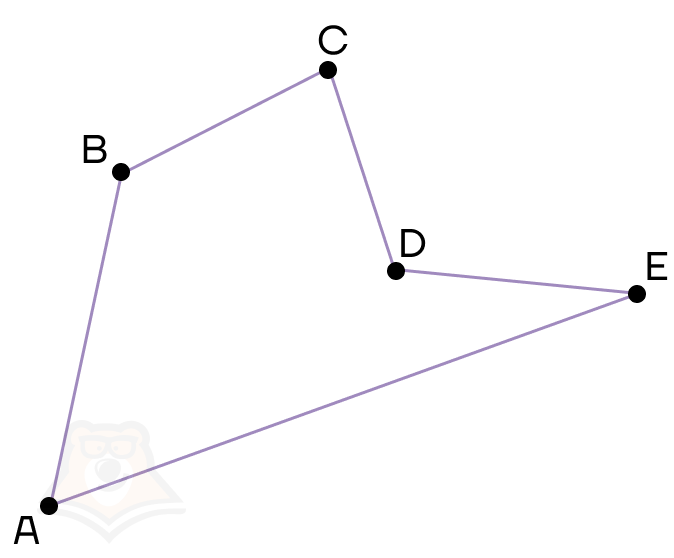
Также в многоугольнике есть важный элемент — диагональ.
Диагональ — отрезок в многоугольнике, который соединяет две вершины, не лежащие на одной стороне.
Например, AD, AC, BD — диагонали.
Поскольку многоугольник – геометрическая фигура, она занимает определенное место на поверхности. А значит, как и другие фигуры, многоугольник обладает площадью.
Существует несколько видов многоугольника, которые мы рассмотрим чуть дальше. Для многих из них – прямоугольника, квадрата, шестиугольника и т.д. существуют свои формулы для определения площади. Но что делать, если многоугольник имеет более сложную конфигурацию?
В таком случае будет намного удобнее искать площадь составной фигуры.
Составная фигура – это фигура, которую можно разделить на несколько более простых фигур.
Предположим, нам дан следующий многоугольник:
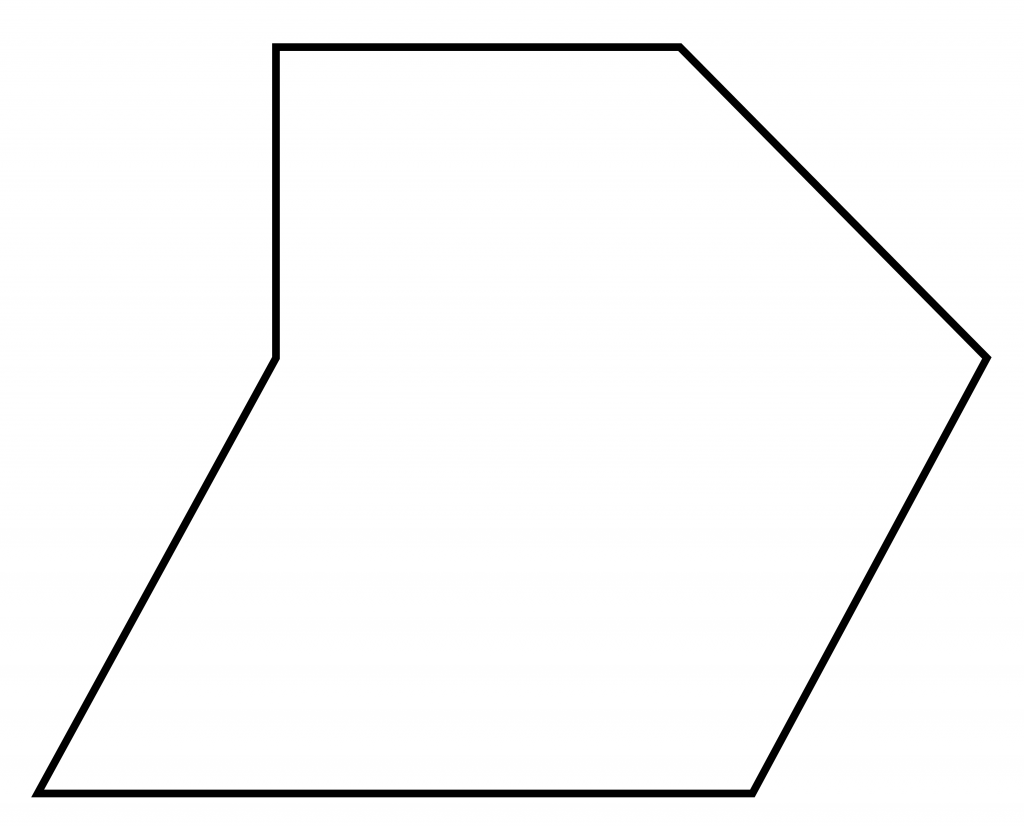
Посчитать его площадь по определенной формуле будет достаточно тяжело. А теперь попробуем разбить его на треугольник, прямоугольник и параллелограмм:
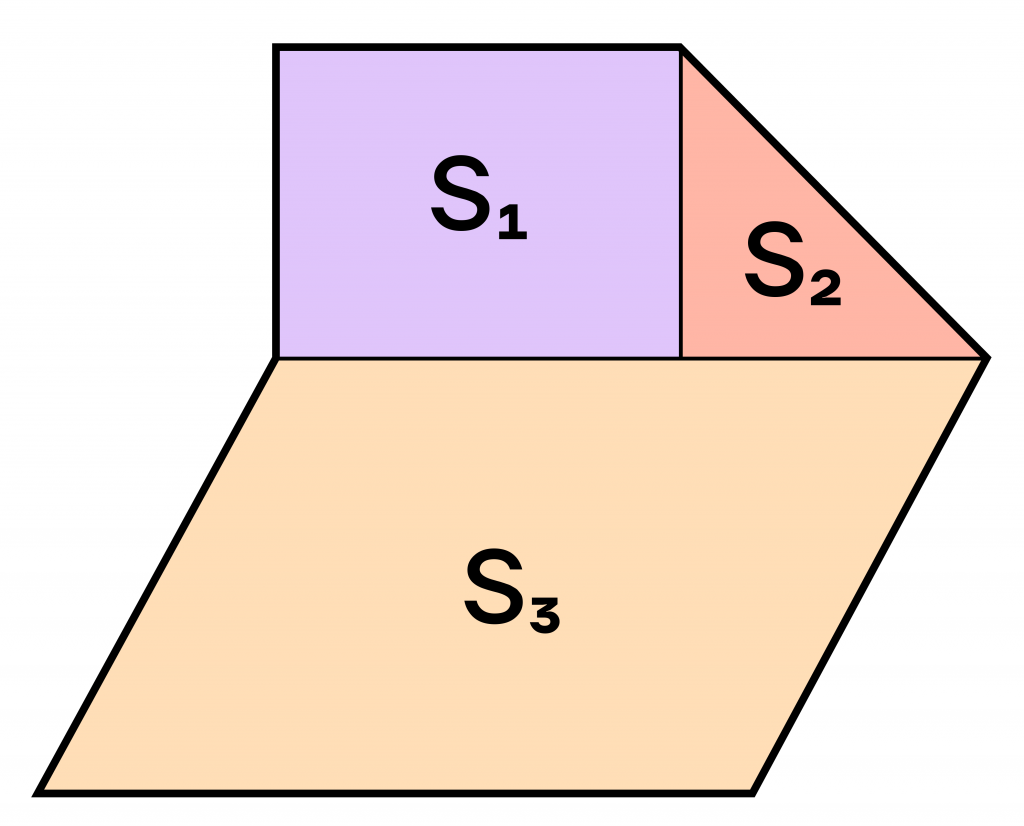
Тогда площадь многоугольника будет равна сумме площадей этих фигур, а именно:
\(S=S_1+S_2+S_3\)
Мы уже упоминали разные названия многоугольников. Существует правило, по которому можно безошибочно правильно назвать многоугольник. Многоугольник называется по количеству сторон.
- Например, если у многоугольника 3 стороны, то это треугольник.
- Если у многоугольника 4 стороны, то это четырехугольник.
- Если у многоугольника 12 сторон, то это двенадцатиугольник.
- Если у многоугольника n сторон, то это n-угольник.
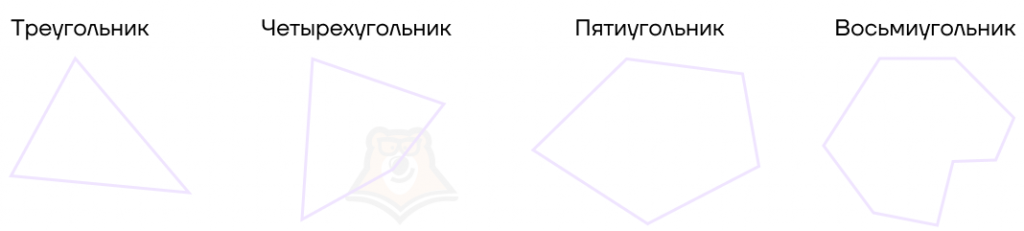
Получается все многоугольники можно разбить на группы по количеству сторон. Но существует ли еще какая-то классификация многоугольников? Поговорим об этом дальше.
Виды многоугольников
Как уже было заметно из рисунков, многоугольники бывают совершенно разные. Но есть два основных вида многоугольника: выпуклый и невыпуклый.

Рассмотрим, чем они отличаются. Построим два пятиугольника и проведем прямые через каждые две соседние вершины, то есть построим прямые, содержащие стороны пятиугольника.
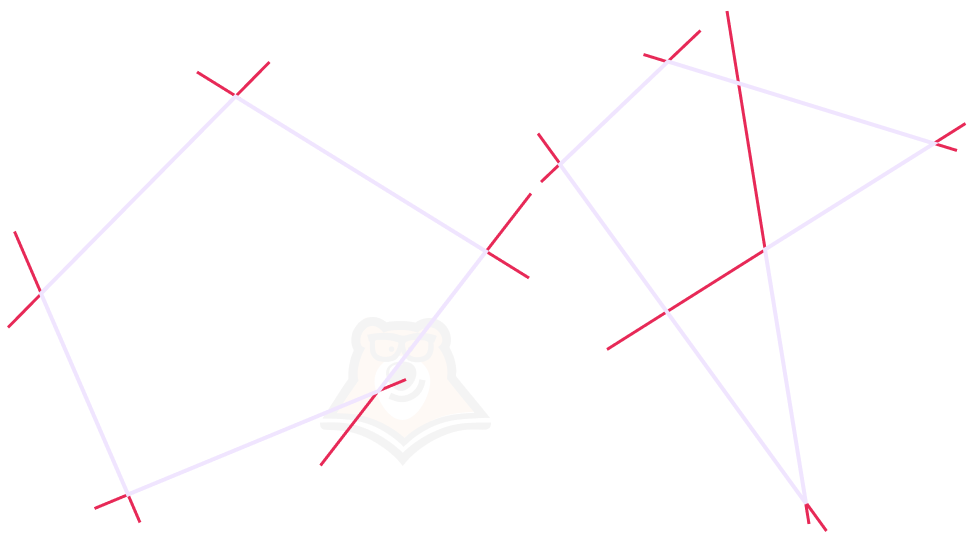
Несложно заметить, что в первом случае, какую бы прямую мы ни рассматривали, вся фигура будет лежать только по одну сторону от этой прямой. Такой пятиугольник и будет называться выпуклым.
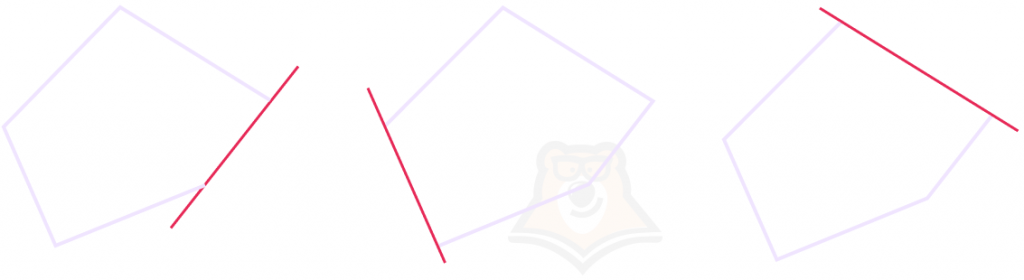
Во втором же пятиугольнике, при рассмотрении некоторых прямых, фигура будет лежать по обе стороны от прямой. Такой многоугольник будет называться невыпуклым.
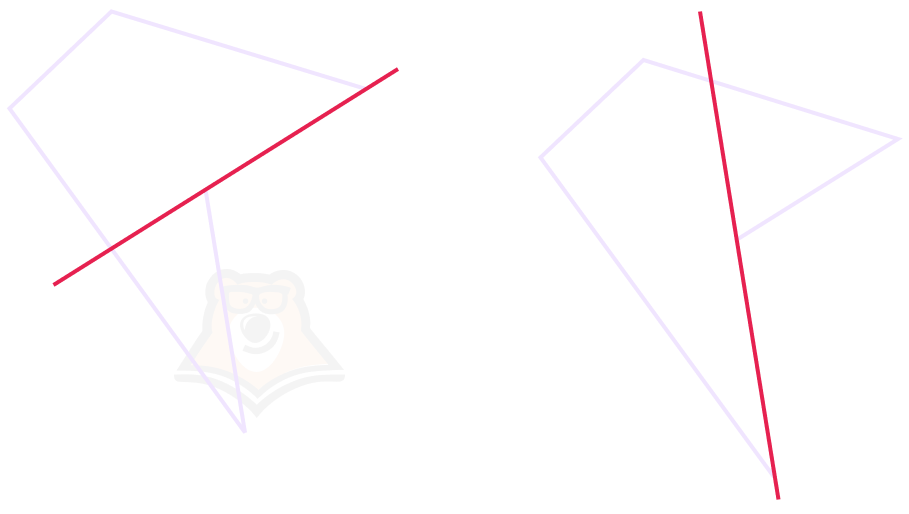
В этом принципиальное различие этих пятиугольников. А если говорить более математическим языком, то первый пятиугольник является выпуклым, а второй нет.
Выпуклый многоугольник — многоугольник, который лежит с одной стороны от любой прямой, содержащей его сторону.
Невыпуклый многоугольник — многоугольник, в котором прямая, содержащая его сторону, делит многоугольник на части.

В дальнейшем материале мы будем рассматривать только выпуклые многоугольники.
Получается, все многоугольники можно разбить на две большие группы. А существуют ли полностью идентичные многоугольники? Можно ли говорить о равенстве многоугольников? Поговорим об этом дальше.
Равные многоугольники
Равными будут называться многоугольники, которые совпадают при наложении.
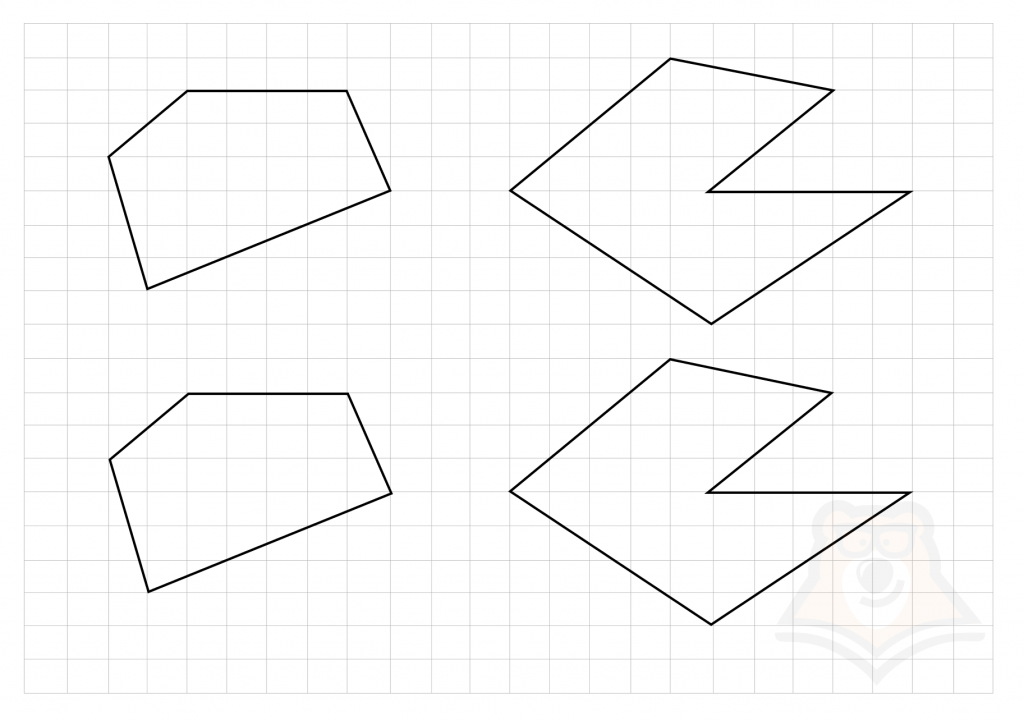
То есть получается что все стороны равных многоугольников должны соответственно равняться друг другу, также равными должны быть и углы между равными сторонами.
Помимо равных многоугольников важно также упомянуть равновеликие многоугольники.
Равновеликими называются многоугольники, площади которых равны.
Возникает вопрос. Все ли равновеликие многоугольники будут равными и наоборот?
Для начала давайте рассмотрим равные многоугольники. Поскольку равные многоугольники совпадают при наложении, получается, что площадь, которую они занимают будет одинаковой. Особенно хорошо это можно увидеть на квадратной решетке.
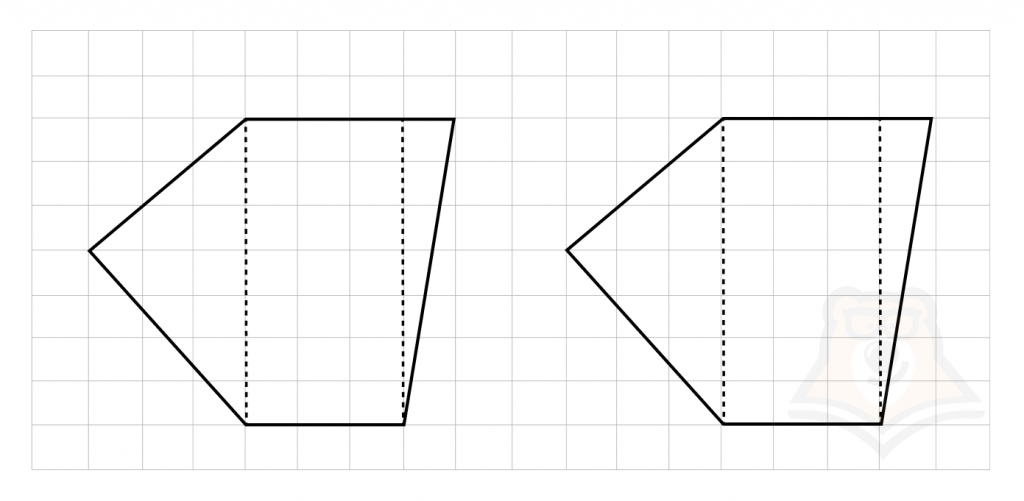
То есть получается, что все равные многоугольники являются равновеликими.
Немного сложнее обстоят дела с обратным утверждением. Давайте рассмотрим два неравных многоугольника и попробуем доказать, что их площади равны, то есть они являются равновеликими.
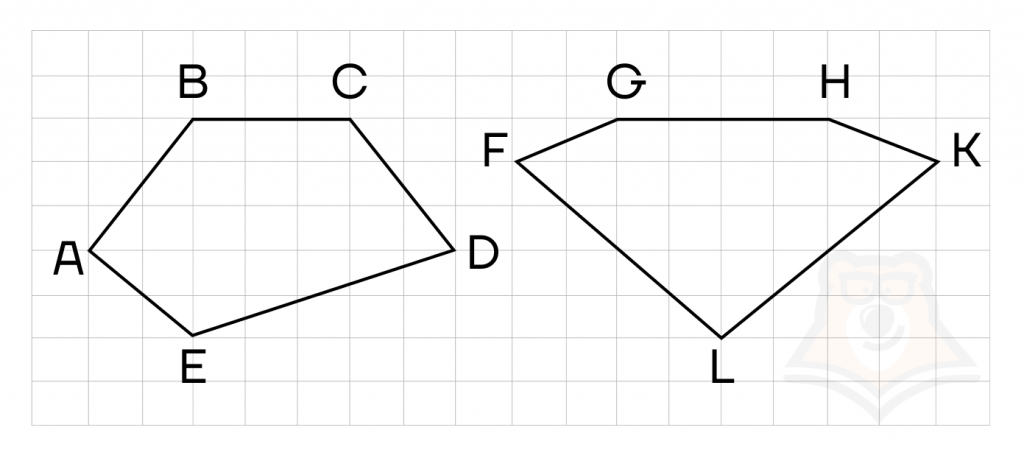
Разобьем каждый из многоугольников на более простые фигуры.
В пятиугольнике \(ABCDE\) проведем диагональ \(AD\) и \(BB_1 \bot AD, CC_1 \bot AD\). Получается, мы разбили пятиугольник на квадрат \(BCC_1B_1\), треугольники \(\triangle AED, \triangle ABB_1, \triangle CC_1D\).
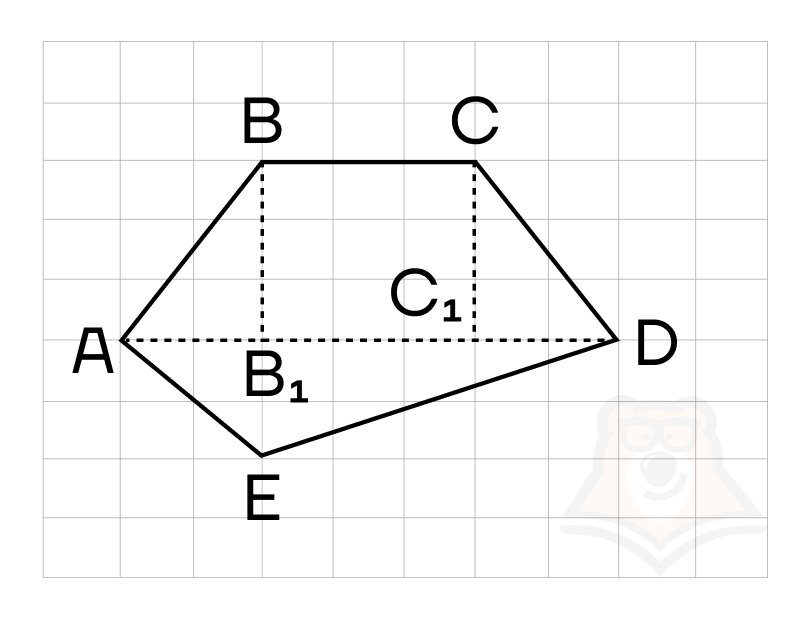
Площадь пятиугольника \(ABCDE\) будет равна сумме площадей этих фигур:
\(S(BCC_1B_1)=3*3=9\)
\(S(\triangle ADE)=\frac{1}{2}*2*7=7\)
\(S(\triangle ABB_1)=\frac{1}{2}*3*2=3\)
\(S(\triangle CC_1D)=\frac{1}{2}*3*2=3\)
\(S(ABCDE)=9+7+3+3=22\)
В пятиугольнике \(FGHK\) проведем диагональ \(FK\) и \(GG_1 \bot FK, HH_1 \bot FK\). Получаем \(\triangle FLK, \triangle FGG_1, \triangle HH_1K\) и прямоугольник \(GHH_1G_1\).
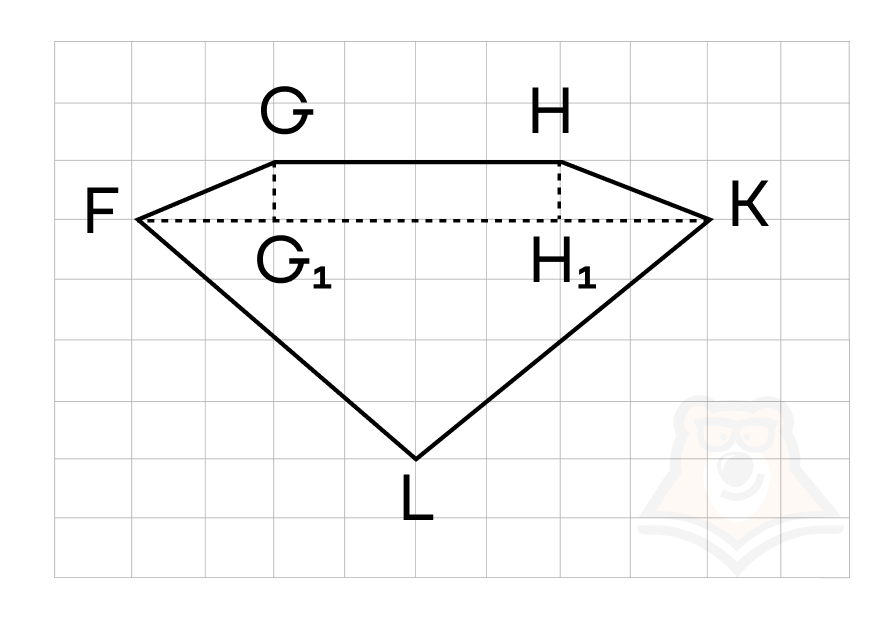
Найдем площади всех фигур и итоговую площадь пятиугольника:
\(S(\triangle GHH_1G_1)=4*1=4\)
\(S(\triangle FLK)=\frac{1}{2}*4*8=16\)
\(S(\triangle FGG_1)=\frac{1}{2}*1*2=1\)
\(S(HH_1K)=\frac{1}{2}*1*2=1\)
\(S(FGHKL)=4+16+1+1=22\)
То есть получается что равновеликие многоугольники не всегда являются равными. Более того, равновеликими могут быть и многоугольники с разным количеством вершин.
Далее давайте более подробно обсудим элементы многоугольников. Начнем со сторон.
Стороны многоугольника
Мы знаем, что существует неравенство треугольника, согласно которому любая сторона треугольника меньше суммы двух других его сторон. Существуют ли подобные ограничения для многоугольников? Давайте разбираться.
Мы не просто так вспомнили про неравенство треугольника, с помощью этого неравенства можно легко доказать одну важную теорему:
Длина отрезка, соединяющего концы ломаной, не превосходит длины этой ломаной.
Попробуем доказать.
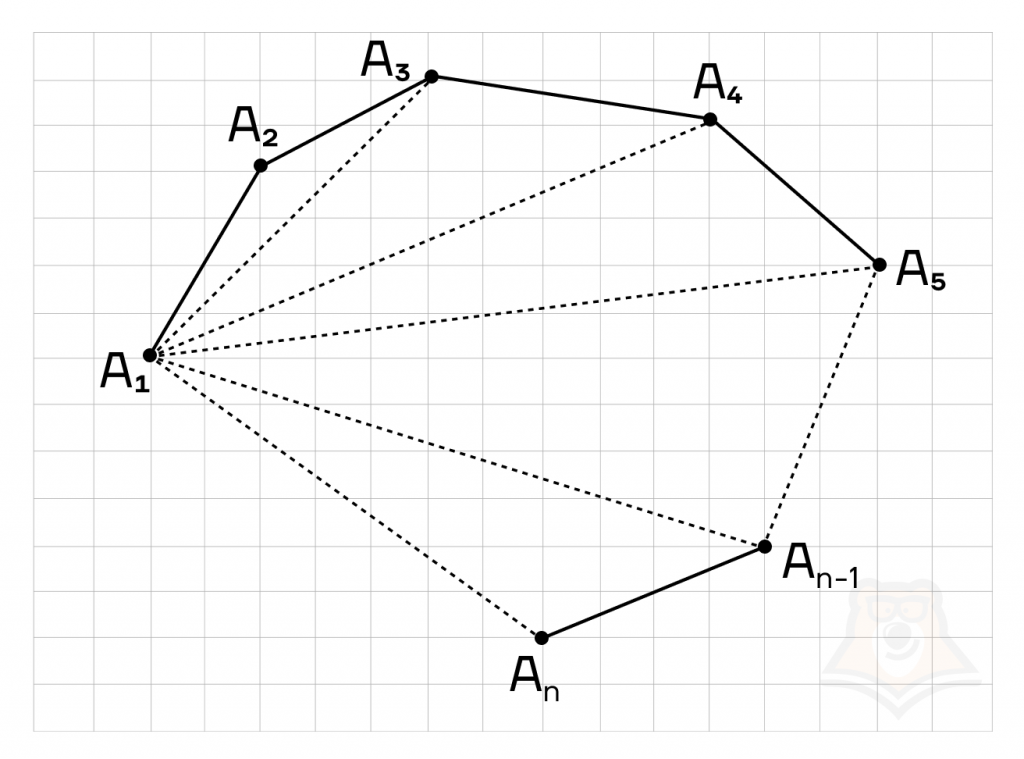
Пусть наша ломаная — \(A_1A_2A_3…A_n\), то есть в ней \(n\) звеньев.
Заменим соседние стороны \(A_1A_2\) и \(A_2A_3\) стороной \(A_1A_3\), согласно неравенству треугольника \(A_1A_3<A_1A_2+A_2A_3\).
То есть мы получим ломаную, длина которой короче длины исходной ломаной.
Аналогично заменим стороны \(A_1A_3\) и \(A_3A_4\) стороной \(A_1A_4\). По неравенству треугольника получаем, что \(A_1A_4<A_1A_3+A_3A_4\), а поскольку \(A_1A_3<A_1A_2+A_2A_3\) выходит, что \(A_1A_4<A_1A_2+A_2A_3+A_3A_4\).
Проделав данное преобразование \(n-2\) раз получим, что \(A_1A_n<A_1A_2+A_2A_3+ … +A_{n-1}A_n\). Что и требовалось доказать.
Поскольку многоугольник — это замкнутая ломаная, а «разомкнуть» ее мы можем между любыми двумя вершинами, то согласно данной теореме для любой стороны многоугольника справедливо, следующее:
Каждая сторона многоугольника меньше суммы длин других его сторон.
Мы довольно подробно обсудили многоугольники с точки зрения их сторон, но ведь есть еще и углы.
Сумма внутренних углов в многоугольнике
Мы точно знаем, что в треугольнике сумма углов равняется 180°, а в четырехугольнике 360°. А чему равна сумма углов в пятиугольнике, шестиугольнике, восьмиугольнике и так далее?
Разумеется, мы не учим точное значение для каждого многоугольника. Однако существует формула, по которой можно найти сумму углов в любом многоугольнике.
Пусть n — количество сторон многоугольника, \(S\) — сумма углов выпуклого многоугольника, тогда ее можно найти по следующей формуле:
\(S=180॰(n-2)\)
Проверим на известных нам треугольнике и четырехугольнике.
В треугольнике \(n = 3: 180॰(3-2) = 180॰*1 = 180॰\).
В четырехугольнике \(n = 4: 180॰(4-2)=180॰*2=360॰\). Все верно.
А теперь найдем для примера сумму углов многоугольника при разных значениях \(n\).
\(n = 6: 180॰(6-2) = 180॰*4 = 720॰\).
\(n = 10: 180॰(10-2) = 180॰*8 = 1440॰\).
\(n = 25: 180॰(25-2) = 180॰*23 = 4140॰\).
Таким образом, зная формулу, мы можем найти сумму углов в многоугольнике с любым количеством сторон.
Но помимо внутренних углов, у любой фигуры есть и внешние углы. А как обстоят дела с ними? Существуют ли какие-то правила и формулы, касающиеся внешних углов многоугольника?
Сумма внешних углов многоугольника
Мы легко можем посчитать чему равна сумма внешних углов у треугольника, четырехугольника и даже шестиугольника. Но что делать, если количество вершин нашего многоугольника гораздо больше? Да или если нам просто лень высчитывать все это вручную из раза в раз.
В предыдущем пункте мы выяснили, что существует формула, с помощью которой можно найти сумму внутренних углов выпуклого многоугольника, может, существует какое-то правило и для внешних углов? Попробуем разобраться.
На самом деле, если мы начнем высчитывать сумму внешних углов для фигур, в которых это сделать не так сложно и затратно по времени, то мы заметим некоторую закономерность.
Для простоты вычислений, давайте возьмем для примера правильный треугольник и правильный четырехугольник (квадрат).
Рассмотрим правильный треугольник \(ABC\).
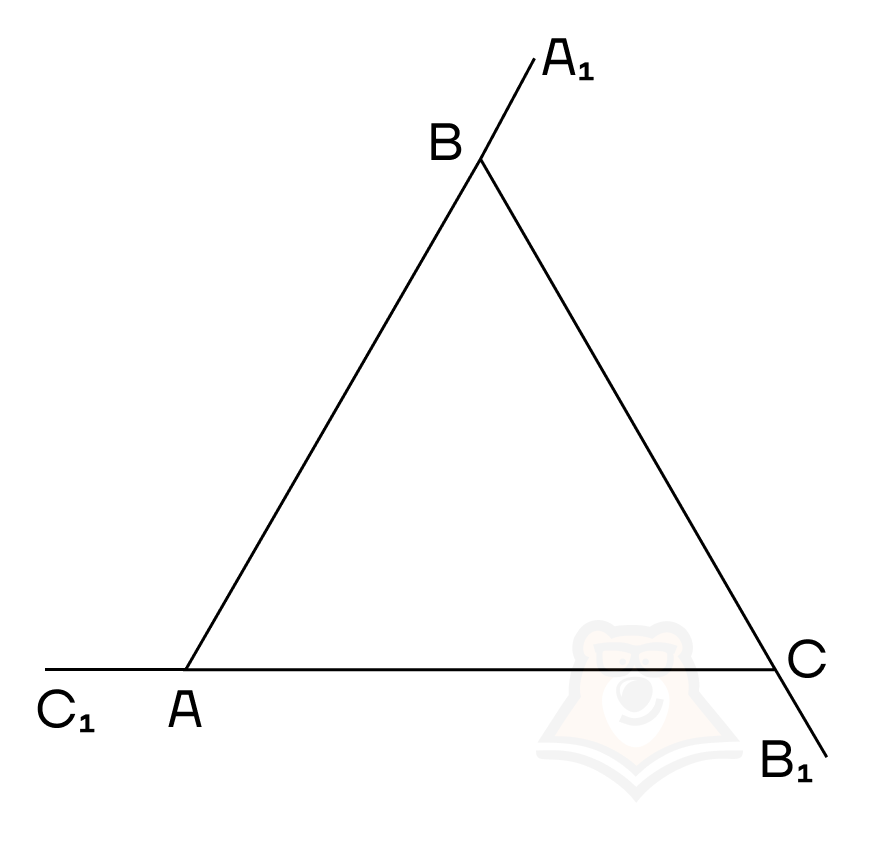
Каждый внутренний угол правильного треугольника равен 60॰:
\(∠BAC=∠ABC=∠BCA=180॰ : 3=60॰\)
Каждый внешний угол будет смежным с внутренним, то есть:
\(∠BAC_1=180॰-∠BAC=180॰-60॰=120॰\)
\(∠A_1BC=180॰-∠ABC=180॰-60॰=120॰\)
\(∠B_1CA=180॰-∠BCA=180॰-60॰=120॰\)
Тогда сумма внешних углов:
\(∠BAC_1+∠A_1BC+∠B_1CA=120॰+120॰+120॰=360॰\)
Теперь рассмотрим квадрат \(ABCD\).
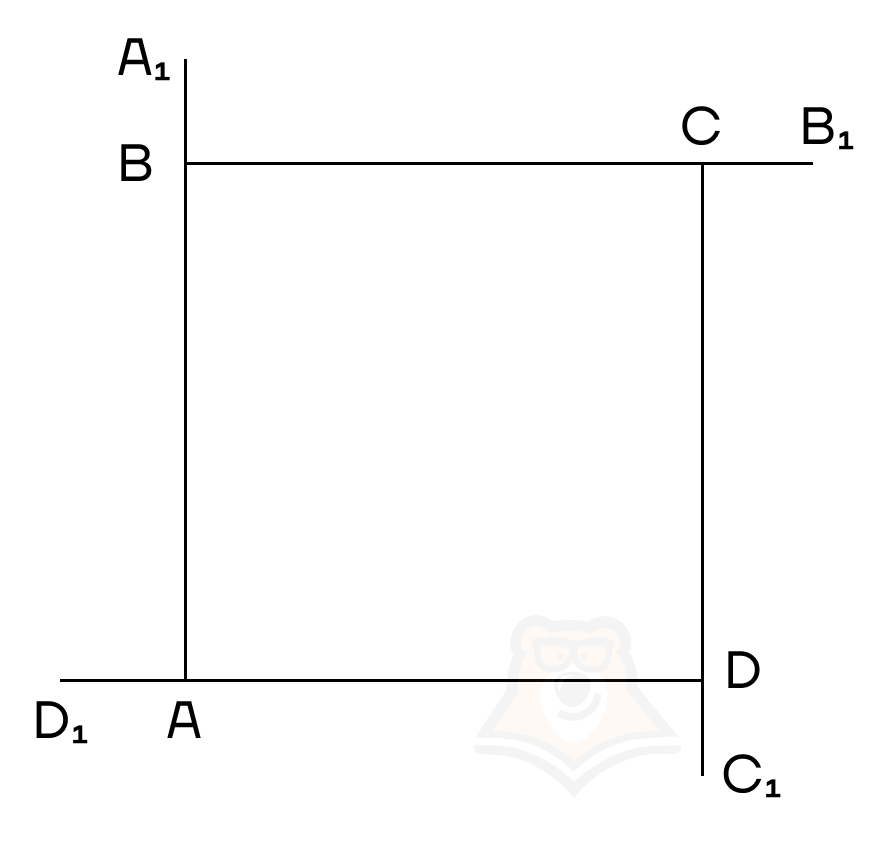
Каждый внутренний угол квадрата равен 90॰:
\(∠BAD=∠ABC=∠BCD=∠CDA=90॰\)
Каждый внешний угол будет смежным с внутренним, то есть:
\(∠BAD_1=180॰-∠BAD=180॰-90॰=90॰\)
\(∠A_1BC=180॰-∠ABC=180॰-90॰=90॰\)
\(∠B_1CD=180॰-∠BCD=180॰-90॰=90॰\)
\(∠C_1DA=180॰-∠CDA=180॰-90॰=90॰\)
Выходит, что сумма внешних углов:
\(∠BAD_1+∠A_1BC+∠B_1CD+∠C_1DA=90॰+90॰+90॰+90॰=360॰\)
Таким образом, получается, что и сумма внешних углов правильного треугольника, и сумма внешних углов квадрата равна 360॰. И на самом деле это не просто совпадение, и несмотря на то что мы рассматривали правильные фигуры, справедливо это будет для любых выпуклых многоугольников.
Рассмотрим доказательство в общем виде, на примере выпуклого n-угольника.
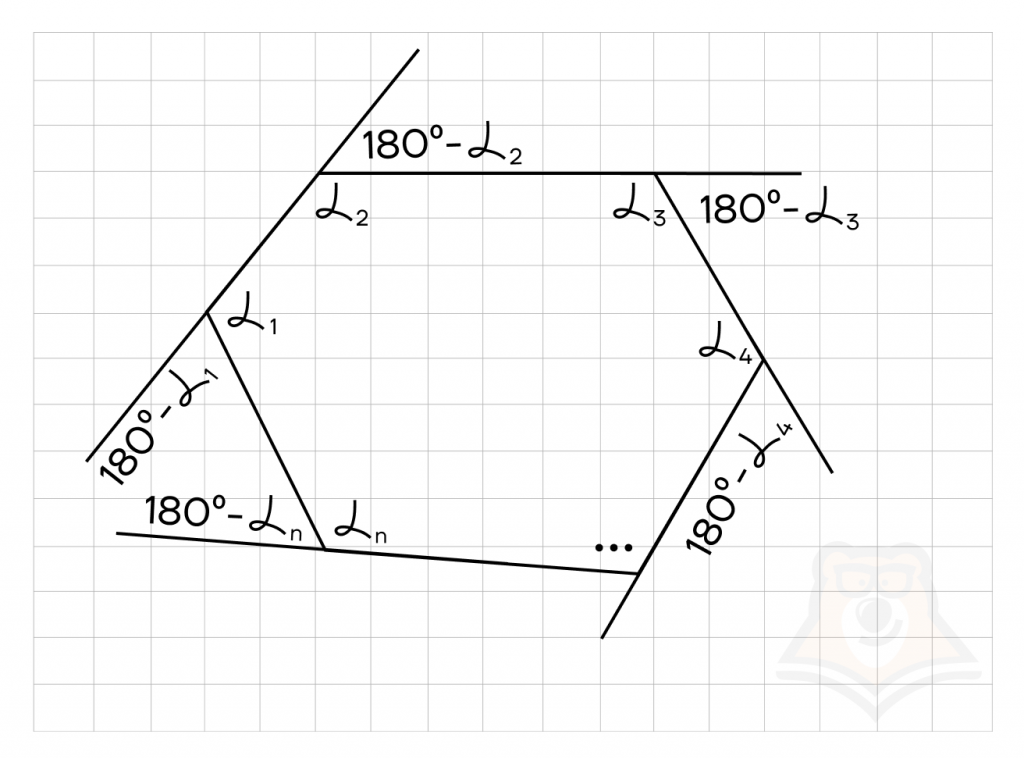
Пусть внутренние углы n-угольника равны \(\alpha_1, \alpha_2, \alpha_3, … , \alpha_n\).
Внешние углы будут смежными с внутренними, значит, будут равны \(180॰-\alpha_1, 180॰-\alpha_2, 180॰-\alpha_3, … , 180॰-\alpha_n\).
Тогда сумма внешних углов:
\(180॰-\alpha_1+180॰-\alpha_2+180॰-\alpha_3+ … +180॰-\alpha_n=180॰*n-(\alpha_1+\alpha_2+\alpha_3+ …+\alpha_n)\)
\((\alpha_1+\alpha_2+\alpha_3+ …+\alpha_n)\) — сумма внутренних углов многоугольника, ее можно найти по формуле: \(S=180॰(n-2)\)
Значит, \((\alpha_1+\alpha_2+\alpha_3+ …+\alpha_n)=180॰(n-2)\).
Подставив это в выражение для суммы внешних углов n-угольника получим:
\(180॰-\alpha_1+180॰-\alpha_2+180॰-\alpha_3+ … +180॰-\alpha_n=180॰n-(\alpha_1+\alpha_2+\alpha_3+ …+\alpha_n)\)
\(=180॰n-180॰(n-2)=180॰n-180॰n+180॰*2=180॰*2=360॰\)
Таким образом, мы получаем следующее утверждение.
Сумма внешних углов выпуклого многоугольника равна 360॰.
Мы подробно рассмотрели все элементы многоугольников, и в целом довольно подробно обсудили произвольные многоугольники, но стоит также обратить внимание на более частный случай — правильные многоугольники.
Правильные многоугольники
Мы знаем, что существует правильный треугольник. Подробнее про него можно прочитать в этой статье. Однако правильным может быть не только он. Правильные многоугольники также существуют.
Правильный многоугольник — это многоугольник, все стороны и углы которого равны.
| Из 2D в 3D. Что там по пространству? Платоновы тела — объемные аналоги правильных многоугольников, то есть это многогранники, гранями которых являются правильные многоугольники. И таких тел существует всего 5. Тетраэдр, октаэдр и икосаэдр, гранями которых являются правильные треугольники. Гексаэдр, больше известный как куб, с квадратными гранями. И, наконец, додекаэдр с гранями пятиугольниками. А доказали этот факт еще более двух тысяч лет назад. |

В правильном многоугольнике очень легко найти углы.
Например, нам дан правильный двенадцатиугольник.
Найдем сумму его углов: \(180(12-2)=180*10=1800\)
В этом многоугольнике всего будет двенадцать углов \(а\), сумма которых равняется \(1800\). То есть \(12а = 1800\), следовательно, один угол многоугольника равен \(\frac{1800}{12}=150°\).
Теперь мы можем вывести формулу. Пусть \(а\) — угол многоугольника, \(n\) — количество его сторон.
\(a=\frac{180(n-2)}{n}\)
Данная формула может пригодиться как для решения простых заданий из первой части, так и при решении более сложных задач, как в ОГЭ, так и в ЕГЭ по математике, поэтому важно знать эту формулу и уметь правильно ее использовать.Например, рассмотрим задание №15 из ОГЭ по математике:
Задание. ABCDEFGHKL — правильный десятиугольник. Найдите угол FGH. Ответ дайте в градусах.
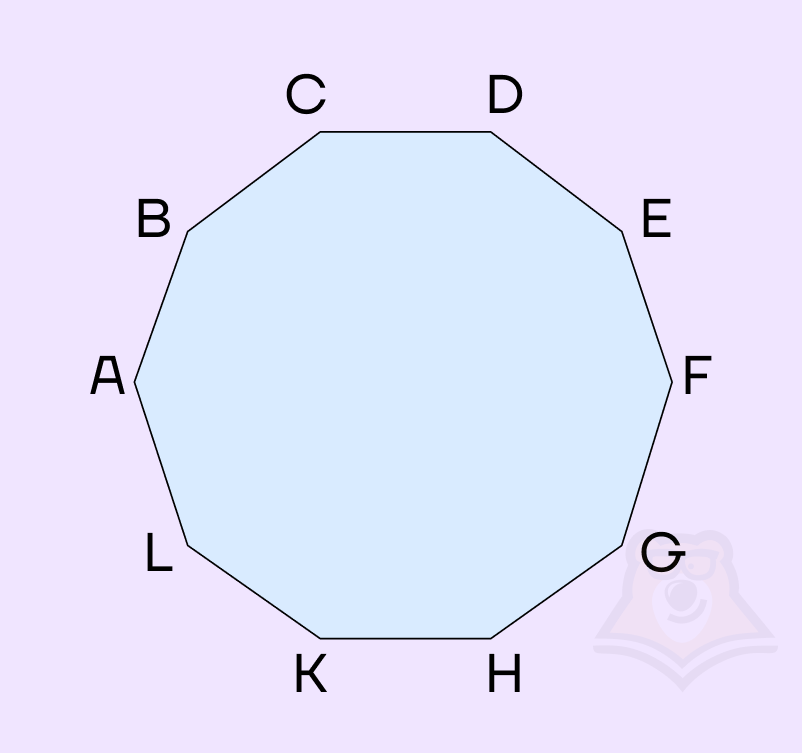
Решение. Воспользуемся формулой для нахождения угла правильного многоугольника:
\(a=\frac{180(n-2)}{n}\)
В нашей задаче речь идет о правильном десятиугольнике, значит n=10. Таким образом, получаем:
\(∠FGH=\frac{180(10-2)}{10}=\frac{180*8}{10}=18*8=144\)
Ответ: 144
Также в правильном многоугольнике достаточно просто найти периметр: нужно умножить количество сторон на их длину. Пусть \(n\) — количество сторон, \(b\) — длина сторон.
\(P=n*b\)
Например, в девятиугольнике сторона равняется \(5\). Тогда его периметр равен \(5*9=45\).
| Каким может быть максимальное количество углов у правильного многоугольника? Считается, что у многоугольника может быть бесконечное количество углов. Но есть один нюанс. Правильный многоугольник с 65 537 углами и 65 537 сторонами визуально уже не отличим от окружности. Называется он: Шестьдеся̀тпятьты̀сячпятисо̀ттридцатисемиуго́льник Больше похоже на заклинание призыва потусторонних сил, не так ли? Его можно запросто построить с помощью циркуля и линейки. |
Многоугольник не просто так связан с окружностью. С ее помощью даже можно построить любой правильный n-угольник! Как это сделать?
Допустим, нам необходимо построить правильный девятиугольник. Для начала начертим окружность с центром О.
Теперь саму окружность нужно разбить на 9 равных треугольников, две стороны которых будут соединять дугу окружности и ее центр. То есть эти стороны будут радиусами, а значит, равны между собой.
Вспомним один из признаков равенства треугольников, о котором мы говорили в статье «Равенство и подобие треугольников». Два треугольника равны в том случае, когда две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.
Мы уже определили, что у наших треугольников будет по две равные стороны (радиусы окружности). Следовательно, чтобы треугольники были равны, нам необходимо, чтобы были равны и углы между ними.
Поскольку треугольников всего 9, то нам нужно разделить окружность на 9 равных углов. Дуга окружности равна 360 градусам, следовательно, один такой угол будет равен:
\(\frac{360°}{9}=40°\)
Если нам будет дан любой другой многоугольник, то для нахождения углов нужно разделить 360° на количество его сторон.
Теперь отложим девять углов по 40 градусов из центра окружности и продлим лучи до пересечения с дугой.
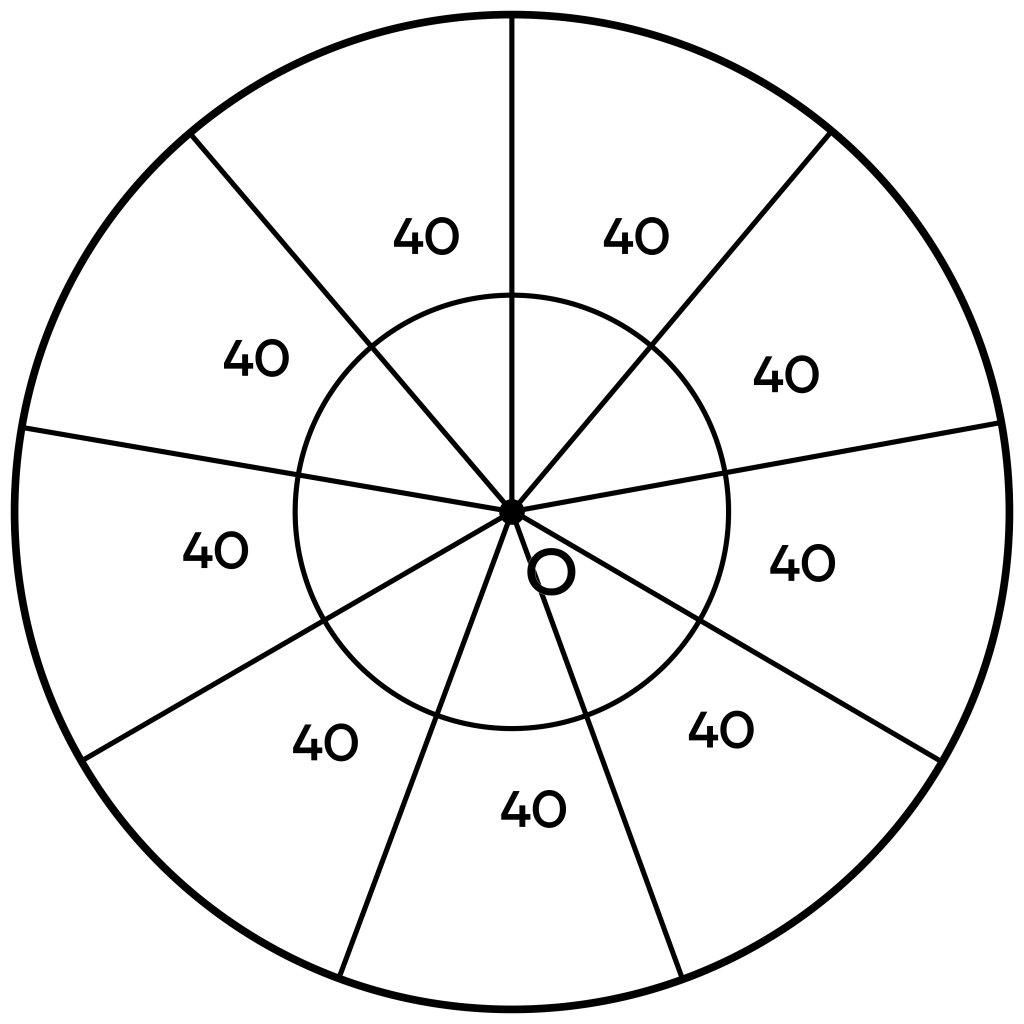
Осталось соединить между собой точки пересечения лучей и дуги окружности, и наш многоугольник готов!
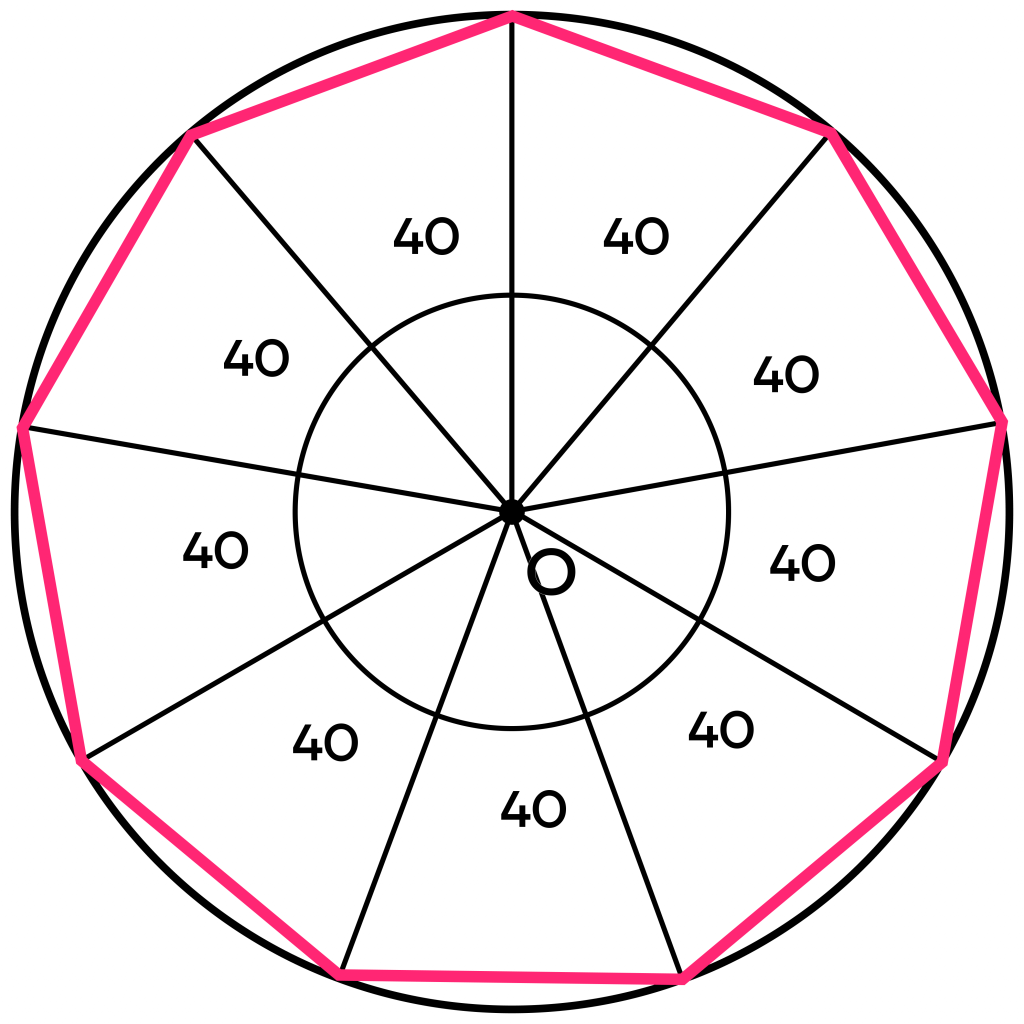
Таким способом можно построить любой многоугольник! Достаточно следовать следующему алгоритму:
1. Начертить окружность.
2. Разделить 360 на количество сторон. Так мы получим градусную меру угла, который будем откладывать дальше.
3. Отложить нужное количество углов и продлить их лучи до пересечения с окружностью.
4. Соединить полученные точки.
Но окружность и многоугольники связаны не только построением, а еще и несколькими интересными свойствами.
Вписанные и описанные многоугольники
Рассмотрим связь многоугольников и окружности.
Вписанный многоугольник — это многоугольник, все вершины которого лежат на окружности.
Описанный многоугольник — это многоугольник, все стороны которого касаются окружности.
Подробнее про вписанные многоугольники можно прочесть в статье «Вписанная и описанная окружность».
В этой же статье чуть подробнее разберем правильные многоугольники.
| Где в природе можно встретить описанный многоугольник? Пчелиные соты — одни из самых совершенных построек насекомых. Шестигранное строение придает сотам необходимую прочность при минимальной толщине стенок – их можно перемещать на далекие расстояния без риска повреждения структуры. Исследования ученых из Китая и Великобритании утверждают, что пчелы изначально строят круглые соты, а затем постепенно формируют шестиугольник. Таким образом, эти «маленькие трудяги» создают правильный описанный многоугольник. Для самых любознательных: почитать об этом исследовании можно по ссылке. |
Любой правильный многоугольник можно вписать в окружность, также как и возле любого правильного многоугольника можно описать окружность.

Вспомним, что центр вписанной окружности лежит в точке пересечения биссектрис, а центр описанной в точке пересечения серединных перпендикуляров. В правильных многоугольниках эти точки совпадают, а значит и центры вписанной и описанной окружности будут лежать в одной точке.
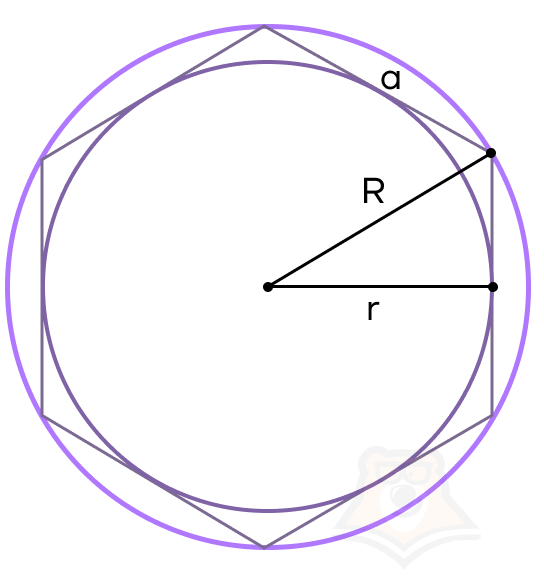
Для правильных многоугольников существует таблица, в которой приведены формулы для радиусов вписанной и описанной окружности, а также площадь многоугольника. Использование этих формул значительно упрощает решение многих задач.

Формулы из данной таблицы могут пригодиться для решения задач из первой части ОГЭ и ЕГЭ, а также как один из элементов решения более сложных задач с развернутым ответом из второй части. В качестве примера рассмотрим задание №1 ЕГЭ по профильной математике.
Задание. Площадь правильного шестиугольника равна \(96\sqrt{3}\). Найдите радиус описанной окружности.
Решение: Обратимся к приведенной выше таблице, площадь правильного шестиугольника можно найти по следующей формуле:
\(S=\frac{3a^2\sqrt{3}}{2}\)
Таким образом, получаем:
\(96\sqrt{3}=\frac{3a^2\sqrt{3}}{2}\)
Умножаем обе части равенства на \(2\), чтобы избавиться от знаменателя:
\(192\sqrt{3}=3a^2\sqrt{3}\)
Далее делим обе части на \(3\sqrt{3}\):
\(64=a^2\)
\(a_1=8, a_2=-8\)
Второй корень нам не подходит, поскольку длина стороны не может быть отрицательной.
Снова возвращаемся к таблице и видим, что радиус описанной окружности связан со стороной правильного шестиугольника следующим образом:
\(R=a\)
Значит, радиус нашей окружности равен:
\(R=8\)
Ответ: 8
В этой статье мы узнали много полезного и интересного о многоугольниках, а также рассмотрели задания, с которыми вы можете встретиться на экзаменах. Но только ли рассмотренными нами свойствами обладают многоугольники? Или есть какие-то особые фигуры, свойства которых мы не затронули? Об этом и многом другом вы можете узнать в статье «Трапеция».
Фактчек
- Многоугольник — это замкнутая ломаная линия, которая ограничивает часть плоскости. В многоугольнике может быть любое количество сторон, причем название конкретного многоугольника будет зависеть от количества его сторон, например, треугольник, четырехугольник, пятиугольник и так далее.
- Многоугольники бывают выпуклые и невыпуклые. Выпуклые многоугольники всегда лежат по одну сторону от прямой, которая содержит любую из его сторон.
- Найти сумму углов в любом многоугольнике можно по формуле 180(n-2), где n — количество сторон.
- Правильный многоугольник — это многоугольник, все стороны и углы которого равны. В любой правильный многоугольник можно вписать окружность, также возле любого правильного многоугольника можно описать окружность. Для правильных многоугольников существуют формулы для поиска радиусов вписанной и описанной окружности, а также площади и периметра многоугольника.
Проверь себя
Задание 1.
Что такое диагональ в многоугольнике?
- Прямая, соединяющая две вершины, принадлежащие одной стороне.
- Прямая, соединяющая две вершины, не лежащие на одной стороне.
- Наклонная прямая, проведенная к многоугольнику и пересекающая его в нескольких точках.
- Наклонная прямая, проведенная к многоугольнику и касающаяся его в одной точке.
Задание 2.
Чему равна сумма углов в семиугольнике?
- 800
- 180
- 360
- 900
Задание 3.
Чему равен один угол в правильном двадцатиугольнике?
- 162
- 160
- 180
- 200
Задание 4.
Периметр правильного восьмиугольника равен 364. Чему равна сторона этого многоугольника?
- 45
- 45,5
- 46
- 50
Задание 5.
Радиус вписанной окружности правильного шестиугольника равен 3√3. Чему равен радиус окружности, описанной около этого шестиугольника?
- 3
- 5
- 6
- 8
Ответы: 1. — 2; 2. — 4; 3. — 1; 4. — 2; 5. — 3.


 к списку статей
к списку статей