Алгебраические дроби и действия с ними

На этой странице вы узнаете

• От чего произошли алгебраические дроби?
• Как любой многочлен превратить в дробь?
• Можно ли сложить две алгебраические дроби и получить 0?

Можно ли разделить букву на букву? Нет-нет, не спешите крутить пальцем у виска, когда вам зададут такой вопрос, ведь алгебра может с уверенностью дать на него положительный ответ.

Дроби часто могут состоять не только из чисел, но и из букв. В этой статье мы разберемся с такими, на первый взгляд, страшными дробями, а также посмотрим, какие действия с ними можно выполнять.

Понятие алгебраической дроби

С понятием обыкновенной дроби мы познакомились в статье «‎Дроби». Алгебраическая дробь отличается от обыкновенной лишь тем, что на месте числителя и знаменателя могут стоять не только числа, но и алгебраические выражения, о которых шла речь в статьях «‎Одночлены и действия с ними» и «‎Многочлены и действия с ними». Чтобы вспомнить, как выполнять действия с многочленами, можно также ознакомиться со статьями «Преобразование алгебраических выражений. Часть 1» и «Преобразование алгебраических выражений. Часть 2».

От чего произошли алгебраические дроби? Изучение математики всегда начинается с понятия числа, арифметических действий над числами. Только после знакомства с числами мы переходим к следующему разделу – алгебре, которая погружает нас в мир букв (переменных). Точно так же и развивалась математика много-много лет назад: сначала появились числа, которые люди использовали для различных целей, главным образом – для счета. Когда появилась необходимость делить что-то, возникли и обыкновенные дроби. Например, кусочек пирога, разделенного на 8 одинаковых частей, теперь могли обозначить как \(\frac{1}{8}\). С возникновением алгебры, когда люди начали использовать математику не только для счета, но и для более общих целей (таких как решение различных физических задач, работы с формулами), понятие обыкновенной дроби дополнилось лишь буквами в ее составе. Так и возникла алгебраическая дробь. Именно поэтому можно считать, что алгебраическая дробь возникла именно от обыкновенной дроби. Все свойства и правила, которые будут разобраны в этой статье, действуют и для обыкновенных дробей. Наша же основная задача – подметить основные нюансы при работе именно с алгебраическими дробями.

Алгебраическая дробь – это запись вида \(\frac{A}{B}\), где A и B – многочлены (а также одночлены), при этом выражение A называют числителем алгебраической дроби, выражение B – знаменателем алгебраической дроби.

Например:

• \(\frac{a+b}{5-x}\);
• \(\frac{kx^2}{y-8}\);
• \(\frac{ax^2+bx+c}{6}\).

Перед обозначением дроби может также стоять знак «-». Например, \(-\frac{5}{7}\), \(-\frac{13}{105}\). Аналогично минус может стоять и перед алгебраической дробью (\(-\frac{x}{8}, -\frac{7+y^2}{x^2+by+6}\)). Этот минус можно «занести» в числитель, то есть записать дробь следующим образом:

\(-\frac{x}{8}=\frac{-x}{8}\)
\(-\frac{7+y^2}{x^2+by+6}=\frac{-(7+y^2)}{x^2+by+6}=\frac{-7-y^2}{x^2+by+6}\)

Такой прием часто используют при выполнении действия с алгебраическими дробями.

Дробная черта (черта между числителем и знаменателем) в алгебраической дроби, так же, как и в случае обыкновенной дроби, означает деление числителя на знаменатель. 

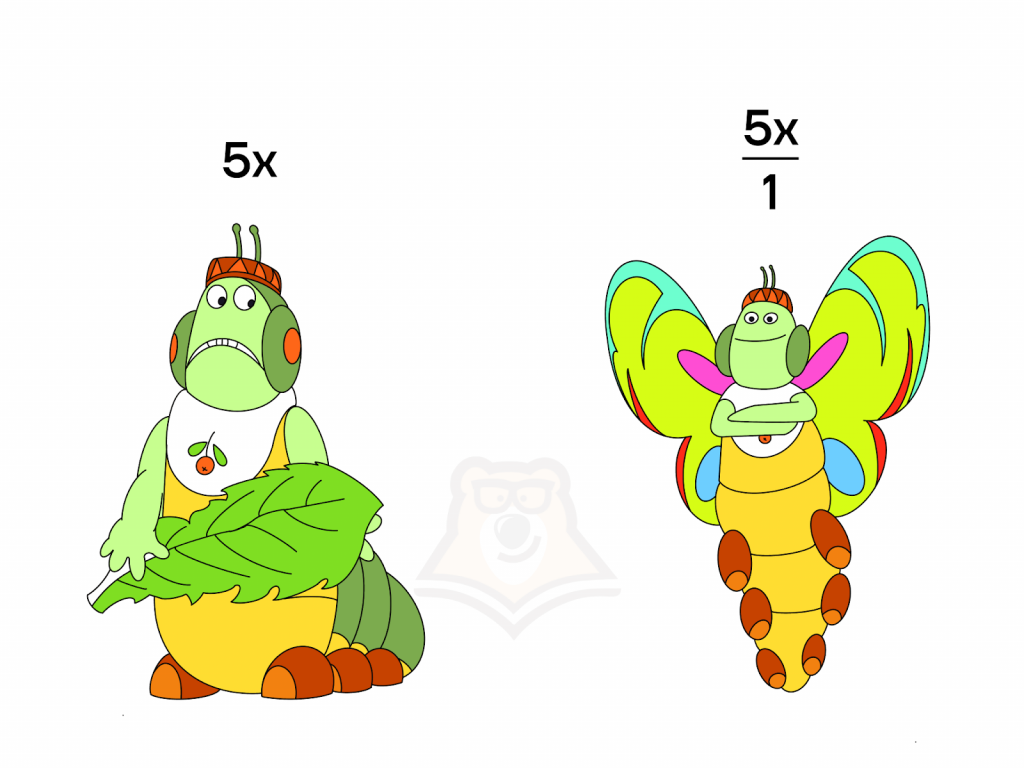
Как любой многочлен превратить в дробь? Одно из основных свойств деления – при делении любого выражения на 1 мы получаем то же самое выражение, то есть \(A :1=A\). Тогда можем записать это следующим образом: \(A=A :1=\frac{A}{1}\) Любой многочлен (в том числе и одночлен) можно представить в виде алгебраической дроби, числителем которой будет являться этот же многочлен, а знаменатель равен 1. Например: \(5x=\frac{5x}{1}\) \(7,3x^3-2y+6=\frac{7,3x^3-2y+6}{1}\)

В дальнейшем в ходе статьи мы не раз будем сталкиваться со степенями и их свойствами, в связи с чем рекомендуем освежить этот материал в памяти, прочитав статью «Действия с натуральными числами». 

Обыкновенную дробь можно видоизменять, не меняя при этом ее значения. Делается это с помощью основного свойства дроби, которым обладает и любая алгебраическая дробь. 

Основное свойство алгебраической дроби

Для начала вспомним основное свойство обыкновенной дроби: в любой обыкновенной дроби и числитель, и знаменатель можно умножить или разделить на одно и то же число, отличное от нуля. Значение дроби от этого не поменяется.

Это свойство не зря называют основным: оно помогает представлять одну и ту же дробь разными способами, что, безусловно, часто используется в математике.

Например, дробь \(\frac{3}{6}\) можно представить как:

• \(\frac{3}{6}=\frac{3*2}{6*2}=\frac{6}{12}\)
• \(\frac{3}{6}=\frac{3:3}{6:3}=\frac{1}{2}\)
• \(\frac{3}{6}=\frac{3*100}{6*100}=\frac{300}{600}\)

В алгебраической дроби и числитель, и знаменатель можно умножить или разделить не только на одно натуральное число, но и на многочлен (в том числе и одночлен).

В любой алгебраической дроби и числитель, и знаменатель можно умножить или разделить на одно и то же выражение, значение которого отлично от нуля. Значение дроби от этого не поменяется.

\(\frac{A}{B}=\frac{A*C}{B*C}\), где \(C\neq0\)
\(\frac{A}{B}=\frac{A:C}{B:C}\), где \(C\neq0\)

Почему же \(C\neq0\)? 

• Числитель и знаменатель нельзя разделить на 0 согласно одному из главных правил математики: делить на нуль нельзя. 
• Если же числитель и знаменатель умножить на 0, то в знаменателе получится 0. Дробь означает деление, то есть, числитель делится на знаменатель. И тут мы снова упираемся в то, что делить на 0 мы не можем.

Приведем пример. В дроби \(\frac{7x}{5+y}\) умножим и числитель, и знаменатель на многочлен \((x+2)\):

\(\frac{7x}{5+y}=\frac{7x*(x+2)}{(5+y)*(x+2)}=\frac{7x^2+7x*2}{5x+yx+5*2+2y}=\frac{7x^2+14x}{5x+yx+10+2y}\)

Получили: \(\frac{7x}{5+y}=\frac{7x^2+14x}{5x+yx+10+2y}\).

Приведем еще несколько примеров:

• \(\frac{13}{x^2+3}=\frac{13*2x}{(x^2+3)*2x}=\frac{26x}{2x^3+6x}\);
• \(\frac{km^3+5m-1}{6k+8}=\frac{(km^3+5m-1)*3}{(6k+8)*3}=\frac{3km^3+15m-3}{18k+24}\);
• \(\frac{d}{d^2}=\frac{d:d}{d^2:d}=\frac{1}{d}\)

Итак, есть два варианта использования основного свойства алгебраической дроби:

1. умножить числитель и знаменатель на одно и то же выражение, значение которого отлично от нуля;
2. разделить числитель и знаменатель на одно и то же выражение, значение которого отлично от нуля.

Второй вариант также называют сокращением дроби. Поговорим подробнее о нем.

Сокращение алгебраической дроби

Сократить алгебраическую дробь – значит разделить числитель и знаменатель этой дроби на выражение, значение которого отлично от нуля.

Так как сокращение напрямую связано с делением, для начала вспомним одно из важных свойств степеней, которое нам понадобится:

\(a^b:a^c=a^{b-c}\)

То есть, при делении двух степеней с одинаковыми основаниями получается степень с таким же основанием, показатель которой равен разности показателей этих степеней. 

Приведем несколько примеров:

• \(a^5:a^2=a^{5-2}=a^3\);
• \(z^{11}:z^7=z^{11-7}=z^4\);
• \(k^{100}:k=k^{100-1}=k^{99}\).

Это свойство понадобится нам для сокращения переменных.

Чтобы сократить алгебраическую дробь, для начала необходимо числитель и знаменатель этой дроби разложить на множители.

Например, рассмотрим дробь \(\frac{x^2+2x+1}{2x+2}\). В числителе этой дроби можно заметить полный квадрат суммы, общая формула которого: \(a^2+2ab+b^2=(a+b)^2\). Получаем:

\(x^2+2x+1=(x+1)^2\)

В знаменателе дроби \((2x+2)\) можно вынести за скобки общий множитель 2 : 

\(2x+2=2(x+1)\)

Подставим получившиеся выражения вместо числителя и знаменателя:

\(\frac{x^2+2x+1}{2x+2}=\frac{(x+1)^2}{2(x+1)}\)

Видим, что в числителе и знаменателе появился общий множитель (x+1), на который мы и можем сократить нашу дробь:

\(\frac{x^2+2x+1}{2x+2}=\frac{(x+1)^2}{2(x+1)}=\frac{(x+1)^2:(x+1)}{2(x+1):(x+1)}=\frac{x+1}{2}\)

Чтобы сократить алгебраическую дробь, необходимо:

1) разложить числитель и знаменатель этой дроби на множители;
2) сократить эту дробь на общие множители числителя и знаменателя, образовавшиеся в результате их разложения на множители.

Рассмотрим еще один пример: сократим дробь \(\frac{3a^2b+6ab^2}{12a^4b^3-18a^2b^5}\).

Числитель \(3a^2b+6ab^2\) разложим на множители, вынеся за скобки общий множитель:

\(3a^2b+6ab^2=3ab(a+2b)\)

Таким же образом разложим знаменатель \(12a^4b^3-9a^2b^5\):

\(12a^4b^3-18a^2b^5=6a^2b^3(2a^2-3b^2)\)

Подставим полученные выражения в числитель и знаменатель дроби:

\(\frac{3a^2b+6ab^2}{12a^4b^3-18a^2b^5}=\frac{3ab(a+2b)}{6a^2b^3(2a^2-3b^2)}\)

Для начала обратим внимание на числовые множители 3 и 6, наибольшим общим делителем которых является число 3. Значит, можем сократить дробь на 3:

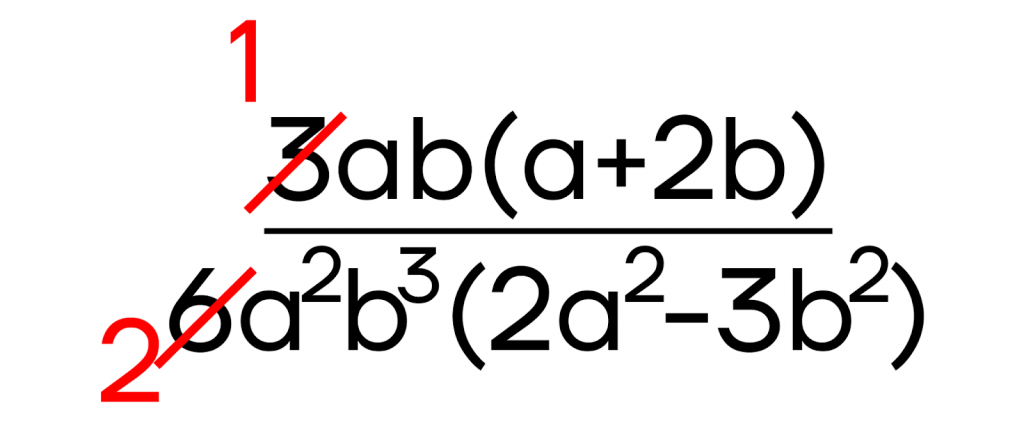
Далее посмотрим на переменную a: она выступает в качестве отдельного множителя и в числителе (в первой степени), и в знаменателе (во второй степени). Значит, на нее мы тоже сможем сократить нашу дробь. Причем сокращать будем на наименьшую из данных степеней, то есть на a (первая степень). Для этого разделим множители a и \(a^2\) на a.

Аналогичная ситуация с переменной b: из двух степеней, встречающихся в числителе (первая степень) и знаменателе (третья степень), мы сократим дробь на наименьшую степень, то есть на b (первая степень).

Получим:

Оставшиеся множители \((a+2b)\) в числителе и \((2a^2-3b^2)\) в знаменателе сократить никак не получится, ведь это два разных выражения, не имеющих общих множителей. Тогда дробь можем считать оканчательно сокращенной.

Такой способ сокращения и используют в алгебре: вместо того, чтобы сокращать сразу два больших «страшных» выражения, можно сокращать по отдельности их множители, то есть отдельно сокращать числовые множители, отдельно – степени с одинаковым основанием.

Разберем пример задания №8 из ОГЭ по математике.

Задание. Упростите выражение \(\frac{9k^2-12k+4}{6k-4}\) и найдите его значение при \(k=2\).

Решение. Для начала разложим числитель и знаменатель данной дроби на множители:

\(9k^2-12k+4=(3k)^2-2*3k*2+2^2=(3k-2)^2\)
\(6k-4=2(3k-2)\)

Подставим получившиеся выражения в дробь и выполним сокращение:

\(\frac{(3k-2)2^2}{(3k-2)}=\frac{3k-2}{2}\)

При \(k=2\) получаем: 

\(\frac{3k-2}{2}=\frac{3*2-2}{2}=\frac{4}{2}=2\)

Ответ: 2

Также важно отметить, что далеко не все алгебраические дроби можно сократить. Например, дроби \(\frac{1}{x}, \frac{x^2+y-2}{z+8x+y}\) сократить никак не получится. В таком случае их называют несократимыми.

Дроби, которые можно сократить, называют сократимыми.

Полностью сократить дробь – значит преобразовать ее до несократимой дроби.

Сокращение позволяет нам совершать значительные преобразования над дробями, упрощать их. При этом на сокращении наши возможности не останавливаются, ведь над алгебраическими дробями можно также совершать различные действия – сложение, вычитание, умножение, деление. Остановимся подробнее на каждом из них.

Сложение и вычитание алгебраических дробей с одинаковым знаменателем

Сложение и вычитание алгебраических дробей с одинаковыми знаменателями происходят по аналогии со сложением и вычитанием обыкновенных дробей с одинаковыми знаменателями.

Сумма или разность алгебраических дробей с одинаковыми знаменателями есть алгебраическая дробь, числителем которой является сумма или разность числителей исходных дробей, а знаменатель равен знаменателю этих дробей.

\(\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}\)
\(\frac{a}{c}-\frac{b}{c}=\frac{a-b}{c}\)

Приведем несколько примеров:

1. \(\frac{2a-3b}{x^2}+\frac{2a}{x^2}=\frac{(2a-3b)+(2a)}{x^2}=\frac{2a-3b+2a}{x^2}=\frac{4a-3b}{x^2}\)
2. \(\frac{zk+8y+5}{kx+b}+(-\frac{8y+4}{kx+b})=\frac{zk+8y+5}{kx+b}+\frac{-8y-4}{kx+b}=\frac{(zk+8y+5)+(-8y-4)}{kx+b}=\frac{zk+8y+5-8y-4}{kx+b}=\frac{zk+1}{kx+b}\)
3. \(\frac{9m+x^3y}{2c^5-1}-\frac{9m^2-6m+8}{2c^2-1}=\frac{(9m+x^3y)-(9m^2-6m+8)}{2c^2-1}=\frac{9m+x3y-9m2-6m+8}{2c^2-1}=\frac{3m+x^3y+9m^2+8}{2c^2-1}\)

То есть, главное при таком сложении/вычитании – правильно раскрыть скобки и привести после этого подобные слагаемые.

Таким образом, с дробями с одинаковым знаменателем все просто: складываем или вычитаем числители, а знаменатель оставляем таким же. Как же быть с алгебраическими дробями с разными знаменателями?

Сложение и вычитание алгебраических дробей с разными знаменателями

Для начала вспомним: чтобы выполнить действия сложения или вычитания дробей с разными знаменателями, необходимо для начала привести их к общему знаменателю.

То же самое действует и для алгебраических дробей.

Чтобы выполнить действия сложения или вычитания алгебраических дробей с разными знаменателями, необходимо:
1. привести эти дроби к общему знаменателю;
2. выполнить действие сложения/вычитания дробей с одинаковым знаменателем.

Общий знаменатель – это общее кратное знаменателей всех дробей, над которыми выполняются действия сложения/вычитания. 

Как же найти общее кратное двух многочленов? Разберемся в этом, рассмотрев пример:

\(\frac{7}{4y(x+y)^2}+\frac{9}{6k(x+y)}\)

Наша основная задача сейчас – свести дроби к общему знаменателю, то есть преобразовать дроби так, чтобы знаменатели у них стали одинаковыми. 

Здесь можно представить себя строителями. Каждый знаменатель мы будем «достраивать» до общего.

Начнем с числовых множителей знаменателей 4 и 6. Наименьшим общим кратным этих двух чисел является число 12 \((12:4=3; 12:6=2)\). Поэтому в первой дроби, согласно основному свойству дроби, мы можем и числитель, и знаменатель умножить на 3, во второй дроби – на 2. Напишем это следующим образом:

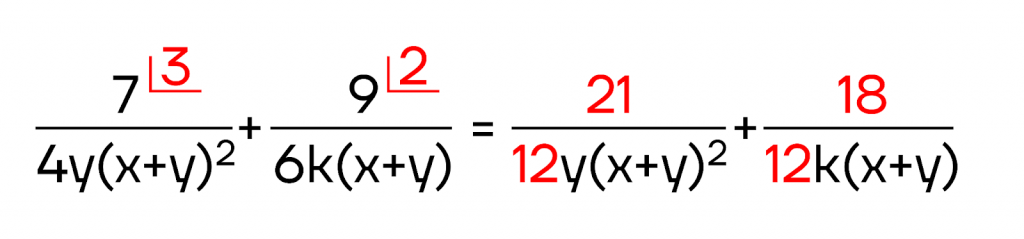
На этом наше строительство, разумеется, не заканчивается, ведь знаменатели все еще разные.

Далее мы можем «уравнять» показатели степеней у множителя (x+y), который есть и в первом (вторая степень), и во втором (первая степень) знаменателе. Для этого домножим вторую дробь на (x+y):

Остался последний шаг на пути к общему знаменателю. В первой дроби в знаменателе есть множитель y, которого нет в знаменателе второй дроби. Поэтому вторую дробь можем домножить на y (чтобы он там «появился»). Аналогично первую дробь домножим на k:

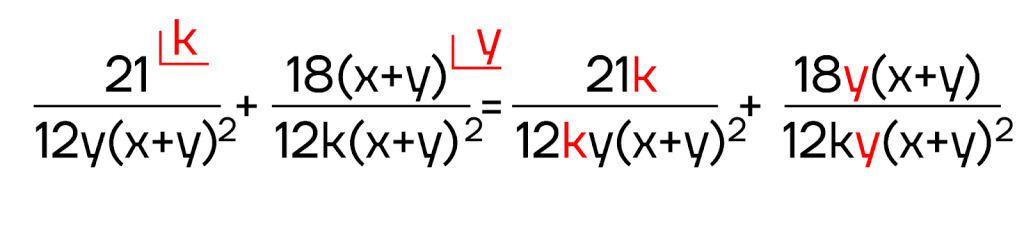
И вот, мы получили общий знаменатель в обеих дробях, наше строительство на этом подходит к концу. Осталось только сложить эти дроби так, как мы это делали с дробями с одинаковыми знаменателями:

\(\frac{21k}{12ky(x+y)^2}+\frac{18y(x+y)}{12ky(x+y)^2}=\frac{21k+18y(x+y)}{12ky(x+y)^2}=\frac{21k+18yx+18y^2}{12ky(x+y)^2}\)

В рассмотренном примере мы сложили две алгебраические дроби с разными знаменателями \({4y(x+y)^2\) и \(6k(x+y)\), в ходе чего привели эти дроби к общему знаменателю \(12ky(x+y)^2\). Этот общий знаменатель является общим кратным знаменателей двух складываемых дробей. Как видим, он «включает» в себя оба этих знаменателя:

Тогда все действие приведения к общему знаменателю можно записать следующим образом:

Множители \(3k\) и \(2y(x+y)\) в этом случае также называют дополнительными множителями.

По аналогии можно привести к общему знаменателю любые взятые алгебраические дроби.

Обращаем внимание: в рассмотренном примере знаменатели двух дробей изначально были разложены на множители. В иных случаях эту операцию необходимо проделать самостоятельно перед началом приведения дробей к общему знаменателю.

Чтобы привести алгебраические дроби к общему знаменателю, необходимо:

1) разложить знаменатели этих дробей на множители;

2) найти наименьшее общее кратное числовых множителей в знаменателях и привести к нему обе дроби;

3) общие множители в знаменателях «уравнять» в степенях, то есть привести их к наибольшей степени из присутствующих;

4) умножить и числитель, и знаменатель каждой дроби на множители, которые являются множителями в знаменателях других дробей, но не являются множителями в знаменателе этой дроби.

Рассмотрим еще один пример: \(\frac{x+8}{ba^2+2ab+b}-\frac{c^2}{3a^2b^3-3b^3}\).

Для начала разложим на множители числители обеих дробей:

\(ba^2+2ab+b=b(a^2+2a+1)=b(a+1)^2\)
\(3a^2b^2-3b^2=3b^2(a^2-1)=3b^2(a-1)(a+1)\)

Подставим получившиеся выражения вместо знаменателей:

\(\frac{x+8}{ba^2+2ab+b}-\frac{c^2}{3a^2b^3-3b^3}=\frac{x+8}{b(a+1)^2}-\frac{c}{3b^3(a-1)(a+1)}\)

1. Числовой коэффициент первого и второго знаменателей равны 1 и 3 соответственно, значит, первую дробь можем домножить на 3.
2. Чтобы «уравнять» степени множителей \((a+1)^2\) и \((a+1)\) в знаменателях первой и второй дроби соответственно, домножим вторую дробь на \((a+1)\).
3. Чтобы «уравнять» степени множителей \(b\) и \(b^3\) в знаменателях первой и второй дроби соответственно, домножим первую дробь на \(b^2\).
4. Первую дробь домножим на множитель \((a-1)\), которого нет в ее знаменателе.

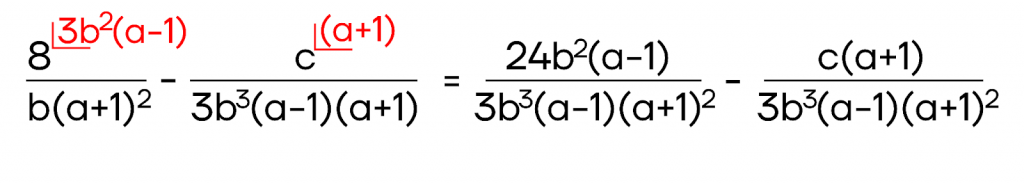
Осталось выполнить вычисления, получим: 

\(\frac{24b^2(a-1)}{3b3(a-1)(a+1)2}-\frac{c(a+1)}{3b^3(a-1)(a+1)^2}=\frac{(24b^2a-24b^2)-(ca+c)}{3b^3(a-1)(a+1)^2}=\frac{24b^2a-24b^2-ca-c}{3b^3(a-1)(a+1)^2}\)

Разберем пример задания №6 из ЕГЭ по профильной математике.

Задание. Найти значение выражения \((a^2-b^2)(\frac{1}{a-b}-\frac{1}{a+b})-a\) при \(a=1000, b=501\)

Решение. В первую очередь выполним вычитание алгебраических дробей в скобках \(\frac{1}{a-b}-\frac{1}{a+b}\). Общим знаменателем в этом случае будет выражение \((a-b)(a+b)\), первую дробь домножим на \((a+b)\), вторую – на \((a-b)\):

\(\frac{1}{a-b}-\frac{1}{a+b}=\frac{a+b}{(a-b)(a+b)}-\frac{a-b}{(a-b)(a+b)}=\frac{a+b-(a-b)}{(a-b)(a+b)}=\frac{a+b-a+b}{(a-b)(a+b)}=\frac{2b}{a^2-b^2}\)

Подставим получившуюся дробь в исходное выражение:

\((a^2-b^2)(\frac{1}{a-b}-\frac{1}{a+b})+2a=(a^2-b^2)*\frac{2b}{a^2-b^2}-a\)

Выполним первое действие – умножение: 

\((a^2-b^2)*\frac{2b}{a^2-b^2}=\frac{a^2-b^2}{1}*\frac{2b}{a^2-b^2}=\frac{(a^2-b^2)2b}{a^2-b^2}=\frac{2b}{1}=2b\)

Подставим в выражение: 

\((a^2-b^2)*\frac{2b}{a^2-b^2}-a=2b-a\)

При \(b=501\) и \(a=1000\) получим:

\(2b-a=2501-1000=1002-1000=2\)

Ответ: 2

Можно ли сложить многочлен с алгебраической дробью? Конечно, для этого нужно сначала представить этот многочлен в виде дроби со знаменателем 1, а затем выполнить сложение получившихся дробей. Например:

\(7k^4+\frac{k^4-1}{9}=\frac{7k^4}{1}+\frac{k^4-1}{9}=\frac{7k^4*9}{1*9}+\frac{k^4-1}{9}=\frac{63k^4}{9}+\frac{k^4-1}{9}=\frac{63k^4+k^4-1}{9}=\frac{64k^4-1}{9}\)

Общим знаменателем в этом случае будет являться знаменатель второй дроби (9), который также будет дополнительным множителем для первой дроби (7k41).

Можно ли сложить две алгебраические дроби и получить 0? Действительно, существуют такие дроби. Приведем пример: \(\frac{2x}{10-x^2}+(-\frac{2x}{10-x^2})=\frac{2x}{10-x^2}+\frac{-2x}{10-x^2}=\frac{2x+(-2x)}{10-x^2}=\frac{0}{10-x^2}=0\) То есть, при сложении дробей \(\frac{2x}{10-x^2}\) и \(-\frac{2x}{10-x^2}\) мы получили 0. Такие дроби также называют противоположными.  \(\frac{a}{b}+\frac{c}{d}=0 \rightarrow \frac{a}{b}\) и \(\frac{c}{d}\) – противоположные Как можно заметить, дроби с одинаковыми знаменателями являются противоположными, если сумма их числителей после выполнения всех преобразований равна 0.  Приведем еще пример: \(\frac{-10+6y}{8}+\frac{2(3y-5)}{8}=\frac{-10+6y}{8}+\frac{6y-10}{8}=\frac{-10+6y+6y-10}{8}=\frac{0}{8}=0\) Таким образом, дроби \(\frac{-10+6y}{8}\) и \(\frac{2(3y-5)}{8}\) также являются противоположными. Чтобы понять, являются ли две дроби с разными знаменателями противоположными, необходимо для начала привести их к общему знаменателю, после чего выполнить сложение. Рассмотрим пример: \(\frac{x^2+x}{2x}+\frac{-x-1}{2}=\frac{x^2+x}{2x}+\frac{(-x-1)*x}{2*x}=\frac{x^2+x}{2x}+\frac{-x^2-x}{2x}=\frac{x^2+x-x^2-x}{2x}=\frac{0}{2x}=0\) Сделаем вывод: дроби \(\frac{x^2+x}{2x}\) и \(\frac{-x-1}{2}\) также являются противоположными.

Процесс приведения алгебраических дробей, может быть, и кажется чем-то слишком сложным, но если в нем разобраться, понять суть, то оказывается, что это может быть очень увлекательно, особенно с «длинными» выражениями. 

Итак, со сложением и вычитанием алгебраических дробей мы разобрались. Как насчет умножения?

Умножение алгебраических дробей

Как мы уже поняли, многие действия с алгебраическими дробями выполняются так же, как и с обыкновенными дробями. Умножение здесь не стало исключением.

Произведение алгебраических дробей равно алгебраической дроби, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.

\(\frac{a}{b}*\frac{c}{d}=\frac{a*c}{b*d}\)

Приведем пример:

\(\frac{x2}{10y}*{5y}{x+10}=\frac{x^2*5y}{10y(x+10)}\)

Перед тем, как раскрыть скобки в знаменателе, вспомним, что при умножении дробей мы можем сокращать множители. То же самое касается и алгебраических дробей: согласно основному свойству алгебраической дроби, 5 и 10 можно сократить на 5, а также можно сократить y в числителе и в знаменателе:

Получаем:

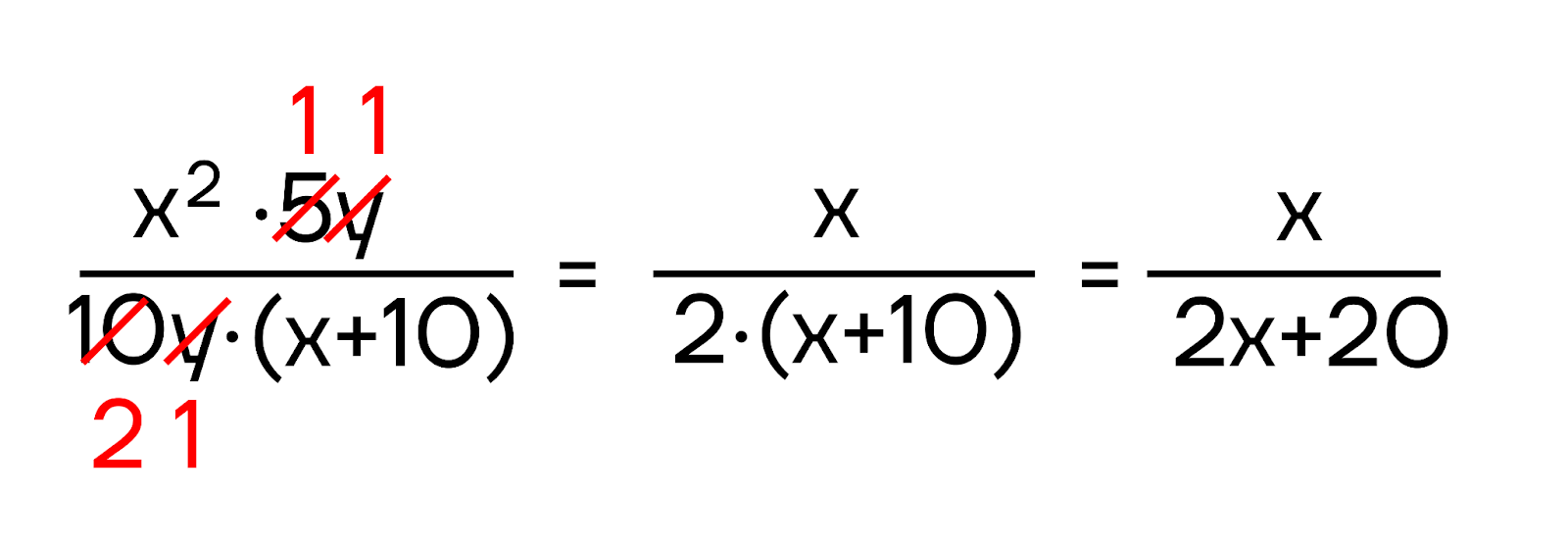
Рассмотрим еще один пример:

\(\frac{6y+1}{7m^2}*\frac{m^2}{18y+3}=\frac{(6y+1)*m^2}{7m^2*(18y+3)}\)

Можно заметить, что в множителе \(18y+3\) можно вынести общий множитель за скобки:

\(\frac{(6y+1)*m^2}{7m^2*(18y+3)}\)=\frac{(6y+1)*m^2}{7m^2*3(6y+1)}\)

Полученную дробь можно сократить на \((6y+1)\) и \(m^2\):

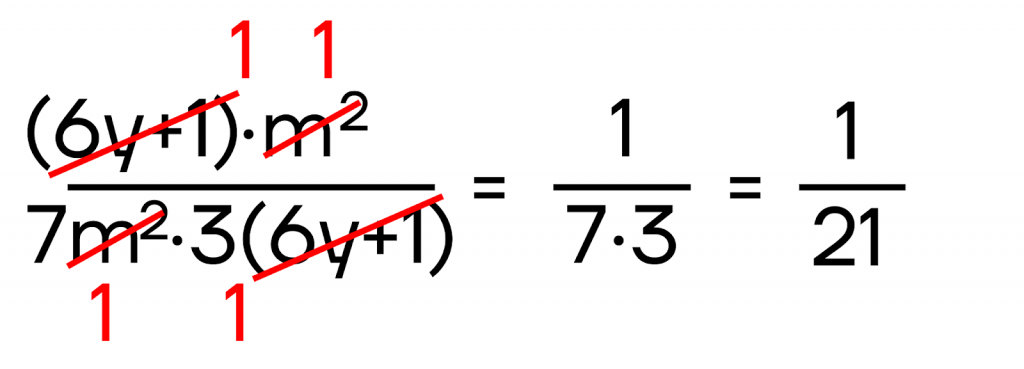
Таким образом, перед тем, как выполнять само умножение, всегда лучше проверить, нельзя ли выделить пары множителей, которые можно сократить друг с другом. Часто это очень сильно упрощает вычисления.

Помимо умножения дроби на дробь, можно также умножить алгебраическую дробь на выражение. Для этого сначала нужно представить это выражение в виде дроби со знаменателем 1. Например:

\((2x-1)*\frac{3y}{2x+8}=\frac{2x-1}{1}*\frac{3y}{2x+8}=\frac{(2x-1)*3y}{1*(2x+8)}=\frac{6xy-3y}{2x+8}\)

Алгебраические дроби, произведение которых равно 1, называют обратными алгебраическими дробями.

Например, \(\frac{9}{x+8}\) и \(\frac{x+8}{9}\):

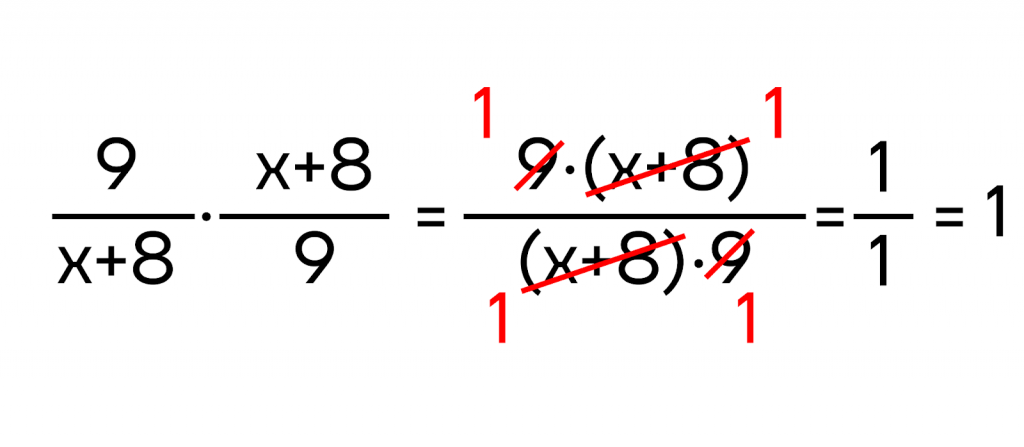
Дробь, обратная данной дроби, часто выглядит просто как «перевернутая» дробь, как в рассмотренном выше примере: дробь \(\frac{x+8}{9}\), обратная дроби \(\frac{9}{x+8}\). Однако одна и та же дробь может принимать разные «образы».

Например, дроби \(\frac{4x^2-4x+1}{5x+5}\) и \(\frac{5(x+1)}{(2x-1)^2}\) также являются обратными:

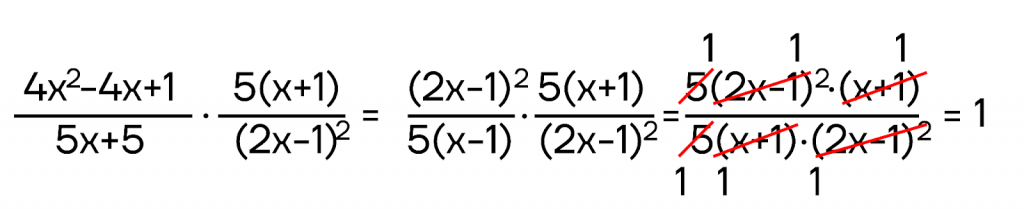
Конечно, там, где есть умножение, есть и возведение в степень. Разберемся с этим подробнее.

Возведение алгебраической дроби в степень

И снова обратимся к обыкновенным дробям, ведь возведение алгебраических дробей в степень происходит таким же способом:

\((\frac{a}{b})^n=\frac{a^n}{b^n}\)

Чтобы возвести алгебраическую дробь в степень, необходимо возвести в эту степень числитель и знаменатель дроби.

Например:

\((\frac{7k^3z}{x+8})^2=\frac{(7k^3z)^2}{(x+8)^2}=\frac{49k^6z^2}{x^2+16x+64}\)

\((\frac{y^4-3x}{2m^5})^3=\frac{(y^4-3x)^3}{(2m^5)^3}=\frac{y^{12}-9y^8x+27y^4x^2-27x^3}{8m^{15}}\)

Осталось разобрать последнее действие, которое можно совершать с алгебраической дробью – деление. Сделаем это в следующем разделе.

Деление алгебраических дробей

Как же происходит деление алгебраических дробей? Конечно, так же, как и деление обыкновенных дробей.

Чтобы разделить одну алгебраическую дробь на другую, необходимо первую дробь умножить на дробь, обратную второй алгебраической дроби.

\(\frac{a}{b}:\frac{c}{d}=\frac{a}{b}*\frac{d}{c}\)

Проще говоря, необходимо просто первую дробь умножить на «перевернутую» вторую дробь.

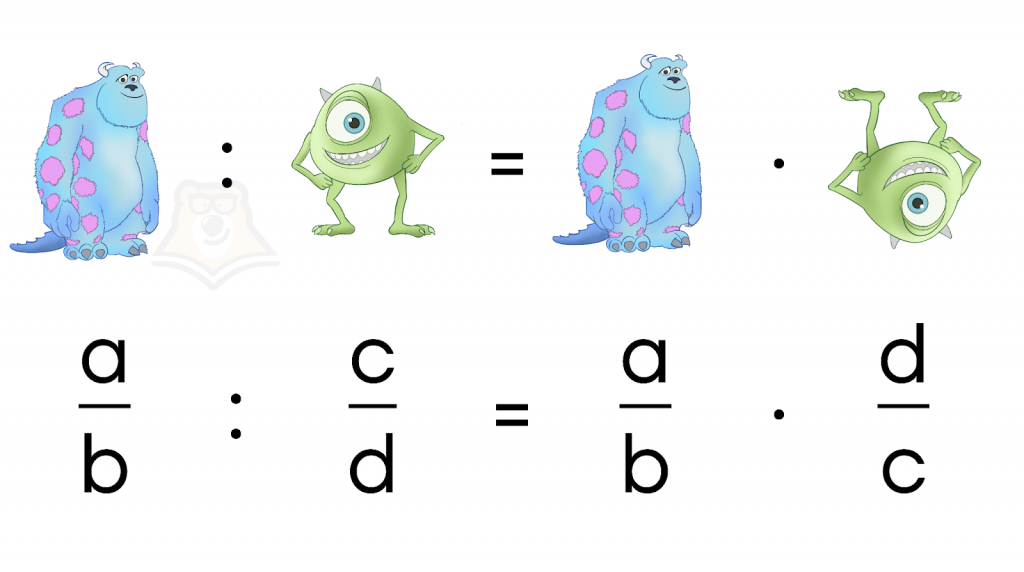
Разберем некоторые примеры:

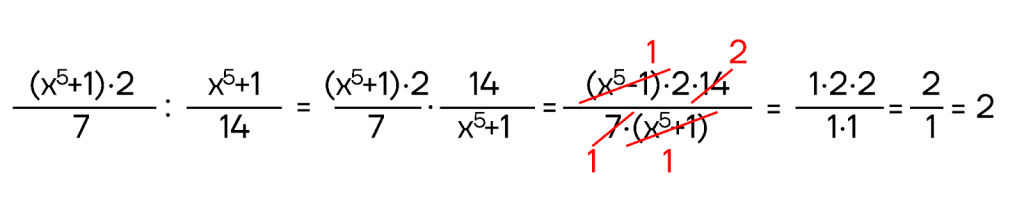
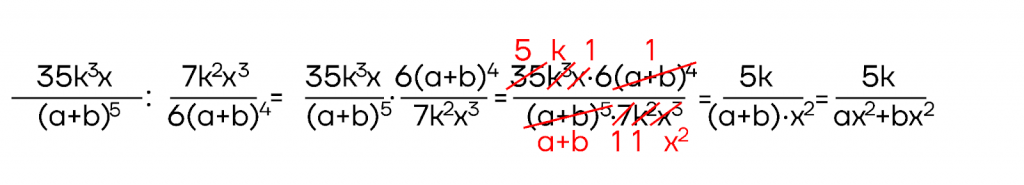
Как можем еще раз заметить: от деления мы переходим к умножению, а далее действуем по известному алгоритму.

Чтобы поделить выражение на алгебраическую дробь или алгебраическую дробь на выражение, необходимо сначала это выражение представить в виде дроби со знаменателем 1. Приведем пару примеров:

\(3k:\frac{2+k^2}{3+8k}=\frac{3k}{1}:\frac{2+k^2}{3+8k}=\frac{3k}{1}*\frac{3+8k}{2+k^2}=\frac{3k(3+8k)}{2+k^2}=\frac{9k+24k^2}{2+k^2}\)

\(\frac{11+x}{y^3}:(3z)=\frac{11+x}{y^3}:\frac{3z}{1}=\frac{11+x}{y^3}*\frac{1}{3z}=\frac{(11+x)*1}{y^3*3z}=\frac{11+x}{3y^3z}\)

На этом статья об алгебраических дробях подходит к своему завершению. Данные дроби играют большую роль в математике и часто используются для решения различных задач, поэтому особенно важно знать, как и какие действия с ними выполнять. 

Если вам понравилась эта статья, рекомендуем скорее перейти к еще одной немаловажной теме – «Линейные, квадратные и кубические уравнения».

Термины

Алгебраическое выражение – это запись, состоящая из чисел и переменных (букв), арифметических действий между ними (сложения, вычитания, умножения, деления), а также, при необходимости, скобок.

Натуральные числа – это числа, используемые при счете (1;2;3;4; и так далее). 

Обыкновенная дробь – запись вида \(\frac{m}{n}\), где m,n любые натуральные числа.

Фактчек

• Алгебраическая дробь – это запись вида \(\frac{A}{B}\), где A и B – многочлены (а также одночлены), при этом выражение A называют числителем алгебраической дроби, выражение B – знаменателем алгебраической дроби.
• Любая алгебраическая дробь обладает основным свойством алгебраической дроби: в любой алгебраической дроби и числитель, и знаменатель можно умножить или разделить на одно и то же выражение, значение которого отлично от нуля.
• Чтобы сократить алгебраическую дробь, необходимо числитель и знаменатель разделить на выражение, отличное от 0. 
• Так же, как и над обыкновенными дробями, над алгебраическими дробями можно выполнять действия сложения, вычитания, умножения и деления, а также любую алгебраическую дробь можно возвести в степень.

Проверь себя

Задание 1.
Запись \(\frac{45x^2+9x-10}{7}\):

1. является обыкновенной дробью;
2. является алгебраической дробью;
3. не является дробью;
4. является и обыкновенной, и алгебраической дробью.

Задание 2.
Дробь \(\frac{55x^2y}{11xy^2}\) можно сократить на:

1. x;
2. y;
3. 11;
4. все варианты верны.

Задание 3.
Сумма дробей \(\frac{5x^3}{x+y}\) и \(\frac{x^3}{y+x}\) равна:

1. \(\frac{6x^3}{x+y}\);
2. \(\frac{5x^3}{x+y}\);
3. \(\frac{6x^3}{2x+2y}\);
4. \(\frac{5x^3}{2x+2y}\).

Задание 4.
Общим знаменателем дробей \(\frac{1}{5x^2(2x+2)}\) и \(\frac{1}{10x^2(2x+2)^2}\) является выражение:

1. \(50x^3(2x+2)^3\);
2. \(5x(2x+2)\);
3. \(10x^2(2x+2)^2\);
4. \(2x(2x+2)\).

Ответы: 1. – 2; 2. – 4; 3. – 1; 4. – 3