Графики тригонометрических функций

На этой странице вы узнаете

• Что означают слова тригонометрия, синус, косинус, тангенс и котангенс?
• Куда уехали синус и косинус?
• Где у тригонометрических функций противоречие? 

Любую функцию в математике можно изобразить графически. Тригонометрические функции не исключение. В статьях «Тригонометрическая окружность. Часть 1» и «Тригонометрическая окружность. Часть 2» мы уже разбирали один из видов графического изображения функции. 

Однако окружность — не единственный график тригонометрических функций. Их можно изобразить в стандартной для нас системе координат — то есть на осях х и у. Разберем чуть подробнее, как выглядят графики синуса, косинуса, тангенса и котангенса. 

Графики тригонометрических функций

К тригонометрическим функциям относятся синус, косинус, тангенс и котангенс. И все они неразрывно связаны со сторонами прямоугольного треугольника. Как это происходит и почему мы подробно обсуждаем в статье «Тригонометрическая окружность. Часть 1». 

Что означают слова тригонометрия, синус, косинус, тангенс и котангенс? Тригонометрия — это слово греческого происхождения. В буквальном переводе оно означает «измерение треугольников»: trigwnon — треугольник, metrew — измеряю. Под измерением треугольников понимается их решение, то есть определение сторон, углов и других элементов треугольника, когда известны лишь некоторые из них. С древних времен и до наших дней большое количество задач, связанных с плоскими и объемными фигурами геометрии, а также практических моментов астрономии, строительного дела и других наук приводятся к задаче решения треугольников. Слово «синус» пришло к нам из Древней Индии. Отрезок АМ на изображении индийцы называли ардхаджива, что переводится как «половина тетивы лука». Позднее это слово несколько видоизменялось и окончательно было заменено латинским sinus при переводе текстов на латынь. Слово косинус — это сокращение латинского выражения completely sinus, то есть «дополнительный синус» или «синус дополнительной дуги»: \(cos x=sin(90°-x)\). Название тангенса происходит от латинского tanger и переводится как «касающийся», ведь линия тангенсов — касательная к единичной окружности. А cotangens в переводе с латыни означает «соприкасающийся». Это переформулированное слово от изначального названия тангенса.

Сейчас кратко вспомним, что:

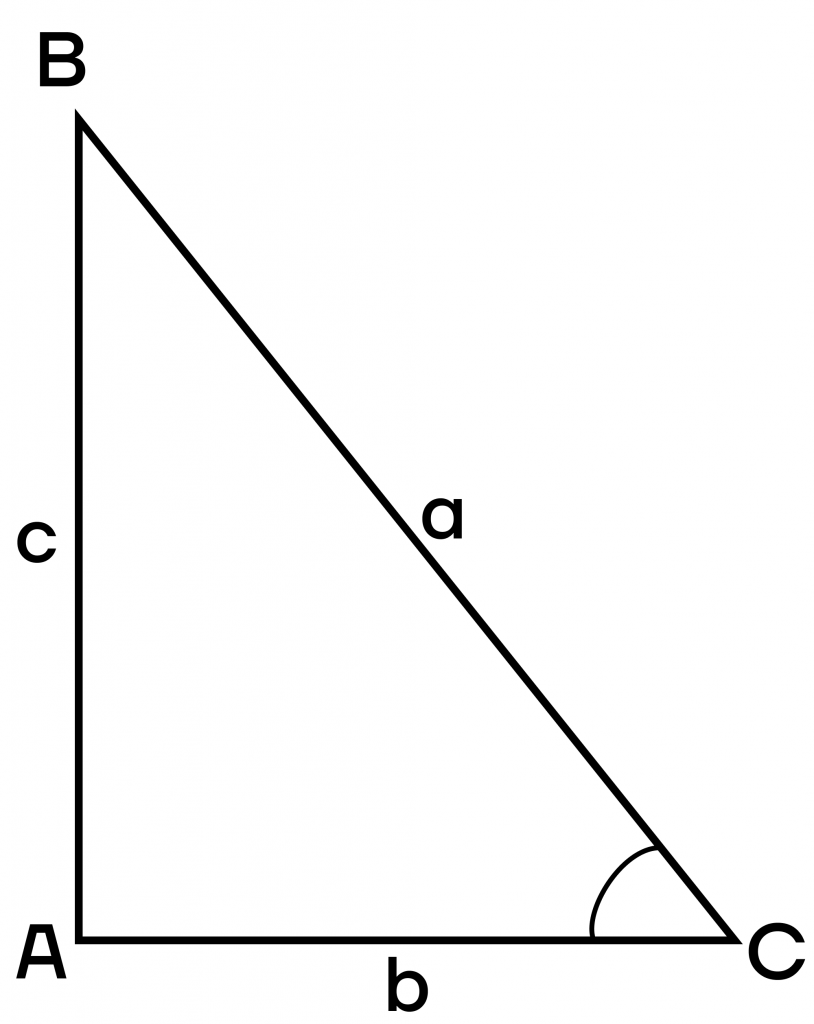
• Синус — это отношение противолежащего катета к гипотенузе: \(sinC=\frac{c}{a}\).
• Косинус — это отношение прилежащего катета к гипотенузе: \(cosC=\frac{b}{a}\). 
• Тангенс — это отношение противолежащего катета к прилежащему катету: \(tgC=\frac{c}{b}\).  
• Котангенс — это отношение прилежащего катета к противолежащему катету: \(ctgC=\frac{b}{c}\). 

В статье «Тригонометрическая окружность. Часть 2», мы обсуждали, что их значения можно обозначить на тригонометрической окружности. 

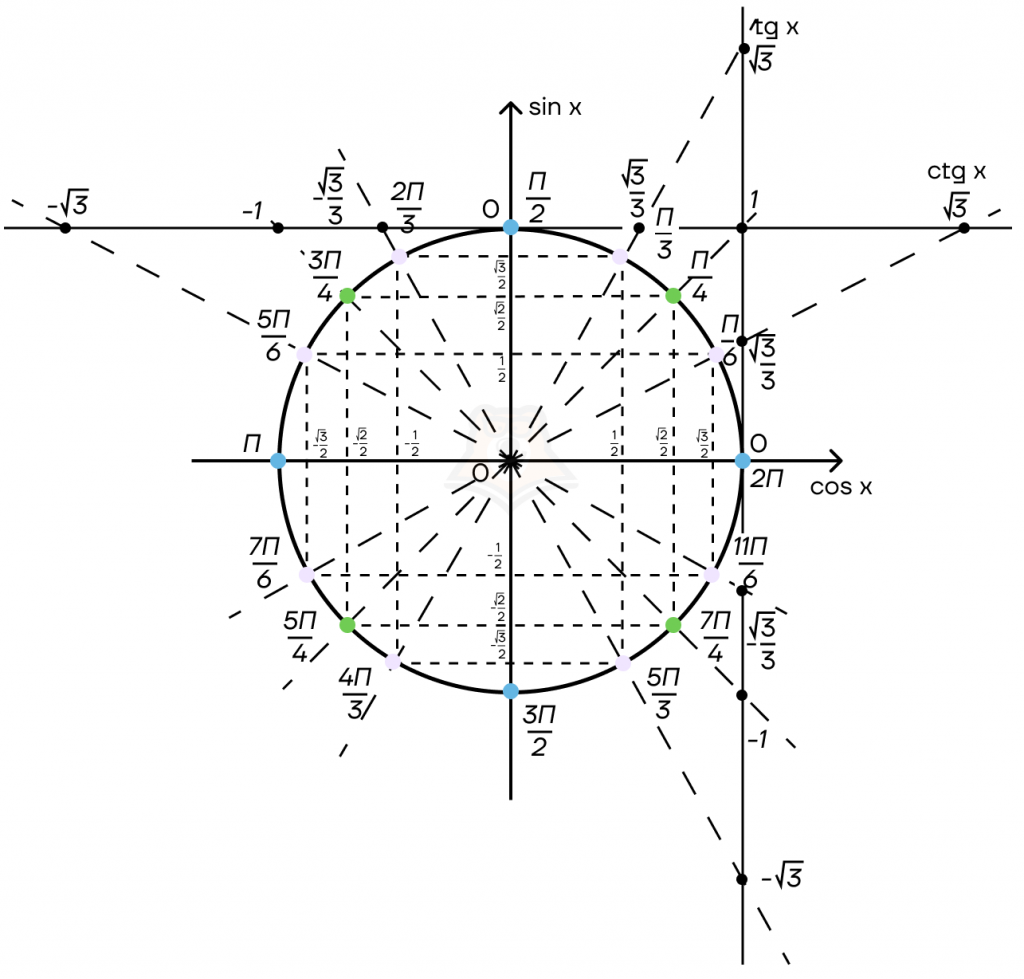
Если рассматривать значения синуса, косинуса, тангенса и котангенса на тригонометрической окружности, то можно заметить, что эти функции периодические. Что это значит? 

Периодическая функция — это функция, значения которой повторяются через определенный промежуток, называемый периодом. 

Теперь рассмотрим подробнее графики таких функций. 

Как мы обычно строим график функции? Находим значения у для разных значений х и соединяем точки. Также и с графиками тригонометрических функций. Этим способом можно получить следующие графики функций.

График \(y=sin x\) — синусоида.

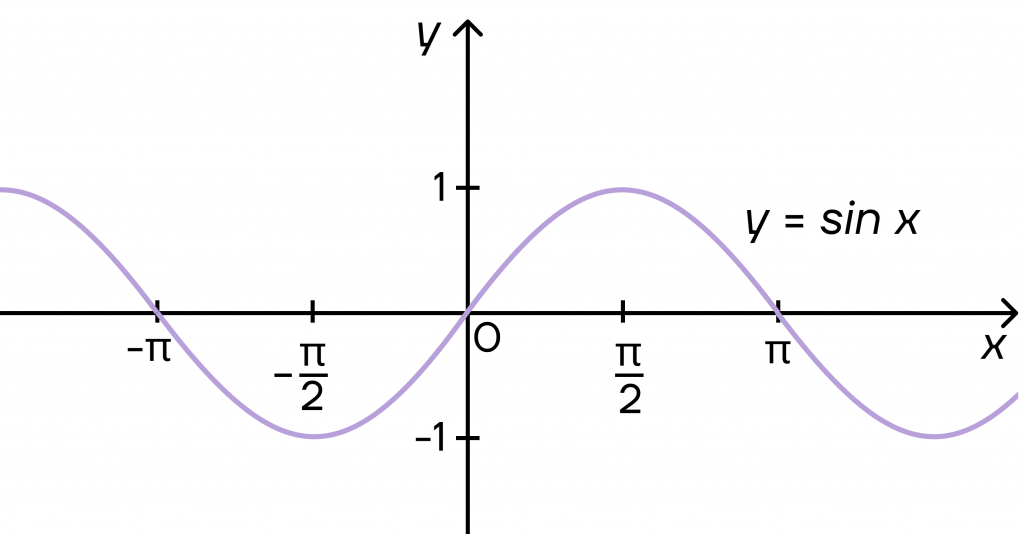
График \(y=cos x\) — косинусоида.

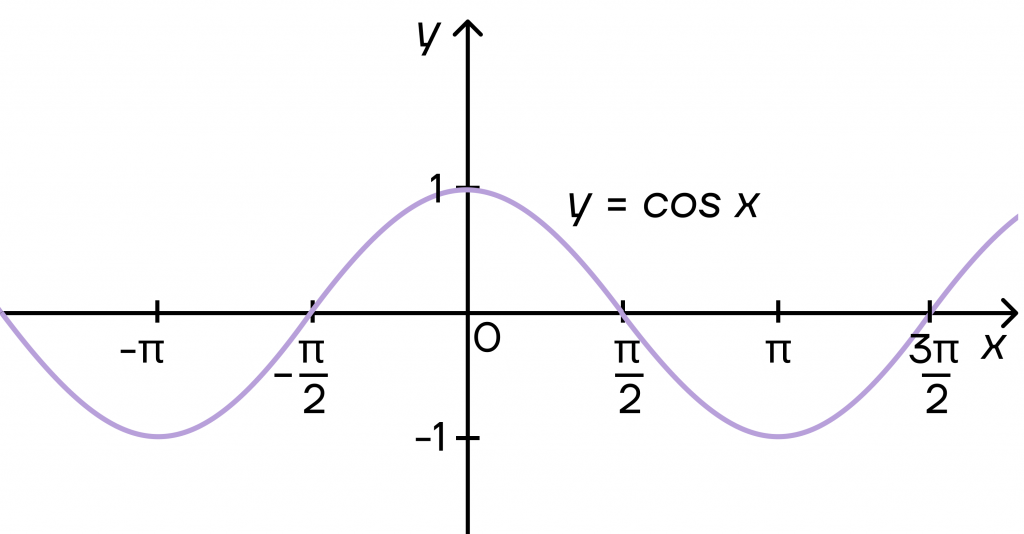
Периодом синусоиды и косинусоиды будет \(2\pi\). То есть одно и то же значение будет повторяться через каждые \(2\pi\). Например, косинус будет равен 1 в точках 0 и \(2\pi\), а дальше он примет это значение в точках \(4\pi\), \(6\pi\) и т.д.

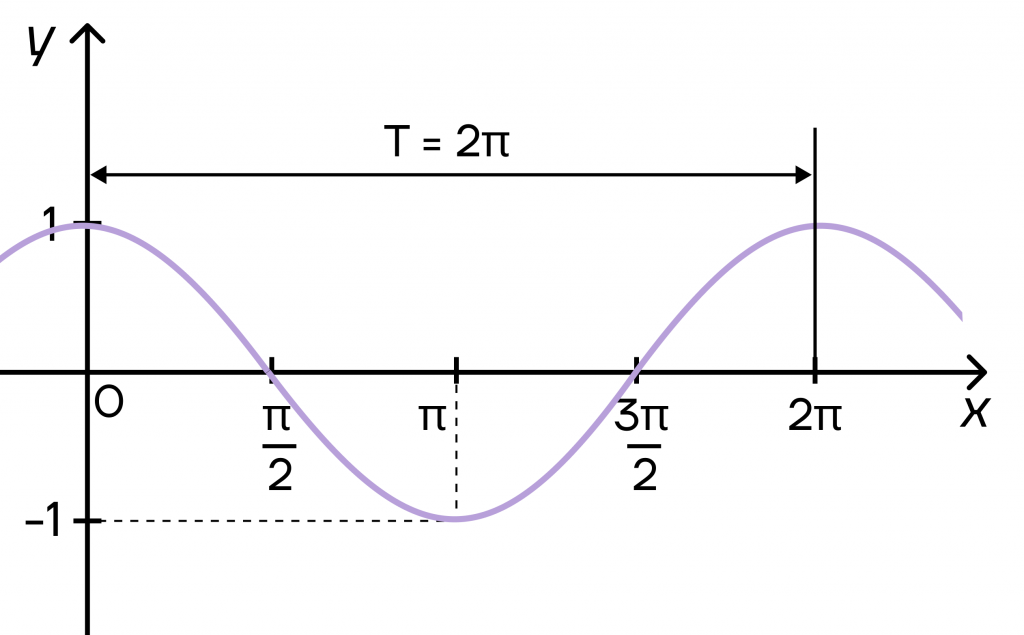
Куда уехали синус и косинус? Поскольку и на тригонометрической окружности, и на обычном графике синус и косинус сами по себе не меняются, то и оба графика зависят друг от друга. Представить это можно так: окружность будет стрелкой часов, движение которой мы отобразим по оси х. Эта стрелка будет оставлять свой след, он и превратится в синусоиду и косинусоиду.

А как выглядят графики тангенса и котангенса? В отличие от синусоиды и косинусоиды, они прерываются через период . С чем это связано?

Выразим тангенс и котангенс через синус и косинус. Для этого нам нужно воспользоваться тригонометрическими формулами, подробнее про которые вы можете прочесть в статье «Формулы тригонометрии и простейшие уравнения»:

\(tg x=\frac{sin x}{cos x}\)
\(ctg x=\frac{cos x}{sin x}\)

Рассмотрим тангенс. В знаменателе стоит косинус, а значит, мы должны ввести ограничение: косинус не может быть равен 0 (поскольку на 0 делить нельзя). Таким образом, как только мы видим тангенс, у нас сразу появляется условие: 

\(cos x \neq 0\).

С помощью тригонометрической окружности определяем, что косинус равен 0 при \(x=\frac{\pi}{2}+\pi n, n \in Z\) (подробнее про запись \(\pi n, n \in Z\) можно прочесть в статье «Тригонометрическая окружность. Часть 2»). 

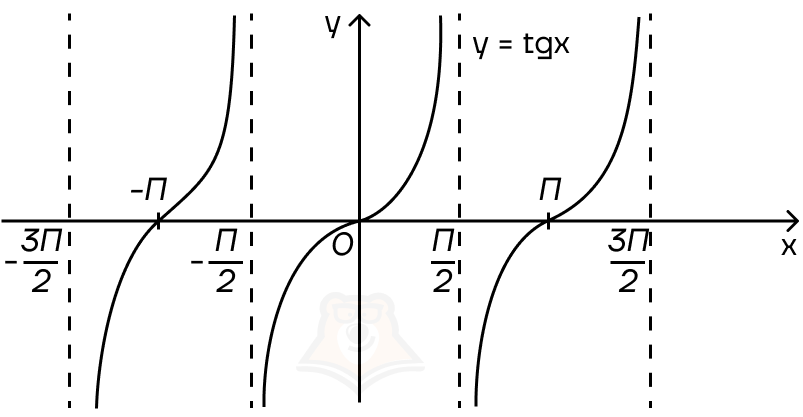
То есть получается, что тангенс не существует в точках \(\frac{\pi}{2}, \frac{3\pi}{2}, \frac{5\pi}{2}, \frac{7\pi}{2}\) и т.д. 

Для тангенсоиды эти точки откладываются на оси х и чертятся асимптоты. 

Асимптота — это прямая, к которой стремится график функции, но которую он никогда не пересекает. 

График \(y=tgx\) — тангенсоида.

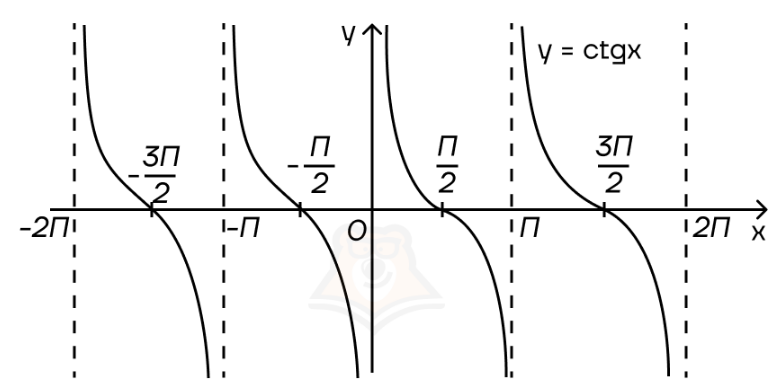
Для котангенса у нас появляется условие \(sin x \neq 0 => x \neq \pi n, n \in Z\). Следовательно, асимптотами котангенсоиды будут \(\pi, 2\pi, 3\pi\) и т.д. 

График \(y=ctgx\) — котангенсоида.

Мы рассмотрели и построили графики для синуса, косинуса, тангенса и котангенса. Но можем ли мы их изменить? Да. Каждую из рассмотренных выше функций можно сдвигать по осям х и у и растягивать по оси у. Давайте узнаем, как это сделать. 

Коэффициент перед тригонометрической функцией

Как мы можем преобразовать саму функцию? Первым делом, поставить перед ней коэффициент, то есть числовой множитель.

Давайте рассмотрим, что произойдет с функцией, если поставить перед ней коэффициент. Для примера возьмем график синуса.

Пусть у нас есть функция \(y=sin 30\). Тогда с помощью тригонометрической окружности определяем, что \(y=\frac{1}{2}\).

А теперь подставим коэффициент: \(y=4*sin 30\). 

Решим это уравнение: \(y=4*\frac{1}{2}=2\). 

Сравнивая числа \(\frac{1}{2}\) и 2, мы можем заметить, что значение функции увеличилось в 4 раза. 

А теперь найдем значение функции \(y=\frac{1}{2}sin 30\):

\(y=\frac{1}{2}*\frac{1}{2}=14\)

В этом случае значение функции уменьшилось в два раза. И все благодаря коэффициенту: во сколько раз увеличивается функция, во столько раз меняется ее значение. 

Для наглядности построим графики трех рассмотренных функций: 

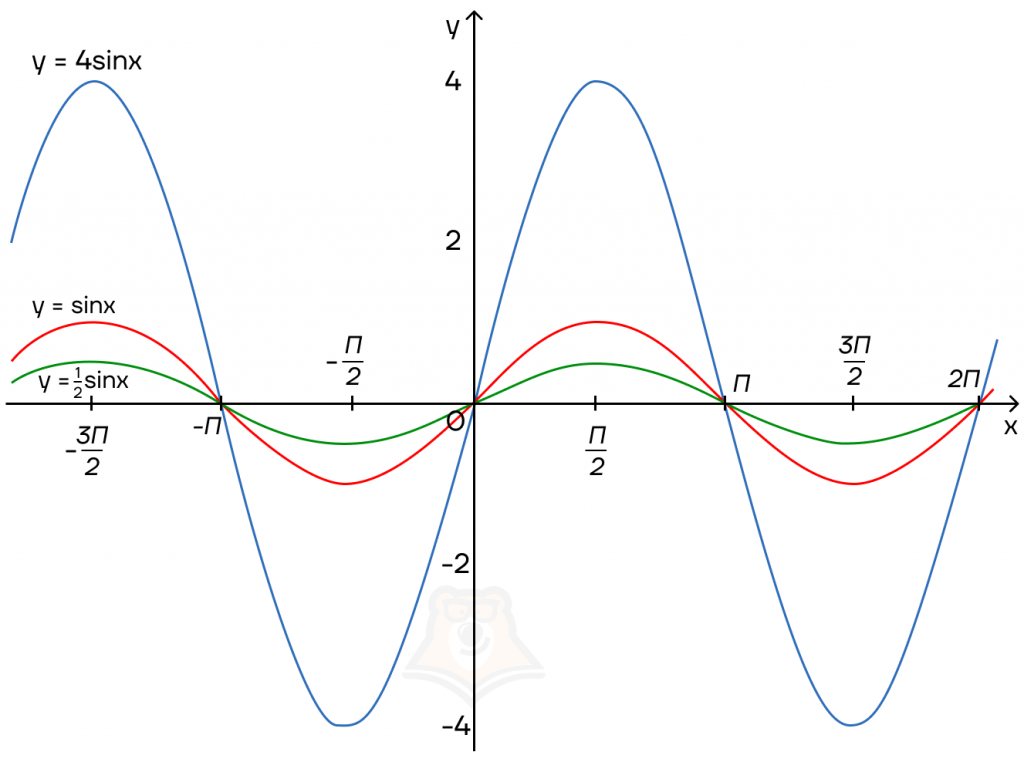
Заметим, что чем больше коэффициент перед тригонометрической функцией, тем сильнее она вытягивается по вертикали. 

Итак, мы рассмотрели пример с синусоидой. Поскольку синусоида и косинусоида похожи, то график косинусоиды будет меняться похожим способом. 

А что же происходит с тангенсоидой и котангенсоидой? Также рассмотрим три функции:

\(y=tg 45\) \(y=1\)

\(y=\frac{1}{2}*tg 45\) \(y=\frac{1}{2}*1=\frac{1}{2}\)

\(y=4*tg 45\) \(y=4*1=4\)

Значения тангенса также менялось в зависимости от коэффициента перед тригонометрической функцией. Построим графики полученных функций:

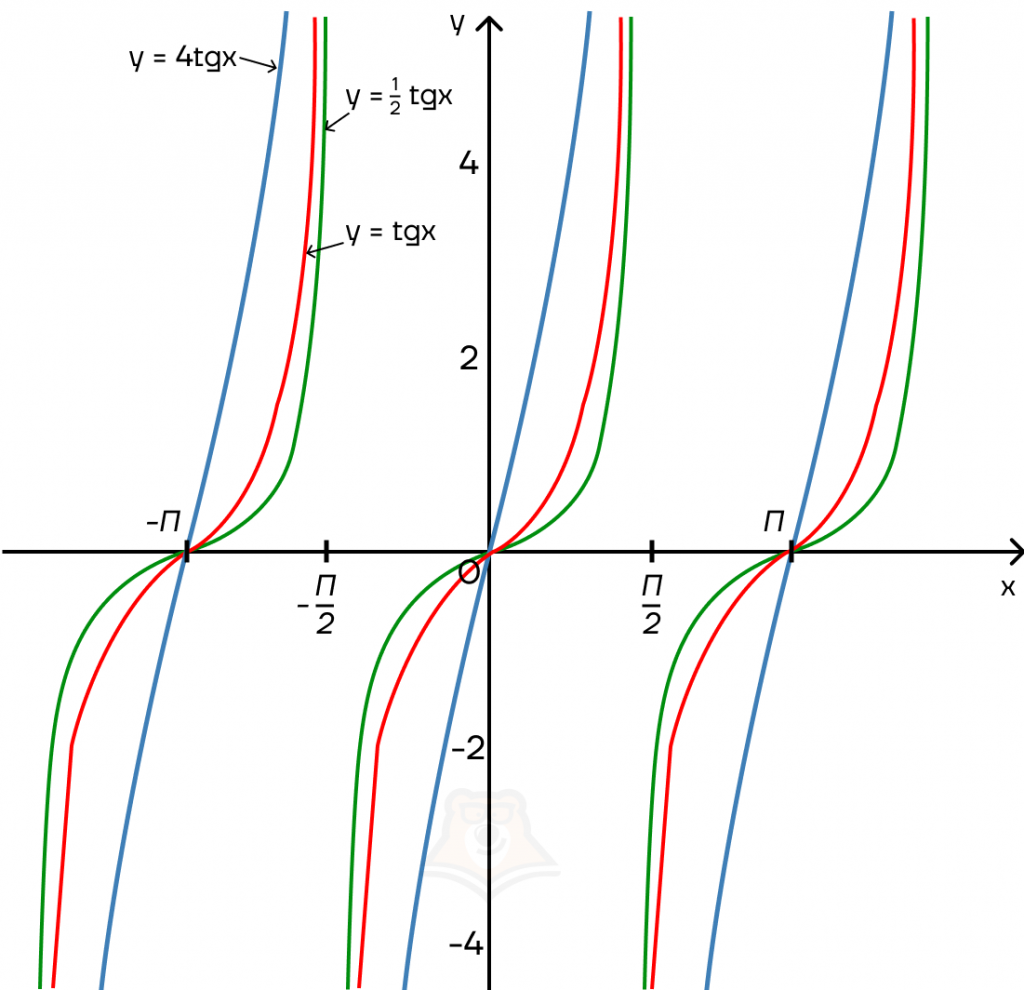
Заметим, что в этом случае у нас меняется искривление тангенсоиды: чем больше коэффициент, тем меньше искривляется кривая. 

Косинусоида будет изменяться аналогичным способом. 

Сдвиг по оси Y

Как мы уже упоминали в самом начале этой статьи, график можно сдвинуть по оси у. Как это можно сделать? 

Если до этого мы умножали график, то теперь попробуем воспользоваться сложением и вычитанием. Рассмотрим три графика: 

\(y=sin 30-3\) \(y=\frac{1}{2}-3=-2,5\)

\(y=sin 30\) \(y=\frac{1}{2}=0,5\)

\(y=sin 30+3\) \(y=\frac{1}{2}+3=3,5\)

Заметим, что в этот раз графики отличаются не в несколько раз, а на некоторое число. То есть какое бы число мы ни прибавили, на такое число и увеличится (уменьшится) график. 

Рассмотрим, как это будет выглядеть на графике. 

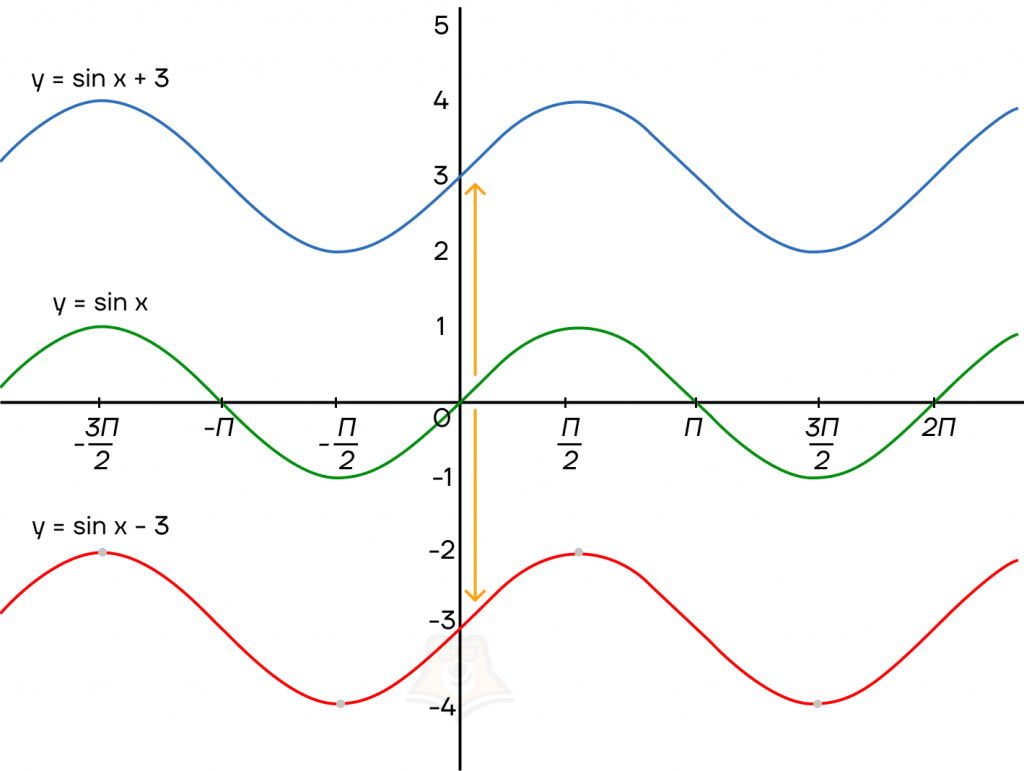
График тригонометрической функции сдвигается по оси у на прибавленную к значению y константу. 

Константой мы называем число, которое не зависит от переменной и не меняется вслед за ней. 

Еще раз напомним, что синусоида и косинусоида меняются схожим образом. 

Рассмотрим также на примере тангенсоиды. Котангенсоида будет меняться похожим способом.

\(y=tg 45-3\) \(y=1-3=-2\)

\(y=tg 45\) \(y=1\)

\(y=tg 45+3\) \(y=1+3=4\)

Также, как и синусоида, тангенсоида будет меняться на 3. В этом случае мы как бы «переносим» график на три единицы вверх или вниз. 

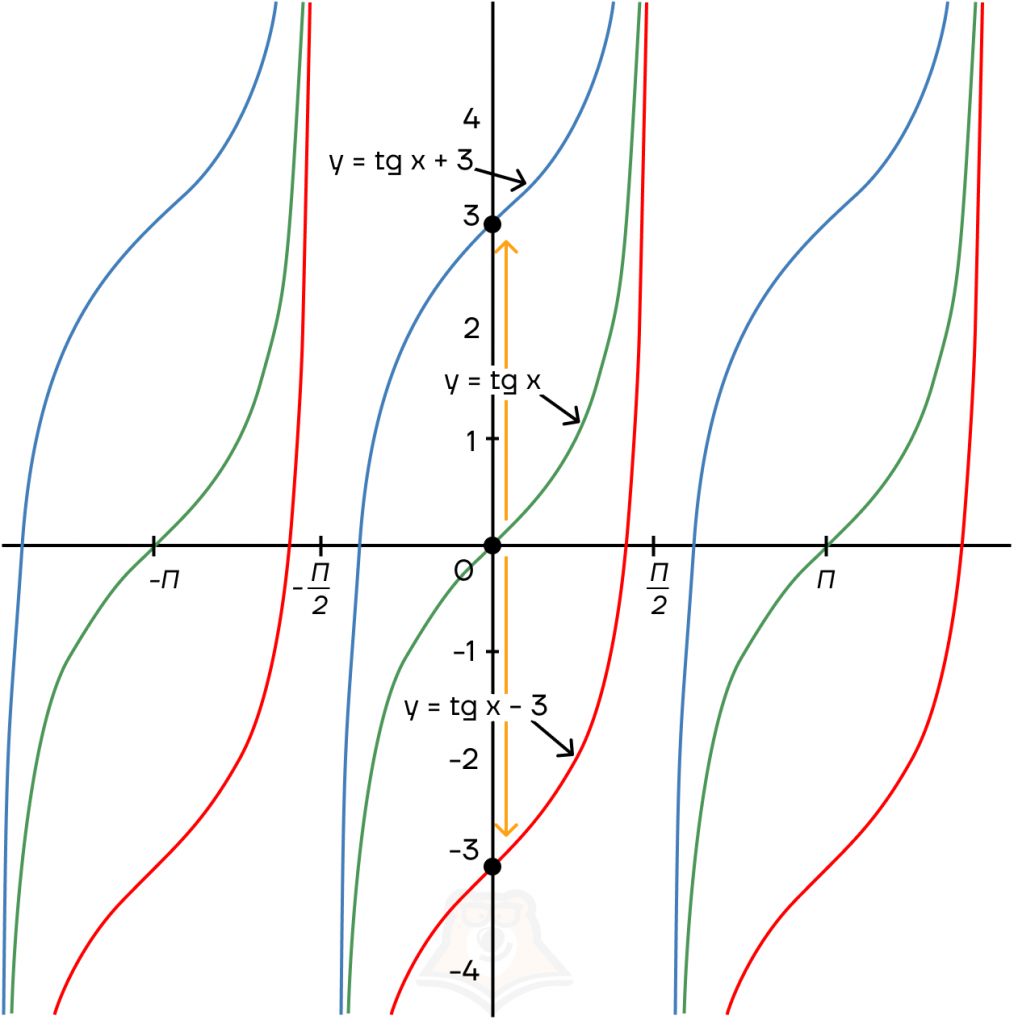
Графики тригонометрических функций можно встретить в №10 ЕГЭ по профильной математике. 
На рисунке изображен график функции \(y=m*cos x-n\). Найдите n.

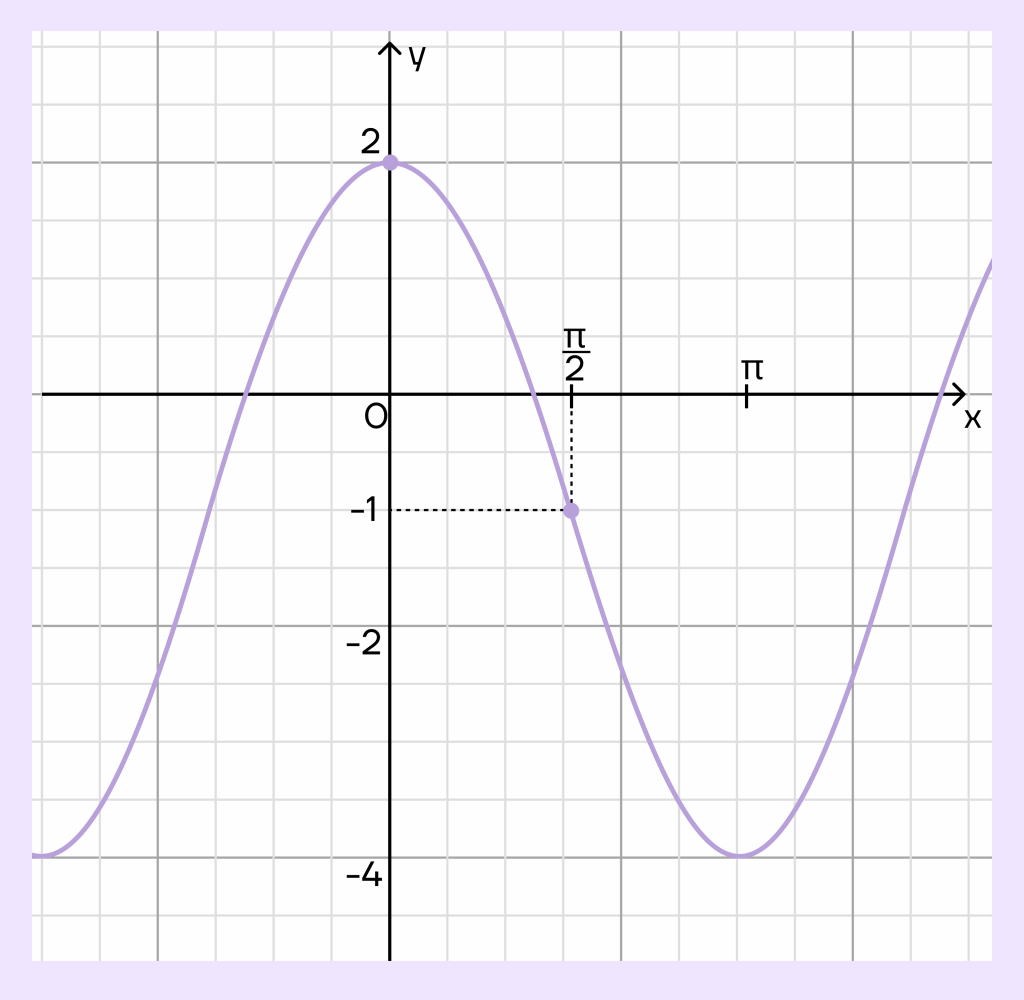
Решение. Заметим, что нам даны точки \((0;2)\) и \((\frac{\pi}{2};-1)\).

Подставим координаты из второй точки в уравнение. Вспомним, что координаты записываются следующим образом: (х;у). 

\(-1=m*cos(\frac{\pi}{2})-n\)

По тригонометрической окружности определяем, что \(cos(\frac{\pi}{2})=0\), тогда получаем уравнение:

\(-1=m*0-n\)
\(-1=-n |*(-1)\)
\(n=1\)

Задание решено.

Ответ: 1.

Сдвиг по оси Х

Мы разобрались, как двигать график по оси y. Есть ли возможность сдвинуть его по оси х? Разумеется! 

Снова рассмотрим на примере синусоиды и тангенсоиды. 

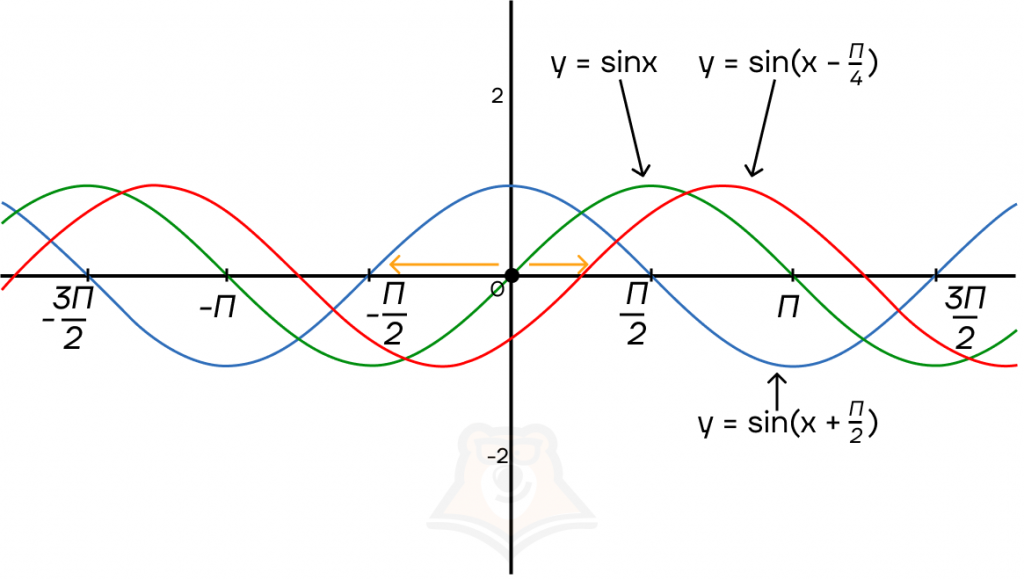
График тригонометрической функции сдвигается по оси х на прибавленную к значению х константу. 

Например, вместо функции \(y=sin x\) мы запишем функцию \(y=sin(x+\frac{\pi}{2})\). В этом случае у нас график сдвинется на 2 влево. 

А вот если мы вычтем из аргумента какое-то значение, то график сдвинется вправо. Например, для функции \(y=sin(x-\frac{\pi}{4})\) мы будем двигать синусоиду на \(\frac{\pi}{4}\) вправо. 

Где у тригонометрических функций противоречие? В случае сдвига функции по оси у мы не сталкиваемся с противоречиями: — если мы прибавляем константу к функции, то двигаем график в положительную сторону по оси у, — если вычитаем константу — то в отрицательную сторону.  В случае со сдвигом по оси х ситуация прямо противоположна, и, можно сказать, даже противоречива: — если мы прибавляем константу к аргументу функции, то график сдвигается в отрицательную сторону по оси х. — если мы вычитаем константу из аргумента функции, то график сдвигается в положительную сторону по оси х.

Рассмотрим, почему так происходит. 

Допустим, у нас есть две функции:

\(y=sin x\) и \(y=sin(x+\frac{\pi}{4})\), при этом пусть \(x=\frac{\pi}{2}\). 

Тогда для первой функции получим: \(y=sin\frac{\pi}{2}=1\).

А для второй: \(y=sin(\frac{\pi}{2}+\frac{\pi}{4})=sin\frac{3\pi}{4}=\frac{\sqrt2}{2}\approx 0,7\).

Заметим, что несмотря на то, что мы увеличили аргумент, значение самой функции уменьшилось. Поэтому, чтобы добиться «равновесия», график функции сдвигается в противоположную сторону. 

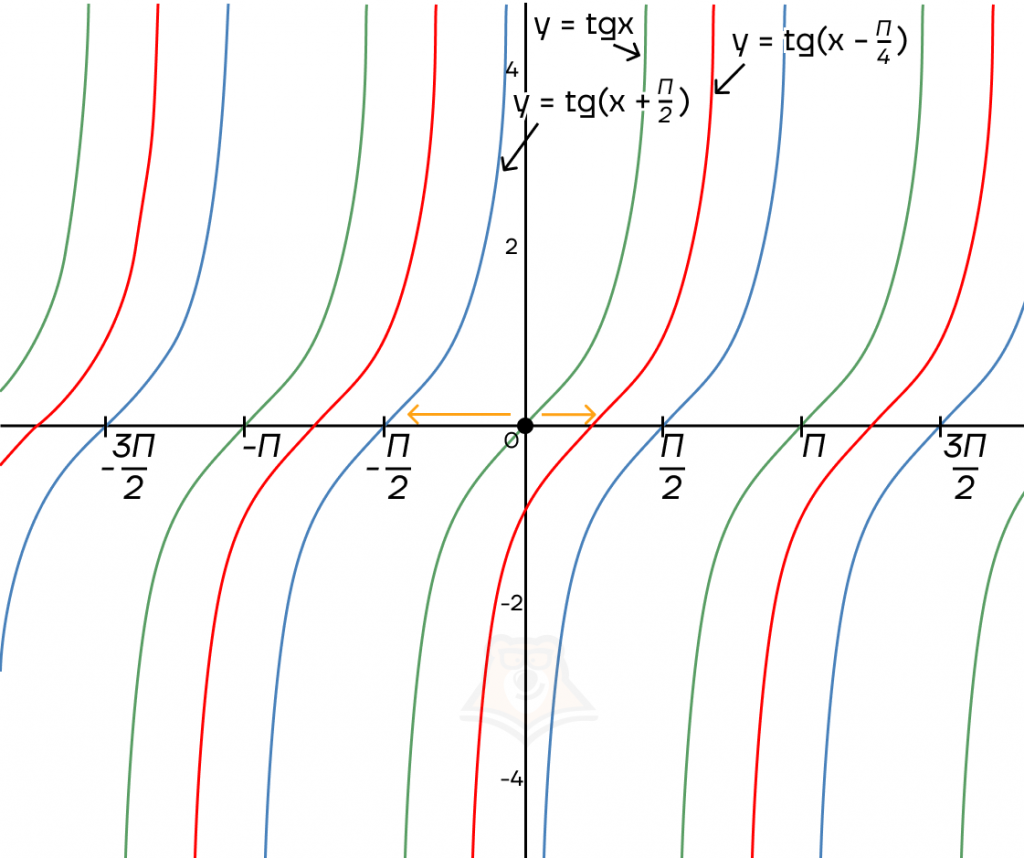
Аналогичным образом будет сдвигаться тангенсоида. 

Для функции \(y=tg(x+\frac{\pi}{2})\) необходимо сдвинуть график на \(\frac{\pi}{2}\) влево, а для функции \(y=tg(x-\frac{\pi}{4})\) нужно сдвинуть график на \(\frac{\pi}{4}\) вправо. 

Разберем еще один вариант задания с графиками тригонометрических функций из №10 ЕГЭ по профильной математике.

На рисунке изображен график функции \(y=a*cos(\pi x+b)+c\), где a,b,c — целые числа. Найдите \(f(\frac{17}{2})\).

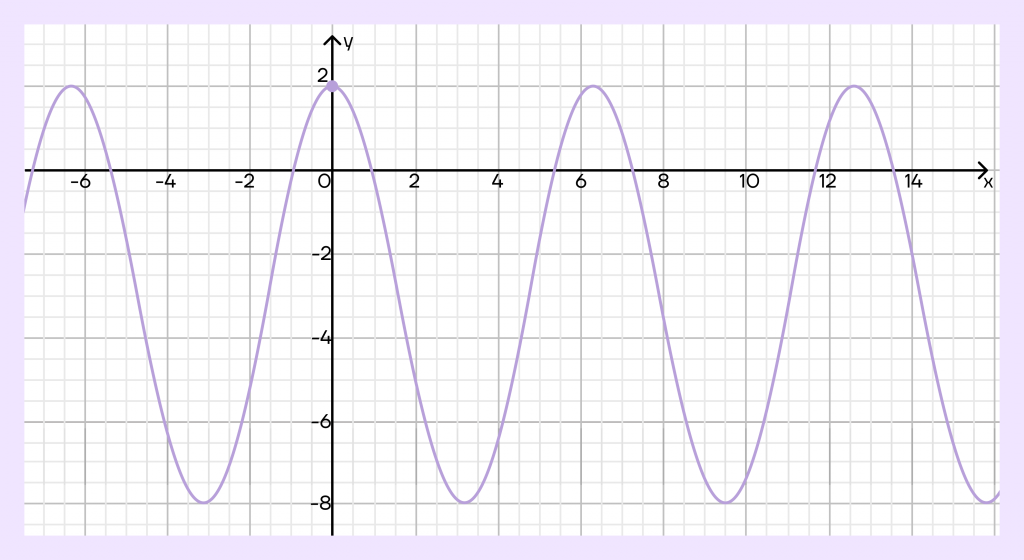
Решение.
По заданию перед нами косинусоида. Если мы вспомним, как выглядит ее график, то заметим, что она проходит через точку (0;1), то есть ее вершина лежит на оси у так же, как и на графике выше. Следовательно, смещения по оси х у нас нет, и \(b=0\). Тогда функция принимает вид \(y=a*cos(\pi x)+c\).

Коэффициент a отвечает за «растяжение» и «сжатие» функции. Обычная косинусоида идет в промежутке от -1 до 1. В нашем случае это промежуток от -8 до 2, то есть косинусоида занимает 10 единиц вместо 2. Следовательно, она растянута в пять раз, значит, \(a=5\).

Коэффициент c отвечает за сдвиг функции вдоль оси у. Без сдвига функция должна занимать промежуток от -5 до 5, в нашем случае она занимает промежуток от -8 до 2. Следовательно, график функции сдвинут на 3 единицы вниз. Значит, \(c=-3\).

Получаем функцию \(y=5cos(\pi x)-3\).

Осталось найти значение функции в точке \(x=\frac{17}{2}\). Подставим это значение в нашу функцию:

\(y=5cos(\frac{17\pi}{2})-3\)

Заметим, что \(\frac{17\pi}{2}=8,5\pi\). То есть это \(\frac{\pi}{2}\) плюс четыре круга: 

\(\frac{\pi}{2}+4*2\pi=\frac{\pi}{2}+8\pi=\frac{17\pi}{2}\)

Тогда косинус в этой точке равен тому же значению, что и косинус в точке \(\frac{\pi}{2}\). Следовательно, \(cos(\frac{17\pi}{2})=0\).

Получаем выражение:

\(y=5cos(\frac{17\pi}{2})-3=5*0-3=-3\)

Ответ: -3

Тригонометрические функции можно усложнить: умножить функцию на коэффициент, или прибавить константу к функции или аргументу. Чтобы понимать, что именно происходит в этот момент с функцией, тригонометрической окружности недостаточно, и в этом случае на помощь приходят графики тригонометрических функций. Более того, они являются еще одним способом изобразить на плоскости тригонометрическую функцию. 

Однако графиков и окружности недостаточно для решения тригонометрических уравнений или неравенств. Нам также нужно знать формулы, с помощью которых мы можем преобразовывать выражения. Познакомиться с ними вы можете в статье «Формулы тригонометрии и простейшие уравнения». 

Термины

Аргумент функции — независимая переменная, значение которой может меняться. 

Значение функции — зависимая переменная, которая меняется в зависимости от аргумента. Другими словами, это величина, которой равна функция после того, как выполнены все преобразования при конкретно заданном значении аргумента. 

Прямоугольный треугольник — это треугольник, один из углов которого прямой, то есть равен 90°. Подробнее о нем можно прочитать в статье «Равнобедренный, равносторонний и прямоугольный треугольник».

Целые числа — это натуральные числа, нуль, а также противоположные натуральным числам (то есть со знаком минус). 

Фактчек

• График функции — это представление функции на координатной плоскости. Наравне с тригонометрической окружностью, это способ графически изобразить функции синуса, косинуса, тангенса или котангенса.
• Графики тригонометрических функций называются синусоида, косинусоида, тангенсоида и котангенсоида. 
• У тангенсоиды и котангенсоиды существуют асимптоты, то есть значения, к которым график стремится, но которые никогда не пересечет. 
• График тригонометрической функции можно «изменить» тремя способами: умножить на коэффициент, добавить константу к функции или добавить константу к аргументу функции. 
• Коэффициент перед функцией отвечает за растяжение графика функции вдоль оси Y.
• Константа, прибавляемая к х или y, отвечает за сдвиг функции относительно изначального значения. 

Проверь себя

Задание 1.
Как называется график функции \(y=sin x\)?

1. синусоида
2. синус
3. синусоид
4. определенного названия нет 

Задание 2.
Какое уравнение соответствует асимптотам тангенсоиды?

1. \(x=\pi n, n \in Z\)
2. \(x=\frac{\pi}{2}+\pi n, n\in Z\)
3. \(x=2\pi n, n\in Z\)
4. \(x=\frac{\pi}{2}+2\pi n, n\in Z\)

Задание 3.
Какое уравнение соответствует асимптотам котангенсоиды?

1. \(x=\pi n, n \in Z\)
2. \(x=\frac{\pi}{2}+\pi n, n\in Z\)
3. \(x=2\pi n, n\in Z\)
4. \(x=\frac{\pi}{2}+2\pi n, n\in Z\)

Задание 4.
Куда будет сдвиг графика функции \((sin(x+\frac{4\pi}{3})\)?

1. вправо
2. влево
3. вверх
4. вниз

Задание 5.
Куда будет сдвиг графика функции \(ctg x+2\)?

1. вправо
2. влево
3. вниз
4. вверх

Ответы: 1. — 1; 2. — 2; 3. — 1; 4. — 2; 5. — 4.