Вписанная и описанная окружности. Основные формулы треугольника
На этой странице вы узнаете
- Чем отличается медиана и серединный перпендикуляр?
- Еще больше теорем! В чем заключаются теоремы синусов и косинусов?
Казалось бы, окружность и треугольник — совершенно разные фигуры. Могут ли они как-то пересекаться или взаимодействовать друг с другом? А вдруг у них есть свои личные секреты, которые мы можем узнать? Ответы на эти вопросы ждут вас в статье.
Вписанная и описанная окружности
Чуть подробнее рассмотрим, как окружности могут взаимодействовать с треугольником.
Описанная окружность — это окружность, которая проходит через все вершины треугольника.
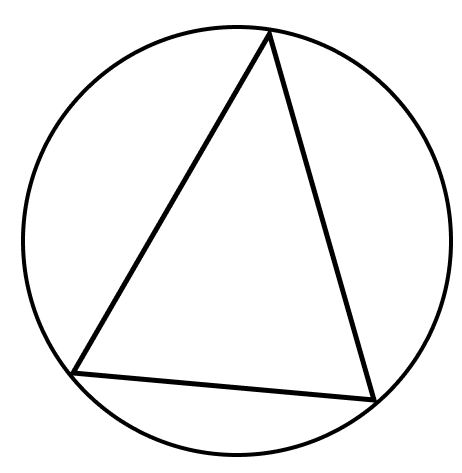
Центр такой окружности равноудален от вершин треугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров треугольника.
Представим, что в центре окружности стоит именинник, а вокруг него водят хоровод три человека. Поскольку они держатся за вытянутые руки, то они будут на одинаковом расстоянии от именинника. Таким образом, именинник — центр окружности, а его друзья — вершины треугольника.
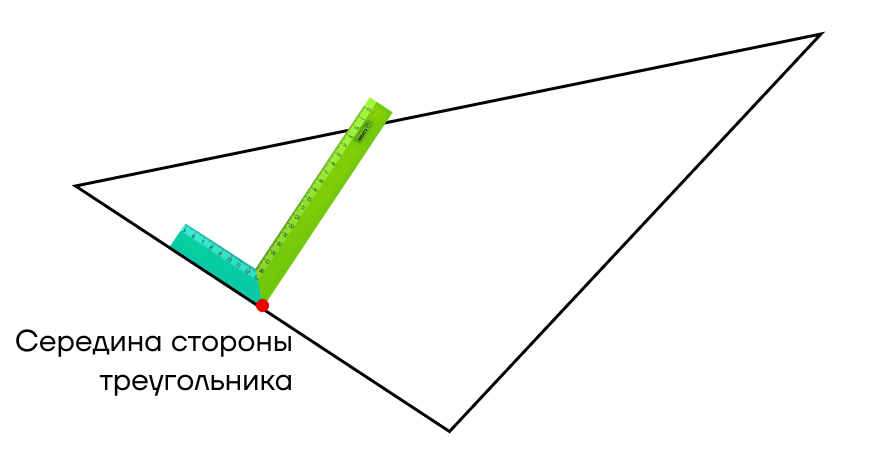
Серединный перпендикуляр — это перпендикуляр, проведенный к середине стороны треугольника.
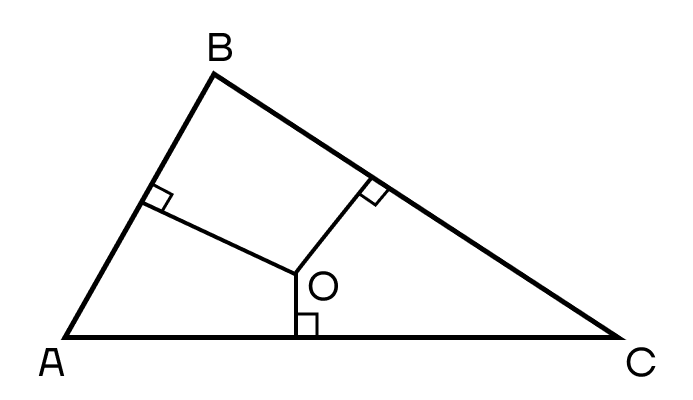
Вспомним строительный уголок. Серединный перпендикуляр и будет этим уголком, который приложен к центру стороны треугольника.
Точка пересечения серединных перпендикуляров будет лежать:
- В остроугольном треугольнике «внутри» треугольника.
- В прямоугольном треугольнике на середине гипотенузы.
- В тупоугольном треугольнике за пределами треугольника.
| Чем отличается медиана и серединный перпендикуляр? Серединный перпендикуляр — это перпендикуляр, проведенный к середине стороны треугольника. Важно заметить, что это не медиана, поскольку медиана — это просто отрезок, проведенный из вершины треугольника к середине стороны, при этом этот отрезок не обязательно будет перпендикулярен этой стороне. |

| Важно запомнить, что вокруг любого треугольника можно описать окружность, причем только одну. Также в любой треугольник можно вписать окружность, причем только одну. |
Вписанная и описанная окружности активно участвуют в свойствах треугольника. На окружностях строятся несколько важных теорем, а также их радиусы часто встречаются в формулах треугольника.
Благодаря свойствам углов и касательных, вписанная и описанная окружности могут стать незаменимым инструментом в решении сложных задач. Подробнее про касательные и углы в окружности можно прочесть в статьях «Касание к окружности» и «Окружность и круг».
Вписанная окружность — это окружность, которая касается всех сторон треугольника.
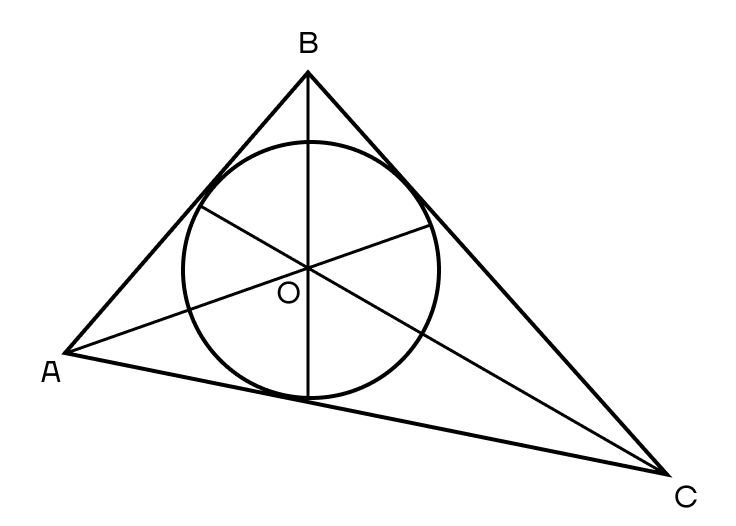
Центр вписанной окружности лежит в точке пересечения биссектрис треугольника.
Основные теоремы
Рассмотрим еще две интересные теоремы, которые можно применить в треугольнике.
Теорема синусов:
Отношения сторон треугольника к синусам противолежащих углов равны.
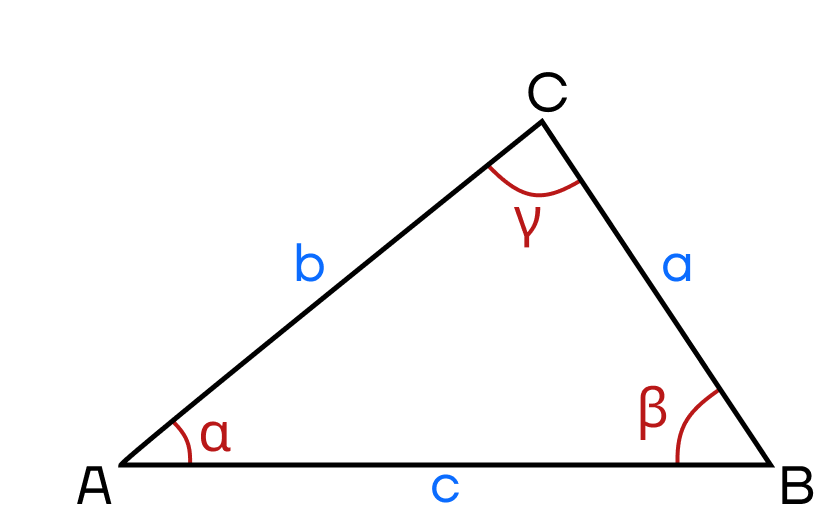
В теореме синусов выполняется следующее равенство:
\(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\).
Также теорему синусов можно связать и с описанной окружностью: отношение сторон к синусам углов будет равно двум радиусам:
\(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\).
Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
\(c^2 = a^2 + b^2 — 2ab \cos C\)
Теорему косинусов можно составить для любой стороны в треугольнике.
| Еще больше теорем! В чем заключаются теоремы синусов и косинусов? Вспомним, что чем больше угол треугольника, тем больше противолежащая ему сторона. Теорема синусов не только иллюстрирует это, но и позволяет нам найти численное значение этих отношений. Почему теорема синусов будет иллюстрировать это свойство треугольника? Заметим, что чем больше угол, тем большее значение будет принимать его синус. Например, синус 30° равен 0,5, а синус 45° примерно равен 0,7. Получим отношение \(\frac{a}{0,5} = \frac{b}{0,7}\). Теперь вопрос: что будет больше, а или b? Разумеется, b. Таким образом, получаем, что чем больше сторона, тем больше угол напротив нее. А с помощью теоремы синусов можно еще и найти неизвестные нам стороны, углы или радиус описанной окружности. Для чего можно применить теорему косинусов? Чтобы найти сторону треугольника через две другие. В прямоугольном треугольнике мы можем для этого воспользоваться теоремой Пифагора. А что делать с произвольными треугольниками? И тут к нам приходит теорема косинусов: для нее нам нужно знать только две стороны треугольника и угол между ними. Кстати, теорема Пифагора совпадает с теоремой косинусов. Пусть а, b — катеты, с — гипотенуза. Напротив гипотенузы лежит прямой угол, а значит, мы можем использовать теорему косинусов: \(c^2 = a^2 + b^2 — 2 * a * b* \cos 90^о = a^2 + b^2 — 2 * a * b * 0 = a^2 + b^2\) |
Основные формулы
Ниже приведена таблица со всеми основными формулами, которые могут пригодиться для решения задач. Важно знать их наизусть.
| Формула | Обозначения |
| P = a + b + c \(p = \frac{a + b + c}{2}\) | P — периметр; p — полупериметр; a, b, c — стороны треугольника. |
| \(S = \frac{1}{2}ah\) \(S = \frac{1}{2}ab \sin \alpha \) \(S = pr\) \(S = \frac{abc}{4R}\) \(S = \sqrt{p(p — a)(p — b)(p — c)}\) Для равностороннего треугольника: \(S = \frac{\sqrt{3}a^2}{4}\) | S — площадь; a, b, c — стороны треугольника; h — высота; p — полупериметр; r — радиус вписанной окружности; R — радиус описанной окружности. |
| \(m_c = \frac{\sqrt{2a^2 + 2b^2 — c^2}}{2}\) | mc — медиана; a, b, c — стороны. |
| В равностороннем треугольнике \(h = \frac{a \sqrt{3}}{2}\) \(R = \frac{a \sqrt{3}}{3}\) \(r = \frac{a \sqrt{3}}{6}\) \(R = 2r\) | h — высота; a — сторона равностороннего треугольника; R — радиус описанной окружности; r — радиус вписанной окружности. |
| Теорема Пифагора: \(c^2 = a^2 + b^2\) | c — гипотенуза; a, b — катеты. |
| Теорема синусов: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R\) | a, b, c — стороны; A, B, C — углы треугольника; R — радиус описанной окружности. |
| Теорема косинусов: \(c^2 = a^2 + b^2 — 2ab \cos C\) | a, b, c — стороны; C — угол треугольника. |
Фактчек
- Любой треугольник можно вписать в окружность, а также описать вокруг него окружность. Центр вписанной окружности будет лежать на пересечении биссектрис, центр описанной окружности будет лежать на пересечении серединных перпендикуляров (ортоцентре).
- Теорема синусов гласит, что отношение сторон треугольника к синусам противолежащих углов равны. Также эти отношения можно приравнять к удвоенному радиусу.
- С помощью теоремы косинусов можно найти любую сторону треугольника. Теорема косинусов гласит, что квадрат стороны равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
- Для решения задач необходимо хорошо знать и свободно владеть основными формулами.
Проверь себя
Задание 1.
В какой точке лежит центр описанной окружности треугольника?
- в точке пересечения биссектрис
- в точке пересечения высот
- в точке пересечения медиан
- в точке пересечения серединных перпендикуляров
Задание 2.
В какой точке лежит центр вписанной окружности треугольника?
- в точке пересечения биссектрис
- в точке пересечения высот
- в точке пересечения медиан
- в точке пересечения серединных перпендикуляров
Задание 3.
Где будет лежать точка пересечения серединных перпендикуляров в прямоугольном треугольнике?
- «внутри» треугольника
- «снаружи» треугольника
- на середине гипотенузы
- на середине одного из катетов
Задание 4.
Периметр треугольника равен 8, а радиус вписанной окружности равен 4. Чему равна площадь этого треугольника?
- 32
- 16
- 2
- 64
Задание 5.
Площадь треугольника равна 30, основание равно 12. Чему равна высота треугольника, проведенная к этому основанию?
- 5
- 2,5
- 10
- 6
Ответы: 1. — 4; 2. — 1; 3. — 3; 4. — 2; 5. — 1.


 к списку статей
к списку статей





