Тригонометрические уравнения

На этой странице вы узнаете

• Существует ли ОДЗ в реальной жизни?
• Почему синус и косинус не могут быть больше 1?
• Почему в однородных тригонометрических уравнениях можно делить на переменную? 

Что общего у астрономии, компьютерной графики, архитектуры и медицины? Измерить расстояние до звезд или провести обследование сердца, спроектировать небоскреб в центре города и нарисовать локацию в игре — это и многое другое невозможно без решения задач тригонометрии.

Предыстория

Тригонометрия связана со значениями углов, но здесь перед нами открывается масса возможностей. Мы можем:

• выразить угол в градусах — например, 90° или 180°;
• или выразить угол в радианах — например, \(\frac{\pi}{2}\) или \(\frac{7\pi}{6}\);
• а также посчитать его численное значение — например, 0, 1 или \(\frac{\sqrt3}{3}\). 

Для этого нам понадобятся синус, косинус, тангенс и котангенс. Подробнее про эти функции и работу с ними можно узнать в статьях: 

• «Тригонометрическая окружность. Часть 1»;
• «Тригонометрическая окружность. Часть 2»;
• «Графики тригонометрических функций».

Однако на практике нам почти не встречаются функции в «чистом» виде, то есть просто sin x, cos x, tg x или ctg x. Они либо усложнены, либо вовсе являются частью уравнения или неравенства. Про то, как преобразовывать «усложненные» тригонометрические функции мы говорили в статье «Формулы тригонометрии и простейшие уравнения». А вот как работать с тригонометрическими уравнениями нам предстоит разобраться в этой статье.

ОДЗ тригонометрических функций

Однако прежде, чем переходить к решению уравнений, необходимо вспомнить про область допустимых значений (ОДЗ). 

Область допустимых значений — это значения переменной, при которых выражение будет существовать. 

Все значения, которые не входят в ОДЗ, не могут являться ответом, поскольку в этих точках уравнение не будет существовать. 

Существует ли ОДЗ в реальной жизни? В своей повседневной жизни мы часто встречаемся с условиями ОДЗ, просто не всегда их замечаем.  Допустим, дома вас ждет очень голодный кот, а в кошельке всего 250 рублей. Из них 48 рублей очень нужны на проезд, а пакетик кошачьего корма стоит 32 рубля. Нужно рассчитать, сколько кошачьего корма мы можем купить? Возьмем за х — количество пакетиков с кормом. При этом \(x\geq1\), так оставить кота голодным мы не можем. Тогда: \(x=\frac{250-48}{32}\) \(x=6\) (и остаток 10 рублей).  Получаем, что мы можем купить \(1\leq x\leq 6\) пакетиков кошачьего корма. Это и будет ограничение на его количество. А в математике поиск таких ограничений называется ОДЗ.

Тригонометрические функции накладывают свои ограничения, которые важно учитывать при решении тригонометрических уравнений и неравенств. Рассмотрим их.  

1. ОДЗ синуса и косинуса.

Важно помнить, что эти тригонометрические функции могут принимать значения от -1 до 1 включительно:

\(-1\leq cos x \leq1\) и \(-1\leq sin x \leq 1\)

Наглядно это можно увидеть на графиках синусоиды и косинусоиды: «волна» идет в пределах от – 1 до 1 по оси y. 

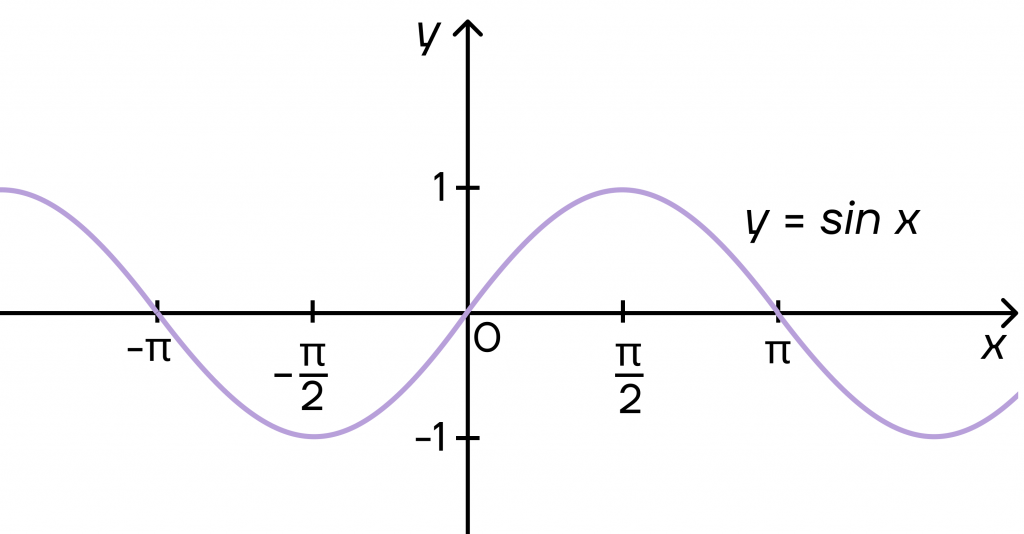
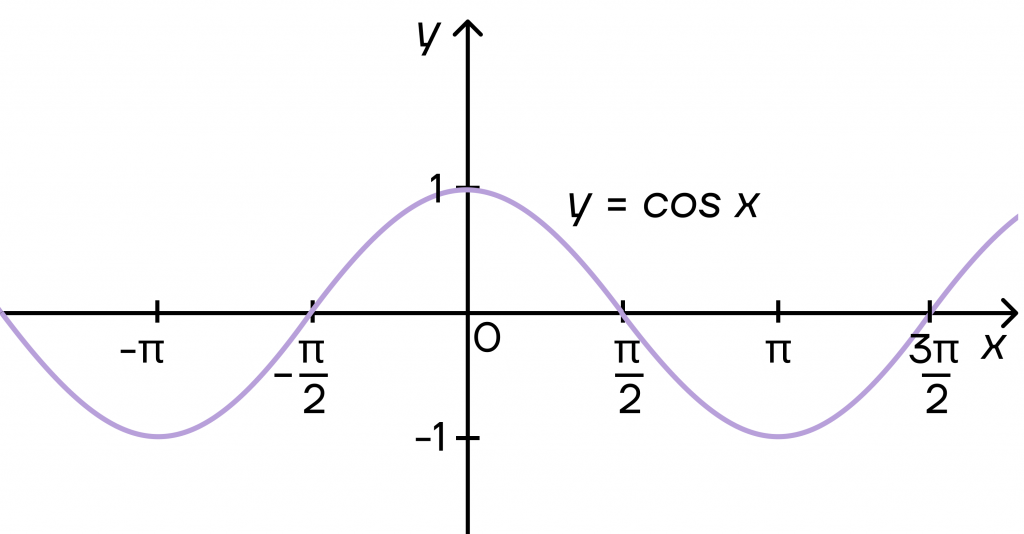
Если же в решении мы получим значения меньше – 1 или больше 1, например, \(sin x=-3\) или \(cos x=1,2\), то решений у этого уравнения не будет. 

Почему синус и косинус не могут быть больше 1? Чтобы ответить на этот вопрос, нам предстоит вспомнить некоторые свойства прямоугольного треугольника. Синус — это отношение противолежащего катета к гипотенузе, а косинус — отношение прилежащего катета к гипотенузе. В треугольнике напротив большего угла лежит большая сторона. Для прямоугольного треугольника этой стороной всегда будет гипотенуза (поскольку угол 90° самый большой). Получается, что если мы будем делить длину катета на длину гипотенузы, то это всегда будет деление меньшего числа на большее. Значит, результат такого вычисления всегда будет меньше 1.

2. ОДЗ тангенса и котангенса.

Вспомним, что эти тригонометрические функции можно выразить через синус и косинус:

\(tg x=\frac{sin x}{cos x}\)
\(ctg x=\frac{cos x}{sin x}\)

Поскольку у нас появляется дробь, ее знаменатель не может быть равен 0. Поэтому: 

• Если в примере появляется тангенс, то \(cos x\neq0\). Следовательно, \(x\neq\frac{\pi}{2}+\pi n, n\in Z\). 
• Если в примере появляется котангенс, то \(sin x\neq0\). Следовательно, \(x\neq \pi n, n\in Z\). 

Эти зависимости легко проследить на графиках тангенса и котангенса: их асимптоты как раз совпадают с наложенными ограничениями. 

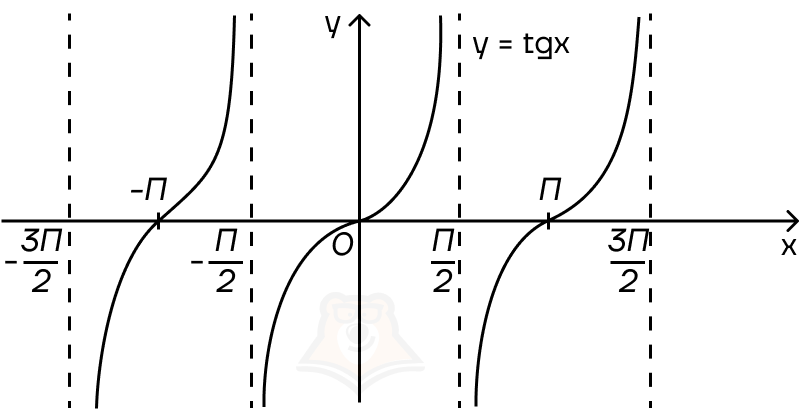
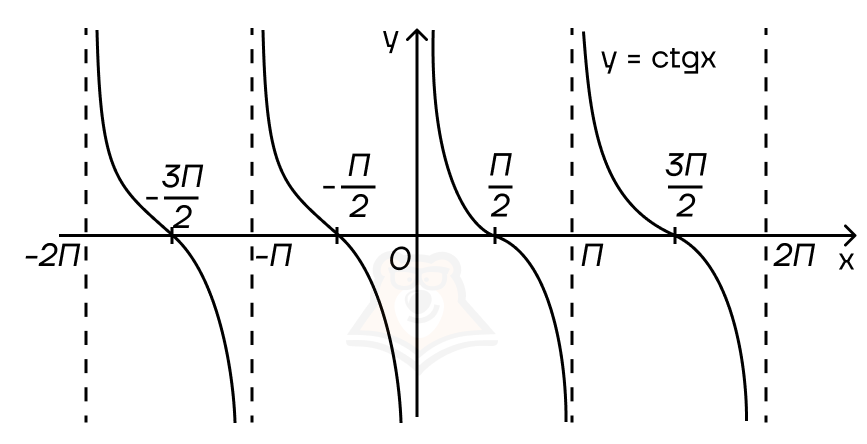
Заметим интересную закономерность: для синуса и косинуса ограничения наложены на ось у (область значений), а на оси х (область определений) никаких ограничений нет. Для тангенса и котангенса ситуация прямо противоположна: мы имеем ограничения в области определений, но не имеем ограничений в области значений. 

3. Другие случаи ОДЗ.

Помимо ограничений на сами тригонометрические функции, могут возникнуть ситуации, когда они стоят в «опасных» местах. К таким ситуациям можно отнести:

• Тригонометрическая функция стоит в знаменателе. В этом случае знаменатель не равен 0.

Например, для выражения \(\frac{1}{sin x}\) ограничением будет \(sin x \neq 0\).

• Тригонометрическая функция стоит под знаком корня. В этом случае подкоренное выражение должно быть больше или равно 0.

Например, \(\sqrt{cos x}=0 => cos x\geq 0\). 

Теперь, зная все «опасные» места, мы можем перейти к решению тригонометрических уравнений. 

Основные способы решения тригонометрических уравнений

Тригонометрическое уравнение — это уравнение, в котором переменная содержится под знаком тригонометрической функции.

Существует огромное множество тригонометрических уравнений. Но есть отличная новость: чтобы решить их, не нужно знать особенности каждого вида уравнений, достаточно воспользоваться лишь одним из способов их решения. 

Способ первый: введение новой переменной

Представим, что мы владеем магазином пряжи. Ожидается, что сегодня к нам придет много покупателей, которые хотят связать свитера по одной и той же схеме. Для каждого свитера им нужно три мотка ниток: голубые, синие и бежевые. Разумеется, каждый цвет лежит у нас на отдельном стеллаже. 

Будет уходить много времени, если мы будем собирать набор для каждого покупателя отдельно. Чтобы упростить работу, можно заранее собрать в отдельные пакеты необходимые цвета, и продавать пряжу уже наборами. 

Так, мы упростили действие «собрать с отдельных полок пряжу синего, голубого и бежевого цвета» до «продать набор с пряжей». По этому же принципу работает и введение новой переменной: мы упрощаем «страшное» выражение до более понятной и приятной переменной, с которой намного проще решать уравнение. 

1. Рассмотрим следующее уравнение:

\(3cos^2x-5cos x-2=0\)

Решать уравнение с функцией косинуса неудобно, да и не особо привычно. Но мы можем «упростить» его и ввести более понятную нам переменную! 

2. Введем новую переменную. Не забудем указать, что cos x может принимать значения только от -1 до 1. 

\(cos x =t, -1 \leq t \leq 1\)
\(3t^2-5t-2=0\)

И вот мы получили обычное квадратное уравнение. Теперь мы можем решить его с помощью дискриминанта. 

3. Найдем дискриминант: 

\(D=b^2-4ac=5^2-4*3*(-2)=25+24=49\)

Тогда корнями уравнения будут:

\(t_1=\frac{-b+\sqrt{D}}{2a}=\frac{5+7}{6}=2\)
\(t_2=\frac{-b-\sqrt{D}}{2a}=\frac{5-7}{6}=-\frac{1}{3}\)

И вот, мы решили уравнение, можно записывать ответ? Еще рано: мы нашли значение только нашей переменной, а нам необходимо найти решение того, что у нее «внутри». 

Иными словами, когда мы придем домой с купленным набором пряжи, чтобы сделать свитер, нам необходимо будет провести обратную операцию: разобрать пакет на отдельные мотки ниток. 

В математике это действие называется обратная замена. 

4. Сделаем обратную замену. Для этого в уравнение \(cos x=t\) подставим значения переменной. Получаем \(cos x=2\) и \(cos x =-\frac{1}{3}\).

Первый корень не подходит, так как не находится на промежутке от -1 до 1.

Рассмотрим второй корень. Поскольку \(-\frac{1}{3}\) не является табличным значением косинуса, решить это уравнение можно только через аркфункцию.

Аркфункция — это функция, обратная тригонометрической. 

С ее помощью мы можем узнать, чему равен аргумент тригонометрической функции, иными словами, найти значение угла. Подробнее про решение уравнений через аркфункцию мы рассказали в статье «Формулы тригонометрии и простейшие уравнения». 

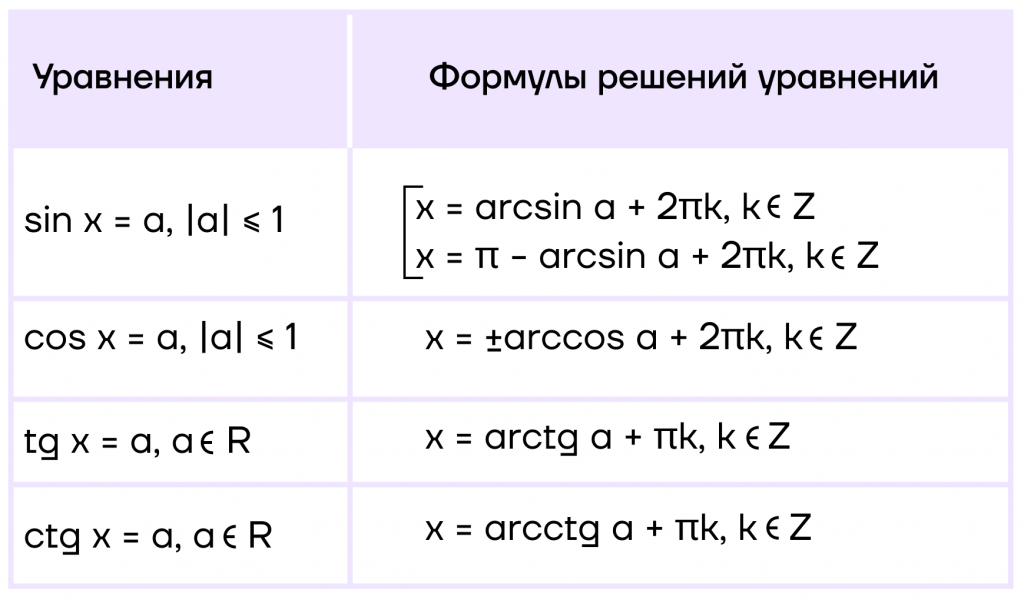
Если мы решаем уравнение с табличными значениями (о них мы сейчас тоже поговорим), то все равно пользуемся этими формулами, просто ответ в конце получается «красивый». В иных случаях достаточно указать аркфункцию. 

\(cos x =-\frac{1}{3}\)
\(x=\pm arccos\frac{1}{3}+2\pi k, k\ in z\)

Данная запись и является ответом. 

Способ второй: разложение на множители

Перейдем ко второму способу решения тригонометрических уравнений: разложение на множители. Не все тригонометрические уравнения сводятся к квадратным, то есть дискриминант и теорема Виета не всегда могут прийти нам на помощь. Однако это не значит, что мы не можем упростить запись.

Решим следующее уравнение:

\(sin x * cos x -cos x =0\)

Заметим, что косинус — общий множитель в каждой части, то есть мы можем вынести его за скобку и получить произведение:

\(cos x * (sin x -1)=0\)

Что делать дальше? Вспомнить одно простое правило: если произведение множителей равно 0, то каждый из этих множителей равен 0. 

Для решения данного уравнения нам необходимо, чтобы хотя бы один из множителей был равен 0. Следовательно, либо \(cos x = 0\), либо \(sin x-1=0 => sin x=1\). Запишем эти выражения в виде совокупности уравнений:

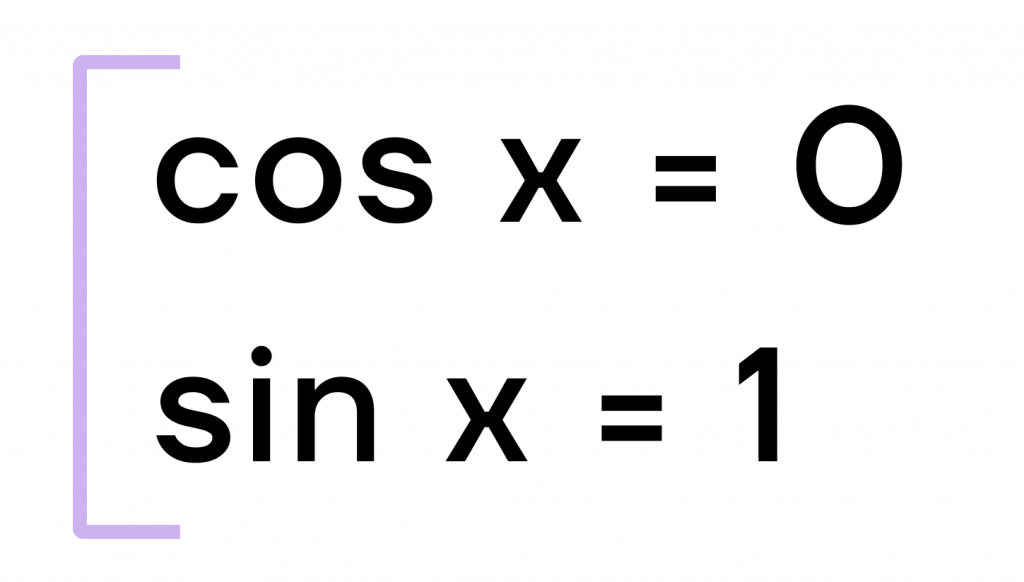
 В совокупности мы получили табличные значения тригонометрических функций.

Рассмотрим таблицу. Мы уже пользовались ей при решении простейших тригонометрических уравнений.

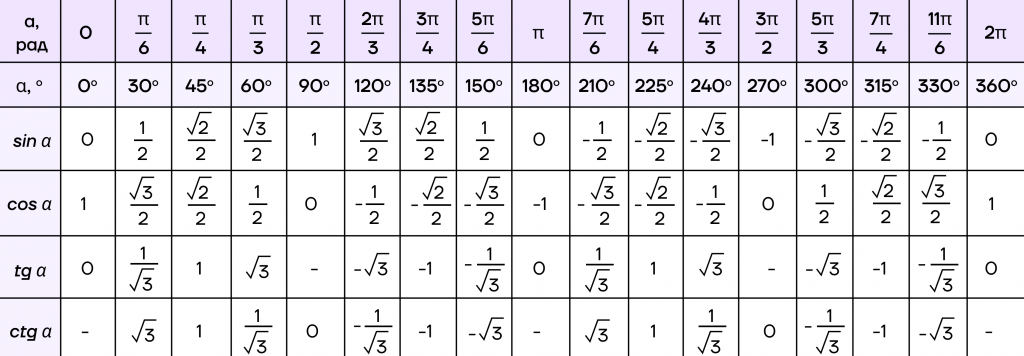
Вспомним, как работать с ней при нахождении корней. Нам нужно найти пересечение нужной функции и ее значения, а после записать полученный радиан. 

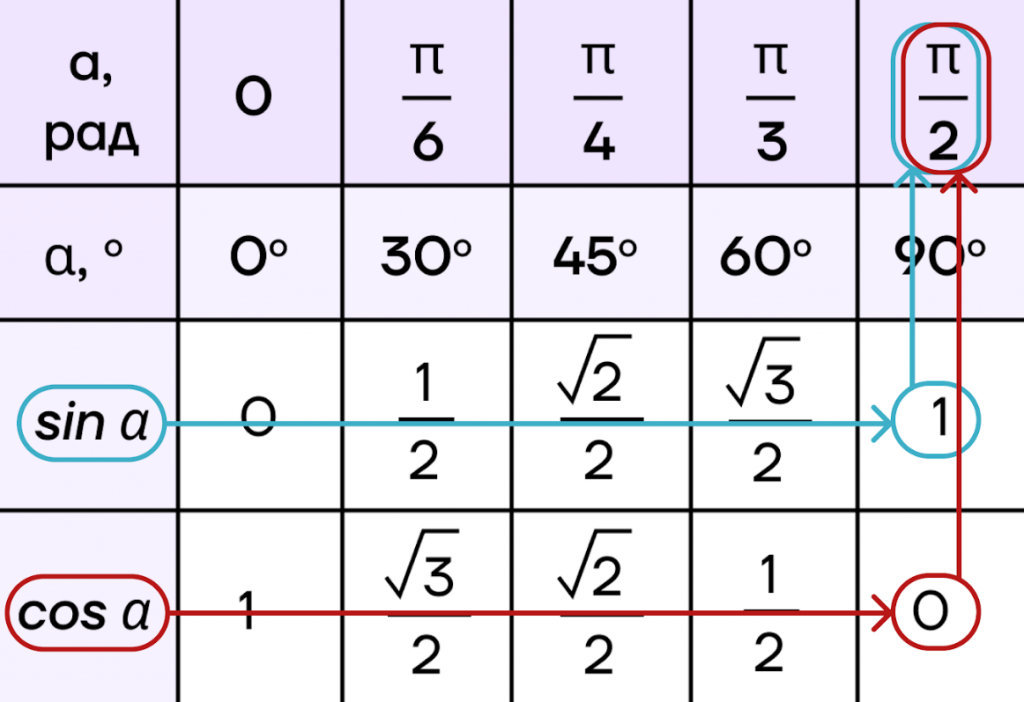
По таблице получаем:

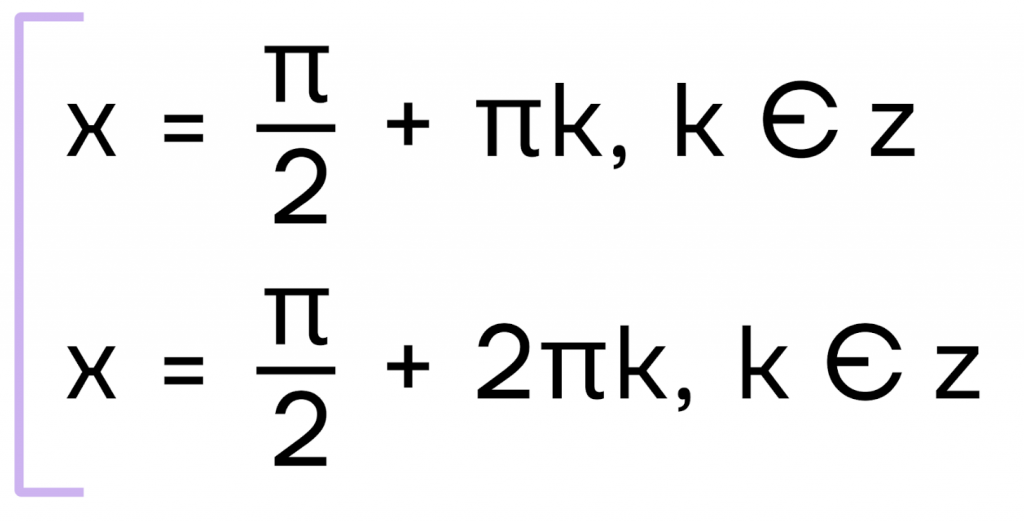
Если присмотреться, то корни уравнения похожи. Рассмотрим их на тригонометрической окружности: расположение корней первого уравнения будет отмечены красными стрелками, а второго — синими. 

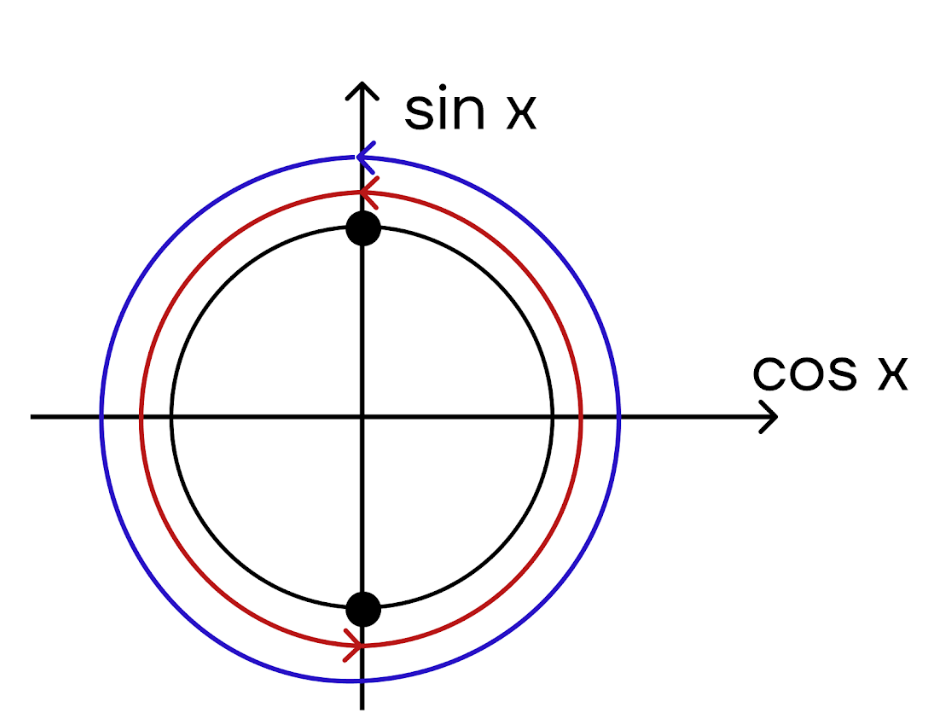
Заметим, что второй корень делает полный оборот по кругу, а вот первый делает «остановку» посередине. Однако сами точки не меняются, а значит, корни можно объединить в один. 

Так как решения второго уравнения одновременно являются и решениями первого уравнения, в ответ запишем следующее \(x=\frac{\pi}{2}+\pi k, k\in z\).

Тригонометрические уравнения могут встретиться в №5 ЕГЭ по профильной математике. Рассмотрим одно из таких уравнений. 

Решите уравнение \(ctg\frac{\pi x}{3}=\sqrt3\). В ответ запишите наименьший положительный корень.

Решение.
Перед нами простейшее тригонометрическое уравнение с немного усложненным аргументом. По таблице найдем значение аргумента (вместо х слева нужно будет записать аргумент без изменений):

\(\frac{\pi x}{3}=\frac{\pi}{6}+\pi n, n \in Z\)

Теперь из этого уравнения нам нужно выразить х. Чтобы его выразить, нужно преобразовать уравнение так, чтобы слева стоял только х без коэффициентов. 

Избавимся от дробей. Для этого умножим уравнение на 6: 

\(\frac{\pi x}{3}=\frac{\pi}{6}+\pi n, n \in Z| *6\)
\(2\pi x=\pi +6\pi n, n \in Z\)

Считать ответ, когда в уравнении есть число очень неудобно. Однако поскольку стоит в каждом слагаемом, мы можем разделить уравнение на него:

\(2\pi x=\pi +6\pi n, n \in Z|:\pi \)
\(2x=1+6n, n \in Z |:2\)
\(x=\frac{1}{2}+3n, n\in Z\)

По условию нам нужно найти наименьший положительный корень. Чтобы его определить, нужно вместо n подставить целые числа. 

Если мы попробуем уменьшить \(\frac{1}{2}\), то получим отрицательное число. Чтобы проверить это, подставим \(n=-1\):

\(x=\frac{1}{2}-3=-\frac{5}{2}\)

Если \(n=0\), то получим ответ \(x=\frac{1}{2}=0,5\).

Если \(n=1\), то \(x=\frac{1}{2}+3=\frac{7}{2}=3,5>0,5\). 

При дальнейшем увеличении n значения х будут только увеличиваться. Следовательно, наименьший положительный корень будет равен 0,5. 

Ответ: 0,5

Однородные тригонометрические уравнения

Мы разобрались в основных способах решения тригонометрических уравнений. Однако существуют такие уравнения, которые могут потребовать особых действий, немного отличных от приведенного выше алгоритма. 

Например, такими являются однородные тригонометрические уравнения.

Однородное тригонометрическое уравнение — уравнение, каждое из слагаемых которого содержит одинаковое количество множителей. 

Однородные тригонометрические уравнения принято делить на два вида:

• однородное тригонометрическое уравнение первой степени;
• однородное тригонометрическое уравнение второй степени.

Их различие описано в самом названии: степень некоторых множителей будет отличаться. Начнем их разбор по порядку. 

Однородное тригонометрическое уравнение первой степени — это уравнение вида \(a*sin x+b*cos x=0\). 

При этом коэффициенты \(a\neq 0\) и \(b\neq 0\), поскольку в ином случае мы перейдем к уравнениям \(a*sin x=0\) или \(b*cos x=0\), а они не являются однородными. 

Почему в однородных тригонометрических уравнениях можно делить на переменную?  Могут ли быть равны 0 сами синус и косинус? Допустим, \(sin x=0\), тогда получаем уравнение: \(a*0+b*cos x=0\) \(b*cos x=0\) Поскольку \(b\neq 0\), то решением этого уравнения будет \(cos x=0\), что невозможно, так как у нас уже синус равен 0. Может возникнуть вопрос, почему и синус, и косинус не могут быть равны 0 одновременно? Это связано с основным тригонометрическим тождеством: \(sin^2x+cos^2x=1\) И если мы подставим синус и косинус, равные 0, то получим: \(0^2+0^2\neq 1\) Следовательно, тождество не выполняется и такой ситуации существовать не может.  Получаем, что \(sin x\neq 0\) и \(cos x\neq 0\).

Чем нам может помочь эта информация? Вспомним, что уравнения нельзя делить на переменную, поскольку есть шанс потерять одно из значений корней, а именно то, при котором переменная равна 0. Однако теперь мы точно знаем, что ни синус, ни косинус не равен 0, тогда мы можем спокойно разделить уравнение на них!

Рассмотрим пример решения однородного уравнения первой степени на примере \(3sin x-\sqrt{3}cos x=0\). 

Разделим обе части уравнения на \(cos x\):

\(\frac{3sin x}{cos x}-\frac{\sqrt{3}cos x}{cos x}=0\)

Вспомним, что tg x=sin xcos x. Тогда получаем:

\(3tg x-\sqrt3*1=0\)
\(3tg x=\sqrt3\)
\(tg x=\frac{\sqrt3}{3}\)

Мы получили простейшее тригонометрическое уравнение. Осталось решить его с помощью таблицы. Получаем:

\(x=\frac{\pi}{6}+\pi n, n\in Z\)

Алгоритм решения однородного тригонометрического уравнения 1-ой степени:

1. Записать данное уравнение.
2. Разделить обе части уравнения на \(cos x\) или \(sin x\).
3. Перейти к уравнению с тангенсом или котангенсом.
4. Решить простейшее тригонометрическое уравнение и найти его корни. 

Итак, мы разобрались с однородными уравнениями первой степени. Чем же от них отличаются уравнения второй степени?

Однородные тригонометрические уравнения второй степени — это уравнения вида \(a*sin^2x+b*sin x*cos x+c*cos^2x=0\). 

Заметим, что в этом случае коэффициенты a и с должны быть отличны от 0. 

• Если \(a=0\), то получаем уравнение вида \(b*sin x*cos x+c*cos^2x=0\), которое решается с помощью вынесения общего множителя за скобку:

\(cos x(b*sin x+c*cos x)=0\)

• Аналогичная ситуация получится, если \(c=0\). 

• А вот если \(a=c=0\), мы получаем уравнение вида \(b*sin x*cos x=0\). Тут стоит вспомнить, что если произведение множителей равно 0, то каждый из множителей равен 0. Тогда решением такого уравнения будет \(cos x=0\) и \(sin x=0\). 

Как мы уже рассуждали раньше, синус и косинус не могут быть равны 0. Значит, уравнение можно разделить на переменную. 

Решим уравнение \(sin^2x+(\sqrt3-1)sin x*cos x-\sqrt3cos^2x=0\). В этот раз разделим уравнение на \(cos^2x\):

\(\frac{sin^2x}{cos^2x}+\frac{(\sqrt3-1)sin x*cos x}{cos^2x}-\frac{\sqrt3cos^2x}{cos^2x}=0\)
\(tg^2x+\frac{(\sqrt3-1)sin x}{cos x}-\sqrt3=0\)
\(tg^2x+(\sqrt3-1)tgx-\sqrt3=0\)

Сделаем замену: \(tg =t\), тогда:

\(t^2+(\sqrt3-1)t-\sqrt3=0\)

Решим с помощью теоремы Виета: 

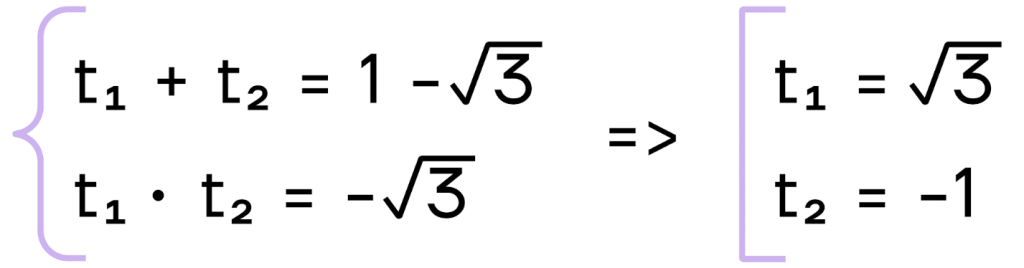
Сделаем обратную замену: \(tg x=\sqrt3\) и \(tg x=-1\). С помощью таблицы решим простейшее тригонометрическое уравнение и получим:

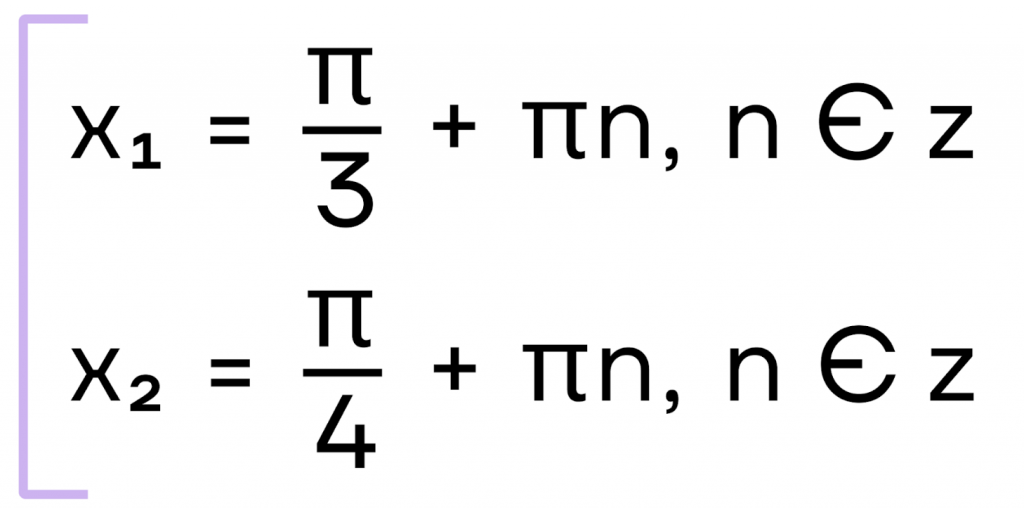
Алгоритм решения однородного тригонометрического уравнения 2-ой степени:

1. Записать данное уравнение.
2. Разделить обе части уравнения на \(cos^2 x\) или \(sin^2 x\).
3. Перейти к уравнению с тангенсом или котангенсом.
4. Решить уравнение и найти его корни. 

Мы разобрали однородные тригонометрические уравнения. Какой еще тип уравнений можно выделить? 

Наверняка вы слышали уже ставшее крылатым выражение «сборная солянка». А что, если в нашу солянку намешать тригонометрию, дроби, корни, логарифмы и все-все, что душе угодно? У нас получится комбинированное уравнение!

Комбинированные тригонометрические уравнения

Само название говорит, что мы комбинируем несколько видов уравнений в одном. На самом деле, в них нет ничего сложного, но такие уравнения решаются чуть-чуть по-другому. Главное правило: необходимо перейти от комбинированного уравнения к уравнению обычного вида и найти все корни. 

Комбинированные уравнения или уравнения смешанного типа могут встретиться в №12 ЕГЭ по профильной математике. Разберем, как решать подобный тип уравнений.
а) Решите уравнение \({(121^{cos x})}^{sin x}=11^{\sqrt2*sin x}\).
б) Найдите корни уравнения, принадлежащие отрезку [\(4\pi;\frac{19\pi}{4}\)]. 

Решение.
Итак, перед нами показательное уравнение, однако вместо переменной стоят тригонометрические функции. Наша главная задача максимально упростить уравнение. 
Начнем решать уравнение как показательное. Подробнее про этот тип уравнений можно прочесть в статье «Показательные уравнения и неравенства». 

Для начала раскроем скобки по свойству степеней \({(a^n)}^m=a^{n*m}\):

\(121^{cos x*sin x}=11^{\sqrt2sin x}\)

Заметим, что \(121=11^2\). Тогда:

\({(11^2)}^{cos x*sin x}=11^{\sqrt2sin x}\)

Снова применим то же свойство степеней:

\(11^{2cos x*sin x}=11^{\sqrt2sin x}\)

Поскольку основания у нас равны, мы можем отбросить их и перейти к уравнению со степенями: 

\(2cos x*sin x=\sqrt2sin x\)

Итак, мы перешли к обычному тригонометрическому уравнению! Перенесем слагаемые в одну сторону и вынесем общий множитель:

\(2cos x*sin x-\sqrt2sin x=0\)
\(sin x(2cos x-\sqrt2)=0\)

Если произведение множителей равно 0, то каждый множитель равен 0. Получаем совокупность: 

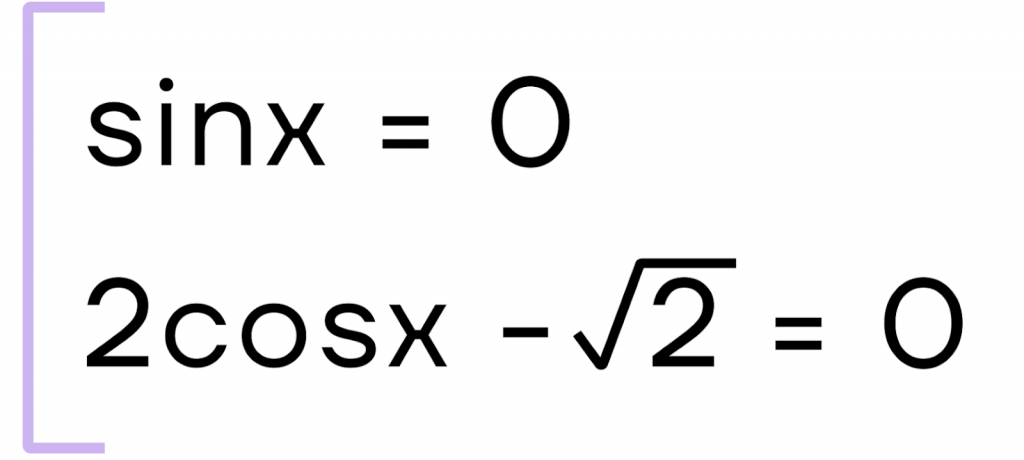
Решим первое уравнение совокупности \(sin x=0\). Это частный случай, следовательно, \(x=\pi n, n\in Z\). 

Решим второе уравнение совокупности. 

\(2cos x-\sqrt2=0\)
\(2cos x=\sqrt2\)
\(cos x=\frac{\sqrt2}{2}\)
\(x=\pm \frac{\pi}{4}+2\pi n, n\in Z\)

Мы нашли все корни уравнения. 

б) Теперь с помощью тригонометрической окружности отберем корни на отрезке [\(4\pi;\frac{19\pi}{4}\)]. Отметим промежуток и полученные точки на окружности: 

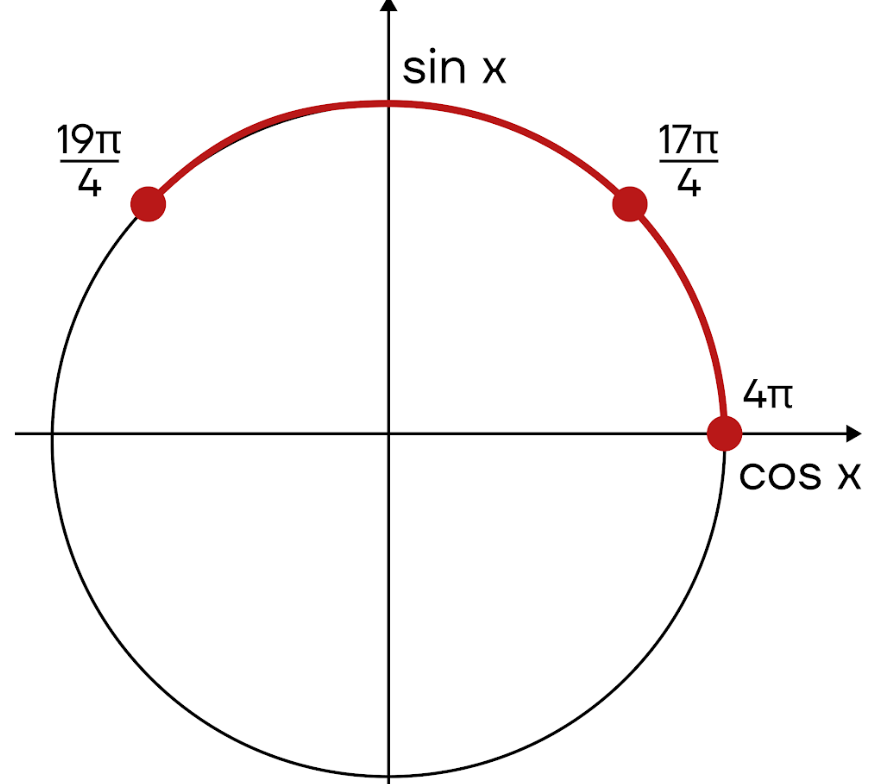
В данном отрезке лежат точки \(4\pi\) и \(\frac{17\pi}{4}\).

Ответ: а) \(n\pi, n\in Z \pm \frac{\pi}{4}+2\pi n,n\in Z\), б) \(4\pi\, \frac{17\pi}{4}\)

Мы научились решать тригонометрические уравнения, узнали про однородные уравнения первой и второй степени и даже немного поговорили про солянку. Но уравнения всегда близко идут с неравенствами, узнать подробнее о которых вы можете в статье «Тригонометрические неравенства». 

Термины

Радиан — это способ измерения угла с помощью числа пи (\(\pi\)). Чтобы считать углы в радианах, нужно помнить, что \(\pi=180°\), тогда \(90°=\frac{\pi}{2}, 360°=2\pi\) и т.д. 

Переменная — это математический объект, который занимает некоторое множество значений (как правило, числовых) и может изменять свое значение в его пределах.

Дискриминант в квадратном уравнении — это выражение, которое ищется по формуле \(D=b^2-4⋅a⋅c\), где а, b и с берутся из уравнения. Подробнее о нем рассказано в статье «Линейные, квадратные и кубические уравнения». 

Корень уравнения — это число, которое при подстановке вместо буквы обращает уравнение в верное числовое равенство.

Асимптота – прямая, к которой неограниченно близко приближается график функции, но никогда ее не пересекает. 

Фактчек

• Тригонометрические функции имеют свои ограничения, которые важно учитывать в ОДЗ. Так, синус и косинус не могут быть меньше – 1 и больше 1. Если появляется тангенс, то косинус не равен 0. А если появляется котангенс, то не равен 0 уже синус. 
• Тригонометрические уравнения могут решаться методами введения новой переменной и разложения на множители.
• Среди тригонометрических уравнений можно выделить однородные уравнения первой и второй степени. 
• Однородное тригонометрическое уравнение первой степени — это уравнение вида \(a*sin x+b*cos x=0\). 
• Однородные тригонометрические уравнения второй степени — это уравнения вида \(a*sin^2x+b*sin x*cos x+c*cos^2x=0\). 

Проверь себя

Задание 1.
Какое ОДЗ у синуса?

1. \(-1<sin x<1\)
2. \(-1\leq sin x\leq 1\)
3. \(-1\leq x\leq 1\)
4. \(-1<x<1\)

Задание 2.
Какое ОДЗ тангенса?

1. \(sin x\neq 0\)
2. \(cos x\neq 0\)
3. \(x\neq 0\)
4. У тангенса нет ОДЗ. 

Задание 3.
Решите уравнение \(2cos x +4cos x sin x =0\).

1. \(-\frac{\pi}{2}+\pi k, k\in z\)
2. \(-\frac{5\pi}{6}+2\pi k, k\in z;-\frac{\pi}{6}+2\pi k, k\in z;-\frac{\pi}{2}+\pi k, k\in z\)
3. нет решений
4. при любом х

Задание 4.
Выберите однородное тригонометрическое уравнение первой степени:

1. \(sin x-sin x*cos x=0\)
2. \(sin x=0\)
3. \(sin x-3cos x=0\)
4. \(sin x*cos x=0\)

Задание 5.
Выберите однородное тригонометрическое уравнение второй степени:

1. \(cos^2x-cos x=0\)
2. \(sin^2x+sin x*cos x=0\)
3. \(sin x*cos x=0\)
4. \(sin^2x-cos^2x=0\)

Ответы: 1. — 2; 2. — 2; 3. — 2; 4. — 3; 5. — 4.